A Simulation Study of Relative Efficiency and Bias in the Nested Case–Control Study Design

Abstract

Purpose

The nested case–control study design, in which a fixed number of controls are matched to each case, is often used to analyze exposure–response associations within a cohort. It has become common practice to sample four or five controls per case; however, previous research has shown that in certain instances, significant gains in relative efficiency can be realized when more controls are matched to each case. This study expanded upon this and investigated the effect of (i) the number of cases, (ii) the strength of the exposure–response, and (iii) the skewness of the exposure distribution on the bias and relative efficiency of the conditional likelihood estimator from a nested case–control study.

Methods

Cohorts were simulated and analyzed using conditional logistic regression.

Results

The relative efficiency decreased and bias away from the null increased, as the true exposure–response parameter increased and the skewness of the exposure distribution of the risk-sets increased. This became more pronounced when the number of cases in the cohort was small.

Conclusions

Gains in relative efficiency and a reduction in bias can be realized by sampling more than four or five controls per case generally used, especially when there are few cases, a strong exposure–response relation, and a skewed exposure variable.

Introduction

Cohort studies are frequently conducted to evaluate the effect of exposure to a particular physical or chemical agent on the occurrence of or death from a particular disease. The Cox proportional hazard model (Cox, 1972) is a common method used to evaluate an exposure–response relation between the exposure and outcome of interest. However, performing this analysis on a full cohort often requires collecting detailed, time-dependent exposure history information on each member of the cohort, which can be quite expensive in time and money. The nested case–control study design eases this burden (Mantel, 1973; Thomas, 1977). In a nested case–control study, individuals of the cohort who experience the outcome of interest (referred to as cases) are identified, and for each case, the risk-set is formed. The risk-set for a case includes the case and all cohort members who are under observation, and are therefore considered at risk, just prior to the failure time of the case. Members of each risk-set excluding the case are then randomly sampled without replacement (and are referred to as controls). It is possible that a case may serve as a control in an earlier risk-set and that the same control may appear in multiple risk-sets. Covariate information for all sampled controls of a risk-set is evaluated at the failure time of the case, and the sampled risk-sets are then analyzed using conditional logistic regression. Generally, since the outcome of interest is death or occurrence of a particular disease, age is used as the time scale (as opposed to calendar time or time on study) because age is one of the most important risk factors for most diseases, and using age as the time scale matches exactly on age (Breslow et al., 1983).

It has been shown that unbiased exposure–response estimates could be obtained by analyzing a sample of the cohort using the conditional likelihood (Breslow et al., 1978; Prentice and Breslow, 1978; Breslow, 1981). Additionally, Goldstein and Langholz (1992) further proved that (a) the exposure–response parameter estimate from performing conditional logistic regression on the sampled risk-sets is asymptotically unbiased and (b) when there is no exposure–response relation, the asymptotic relative efficiency from performing conditional logistic regression on the sampled risk-sets, with m controls matched to each case, compared to analyzing the full risk-sets (which is equivalent to performing Cox proportional hazard regression on the full cohort) is $\frac{m}{m+1}$, regardless of the distribution of the exposure variable. For instance, the asymptotic relative efficiency of sampling one control for each case is $\frac{1}{2}$, which means that the variance of the estimate from the sampled risk-set analysis is twice as large as the variance of the estimate obtained if the full cohort was analyzed. In addition, Ury (1975) provided a similar result for the asymptotic relative efficiency in the context of a matched case–control study. In fact, a nested case–control study can be thought of as a matched case–control study where the risk-sets of the cohort from which controls are sampled serve as the stratified sample population in the matched case–control study.

However, these results are asymptotic properties; that is, they apply as the size of the cohort (and, therefore, the number of cases in the cohort) approaches infinity. It is not clear how these results hold in situations with small sample sizes, or when there are few observed cases in the cohort due to a rare outcome.

In addition, it seems to have become common practice to simply sample four or five controls per case, even with a rare outcome such as death from leukemia. For example, a recent PubMed search for “nested case–control” and “leukemia” articles published in 2012 returned nine studies. Two of these studies analyzed the full cohort and were not considered. Of the remaining seven studies, six matched five or fewer controls per case, including three studies that only observed 22, 64, and 118 cases. The remaining study observed 71 cases and sampled 10 controls per case. The properties of the conditional logistic regression estimator in these scenarios would not be guaranteed by the asymptotic theory and may be biased and/or inefficient.

While previous work has stated that sampling four or –five controls per case in a matched case–control study is sufficient and there is little to be gained in sampling more controls per case (Gail et al., 1976; Walter, 1980; Taylor, 1986), it has been shown that when the relative risk is large and the exposure is rare, there is considerable value in sampling more controls per case than the 4–5 generally recommended (Breslow et al., 1983, 1987). However, their findings were based upon a dichotomous exposure variable, and the focus was on improving only the relative efficiency.

This article hopes to expand upon these findings through a simulation study by also considering a continuous exposure variable as well as considering potential bias due to small samples. In particular, this article will investigate the effect of (i) the number of cases, (ii) the strength of the exposure–response, and (iii) the skewness of the exposure distribution on the bias and relative efficiency of the conditional likelihood estimator from a nested case–control study.

Materials and methods

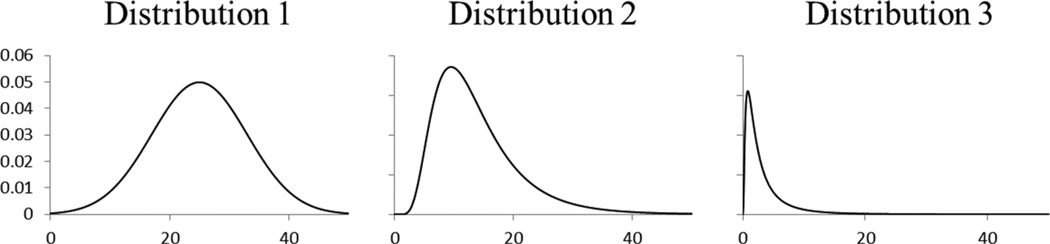
Simulations were conducted using SAS Software (version 9.1.3, SAS Institute Inc., Cary, NC). Cohorts were simulated based on methods developed by Richardson and Loomis (2004) and further used by Hein et al. (2009). Thirty-six simulation scenarios were performed defined by the number of cases in the cohort (~30, ,100, and ~300), the exposure–response relation (hazard ratio per unit exposure = 1, 1.005, 1.010, and 1.015), and the distribution of the exposure intensity [distribution 1: normal(μ = 25, σ² = 64) – truncated between 0 and 50; distribution 2: log-normal(μ = 2.5, σ² = 0.25) – truncated between 0 and 50; and distribution 3: log-normal (μ = 0.75, σ² = 1) – truncated between 0 and 50]. These distributions were chosen to study the effect of skewness on bias and relative efficiency. Distribution 1 is symmetric (skewness of 0), distribution 2 is slightly right-skewed (skewness of about 1.35), and distribution 3 is very right-skewed (skewness of about 3.7). Graphs of the probability density functions for the three distributions are presented in Figure 1.

Figure 1.

Graph of the probability density function for the distributions used in the simulations. Distribution 1: normal (μ = 25, σ² = 64) – truncated between 0 and 50, distribution 2: log-normal (μ = 2.5, σ² = 0.25) – truncated between 0 and 50, and distribution 3: log-normal (μ = 0.75, σ² = 1) – truncated between 0 and 50

Each simulated cohort consisted of 5,000 workers. For each scenario with ~30 cases, 10,000 cohorts were simulated, for each scenario with ~100 cases, 3,000 cohorts were simulated, and for each scenario with ~300 cases, 1,000 cohorts were simulated. The number of cohorts varied, since precision is inversely proportional to the number of cases and therefore, the results from the simulations with ~30 cases require 10 times the simulations as those with ~300 cases to achieve the same level of precision. Hence, 10,000 and 1,000 cohorts were simulated.

Each worker was randomly assigned values for age at first exposure (18 years plus a random exponential variable with mean 10) and maximum follow-up time (40 years minus a random exponential variable with mean 5). Each worker was also assigned a maximum exposure duration of 15 years. Therefore, since the exposure intensity was truncated to be below 50, the maximum exposure an individual could accumulate is 750 units (50 units/year × 15 years).

At each year of a worker’s maximum follow-up time, the worker’s current age and cumulative exposure (equal to the worker’s exposure intensity multiplied by exposure duration) were calculated. Also, at each year, a conditional probability of mortality from the outcome of interest (conditional on survival to that age), h, was assigned to each worker based on the worker’s age and cumulative exposure, cumexp, by the following formula:

$$h=e^{\alpha +{1.5}^{*}\text{ln}\left(\frac{\text{age}}{55}\right)+{\beta }^{*}\text{cumexp},}$$

where β is the exposure–response parameter (and, therefore, the hazard ratio per unit of exposure is e^β). The parameter α is an intercept parameter which varied in each simulation scenario and was chosen to obtain the desired number of cases (on average). It is not possible to completely control the number of cases in each cohort through this method; rather the number of cases in each simulated cohort will vary.

Additionally, at each follow-up year, a conditional probability of mortality from any other outcome (conditional on survival to that age), c, was assigned to each worker based only on the worker’s age by the following formula:

$$c=e^{-5+5^{*}\text{ln}\left(\frac{\text{age}}{55}\right).}$$

Specific parameters for these conditional probabilities (hazard rates) were used by Richardson and Loomis (2004) as well as Hein et al. (2009).

Two Bernoulli random variables were assigned to each worker at each year, one with probability h and one with probability c. A Bernoulli random variable of 1 represents a death in that year. A worker was followed up until his first death. A worker was treated as if he were censored if his first death is from another outcome or if he survived all years of his maximum follow-up time with no deaths. A worker was considered a case if his first death is from the outcome of interest. The final cohort consisted of 5,000 workers with variables indicating for each worker the age at first exposure, age at death/censor, age at last exposure (which is the minimum of: (i) age at first exposure plus 15 and (ii) age at death/censor), exposure intensity, and case-status.

At first glance, the hazard ratios chosen may seem very small. However, it is important to note that these hazard ratios are per unit of exposure for an exposure where it is possible to accumulate 750 units. To relate these hazard ratios to a specific study, the results must be appropriately scaled. For example, in a study of gold miners exposed to silica, Steenland and Brown (1995) reported a strong hazard ratio of 4.7 per unit of logged cumulative exposure (the exposure metric that was determined to give the best fit). The logged cumulative exposure ranged from 5.6 to 12 units. This hazard ratio of 4.7 would scale to:

$${4.7}^{\frac{12-5.6}{750}}=1.013$$

per unit of an exposure which ranges from 0 to 750 units.

Analysis

Risk-sets were created for each cohort, with age as the time scale. For each case, 1, 5, 10, 15, and 20 controls were randomly sampled from the risk-sets. The full as well as the sampled risk-sets were analyzed using conditional logistic regression (procedure PHREG in SAS) to obtain estimates of the exposure–response parameter. The Breslow option (1974) in the PHREG procedure was used to handle tied survival times. For each scenario, 10,000, 3,000, and 1,000 estimates of the exposure–response parameter were obtained from the analysis of the full risk-sets and for each of the sampled risk-sets from the cohorts with ~30, ~100, and ~300 cases, respectively. Relative efficiency of 1:m sampling was estimated by dividing the sample variance of the parameter estimates obtained from the full risk-set analyses by the sample variance of the parameter estimates obtained from the m-sampled risk-set analyses. Bias was estimated by subtracting the true exposure–response parameter (i.e. the log of the true hazard ratio) from the mean of the estimated parameters and is reported, for non-null associations, as a percentage of the true parameter estimate.

The PHREG procedure will not converge if, in every risk-set, the case’s exposure is higher (lower) than the maximum (minimum) exposure of the corresponding controls in the risk-set, because the maximum likelihood estimate is infinity (–infinity). In this situation, PHREG will report the last estimate when the optimization algorithm stopped, which most likely will be a very large estimate with a large standard error. When summarizing the simulated results, observations for which the resulting standard error was greater than 1 were excluded, because this was taken as an indication that the procedure had trouble converging. As a result of removing these extreme results, all analyses will be conditional on the algorithm converging, and any summary statistics may be underestimated.

Results

Results from simulations based on distributions 1 and 2; true hazard ratios of 1, 1.005, and 1.015; and ~30 cases and ~100 cases are presented in all tables and figures; complete results can be found in the Online Appendix.

The parameter estimates from each scenario using distribution 1 are summarized in Table 1, and the results using distribution 2 are summarized in Table 2. In most of the simulation scenarios, no observations were excluded from the analysis because of convergence problems. The most severe scenario was distribution 2, ~30 cases per cohort and a true hazard ratio of 1.015, for which more than 20% of the simulated cohorts appeared to have convergence problems when one control was matched to each case. The issue was much less severe for cohorts with ~100 cases or a true hazard ratio of 1.005 or 1. As a result of excluding these cohorts, the results in Tables 1 and 2 summarize the parameter estimates and standard errors given that the procedure converged.

Table 1.

Summary statistics of the exposure–response parameter estimates for each scenario with exposure intensity distribution 1

True hazard ratio	Match	~30 cases per cohort					~100 cases per cohort
		Na	Meanb	Empirical standard errorc	Estimated standard errord	Relative efficiencye (%)	Na	Meanb	Empirical standard errorc	Estimated standard errord	Relative efficiencye (%)
1	1:01	10,000	1.0000	2.16E–03	2.02E–03	38.7	3,000	1.0000	1.13E–03	1.11E–03	48.1
	1:05	10,000	1.0000	1.52E–03	1.48E–03	78.3	3,000	1.0000	8.52E–04	8.45E–04	84.5
	1:10	10,000	1.0000	1.43E–03	1.41E–03	88.7	3,000	1.0000	8.20E–04	8.07E–04	91.4
	1:15	10,000	1.0000	1.40E–03	1.39E–03	92.6	3,000	1.0000	8.10E–04	7.95E–04	93.5
	1:20	10,000	1.0000	1.38E–03	1.38E–03	94.0	3,000	1.0000	8.08E–04	7.88E–04	94.0
	Full	10,000	1.0000	1.34E–03	1.34E–03		3,000	1.0000	7.84E–04	7.69E–04
1.005	1:01	10,000	1.0056	5.80E–03	2.63E–03	5.9	3,000	1.0052	1.41E–03	1.37E–03	33.4
	1:05	10,000	1.0051	1.71E–03	1.66E–03	68.4	3,000	1.0050	9.59E–04	9.43E–04	72.1
	1:10	10,000	1.0051	1.57E–03	1.54E–03	81.4	3,000	1.0050	8.84E–04	8.78E–04	84.9
	1:15	10,000	1.0051	1.52E–03	1.49E–03	86.7	3,000	1.0050	8.52E–04	8.54E–04	91.3
	1:20	10,000	1.0050	1.49E–03	1.47E–03	90.2	3,000	1.0050	8.58E–04	8.42E–04	89.9
	Full	10,000	1.0050	1.41E–03	1.40E–03		3,000	1.0050	8.14E–04	8.05E–04
1.015	1:01	9,782	1.0189	1.50E–02	8.47E–03	1.2	3,000	1.0160	4.15E–03	3.34E–03	5.2
	1:05	9,999	1.0158	3.56E–03	3.11E–03	21.6	3,000	1.0152	1.81E–03	1.72E–03	27.3
	1:10	10,000	1.0154	2.68E–03	2.49E–03	38.0	3,000	1.0152	1.46E–03	1.43E–03	42.0
	1:15	10,000	1.0153	2.40E–03	2.26E–03	47.6	3,000	1.0151	1.31E–03	1.31E–03	51.8
	1:20	10,000	1.0153	2.25E–03	2.13E–03	54.1	3,000	1.0151	1.25E–03	1.24E–03	57.8
	Full	10,000	1.0151	1.65E–03	1.62E–03		3,000	1.0150	9.46E–04	9.70E–04

Notes:

^aN is the number of parameter estimates with corresponding standard error less than 1 as calculated by the PHREG procedure.

^bMean is the exponential of the mean of the estimated log hazard ratios.

^cEmpirical standard error is the sample standard deviation of the estimated log hazard ratios.

^dEstimated standard error is the mean of the estimated standard errors.

^eRelative efficiency of 1:m sampling was estimated by dividing the empirical variance obtained from the full risk-set analyses by the empirical variance obtained from the m-sampled risk-set analyses.

Table 2.

Summary statistics of the exposure–response parameter estimates for each scenario with exposure intensity distribution 2

True hazard ratio	Match	~30 cases per cohort					~100 cases per cohort
		Na	Meanb	Empirical standard errorc	Estimated standard errord	Relative efficiencye (%)	Na	Meanb	Empirical standard errorc	Estimated standard errord	Relative efficiencye (%)
1	1:01	10,000	1.0000	2.84E–03	2.62E–03	36.9	3,000	1.0000	1.42E–03	1.40E–03	44.7
	1:05	10,000	0.9999	1.95E–03	1.89E–03	78.5	3,000	1.0000	1.06E–03	1.00E–03	80.1
	1:10	10,000	0.9998	1.84E–03	1.80E–03	88.3	3,000	1.0000	1.01E–03	1.00E–03	89.4
	1:15	10,000	0.9998	1.80E–03	1.76E–03	92.1	3,000	1.0000	9.96E–04	9.96E–04	91.2
	1:20	10,000	0.9998	1.78E–03	1.75E–03	93.9	3,000	1.0000	9.80E–04	9.87E–04	94.2
	Full	10,000	0.9998	1.73E–03	1.70E–03		3,000	1.0000	9.51E–04	9.63E–04
1.005	1:01	9,999	1.0058	4.00E–03	3.09E–03	11.3	3,000	1.0052	1.50E–03	1.40E–03	20.8
	1:05	10,000	1.0051	1.87E–03	1.79E–03	52.1	3,000	1.0050	9.12E–04	9.04E–04	56.4
	1:10	10,000	1.0051	1.64E–03	1.59E–03	67.4	3,000	1.0050	8.14E–04	8.06E–04	70.8
	1:15	10,000	1.0050	1.57E–03	1.50E–03	74.0	3,000	1.0050	7.74E–04	7.68E–04	78.4
	1:20	10,000	1.0050	1.51E–03	1.46E–03	80.1	3,000	1.0050	7.51E–04	7.47E–04	83.1
	Full	10,000	1.0049	1.35E–03	1.31E–03		3,000	1.0049	6.85E–04	6.79E–04
1.015	1:01	7,911	1.0206	2.20E–02	1.51E–02	0.3	2,992	1.017	6.62E–03	4.50E–03	1.0
	1:05	9,897	1.0175	1.09E–02	5.51E–03	1.3	3,000	1.0154	2.07E–03	1.90E–03	10.4
	1:10	9,987	1.0164	7.74E–03	3.51E–03	2.5	3,000	1.0153	1.55E–03	1.40E–03	18.5
	1:15	9,996	1.0159	3.82E–03	2.79E–03	10.3	3,000	1.0152	1.37E–03	1.30E–03	23.7
	1:20	9,996	1.0157	3.24E–03	2.48E–03	14.3	3,000	1.0152	1.23E–03	1.20E–03	29.4
	Full	10,000	1.0152	1.22E–03	1.20E–03		3,000	1.0150	6.68E–04	6.92E–04

Notes:

^aN is the number of parameter estimates with corresponding standard error less than 1 as calculated by the PHREG procedure.

^bMean is the exponential of the mean of the estimated log hazard ratios.

^cEmpirical standard error is the sample standard deviation of the estimated log hazard ratios.

^dEstimated standard error is the mean of the estimated standard errors.

^eRelative efficiency of 1:m sampling was estimated by dividing the empirical variance obtained from the full risk-set analyses by the empirical variance obtained from the m-sampled risk-set analyses.

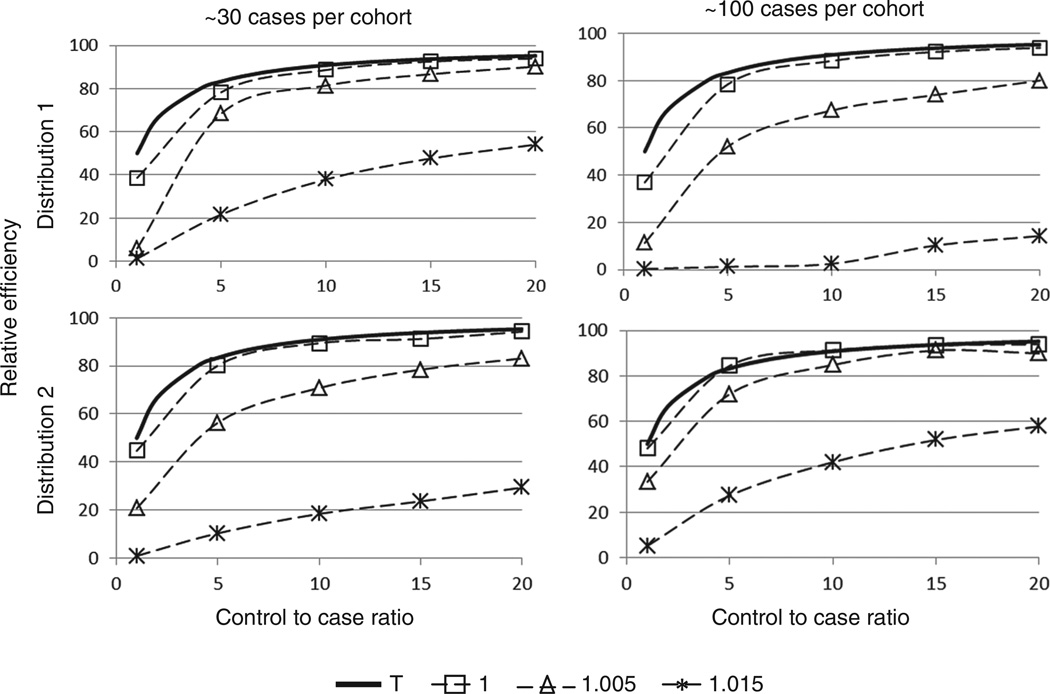
Figure 2 provides a graphical representation of the relative efficiency for each scenario. Generally, relative efficiency improved with the number of matched controls. The empirical relative efficiency when the true hazard ratio is 1 was close to the asymptotic $\frac{m}{m+1}$ for 1:m matching, and it gets closer to this value as the number of cases increases. However, when the true hazard ratio increased, the relative efficiency decreased substantially, particularly when the number of matched controls was low or the exposure distribution was skewed. For example, with ~100 cases per cohort, exposure intensity distribution 2, and true hazard ratio 1.015, the relative efficiency of 1:5 matching is ~10.4%, which is considerably lower than the theoretical estimate of 5/6 or 83% under the null hypothesis. In fact, in this scenario to obtain 80% relative efficiency, ~50 controls would need to be matched per case (assuming a linear trend). Additionally, the relative efficiency was dependent on the distribution of exposure intensity (and consequently dependent on the distribution of cumulative exposure of the risk-sets of a cohort). The distribution 1 simulations yielded higher relative efficiencies for a fixed true hazard ratio and approximate number of cases than the corresponding simulations using distribution 2, indicating that the relative efficiency is smaller when the distribution of the exposure variable is right-skewed.

Figure 2.

Relative efficiency vs control-to-case ratio by true hazard ratio. The solid curve T represents the graph of the equation $\frac{m}{m+1}$ which is the asymptotic relative efficiency when β = 0 (i.e. a hazard ratio of 1) for m matched controls per case.

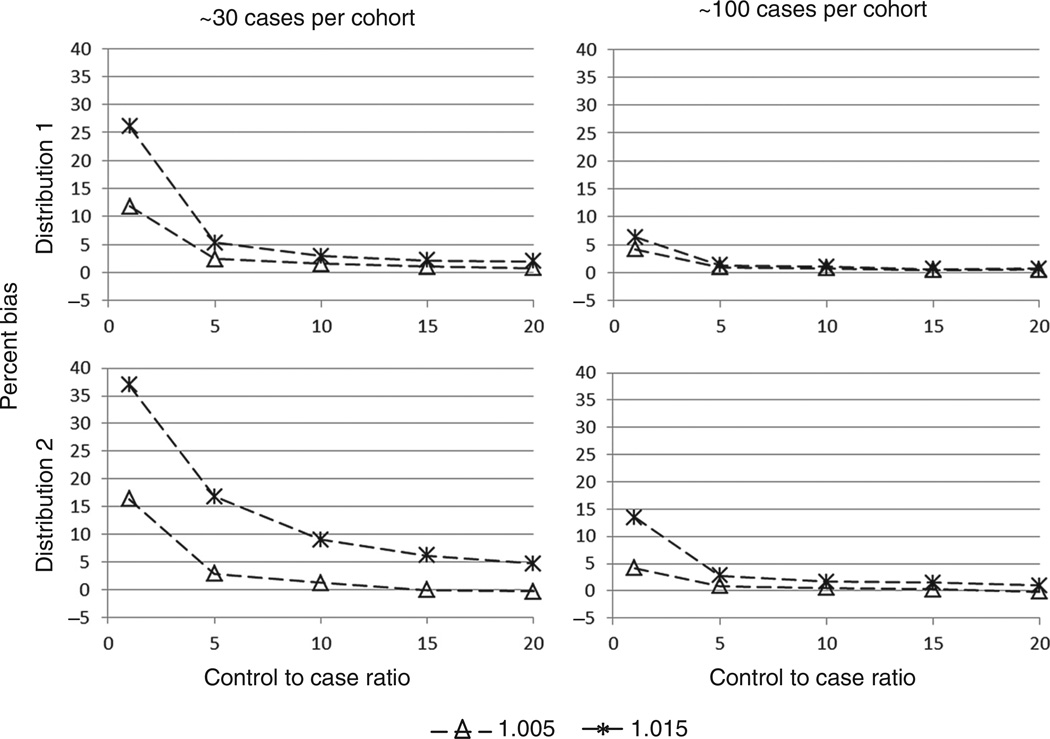
The bias in each scenario was also calculated (Figure 3). Generally, bias decreased, as the number of matched controls increased. The bias was larger with a stronger exposure–response relation or with a more right-skewed distribution and this bias tended to be away from the null. However, the bias was most affected by the number of cases in a cohort, and the bias decreased substantially as the number of cases increased. In fact, for all simulations with ~100 cases, when five or more controls were matched to each case, the bias was never more than 3%.

Figure 3.

Percent bias vs control-to-case ratio by true hazard ratio

The results from scenarios with ~300 cases and distribution 3 continue the trends summarized above. Namely, bias decreased with more cases but increased as the skewness of the exposure distribution increased. Also, relative efficiency increased with more cases and decreased as the skewness increased. Specific results can be found in the Online Appendix.

Discussion

Previous work has stated that sampling four or five controls per case in a matched case–control study is sufficient, and there is little to be gained in sampling more controls per case (Gail et al., 1976; Walter, 1980; Taylor, 1986). However, these studies are based upon asymptotic properties of the power of tests for detecting a non-null exposure–response. Power was also considered in this study (results not shown), and as is often seen, power increased as the strength of the exposure–response relation increased. Therefore, detecting a significant non-null parameter estimate was not an issue for large hazard ratios. However, the relative efficiency decreased as the exposure–response increased, which would result in wide confidence intervals and, therefore, imprecise estimates of the true exposure–response parameter.

When the goal is to obtain a precise risk estimate rather than simply detecting a significantly positive estimate, such as in a risk assessment study, more controls should be matched to each case. For example, Rinsky et al. (1987) investigated the effect of benzene exposure on leukemia mortality for a cohort of rubber workers to evaluate the appropriateness of the Occupational Safety and Health Administration (OSHA) occupational-exposure limit. The cohort consisted of 1,165 white males, and nine cases of leukemia were observed. In analyses based on the nested case–control study design with ten controls matched to each case, cumulative exposure, which was highly skewed and determined to fit the data best, gave a strong, significant exposure–response (β = 0.0126 per ppm-year, SE = 0.005). In our study, these conditions (few cases, skewed exposure distribution, and strong exposure–response) were associated with reduced relative efficiency; thus, greater precision could have been realized by selecting more controls per case.

In addition to lower precision, such conditions also resulted in bias away from the null in the simulations of this study. For example, in the simulations with ~30 cases, a skewed distribution, and a comparable true hazard ratio of 1.015, the bias was over 15% with five controls matched to each case and 8% with ten controls. Presumably, with only nine cases, the bias in the rubber workers cohort study would be more extreme and could be reduced by sampling additional controls per case. Greater precision and reduced bias would have been desirable to adequately evaluate the effectiveness of the OSHA occupational-exposure limit.

It has been shown previously that relative efficiency decreases as the strength of the exposure–response increases. In fact, Breslow et al. (1983) provided a general formula for the asymptotic relative efficiency in the case of a binary exposure variable and noted that there is a considerable value in sampling more controls per case than the four or five generally recommended when the relative risk is large and the exposure is rare. These simulations support this fact and further show a relationship between the efficiency and the distribution of the exposure variable for a continuous exposure.

In addition, alternative methods have been proposed to improve the relative efficiency. In particular, Langholz and Borgan (1995) proposed the idea of counter-matching where controls are matched to each case based on knowledge of a surrogate for exposure for the entire cohort. This method of sampling has been shown to provide improvements in efficiency compared to the simple random sampling considered in this study (Borgan and Olsen, 1999), and if information on a surrogate of exposure is available for the entire cohort, this method could be implemented. Furthermore, there have been new estimators proposed to improve the efficiency; see Samuelsen (1997) and Chen (2004). In specific scenarios, each of these estimators may provide improvements in risk estimation.

Bias away from the null has also been noted before in the literature for matched case–control studies. A study by Greenland (2000) noted that bias is quite severe in a 1:1 matched case–control study when there is a small sample size and further described and evaluated possible corrections for this bias that may be used in the analysis. This observation is consistent with the current simulation study. The bias away from the null was severe (as high as 35%) when only one control was matched to each case, especially when there were few cases. In fact, even with ~100 cases, the bias was as high as 13% with a skewed distribution and a true rate ratio of 1.015. However, the bias decreased dramatically when more controls were matched to each case, and for most scenarios, decreased to below 5% with 1:5 matching. Still, 20 controls were needed for each case to reduce the bias to below 5% with a skewed exposure distribution and few cases.

Lastly, in addition to decreased relative efficiency and greater bias, having few cases, a skewed exposure distribution, and a strong exposure–response resulted in an increased number of analyses that did not converge. However, this was only a major issue when one control was matched to each case. When at least five controls were matched to each case, the worst scenario only had a 1.0% of the analyses not converge and this decreased to 0 when there were at least ~100 cases in the study. Therefore, sampling more controls per case, especially when there are a few cases, will help ensure that the resulting analysis will converge and provide a meaningful exposure–response estimate.

A limitation of this study is that it only considered scenarios with one covariate. It is not completely clear how these results would generalize to scenarios with more than one covariate in the model, and this could be the topic of a future study.

In summary, we found that the relative efficiency decreases, as the strength of the exposure–response parameter increases and as the skewness of the exposure distribution increases. Also, considerable bias away from the null was observed when the number of cases in the study was small, however, selecting more controls per case reduced this bias. Consequently, the results of this article (including the complete results listed in the Online Appendix) can be used to aid in the planning of a nested or matched case–control study. By considering the number of cases, the expected exposure distribution, and the expected strength of the exposure–response of a study, these results can help guide the decision on the number of controls needed per case to achieve a desired relative efficiency and bias.