Statistical identifiability and sample size calculations for serial seroepidemiology

Highlights

• •We investigate whether disease dynamics can be inferred by repeated serum collections.
• •Measuring antibody waning is critical for inference in serological time series.
• •Collecting 200 samples every 2 months allows for inference of transmission parameters.
• •Low-level seasonality is difficult to detect statistically.

Abstract

Inference on disease dynamics is typically performed using case reporting time series of symptomatic disease. The inferred dynamics will vary depending on the reporting patterns and surveillance system for the disease in question, and the inference will miss mild or underreported epidemics. To eliminate the variation introduced by differing reporting patterns and to capture asymptomatic or subclinical infection, inferential methods can be applied to serological data sets instead of case reporting data. To reconstruct complete disease dynamics, one would need to collect a serological time series. In the statistical analysis presented here, we consider a particular kind of serological time series with repeated, periodic collections of population-representative serum. We refer to this study design as a serial seroepidemiology (SSE) design, and we base the analysis on our epidemiological knowledge of influenza. We consider a study duration of three to four years, during which a single antigenic type of influenza would be circulating, and we evaluate our ability to reconstruct disease dynamics based on serological data alone. We show that the processes of reinfection, antibody generation, and antibody waning confound each other and are not always statistically identifiable, especially when dynamics resemble a non-oscillating endemic equilibrium behavior. We introduce some constraints to partially resolve this confounding, and we show that transmission rates and basic reproduction numbers can be accurately estimated in SSE study designs. Seasonal forcing is more difficult to identify as serology-based studies only detect oscillations in antibody titers of recovered individuals, and these oscillations are typically weaker than those observed for infected individuals. To accurately estimate the magnitude and timing of seasonal forcing, serum samples should be collected every two months and 200 or more samples should be included in each collection; this sample size estimate is sensitive to the antibody waning rate and the assumed level of seasonal forcing.

1. Introduction

Analyzing time series of infectious disease case reports is the most common way to gain an understanding of disease dynamics. One advantage of this approach is that time series from hospital reporting, community reporting, and sentinel surveillance are readily available. Because some surveillance systems have been running for decades, this is a good way to investigate the long-term dynamics of many diseases. Two drawbacks of this approach are that it only counts symptomatic and reported cases, and that reporting patterns will vary across studies and sites so that two time series will usually not be directly comparable. One way of circumventing these drawbacks and still capturing general-population disease dynamics is to base a study on serology rather than symptoms and reporting patterns. A cross-sectional seroepidemiology study will give us details on past dynamics if we assume (i) that the infection process is independent of age, and (ii) that immunity is lifelong (Grenfell and Anderson, 1985; Ferguson et al., 1999), but the inferred dynamics will be coarsely broken up by year, unless individuals’ ages are specified to one or two decimal places. However, if consecutive cross-sectional studies are performed, general population incidence can be measured from any pair of consecutive cross-sectional collections, and long-term dynamics can be analyzed for the duration that repetitive cross-sectional samples are being collected.

In this paper, we analyze the usefulness of a serial seroepidemiology (SSE) study design, which we define as a study consisting of periodic collections of cross-sectional population-representative serum samples. We base our analysis on influenza virus, although the concepts are readily applied to other acute infectious diseases. Studies resembling SSE study designs have been carried out with two or three serum collections (Baguelin et al., 2011; Iwatsuki-Horimoto et al., 2011; McLeish et al., 2011; Soh et al., 2012; Yang et al., 2012), with continuous serum collection (Wu et al., 2011, 2014), and in southern Vietnam with long-term periodic collections (Boni et al., 2013; Todd et al., 2014). In this study, we analyze the power of such a study to infer the basic reproductive number of a pathogen as well as the timing and strength of its seasonal dynamics. We describe certain parts of the dynamical process that may not be identifiable under various conditions. We show that certain intuitive assumptions about disease dynamics need to be revisited when dynamical inference is based on serological data, the reason being that observations in an SSE study are made on recovered/susceptible individuals instead of infected individuals. The dynamics of recovered individuals are not normally studied in detail, but when viewing serological time series, it is these dynamics that provide the necessary information to reconstruct past epidemic dynamics. We show that accurate measurement of the antibody waning process is critical for inference in other parts of the system, and we present a power analysis showing how the epidemiological scenario, duration of the study, and the sample size of each collection affect likelihood-based statistical inference in this system.

2. Model and inference

We define a serial seroepidemiology study design as one in which N cross-sectional serum samples are collected every M months from the general population, or a pool of blood donors, patients, or other individuals who may be representative of the general population. Serum collections like these would in general be age-stratified, but we do not take advantage of the age information in the analysis presented here. We will base the analysis that follows on influenza serology, although easy parallels are drawn for other diseases, and we will assume that serum samples are analyzed via haemagglutination inhibition (HI) assays or microneutralization (MN) tests to a single virus or antigen. These dilution-based assays typically yield one of nine possible titer measurements, ranging from 10 to 2560 by two-fold increases, with 2560 corresponding to the highest measurable level of antibody in a sample and 10 corresponding to the lowest detectable level; we also include a class “<10” for undetectable antibody. Different dilution series are used sometimes, and the model structure is easily modifiable to take this into account.

The purpose of the analysis is to reconstruct the disease dynamics during the time that serum samples are being collected. Normally such dynamics would be inferred by fitting a dynamical model to a time series of symptomatic and reported cases of disease, and the statistical procedure would infer a reporting parameter describing the fraction of cases that are reported to a surveillance system. When using cross-sectional serum samples from an SSE, it is not necessary to infer a reporting parameter as the sample collections are believed to be representative of the population as a whole. In this way, an SSE study will infer the complete disease dynamics of all symptomatic and asymptomatic infections, as opposed to a study based on case reporting which will bias the inferred dynamics to the dynamics of symptomatic and/or reported cases only.

2.1. General dynamical model

In building a general dynamical model for inference in an SSE, it is important to remember that the observed variables are recovered individuals, and not infected individuals. Therefore, the model structure should include the observed variation in recovered individuals as measured by an immunological assay such as an HI test or a MN test, and we achieve this by including ten separate population classes for recovered individuals, R₁ through R₁₀. Many variations of such models have been studied in the past (Hethcote et al., 1981; Thieme and Yang, 2002; King et al., 2008). The specific dynamical equations we use are:

$$\begin{array}{ccc}\hfill \dot{E}& \hfill =\hfill & \lambda (t)\sum _{i=1}^{10}(1-{\varepsilon }_i)R_i-\mathrm{hE}\hfill \\ \hfill \dot{I}& \hfill =\hfill & \mathrm{hE}-\nu I\hfill \\ \hfill \dot{P}& \hfill =\hfill & \nu I-\sigma P\hfill \\ \hfill {\dot{R}}_1& \hfill =\hfill & p_1\sigma P-\lambda (t)(1-{\varepsilon }_1)R_1-{\rho }_1{R}_1\hfill \\ \hfill {\dot{R}}_i& \hfill =\hfill & p_i\sigma P+{\rho }_{i-1}{R}_{i-1}-\lambda (t)(1-{\varepsilon }_i)R_i-{\rho }_i{R}_i\mathrm{for}2\le i\le 9\hfill \\ \hfill {\dot{R}}_{10}& \hfill =\hfill & p_{10}\sigma P+{\rho }_9{R}_9-\lambda (t)(1-{\varepsilon }_{10})R_{10}\hfill \\ \hfill & \hfill \hfill & \hfill \end{array}$$ (1)

with a seasonal force of infection

$$\lambda \left(t\right)=\beta \left(1+A{cos}^{+}\left(\frac{2\pi t}{365}+\phi \right)\right)I,$$

where cos ⁺ refers to the non-negative part of the cosine function. The host compartments in the model are exposed individuals (E), infected individuals (I), recovered individuals who have not yet mounted a full antibody response (P), and recovered individuals whose specific antibody levels would give a result i in an immunological assay (R_i). For example, hosts in classes R₈ and R₉ would have test outcomes of 20 and 10, respectively, in HI or MN assays, and these hosts are considered to be almost fully susceptible.

It is important to note that when applying this model to influenza epidemiology, the model is only valid for one antigenic type (Smith et al., 2004). For collections over the past few years, it would be assumed that individuals were infected with either the original 2009 H1N1 pandemic strain (A/California/7/2009) or an H3N2 strain similar to the A/Victoria/361/2011-like or A/Texas/50/2012-like viruses. To use a model like this for analysis of a longer-term data set (>10 years), two types of antibody waning would need to be accounted for. The first is the natural waning of antibody levels that we have included in Eq. (1). The second is the antibody waning that occurs as a result of antigenic drift in the virus. As an example, an individual classified as R₇ (HI titer of 40) may have his or her neutralizing antibodies “wane” to class R₈ or R₉ if an antigenically novel virus enters the population. For the remainder of the analysis, we assume that there is only one antigenic type.

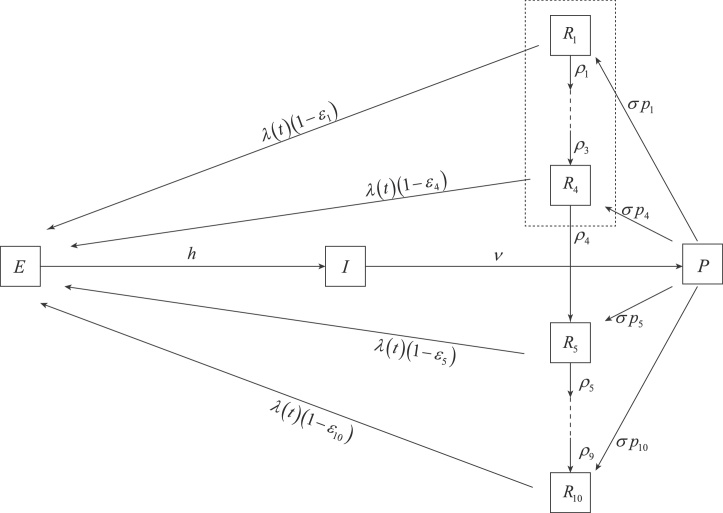
Model parameters have the expected interpretations as in standard epidemiological models (see Table 1). The parameters ρ_i describe the process of antibody waning after the initial immune response. The parameters p_i sum to one, and describe the distribution of antibody measurements expected shortly after a host recovers from infection. The parameters ɛ_i fall between zero and one, and describe the degree to which a host is protected from infection based on that host's current immune status or antibody level; note that we will have ɛ_i ≥ ɛ_j for i < j. See Fig. 1 for a class diagram of the model.

Table 1.

Model parameters.

Parameter	Description	Value/range
β	Transmission parameter	0.25 ≤ β ≤ 0.45
A	Amplitude of seasonal forcing function	0.1, 0.2
φ	Phase parameter; timing of peak transmission	π
ν−1	Infection duration	5 days
h−1	Incubation period	3 days
σ−1	Number of days post-infection before antibody response is generated	14 days
pi	Probability of immediate post-infection titer of Ri	(*)
ɛi	Susceptibility reduction (i.e. level of protection) for hosts in Ri	(*)
ρi	Antibody waning rate from Ri to Ri+1	(*)
μ	Parameter for post-infection titer distribution, defined by (2)	0.2, 2.0, 20.0
γ	Susceptibility reduction parameter, defined by (3)	0.4 ≤ γ ≤ 2.0
$w$	Duration of antibody waning from class R1 to R2	50 days
c	Inflation parameter describing how antibody waning slows down	0.2 ≤ c ≤ 0.7
	as Individuals move from Ri to Ri+1 to Ri+2, etc.
e	Probability that a serum sample is misclassified with an error of one two-fold dilution	0.05

(*) In general, these parameters can vary freely, but normally we constrain them with Eqs. (2)–(4)

Fig. 1.

Class diagram for model (1). Population classes are exposed individuals (E), infected individuals (I), recently recovered individuals who have not yet mounted a specific antibody response (P), and recovered individuals with antibody titer i (R_i). Using constraints (2) and (3), hosts inside the dashed box are completely refractory to reinfection.

Very few studies exist describing a complete antibody waning process for an infectious disease. For influenza, it is believed that the longest-lived antibody responses are those generated by infections experienced during childhood, a phenomenon that is referred to as original antigenic sin (Fazekas De et al., 1966; Lessler et al., 2012), and that these antibody responses are detectable at high levels for decades (Yu et al., 2008). The longevity of antibody responses to “non-original” infections is known less well, although our best guess is that that antibody titers stay above the commonly used threshold HI titer of 40 for years (Horsfall, 1940; Grilli et al., 1986; Severson et al., 2012; Ng et al., 2013), as opposed to decades or months. This is likely to depend on strain, age, the degree to which a virus cross-reacts immunologically with other circulating viruses, and whether the estimates come from vaccinees or individuals who were naturally infected. There is much less data on antibody dynamics in the months following an infection, but Horsfall (1940) and Horsfall and Rickard (1941) showed in a small group of patients that antibody concentrations fall between 1.0 and 1.5 units on a 2-fold dilution scale in the ninety days following infection; similarly Ng et al. (2013) show a two-fold decline in antibody concentrations occurring after 100–200 days, depending on vaccination status and influenza type.

One notable feature of many seroepidemiological studies is that there are typically very few individuals in the highest titer classes (e.g. 2560, 1280, 640), even when samples are taken soon after a pandemic or epidemic wave (Miller et al., 2010; Deng et al., 2010; Iwatsuki-Horimoto et al., 2011; Lessler et al., 2011; Dudareva et al., 2011; Bone et al., 2012; Cauchemez et al., 2012). There are several possible reasons for this. One is that individuals who seroconvert to high titers do not sustain high titers for a long time. A second reason is that seroconverters frequently seroconvert to the intermediate titer classes (e.g. 160, 80, 40) without passing through the high titer classes (Chen et al., 2010; Cauchemez et al., 2012). For the purposes of this study, we assume that both of these processes occur to varying degrees, parameterized by p_i and ρ_i.

A major challenge in the analysis will be obtaining estimates of antibody waning (ρ_i), partial immunity (ɛ_i), and the post-infection titer distribution (p_i). In order to reduce the degrees of freedom in these parameters, we introduce some constraints. For hosts recovering from infection, we assume that their immediate post-infection titer distribution will be a truncated Poisson distribution

$$\begin{array}{cc}{p}_i=C_0{e}^{-\mu }\frac{{\mu }^{i-1}}{(i-1)!}\hfill & \mathrm{for}1\le i\le 4\hfill \\ p_i=0\hfill & \mathrm{for}i>4\hfill \\ \hfill & \hfill \end{array}$$ (2)

where C₀ is a normalization constant. This constraint allows us to weight the post-infection titer distribution to the higher titers or the middle titers with a single parameter μ. The three μ values we will use for sensitivity analysis are μ = 0.2 (approximately 82% of hosts would enter R₁ after infection), μ = 2.0 (an approximately uniform distribution of post-infection titers), and μ = 20.0 (approximately 86% of hosts would enter R₄ after infection).

Reduced susceptibility is modeled via

$$\begin{array}{cc}1-{\varepsilon }_i=0\hfill & \mathrm{for}1\le i\le 4\hfill \\ 1-{\varepsilon }_i=2^{{((i-4)/6)}^{\gamma }}-1\hfill & \mathrm{for}i>4\hfill \\ \hfill & \hfill \end{array}$$ (3)

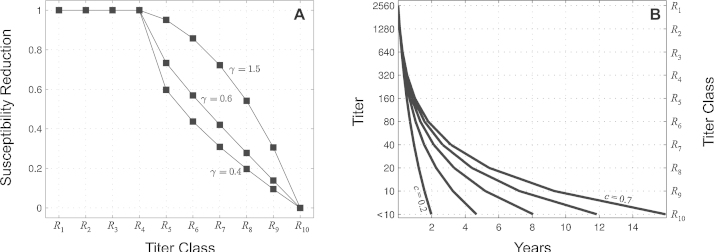
This parametrization with γ allows susceptibility to increase from 0 to 1 as individuals pass through the R-classes (see Fig. 2). The plausible range of this parameter is γ ∈ [0.4, 2.0]. For γ = 0.4, the susceptibility reduction of hosts in R₅ is 60%. For, γ = 2.0, the susceptibility reduction in R₅ is 98%, and the susceptibility reduction in R₈ is approximately 64%. The default value that we use is γ = 0.6, which corresponds to a 42% susceptibility reduction for hosts in R₇ (HI titer of 40) which is consistent with measurements obtained from influenza cohort studies, although it should be noted that there is substantial variation in these measurements (Hobson et al., 1972; Potter and Oxford, 1979; Couch et al., 2012; Ng et al., 2013; Tsang et al., 2014). The classes R₁–R₄ are completely refractory to infection, consistent with assumptions in previous models that recovered individuals cannot be immediately reinfected (Ferguson et al., 2003; Tria et al., 2005; Minayev and Ferguson, 2009; Bedford et al., 2012).

Fig. 2.

(A) Susceptibility reduction (ɛ_i) in the different R-classes. Three values of γ are shown. (B) Five different antibody waning rates explored in this analysis. From left to right the five lines are for c = 0.2, 0.4, 0.53, 0.625, 0.7.

Antibody waning will be parameterized by c and $w$ using

$${\rho }_i^{-1}=w·{\left(1+c\right)}^{i-1}\mathrm{for}1\le i\le 9$$ (4)

as the duration of time that a host spends in class R_i. The parameters c and $w$ will be constrained to reflect the fact that the rate of antibody waning in very immune individuals is faster than in less immune individuals. The parameter $w$ in this situation is the number of days an individual stays in the R₁ class after recovering. Plausible ranges for these parameters are c ∈ [0.2, 0.9] and $w\in [20,90]$.

2.2. Reduced dynamical model

One of our goals is to evaluate our ability to estimate the parameters μ, γ, $w$, and c from SSE data. The limited number of serum samples we would expect to see in the high-titer classes (R₁ through R₄) may make it impossible to estimate the parameter μ. To obviate this problem, we use a reduced model that collapses classes R₁–R₄ into a single population class R_(1,4) which heuristically corresponds to recently infected individuals. The dynamical equations for the reduced model are

$$\begin{array}{ccc}\hfill \dot{E}& \hfill =\hfill & \lambda (t)\sum _{i>4}(1-{\varepsilon }_i)R_i-\mathrm{hE}\hfill \\ \hfill \dot{I}& \hfill =\hfill & \mathrm{hE}-\nu I\hfill \\ \hfill \dot{P}& \hfill =\hfill & \nu I-\sigma P\hfill \\ \hfill {\dot{R}}_{(1,4)}& \hfill =\hfill & \sigma P-{\rho }_{(1,4)}{R}_{(1,4)}\hfill \\ \hfill \dot{R_5}& \hfill =\hfill & {\rho }_{(1,4)}{R}_{(1,4)}-\lambda (t)(1-{\varepsilon }_5)R_5-{\rho }_5{R}_5\hfill \\ \hfill \dot{R_i}& \hfill =\hfill & {\rho }_{i-1}{R}_{i-1}-\lambda (t)(1-{\varepsilon }_i)R_i-{\rho }_i{R}_i\mathrm{for}6\le i\le 9\hfill \\ \hfill {\dot{R}}_{10}& \hfill =\hfill & {\rho }_9{R}_9-\lambda (t)(1-{\varepsilon }_{10})R_{10}\hfill \end{array}$$ (5)

The constraints (2)–(4) are used to reduce the dimensionality of parameter space. The parameter ρ_(1,4) is defined as

$${\rho }_{(1,4)}^{-1}=\sum _{j=1}^4{p}_j\sum _{i=j}^4{\rho }_i^{-1},$$ (6)

and thus still depends on μ, but model dynamics are not very sensitive to μ.

2.3. Likelihood framework

To determine how easily one can infer the epidemiological and immunological parameters in systems (1)–(5), with or without the constraints (2)–(4), we define a likelihood framework that describes the probabilities of sampling recovered individuals with particular antibody titers. We define an error function that allows a serum sample to be misclassified one titer class higher or lower with probability e; a serum sample is correctly classified with probability 1 − 2e. Individuals sampled from classes R₁ and R₁₀ can only be misclassified into one neighboring titer class with probability e, and are correctly classified with probability 1 − e. Individuals sampled from classes E, I, and P are assumed (as an approximation) to have the same antibody titer as the class R₁₀. We simulate this system until it reaches an equilibrium or stable oscillating behavior, and we generate sample sets of size N every M months with multinomial sampling, using e = 0.05.

The probability that at time t, a serum sample s_t falls in titer class i is:

$$P(s_t=i)=\left\{\begin{array}{cc}(1-e)r_1(t)+e{r}_2(t)\hfill & i=1\hfill \\ e{r}_{i-1}(t)+(1-2e)r_i(t)+e{r}_{i+1}(t)\hfill & 2\le i\le 9\hfill \\ e{r}_9(t)+(1-e)r_{10}(t)\hfill & i=10,\hfill \end{array}\right)$$ (7)

where the r_i(t) variables represent the proportions of individuals in the population that have an antibody titer i at time t. When performing inference with the reduced model, the probability is

$$P(s_t=i)=\left\{\begin{array}{cc}(1-e^{*})r_{(1,4)}(t)+e{r}_5(t)\hfill & i=\left(1,4\right)\hfill \\ e^{*}{r}_{(1,4)}(t)+(1-2e)r_5(t)+e{r}_6(t)\hfill & i=5\hfill \\ e{r}_{i-1}(t)+(1-2e)r_i(t)+e{r}_{i+1}(t)\hfill & 6\le i\le 9\hfill \\ e{r}_9(t)+(1-e)r_{10}(t)\hfill & i=10.\hfill \end{array}\right)$$ (8)

The misclassification parameter e^* is computed from the data using

$$e^{*}=e·\frac{\text{number of serum samples in}{R}_4}{\text{number of serum samples in}{R}_{(1,4)}}$$

which gives us an approximation of the number of serum samples in R₁ through R₄ whose antibody titer would be misclassified as R₅. The full likelihood is defined as the product across all samples, and the log-likelihood is maximized over the parameters β, A, and φ using a standard Nelder-Mead method (Nelder and Mead, 1965) in Matlab (Mathworks, Natick, MA). Confidence intervals for parameter estimates are computed using likelihood profiles. Confidence intervals are presented as medians over ten simulated data sets; the median upper bound is taken and the median lower bound is taken so that the presented confidence interval may not correspond to any particular simulation that was run.

2.4. Assessing statistical identifiability

A key question when performing statistical inference on disease dynamics using serological data is whether the three processes of (i) reinfection, (ii) post-infection antibody generation, and (iii) antibody waning are statistically identifiable from one another. When there is no seasonal forcing in the model (A = 0), the dynamics settle to a non-oscillating endemic equilibrium – as any standard Susceptible-Infected-Recovered-Susceptible (SIRS) model would – but this endemic equilibrium will not be associated with a unique set of parameters describing infection rate (β and ɛ_i), antibody generation (p_i), and antibody waning (ρ_i). This is a general property of SIRS-like dynamical systems. As an example, in a standard SIRS model, we can always increase the waning rate and reduce the transmission rate in a way that keeps the endemic equilibrium prevalence unchanged. Therefore, given a data set from a real-world SIRS-like epidemiological system, it may be difficult or impossible to infer the values of the parameters β, ɛ_i, p_i, and ρ_i.

To illustrate this property and test its robustness to other features of the system, we chose a parameter combination

$${\mathrm{\Theta }}_0=(\beta ,{\varepsilon }_1,\dots ,{\varepsilon }_{10},p_1,\dots ,p_{10},{\rho }_1,\dots ,{\rho }_9)$$ (9)

corresponding to an endemic equilibrium prevalence of 1.1%; Θ₀ corresponds to 30 parameter values. We then generated 100 ‘false’ parameter combinations ${\{{\mathrm{\Theta }}_j\}}_{j=1,\dots ,100}$ corresponding to the same endemic equilibrium, in order to determine if they can be distinguished from the true parameters Θ₀.

False parameter combinations Θ_j were chosen according to the following procedure. First, we let β_i = β(1 − ɛ_i) and chose ten β_i parameters uniformly on (0,1); we sorted and renumbered so that β₁₀ was largest. Summing up the right-hand sides of the dynamical equations for R₁ through R₁₀ in the general model (1), we obtain

$$\sigma P-\sum _{i=1}^{10}{\beta }_i{\hat{R}}_i\hat{I}=0$$

and we rescale the β_i so that the equation above is satisfied. We let β = β₁₀, which results in ɛ₁₀ = 0. Second, the 10 p_i parameters were also chosen uniformly and within 10% of their true values, and they were normalized so that they summed to unity. The ρ_i parameters were then obtained by solving the dynamical equations for R_i assuming endemic equilibrium. The parameters from this second step were accepted only if the ρ_i parameters satisfied ρ_i > ρ_j > 0 for all i > j; if this condition was not met, the second step was repeated. If the inferential system possesses statistical identifiability and no bias, then the likelihood values of all the Θ_j combinations should be strictly lower than the likelihood value of Θ₀.

Using the true parameters Θ₀ and assuming no seasonality in the dynamics (A = 0), a data set X₀ of titer measurements was generated by sampling from the dynamical system (1). Dynamics were simulated until equilibrium, after which 200 recovered individuals were sampled at random every two months for four years to generate a data set X₀ with 4800 total data points. Using Eq. (7), the log-likelihood L(Θ₀|X₀) was compared with the log-likelihoods L(Θ_j|X₀) to determine if the true set of parameters Θ₀ could be distinguished from false sets of parameters using likelihood methods. In order to determine if low amplitudes – ones that cause dynamics to oscillate around the endemic equilibrium – could improve statistical identifiability, data sets X_A for small positive values of A were generated using the general model (1) and parameters Θ₀. Likelihood comparisons were also done using the data sets X_A.

The analysis was repeated using system (1) with constraints (2)–(4). A constrained parameter set

$${\mathrm{\Theta }}_0^{\prime }=(\beta ,\gamma ,\mu ,c,w)$$ (10)

was chosen to correspond to an endemic equilibrium prevalence of 0.9%; the parameter set was ${\mathrm{\Theta }}_0^{\prime }=(0.45,0.6,20.0,0.2,50)$. In this case, false parameter combinations ${\mathrm{\Theta }}_j^{\prime }$ that correspond to the exact endemic equilibrium of ${\mathrm{\Theta }}_0^{\prime }$ could not be found easily; therefore, we chose false parameter combinations ${\mathrm{\Theta }}_j^{\prime }$ that corresponded to an endemic equilibrium close to the original one. First, we chose μ ∈ U(15, 25), c ∈ U(0.18, 0.22), and $w\in U(40,60)$. Second, we optimized β and γ and checked to see if the L¹-distance from the false equilibrium to the true equilibrium was less than 0.5% of the total population size. If this condition was not met, we began with a new random draw of μ, c, and $w$. Data sets $X_0^{\prime }$ and $X_A^{\prime }$ were generated as above.

3. Results

3.1. Statistical identifiability

In general, it is clear that there is a statistical identifiability problem among the processes of antibody generation, antibody waning, and reinfection. This is intuitive, as in many epidemiological models it may be expected that speeding up or slowing down all of these processes by the same factor may result in no change or little change in the system's mean long-term dynamics. This is particularly true if there is no seasonal forcing in the model.

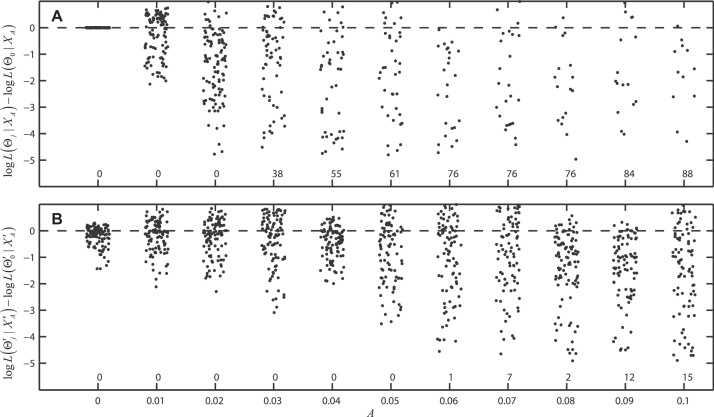
When the model is seasonally forced, the shape of the seasonal dynamics improves statistical identifiability among antibody generation, antibody waning, and reinfection. We describe the degree of statistical identifiability in our system by evaluating a data set X_A, generated with a set of true parameters Θ₀, and computing the probability that X_A could have been generated with sets of false parameters ${\{{\mathrm{\Theta }}_j\}}_{j=1,\dots ,100}$. Simulating system (1) with Θ₀ and amplitude A, we generate data sets X_A and expect that L(Θ₀|X_A) > L(Θ_j|X_A) for all j. However, Fig. 3A shows that when the dynamics are not seasonally forced (A = 0.0), the likelihoods of the false parameter combination Θ_j are identical to that of the true parameter combination Θ₀, making it impossible to estimate the true parameters. As the amplitude is increased slightly, the likelihoods of the different scenarios Θ_j begin to differentiate as the shapes of the oscillating trajectories will be dependent on whether the individual processes of antibody waning and reinfection are fast or slow. Fig. 3B shows a similar behavior for model (1) simulated with constraints (2)–(4). Increasing A also improves statistical identifiability. Note that in this case, the false parameter combinations ${\mathrm{\Theta }}_j^{\prime }$ were more difficult to generate than Θ_j, and they are, in general, quite close in parameter space to the true parameters ${\mathrm{\Theta }}_0^{\prime }$. For this reason, the likelihoods in Fig. 3B cluster together more closely than the likelihoods in Fig. 3A.

Fig. 3.

Difference in log-likelihood values between the true parameter combination Θ₀ (used to generate data sets X_A) and false parameter combinations Θ_j that generate similar dynamics. Panel A shows free parameter sets Θ_j as defined by (9), and panel B shows constrained parameters sets ${\mathrm{\Theta }}_j^{\prime }$ as defined by (10). Each point corresponds to one of 100 false parameter combinations, and a negative number on the ordinate indicates that a particular Θ_j had lower log-likelihood than Θ₀. When the log-likelihood difference is greater than five, no point is plotted; instead the number of points for which the log-likelihood difference is greater than five is indicated above the tick marks on the horizontal axis. The amplitude A is shown on the horizontal axis. Likelihoods are computed given eleven different data sets X_A with different seasonal forcing amplitudes. As seasonal forcing increases, statistical identifiability improves.

Equilibrium prevalence in the above simulated data sets is approximately 1.0%. A similar pattern of statistical identifiability is seen as we vary β and consider prevalences between 0.25% and 0.65%. Figs. S1–S3 again show that statistical identifiability improves as the amplitude A increases, but identifiability worsens as β decreases, indicating that inference at very low prevalence levels may be difficult. Thus, in epidemiological scenarios where there are no seasonal dynamics, statistical inference using serological time series may be impossible; likewise, if seasonality is weak and prevalence levels are low, estimation of various epidemiological processes will also be difficult.

Understanding the relationships among antibody generation, antibody waning, and reinfection is crucial for knowing whether a particular serological data set can be used to infer properties of disease dynamics. Ideally, these rates would be estimated independently using patient-level longitudinal data. For influenza, these data sets allow us to approximate the susceptibility reduction parameter at γ ≈ 0.6 (Hobson et al., 1972; Potter and Oxford, 1979; Couch et al., 2012; Ng et al., 2013; Tsang et al., 2014). The formulation of the reduced model (5) allows our simulation and inference to be relatively insensitive to the antibody generation process described by μ. However, very few good estimates exist of the waning rate of influenza antibodies. In the section below, we evaluate our ability to perform inference on transmission and seasonality parameters, given uncertainty in the rate of antibody waning.

3.2. Estimation of transmission and seasonality parameters

In this section, we assume that $w=50$ and that c varies in the range 0.2 ≤ c ≤ 0.7. At the boundaries, this means that individuals’ antibodies wane from a titer of 2560 (class R₁) to a titer of 20 (class R₈) in 1.8 years for the fast-waning scenario (c = 0.2) and in 7.8 years in the slow-waning scenario (c = 0.7). We assume that γ = 0.6, μ = 2.0, and that β = 0.3 corresponding to a basic reproductive ratio of R₀ = 1.5. Seasonal amplitudes of A = 0.1 and A = 0.2 are used, to see if we can statistically identify amplitudes lower than the expected range 0.3 ≤ A ≤ 0.6 for temperate areas (Truscott et al., 2011). The timing of peak transmission is set arbitrarily to φ = π. Using Eqs. (1) with constraints (2)–(4), we simulate our system until it reaches a stable oscillating behavior, and data sets are generated by sampling N individuals every two months for a duration of either three years or four years. Inference is performed using the reduced model (5), and likelihood optimization is performed over the parameters β, A, and φ.

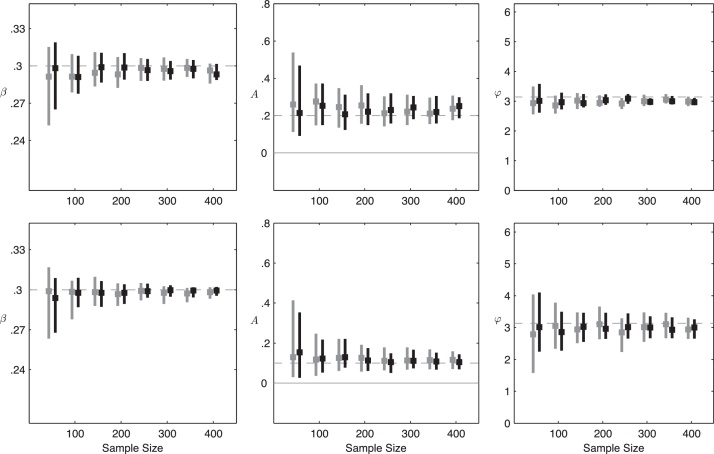
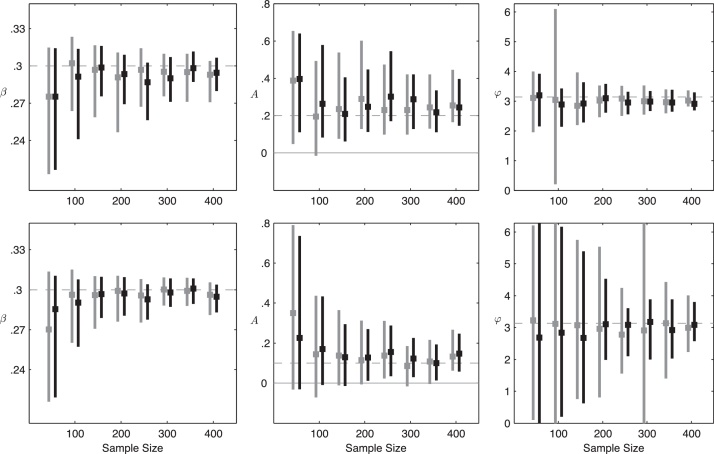
Fig. 4 shows the confidence intervals for our maximum-likelihood estimates of parameters β, A, and φ when antibody waning is fast (c = 0.2; 1.8 years to lose protection). In general β is easy to estimate for sample sizes N ≥ 100. This is to be expected, because in a single cross-sectional set of serum samples, if we know the antibody waning rate, we should be able to estimate the level of endemicity and thus the R₀ value. The 95% confidence intervals for the amplitude parameter A do not include zero, indicating that the presence of seasonality is detectable in an SSE study design with samples collected every two months for ≥3 years. These confidence intervals are not symmetric about the true value, which results from the irregular shape of the likelihood surface near A = 0.0. The maximum likelihood estimates of A appear to be biased slightly upwards, but this is difficult to know with certainty due to there being only ten estimates per sample size. The time of peak transmission (i.e. the phase φ of the forcing function) can also be reasonably estimated. For N = 150 and four years of data, the 95% confidence intervals for φ span a period covering 26 days (A = 0.2) or 53 days (A = 0.1), indicating that the pattern of seasonal forcing is correctly identified. Note that when A is smaller, we are closer to the endemic equilibrium and estimation of β is easier; however, oscillations are of lower magnitude, and hence estimation of A and φ is more difficult.

Fig. 4.

Confidence intervals for parameters β, A, and φ as a function of the sample size N, under a scenario of fast antibody waning (1.8 years to immune loss). Amplitudes of A = 0.2 (top row) and A = 0.1 (bottom row) are used. Gray lines correspond to a three-year data set and black lines to a four-year data set, and the dashed lines indicate the true parameter values. Data are simulated with system (1) and constraints (2)–(4), and inference is performed with the reduced model (5). Parameters are $\gamma =0.6,\mu =2.0,w=50,c=0.2$. Confidence intervals shown are medians over ten simulated data sets, and the square on each line is the mean maximum-likelihood estimate.

Estimating transmission intensity and identifying the transmission season is more difficult when antibodies persist longer. With a slightly slower rate of antibody waning (c = 0.4; 3.3 years from a titer of 2560 to a titer of 20), transmission and seasonality are difficult to estimate for small samples sizes. When seasonal forcing is weak (A = 0.1), the presence or absence of seasonality may be impossible to infer with an SSE study design if the antibody waning process is slow. The bottom panels of Fig. 5 show that even for large sample sizes, locating the timing of peak transmission (φ) may be impossible; this also means that the corresponding confidence intervals for the amplitude A are epidemiologically meaningless as the inference in this case is simply capturing noise in the system and not any true seasonal behavior. If the true seasonal amplitude is slightly larger (A = 0.2), we can hope to estimate it with large sample sizes (N ≥ 200), and the transmission parameter β should also be estimated to within 20% of its true value. The confidence intervals computed in this section are not sensitive to the parameter μ when antibody waning is fast (Figs. S4 and S5); they are somewhat sensitive to μ when the antibody waning rate is slow (Figs. S6 and S7). The confidence intervals in Figs. S8 and S9 show that if samples are collected every four months (M = 4), statistical identifiability is considerably worse, even for fast antibody waning. Figs. S10–S17 present all confidence computed in this part of the analysis.

Fig. 5.

Confidence intervals for parameters β, A, and φ as a function of the sample size N, under a scenario of moderate antibody waning (3.3 years to immune loss). Amplitudes of A = 0.2 (top row) and A = 0.1 (bottom row) are used. Gray lines correspond to a three-year data set and black lines to a four-year data set, and the dashed lines indicate the true parameter values. Data are simulated with system (1) and constraints (2)–(4), and inference is performed with the reduced model (5). Parameters are $\gamma =0.6,\mu =2.0,w=50,c=0.4$. Confidence intervals shown are medians over ten simulated data sets, and the square on each line is the mean maximum-likelihood estimate.

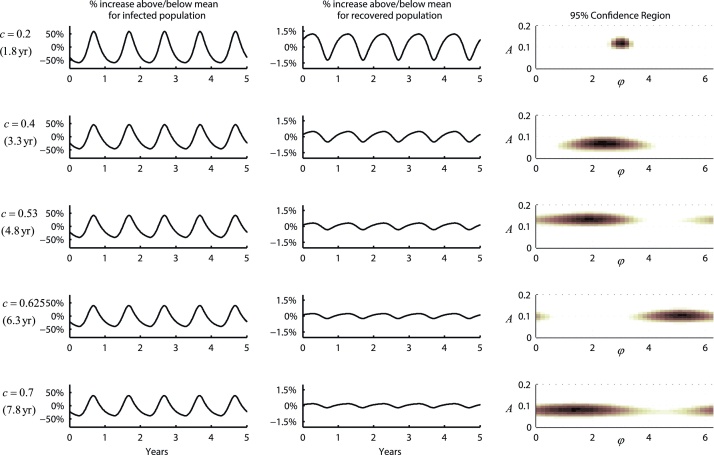
In general, estimation of the seasonality parameters A and φ is very sensitive to the rate of antibody waning. The reason for this is that these parameters are estimated based on oscillations in data collected on the recovered classes R₁–R₁₀, and these oscillations are sensitive to the waning rate: a slow rate of waning will cause individuals to stay in the R-classes longer and will dampen the oscillations. This is a reminder that in a serology-based field study, observations are made on recovered or susceptible individuals, and oscillations in the recovered/susceptible population behave differently than oscillations in the infected population. Fig. 6 shows changes in these oscillations as the rate of antibody waning is slowed down. The left and middle columns of Fig. 6 show the relative magnitude of oscillations to their long-term average, both in the infected population (left column) and in the recovered/susceptible population (middle column). The relative magnitude of oscillations in infected individuals is large and insensitive to changes in the rate of antibody waning. However, oscillations in the R classes are of smaller magnitude and dampen substantially with slower waning. The likelihood surfaces on the right show that for A = 0.1, the transmission season cannot be identified reliably if immune loss takes longer than four years. Fig. S18 shows that statistical identifiability is improved when A = 0.2.

Fig. 6.

Effect of antibody waning on our ability to perform inference on seasonality parameters. Plots show equilibrium dynamics (left and middle columns) and likelihood surfaces (right column) for five different rates of antibody waning; the c parameter and time to immune loss are shown on the left. The first column of figures shows the dynamics of I(t) relative to its long-term mean value, and the second column shows the dynamics of ∑R_i(t) relative to its long-term mean value. As the rate of antibody waning slows down, the relative magnitude of oscillations in the recovered classes decreases, making these oscillations more difficult to detect. The right column shows the 95% confidence region for A and φ, with the darker regions having highest likelihood. When antibody waning is slow (c > 0.5), detecting the phase φ may be impossible. Simulations and inference were performed with system (1) with constraints (2)–(4). Parameters used in the simulation were A = 0.1, φ = π, γ = 0.6, μ = 2.0, β = 0.3, and $w=50$. Inference was performed on a 4-year data set with 200 samples collected every two months.

4. Discussion

If seroepidemiology is to become a useful tool for performing inference on disease dynamics, we must understand which disease processes have the largest effects on observations made in serological studies. From the analyses presented here, it is apparent that the antibody waning rate is a crucial process that must be understood and measured precisely, in order to be able to perform accurate inference from a serially sampled set of cross-sectional serum collections. In addition, understanding antibody waning is also critical for traditional seroepidemiological studies with a single cross-section. For infections whose antibody responses are expected to wane, a cross-sectional sample only tells us the recent history of the individuals in that sample, the degree of recency depending on the rate of antibody waning. For diseases that confer life-long immunity, seroprevalence in a cross-sectional sample will correspond to lifetime attack rate, but only if serological cutoffs are chosen with care so that low-level antibody concentrations indicative of past infection are counted as such. Knowing whether a basic seroepidemiology study reports a disease's attack rate over the past several months or past several years is critical for estimating disease burden and public health planning.

Direct measurements of the antibody waning process are rare (Horsfall, 1940; Horsfall and Rickard, 1941; Buchy et al., 2010; Severson et al., 2012). One assumption we have made in this analysis is that the antibody waning rate is not constant. We assume that there is a shorter transition time among the high-titer classes (2560, 1280, …) than among the low-titer classes (80,40, …) and that individuals maintain lower antibody titers for much longer periods of time. We made this assumption based on the fact that individuals are not typically observed to have high titers in many cross-sectional studies. If this assumption holds true, it means that the slow part of the waning process will be difficult to measure precisely, and not very useful for statistical inference as estimates will almost certainly come with a high variance. In other words, given an individual with a protective but low antibody titer, it would be impossible to infer the date of that individual's most recent infection. However, if we observe an individual in the fast-waning part of the process, a high titer may be informative in estimating a time window in the recent past when that individual experienced an infection.

Finally, antibody waning will depend on age (Cauchemez et al., 2012; Ng et al., 2013), which would also indicate that titer cut-offs should be age-dependent. Current seroepidemiological studies do not take this potential age-dependence into account, partially because few studies are large enough, both in terms of numbers of patients and duration of follow-up, to determine the nature of this age-dependence. The waning rate will also be sensitive to immunodominance relationships among strains, and specifically to whether a host's antibody profile has arisen in response to that host's first influenza infection. There will likely be other causes of variation in the waning process, as is evidenced in most cross-sectional studies by the presence of some individuals with long-lived high titers that do not seem to be the result of original antigenic sin. This is evident in the data used by Lessler et al. (2011, 2012) which show a noticeable minority of the study population with high antibody titers to certain influenza strains that have been out of circulation for ten or twenty years. Teasing out the effects of age, strain, and original antigenic sin as contributors to variation in antibody titer is a major challenge for influenza serology. Understanding the slower part of the antibody waning process will be critical for studies aimed at long-term collection of serological data.

Two immediate benefits of performing inference on serological time series are the ability to reconstruct complete disease dynamics – i.e. the dynamics of both symptomatic and asymptomatic individuals – and the avoidance of a reporting parameter. The study of complete disease dynamics is not something that has yet gained significant traction among field epidemiologists. However, with better access to time-stratified serological collections (Wu et al., 2011, 2014; de Bruin et al., 2014) and new high-throughput serological assays (Koopmans et al., 2011; Baas et al., 2013; Huijskens et al., 2013), these types of studies may become more common. Public health benefits of SSE-like study designs include the ability to distinguish a large influenza epidemic from a severe influenza epidemic. Additionally, we may be able to learn something about the variation in the symptomatic or asymptomatic natures in the epidemics dynamics of certain diseases. This is particularly important for dengue virus as it is has been observed, by comparing case reporting to serological data, that dengue epidemics can vary substantially in their symptomatic/asymptomatic ratio (Sangkawibha et al., 1984).

For tropical influenza specifically, study designs based on serological time series may hold a lot of promise as the dynamics of tropical influenza are qualitatively different from those of temperate influenza epidemics. In tropical regions, as far as we know, it is not possible to perform influenza surveillance using syndromic data alone, as case numbers for influenza-like illness (ILI) do not seem to correlate well with case numbers for confirmed influenza (Nguyen et al., 2009; Vongphrachanh et al., 2010), although more study is needed in this area. Inferring dynamics from time series of confirmed influenza cases gives a clearer picture of influenza dynamics, but even this type of surveillance may miss one of the larger features of tropical influenza epidemiology, namely, that some regions in the tropics or sub-tropics may support year-round circulation of viruses (Le et al., 2013; Nelson et al., 2014). We have not yet powered the SSE study design to determine how low of a level of persistent circulation we should be able to detect. The analyses presented here were all performed on epidemiological scenarios with endemicity levels ranging from 0.2% to 1.1%; however, persistence levels during low-influenza periods may be even lower than this. A second important feature of tropical influenza that needs to be understood is the regularity and amplitude of seasonality. Despite recent attempts to classify the seasonality of influenza in tropical regions (Tamerius et al., 2013; Saha et al., 2014), it is still unclear whether a true influenza season exists in many tropical countries. In addition, the shape and duration of the peak transmission season has not been determined for most parts of the world, and this transmission curve is not guaranteed to take on the sinusoidal shape assumed in most seasonally-forced epidemic models. Thus, in addition to determining the presence or absence of seasonal forcing, a part of the inferential procedure should be focused on determining its shape. If seasonal forcing does exist in the tropics, it is likely to be much weaker than that observed in temperate regions, and for this reason in the present study we evaluated our ability to statistically identify low-level seasonality.

Given the importance of tropical influenza to global influenza dynamics (Russell et al., 2008; Rambaut et al., 2008; Bedford et al., 2010; Bahl et al., 2011), and the possibility that persistence in tropical regions may have an effect on the rate or fixation probability of antigenic changes in influenza (Boni et al., 2006; Russell et al., 2008; Rambaut et al., 2008; Boni, 2008; Adams and McHardy, 2011), it is critical that we continue gathering high-quality data that can shed light on influenza's persistence and seasonality patterns in tropical countries. The serial seroepidemiology study design presented here is one method of gathering consistent and continuous sample sets that will allow for reconstruction of complete disease dynamics, and improve our understanding of the dynamic patterns of influenza circulation in the tropics.

Appendix A. Supplementary data

The following is the supplementary data to this article: