Anisotropic thermoelectric behavior in armchair and zigzag mono- and fewlayer MoS₂ in thermoelectric generator applications

Abstract

In this work, we have studied thermoelectric properties of monolayer and fewlayer MoS₂ in both armchair and zigzag orientations. Density functional theory (DFT) using non-equilibrium Green’s function (NEGF) method has been implemented to calculate the transmission spectra of mono- and fewlayer MoS₂ in armchair and zigzag directions. Phonon transmission spectra are calculated based on parameterization of Stillinger-Weber potential. Thermoelectric figure of merit, ZT, is calculated using these electronic and phonon transmission spectra. In general, a thermoelectric generator is composed of thermocouples made of both n-type and p-type legs. Based on our calculations, monolayer MoS₂ in armchair orientation is found to have the highest ZT value for both p-type and n-type legs compared to all other armchair and zigzag structures. We have proposed a thermoelectric generator based on monolayer MoS₂ in armchair orientation. Moreover, we have studied the effect of various dopant species on thermoelectric current of our proposed generator. Further, we have compared output current of our proposed generator with those of Silicon thin films. Results indicate that thermoelectric current of MoS₂ armchair monolayer is several orders of magnitude higher than that of Silicon thin films.

The advent of Graphene¹,²,³, a two-dimensional (2D) sheet of carbon atoms in honeycomb lattice, has stimulated great interest and intensive research on the properties of 2D materials. More recently, a new family of 2D materials has been proposed, namely Transition Metal Dichalcogenides (TMDs). The presence of a bandgap in some members of TMD family, a crucial property for microelectronics applications, has attracted much attention in comparison with the gapless Graphene. Among all semiconducting TMDs, Molybdenum disulfide (MoS₂) is the most representative, widely interesting and intensively studied one⁴,⁵,⁶, partially because it is relatively stable and readily available. MoS₂ has been used as a dry lubricant in automobile industry due to its low friction properties. Recently, it has been studied for applications in field effect transistors⁷,⁸,⁹, photovoltaics¹⁰ and photocatalysis¹¹.

In general, bulk TMDs has a layered structure. Each layer is formed by a plane of transition metal atoms sandwiched between two planes of chalcogen atoms in trigonal prismatic arrangements as illustrated in Fig. 1. Strong intralayer covalent bonding, in contrast to weak interlayer van der Waals forces¹² make it possible to fabricate high-quality monolayer MoS₂ by exfoliation technique¹²,¹³,¹⁴. A desirable bandgap¹²,¹³,¹⁴,¹⁵, comparable carrier mobility with those of Si thin film and Graphene nanoribbons¹⁴,¹⁶,¹⁷ together with excellent thermal stability¹⁴ and surface free from dangling bonds¹⁸,¹⁹, makes 2D MoS₂ a very attractive candidate for device applications²⁰,²¹.

Figure 1. Atomic structure of MoS₂.

(a) Monolayer of MoS₂ is made of a honeycomb sheet of Molybdenum atoms covalently sandwiched between two honeycomb sheets of Sulphur atoms. Bulk of MoS₂ is formed by monolayers stacked and held on top of each other by van der Waals forces. Side view of mono-, bi-, tri- and quadlayer is illustrated in parts (b–e), respectively.

Compared to the research progress in its electronic and mechanical characteristics²²,²³,²⁴, thermoelectric (TE) properties of MoS₂ have not been widely studied. Thermoelectrics provide a way of converting thermal energy into electricity²⁵. Thermoelectric generator is expected to play an important role in increasing demand for clean energy in future³³. In general, a TE generator module is made of an array of thermocouples. As illustrated in Fig. 2, each thermocouple, the basic unit of a TE generator, is made of a p-type and an n-type semiconductor, named as legs, connected thermally in parallel and electrically in series. Temperature gradient across thermocouple is the driving force inducing electrical current.

Figure 2. Structure of proposed thermoelectric generator based on monolayer MoS2.

It is composed of a p-type and an n-type semiconductor, known as legs. Temperature gradient across thermocouples will induce an electrical current through thermocouple based on thermoelectric phenomenon.

The research on thermoelectric materials has been one of the major topics since 1950 s when basic science of thermoelectrics was well founded²⁶. Bi₂Te₃ and the similar alloys have played a main role in the application of thermoelectric devices. It is well-known that efficiency of thermoelectric conversion can be evaluated by a dimensionless figure of merit , in which , , k_e, k_ph and T are electrical conductance, Seebeck’s coefficient, electronic contribution to thermal conductance, phonon contribution to thermal conductance and absolute temperature, respectively²⁶. In order to have a high ZT, it is desirable to have a high electrical conductance and large Seebeck’s coefficient and low thermal conductance. These parameters mainly depend on the intrinsic properties of materials and they are generally coupled with each other. Enhancement to one of them may degrade the other and the overall effect will not change. In three decades after 1950 s, only incremental progress was made due to the difficulty in fine-tuning of these parameters²⁷.

Recently, new wave of research on thermoelectric field has been initiated because nanoscale structures may enhance thermoelectric efficiency. It was shown that quantum confinement of charge carriers in quantum-well super-lattices²⁸, quantum-wires²⁹ as well as bulk samples containing nanostructured constituents²⁷ will enhance thermoelectric conversion. It is known that Density of States (DOS) of low-dimensional materials exhibits sharp changes around Fermi level²⁷,²⁸,²⁹. As a result, Seebeck’s coefficient, which depends on logarithmic derivative of DOS, is significantly enhanced, and hence, the ZT increases. In addition to an increase in Seebeck’s coefficient, low dimensional materials are known to benefit from higher phonon scattering and consequently lower phonon thermal conductance²⁷. Low phonon thermal conductivity (k_ph) has been already reported for TMDs: ph of MoS₂ thin films and disordered layered WSe₂ are about 0.1 W/mK to 1 W/mK³⁰ and 0.05 W/mK³¹, respectively. In addition, it has been reported that MoS₂ has anisotropic thermal properties³², which provides another degree of freedom to optimize TE conversion performance. The advantage of nano-scale structures with respect to their bulk counterparts motivates us to study thermoelectric properties of 2D MoS₂ in both armchair and zigzag orientations.

In this work, thermoelectric properties of mono-, bi-, tri- and quadlayer MoS₂ in armchair and zigzag directions have been studied for electricity generation. ZT of bulk MoS₂ has already been reported to be 0.1 at 700 K³³. In a later study, effect of pressure on thermoelectric properties of MoS₂ has been investigated³⁴. ZT has been reported to increase up to 0.65 in a wide range of pressure and temperature. Thermoelectric performance of monolayer MoS₂ has been studied and ZT is reported to reach 0.58 in room temperature³⁵. In this study, ZT values up to 1.2 in armchair direction has been achieved which is higher than ZT values reported for omnidirectional MoS₂ structures. Well-established thermoelectric materials include PbTe³⁶,³⁷ and Bi₂Te₃³⁸ based alloys, from which higher ZT values around 2.4 have been already achieved at 900 K. However, their substitution with abundant materials is favorable due to scarcity of Te element. This study aims to investigate the possibility of forming high performance thermoelectric generator based on highly available MoS₂. In addition to abundance of MoS₂, mono- and fewlayer structures have benefits of possibility of forming high density thermoelectric modules, due to their nano-scale size. In this study, it is found that as the number of layers increases from monolayer to quadlayer, both transmission spectrum and phonon thermal conductance increase. In addition, strong electronic and thermal transport anisotropy is found between zigzag and armchair orientations. Transmission coefficient and phonon thermal conductance of zigzag orientation is higher than those of armchair with the same number of layers. Their effect on ZT has been studied in this work. In addition, TE conversion of Si thin film TE generator with the same thickness as MoS₂ armchair mono- and fewlayer TE generator has been studied by using Synopsys TCAD software. The comparison indicates that proposed MoS₂ generator exhibits superior TE conversion efficiency.

Method

The computational model used in this paper is based on self-consistent density functional theory (DFT) using non-equilibrium Green’s function (NEGF) method³⁹,⁴⁰ implemented in QuantumWise ATK software package. Prior to the calculations of carrier transport, the structure has been relaxed to optimized force and stress of 0.05 eV/Å and 0.05 eV/ ų, respectively. The relaxation calculations is implemented by using Generalized Gradient Approximation (GGA) exchange correlation with a Double Zeta Polarized (DZP) basis set and a mesh cut-off energy of 75 Ha.

Top view of structures studied in this paper is illustrated in Fig. 3. They can be divided into three regions: left, right and central. Left and right regions are called electrodes, treated with semi-infinite boundary conditions. Their properties can be described by solving for the bulk material. The voltage and temperature bias are applied on electrode regions. Central region includes a repetition of each electrode region in order to screen out perturbations introduced in the scattering regions. In order to have an insight on the effect of lattice orientation and thickness on the intrinsic TE properties of MoS₂, no perturbation is introduced in the scattering region in calculating ZT.

Figure 3. Simulated structures in this paper.

Armchair-oriented and zigzag-oriented MoS₂ are shown in part (a,b), respectively. Each device is comprised of three regions: left electrode, central region and right electrode. Central region, itself, contains an extension of electrode regions on both sides and scattering region in the middle. Electrode regions are treated semi-infinitely. Their properties are computed by solving for bulk material. Temperature gradient is biased on electrode regions. Extension of electrode regions in central region, are used to screen out any perturbation introduced in scattering region.

Central region shown in Fig. 3, should be large enough to accommodate both the voltage and temperature drop within itself. Due to computational constraints, we used 149, 299, 449 and 599 atoms supercell as central region in mono-, bi-, tri- and quadlayer structures, respectively. Using infinitesimal voltage and temperature drop, i.e. working in linear regime, makes our approximation valid. In addition, a vacuum spacing of 20 Å is added to each side of the structure super cell to suppress any interaction caused by periodic boundary condition at out-of-plane direction.

In order to calculate linear transport properties of the system, Landauer-Buttiker⁴¹ formula is used, in which transport coefficients are calculated from Green’s function. This formulism is correct in absence of inelastic scattering and phase-changing mechanisms. DFT-NEGF method is chosen since it is proven to be a fast and computationally efficient method for a systems containing a large number of atoms⁴²,⁴³. For DFT calculations, Monkhorst-Pack k-grid⁴⁴ of 1 × 1 × 100 with a density mesh cut-off of 10 Ha is used for supercell within Localized Density Approximation (LDA)⁴⁵ with DZP basis set.

Electrical current in the linear transport regime is given by:

where factor 2 counts for spin degeneracy, q is electrical charge of carrier, h is Planck’s constant, is transmission spectrum coefficient, 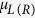is chemical potential of left (right) electrodes and is the Fermi distribution of left (right) electrode. In linear response regime, it is assumed that 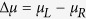and are infinitesimally small. As a result, equation (1) will be reduced to:

Electronic contribution to TE properties, which is including electrical conductance (), Seebeck’s coefficient () and electronic thermal conductance (), can be calculated by using the followings:

where is expressed as:

Phonon transmission spectrum is calculated based on parameterization of Stillinger-Weber⁴⁶ potential for MoS₂⁴⁷ as implemented in Quantum Wise ATK package. Phonon thermal conductance (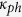) can be calculated as:

where is phonon transmission spectrum; and are Bose-Einstein distribution of the left and right electrodes, respectively; is temperature of left(right) electrode and is energy of phonon. In linear response regime, and equation (7) becomes:

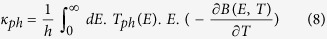It is worth mentioning that the phonon thermal conductance calculations in this paper are performed in the absence of any phonon decaying mechanisms. Hence, the calculations set the upper limit for phonon thermal conductance of pure MoS₂. In reality however, there would be a few mechanisms which tend to suppress phonon conduction such as rough surface, edge imperfectness, scattering centers, etc. ZT values calculated in this paper, therefore is the minimum of what actually can be achieved by these materials. TE figure of merit is calculated by using the above information:

Results and Discussion

Transmission spectrum characterizes the electrical behavior of the proposed devices. Electrical factors that affect TE figure of merit include electrical conductance (), electronic thermal conductance () and Seebeck’s coefficient (). These factors can be derived from transmission spectrum as described in the previous section. Transmission spectrums for monolayer and fewlayer MoS₂ in armchair and zigzag orientations are illustrated in Fig. 4. Fermi level for is located at . Further study of Fig. 4 indicates that as the number of layers increases from one to four layers, the band gap decreases from eV to eV which is in good agreement with previously reported values⁴,⁵,⁶. In addition, the amplitude of transmission spectrum coefficient increases as number of layers increases from one to four, indicating that each layer provides an independent channel to conduct carriers⁴⁸. Furthermore, zigzag orientation is found to have higher transmission coefficients in comparison with armchair. It is expected to be more conductive than armchair consequently.

Figure 4. Transmission spectra.

Transmission spectrum of (a) armchair-oriented and (b) zigzag-oriented for mono-, bi-, tri- and quadlayer MoS₂ calculated based on DFT-NEGF method. Band gap is increasing as number of layers decreases. Transmission coefficients are higher for fewlayer structures, suggesting that each layer provides a conductive channel for carriers.

In semiconducting materials, phonon thermal conductance () is several times larger than and outplays the impact of on TE figure of merit. ph of monolayer and fewlayer for armchair and zigzag orientations vs. temperature are illustrated in Fig. 5. As shown in Fig. 5, ph is almost independent of temperature. It is closely a constant in a wide range of temperatures (from 200 K to 500 K). In addition, zigzag orientation shows larger than armchair as was pointed out by Jiang³² due to the alignment of one vibrational mode in transport direction along zigzag orientation. These results also suggest that of both zigzag and armchair orientations increases as the number of layers increases. The rate of increase in is more in zigzag than in armchair orientation. Our results of for monolayer MoS₂ is in a good agreement with findings by Huang³⁵.

Figure 5. Phonon thermal conductance.

(a) 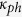vs. temperature for monolayer and fewlayer armchair- and zigzag-oriented MoS₂. (b) 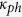vs. number of layers for armchair- and zigzag-oriented MoS₂ at T = 300k. for zigzag orientation shows higher values and greater rate of increase as number of layers increases from monolayer to quadlayer than those for armchair orientation.

From factors playing role in TE figure of merit, and follow the profile of transmission spectrum, i.e. as the Fermi level moves into valence or conduction bands, transmission increases, and hence, there are more carriers to be conducted both thermally and electrically. In contrast to and , it is typical for semiconductor materials that Seebeck’s coefficient () decreases as Fermi level moves into valence and conduction bands. Therefore and are competing with each other and their product in the form of 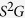, known as power factor, reaches its maximum at an optimum position of Fermi energy²⁷,³⁵.

ZT values of monolayer and fewlayer MoS₂ in armchair and zigzag orientations vs. Fermi level position at four temperatures are illustrated in Fig. 6. There are two main peaks in ZT, separated by a bandgap, corresponding to valence band and conduction band. Valence band maximum (VBM) and conduction band minimum (CBM) are specified in each plot by vertical dashed lines. In this study, TE figure of merit is referred to as ZT of n-doped or ZT of p-doped as Fermi level is approaching conduction band or valence band, respectively. It is shown in Fig. 6 that for all monolayer and fewlayer structures, ZT values of n-doped are higher than those of p-doped.

Figure 6. Thermoelectric figure of merit.

ZT for monolayer and fewlayer armchair- and zigzag-oriented MoS₂ vs. Fermi level position for four temperatures. Conduction band minimum (CBM) and valence band maximum (VBM) are shown by vertical dashed lines in each plot.

As temperature increases, amplitude of ZT also increases since ZT is proportional to the temperature. In addition, rising temperature broadens Fermi distribution. This broadening will populate states in energies higher than Fermi level, which were unpopulated in lower temperatures. These newly occupied states contribute to both electrical and thermal conduction. It means that electrical conductance increases in energies which has insignificant contribution to conduction in lower temperatures, resulting in broadening of ZT peaks vs. energy. Further study of Fig. 6 shows that profile of ZT broadens as number of layers increases for both armchair and zigzag orientations. This behavior can be attributed to the broadening of transmission spectra of both armchair and zigzag orientations as number of layer increases as illustrated in Fig. 4. Despite the increase in transmission coefficients from monolayer to quadlayer, ZT values tend to decrease as number of layers increases. This may be contrary to what is expected. One may expect that higher transmission coefficients is equivalent to more conductivity and hence higher ZT value. The reason for this behavior is due to suppression of out-of-plane vibrational mode in monolayer structures. As it can be seen from Fig. 6, ZT values undergo a sharp drop as structure changes from monolayer to bilayer for both orientations. This drop in ZT value is less pronounced when structure changes from bilayer to quadlayer. In addition, Fig. 6 suggests that ZT value of p-doped structures are smaller than those of n-doped for both orientations. This characteristic can be attributed to lower growth rate in transmission modes as Fermi level moves into valence band compared to when it moves into conduction band as illustrated in Fig. 4.

Peak values of ZT for monolayer and fewlayer armchair and zigzag orientations vs. temperature are shown in Fig. 7. As it was expected from equation (9), ZT is quite linear with temperature. ZT value is monotonously decreasing as number of layers increases. ZT value is larger than unity in n-doped armchair-oriented monolayer at . This structure has also the highest p-doped ZT value. Therefore, for both n-type and p-type legs in thermocouple, armchair-oriented monolayer MoS₂ is the best choice among all structures studied in this paper.

Figure 7. Maximum thermoelectric figure of merit.

Maximum ZT for p-doped and n-doped monolayer and fewlayer in both armchair and zigzag orientations vs. temperature.

As illustrated in Fig. 6, in order to take advantage of the highest ZT value possible, MoS₂ should be doped in order to shift Fermi level to the optimum energy of peak value of ZT profile. Substitutional doping of TMD samples has been observed experimentally under exposure to 80 keV electron beam irradiation⁴⁹. Also, a first principal study of effect of this doping approach for transition metal dopants as well as non-metal dopants is reported⁵⁰. In order to examine the TE current of MoS₂, we have simulated a monolayer MoS₂ in armchair orientation doped with various dopant species. We followed the same substitutional approach for doping our structure. Transition metal atoms (Re, Ru and Ta) are used as the replacing dopants for Molybdenum, and non-transition metal atoms (As, Br, Cl and P) are used for Sulphur⁵¹. In order to screen out the perturbation caused by doping properly, only one dopant atom was inserted in central region of device. A temperature gradient has been set across the nanoribbon by fixing the temperature of right electrode to and changing temperature of left electrode from to (for device configuration, see Fig. 3). Results are shown in Fig. 8. TE current of monolayer armchair MoS₂ shows strong dependence on the type of dopant atom. While Arsenic does not show any effect on thermoelectric current, P and Ta showed a similar boost to current. For n-type dopant, Ru exhibits the best current boost in comparison with other dopants. It should be noted that doping in MoS₂ monolayer at nanoscale will induce device to device performance variation⁵².

Figure 8. Thermoelectric current of doped armchair-oriented monolayer MoS₂.

(a) Thermoelectric current of armchair-oriented monolayer MoS₂ substitutionally doped with various dopants vs. temperature gradient across it. Transition metal dopants replace Molybdenum and non-metal dopants replace Sulfur. (b) Thermoelectric current of Si thin films doped p-type for different film thicknesses vs. temperature gradient across them.

These results are compared with TE current of Si thin film doped with acceptor (B) concentration of with various film thicknesses (also shown in Fig. 8). For Si thin film with film thickness of , TE current density reaches 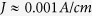at . In comparison, monolayer Ru-doped MoS₂ has TE current density at 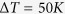, more than two orders of magnitude larger. Decreasing thickness of Si film makes them more resistive and TE current decreases consequently, as shown in Fig.8. Superiority of MoS₂-based thermocouples will be more dramatic if we compare its TE performance with those of thinner Si films, especially -thick Si films which is almost the same thickness of monolayer MoS₂.

Thermocouples, as was mentioned in previous section, are made of both p-type and n-type semiconductors. In order to compare the performance of monolayer MoS₂-based and Si-based thermocouples, TE current of both of these materials is illustrated in Fig. 9. For Si-based thermocouples, p-doped (B) and n-doped (As) films with thickness of and with doping concentration of is used. For monolayer MoS₂ TE conversion, Ru-doped and P-doped are the best n-type and p-type structures, respectively. These two structures are chosen to construct the thermocouple based on monolayer MoS₂. Fig. 9 shows that thermocouples based on monolayer MoS₂ are far more superior to thermocouples based on Si thin films.

Figure 9. Si thin film vs. armchair-oriented monolayer MoS₂.

Thermoelectric current of thermoelectric generators based on Si thin film in comparison with that of based on doped monolayer MoS₂.

Conclusion

In summary, we proposed a TE generator based on monolayer armchair-oriented MoS₂. In order to find the optimum structure for the proposed thermocouple, first-principle simulation has been performed to calculate TE figure of merit, ZT, for monolayer and fewlayer MoS₂ in armchair and zigzag orientations. Results indicate that by increasing number of layers, ZT value tends to decrease. This behavior is in contrast to the fact that fewlayer MoS₂ is more conductive than monolayer in both directions and can be explained by suppression of out-of-plane vibrational modes in monolayer structures. Among all structures studied, monolayer armchair-oriented MoS₂ is shown to have the highest ZT value as both n-type and p-type semiconducting legs. Moreover, compared to Si thin films, TE current of monolayer MoS₂ is two orders of magnitude higher.

Additional Information

How to cite this article: Arab, A. and Li, Q. Anisotropic thermoelectric behavior in armchair and zigzag mono- and fewlayer MoS₂ in thermoelectric generator applications. Sci. Rep. 5, 13706; doi: 10.1038/srep13706 (2015).