Digital Single-Cell Analysis of Plant Organ Development Using 3DCellAtlas

A tool was developed to extract biologically relevant information from quantitative 3D image data, allowing the relationship between diverse regulatory networks and 3D organ growth to be revealed.

Abstract

Diverse molecular networks underlying plant growth and development are rapidly being uncovered. Integrating these data into the spatial and temporal context of dynamic organ growth remains a technical challenge. We developed 3DCellAtlas, an integrative computational pipeline that semiautomatically identifies cell types and quantifies both 3D cellular anisotropy and reporter abundance at single-cell resolution across whole plant organs. Cell identification is no less than 97.8% accurate and does not require transgenic lineage markers or reference atlases. Cell positions within organs are defined using an internal indexing system generating cellular level organ atlases where data from multiple samples can be integrated. Using this approach, we quantified the organ-wide cell-type-specific 3D cellular anisotropy driving Arabidopsis thaliana hypocotyl elongation. The impact ethylene has on hypocotyl 3D cell anisotropy identified the preferential growth of endodermis in response to this hormone. The spatiotemporal dynamics of the endogenous DELLA protein RGA, expansin gene EXPA3, and cell expansion was quantified within distinct cell types of Arabidopsis roots. A significant regulatory relationship between RGA, EXPA3, and growth was present in the epidermis and endodermis. The use of single-cell analyses of plant development enables the dynamics of diverse regulatory networks to be integrated with 3D organ growth.

INTRODUCTION

Advances in confocal imaging techniques have enabled the acquisition of 3D (Moreno et al., 2006; Truernit et al., 2008; Bassel et al., 2014; Yoshida et al., 2014) and 4D data sets (Fernandez et al., 2010; Maizel et al., 2011; Sena et al., 2011), such that the extent and dynamics of cellular structures in plants can be captured. Key advantages to higher dimension imaging include the more accurate and complete representation of the biological system being analyzed. This is required for the inclusive understanding of plant growth and can provide insight not possible using 2D imaging (Fernandez et al., 2010; Bassel et al., 2014; Yoshida et al., 2014).

The comprehensive quantification of cellular growth is a central objective in the analysis of image data sets, and procedures capable of quantifying cell elongation using 2D images have been developed (Federici et al., 2012; French et al., 2012). These approaches are limited to the select number of cells being imaged and are susceptible to measurement errors due to oblique optical sectioning. A full 3D representation of cellular structure is required both for accurate quantitative measurement and comprehensive representation (Fernandez et al., 2010).

The ability to identify unique cell types from 3D images creates the possibility to perform virtual cell-type-specific analyses. This can be accomplished through the introduction of distinct cell lineage markers (Long et al., 2009; Federici et al., 2012) or the creation of user-defined cellular reference lookup (Busch et al., 2012; Schmidt et al., 2014). The ability to extend these approaches to different organs and contexts relies upon additional user input to define either novel reference atlases or to introduce lineage markers into additional genetic backgrounds. Neither of these approaches provides complete cell shape information.

The molecular networks underlying plant growth and development are being uncovered by the efforts of the research community through large-scale biological interaction network data at multiple scales (Schauer and Fernie, 2006; Brady et al., 2007; Braun et al., 2011; Bassel et al., 2012; Rhee and Mutwil, 2014). However, the ability to quantify the dynamic spatial and temporal relationships between these components and their interactions within the context of multicellular organ development remains limited.

In order to investigate whole-organ growth and integrate regulatory networks at single-cell resolution, we developed 3DCellAtlas. This rapid and modular computational approach to generate quantitative 3D cellular atlases of plant organ growth simultaneously identifies cell types and quantifies 3D cellular anisotropy using the intrinsic geometric properties of distinct cell types. This is achieved with greater accuracy than other published approaches and does not require user-defined reference atlases or cell lineage markers. This approach may be applied directly to diverse radially symmetric plant organs. The ability to quantify reporter abundance within individual cells in 3D facilitates cell-type and position-specific analyses to establish the relationship between regulatory network components and organ growth at a cell-type-specific resolution. The implementation of 3DCellAtlas within the existing publicly available software MorphoGraphX (www.MorphoGraphX.org) makes this procedure easily accessible and allows quantitative outputs to be rapidly visualized in situ within the context of the cellular structure of 3D organs.

The development of this methodology, which we used in the analysis of Arabidopsis thaliana, enables whole 3D organ growth patterns at single-cell resolution to be investigated, and it allows the simultaneous integration of regulatory components within these individual cells.

RESULTS AND DISCUSSION

Primary Image Acquisition and 3D Segmentation

Cleared samples were imaged using confocal microscopy as previously described (Truernit et al., 2008; Bassel et al., 2014) and z-stacks opened within MorphoGraphX (www.MorphoGraphX.org) (Kierzkowski et al., 2012) (Figures 1 and 2A). A curved line, termed a Bezier line, was placed through the geometric center of the organ (Figure 1B; Supplemental Movie 1), and cells were segmented using ITK Autoseeded Watershed, an image processing algorithm (Figure 2C) (Supplemental Figure 1) (Bassel et al., 2014; Yoshida et al., 2014).

Figure 1.

Workflow for the Generation of Quantitative 3D Cellular Atlases.

Figure 2.

Label-Free Geometry-Based Identification of Cell Types from 3D Images.

(A) Embryonic Arabidopsis axis z-stack maximum intensity project.

(B) Alignment of a Bezier curve (white line) through the axis in (A).

(C) 3D segmented axis in (A) with different colors indicating unique segments.

(D) The mesh describing the surface of the organ is represented in white.

(E) A section of the hypocotyl of the embryo in (A) where the cells are segmented (in blue) and the white line indicates the location of the Bezier curve. The surface mesh is shown in light red surrounding the organ axis. Bar = 30 μm.

(F) Hypocotyl cross section showing alignment of axes in 2D and a single cell in 3D. The location of the Bezier is represented by a pink dot.

(G) and (H) Aligned local axes within an individual cortical cell (G) and across the epidermal cells (H) of the hypocotyl from (E).

(I) Cells false colored by their circumferential length in the hypocotyl section in (E) with the scale in microns.

(J) Clustering of cell types based on their circumferential length and scaled radial distance from the Bezier.

(K) Annotation of the cell clusters in (J).

(L) and (M) Identified cell types in the Arabidopsis hypocotyl given unique colors in longitudinal and cross section. Bars = 50 μm.

(N) and (O) Identified cell types in the Arabidopsis root in a virtual longitudinal section before (N) and after (O) the assignment of the columella. Bar = 20 μm.

(P) Mature root in a virtual cross section. Bar = 20 μm.

(Q) to (S) Identified cell types in the Arabidopsis embryo axis.

(Q) Virtual cross section. Bar = 10 μm.

(R) and (S) Longitudinal section before the assignment of the columella (R) and after the assignment of the columella (S). Bar = 20 μm.

(T) Longitudinal section of a poppy hypocotyl. Bar = 50 μm.

(U) Cross section of a poppy hypocotyl. Bar = 50 μm.

Local Axis Alignment

The cells of many radially symmetric plant organs have an approximately cuboid geometry (Bassel et al., 2014), such that three principle axes describe each of their three dimensions of anisotropic growth. 3DCellAtlas uses a combination of a central Bezier curve and a mesh defining the surface of the organ to align these local axes within the natural coordinate system for the organ (Figures 2B and 2E; Supplemental Figure 2) (Hejnowicz, 1984). The use of a Bezier curve better describes the contours of plant organs than a straight line (Bassel et al., 2014) owing to the curved nature of their growth habit.

Meshes describing cell surfaces were generated by segmenting the stack in 3D using the ITK Morphological watershed filter and then using the marching cubes algorithm (Lorensen and Cline, 1987). An additional mesh describing the overall surface of the organ was also extracted (Figures 2D and 2E; Supplemental Figure 1). Cell dimensions were determined using the directions defined by the coordinate system, with the three principal directions of each cell, representing the longitudinal, radial, and circumferential axes, measured from the centroid position within each individual cell (Figures 2F to 2H; see Methods). The length of each of these axes represents the simplified 3D dimensions of each cell.

Non-strictly symmetric features, for example, the circumferential flaring of the Arabidopsis embryo (Supplemental Figure 3) or tapering of roots and embryos (Supplemental Figure 4), were incorporated through linear interpolation of the Bezier and surface axes (Methods), enhancing the accuracy of the axis alignment.

Geometry-Based Identification of Cell Types

Different cell types in plant organs frequently have unique shapes, an intrinsic property that this method uses to differentiate them without additional information. For example, the hypocotyl of the mature Arabidopsis embryo shows cell-type specificity with respect to circumferential cell lengths, with greater lengths observed in the cortical cells relative to the epidermis and endodermis (Figure 2I).

By plotting a distinguishing linear dimension of cell geometry on one axis, and the scaled radial distance of the cell from the central Bezier on the other axis, clusters of distinct cell types are produced on 2D heat map plots (Figure 2J; Supplemental Figure 5). Selection of these cell-type-specific clusters within a graphical user interface (GUI) implemented in 3DCellAtlas enables user-defined annotations of these clusters to demarcate distinct cell types. Within the GUI, clusters in the 2D heat map are seeded with clicks and annotated by the user with numbers. These numbers represent annotation labels for selected cell types and are stored within the “parents” variable for each segmented cell in MorphoGraphX. Diverse organs may have different geometric features in their cells that may represent unique geometric properties of a given cell type that can be used to uniquely identify it. Users may select any of the three principal directions to generate 2D heat map plots and generate distinct clusters of cell types (Supplemental Figure 5).

Following the user-defined assignment of unique cell-type numbers to clusters in the 2D GUI heat map, the cells of 3D segmented organs in the active window are immediately false colored using distinct colors for each assigned parent label or cell type. By painting unique selected cell types with different colors, users can evaluate the quality of the cluster selection that has been performed. If there are inaccuracies, the user can return to the cell cluster selection GUI to iteratively adjust the locations of the seeds and enhance the accuracy with which distinct cell types are identified. This real-time iterative adjustment of cluster seeding provides users the opportunity to rapidly increase cellular annotation accuracy. Cells that are not segmented properly represent inaccurate geometric representations and cannot be accurately identified owing to their geometric irregularities. They should as well be disregarded from future statistical analyses for the sake of their geometric inaccuracies.

In addition to the segmentation of cells, air spaces between cells (Cloetens et al., 2006) are also captured. These segments do not represent genuine cellular data points, but nonetheless require accurate identification and annotation to facilitate their removal to avoid confounding further analyses. Air spaces typically have shorter dimensions and are generally located between adjacent cell layers within the 2D heat map plots displaying cell geometries. These can be selected within the GUI and assigned a unique parent label enabling their removal from future analyses (Figure 2K; Supplemental Figure 5).

This approach works on diverse radially symmetric organs from Arabidopsis, including hypocotyls (Figures 2L and 2M), roots (Figures 2N to 2P), and mature embryo axes (Figures 2Q to 2S). While these examples are provided using Arabidopsis organs, this method is applicable to any radially symmetric organ, for example, a poppy (Papaver rhoeas) hypocotyl (Figures 2T and 2U).

Assignment of the Columella

Up to this stage, the annotation of cells in organs started from the first cortical cell onwards, leaving the columella in roots and embryo radicles unannotated (Figures 2N and 2R). To complete the assignment of an identity to these cells, a single click of the “assign columella” annotates the unassigned cells (Figures 2O and 2S). The columella is annotated as those cells not already having been assigned a label, and the surrounding lateral root cap identified as separate from the columella based on these cells having a deficiency in shared surface area with their adjacent cells (see Methods).

Topological Identification of Misannotated Cells

Radially symmetric plant organs by definition consist of concentric rings of cells. The physical associations between these adjacent cell types are therefore conserved through organs having this topology. We used this feature to automatically identify cells which were misannotated using the initial geometry-based cell identification.

To achieve this, physical cellular interaction networks between cells from whole segmented organs were generated by identifying shared triangles between the surface meshes of adjacent cells (Figures 3A to 3C; Supplemental Figure 6; see Methods) (Yoshida et al., 2014). Cellular connectivity graphs were annotated by cell type using the geometry-based cell identification method described above. Topological validation using the cellular interaction network data was performed to identify misannotated cells (Long et al., 2008). Using the process “topological check,” the frequencies of edges between cell types were established, and low-frequency or “impossible” edges in the graph were identified (Figure 3D). These edges highlight the presence of a misannotated cell that can then be identified and are selected as part of the process (Figures 3E and 3F). This method is effective at highlighting the presence of misannotated cells, while cells adjacent to errors can also become highlighted given their association to incorrect cells (Figure 3F). The manual correction of these annotation errors facilitates the correct labeling of all cells within segmented organs in the minority of instances where the semiautomated method fails.

Figure 3.

Topological Identification and Correction of Misannotated Cells.

(A) Surface rendering of radial section of segmented embryonic hypocotyl cells. Bar = 10 μm.

(B) Close-up of (A) showing the mesh defining the cell surfaces.

(C) Cellular connectivity network depicting the cells in (A) and their associations in 2D. Distinct cell types in the network are given unique colors.

(D) Schematic cellular connectivity network illustrating the identification of impossible edges. Unique cell types are illustrated using the same color scheme for cell types used in (C). A misannotated cell is identified based on the “impossible” association between the orange endodermal cell and the cyan outer cortical cell. Impossible edges are colored red in this schematic.

(E) Embryonic Arabidopsis hypocotyl following the assignment of cell types.

(F) Output of the topological check identifying misannotated cells.

(G) Correction of misannotated endodermal cells by the “check vasculature” process.

An automatic method to correct cell annotation errors was also developed. A common error is the misannotation of endodermis as vasculature given the close proximity of these two cell types in the 2D heat maps. Using the “examine vasculature” process, endodermal cells that have been incorrectly annotated are automatically identified based on their similar distance and geometry to correctly annotated endodermal cells, as identified using topological validation. The labels of these cells are adjusted accordingly, which increases the accuracy of cellular annotations for this cell type (Figure 3G).

This annotation method combined with topological correction has a minimum of 98.2% accuracy for Arabidopsis hypocotyls, mature embryos, and roots (Table 1) and was accurate to a minimum of 97.8% in poppy hypocotyls.

Table 1. Accuracy of Geometry-Based Cell-Type Identification within 3D Images of Radially Symmetric Plant Organs.

	Epidermis		Outer Cortex		Inner Cortex		Endodermis
	No. of Cells Analyzed	Accuracy	No. of Cells Analyzed	Accuracy	No. of Cells Analyzed	Accuracy	No. of Cells Analyzed	Accuracy before “Examine Vasculature”	Endodermis after “Examine Vasculature”
Arabidopsis root	399 ± 22	98.9 ± 0.2	180 ± 11	98.4 ± 0.2	N/A	N/A	213 ± 15	90.5 ± 0.7	98.2 ± 0.11
Arabidopsis hypocotyl	291 ± 65	99.5 ± 0.9*	138 ± 28	98.9 ± 0.5	74 ± 25	100 ± 0	86 ± 25	97.7 ± 4.0	99.4 ± 1.0
Arabidopsis mature embryo axis	837 ± 43	99.7 ± 0.1	394 ± 21	99.4 ± 0.7	203 ± 25	99.3 ± 0.2	239 ± 48	92.9 ± 2.3	98.7 ± 0.8
Poppy hypocotyl	584 ± 230	99.9 ± 0.1	412 ± 18	99.1 ± 0.8	228 ± 30	98.7 ± 1.9	179 ± 28	90.8 ± 4.9	97.8 ± 3.4

The number of cells of each cell type present in the organs analyzed is indicated along with the standard deviation across the three samples analyzed. Accuracy is represented as the percentage of cells whose identity was correctly identified from the total number of cells for a given cell type in a given organ. The variation is the standard deviation of the percentage accuracy for each of the three samples per organ analyzed. The percentage accuracy both before and after running the “examine vasculature” process in the endodermis is indicated in the final two columns. A total of three samples for each organ was analyzed to generate these accuracy count data. Asterisk indicates that the upper limit of the variation in accuracy counts was truncated at 100%. N/A, not applicable.

A Cortical Reference System for Comparative Analyses

In order to assign individual cells within organs to an indexed system, an internal cellular referencing system was established. This enables direct comparison of organ properties between different organs at different stages of development at the resolution of individual cells. The cortical cells of roots, hypocotyls, and embryos show the greatest geometric uniformity (Bassel et al., 2014) and are relatively evenly distributed across the circumferential arrangement of plant organs. Cortical cells were therefore chosen to establish an intrinsic positional referencing system.

To establish the cellular referencing system, the first cortical cell in a sample is selected by the user (Figure 4A), which assigns this cell a position number of 1. The “assign cortical cells” process uses this reference point to index all cells in the organ. Sequential cells following the same linear file of cortical cells along the axis are assigned incremental position numbers, and these positional values were projected radially across the organ. All other cells within the same longitudinal position are given the same cell number position, along with other cell types that lay within the window of this cell position (Figure 4B). In this way, all cells within the organ are assigned a cell type and a cell position. These quantitative values can be visualized by false coloring axes within the “display cell data” process of the 3DCellAtlas plug-in and selecting “associated cortical cell.” This process also enables the volume (Figure 4C), surface area (Figure 4D), longitudinal cell length (Figure 4E), radial cell length (Figure 4F), and circumferential cell length (Figure 4G) of individual cells to be visualized in situ through the false coloring of segmented organs.

Figure 4.

Internal Reference System and Whole Organ Quantification of 3D Cell Geometry.

(A) Longitudinal section of a segmented mature Arabidopsis root with the first cortical cell selected (in red) used to align local cell position reference system. Bar = 20 μm.

(B) False coloring of all cell types along the length of the root, which have been assigned an associated cortical cell position based on their longitudinal position along the Bezier curve. The scale indicates cortical cell position, with cells in the columella assigned a position of 0.

(C) Cell volumes along the length of the root false colored using cubic microns on the scale.

(D) Cell surface area false colored on the axis using square microns on the scale.

(E) Cell length parallel the Bezier curve.

(F) Radial cell length emanating from the center of the organ.

(G) Cell circumferential length going around the radial orientation of the organ.

Quantitative data from 3DCellAtlas can be saved and loaded from within the plug-in using the “save cell data” and “load cell data” processes, respectively. Saved text files contain cell geometric data including cell volume, surface area, longitudinal length, radial length, and circumferential length, the cell position within the internal referencing system, and the parent labels that define cell identity. The locations where seeds were placed within 2D heat map GUIs to select cell type clusters are also saved and can be loaded from saved files, which allows modifications to a previous work flow to be made. Exported text files from multiple samples or time points enable the statistical analysis of these quantitative cellular geometric data.

Single-Cell 3D Phenotyping of Hypocotyl Growth

Studies have previously examined the elongation of epidermal cells during hypocotyl growth in Arabidopsis (Gendreau et al., 1997), yet the growth of cells within this multicellular organ and their 3D anisotropy have yet to be examined. We sought to quantify the organ-wide cell-type-specific 3D anisotropy driving seedling establishment in the Arabidopsis hypocotyl using the cellular geometric data generated by 3DCellAtlas. The growth of the hypocotyl up to 4 d of development does not involve significant cell divisions (Gendreau et al., 1997), enabling multiple fixed samples at different stages to be used in statistical analyses of 3D growth. The hypocotyl within the mature embryo axis was used as the baseline unexpanded state, and cell geometries were compared with seedlings grown for 4 d.

The use of the cortical referencing system defined cell positions within samples, enabling equivalent individual cells from different samples to be quantitatively compared. A total of four samples for each the unexpanded (embryonic hypocotyl) and expanded states (4 d hypocotyl) were collected. Statistical analyses were performed on these pooled data (see Methods), whereby output files from these multiple samples were compiled into a single directory and analyzed at cell-type and position-specific resolution using the “3D cell growth analysis” process (Figure 5). Outputs of the 3D cell growth analysis process include text files that can be used to plot the mean and confidence intervals for data on a cell-type and position-specific basis (Supplemental Figure 7). Importing these text files as a heat map in MorphoGraphX allows for the false coloring of a 3D segmented organ mesh and the in situ visualization of differences in cell size within the cellular context of the organ. The data presented in Figure 5 represent the false-colored means of these analyses.

Figure 5.

Single-Cell 3D Phenotyping at Cell-Type and Position-Specific Resolution in Arabidopsis Hypocotyls.

(A) to (E) 3D quantification of a wild-type Arabidopsis hypocotyl grown in the light for 4 d with false coloring indicating mean relative changes in cell volume (A), cell surface area (B), longitudinal length (C), radial length (D), and circumferential length (E). Scales represent the ratio of growth above the embryo hypocotyl control.

(F) to (J) 3D quantification of a wild-type Arabidopsis hypocotyl grown in the light and in the presence of 30 μM ACC for 4 d with false coloring indicating mean relative changes in cell volume (F), cell surface area (G), longitudinal length (H), radial length (I), and circumferential length (J). Scales represent the ratio of growth above the embryo hypocotyl control.

Bars in (A) and (F) = 50 μm.

(K) Ratio of cell volume of ACC-treated hypocotyls over controls.

(L) Ratio of cell surface area of ACC-treated hypocotyls over controls.

(M) Ratio of longitudinal cell length of ACC-treated hypocotyls over controls.

(N) Ratio of radial cell length of ACC-treated hypocotyls over controls.

(O) Ratio of circumferential cell length of ACC-treated hypocotyls over controls.

(P) and (Q) Longitudinal E-factors in light-grown (P) and ACC-treated (Q) hypocotyls.

(R) and (S) Radial E-factors in light-grown (R) and ACC-treated (S) hypocotyls.

(T) and (U) Circumferential E-factors in light-grown (T) and ACC-treated (U) hypocotyls. Scales indicate absolute E-factor values.

During the elongation of hypocotyls in the light, relative volumetric cell expansion is greatest in the inner cell layers and decreases progressively toward outer cell layers (Figure 5A). A gradient of expansion of high to low growth was observed from the base of the hypocotyl moving upwards in the epidermis and outer cortical cells. A similar gradient of increase in relative surface area was observed in both cortical cell layers and to a lesser extent in the epidermis (Figure 5B). The endodermis underwent the greatest increase in surface area growth.

Relative longitudinal cell expansion was greatest at the base of the hypocotyl as previously reported (Gendreau et al., 1997) and evenly distributed across cell types (Figure 5C). Radial cell elongation was greatest in the cortical cells of light-grown hypocotyls and significantly less in the epidermis and endodermis (Figure 5D). Conversely, circumferential growth was greatest in the epidermis and endodermis and much less in the cortex (Figure 5E). A gradient of increasing circumferential growth was observed in the endodermis and epidermis moving up the hypocotyl.

The calculation of organ-wide 3D cell anisotropy driving hypocotyl elongation in the light confirmed the previous observation that there is a gradient of decreasing cell elongation moving up the hypocotyl (Gendreau et al., 1997). It has also provided information as to the anisotropies of the epidermis and inner cell types, including both cortical cell layers and endodermis during hypocotyl growth. These data collectively demonstrate the cortex to be growing more in the radial direction and possibly compressing the epidermis and endodermis, respectively.

Ethylene Modulates Hypocotyl 3D Cellular Anisotropy

A previous study reported that the treatment of light grown hypocotyls with the ethylene precursor 1-aminocyclopropane-1-carboxylic acid (ACC) leads to increased epidermal cell elongation in Arabidopsis hypocotyls (Smalle et al., 1997). To quantify the influence of this hormone treatment on the organ-wide cell-type-specific 3D anisotropy of hypocotyl growth in the light, we subjected 4-d-old ACC-treated light grown hypocotyls to quantitative cellular phenotyping using 3DCellAtlas (Figures 5F to 5J).

The maximum relative increase in cell volume doubled in hypocotyls treated with ACC relative to control samples (Figures 5A and 5F; Supplemental Figure 8). This supports the finding that ethylene inhibits the light-mediated limitation of cellular expansion in Arabidopsis hypocotyls.

The pattern of 3D cell anisotropy in ACC-treated hypocotyls also differed from light controls. To visualize these differences, false-colored axes showing the ratio of ACC cell growth over that in the wild type were generated (Figures 5K to 5O).

The overall expansion of the inner cell layers in ACC-treated hypocotyls was greatest and decreased progressively toward the outer cell layers (Figure 5K). Both cell expansion and cell elongation (Figure 5M) were greater in the lower section of the hypocotyl in ACC-treated samples than in light grown controls, particularly in the endodermis. These data indicate ethylene-mediated enhanced cell expansion in hypocotyls to be greatest both in the inner cell layers and toward the base of this organ.

The radial expansion of endodermal cells was up to 50% greater in ACC-treated samples and decreased progressively toward the outer cell layers with the epidermis showing little difference with control hypocotyls (Figures 5I and 5N). The circumferential growth of the endodermis was very similar between treatment and control samples, with the outer cortex showing the greatest increase growth in this direction in ACC samples (Figure 5O).

Collectively, these data indicate the growth response of the endodermis to be most affected by ACC treatment in light grown hypocotyls. The observed anisotropic growth in this cell type could either be due to enhanced ethylene response within this cell type, an intrinsic anisotropy of this tissue, or to the loosening of the neighboring cortical cell wall, leading to radial expansion.

Visualizing 3D Cellular Anisotropy

Patterns of dominant cell anisotropy in 3D were quantified by calculating the elongation factors (E-factors) of cell expansion in each of the three principal directions. E-factors represent the ratio of cell growth in a given direction divided by the sum of elongation in all three directions (Methods). In this way, the relative elongation in a given direction relative to total elongation may be determined.

E-factors for each light-grown and ACC-treated hypocotyl were calculated using the “3D cell growth analysis” process. False coloring of the active 3D segmented sample in the MorphoGraphX window with each of the three principal E-factor directions can be achieved by importing the text files containing these data as a heat map.

Anisotropy in the longitudinal direction was strikingly similar between control and treated hypocotyls (Figures 5P and 5Q), with only slightly less extension in the lower epidermis and outer cortex in ACC-treated samples. This indicates that despite ACC leading to larger and thicker hypocotyls, this treatment does not influence longitudinal anisotropy relative to total cell elongation along all three principal directions of growth.

Radial anisotropy was slightly greater in the lower cortical cells of ACC-treated samples than corresponding controls and much greater in the endodermal cells (Figures 5R and 5S). This calculation reflects the greater relative radial expansion of the endodermis in ACC-treated samples relative to untreated light grown counterparts (Figures 5D and 5I).

The pattern of circumferential anisotropy between light-grown and ACC-treated hypocotyls was similar with the exception of greater growth in this direction within the endodermis of light-grown samples (Figures 5T and 5U). This observation is also not intuitive given the strong differences in the pattern of relative circumferential extension between each light-grown and ACC-treated hypocotyls (Figures 5E and 5J).

These data collectively demonstrate the anisotropic growth of the endodermis, and to a limited extent the epidermis, to be differentially regulated by the ethylene signaling pathway. ACC application increases radial anisotropy of the endodermis while decreasing circumferential elongation according to these observations. These analyses are aided by the visualization of organ-wide cell-type-specific cellular anisotropy using E-factors so that unintuitive patterns of growth can be revealed.

Collectively, these analyses demonstrate the endodermis to be a cellular site of preferential growth in response to ethylene in Arabidopsis hypocotyls and specifically its anisotropic growth in the radial and circumferential directions.

Quantification of Reporter Abundance within Individual Cells and Relationship with 3D Growth

Multichannel confocal imaging enables both the cellular structure and abundance of reporter constructs to be captured simultaneously. Following the 3D segmentation of plant cells, the total abundance of signal within the defined boundaries of individual cells can be quantified (Figures 6A to 6D) (Yoshida et al., 2011). The quantification of reporter abundance within individual cells together with cell position, identity, and 3D anisotropy enables single-cell multidimensional imaging using 3DCellAtlas. Quantification of reporter abundance in 3D is more accurate than that in 2D, which may be subject to errors due to incomplete imaging of cells and partial measurements depending on the plane that is imaged.

Figure 6.

Multidimensional Quantification of Cell Size, DELLA Protein Abundance, and Expansin Promoter Activity in the Mature Arabidopsis Root.

(A) Surface rendering of segmented embryonic cortical cells.

(B) 3D capture of GUS reporter activity by collection of reflectance of crystals generated following GUS assays using 5-bromo-4-chloro-3-indolyl-β-d-glucuronic acid as a substrate.

(C) Encapsulation of GUS activity within individual 3D segmented cells.

(D) False coloring of the total concentration of GUS reporter activity within individual cells in 3D in relative units.

(E) Concentration of the endogenous RGA protein within individual cells types at specific cell positions along the mature Arabidopsis root.

(F) Cell type and position specific activity of the EXPA3 promoter along the length of the mature Arabidopsis root. The scales in (E) and (F) are frequency normalized to the total amount of reporter signal within each sample.

(G) Plot of average RGA protein abundance, EXPA3 promoter activity, and average cell volume in the root epidermis by cortical cell position.

(H) Same as (G) in root cortical cells.

(I) Same as (G) in the root endodermis. Reporter values in (G) to (I) are frequency normalized to illustrate relative abundances.

Spatial Distribution of Endogenous DELLA Protein Concentration during Root Growth

DELLA proteins are well characterized repressors of cell growth (Harberd et al., 2009). The selective proteolysis of DELLA proteins following the stimulus for a cell to grow, including the response to the hormone gibberellic acid (GA), leads to the repression of this repressor and a reversible growth switch (Harberd et al., 2009). While the repressive function of DELLAs is well characterized on a biochemical level, less is known about the spatial and temporal regulation of these endogenous proteins in relation to organ development.

We sought to explore the relationship between the cell-type-specific abundance of the DELLA protein RGA (REPRESSOR OF ga1-3) and cell expansion patterns during Arabidopsis root development to understand how the abundance of this growth repressor relates to observed growth. We generated a RGA:RGA-GUS (β-glucuronidase) translational fusion that could be quantified within the context of individual cells across growing roots. The total reflectance of GUS crystals formed following GUS staining (Truernit et al., 2008; Bassel et al., 2014) was used to identify the relative concentration of reporter within individual cells of the Arabidopsis root meristem.

The concentration (volume normalized abundance) of the endogenous RGA protein was false colored onto a 3D segmented root (Figure 6E) to visualize its cell-type-specific distribution. The relative abundance of the RGA protein reporter shows successive peaks emanating from the tip of the root, with that in the epidermis being closest to the quiescent center, followed by an intermediately positioned peak in the cortex and a distal protein abundance peak in the endodermis. These data were plotted together with changes in cell volume for each cell type (Figures 6G to 6I). Reporter data were frequency normalized for comparative purposes in these graphs to explore the cell-type-specific relationships between these components. The average volumes for each cell type at defined positions were calculated as described for the hypocotyl. Absolute volumetric cell expansion increased progressively along the length of the root tip, while the observed decrease in endodermal cell volume can be accounted for by the enhanced cell division rate in this cell type.

Peaks of RGA protein concentration do not relate to the progressive expansion of cells along the length of the root longitudinal axis. The relationship between RGA protein concentration and cell volume across the different cell types of the root was established statistically using linear regression (Table 2). The regression analysis revealed no evidence of a significant relationship (P value > 0.05) between RGA protein concentration and change in cell volume for any of the cell types examined.

Table 2. Output of Linear Regression between RGA Protein Concentration and EXPA3 Promoter Activity and Cell Volume across Different Cell Types of the Expanding Arabidopsis Root.

	Coefficient		se		t-Value		P Value
Cell Type	RGA and Cell Vol.	EXPA3 and Cell Vol.	RGA and Cell Vol.	EXPA3 and Cell Vol.	RGA and Cell Vol.	EXPA3 and Cell Vol.	RGA and Cell Vol.	EXPA3 and Cell Vol.
Epidermis	−0.00575	0.10873	0.023	0.013	−0.242	8.482	0.809	3.71·10−16
Cortex	0.00512	0.07099	0.012	0.012	0.426	5.714	0.671	4.88·10−8
Endodermis	0.00487	0.14115	0.018	0.0164	0.278	8.614	0.781	2.77·10−15

Roots were imaged and both cell geometric data and quantitative protein concentration used to fit linear models to explain these quantitative relationships. A P value < 0.05 indicates a significant relationship.

Integration of Endogenous DELLA Protein Abundance with Downstream Expansin Expression and Cell Growth

One proposed mechanism by which DELLAs limit cell expansion is through the inhibition of expansin gene expression (Cao et al., 2006). Expansins are a well characterized class of cell wall protein that promotes the loosening of cell walls and enable cell expansion (Cosgrove, 2005). EXPANSIN-A3 (EXPA3) is expressed during Arabidopsis root development, and expression of this gene is increased following GA application in the GA-deficient background ga1-5 (Goda et al., 2008), suggesting transcription of this gene and activity of the upstream promoter is regulated by DELLA proteins. Using the multidimensional imaging approach provided by 3DCellAtlas, we examined the spatiotemporal relationship between the abundance of the endogenous RGA protein, activity of the EXPA3 promoter, and cell expansion in a growing Arabidopsis root.

The activity of the EXPA3 promoter increases progressively along the length of the root in the epidermis, cortex, and endodermis in a roughly similar pattern to cell volume increase (Figures 6F to 6I). Using linear regression across the different cell types for each EXPA3 promoter activity and cell volume, a significant positive relationship between the activity of this promoter and cell expansion is observed in all cell types of the root (P value < 0.05) (Table 2).

To determine whether a significant relationship between the RGA protein and EXPA3 promoter activity is present, we performed a linear regression comparing the means of each of these components at defined cell positions across distinct cell types. The R² values and P values from this analysis are given in Table 3. There is evidence of a significant relationship for the epidermis and endodermis (P = 0.014 and P = 0.044, respectively), but not in the cortex. In both cases, the relevant regression coefficient was negative, suggesting a weakly significant negative relationship between RGA and EXPA3 as expected based on DELLA regulation of expansins.

Table 3. Output of the Linear Regression between RGA Protein Abundance and EXPA3 Promoter Activity across Different Cell Types of the Arabidopsis Root.

Cell Type	R2	P Value
Epidermis	0.512	0.014
Cortex	0.114	0.457
Endodermis	0.381	0.044

R² indicates the fraction of the variation in EXPA3 promoter activity accounted for by RGA. A P value < 0.05 represents a significant relationship.

These observations collectively suggest that the activity of the EXPA3 promoter strongly correlates with cell size in all cell types of the root examined. The regulation of the endogenous RGA protein does not directly correlate with cell volume and only weakly relates to EXPA3 promoter activity in the epidermis and endodermis. The lack of a significant relationship between the RGA protein and cell volume suggests that other factors downstream of RGA that determine cell volume have not been observed or accounted for in this analysis and that RGA regulates cell volume in the root through more than just EXPA3. This observation fits with there being many more genes that promote cell expansion being expressed in the root than just EXPA3 (Brady et al., 2007).

The ability to map single-cell data from diverse samples into a common framework for comparative purposes using 3DCellAtlas enables the quantitative relationships between various regulatory components at cell-type-specific resolution to be established. This represents a powerful approach to understand the relationship between gene regulatory networks and cellular growth across whole organs. The data also provide a means to parameterize models to recapitulate these observed behaviors (Band et al., 2012, 2014).

While this example uses GUS reflectance, the quantification of signal within individual cells may be performed using any reporter construct including fluorescence. The use of ratiometric quantification of a reporter relative to an internal control using existing software may facilitate the quantitative analysis of reporter abundance in individual cells (Federici et al., 2012; Pound et al., 2012; Liao et al., 2015).

Quantitative 3D imaging of plant development is an increasingly important approach in the study of plant developmental biology. With the growing use of this approach comes an increased need for computational tools capable of extracting biologically relevant information from these data.

3DCellAtlas is a rapid and modular computational approach to generate quantitative cellular level atlases of plant organ development. This pipeline enables the quantification of organ-wide 3D cell anisotropy driving organ growth at single-cell resolution. Atlases generated also allow for multiple reporters and data types to be quantified and mapped onto a common cellular level template. The quantitative and integrative analysis of diverse network components can then be explored within the spatial and temporal context of 3D cell shape changes across developing organs.

A key advance in computational methodology provided by 3DCellAtlas is the use of a warped 3D coordinate system (Figure 2H). This can accommodate the nonlinear growth of plant organs, and it enables the accurate alignment of axes representing the principal directions of growth in radially symmetric organs. These accurately aligned axes facilitate the rapid label-free identification of cell types from 3D images without the need for transgenic lineage markers or reference atlases, as well as the complete quantification of 3D anisotropy across whole organs and cell types.

Another key advance provided by 3DCellAtlas is the generation of an internal cellular referencing system within whole-plant organs. This enables data from diverse samples to be integrated onto a common template at cell-type- and position-specific resolution.

These advances enable virtual single cell analyses to be performed across whole organs and the integration of diverse network components within the context of 3D cell shape changes.

The organ-wide cell-type-specific 3D cell anisotropy driving Arabidopsis hypocotyl elongation in the light was quantified. Differences in the radial cell anisotropy of the endodermis, relative to other cell types, was captured.

The influence of ethylene on 3D cell anisotropy in the hypocotyl was also quantified and led to the identification of the endodermis as a cellular site of preferential growth in response to ethylene application in hypocotyls. The role for GA signaling in the endodermis regulating root elongation has been demonstrated previously (Ubeda-Tomás et al., 2008). The preferential growth of the endodermis in response to ethylene suggests this cell layer may facilitate hypocotyl growth in response to this hormone. These analyses also revealed the presence of a gradient of increased cell growth toward the inner cell layers in the hypocotyl in response to ethylene.

This approach is not limited by species, and the accurate identification of cell types using the quantification of 3D cellular geometric properties is possible in other species, including P. rhoeas (Figures 2T and 2U).

The ability to investigate the quantitative spatiotemporal dynamics of multiple components of a regulatory network across organ growth at cell-type-specific resolution was also demonstrated by examining the relationship between the DELLA protein RGA, the promoter activity of the expansin gene EXPA3, and observed cellular growth in Arabidopsis roots. A strong positive relationship between EXPA3 promoter activity and cell expansion was observed in all cell types examined, while no significant relationship between RGA protein abundance and cell volume was observed. A marginally significant relationship between the RGA protein and EXPA3 promoter activity was identified in the epidermis and endodermis. These quantitative relationships collectively demonstrate that EXPA3 expression is closely related to cell expansion in roots. In addition, the RGA protein regulates cell expansion through more than just EXPA3, an observation consistent with the large number of cell-wall-related genes whose expression is influenced by DELLA proteins (Cao et al., 2006).

The quantitative description of this network integrated within the context of 3D cellular growth across a whole plant organ was facilitated by the methodology presented here. These results are able to identify and quantitatively characterize the complexity of the genetic regulation of growth in the root.

As an increasing number of reporters and key interactions regulating plant development are generated and described, the need to integrate this into the spatial and temporal context of multicellular organ growth will increase. The robust nature of this approach will facilitate these integrative multidimensional studies. The simultaneous identification of cell type, quantification of 3D cell shape changes, and reporter abundance within individual cells allows the relationships between these variables to be established and the modulation of cellular growth by regulatory network activity to be defined at single-cell resolution. These data may be used to parameterize models of dynamic organ growth at cell-type-specific resolution (Band et al., 2012, 2014).

The ability to map these diverse components onto a common template using 3DCellAtlas also provides a means to generate digital single cell databases of plant organ development through the community deposition of reporter data sets into a common cellular atlas framework. The generation of compiled single-cell data would enable meta-analyses to uncover previously undescribed biological relationships at great resolution.

As imaging technologies improve and greater number and diversity of whole-organ 3D data sets are generated, 3DCellAtlas will enable their discretization, analysis, and integration.

METHODS

Plant Materials and Growth Conditions

Arabidopsis thaliana plants were grown to maturity in environmentally controlled cabinets using 16 h light (light intensity 150 to 175 μmol m² s⁻¹) at 22°C and 8 h dark at 18°C. Seeds were harvested, cleaned through a 500-μm mesh, and stored at 24°C in glassine bags. The line harbored pRGA:RGA-GUS C-terminal GUS fusion within the Gateway vector pGWB433 and included 2000 bp of promoter sequence. The promoter reporter EXPA3:GUS was generated within the pKANGWFS7 Gateway vector with 2000 bp of promoter sequence. GUS staining was performed as previously described (Bassel et al., 2014).

Sample Preparation and Image Acquisition

All seeds were surface sterilized using 10% (v/v) Parazone (commercial bleach) for 5 min and rinsed five times with sterile distilled water. Seeds were then pipetted onto Petri dishes containing 0.5× Murashige and Skoog basal salts (Melford) and 0.8% or 1% (w/v) agar (Fisher), pH 5.7. Mature embryo samples were imbibed for 3 h on agar plates before being placed upon moist filter paper and dissected using a binocular microscope before being fixed in 3:1 (v/v) ethanol:acetic acid. Roots at 7 d and hypocotyls at 4 d were prepared by growing plants on vertical 1% (w/v) agar plates.

For embryos, roots, and hypocotyls, following one night of fixation, samples were placed in 1% SDS and 0.2 n NaOH overnight and then washed in distilled water before being enzymatically treated with α-amylase as previously described (Wuyts et al., 2010). Following amylase treatment, samples were stained with propidium iodide as described previously (Truernit et al., 2008).

z-Stacks of fixed cleared samples were collected using a 25× oil objective on a Zeiss LSM 710 confocal microscope at 0.6 Airy units and a slice interval of 0.4 μm as 16-bit images at 2048 × 2048 resolution. Identical settings were used for all experiments. GUS signal detection was collected as previously described (Truernit et al., 2008) with the detector set to reflectance, gain typically at 400, and offset at −5600. Image stacks were saved in the Zeiss LSM format, exported into TIFF stacks using ImageJ, and then imported into MorphoGraphX for segmentation.

3D Segmentation of Plant Cells

TIFF image stacks of whole plant organs were blurred using the ITK Gaussian Blur with a radius of 0.5 μm before being segmented using the ITK Autoseeded Watershed (www.itk.org) at a threshold between 500 and 800. Segmented bitmap stacks were manually corrected for oversegmentation errors within MorphoGraphX by fusing together multiple labels into the single cells, which were represented using a combination of the select and paint bucket tools in MorphoGraphX (Kierzkowski et al., 2012; Roeder et al., 2012). Meshes were generated using the marching cubes algorithm (Lorensen and Cline, 1987) at a cube spacing of 2 μm and were not smoothed.

Defining the Intrinsic Coordinate System

A Bezier line containing five control handles was oriented to extend through the center of the axis of sample roots, hypocotyls, and embryos. A mesh defining the surface of the organ was generated by first blurring the whole organ by 5 μm and then generating a two-dimensional curved surface mesh using the marching cubes surface algorithm at a spacing of 5 μm and a threshold of 3000 (Kierzkowski et al., 2012). The end of the mesh, corresponding to the place where the imaging of the organ was limited due to the objective, was removed within MorphoGraphX using clipping planes.

With the mesh defining the cells of the organ in Mesh 1, and the surface mesh in Mesh 2 within MorphoGraphX, the process named “analyze cells 3D” is run. For each triangle in the surface mesh of cell , a tetrahedron is formed from the axis origin and the three triangle vertices , labeled in an anticlockwise manner when viewed from within the cell. The signed volume of each tetrahedron is calculated, and the sum of these signed volumes then gives the cell volume,

The centroid of the cell is then calculated by summing the midpoints of the tetrahedral, weighted by their signed volume,

We then calculate the coordinates of each centroid in terms of an intrinsic coordinate system, using length from the organ tip (longitudinal coordinate ), radial distance from the Bezier (radial coordinate ), and angle around the organ (circumferential coordinate ) (Supplemental Figure 2). For each centroid, the closest point on the Bezier is found, associating each cell with a position along the Bezier (longitudinal coordinate) and a radial coordinate . The circumferential coordinate is calculated by defining a plane

that cuts radially through the organ. Here, is the direction of an arbitrary cell to the Bezier and is the tangent to the Bezier at that point. For each centroid, the closest point on the plane is calculated, which together with the closest point to the Bezier gives two sides of a right-angled triangle, giving the circumferential angle .

Having calculated intrinsic coordinates for each cell , we calculate a scaled radial coordinate that maps each centroid to a unique point of the interior of a cylinder of unit radius, with each successive layer of different cell types occupying approximately annular shells of different average radii (Supplemental Figures 1 to 3). This is done by considering all points on the surface mesh with longitudinal distance 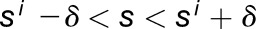for small, positive and then selecting the point on the surface mesh such that the difference in coordinate is minimized. We can then calculate a scaled radial coordinate , where is the shortest distance from to the centerline Bezier.

To inform the radially symmetric portion along the longitudinal distance of the organ, the first true cortical cell is demarcated, eliminating the topologically nonradially symmetric columella from the analysis. This completes the intrinsic description of the organ in terms of the body coordinates .

Local Cell Axis Alignment

To find the morphology of each cell in terms of intrinsic longitudinal, radial, and circumferential lengths, we must know the alignment of that cell with respect to the full organ. Thus, for each cell it is necessary to find a local set of “cell” axes. For each cell, we calculate the three local directions defining its orientation then walk along them to find the cell lengths using a ray triangle intersect algorithm.

The three local directions are determined in the following way. For a radially symmetric organ, a local radial axis is given by the direction from the cell centroid to its nearest point on the Bezier curve. However, because our organs are not perfectly radially symmetric, we also calculate the direction to the closest point on the surface mesh . The cell radial axis is approximated as a combination of the two directions. Given that cells closer to the outside of the organ will be more aligned with the surface mesh, and vice versa for cells on the inside of the organ with the Bezier, we use the scaled radial coordinate to scale the contribution of these two reference axes over the radial distance of the organ using the linear combination,

To approximate the cell longitudinal direction , we require unit tangent to the Bezier associated with the cell centroid and the normalized unit vector of the projection of onto the surface mesh at point . The local cell tangent is then also modeled by a combination of and linear in the scaled radius ,

so that cells close to the outside match and cells close to the inside match . This model is the simplest that allows for changes in the organ radius as a function of longitudinal distance resulting from changing cell alignment and morphology, as occurs for example toward the root tip (Supplemental Figure 3). The circumferential axis is then given by the cross-product . To determine cell lengths along these three oriented local directions 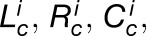a ray is projected from the centroid in the three local directions (longitudinal, radial, and circumferential), in both the positive and negative directions. The distance between the points where the positive and negative rays hit the perimeter of the cell defines the cell length along this local axis.

Geometry-Based Clustering and Identification of Cell Types

Using the “assign cell types” process, cell types were clustered in a two-dimensional heat map plotting a combination of the radial coordinate and either the circumferential, longitudinal, or radial length. Whichever coordinates are chosen for clustering, the values are scaled by their minimum and maximum value and spread over the range of the heat map space . We generated a two-dimensional function from a sum of Gaussians centered around the two chosen coordinate values of each cell i. For a given point on the heat map (x, y), the heat value is calculated as

with the smoothing parameter that can be manually adjusted by the user within the GUI. Because this smooth function has defined peaks and valleys, demarcation of cell types along these maxima and minima is possible and performed through the GUI implemented within MorphoGraphX.

Using the “assign columella” process, cells beyond the radially symmetric portion of the organ are labeled as columella. To determine which columella cells form part of the root cap, the ratio of the total surface area of each columella cell to the sum of the areas interacting with its neighboring cells is calculated. Those cells that are root cap lie on the outside of the organ, and as such there is a significant deficit (at least 20%) in these areas compared with interior cells. This measure taken together with scaled radius is used to differentiate the root cap cells lying over the columella.

Cell identity labels are stored as “parents” within MorphoGraphX. The geometric properties of cells within a given sample can be visualized in situ within MorphoGraphX using the “display cell data” process. A drop-down menu allows for the different geometric features to be visualized individually.

Identification of Mislabeled Cells Using Graph Topology

Triangular meshes containing the 3D cell geometry and arrangement of cells within plant organs were used to determine and quantify the interfaces between cells as previously described (Yoshida et al., 2014). Triangles that were shared between adjacent cells were identified and defined edges within the connectivity network. Using the cellular connectivity network data and cellular annotation of the labels, the pairwise relationships between cells can be examined (Long et al., 2009). In this way, cells that have been incorrectly annotated can be identified based on the impossibility of their association with their neighbors. An association between the vasculature and cortex indicates the absence or mislabeling of an endodermal cell and is the most common misannotation error (Table 1). Using the “topological check” feature, cells or nodes possessing a user-defined threshold of impossible edges are identified by examining all connections and comparing them with lists of possible connections. Nodes with a greater number of impossible edges than the threshold are identified as misannotated.

Cells that have been mislabeled as vasculature are relabeled as endodermis or air spaces depending on their circumferential lengths based on the length value of previously accurately labeled cells. All other potentially misannotated cell labels can be highlighted within MorphoGraphX where they are visually inspected and reassigned to their proper annotation.

Cortical Cell Referencing System

Following the identification of cell types using the “assign cell types” process, the cortical cell referencing system was set up using “assign cortical cells.” Here, the cortical cell in a user-defined position is selected, the tangential lengths of every cortical cell are taken as a function of the cells’ longitudinal coordinates, and the data are fitted to a third order polynomial via a least-squares method. This creates an average “fitted length” of cortical cells as a function of their longitudinal coordinate, which is used to divide the cells into bins. Each cell is then associated with this intrinsic cortical numbering system via nearest-neighbor interpolation on its longitudinal coordinate.

Statistical Analysis of Growth Data

The process “3D cell growth analysis” was used to analyze the cellular geometric data generated by 3DCellAtlas. Data from individual samples were saved and placed within a single directory where they were analyzed. Ratios of means for cell size metrics () were measured by reading data calculated in MorphoGraphX from multiple stacks and grouping the data by cell type, and then associated cortical cell; from these vectors, the was calculated using

where and are arrays containing the natural logarithms of the treatment and control data, respectively, and and are their corresponding sample mean values. Approximate confidence intervals were calculated as

where is the critical value of the t-distribution at the percentile point with degrees of freedom. Here, α was set to 0.05 to produce 95% confidence intervals. and are the variances of the natural logarithm data sets, and and are the sample sizes of the T and C data sets.

E-factors were defined for the differences in radial , longitudinal , and circumferential cell lengths measured at the beginning and the end of the experiment using the same vectors as previously, with the following:

Data presented were smoothed using a sliding window average of three associated cortical cell positions, one cell on either side. Cells in the first and last position within samples were reduced to the average of two cells, that being their single neighbor.

Statistical Analysis of Reporter Data

Reporter concentration within the context of the 3D segmented organ mesh was determined by taking the signal average interior signal value from the MorphoGraphX heat map function. These data were saved as CSV files from within this process and analyzed using 3DCellAtlas with the “reporter abundance analysis 3D” process. The reporter concentration values for each cell were assigned to the appropriate cell type and position (associated cortical cell) by matching these data with corresponding files generated from cell type and indexing in previous processes described above. Data from multiple samples were pooled together into bins representing unique cells.

The statistical analysis of reporter cellular concentrations calculated the mean reporter concentration for each cell type and associated cortical cell as vectors, as described above for cell geometry data. The 95% confidence intervals were computed using bootstrapping, with a minimum sample size of seven cells.

These data were projected onto heat maps for visualization in MorphoGraphX by joining the computed metrics by cell type and associated cortical cell to a selected 3D segmented organ present in the active window. Text files containing the mean and confidence interval for calculated reporter data are exported from the process for further use.

The statistical relationships between reporters and cell volume were established by performing linear regression after log-transforming data on each cell type separately, with these comparisons being performed on the same imaged materials. The relationship between RGA and EXPA3 measurements was collected from different experimental materials so it was not possible to assess this relationship directly. Here, RGA and EXPA3 data were averaged at each cell type and associated cortical cell level, and a linear model was fit to examine their relationship for each cell type.

Accession Numbers

Sequence data from this article can be found in the GenBank/EMBL libraries under accession numbers: At2g37640 (EXPA3) and At2g01570 (RGA).

Supplemental Data

• Supplemental Figure 1. 3D segmentations of an Arabidopsis root, hypocotyl, and embryo.

• Supplemental Figure 2. Cylindrical coordinate system used to orient radially symmetric plant organs.

• Supplemental Figure 3. Calculation of scaled radial distance.

• Supplemental Figure 4. Use of scaled radial distance to adjust for geometric irregularities.

• Supplemental Figure 5. Heat maps and cell-type cluster selection.

• Supplemental Figure 6. The conversion of shared triangles in meshes between adjacent cells and a cellular connectivity network.

• Supplemental Figure 7. Plots showing hypocotyl 3D anisotropy as a function of associated cortical cell in a light-grown Arabidopsis hypocotyl 4 d after germination.

• Supplemental Figure 8. Plots showing hypocotyl 3D anisotropy as a function of associated cortical cell in an ACC-treated light-grown Arabidopsis hypocotyl 4 d after germination.

• Supplemental Movie 1. Demonstration of cell type identification and topological correction on an Arabidopsis embryonic hypocotyl using 3DCellAtlas.

Glossary

GUI

graphical user interface

ACC

1-aminocyclopropane-1-carboxylic acid

GA

gibberellic acid