Phylogenetic niche conservatism – common pitfalls and ways forward

Abstract

1. The prevalence of phylogenetic niche conservatism (PNC) in nature is still a conflicting issue. Disagreement arises from confusion over its precise definition and the variety of approaches to measure its prevalence. Recent work highlighted that common measures of PNC strongly depend on the assumptions of the underlying model of niche evolution. However, this warning has not been well recognized in the applied literature and questionable approaches are still frequently applied.

2. The aim of this paper is to draw attention to the assumptions underlying commonly applied simple measures of PNC. We used a series of simulations to illustrate how misleading results can be if assumptions of niche evolution are violated, that the violation of assumptions is a common phenomenon and that testing assumptions requires in-depth pre-test.

3. We conclude that the seemingly simple measures of PNC, such as phylogenetic sign6al and evolutionary rate, are not so easy to apply if one accounts for the necessity to test model assumptions. In addition, these measures can be difficult to interpret. The common assumption that strong phylogenetic signal indicates PNC will be often invalid. In addition, the interpretation of some measures, e.g. the conclusion that evolutionary rate is slow enough to indicate PNC, requires a comparison with another clade, another trait or well-developed null model assumptions and thus additional data.

4. We suggest that studies investigating PNC should always compare alternative evolutionary models, and that model comparisons should in particular include flexible niche evolution models such as multiple-optima OU models, although these are computational intensive. These models are directly inherited from the concept of macro-evolutionary adaptive landscape, and can indicate PNC either by relative few peak shifts or by narrow peaks in the adaptive landscape. A test of PNC thus requires comparing these parameters of the macroevolutionary landscape between clades or time periods.

5. The general prevalence of PNC in nature should be evaluated only based on studies keeping up to the high standards of communicating the used definition of PNC, testing the assumptions made in the modelling approaches and including newly developed models in a model comparison approach.

The interplay between ecological and evolutionary processes drives the distribution and dynamics of biodiversity (Ricklefs 1987; Lavergne et al. 2010). A signature of these processes is contained in phylogenetic trees and in the distribution of species’ ecological characteristics along these trees (Webb et al. 2002). One of the most striking and long recognized signatures is the similarity of ecological niches among closely related species (Wiens and Graham 2005; Losos 2008a; Pearman et al. 2008). The degree to which observable species characteristics contain information about phylogenetic relationships can be broadly defined as ‘phylogenetic signal’ (PS, e.g. Hillis & Huelsenbeck 1992), but this definition may encompass several different metrics. A commonly used and operational perspective, which we will use in the following, is to define PS as the tendency for related species to resemble each other more than they resemble species drawn at random from the phylogenetic tree (Blomberg & Garland 2002).

Already Darwin (1859) identified the relatively recent common ancestry of related species as the primary reason for their ecological similarity (the pattern that much later has been termed PS). Grafen (1989) was one of the first to suggest that niche similarity of related species is not only due to shared ancestry but also due to shared environmental constraints and biogeographic history. He hypothesised that closely related species tend to have similar niches and to live more or less closely together. They should thus have high chances to enter the same new niches when they emerge. Over time they should then be exposed to similar adaptive forces in these new niches, which should lead them to be more similar ecologically than expected under neutral drift (Grafen 1989). Grafen’s explanation was then revisited by Harvey and Pagel (1991), who defined the ecological and evolutionary processes resulting in the tendency of species or lineages to retain their ancestral niches over time as phylogenetic niche conservatism (PNC). Recent theoretical work has shown that PS and PNC are not the same thing. Even under strong PNC species niche differences can be unrelated to phylogenetic distances (no PS) and labile niches can sometimes lead to a strong relation between niche differences and phylogenetic distance (strong PS, Revell, Harmon & Collar 2008).

The recent rise of large and dated molecular phylogenies (Bininda-Emonds et al. 2008; Thuiller et al. 2011; Jetz et al. 2012; Pyron, Burbrink & Wiens 2013; Zanne et al. 2014) allows for testing multiple hypotheses related to PNC and past biodiversity dynamics and has led to an increased interest in PNC (Pearman et al. 2014). However, the concept was expanded and conflicting ideas emerged around two key questions: First, is PNC a process or a pattern? Harvey and Pagel (1991, p. 38) introduced PNC as an adaptive ecological and evolutionary process. This initial interpretation may have been based on a population dynamic perspective where different factors, such as strong stabilizing selection, lack of appropriate genetic variation, genetic or functional constraints due to epistatic or pleiotropic effects, and gene flow impeding the emergence of novel adaptations, can lead to PNC (Hansen & Houle 2004; Walsh & Blows 2009; Lavergne et al. 2010). From this viewpoint PNC always emerges from an impossibility of niche novelties to emerge due to conditions that restrict population growth (Holt 1996; Gomulkiewicz & Houle 2009). In contrast to this process perspective, other authors have suggested that PNC can be either a process or a pattern depending on the perspective from which the research question is asked (Wiens 2008; Wiens et al. 2010). Finally, it has been claimed that a pure pattern perspective would be adequate as it allows for directly measuring phylogenetic niche conservatism instead of just assuming its presence (Losos 2008). For Losos, PNC in itself cannot explain anything but can result from several processes (genetic constraints, stabilizing selection). Thus a hypothesis about one given underlying process can never be confirmed with a pure-phylogenetic approach. However, comparative approaches may be useful to reject certain classes of processes (Losos 2011).

Second, which constraints are needed to produce PNC? Some authors have suggested that kinship between species relations and resulting niche similarity between related species are not only essential but also sufficient, i.e. that neutral drift is enough to drive PNC (Wiens 2008; Cooper, Jetz & Freckleton 2010; Wiens et al. 2010). Other authors have postulated that PNC requires additional constraints such as environmental filtering which induces pervasive stabilizing selection (Harvey & Pagel 1991; Desdevises et al. 2003; Losos 2008) or limits to adaptive evolution (Holt 1996; Gomulkiewicz & Houle 2009). This is what motivated Losos (2008) to propose that the concept of PNC should be restricted to situations where conservative forces (among the ones listed above) are exerted on phylogenetically related taxa, ultimately resulting in niches diversifying so slowly that closely related species should resemble each other more than expected under neutral drift.

These conflicting ideas about what is and what is not PNC have resulted in a strong debate on its prevalence in nature. While some studies have reported support for PNC (Ackerly 2004; Gomez, Verdu & Perfectti 2010; Burns & Strauss 2011), others have provided counter-examples (Evans et al. 2009; Boucher et al. 2012; Pearman et al. 2014) and some studies have demonstrated its dependency on studied systems, time scales and niche-related traits (Peterson, Soberon & Sanchez-Cordero 1999; Freckleton & Jetz 2009; Cooper, Freckleton & Jetz 2011). However, as the different studies define PNC differently and accordingly utilize different measures they are not directly comparable (Revell, Harmon & Collar 2008; Ackerly 2009), and inevitably lead to inconsistent conclusions about the prevalence of niche conservatism (Losos 2008). Recent conceptual reviews have aimed at disentangling the different viewpoints on PNC and have highlighted that the performance of different measures strongly depends on the assumptions of a certain model of niche evolution (e.g. Cooper, Jetz & Freckleton 2010; Crisp & Cook 2012). However, in applied studies, PNC is still measured with one or the other approach without adequately testing for the underlying evolutionary process (e.g., Buckley et al. 2010). Also, questionable approaches are still frequently used (e.g. methods only relying on taxonomic topologies, Peterson, Soberon & Sanchez-Cordero 1999; Prinzing et al. 2001) and general conclusions on the prevalence of PNC in nature rely on these biased studies (Wiens et al. 2010). In fact, despite the fact that the term PNC was almost unknown at the turn of last century, its use has expanded in recent literature and nobody seems to really agree anymore on what it really is (Crisp & Cook 2012).

In the following, our paper re-visits earlier work on the different approaches for measuring PNC and on the assumptions underlying these approaches (Revell, Harmon & Collar 2008; Ackerly 2009; Cooper, Jetz & Freckleton 2010; Wiens et al. 2010; Crisp & Cook 2012). We go beyond this earlier work by incorporating recent advances in modelling PNC with flexible evolutionary models with no a priori about where niche shifts occur in the phylogeny. We further illustrate with simulated data that violations of basic assumptions of niche evolution models frequently lead to erroneous conclusions and highlight the challenges to test these assumptions. Finally, we suggest ways forward in the study of PNC hopefully contributing to a better common practice and thus to better comparable studies on the prevalence of PNC in nature.

Limitations of commonly applied measures of PNC

The niche of a species is usually defined as the set of abiotic and biotic conditions in which species are able to persist and maintain stable populations (Hutchinson 1957; Wiens and Graham 2005). For the sake of simplicity, we will assume in the following that species’ niches can be described by a single continuous trait capturing the adaptation to those environmental conditions in which a species can thrive. We acknowledge that this is an over-simplification of reality, but this choice is driven by the availability of sophisticated models for the evolution of continuous traits on phylogenies (see below). Furthermore, extending this framework to include intra-specific variability, measurement error, or to consider simultaneously multiple traits describing the niche is theoretically possible (although not implemented in all modelling approaches).

It is well established that the performance of different tests of PNC depends on assumptions of underlying niche evolution models (Cooper, Jetz & Freckleton 2010; Crisp & Cook 2012). Nevertheless, PNC approaches are often applied without knowing which model of niche evolution best describes the data. Two arguments could support this practice. First, PNC approaches could be robust to moderate violations of model assumptions. Second, the often-assumed simple models, such as Brownian motion (see below), could well represent the vast majority of studied cases of niche evolution. In the following we complete recent conceptual reviews with a series of simulations to illustrate that both of these arguments fail in practice. In our simulations we model the evolution of a single niche trait. In a first step phylogenetic trees are simulated under a Yule process. Then niche evolution along these phylogenies is simulated through a discretized continuous time process following various niche evolution models (see below and Appendix S1 for more details). Finally, different measures of PNC are applied to the simulated data and results are compared.

Models of niche evolution: the basics

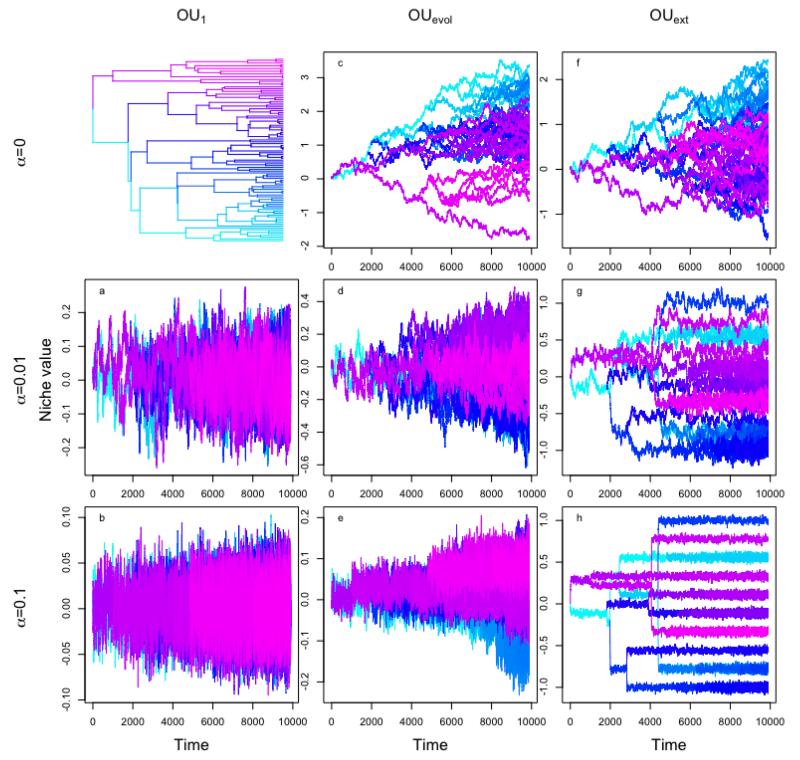
The models of niche evolution introduced here describe the evolution of quantitative characters on phylogenies. Stochasticity, branch lengths and internal or external constraints can influence niche evolution depending on the underlying model. Different niche evolution models can result in very different patterns of niche trait values amongst the tips of the phylogenies (i.e. species, see Fig. 1).

Figure 1.

Niche evolution over time for an OU₁ (left column), OU_evol (middle column) and OU_ext (right column) model with different strength of selection (α). The upper left plot shows the phylogeny; the middle and the upper right plot show two realizations of BM. Colours indicate the position of branches in the phylogeny. When considering only the final distribution of niche values in the tips, then a OU₁ model with strong α can be easily misidentified as a white noise model and an OU_ext model with moderate α can be easily misidentified as a BM model

The Brownian motion

Under Brownian motion (BM, Felsenstein 1985), a continuous trait evolves according to a suite of random steps (i.e. random walk process), with no preferred direction. BM is thus typically used to represent neutral drift over macroevolutionary timescales, but BM-like evolution can arise by a number of other processes such as selection in a quickly fluctuating environment (Hansen & Martins 1996). The size of the random steps depends only on evolutionary rate, i.e. on the rate of phenotypic change in a given lineage.

The Ornstein-Uhlenbeck model

For the purpose of modelling evolution towards a selective optimum, the Ornstein-Uhlenbeck model was introduced to comparative analyses (OU, Hansen 1997; Butler & King 2004). This model is an extension of BM where an additional term describes attraction towards an optimal niche value. Even though its formulation is identical to Lande’s model of stabilizing selection within a population (Lande 1976), the macroevolutionary OU model is only phenomenological, as it mimics (but does not demonstrate) stabilizing selection, constrained evolution in bounded phenotypic space (Boucher et al. 2014), or evolution towards shifting niche optima (Hansen 2012). Under an OU model, the evolution of the niche value (x) is governed by the following differential equation:

$$x(t+\mathit{dt})=x\left(t\right)+\alpha \left(\theta \right(t)-x(t\left)\right)\mathit{dt}+\sigma \mathit{dt}\epsilon .$$

In this equation, ω ~ N (0,1), σ is the Brownian motion rate, θ the optimal value (that can depend on time), α the selection strength, and dt is an elementary unit of time. BM is a special case of the OU model with no selection (α=0). When niche evolution has been so fast that all traces of shared ancestry are lost, niches are said to follow a white noise model (WN), which is equivalent to random draw of niche values independently of the phylogeny. WN is a special case of the OU model where the selection strength tends to infinity (see Appendix S1 for more information).

Further extensions

Multiple variations of the BM and the OU models have been proposed: BM with rates that vary over time like the ACDC model (Blomberg, Garland & Ives 2003) that becomes the Early Burst model when there is slowdown over time (Harmon et al. 2010) or vary in different parts of the phylogeny (O’ Meara et al. 2006; Thomas, Freckleton & Szekely 2006; Eastman et al. 2011), OU with different selective optima applied to different parts of the phylogeny (Butler & King 2004), and even OU models with different selective optima, where rate of drift and selection strength can also vary around different niche optima (Beaulieu et al. 2012). Taking into account heterogeneity in the process of niche evolution is important since simple homogeneous models frequently happen to be very poor descriptors of the data (Pennell et al. 2014). Furthermore, this allows for testing for more complex scenarios and hypotheses of niche evolution. It is, however, important to note that different niche evolution models can cause either completely different or the same niche distribution patterns. For example, neutral drift and adaptation to quickly changing environments can lead to the same BM-like patterns even though underlying processes are very different. Therefore, sometimes, in the analysis of phylogenetic patterns of species niches, several models seem equally plausible in terms of statistical explanatory power, but they may not all be as biologically plausible. Choosing from the seemingly plausible models one that describes a biologically unrealistic process obviously bears the strong risk of drawing wrong conclusions about PNC.

Are common measures informative?

Phylogenetic signal, evolutionary rate, the selection strength in an OU model and model comparison analyses are commonly used to study PNC (Cooper, Jetz & Freckleton 2010; Wiens et al. 2010; Crisp & Cook 2012). The conflicting ideas about PNC (Is it a process or a pattern? Which constraints are needed to produce PNC?) resulted in a debate on which of these approaches are most appropriate. The different measures and the underlying philosophy are shortly outlined in the following together with their limitations (e.g. Revell, Harmon & Collar 2008; Ackerly 2009; Hunt 2012; Ho & Ane 2013).

Phylogenetic signal

Phylogenetic signal takes a pure pattern perspective. Different authors suggested different values of phylogenetic signal to be sufficient for PNC: While Wiens et al. (2008; 2010) state that a pattern expected under neutral drift alone is sufficient and thus states that PNC can be produced by a random walk without additional constraints, others demand that there should be additional constraints (e.g. a strong stabilizing selection favouring the ancestral niche over time) leading to a PS that is stronger than expected under random walk (Losos 2008).

A strong limitation of this approach is that phylogenetic signal can be used to measure PNC unambiguously only under the assumption of a BM-like evolutionary process (Revell, Harmon & Collar 2008; Cooper, Jetz & Freckleton 2010, Fig. 1c, f). The analysis of our simulated data demonstrates how violations of the BM assumption can produce strongly misleading patterns of phylogenetic signal (Fig. 2). For instance, when niches evolve according to an OU process with a single optimum (Fig. 1a, b), strong constraints (leading to niches with only very little variation over time and thus to strong PNC in our simulations) result in low phylogenetic signal. Conversely, when niches evolve under an OU model with multiple optima in different parts of the phylogeny (Fig. 1g, h, which could be interpreted as labile niches, at least in the early history of the clade, see Appendix S1) phylogenetic signal is higher than expected under BM. In addition to the consequences of violating models’ assumptions, there is also the problem that several indices are available to measure phylogenetic signal and since they capture different aspects of the concept, they can give significantly different answers (e.g. Blomberg’s K, Pagel’s λ, Moran’s I and Abouheif’s Cmean, see Münkemüller et al. 2012 for a comparison).

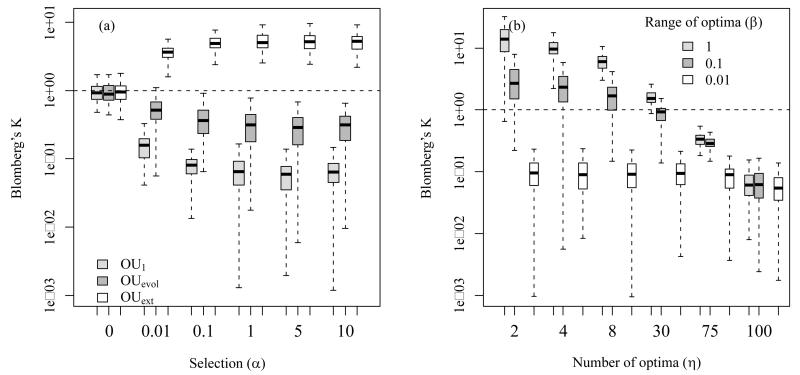
Figure 2.

We measured phylogenetic signal (PS, based on Blomberg’s K) in virtual data that we simulated with different niche evolution models. In the simulations niche values evolved along phylogenetic trees under three different niche evolution models: OU₁ is a single optimum OU model where we set the optimum value equal to the root value; OU_evol is a OU model where we set the optima of nodes to the niche values of the respective ancestor nodes; OU_ext is a OU model where η different clades differ strongly in their external selective optima (β indicates the range of different optima) and these optima also differ strongly from the root value (see Appendices S1 and S2 for more detail).

We found that, phylogenetic signal decreased with parameter changes assumed to increase PNC, such as high values of selection strength (α) in the OU₁ and OU_evol model. Phylogenetic signal, however, increased with parameter changes assumed to increase niche lability in the OU_ext model, such as moderate to high values of selection strength (α, panel a), high numbers of distinct selective optima (η, panel b) and increased ranges of selective optima niche values (high β, panel b). In all simulations, the variance of BM was set to σ=0.01. In plot a, the three models are parameterized as follows: η=1 for OU₁, η=10 and β=1 for OU_ext and for OU_evol the optima are equal to the ancestor nodes; in plot b, α=1. Each boxplot represents 100 repetitions. Note that y-axes are logarithmic and that outliers were not plotted.

In summary, phylogenetic signal is only a useful measure of PNC if the underlying process of evolution is BM-like. Otherwise it can be completely unrelated to PNC and even give spurious answers in respect to the underlying process. Showing evidence of PNC based on phylogenetic signal thus requires to test whether BM is the underlying model of evolution and (if this is fulfilled) to accept a definition of PNC that basically equals BM. To us this is problematic since the expression PNC itself suggests that some conservative forces should slow down niche evolution whereas BM alone is not a conservative force at all.

Evolutionary rate and related measures

Evolutionary rate measures the rate of phenotypic changes over evolutionary time in a given lineage. Since PNC implies a certain resistance to change, it should be characterized by relatively slow rates of niche evolution (Ackerly 2009). However, using this measure requires a comparison, for example between clades or between different periods of time, in order to identify which rates can be termed relatively ‘high’ vs. ‘low’. To allow for such a comparison, Pagel’s δ (Pagel 1999) has been suggested to measure niche retention, i.e. whether most niche variance has accumulated early rather than late in the history of a clade (see also O’Meara et al. 2006; Thomas, Freckleton & Szekely 2006 for a method to test for different rates of evolution between clades). Pagel’s δ is a scaling parameter that affects branch lengths according to their depth in the phylogenetic tree (Pagel 1999). Under the assumption that niche evolution along a δ-transformed phylogeny follows BM, values below unity indicate PNC in the more recent history in comparison to more labile niches in the past.

We would like to note that, in order to standardize the measure of evolutionary rate for comparison of different traits and/or different clades, trait values should be ln-transformed (Ackerly 2009). For example, if all species in the focal clade are small and all species in a related clade are large, and we are interested in relative changes in body size then a log transformation of body sizes would be appropriate to calculate evolutionary rates (Harmon et al. 2010).

Comparably to phylogenetic signal, the measure of evolutionary rate depends on the assumption of an underlying niche evolution model and can only meaningfully be interpreted as a parameter of this model (Hunt 2012). Often these models assume that evolutionary rate is constant across the entire phylogeny, which is a strong and (in most cases) unrealistic assumption and can lead to highly misleading results. For example, when evolutionary rate is measured via the variance of phylogenetic independent contrasts then it is assumed that the underlying process of niche evolution can be meaningfully approximated by a BM-like process (Felsenstein 1985; Hansen & Martins 1996). The analysis of our simulated data illustrates how misleading estimates of evolutionary rates can be if these assumptions are violated. Indeed, an evolutionary rate inferred as the variance of phylogenetic independent contrasts is wrongly estimated if data are simulated with an Ornstein-Uhlenbeck (OU) model (Fig. 3a). This is because the OU model has a finite stationary variance (σ²/2α) that depends on α (see Appendix S1 and Fig. 1 for more information). The variance of niches under an OU process thus remains constant when the age of the clade increases (see Fig. 3 in Harmon et al. 2010), leading to a decrease in the overall evolutionary rate estimated on the phylogeny (Fig. 3a). Accordingly, Pagel’s δ indicates that most variance accumulated close to the tips of the phylogeny (Fig. 3b). This is statistically true but should not be interpreted as evidence that niche evolution has accelerated recently, because in the simulations the OU process has remained constant through time.

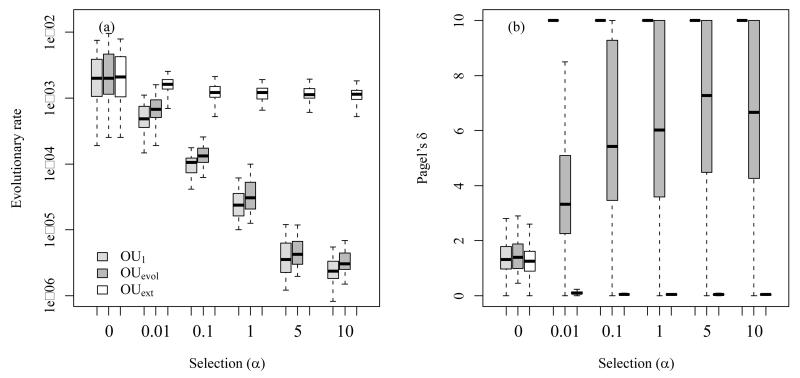
Figure 3.

We measured evolutionary rates (panel a), and Pagel’s δ (panel b) in virtual data that we simulated with different niche evolution models (see the legend of Fig. 2 and Appendices S1 and S2 for more detail). Evolutionary rates decreased for parameter changes commonly assumed to increase PNC (high values of selection strength, α, in the OU₁ and OU_evol model) and remained constant for parameter changes that increase the lability of niches (moderate to high values of selection strength in the OU_ext model; panel a). The retention parameter Pagel’s δ, in contrast, increased for parameter changes commonly assumed to increase PNC and thus suggested more labile niche evolution towards the tips of the phylogeny. For parameter changes that increase the lability of niches Pagel’s δ decreased, which should indicate PNC according to common expectation (Fig. 3b). In addition, Pagel’s δ had strong convergence problems. Note that outliers were not printed and that the y-axis in plot (a) is logarithmic.

In summary, evolutionary rates are a useful means of comparing the relative speed of niche evolution (and thus the strength of PNC) for different traits or different clades but cannot provide an absolute answer on the presence vs. absence of PNC. They provide an accurate description of the process only if the right evolutionary model (BM if estimated via the variance of phylogenetic independent contrasts) is assumed. Models with variable BM rates could be useful to compare rates of niche evolution in different clades (O’Meara et al. 2006).

Parameters of a single optimum OU model

The single optimum OU model mimics constrained evolution around an optimal value (cf. Fig 1a, b) and its parameterization can be used to estimate PNC (Hansen 2012). Interpreting the estimated value of the α parameter in an OU model is appealing because it should in theory be related to the strength of constraints on niche evolution.

However, the use of the α estimate (the selection strength) to inform on PNC is limited because it tends to have a bias towards high values. For instance, the analysis of data simulated with a single optimum OU model demonstrates that it is difficult to accurately estimate the simulated α parameter (Fig. 4a, cf. in addition Appendix from Butler & King 2004; Ho & Ane 2013), while the stationary variance of the OU process (σ²/2α) can be much more reliably estimated (Fig. 4b). It seems that this happens only when α is rather large compared to σ (as is the case in our simulations). However, α can be reliably estimated when it is small, and in this case the stationary variance is wrongly estimated (C. Ané, personal communication). Since the stationary variance of the OU process quantifies the relative strength of drift vs. selection, we believe it is the most important quantity to report and interpret in empirical studies. In addition, rather than directly reporting values of α, one should report the phylogenetic half-life (i.e. ln(2)/α), which measures the time necessary for half of the information contained in phylogenetic relationships to be erased. This quantity is expected to decrease with the strength of PNC, as phylogenetic information contained in the covariance structure of the tree will be erased when selective constraints are too large.

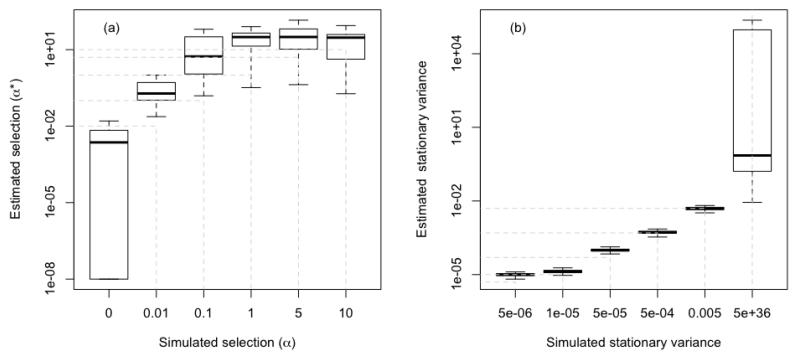
Figure 4.

We compared estimated parameters (backwards estimation from virtual data) against simulated parameters in a single optimum OU model (OU₁ model, see Appendices S1 and S2 for more detail). Results show strong overestimations of the strength of stabilizing selection (α*), especially if simulated selection strengths were low (Fig. 4a). In contrast, the estimates of the stationary variance were more accurate, at least if selection strength was not too high in comparison to the variance of the Brownian motion sub-process in the simulations (Fig. 4b). Each boxplot represents 100 repetitions. Note that outliers were not printed and that the y-axes are logarithmic.

We should mention that there is another limitation that relates equally to α and the stationary variance. Before interpreting the estimated parameters of an OU model, a model comparison test should be performed to decide whether a white noise model, a BM model or an OU model best fits the data. Unfortunately simulations showed that this test has very low power to detect a single optimum OU model, at least if one follows common practice and includes a white noise model in the model comparison (see Fig. 5 and next subsection). In sum, if the parameters of a single optimum OU model are used to infer on PNC then the stationary variance and eventually the phylogenetic half-life should be used rather than the selection strength. The underlying assumption is a single optimum OU model, which in fact might be rarely a good expectation for an entire clade.

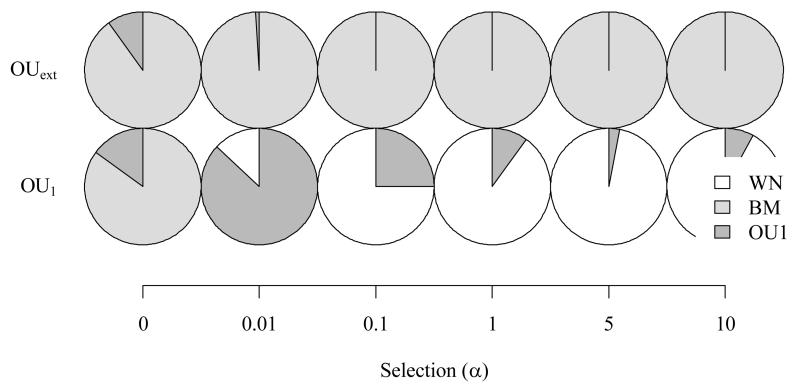
Figure 5.

Results of a model comparison analysis as is frequently done in the literature including white noise (WN), Brownian motion (BM) and single optimum OU models (OU₁) applied to virtual data simulated with two different niche evolution models (see Appendices S1 and S2 for more detail). The data for this analysis were simulated with varying strength of stabilizing selection (α) and under two different OU-models (OU_ext, which simulates multiple external constraints and OU₁, which simulates a single external constraint). A perfectly performing model comparison should identify BM for all simulations where α=0 and OU₁ for data simulated under OU₁ with α>0. Note, that we did not include more complex OU model fitting in the model comparison, as we wanted to show results of common practice. Pie charts indicate how often which model was chosen in the 100 repetitions.

The most striking results are that a single optimum OU process is in the great majority of cases misinterpreted as white noise, and that a multiple optima OU process (OU_ext) is even more often misinterpreted as Brownian motion (BM). However, note that if a more complex model with several optima was fitted, it would almost always outperform BM (not shown results).

Model comparison

It has been suggested that a model comparison of white noise, BM and OU-models can be used to inform on PNC (Cooper, Jetz & Freckleton 2010). The expectation is that an OU model with a single optimum and high selection strength should be chosen when niches have been conserved throughout the evolutionary history of the clade under study. Very recent methodological developments allow to extend this model comparison approach towards multiple optima OU models without any a priori on the nodes where shifts between selective regimes would occur (see the recent SURFACE algorithm by Ingram & Mahler 2013; see Ingram & Kai 2014 for a recent application), to compare different models using AIC (Akaike 1974) and to test whether more complex models are chosen solely because they have more free parameters or because they better describe the process based on a power analysis (phylogenetic Monte Carlo approach, Boettiger, Ralph & Coop 2011). These developments build on earlier work testing for a priori defined selective regimes on a phylogeny (Hansen 1997; see the R package ouch, Butler & King 2004; Beaulieu et al. 2012), constraining the adaptation of a trait to an optimum influenced by continuous, randomly changing predictor variables (see slouch algorithm, Hansen, Pienaar & Orzack 2008) and locating evolutionary shifts on a phylogeny using data-driven algorithms (Thomas & Freckleton 2012).

A major limitation of the frequently applied model comparison between white noise, BM and OU models is that, first, a single optimum OU process is often misidentified as white noise and, second, a multiple optima OU process is often misidentified as BM (see Fig. 5 for a demonstration with simulated data). The first misidentification is problematic since white noise is often interpreted as a model of lability while OU with one optimum is supposed to identify PNC (see Fig. 1 for the cause of this misidentification). The second limitation is problematic as BM is an assumption of many simple measures of PNC that can give biased results under a multiple optima OU process. It is caused by the fact that a scenario where optima are too different from each other can reasonably resemble BM (Uyeda et al. 2011). More generally, it can as well be that simple models of flat or single-peak adaptive landscapes may simply be over-simplistic (Hansen 2012). This problem can be avoided by including multiple optima OU models in the model comparison analysis. If they are included then more complex models with several optima almost always outperform more simple model choices (see following section: Are common assumptions frequently fulfilled?). To avoid that the choice of the more complex models is due to overfitting, a Monte Carlo based power analyses should be applied to verify the model choice (Boettiger, Ralph & Coop 2011). Besides the risk of overfitting, the inclusion of more complex models in the model comparison makes the analysis more data demanding. Sometimes it may also simply not be possible to fit the parameters of a multi-peak OU model due to correlations between parameters and resulting ridges in the likelihood landscape (Beaulieu et al. 2012). In addition, interpretation is more difficult as it is not anymore based on testing a single value against null expectations but on the distribution of peeks and steepness in the estimated macro-evolutionary adaptive landscape (Ingram & Mahler 2013; Mahler et al. 2013, see the following section for more detail).

In summary, model comparison approaches should always consider the inclusion of more complex OU models since otherwise more complex niche evolution processes are easily confounded with BM. However, there may be reasons for discarding these models based on expert knowledge, for example, when evolution is known to have taken place more gradually than assumed in the multi-peak OU model (Pennell, Harmon & Uyeda 2014). We also suggest changing the common practice and excluding the white noise model from model comparison. The reason is that the white noise model is misleading, as it has no clear biological interpretation while it produces the same pattern as an OU model with strong attraction strength. Instead, although we stress out again that the OU model is only phenomenological, finding support for an OU model with strong attraction strength at least provides process-based hypotheses for why phylogenetic relationships do not correlate with niche differences in a given group of organisms: the niche might be evolving under strong stabilizing selection (Hansen 2012) or under diversifying selection within certain bounds (Boucher et al. 2014). Finally, we would like to highlight the potentially substantial impact of biological variation and measurement error on model inference and model comparisons. Whenever possible, appropriate methods for incorporating measurement errors should be applied (Hansen & Bartoszek 2012).

Are common assumptions frequently fulfilled?

The most important take home message from revisiting the measures of PNC is that their performance crucially depends on whether or not the underlying assumptions of a particular model of niche evolution are fulfilled. Commonly the critical assumption is a BM model of niche evolution. However, evidence from the literature suggests that BM is rarely the best model to describe the niche evolution process (e.g. Estes & Arnold 2007; Harmon et al. 2010; Uyeda et al. 2011). We support this evidence based on the analysis of body mass evolution in 17 clades of mammals (see Appendix S3). For these mammal data simple BM is never the best description of the underlying niche evolution process (see Appendix Table S1). This result is supported by a Monte Carlo power analysis (Table S1; with one exception: for the Tamias clade the null hypothesis of an underlying BM model could not be rejected, p-value=0.06). Furthermore, our results suggest that an OU model with a single optimum might often not be appropriate either, since in all clades except Tamias, at least two different optima were detected. Finally, naively applying the different approaches of PNC to the mammal data once again demonstrates that results are often conflicting when assumptions of the approaches are not fulfilled (see Appendix Figure S1).

Cautionary notes for future work on PNC

The debate on whether PNC should be defined more strictly or more loosely in concert with the limitations of approaches towards measuring PNC has diluted the concept of PNC and has rendered impossible any conclusion about how frequently PNC can be observed in nature. It seems a considerable challenge to find a single convincing answer to the question ‘how can I test whether there is PNC in my clade of interest?’. Here, we provide two answers to this question. The first one is simple but in our eyes almost useless – or little informative. The second one is informative but may be perceived as unsatisfying as it is more complex and requires rethinking the question.

Simple is not that simple and partly uninformative

The first answer aims at disentangling the conditions under which simple measures can be applied. Simple measures, such as phylogenetic signal, evolutionary rate, the tempo of niche evolution (Pagel’s δ parameter) and the selection strength in an OU model, remain frequently used for measuring PNC in empirical studies. They seem appealing methods to study PNC as they are often thought to allow for a straightforward conclusion on PNC and can be easily applied. However, to acknowledge the limitations outlined in the previous section one would need to follow a much less simple workflow: 1. test assumptions, 2. apply appropriate measure, and 3. interpret results. At least step 1 and 3 of this workflow are not simple.

In step 1 the evolutionary model that best fits the data should be identified to allow judging whether assumptions of the measures of PNC are fulfilled (e,g PS requires BM). Such a model comparisons should not be based on the BM/white noise/OU₁ trilogy (Cooper, Jetz & Freckleton 2010; Wiens et al. 2010) because in doing so, one may misidentify complex scenarios of niche evolution as BM and single optimum OU processes as white noise (see Fig. 5). The necessity to carefully test model assumptions and to account for more complex OU models with different selection regimes in different parts of the phylogeny puts the advantage of simplicity already in a whole different light. In addition, there is good evidence from the literature and from our data that in most cases simple assumptions will not be fulfilled (Estes & Arnold 2007; Harmon et al. 2010; Uyeda et al. 2011).

In step 3 results of the simple measures need to be interpreted or in other words the question of what we learn from the applied simple measures needs to be answered. This interpretation depends on our ideas about PNC (Is it a process or a pattern? Which constraints are needed to produce PNC?). Therefore, calculating PS or the niche retention parameter δ in step 2 makes only sense if we accept that PNC is a pattern and that a random pattern suffices to indicate PNC (given that we can only unambiguously interpret PS when we assume a BM-like process), a view with which the authors of this paper disagree. We would like to highlight that phylogenetic signal of course remains useful when the interest is not in PNC but in measuring how strongly closely related species resemble each other in their niches compared to distantly related species, a question that has a very common application in community assembly studies (Webb et al. 2002).

If a single optimum OU process is identified as the underlying process of niche evolution then we could interpret the stationary variance as an indicator of PNC. Finally, evolutionary rate is a practical and simple informative approach. However, both evolutionary rates and stationary variance only inform us on the relative strength of PNC. So basically we cannot answer the question ‘is there PNC’ but need to reformulate to ‘which clades show more or less PNC than others’. If we want an answer for a specific clade we thus need to extend our analysis to related clades to be able to compare them with our focal clade. Again, this necessity to compare renders these approaches less simple than it seems on the first glance.

Overall, we conclude that a correct application of the simple measures is not simple at all in practice due to the required steps of assumption testing and interpretation. However, we would also like to mention that some simple measures, such as PS and evolutionary rate, could be used as simple preliminary tests of PNC because in many (but not all!) cases they may indicate PNC even if assumptions are not fulfilled. However, when applied without checking underlying assumptions, they should not be interpreted on their own but should only be used to motivate a more in-depth study of PNC.

Interesting but complex

The second answer comes down to the postulate that conclusions on PNC should be based on an improved understanding of the niche evolution process. This requires refining the question and analyses by allowing selective regimes to change over time and to differ between clades. Recent methodological developments provide the toolkit for such refined studies. They make it possible to fit highly flexible models where different processes are allowed to act in different parts of the trees (e.g. OU models with multiple optima, Ingram & Mahler 2013; Mahler et al. 2013). Our analysis of the evolution of body mass in 17 groups of mammals demonstrates that such flexible models with high numbers of parameters are often the ones best fitting the data. As larger and larger phylogenies are published, these models will most probably take an increasing importance in the study of PNC (Cooper, Jetz & Freckleton 2010; Wiens et al. 2010).

These more complex OU models can be intuitively interpreted as representations of the macro-evolutionary adaptive landscape, the analogue of Wright’s adaptive landscape over long periods of time (Simpson 1944; Ingram & Mahler 2013; Mahler et al. 2013). In this landscape, each different optimum of the OU model is an adaptive peak, which width is determined by the stationary variance of the OU process. Strict PNC in this landscape might be evidenced when only one peak is occupied by a clade. However, when comparing the number of different peaks, the number of transitions between them and the width of peaks in different clades, the relative importance of PNC can be assessed. Recent work based on compilations of evolutionary rates and divergence times demonstrated that models of bounded evolution in short timescales, with peak shifts occurring over longer timescales may constitute a good approximation to these processes (Uyeda et al. 2011). If disentangling a multi-peak OU model in its two components, i.e. number of peak sifts and selection strength towards a peak, then PNC is indicated either by relative few peak shifts or by relative strong selection (i.e. narrow peaks in the adaptive landscape). However, there is no null expectation for the number of peak shifts and the strength of adaptation and thus the analyses of a multi-peak OU model is foremost descriptive.

One may wonder how to go beyond this more descriptive interpretation of the fitted OU models and give guidelines to decide whether or not there is PNC in a clade of interest. Such a decision must be based on a comparison. Such a comparison could (1.) either be between the clade of interest and a related clade (more PNC is identified in the clade of interest if it has less and/or narrower adaptive peaks than related clades) or (2.) between the estimated model parameters in the clade of interest and expected values under a certain null hypothesis. (1.) The first comparison requires the availability of data from related clades and ideally some hypothesis of more or less PNC in one of the clades. This comparison between clades can benefit from additional information both on the selective environmental regimes and on species. For example, a very stable niche in one clade in comparison to a quickly changing niche in another clade may be driven by a stable adaptive zone (e.g. riparian habitats for Ginkgo biloba, Royer, Hickey & Wing 2003) in comparison to a more quickly changing environment promoting frequent shifts between adaptive peaks. If the past spatial distributions of the clades and the respective histories of environmental regimes are known, this hypothesis can be tested and an environmental constraint as a driver of PNC can be identified. On the other hand, if not the environmental regimes but multiple trait information are available, one may use these to compare clades. For example, if some traits evolve similarly in different clades while other traits show more PNC in one clade than in the other, this may indicate a very stable environmental regime for this clade that only selects the traits that show increased PNC (see Blomberg, Garland & Ives 2003 for such a comparison of traits with measures of phylogenetic signal). (2.) One may also compare estimated model parameters in the clade of interest and expected values under a certain null hypothesis. This second type of comparison requires a consistent definition of PNC that allows deriving expected values under null models. For example, if one accepts that pure BM can be termed PNC and that no further constraints besides kinship are required (this is, for example, the position of people advocating that PNC can be measured by phylogenetic signal), then either a model comparison test can be applied (PNC is identified if BM is the best model) or a flexile OU process can be fitted (PNC cannot be rejected if fitted selection strengths is not significantly different from zero and evolutionary rate is constant). If one defines PNC more strictly null expectations have to come from additional information. For example, PNC driven by population dynamics or genetic constraints may be identified by significantly fewer niche shifts in a clade than expected given information on the changes of driving selective environmental regimes. Formulating adequate null models and deriving expected values in specific case studies may be challenging and may fuel further debates. However, one of the strong advantages of this approach is that defining a null model requires openly presenting underlying assumptions. We hope that this will strengthen the discussions on conflicting assumptions in the debate on conflicting evidence for PNC in nature.

Conclusions

Revisiting the published work on PNC and analysing additional simulated and real datasets we come to the conclusion that the simple question ‘is there PNC in my clade of interest’ cannot be studied by simply applying a simple measure. The reasons are that

• Simple measures are not that simple as they require in-depth pre-test of the underlying assumption of a specific niche evolution models.

• Some simple measures are uninformative as they require BM but are pre-defined under BM. The common assumption that strong phylogenetic signal indicates PNC will be invalid most of the time.

• Simple measures become less simple if they require comparing values in the clade of interest with values in related clades (e.g. evolutionary rate).

We strongly advocate against being over-simplistic with both the question and the analysis when studying PNC. PNC needs to be well-defined such that the hypothesis of its presence is rejectable and the assumptions of approaches which are then applied need to be fulfilled. To date, the most promising approaches that we see for investigating PNC are

• Model comparisons excluding white noise model and instead including highly flexible OU models combined with a power test to avoid over-fitting

• Fitting flexible OU models that can be descriptively interpreted as macro-evolutionary adaptive landscapes, where PNC is indicated by relative few peak shifts or by relative strong selection strength. Tests of PNC in a focal clade that are based on a comparison either with related clades (for example by comparing evolutionary rates when one is only interested in the pattern perspective) or with well thought through null model expectations

Although parts of the problems that we highlight in this paper have already been published, they have not been considered in many applied studies. We hope that our paper helps to highlight and illustrate some of the most common problems and will pave the way to a better common practice.