Mortality Deceleration and Mortality Selection: Three unexpected implications of a simple model

Abstract

Unobserved heterogeneity in mortality risk is pervasive and consequential. Mortality deceleration—the slowing of mortality’s rise with age—has been considered an important window into heterogeneity that otherwise might be impossible to explore. This paper argues that deceleration patterns may reveal surprisingly little about the heterogeneity that putatively produces them. I show that even in a very simple model—one composed of just two subpopulations with Gompertz mortality—(1) aggregate mortality can decelerate even while a majority of the cohort is frail; (2) multiple decelerations are possible; and (3) mortality selection can produce acceleration as well as deceleration. Simulations show that these patterns are plausible in model cohorts that in the aggregate resemble cohorts in the Human Mortality Database. I argue that these results: challenge some conventional heuristics for understanding the relationship between selection and deceleration; undermine certain inferences from deceleration timing to patterns of social inequality; and imply that standard parametric models, assumed to plateau at most once, may sometimes badly misestimate deceleration timing—even by decades.

Unobserved heterogeneity in mortality is pervasive and consequential. All cohorts are heterogeneous in mortality risk in ways that are often stably ordered over the life course: if one person is higher-risk than another at young ages, they will also be higher-risk at older ages, should they both live that long. This heterogeneity gives rise to mortality selection: the frailest members of a cohort disproportionately succumb to mortality, eventually leaving an intensely selected, relatively robust cohort in its place (e.g., Beard 1959, 1971; Kannisto 1992; Vaupel, Manton, and Stallard 1979; Vaupel and Yashin 1985). This selection will in general occur unequally across social groups with different patterns of heterogeneity and overall levels of mortality risk. Such unequal selection substantially complicates efforts to understand inequalities in mortality risk—including inequalities driven by observable factors—across and within groups.

The challenge posed by mortality selection for accurately modeling differences in mortality arises in part because—unlike in a linear regression context—mortality selection can bias hazard models even when the omitted sources of mortality risk are unrelated at baseline to the covariates included in the model (Rodriguez 1994). There are many examples of the distorting effects of unobserved heterogeneity caused by mortality selection. Perhaps the most well-known is the black-white mortality crossover (e.g., Berkman et al. 1989, Dupre et al. 1996, Kestenbaum 1992, Lynch et al. 2003, Manton et al. 1979, Masters 2012)—one of many documented mortality crossovers (e.g., Rogers 2002)—which confounds racial inequalities operating at old ages with the intensified selection for robustness experienced by African-American cohorts. Other examples abound. A long-running demographic controversy is whether the well-documented narrowing over age of the mortality disparities by educational status reflects a true convergence of mortality trajectories—perhaps implying a biological limit to lifespan that even healthy behaviors and other advantages cannot overcome—or simply the operation of mortality selection among the higher-mortality less educated, masking a protective effect of education that continues into old age (e.g., Robert and House 2000, Zajacova et al. 2009). Assessing demographic theories about the effects of early-life health on later-life outcomes can also be confounded by mortality selection: the cost to individuals of negative childhood conditions can be masked by the robust composition of those who survive such conditions (e.g., Costa 2012, Palloni 2006). Unobserved heterogeneity can be deeply distorting to efforts to understand group-level inequalities and individual determinants of mortality.

The significance of unobserved heterogeneity in disguising how mortality inequalities unfold over a life course stands in stark contrast to the relative dearth of methods for exploring such heterogeneity. Without comprehensive individual-level measures of the determinants of mortality, population scientists can consider only the aggregate mortality of groups, aided by either parametric assumptions about the unobserved distribution of risk within those groups (in a long research tradition beginning with Vaupel et al. [1979]) or qualitative assumptions about the distribution across groups. Simply put, when dealing with a phenomenon that is by definition unobserved, options are limited.

In this context, mortality deceleration has been considered an important window into heterogeneity that otherwise might be impossible to explore. Mortality deceleration—the slowing of mortality’s rise with age—can occur as cohorts are systematically selected by mortality to disproportionately contain those most robust to death (e.g., Beard 1959, 1971; Kannisto 1992; Thatcher et al. 1998; Vaupel et al. 1979; Vaupel and Yashin 1985). Thus, deceleration has often been considered an important indicator of substantial prior selection—and thus of heterogeneity in the original cohort. Similarly, differential deceleration patterns across groups (e.g., cohorts or race and sex groups) has been used as evidence of differences between groups’ patterns of internal heterogeneity (e.g., Horiuchi and Wilmoth 1997, 1998; Lynch and Brown 2001; Lynch et al. 2003). Indeed, in the words of Lynch et al. (2003: 462), “measuring deceleration, compression and crossover is the means by which to examine heterogeneity within and between populations.”

Demographers have, however, also recognized that deceleration patterns are no panacea for understanding heterogeneity since deceleration in mortality risk may arise biologically at the individual level, not only from mortality selection at the group level. In particular, many experimental biodemographic studies have not found heterogeneity alone to be a plausible cause of observed deceleration in insect and animal populations (e.g., Carey et al. 1992, Curtsinger et al. 1992, Drapeau et al. 2000 [but see Steinsaltz 2005], Rauser et al. 2005, Vaupel and Carey 1993), and a smaller number of studies have reached similar conclusions for human data (Mueller et al. 2011, Steinsaltz and Wachter 2006; and see reviews in Vaupel 1997, Wachter and Finch 1997). If deceleration does arise for reasons other than selection, then heterogeneity might or might not interact with individual-level decelerating mortality to influence population-level rates, but deceleration would not constitute straightforward evidence of selection (see Steinsaltz and Evans 2004 for an elaboration of the argument that deceleration patterns alone are not telling evidence for any particular model that might give rise to them).

In this paper, I show that even if deceleration stems entirely from mortality selection on unobserved heterogeneity, those deceleration patterns still may reveal little about the heterogeneity that produced them. The reason is that even an exceedingly simple binary frailty model can produce deceleration and acceleration patterns sufficiently complex so as to defy some conventional models and predictions. In particular, I show that mortality can decelerate even while most of the cohort remains frail; that mortality can decelerate twice, even with only two subpopulations; and that mortality can reaccelerate, not only because mortality selection has already run its course (a possibility discussed by Vaupel and Yashin [1985]), but also—counterintuitively—because of the continued action of selection itself. These possibilities stem from a simple mathematical result: the rate of selection is greatest, ceteris paribus, when the frail and robust are each half of the cohort. Thus, this paper explores the relationship between the level of frailty in a cohort as it ages, its rate of selection, and the deceleration and acceleration patterns produced by those two things.

These results have two additional implications. As I show, parametric mortality models, such as logistic models, may badly misestimate deceleration timing—even by decades. And standard cross-cohort comparisons of deceleration timing may misstate the direction of inequality in mortality risk.

I begin by stating more explicitly some conventional expectations about mortality deceleration that these results call into question. For concreteness, I then provide an example of the kind of counter-intuitive pattern that the analysis shows to be possible, before presenting the key analytical result that provides the intuition for the mortality patterns explored. However, the complexity of the mortality derivatives makes it difficult to assess analytically when such counter-intuitive patterns will arise, so the main body of the paper presents the results of simulation models with parameters drawn from the Human Mortality Database. Simulations show that the surprising patterns described here can be pervasive in models with realistic parameters, and that the resulting problems with parametric mortality models and certain cross-group comparisons may also be widespread. Before concluding, I argue that, since the results explored here are precluded by widely-used gamma-distributed frailty models, these results suggest a need for more direct comparison of heterogeneity models.

Mortality Deceleration and Mortality Selection

Mortality Deceleration

Mortality deceleration is the label given to a class of mortality patterns deviating from the exponential mortality of the Gompertz model, which posits that mortality accelerates at increasing speed as a cohort ages. In operationalizing deceleration, demographers have variously highlighted different degrees of deviation from exponential mortality. Some focus on what I call relative deceleration, which occurs when mortality continues to accelerate, but does so more slowly than at younger ages. This begins when the third derivative (jerk) of aggregate mortality becomes negative, or, equivalently, when the second derivative begins to decline (Rau et al. [2009] compares the alternatives and advocates this measure). Others (Bebbington et al. 2007, Lynch and Brown 2001; Lynch et al. 2003) employ what I call absolute deceleration, which occurs when mortality is no longer accelerating at all: the second derivative (acceleration) is negative, and the first derivative has begun to decline.¹ In principle, cohorts may evince an even more extreme deviation from Gompertz mortality, mortality decline, which occurs when the first derivative (slope) is negative. Table 1 summarizes these measures. Here, I conceive of mortality deceleration as a process that begins with relative deceleration and may progress through absolute deceleration and even mortality decline, or may stop or reverse at any point. This paper is agnostic about which of absolute or relative deceleration, if either, is a preferable measure, and explores the properties of both. Accordingly, the crucial measures defining deceleration and reacceleration in what follows will be the signs of the derivatives of mortality.²

Table 1.

Three definitions of deceleration relative to Gompertz mortality

	Mortality, μ(a)
	Slope, μ′ (a)	Acceleration, μ″(a)	Jerk, μ″′(a)
Increasingly accelerating mortality	>0	>0	>0
Relative deceleration	>0	>0	<0
Absolute deceleration	>0	<0
Mortality decline	<0

Three Common Assumptions about Heterogeneity and Deceleration

Demographic work on mortality selection has been considerably advanced by efforts to articulate explicit intuitions about the conditions for mortality to decelerate. This paper shows that three such intuitions are wrong.

First, demographers frequently adopt the heuristic that mortality decelerates when the percent frail in the cohort reaches some low critical value. That heuristic seems to underlie some analyses of deceleration, particularly those that attempt to explicitly relate deceleration patterns to social inequality. For example, Lynch et al. (2003), which significantly advances the literature by providing one of the most explicit discussions of how characteristics of population heterogeneity affect deceleration timing, argues that:

A population with a large number of frail members relative to robust members will experience deceleration when mortality rates are higher (and potentially at a later age) than a population whose membership is equally distributed across frail and robust groups. In the former case, it simply takes longer for mortality to select out the frailer members [Lynch et al. 2003: 462; emphasis added]³

Heathcote, Puza, and Roberts (2009) makes a similar claim in a paper giving rare explicit consideration of the possibility that selection-induced deceleration may be followed by reacceleration in populations composed of several subgroups. Their paper shows that:

[T]here exist models of mixtures of Gompertz groups such that, depending on the extent of heterogeneity, there may be none, one or several age intervals of deceleration of the population hazard function interspersed with intervals of acceleration. Gompertz-like behaviour may then be resumed at extreme old age. An intuitive explanation is that deceleration occurs when the weakest group is dying out, followed by a brief assertion of Gompertz acceleration before the next weakest group dies out, and so forth. [Heathcote et al. 2009: 482; emphasis added]

Second, demographers commonly assume that mortality decelerates only once—at least if there are only two subpopulations. The assumption of a single deceleration is built into the standard parametric form used to model mortality deceleration, the logistic model (e.g., Bongaarts 2005, Kulminski et al. 2007, Rau et al. 2009, Thatcher 1999), as well as the alternative arctangent form used by Lynch and Brown (2001; Lynch et al. 2003). The expectation that multiple decelerations are precluded in a two-subpopulation model is made explicit in Heathcote et al. (2009), which proposes that, in a cohort with k heterogeneous closed subpopulations, mortality may decelerate in a maximum of k-1 intervals.⁴

Finally, it is common to conceptualize the derivatives of aggregate mortality as a competition between subpopulation acceleration, which leads the aggregate hazards to accelerate, and the declining frailty composition (driven by mortality selection) of the population, which leads the aggregate hazards to decelerate. Thus, reacceleration, when it is considered, is assumed to reflect the accelerating mortality of subpopulations, overwhelming the decelerating effect of selection. Mortality selection per se is assumed to produce only deceleration, never acceleration.⁵

In what follows, I show that each of these assumptions can fail.

An Example: High-Frailty Deceleration and Multiple Deceleration

To make concrete what follows, I begin by introducing as a running example a single simulated cohort, drawn from a class of simulated cohorts described in detail below. This cohort consists of two subcohorts, each with Gompertz mortality, with 75% of the cohort in the frail subpopulation at age 50.⁶

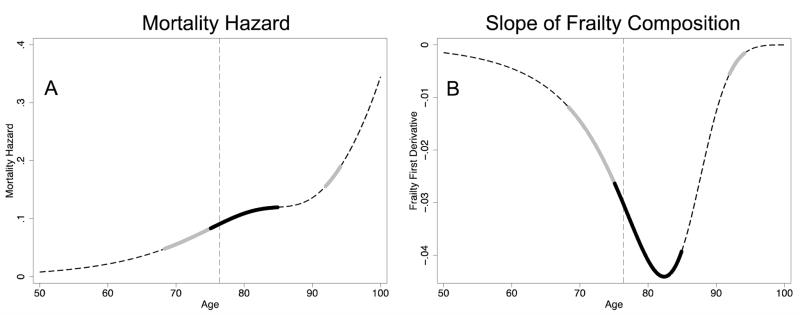
Fig. 1 displays this example cohort from ages 50–100 (by which age the frail are virtually extinct). Panel A of Fig. 1, which gives the aggregate mortality of the cohort over age, illustrates the counter-intuitive patterns at the heart of this paper. In this cohort, mortality increasingly accelerates until age 68, when the first interval of relative deceleration begins, with 66% of the cohort frail. At age 75, with 54% of the cohort frail, mortality decelerates absolutely; the second derivative remains negative until age 84 (16% frail), when a second period of increasingly accelerating mortality begins. This persists until age 91 (0.9% frail), when mortality again decelerates relatively until age 94 (0.2% frail), when the cohort enters increasingly accelerating mortality for the third and final time. Panel B shows the slope of the percent frail of the cohort. We will see that this slope—which, with its sign reversed, is the rate of frailty decline—drives much of the results to follow. In this cohort, frailty declines fastest at age 82, when the frail are 27% of the cohort. The dashed vertical line in both panels marks the point when the frail are half of the cohort, which will be shown to be a turning point in some of the selection dynamics explored in this paper. (The full set of derivatives of mortality and frailty for this cohort are shown in Online Resource 1.)

Figure 1.

Deceleration Intervals in Example Cohort. The left column gives the mortality hazard and the right column gives the slope of the frailty composition (the negative rate of mortality selection), both over age. The dashed dark lines represent Gompertz mortality; the thick grey lines, absolute deceleration; and the thick black lines, relative deceleration. The dashed light vertical line marks the point where the frail become a minority.

Analytical Intuition

High-Frailty Deceleration, Multiple Deceleration, and Selection-Driven Acceleration are Possible in Principle

The surprising mortality patterns shown here to be possible arise from the role played in the mortality derivatives by the rate of change in the cohort’s% frail. Specifically, it turns out that the level of frailty—the percent frail—plays two distinct roles in producing mortality acceleration and deceleration: a direct role (as already shown in Vaupel and Yashin [1985]), and an indirect role via the rate of selection. Here I show the key equations that provide the intuition; Online Resource 1 provides the full analytical results.

The model in this paper assumes that both subcohorts have Gompertz mortality, as shown in Eq. 1:

$${\mu }_r(x)=\alpha e^{\beta ·x}$$ (1a)

$$\begin{array}{r}{\mu }_f(x)=f\alpha e^{\beta ·x}=f·{\mu }_r,\\ f>1\end{array}$$ (1b)

The two subcohorts share a log-slope over mortality, β. That log-slope and the baseline level of robust mortality, α, are assumed to be greater than zero. The frailty multiplier, f, which is the ratio of frail to robust mortality at any age, is assumed to be greater than 1.

Cohort mortality at any age, and its derivatives, are functions of three parameters: the mortality of the robust, μ_r(x) ; the mortality of the frail, μ_f(x) ; and the percent of the cohort that is frail (the frailty composition), π(x), as shown in Eq. 2:

$$\begin{array}{l}\overline{\mu }(x)=\pi (x){\mu }_f(x)+(1-\pi (x)){\mu }_r(x)\\ ={\mu }_r[1+(f-1)\pi (x)]\end{array}$$ (2)

The crucial role in what follows is played by the slope of frailty composition, that is, by the rate at which the cohort is becoming less frail due to mortality selection. Equation 3, which provides the intuition for all results in this paper, shows that this slope is a function of the level of frailty composition and of the difference between frail and robust mortality:

$${\pi }^{\prime }(x)=-\pi (x)(1-\pi (x))\left({\mu }_f(x)-{\mu }_r(x)\right)$$ (3)

All terms in Eq. 3 are non-negative, and so the negative sign means that the slope is always negative: at all ages, mortality selection makes the cohort less frail. The absolute value of this expression can be considered the rate of selection. The binomial variance of the percent frail, π(x)(1 – (x)), is greatest when π(x)=.5. In other words, all else equal, the rate of frailty decline is greatest when half of the cohort is frail and half robust. Yet all else is not equal: the absolute difference between frail and robust mortality, π_f(x) – π_r(x), is greatest when the mortality of each subpopulation is greatest: at the oldest ages.

These two terms create the possibility that selection intensifies, and mortality decelerates, as π (x) hurtles downward toward .5; that selection attenuates, and mortality reaccelerates, as frailty declines further away from .5; and that selection reintensifies, and mortality decelerates again, at very old ages, when π_f (x) π_r (x) is very large (before mortality accelerates a final time with only the robust left alive). Yet the mortality derivatives are sufficiently complex that it is difficult to evaluate analytically whether to expect these patterns in cohorts with realistic parameters. To answer that question, I turn to simulations.

Simulation Results

High-Frailty Deceleration, Multiple Deceleration, and Selection-Driven Acceleration Occur Widely in Model Populations Compatible with the Human Mortality Database

Simulation Procedure

Four parameters define the mortality model: the intercept for robust mortality, α; the log-slope of mortality for both subpopulations, β; the frailty multiplier, or ratio of frail to robust mortality at any age, f; and the baseline percent frail, π₀. All four parameters are unobserved in real data, since subpopulation membership is latent by assumption. Thus, in generating realistic simulations, the goal is to find parameter combinations that generate aggregate cohorts whose parameters match those of real human cohorts. To minimize the role played by assumptions about unobserved parameters and maximize the role played by real data in the selection of simulations, I generate many candidate latent subpopulation models and keep only those whose aggregate parameters are consistent with the life tables of known cohorts.

The mortality hazards are calculated analytically, in instantaneous time. To limit the complexity over four dimensions, one parameter—baseline frailty composition—is set in all simulations at .75, a high value chosen to make visible the selection dynamics when frailty is common as well as rare. The baseline age is 50, which leaves the model agnostic as to whether mortality rises during late adulthood with the same log-slope as it had earlier in life.⁷ The model therefore assumes that 75% of the population surviving to age 50 is frail.⁸ Thus, these simulations represent cohorts in which mortality advantage, rather than disadvantage, is the exceptional condition.⁹ The frailty multiplier is modeled at eight values, ranging in units of .5 from 1.5 to 5; the low end represents fairly modest disadvantage, while the top end is at the extreme of what we might consider plausible for human populations.¹⁰ The intercept for the robust and the log-slope for the two subpopulations are varied nearly continuously, in increments of .001—in the range [.001,.2] for α and [.001,.4] for β. In total, this produces 640,000 simulated cohorts before evaluating the resulting parameters for plausibility.¹¹

To winnow these 640,000 simulated cohorts down to a realistic subset, I estimate a Gompertz model on each aggregated cohort,¹² and keep only the ones that fall inside a parallelogram formed around the intercept and log-slope parameters estimated from the 2,352 historical European cohorts collected in the Human Mortality Database (HMD).¹³ The parallelogram hugs the shape of the HMD cohorts (shown visually in Online Resource 2), so that cohorts included in the final simulation universe generally not only have a Gompertz intercept and slope similar to real (but distinct) cohorts; they have a combination of intercept and slope that is similar to at least one real cohort.¹⁴ The result is a universe of 1,151 simulated cohorts analyzed in this paper.¹⁵

Simulation Results

High-Frailty and Multiple Deceleration

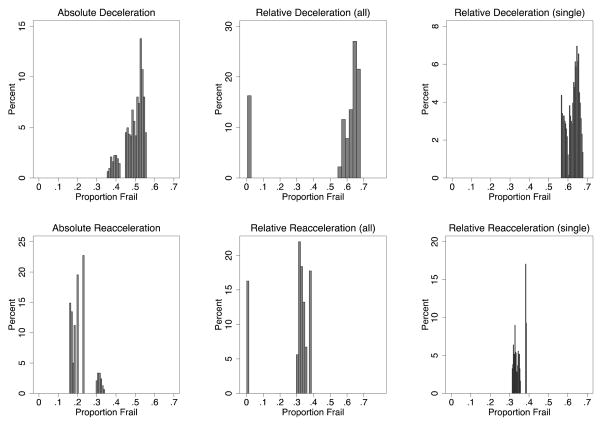
At what percent frail does deceleration and reacceleration occur in this universe? Figure 2 displays the frailty composition at absolute deceleration, relative deceleration as a whole, and relative deceleration restricted to cohorts that decelerate only once (each with their respective reaccelerations reflected in the bottom row). The results demonstrate the problems for the heuristics that mortality decelerates only once (one-third of the cohorts decelerate relatively twice) and only when the frail are nearly depleted. Panel A of Fig. 2 shows that absolute deceleration never corresponds, in these simulations, to the latter heuristic: absolute deceleration can occur when the frail are a majority or a minority, but never occurs here when they are less than 35% of the population. As shown in Panel B, reaccelerations following absolute deceleration, likewise, occur well before frailty depletion, when the frail are 15–34% of the cohort. Panels C and D, which show all relative decelerations, suggest that relative deceleration does sometimes occur as the heuristic would predict, with the cohort decelerating when the frail are nearly gone (in these cohorts, when frailty composition ranges between 0.5–1.2%) and reaccelerating shortly thereafter. But Panels E and F demonstrate that this pattern occurs only in the second of two decelerations. These panels are limited to the 67% of simulated cohorts with only one relative deceleration. They show that when there is a single relative deceleration, the deceleration occurs when most of the cohort is frail. In short, neither absolute nor relative deceleration corresponds to the conventional picture of a single deceleration when the frail are approaching extinction. (An analysis of where in the parameter space high-frailty and multiple decelerations occur is presented in Online Resource 2.)

Figure 2.

Proportion Frail at Deceleration/Reacceleration. The top row is deceleration, and the bottom reacceleration; the columns are, respectively, absolute deceleration, all relative decelerations, and relative decelerations limited to cohorts that decelerate only once.

Selection-Driven Acceleration

It seems intuitive to conceive of acceleration/deceleration as a tradeoff between accelerating subpopulations (producing acceleration) and declining frailty composition (producing deceleration). Yet declining frailty composition can also produce acceleration.

To underscore this point, I offer an artificial calculation as a device for isolating the role of declining frailty composition, illustrating what I call selection-driven acceleration. Starting from the example cohort given above (π₀=.75, f=5, α=.002, and β=.103), imagine that we could hold subpopulation mortality and its derivatives fixed at their levels at age 81—the age when the aggregate second derivative reaches its minimum (with 31% of the cohort frail)—while the percent frail is left varying as in the actual cohort. This calculation isolates the effects of the declining percent frail from those of increasing subpopulation hazards, slopes and accelerations. Figure 3 shows the results: while mortality does not reaccelerate nearly as dramatically without the changes in the subpopulation mortality, nevertheless it does reaccelerate. In this exercise, the declining rate of selection, as frailty falls further below half, leads mortality to reaccelerate even in the absence of subpopulation-level changes. This demonstrates that mortality selection can contribute to acceleration as well as deceleration.

Figure 3.

Acceleration Caused by Mortality Selection. The solid black line gives the artificial derivatives calculated by fixing subpopulation mortality and allowing frailty composition to decline as normal. The dashed dark gray line, provided for reference, is the actual derivative of the underlying cohort. The light gray zero line is provided for reference.

Further Implications

Bias in Estimated Age at Deceleration Using Common Parametric Models

Results so far suggest that, even in an exceedingly simple model, it is possible, indeed plausible, for cohorts to experience at least one period of deceleration followed by reaccelerating mortality. Yet the standard parametric forms used to model older ages—most often, logistic models (e.g., Bongaarts 2005, Kulminski et al. 2007, Rau et al. 2009, Thatcher 1999), and occasionally, very similar arctangent models (Lynch and Brown 2001; Lynch et al. 2003)—assume that mortality decelerates at most once and never reaccelerates. It turns out that this can lead such parametric forms to systematically misestimate deceleration timing.

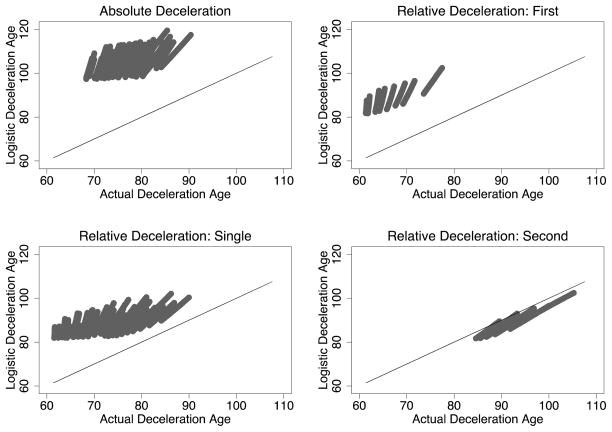
Fig. 4 plots the deceleration timing derived from two-parameter logistic models estimated on the simulated cohorts against the actual deceleration timing of those cohorts, with the main diagonal provided as a reference line.¹⁶ If the logistic models work well, the estimated deceleration ages should fall along (or near) this main diagonal. For most decelerations, they fall very far from it.

Figure 4.

Deceleration Age: Predicted from Logistic Models vs. Actual. The main diagonal is drawn for reference.

Panel A of Fig. 4 shows the results for absolute deceleration. The logistic models badly overestimate the age of deceleration, with the overestimation ranging between 18 and 39 years (28 years on average). Panels B, C, and D show the results for relative deceleration, considering, respectively, single, first, and second relative decelerations. Thus, panel B gives actual vs. estimated deceleration age for those cohorts that decelerate only once. Panels C and D each give the same outcome measure—deceleration timing estimated from logistic models on cohorts that decelerate twice—spread over two different regions on the horizontal axis, reflecting the cohort’s two deceleration points. These panels show that the logistic models fit poorly the deceleration patterns for first and single relative decelerations, and fit well second decelerations. Single deceleration ages are overestimated by 5 to 27 years (16 on average), and first decelerations by 17 to 28 years (22 on average). In contrast, the logistic models underestimate the age at (relatively rare) second relative decelerations by between 1 and 6 years (underestimating by only 3 on average).

Most troublingly, perhaps, the logistic models falsely detect deceleration with alarming frequency. Absolute deceleration is detected in all cohorts that decelerate only relatively. Most strikingly, relative and absolute deceleration are predicted in all cohorts that do not decelerate at all. The estimated age of relative deceleration for these cohorts ranges from 83 to 100 (mean 90), and absolute deceleration from 99 to 117 (mean 107).

These results are especially problematic for two reasons. First, the falsely detected decelerations are found at very similar ages to those identified in previous empirical research on the age at deceleration. Second, the magnitude of the error found in the estimation of age at deceleration—up to several decades—dwarfs the size of differences in deceleration timing interpreted substantively in the empirical literature, which are sometimes only a few years.¹⁷

It is routine in the demographic literature for logistic or similar parametric models to be estimated on mortality data without checking the raw data for evidence of multiple deceleration, or deceleration followed by reacceleration. This might be because the raw data are too noisy to support such investigation non-parametrically, but perhaps it is also because such deceleration patterns are not considered a serious possibility, or a serious source of model bias if they do exist. The latter two ideas are cast into doubt by these results. These results collectively suggest that it would be advisable for demographers whose primary object of study is deceleration not to rely solely on models that assume a single peak in mortality. It may be best to use these conventional parametric approaches alongside some effort to consider whether multiple deceleration, or deceleration with reacceleration, may be present in the data.

Comparing Deceleration across Cohorts

A central motivation for accurately measuring deceleration is that comparing deceleration timing across cohorts or other closed social groups may permit demographers to infer something about the differences in the cohorts’ distributions of mortality risk (Horiuchi and Wilmoth 1997, 1998; Lynch and Brown 2001; Lynch et al. 2003). This endeavor, which links the measurement of deceleration to the study of inequality and change in mortality, necessitates a qualitatively simple relationship between unobserved patterns of heterogeneity and observed patterns of deceleration. Accordingly, such reasoning was advanced considerably by Lynch et al. (2003), which articulated explicit predictions about the circumstances in which one cohort should decelerate at an older age and higher mortality level than another, and used those predictions to infer changes in mortality heterogeneity within racial groups.¹⁸ One of these predictions was quoted above: “A population with a large number of frail members relative to robust members will experience deceleration when mortality rates are higher (and potentially at a later age) than a population whose membership is equally distributed across frail and robust groups” (Lynch et al. 2003: 462). In this section, I show more explicitly how this prediction will sometimes fail.

To test this prediction using all the parameter combinations in the simulation universe, I compare deceleration timing in pairs of cohorts with fixed frailty multiplier f, robust intercept α, and log-slope β, but with baseline frailty composition π₀ varying in units of .05 from .05 to .75. Table 2 reports the proportion of pairs of cohorts for which the mortality or age at deceleration is greater in the cohort with greater baseline percent frail. For absolute decelerations and single relative decelerations, the prediction fares well (albeit imperfectly) for mortality, and poorly for age. For both mortality and age, the prediction is consistently validated for first relative decelerations (when these are separated from both second and single decelerations), but consistently disproved for second (low-frailty) relative decelerations. The latter is particularly important since, as shown above, it is these second relative decelerations, where the prediction fares worst, that are most closely matched by the estimated deceleration in logistic mortality models. In short, it is not necessarily the case that ordering decelerations across cohorts—by mortality or by age—can reveal which cohort had more frail members at birth, even assuming that the cohorts otherwise share the same mortality parameters.¹⁹ (These results are extended to consider the percent frail at deceleration, and an example set of cohorts is offered to illustrate the results in this section, in Online Resource 3.)

Table 2.

Proportion of cohorts for which mortality and age at deceleration increase with baseline percent frail

Deceleration Type	Mortality	Age
Absolute	.97	.23
Relative (single)	.80	.32
Relative (first)	1	1
Relative (second)	0	0
Relative (all)	.80	.35

Parameterizing Heterogeneity

The results in this paper do not readily generalize to the widely used models with gamma-distributed individual frailty and Gompertz individual hazards, since those models aggregate to a logistic (hence single-deceleration) hazard (Beard 1959, 1971). Such gamma-Gompertz models fit many data well (Steinsaltz and Wachter 2006, Missov and Finkelstein 2011) and have been very widely used (e.g., Gampe 2010, Horiuchi and Wilmoth 1998) ever since Vaupel, Manton, and Stallard (1979) pointed out their convenient properties, but whether they are appropriate for all populations or whether competing models might fit equally well is a question that should receive further attention (Steinsaltz and Evans 2004).

In particular, it is not clear which model might be preferable in cases of extreme stratification along unobserved dimensions. Gamma-Gompertz models differ from the dichotomous model used here in two respects: the heterogeneity they estimate is continuously distributed, and it is unimodal. In cases where one unobserved dimension of heterogeneity is so extreme that it swamps other sources of variation between individuals, it is not obvious a priori whether a continuous but single-peak model is a better approximation than a dichotomous one.

To the best of my knowledge, all previous models either capture continuous individual variation at the cost of imposing a unimodal distribution conditional on observed covariates (as in gamma-Gompertz models), or capture the clumping of individual variation that may result from categorical inequalities, such as racial inequality, at the expense of continuous individual variation (in discrete models, such as the model used here). The results presented here suggest that it may be useful to more directly compare discrete and gamma-Gompertz models, particularly in populations that may have unmeasured extreme, categorical stratification, since the models produce such divergent deceleration patterns. Further innovations in modeling heterogeneity, such as mixtures of gamma distributions—which could combine the potential virtues of continuous variation and multiple peaks—should also be explored in future research, including research into the deceleration and acceleration patterns such models may produce.

Since gamma-Gompertz models preclude the deceleration and reacceleration patterns described here, in principle, these theoretical results suggest a test of those models, by looking for multiple decelerations or reaccelerations in empirical data (analogously to Horiuchi and Coale’s [1990] classic work using higher moments to distinguish models generating similar estimated means). In practice, such a test would require very high quality data at old ages, since deceleration would need to be assessed nonparametrically.

Conclusion

Unobserved heterogeneity is a barrier to accurately modeling individual-level risk and group-level inequalities in many domains of mortality research, and options for investigating it are relatively limited. Mortality deceleration has been considered by many a promising avenue for assessing such heterogeneity. This paper has shown that drawing conclusions about heterogeneity from mortality deceleration is problematic for reasons that have not previously been articulated, by demonstrating three unexpected facts about mortality deceleration, which together have three broader implications for demographers. It has shown that even within a single cohort composed of just two subpopulations with proportional Gompertz hazards:

1. Mortality can decelerate even while a majority of the cohort is frail (high-frailty deceleration).

2. Mortality can then reaccelerate while the frail remain a non-negligible part of the cohort. This occurs because the rate of selection is greatest when half the population is frail, so that—counter-intuitively—selection of the frail out of the cohort can cause acceleration, not only deceleration, as the frailty composition dips below half (selection-driven acceleration).

3. Mortality can then decelerate a second time as the frailty composition dips further below half (multiple deceleration), before finally reaccelerating as the robust become such a large part of the cohort that their acceleration dominates over the negligible selection that remains possible.

These facts have three important implications. First, the first two facts challenge a conventional heuristic that has anchored important intuitions in previous demographic work, namely: the heuristic that mortality decelerates only as the frailty composition is ‘nearly’ depleted, and reaccelerates only as the frailty composition is ‘nearly all’ depleted. This paper shows that, while this pattern does occur, it is not the only—or even the main—pattern of deceleration and reacceleration possible in this simple mortality setting. The contribution of mortality selection to deceleration and reacceleration is more complex than has been previously articulated in the literature.

Second, the second and third facts suggest that conventional parameterizations of old-age mortality may lead analysts astray. Parametric forms used to identify the timing of deceleration, such as logistic (Bongaarts 2005, Kulminski et al. 2007, Rau et al. 2009, Thatcher 1999) or arctangent (Lynch and Brown 2001, Lynch et al. 2003) forms, assume a single mortality plateau. Not only will such parametric forms miss reacceleration and multiple deceleration when they occur; when such patterns occur, these parametric forms may misestimate—by decades—the timing of any deceleration point, as they average observations whose derivatives are significantly more complex than the forms assume. This is particularly problematic for purposes that compare deceleration timing across cohorts—and such comparisons are the central way that deceleration timing bears on inequality, within and across cohorts.

Finally, the three facts together qualify the link between deceleration patterns and inequality in one additional way. It turns out that—in contrast to an earlier prediction (Lynch et al. 2003) used to link deceleration patterns to changing heterogeneity among blacks and whites in the United States—all else equal, a cohort with greater baseline frailty composition can sometimes decelerate at lower mortality and younger ages than one with fewer frail members at baseline.

What is perhaps most startling is not only that such counter-intuitive patterns are possible, but that they are possible even in an exceedingly simple mortality model. Reality is bound to be more complex, and more complicated models may or may not create even less predictable deceleration dynamics. These results call for caution in modeling and interpreting mortality deceleration. More broadly, the results in this paper should urge demographers to deepen our theoretical understanding of the surprisingly complex ways that patterns of acceleration and deceleration arise from changing cohort composition. These results highlight the dangers of relying on intuitions about deceleration. They suggest a greater need for formal modeling of deceleration dynamics, and in particular, explicitly comparative modeling that matches the kinds of inferences about heterogeneity and inequality for which deceleration patterns have been used as evidence.