Computational Shape Models Characterize Shape Change of the Left Atrium in Atrial Fibrillation

Abstract

Shape change of the left atrium (LA) and LA appendage in atrial fibrillation (AF) patients is hypothesized to be linked to AF pathology and to play a role in thrombogenesis; however, many aspects of shape variation in the heart are poorly understood. To date, studies of the LA shape in AF have been limited to empirical observation and summary metrics, such as volume and its likeness to a sphere. This paper describes a more comprehensive approach to the study of the LA shape through the use of computationally derived statistical shape models. We describe practical approaches that we have developed to extract shape parameters automatically from the three-dimensional MR images of the patient. From these images and our techniques, we can produce a more comprehensive description of LA geometric variability than that has been previously possible. We present the methodology and results from two examples of specific analyses using shape models: (1) we describe statistically significant group differences between the normal control and AF patient populations (n = 137) and (2) we describe characteristic shapes of the LA appendage that are associated with the risk of thrombogenesis determined by transesophageal echocardiography (n = 203).

Introduction

Atrial fibrillation (AF) is the most common sustained cardiac arrhythmia and is currently estimated to affect around five million Americans.^1,2 AF is characterized by uncoordinated electrical activity and contractions in the left atrium (LA) and is associated with increased mortality and several morbidities, the most notable of which is that because of stroke. It is estimated that AF is the cause of up to 24% (200,000) of strokes in the United States per year.³ The role of the shape of the LA and other heart chambers in AF is not yet well understood, but is hypothesized to be an indicator of the AF pathology and to play a role in the formation of thrombus, a precursor to embolic stroke.^4–6 Thus, a better understanding of the structural changes of the LA because of arrhythmia could inform new diagnostic and therapeutic approaches to treatment and lead to new insights into the causes and maintenance of AF.

Advances in cardiac imaging, including contrast MRI with late gadolinium enhancement (LGE-MRI), have enhanced our ability to noninvasively assess changes to the structure and function of the LA in AF. LGE-MRI can even highlight microstructural changes in endocardial tissues relating to fibrosis, which are implicated in AF.^7–10 However, studies of the LA shape, as it relates to AF and its comorbidities, have traditionally been limited to empirical observation^11,12 and metrics that capture only limited information about the geometry of the heart, such as LA volume, normalized width measurements, or the extent to which its geometry resembles a sphere (“sphericity”).^13–15 The goal of this study was to identify a more descriptive and comprehensive model of the LA shape. To that end, we propose the use of computationally based models and related techniques from the field of medical image analysis to search for new diagnostic and therapeutic approaches.^16–22

Here, we describe a methodology for computational shape analysis of the LA and the left-atrial appendage (LAA) that is based on a technique called particle-based modeling (PBM),^16–19,21 which we have developed and used previously.^37–42 We adapted and validated these techniques for the LA in two studies of AF patient populations. First, we compared the endocardial shape of the LA in subjects with AF to that of healthy control subjects. We show that there are significant shape differences between the AF and non-AF patients who also characterize the severity of AF (paroxysmal vs. persistent). In the second study, we sought to establish a link between the shape of LAA and decreased blood flow in the LAA, a risk factor for the formation of thrombus, which can lead to cardioembolic stroke.⁴ All MRI data for the following studies were obtained retrospectively from a database of AF patient and healthy control MRI (“the Utah AF database”) that is maintained by the Comprehensive Arrhythmia Research and Management (CARMA) Center at the University of Utah. Patients were classified as having paroxysmal AF or persistent AF according to the ACC/AHA/ESC 2006 guidelines. Patient information gathered for the purposes of these studies was de-identified and protected in compliance with HIPAA regulations, and IRB approval was therefore not required.

Methods

Shape analysis pipeline

The image processing steps that we use to produce shape models from the MRI of the LA are as follows: first, AF patients undergo cardiac magnetic resonance angiography (MRA) and LGE-MRI to image the shape of the LA and fibrosis in the LA wall. Next, the LA and associated structures [pulmonary vein (PV) antrum regions, LAA, mitral valve (MV)] are segmented from the MRA and the LGE-MRI. Finally, the shape models are computed directly from the set of image segmentations using an open-source implementation of what is known as the particle-based shape modeling algorithm (PBM). The PBM method generates a set of parameters that represent different aspects of shape variation within the sample of images and forms the basis for statistical comparisons. The other sections describe each of the steps in the pipeline, as we implemented them, in more detail.

Cardiac MRI

Cardiac MR imaging was performed on AF patients presenting at the University of Utah Hospital’s Electrophysiology Clinic. Image sequences include a respiratory and ECG-gated MRA, acquired during continuous gadolinium contrast agent injection (0.1 mmol/kg, Multihance [Bracco Diagnostic Inc.]), followed by a 15-minute postcontrast LGE sequence.²³ Images were acquired on either a 1.5 T or 3 T clinical MR scanner (Siemens Medical Solutions) using phased-array receiver coils. LGE-MRI scans were acquired about 15 minutes after contrast agent injection using a 3D inversion recovery, respiration navigated, ECG-gated, gradient echo pulse sequence. Images were acquired at the end-diastole phase of the cardiac cycle. Figure 1 shows samples of good quality MRA and MRI. Typical image acquisition parameters include the following: free breathing using navigator gating, a transverse imaging volume with voxel size = 1.25 × 1.25 × 2.5 mm (reconstructed to 0.625 × 0.625 × 1.25 mm), and inversion time = 270–320 ms. Inversion times for the LGE-MRI scan were identified using a TI scout scan. Other parameters for the 1.5 T scanner included a repetition time of 5.4 ms, echo time of 2.3 ms, and a flip angle of 20°. Scans performed on the 3 T scanner were done using a repetition time of 3.1 ms, echo time of 1.4 ms, and a flip angle of 14°. ECG gating was used to acquire a small subset of phase encoding views during the diastolic phase of the LA cardiac cycle. The time interval between the R-peak of the ECG and the start of data acquisition was defined using cine images of the LA. Fat saturation was used to suppress the fat signal.

Figure 1.

MRA and LGE-MRI of the LA. (A) A single slice from a 3D MRA sequence of the LA, showing the endocardial boundaries of the LA, the antrum of the RIPV, and the AO. (B) A co-registered slice from the subsequent 3D LGE-MRI sequence of the LA wall, showing enhancement in the LA wall.

Image segmentation

Image segmentation was performed by expert observers on MRA volumes using a semiautomatic approach to delineate the boundaries in 3D of the LA and the LAA. Approximate boundaries of the LA and LAA were first segmented using an automated grow-cut algorithm,²⁴ and then further refined by manual contouring. Further manual segmentation of the LA wall boundary was done on the LGE-MRI, in order to define a region of interest for fibrosis identification and to define the location of attachment of the PVs and the MV. MRA and LGE-MRI were typically in good alignment because they were acquired in the same imaging session; however, to increase alignment accuracy further, we performed affine registration by using maximization of mutual information.²⁵ Fibrotic regions were identified in the LA wall using a supervised thresholding process by expert observers, as described previously in Refs.^7,9,26,27. Total segmentation time for a single patient case was about 45 minutes. We used the Corview software (Marrek, Inc.) for all image processings, which was developed at the University of Utah for cardiac image segmentation. An example of segmentations of an LA endocardial surface, with attached PVs are illustrated in Figure 2, which shows (a) a single slice from an LA segmentation of the endocardial wall and attached structures and (b) a 3D surface rendering of the LA endocardial surface and PVs.

Figure 2.

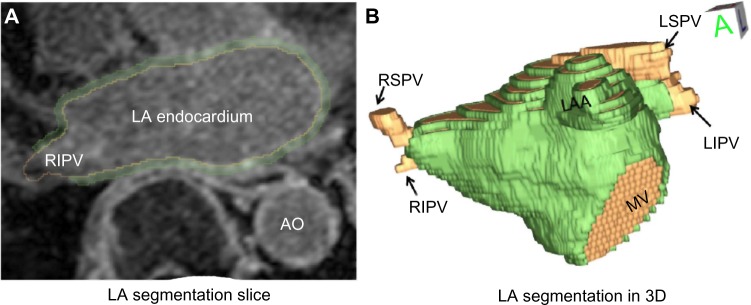
An example of LA segmentation from the MRA and LGE-MRI. (A) A single slice from a segmentation of the LA wall (LGE-MRI). (B) A surface rendering of the LA segmentation, showing attached PVs, MV, and the LAA.

Particle-based shape modeling

A variety of computational shape modeling approaches have been proposed, but two major categories are common. The first strategy is to consider the shape geometry as embedded in the image intensity values at pixels or voxels, and then use nonlinear image registration to map all the sample images to a reference image.^28–33 A second approach to shape modeling, and the one that we used in this study, is to extract surface contours from digital images, and then sample them in a systematic way to produce an arbitrarily dense set of homologous landmark positions. These methods, called point-based models,³⁴ are the computational extension of traditional morphometric landmarking approaches. Morphometric approaches require manual identification of small sets of landmarks on images or physical samples (see Refs.^35,36 for review). By contrast, computationally derived point-based models consist of dense sets of hundreds or thousands of landmarks that are computed automatically. These dense sets of landmarks are called correspondence points and are able to model shape geometry in much greater detail than traditional manual approaches.

In order to compute the correspondence points for our shape models of the LA and LAA, we use a specific optimization algorithm called PBM. The development of PBM is described in a series of papers from our laboratory^20,37–40 and has proven to be effective for the investigation of scientific and clinical questions in a range of applications, including neuroscience,^16,19,39,41 biological phenotyping,^42,43 and orthopedics.^43,44 PBM represents the correspondence points as interacting sets of particles that redistribute themselves under an energy optimization. The optimization finds correspondence positions that minimize the entropy of the model, which is a metric of information content. By minimizing information content, PBM learns the shape parameters that are the most efficient descriptors of the geometry of the LA, thereby maximizing the model’s statistical power and generalizability. PBM is also particularly well suited for the LA (and other heart structures) because its particle system formulation can accommodate holes in a surface, such as the MV openings and PV openings. PBM is also able to capture areas of higher detail, such as folds and ridges, by increasing particle sampling rates in regions of higher surface curvature.¹⁶ For our experiments, we use an open-source distribution of the PBM algorithm called ShapeWorks, which was developed at the University of Utah.

Shape parameters and statistical analysis

The mathematics and theory behind point-based shape models have been developed over the last several decades and is described in many excellent reference texts and papers.^45–48 Here, we briefly summarize the major concepts that are relevant to the results presented in this paper. We define a point-based shape model as a collection of n sets of k correspondence points (3D landmark positions). In our case, n represents the number of LA or LAA segmentations and k is the number of correspondence points placed on each shape. Thus, each LA surface geometry is represented by a unique set of k 3D points. Correspondence among the LA segmentations is determined by running the PBM algorithm to produce a set of k correspondence points x. Point x_i on segmentation number 1 corresponds to point x_i on segmentations 2, 3, 4,…, n, where i = 1,…, k. Note that increasing k allows for a more detailed representation of the LA shape, while decreasing k would produce a model that is more coarse.

The average shape geometry in a point-based model is defined as the set of averages of each of the k correspondence points. Similarly, the variability in geometry can be described by the variability in each of the k correspondence points. All shapes in the model are normalized with respect to scale, such that the root-mean-square distances of the correspondence points to their centroids are equal to one.⁴⁷ Note that normalizing with respect to the scale means that we are analyzing the geometric variability that remains after the scale is removed. Our intention is to perform an analysis that is independent from uniform volume change in the LA, the latter having been previously shown to correlate with AF.^49–52

The geometric variability of a PBM point model can be summarized as a set of shape parameters that are the orthogonal directions of a principal components analysis (PCA) of the correspondence point positions. A complete mathematical description of this process can be found in Refs.^34,47. PCA-based shape parameters allow us to compress the very large amount of geometric information into a much smaller representation of shape that is suitable for traditional statistics, while still retaining most of the geometric information of the shapes. Typically, we choose a finite number of shape parameters m for analysis, either empirically, or by picking a set that accounts for most of the variability in the model (eg, 95% is often chosen). The latter is a standard approach to model the selection that assumes the remaining parameters, containing relatively small amounts of variance, are likely the result of noise from the imaging, segmentations, or other sources. Once the m PCA shape parameters are chosen, every LA shape in the cohort can be represented for statistical analysis as an m-dimensional vector of scalar values, where m is typically less than 10. We can also conduct empirical analysis of the variability in shape by reconstructing shapes from arbitrary combinations of different values of m parameters. For example, we can examine the change in the shape described by each PCA parameter as we move between ±3 standard deviations from the mean in that parameter, a technique we employed for the LA shape analysis, as described below.

Shape analysis experiments

We applied PBM shape modeling in two studies of the shape of the LA and the LAA in AF. The first study was a basic investigation of the shape of the LA endocardial surface in AF patients compared to non-AF controls. The second study addressed the question of whether the shape of the LAA is associated with indicators for stroke risk, specifically the presence or absence of spontaneous echocardiographic contrast (SEC) in transesophageal echocardiography (TEE).

The statistics package R⁵³ was used for all analysis. Continuous variables such as surface area (mm²) are presented as mean ± standard deviation. Shape parameters and other continuous data were analyzed by the unpaired Student’s t-test and Hotelling’s T² test, where normally distributed, or otherwise by permutation testing. A probability value of P < 0.05 was considered to be statistically significant.

Left-atrial endocardial shape in AF

The Utah AF database was queried for patients who underwent MRA of the LA with paroxysmal AF (n = 50), persistent AF (n = 50), and no history of arrhythmia (n = 37). After segmentation of the LA endocardium, we constructed PBM shape models for the LA endocardial surface using 1024 correspondence points per segmentation. We computed the volume of each LA chamber from their endocardial image segmentations. The PVs were excluded prior to shape modeling. We performed PCA to define the characteristic shape parameters and chose the shape parameters describing 95% of the variation for analysis. Summary of patient characteristics for the LA shape study are described in Table 1. We performed multivariate Hotelling’s T² test and Student’s t-test for significant differences in the group mean values of our shape parameters, with the null hypothesis of equivalent mean values across groups.

Table 1.

Patient cohort characteristics for the LA shape study.

	CONTROL (n = 37)	PAROXYSMAL (n = 50)	PERSISTENT (n = 50)
	Mean (std dev)	Mean (std dev)	Mean (std dev)
Age (years)	47.6 (17.2)	67.8 (11.4)	68.0 (11.7)
Height (cm)	169.9 (8.5)	171.0 (10.3)	173.1 (10.1)
Weight (kg)	79.1 (16.9)	82.5 (18.6)	89.4 (23.2)
BMI (kg/m2)	27.1 (5.8)	28.1 (5.5)	29.6 (6.5)
	Number (percent)	Number (percent)	Number (percent)
Female gender	22 (59)	24 (48)	24 (48)
Coronary artery disease	2 (5)	12 (24)	8 (16)
Hypertension	14 (37)	27 (54)	29 (58)
Diabetes mellitus	3 (8)	12 (24)	24 (48)
Mitral valve regurgitation	2 (5)	2 (4)	2 (4)
Congestive heart failure	3 (8)	2 (4)	10 (20)
Stroke	4 (11)	4 (8)	4 (8)

LAA shape and TEE findings

For this study, we identified a cohort of 203 patients from the Utah AF database who had also undergone TEE to evaluate LAA thrombi. These are patients who were imaged before undergoing either radiofrequency ablation or cardioversion for restoration of normal sinus rhythm. In a TEE screening, the LAA was classified as normal, SEC present, or thrombus present. SEC is an indication of decreased blood flow in the LAA and is thus considered a risk factor for thrombus formation. For our study, we identified 57 patients with SEC present and 147 patients classified as normal. The patients with thrombus were excluded because of their relatively low frequency in our database. (AF patients are generally on anticoagulation therapy, and thus unlikely to develop thrombi.) The LAA endocardium was segmented from LGE-MRI for each patient. We constructed PBM shape models of the LAA using 256 correspondence points and identified the shape parameters that described 95% of the variation in the model for analysis. Summary of patient characteristics for the LAA shape study are described in Table 2. We performed multivariate Hotelling’s T² test and Student’s t-test for significant differences in the group mean values of our shape parameters, with the null hypothesis of equivalent mean values across groups.

Table 2.

Patient cohort characteristics for the LAA shape study.

	NO TEE SEC (n = 147)	TEE SEC PRESENT (n = 57)
	Mean (std dev)	Mean (std dev)
Age (years)	64.6 (11.8)	70.1 (9.5)
Height (cm)	174.3 (10.9)	173.7 (12.0)
Weight (kg)	90.14 (19.5)	87.6 (19.5)
	Number (percent)	Number (percent)
Female gender	53 (36)	27 (47)
Coronary artery disease	26 (18)	12 (21)
Hypertension	94 (64)	42 (74)
Diabetes mellitus	18 (12)	17 (12)
Mitral valve regurgitation	17 (12)	3 (5)
Congestive heart failure	16 (11)	9 (16)

Results

Left-atrial endocardial shape in AF

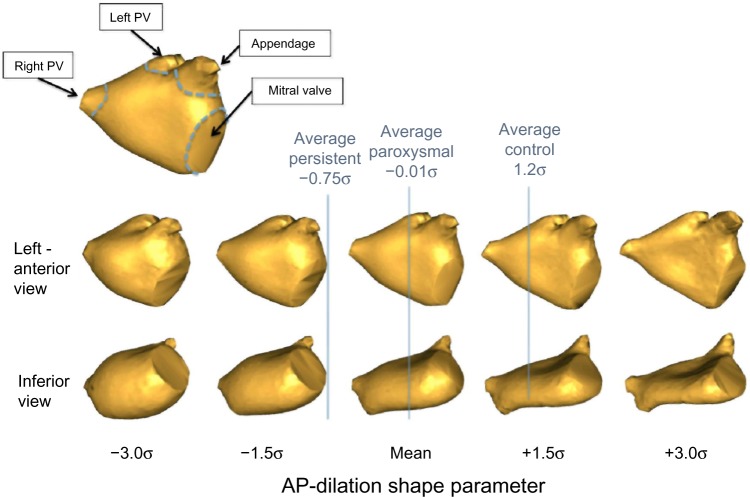
Using the PBM shape model of endocardial LA shape, we performed group-wise comparisons of the mean shapes between the non-AF, paroxysmal AF, and persistent AF groups. We chose the top eight PCA shape parameters from the model for analysis, which collectively account for 95% of the variation. The multivariate Hotelling’s T² test using these shape parameters indicated highly significant differences in group means between the control vs. paroxysmal groups (P < 0.0001), the control vs. persistent groups (P < 0.0001), and the paroxysmal vs. persistent groups (P < 0.001). Closer inspection of the shape parameters revealed that shape parameter 1, which accounts for 21% of the total model variation, captured most of the significant shape differences between the groups. Empirically, the majority of this variation appeared to correspond to a dilation of the LA in the anterior–posterior (AP) direction. Accordingly, we will refer to this shape variation as the AP-dilation parameter. Note that because the AP-dilation parameter was represented in the first PCA mode, expansion in other orthogonal dimensions (inferior–superior, left–right) exhibited lower variability in our population.

Figure 3 compares the distributions of the AP-dilation shape parameter in each of the three groups, along with a right-superior-posterior view of the shape variation described by the parameter. Student’s t-test showed that the means of all these distributions were all well separated (P < 0.001). The interpretation of the LA shape and specifically AP-dilation variation is further illustrated in Figure 4, which depicts two orthogonal views of the mean LA shape, and the shapes corresponding to ±1.5 and ±3 standard deviations of the shape parameter. Labeled vertical lines in the figure also show that the LA shapes from patients with paroxysmal and persistent AF were clustered toward the dilated (negative) end of the spectrum, while shapes from the control population were clustered in the more flattened (positive) end of the spectrum. There was also some shape change in the right–left and inferior–superior directions, though not as pronounced. Finally, we note that the LA shape parameter also appeared to capture some of the variation in the length of the ostia of the PVs. However, given the difficulty in defining consistent boundaries of the ostia during segmentation, it is possible that this apparent variation in the ostia simply reflected segmentation error.

Figure 3.

Distribution by group of the AP-dilation shape parameter. Reconstructed LA shapes described by this parameter are shown in the left. Note that control shapes tend to cluster at the positive, less-dilated end of the spectrum, while AF shapes cluster at the negative, more-dilated end, with persistent AF showing more strongly negative values. (Note that the units are not physical units, but units of the PCA shape parameter.)

Figure 4.

Shape variation described by the AP-dilation shape parameter. Two views of reconstructed LA shapes along a spectrum of ±3 standard deviations (σ) from the mean. The dilation is clearly visible in the inferior view. Positions of the average shapes in each group are also shown.

Shape, as defined by our PBM model, is normalized with respect to the overall scale, which means that the AP shape parameter that we identified as the dominant mode of variation in this patient cohort was independent of any uniform size changes, for example, because of increased volume. To investigate the correlation of the LA shape with volume, we performed a linear regression correlation analysis between volume measurements and the AP-dilation parameter over the entire patient cohort and the control group. LA volume was significantly increased in patients with paroxysmal AF (85.1 mL) relative to controls (57.3 mL), patients with persistent AF (116.9 mL) relative to controls, and between the two symptomatic patient groups (all P < 0.001). Linear regression also showed significant correlation of volume with the AP-dilation parameter over the entire patient cohort (P < 0.0001) and in the control group (P < 0.0001). However, there was no correlation between shape and volume in the paroxysmal and persistent AF subgroups, as shown in Figure 5.

Figure 5.

Correlation of LA volume with the AP-dilation shape parameter. Volume correlates with shape in the entire cohort and with the control group, but is not correlated with shape in the paroxysmal and persistent AF groups.

LAA shape and TEE findings

Using the PBM shape model of the LAA, we performed groupwise comparisons of the mean shapes between the patients whose TEE findings showed SEC (the SEC group, assumed to be at risk of thrombosis) and the patients who had no SEC (the no-SEC group). The first nine PCA shape parameters of our model contained 95% of the model variation, and a multivariate Hotelling’s T² test on these parameters indicated that there were significant differences in shape between the group means (P = 0.007). In particular, the mean values of the first two shape parameters of our LAA model were significantly different, with P = 0.028 for the first parameter and P = 0.004 for the second. These two parameters described 36% and 13% of the total shape variation, respectively.

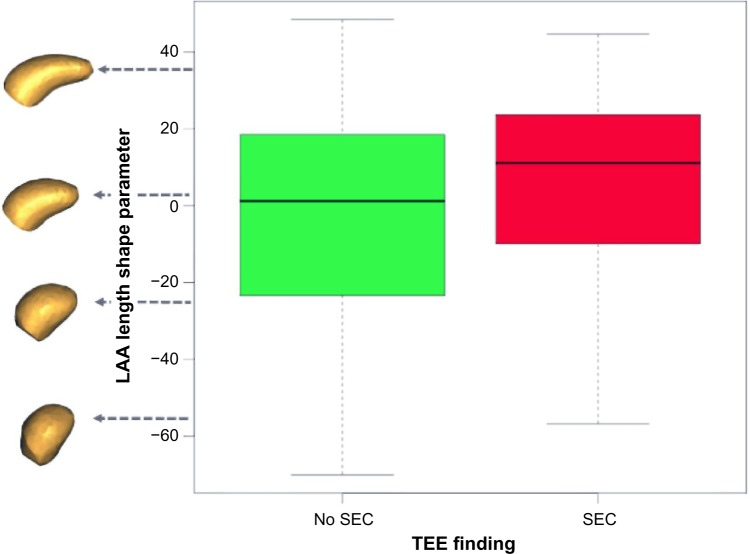
Empirically, the first mode of our shape model appeared to capture a large component of the length of the LAA, as well as describing some of its thickness. We will refer to this parameter as the “length” parameter for brevity. The distribution of this parameter for both the normal (no SEC) and SEC groups is shown with box plots in Figure 6, along with the reconstructed LAA shapes at positions within the distribution, shown at the left edge of the box plots. The top row of the associated Figure 7 depicts reconstructed LAA shapes across a spectrum of ±2 standard deviations (σ) from the mean for the “length” shape parameter (right-anterior-superior view). Higher likelihood of SEC is found at the higher end of the spectrum, where the LAA shapes are longer and thinner.

Figure 6.

The LAA length shape parameter describes significant group differences between patients where SEC is present in TEE examinations and those where no SEC is found, P = 0.028. Longer, thinner LAA shapes tend to show more SEC than shorter, thicker shapes. (Note that units are not physical units, but units of the PCA shape parameter.).

Figure 7.

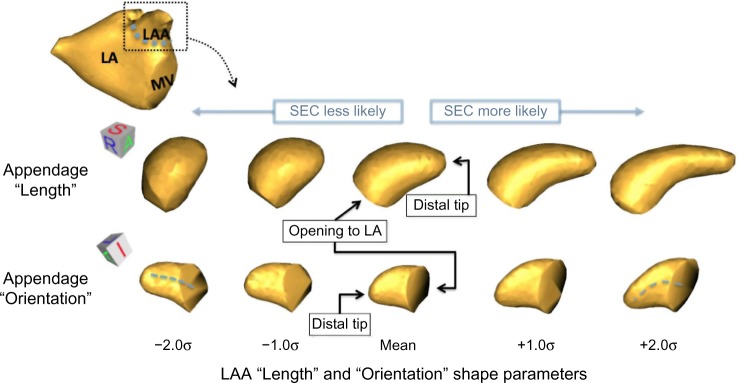
Shape variation of the LAA that describes significant group differences between SEC and non-SEC TEE findings. Reconstructed LAA shapes along a spectrum of ±2 standard deviations (σ) from the mean for the first (“length”) shape parameter (top row) and the second (“orientation”) shape parameter.

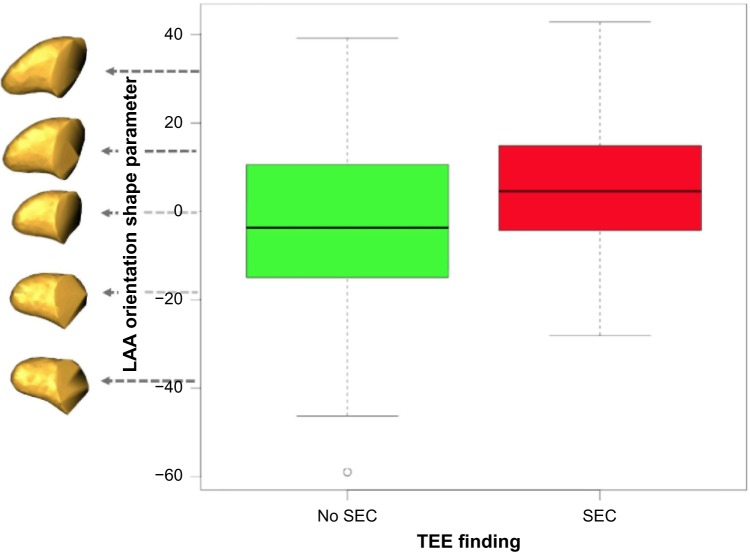
The second shape parameter of our model for LAA variation described more subtle and complex shape changes than the first. Empirically, this shape parameter appeared to capture aspects of the orientation of the LAA, relative to the LA. The distribution of this “orientation” parameter for both the normal (no SEC) and SEC groups is shown with box plots in Figure 8, along with the reconstructed LAA shapes at positions within the distribution. LAA shape along a spectrum of ±2 standard deviations (σ) is shown in the bottom row of the associated Figure 7 (left-anterior-inferior view). From these figures, we see that SEC was more likely to be found in patients whose LAA shape was more curved and extended anteriorly, rather than in a straighter LAA that was oriented in a more superior direction. Other subtle shape differences included a slightly narrowed appendage tip in patients exhibiting SEC.

Figure 8.

The LAA orientation shape parameter describes significant group differences between patients where SEC is present in TEE examinations and those where no SEC is found, P = 0.0004. LAA that are curved anteriorly tend to show more SEC than shapes that extend straight in a left-superior direction. (Note that units are not physical units, but units of the PCA shape parameter.)

Discussion

The purpose of this study was to explore the value of a novel approach to analyzing the shape of the heart in identifying differentiating features in patients with various stages of AF. The study applied recent techniques in particle-based methods (PBM) of statistical shape analysis to high-quality MRI from a cohort of patients and controls, in order to identify relationships between shape variation and the progress and risk factors of AF. Our results indicate that there do appear to be shape parameters that can identify both patients at different phases of AF and even those who may be at risk of subsequent embolic stroke.

Major findings from our PBM analysis of the LA and LAA include: (1) a strong statistical association between AP dilation of the left-atrial chamber and AF, which also increases with the severity of AF and (2) a parameterization of the characteristic shapes of the LAA that are more likely to exhibit decreased blood flow and hence risk of stroke, as measured by TEE.

Our structural findings for the LA in AF populations support and agree with the previous findings in the literature. Bisbal et al describe an association in AF between LA endocardial shape and its degree of “sphericity,” which is defined by a univariate metric of the geometric difference of the LA from that of a sphere. In Refs.^13,14, the authors show a correlation between sphericity and AF recurrence after radiofrequency ablation and a reverse-remodeling toward a less spherical geometry after successful ablations. Given that increased AP dilation is associated with AF, our findings are consistent with earlier studies of sphericity, but provide a more refined and focused description of the nature of the associated shape changes than previously described.

Our AP-dilation shape findings are also similar to those reported using an “asymmetry index” in Nedios et al.¹⁵, who defined asymmetry as an AP LA width measurement that is normalized by LA volume. Nedios et al reported significant (P = 0.002) differences in asymmetry between AF paroxysmal patients and controls, which are consistent with the (scale normalized) AP-dilation findings in our study, though with lower statistical power. Therefore, our results are further evidence that LA dilation in the AP direction correlates with AF burden.

Increase in LA volume is well known to be correlated with an increase in AF burden and has been studied previously.^49–52 Our results also support the hypothesis that LA volume is significantly increased in AF and further increased with AF severity (volumes in patients with paroxysmal AF are larger than in those with persistent AF). Our computational shape analysis using PBM suggests at least one hypothesis that may help explain the specific geometric nature of that volume change, specifically, that the width in the AP direction increases with AF and AF severity, ie, that the volume increase occurs primarily in the AP direction, rather than uniformly. Note that AP dilation, which is independent from volume, was automatically derived in our study without a priori assumptions regarding shape differences. It also provides a higher-power discrimination between our AF and non-AF populations than volume alone (P = 0.0001 vs. P = 0.001).

The LAA is thought to play a significant role in the formation of thrombi in AF that can lead to cardioembolic stroke.^5,54–56 Unfortunately, the characteristic shape of the LAA is particularly difficult to describe, in part because of the significant amount of variability exhibited in the population and the difficulty of obtaining accurate 3D imagery of the structure in vivo. Thrombus formation is likely a complex interaction between hemodynamic factors, the shape of the LAA, and the tissue substrate of the LAA wall. Our results, however, suggest that there may be shape-related indices that can provide insight into risk and mechanism of thrombus and stroke. Specifically, we found two shape parameters that were associated with stagnant blood flow in the LAA (as measured by TEE). One advantage of the PBM modeling approach for the LAA is that it learns optimized shape parameters from the data, conferring a potential advantage for statistical power in highly variable data like LAA shape.

Of the two LAA shape parameters associated with increased SEC in TEE, the first corresponded strongly to overall LAA length and is perhaps more easily interpreted. One hypothesis is that a longer and narrower tubular structure for the LAA might be more restrictive of blood flow in the chamber, leading to increased stagnation and, thus, observed SEC. The second shape parameter, which seemed to correspond in part to the orientation of the LAA, exhibited more complicated and subtle variation. However, the SEC and no-SEC groups were actually better separated statistically based on this parameter than on the first (P = 0.024 in the first vs. P = 0.0004 in the second). Other researchers have recently shown correlation between LAA orientation and embolic stroke risk⁵⁷ that support our findings. However, we are unable to formulate specific hypotheses regarding LAA orientation in our present study because our models do not include the LA shapes. We anticipate that joint PBM models of the LA and LAA will be useful in the future investigation of such questions of LAA positioning and orientation.

All these findings are observational in nature, and further research, ideally using controlled animal models, is clearly needed to investigate hypotheses regarding the mechanisms of shape change in AF, such as the weakening of the wall because of fibrosis and the involvement of structures attached to the LA.

In summary, we have presented translational research in the application of new computational image analysis tools to the study of the heart in AF. We have described an image processing workflow using PBM that may serve as a template for other researches into structural analysis of the heart. Through automated learning of shape descriptors, we remove a priori assumptions of shape and may gain unexpected insights into the function and structure of biological systems. Additionally, the increased geometric detail inherent in computational models can describe much more subtle variation in shape than can be observed directly from the images. While further progress is required to translate and validate complex mathematical tools like PBM for the clinical research domain in general, this study has demonstrated its potential for measuring cardiac shape in the challenging setting of AF.