Abstract
Circadian rhythmicity in humans has been well studied using actigraphy, a method of measuring gross motor movement. As actigraphic technology continues to evolve, it is important for data analysis to keep pace with new variables and features. Our objective is to study the behavior of two variables, interdaily stability and intradaily variability, to describe rest activity rhythm. Simulated data and actigraphy data of humans, rats, and marmosets were used in this study. We modified the method of calculation for IV and IS by modifying the time intervals of analysis. For each variable, we calculated the average value (IVm and ISm) results for each time interval. Simulated data showed that (1) synchronization analysis depends on sample size, and (2) fragmentation is independent of the amplitude of the generated noise. We were able to obtain a significant difference in the fragmentation patterns of stroke patients using an IVm variable, while the variable IV60 was not identified. Rhythmic synchronization of activity and rest was significantly higher in young than adults with Parkinson׳s when using the ISM variable; however, this difference was not seen using IS60. We propose an updated format to calculate rhythmic fragmentation, including two additional optional variables. These alternative methods of nonparametric analysis aim to more precisely detect sleep–wake cycle fragmentation and synchronization.
Keywords: Actigraphy, Fragmentation, Synchronization, Amplitude, Activity, Rest
Background
The rest–activity rhythm in humans is commonly studied using actigraphy, a technology which measures gross motor movement. Adjusting a cosine function to actigraphic data provides parameters that are used in circadian rhythmicity studies. The parameters that describe rhythm characteristics include: amplitude, mesor, acrophase, and period. However, as the rest–activity rhythm does not behave exactly as a cosine function, other variables have been studied and new methodologies have been developed. Since these variables are not associated with parameters of a known function, they are called nonparametric.
In 1990, such nonparametric variables were primarily proposed by Witting et al., who had studied the effect of age and Alzheimer׳s disease on rest–activity rhythm [12]. These variables quantify the main characteristics of the rest–activity circadian rhythm, such as intradaily variability (IV), which quantifies the rhythm fragmentation; interdaily stability (IS), which quantifies the synchronization to the 24-h light–dark cycle; the average activity during the least active 5-h period, or nocturnal activity (L5); and the average activity during the most active 10-h period, or daily activity (M10).
Rhythmic fragmentation and synchronization are measured, respectively, by IV and IS. Intradaily variability quantifies the frequency and extent of transitions between periods of rest and activity on an hourly basis [12,10,11]. High IV values indicate the occurrence of daytime naps and/or nocturnal activity episodes. Interdaily stability quantifies rhythm׳s synchronization to zeitgeber׳s 24-h day–night (or light–dark) cycle.
Studies have shown that IV is an excellent variable for analysis, as it serves as a marker of sleep–wake cycle disturbances [6]. Assessment of interdaily variability in an elderly population shows a more fragmented rest–activity rhythm (high IV values) [6]. Researchers have also observed higher values of IV in patients with Alzheimer׳s disease when compared to controls [12,5]. Aging and Alzheimer׳s disease are factors that contribute to the degeneration of the suprachiasmatic nucleus [9,13], which may explain rhythm fragmentation. Furthermore, it was demonstrated that high IV (high rhythm fragmentation) is associated with decreased sleep quality [3], decreased cognitive functions [7] and decreased circadian rhythm amplitude [12,10].
On the other hand, high IS values indicate good synchronization of zeitgeber׳s 24 h cycle, and good operation of the circadian timing system׳s (CTS) components, which are connected to photic and nonphotic synchronizations. This synchronization can be influenced by age, neurological disorders, and lifestyle. In terms of aging, the synchronization to zeitgeber׳s cycle increases the CTS maturity level [14]. The rhythm stability measured by IS has a direct relationship with quality of life measures. Studies have shown that IS is directly related to rhythm amplitude and light exposure [12,10], Mini Mental State Examination [4], and sleep quality [3]. A well synchronized rhythm is associated with less fragmentation, less nocturnal activity, and better cognitive, behavioral, and emotional functioning [12,4].
Studies using the nonparametric approach, such as those cited above, have calculated the fragmentation and stability of rhythm using a 1 h interval for analysis. However, new actimetry sensor models have been developed, and with the increase in storage capacity, limitations on sampling rates have been overcome. Now that current actimetry sensors are able to record data at a variety of intervals instead of only 1 h, it is possible for rhythm fragmentation data to be analyzed at different intervals. For this reason, we propose a new method of quantifying fragmentation and synchronization data by extracting sampling intervals from 1 min to 60 min. In our study, we used a simulated time series of human and experimental animal rest–activity records obtained by the use of three different devices.
Methods
In the present study we used an artificially created time series with known behavior and data recorded from human and experimental animal studies. The simulated data allowed us to verify the performance and robustness of the new methodology. The rest–activity experimental records were obtained using three different devices, data from human studies, and animal models.
Simulated series
To construct the simulated data we used two types of time series: (i) random data with normal distribution (equal to 1 mean) known in physics as noise, and (ii) a sinusoidal wave with amplitude equal to 1 and whose negative values were replaced with zeros. The duration of these series corresponded to 60 cycles of 1440 min each, thus simulating 60 days with a sampling rate of 1 min.
Based on these two types of time series, we created three types of simulated data. The first consisted of a sinusoidal wave with a period equal to 1440 min multiplied by a noise (mean=1 and standard deviation varied). The second set was similar to the first; however, the mean of the noise (which in previous conditions was equal to 1) varied every 30 min. The third set consisted of sinusoids with periods of 480, 1440, 1470, and 1500 min.
Experimental data
Our data were obtained from three different systems: (i) an actimetry sensor Actiwatch®-16, trademarked by Mini-Mitter Co., which recorded the acceleration variation in three axes at a 32 Hz frequency and stored the accumulated value each minute; (ii) an actimetry sensor by Tempatilumi, CE Brasil, which recorded the variation in acceleration that occurred each minute; and (iii) infrared motion sensors that recorded the locomotor activity and stored the total movements every 5 min. These three systems were used to verify the behavior of variables IV and IS in connection with the proposed method to analyze the data obtained by different devices. In addition, we have used two different animal models, rat (nocturnal and polyphasic) and marmoset (daytime and biphasic).
The Actiwatch was used to record the locomotor activity during one week in two groups: (i) 24 healthy people (38–69 years), and (ii) 52 patients with cerebrovascular accident (55–75 years). The motor activity of 26 patients with Parkinson׳s disease (42–76 years) and 24 healthy young individuals (18–23 years) were analyzed using Tempatilumi during one week. In the animal studies, the motor activity of 6 rats and 8 marmosets was recorded during one week using the sensor system as they remained in cages. The animals were kept in light conditions with a cycle of 12 h light and 12 h dark.
The study was approved by the Federal University of Rio Grande do Norte׳s Institutional Review Board (CEP-HUOL: the University Hospital Onofre Lopes׳ research ethics committee code: 048/09 and 302/09), and conducted in accordance with the criteria established by Resolution 196/96 of the Brazilian National Health Council.
Data analysis
From the actigraphy experimental data, four nonparametric variables were calculated: IS, IV, M10, and L5 [12]. In our study we modified the method of calculation for IV and IS by modifying the time intervals of analysis. The fragmentation (IV) was calculated as the ratio of the mean squares of the first derivative and its population variance. The interdaily variability (IV) was calculated for resampled ranges between 1 and 60 min. The IV, calculated with a 1 h interval, was named IV60. Based on the IV profile, we estimated two parameters of interest: (i) mean IV for each sampling interval (IVm); and (ii) IV for an interval equal to 60 min (IV60). The existing normalization in IV calculation can make this index insensitive to large variations in data amplitude. To verify this, two time series formed by simple noise were used with variance equal to 0.05 and 0.5.
Interdaily stability (IS) was calculated with data sampled every 60 min (IS60); and the mean IS for the sampling intervals divisors of 1440 between 1 and 60 min (ISm). The intervals were 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 32, 36, 40, 45, 48 and 60 min.
We used various sizes of simulated data to verify variable IS behavior. The analysis was performed in two sine functions: one with a period equal to 1470 and the other at 1500 min. Moreover, in this data, IS was calculated simulating different records sizes.
Results
Simulated data
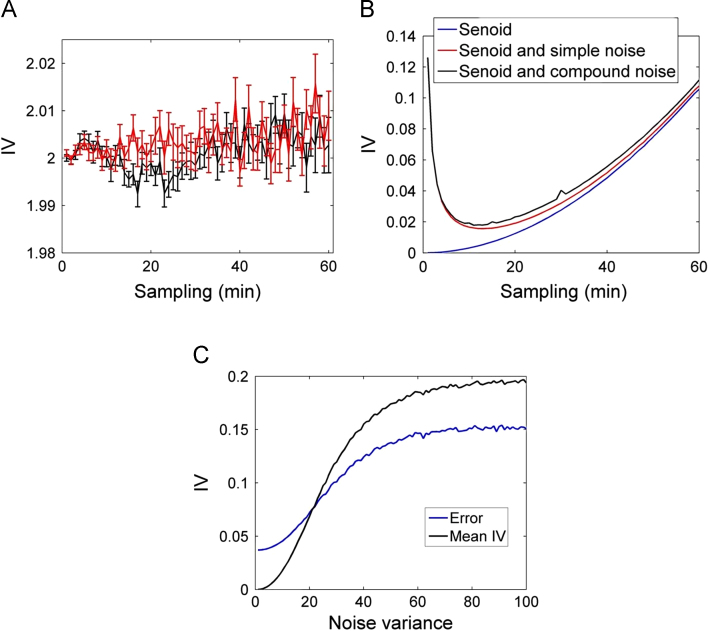
The first analysis was performed using two random data groups with a normal distribution. Both presented a mean of 1, but the first group׳s variance was 0.05 and the other presented variance equal to 0.5. The IV calculation (Fig. 1A) showed noise amplitude and sampling rate independence. There were no significant differences between groups regarding the sampling method (n=100).
Fig. 1.
Calculation of fragmentation simulated data in different conditions. (A) Profile IV calculated for randomly distributed data with equal variances 0.05 and 0.5; (B) IV calculated for three types of simulated signals, pure sine wave, sine and noise with single sinusoid plus noise compound; (C) analysis of behavior of IVerro and IVm parameters for different intensities of noise modulated by a sinusoid.
Interdaily variability was calculated for each simulated time series group: the pure rectified sinusoid function, sinusoid with simple noise, and sinusoid with compound noise (Fig. 1B). For all calculated IV intervals, the time series with compound noise showed the highest values, whereas the series with pure sinusoid showed the lowest IV values. An increase in the compound noise IV profile was observed after 30 min.
In order to evaluate the noise effect on IV values, we changed the noise value modulated by sinusoid variance from 0 to 2, and calculated IVm and IVerror. By increasing the noise variance value, we also increased IVm and IVerror (Fig. 1C).
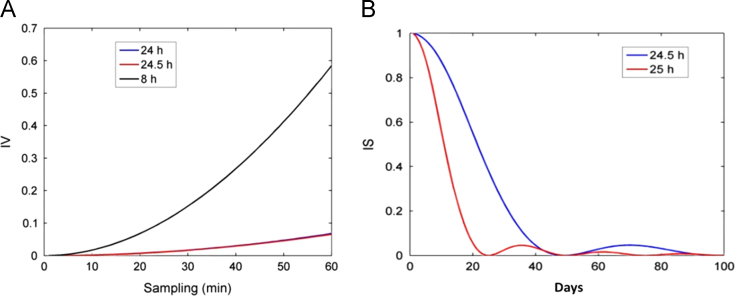
Nonparametric variables were also calculated for different periods of sine functions: 8, 24 and 24.5 h (Table 1). The IV profile for sin24 and sin24.5 were found to be similar; however, it differed from the sin8 IV profile (Fig. 2A). In order to evaluate rest–activity rhythm stability, IS60 and ISm were calculated for series of the same amplitude but with different periods and durations. IS60 and ISm values were equal to 1 for both sin8 and sin24, as the other variables presented different values; this is explained because 8 h is a multiple of 24 h. Functions sin24 and sin24.5 presented different IS values, although the other variables presented similar values. In addition, the IS60 value for sin24.5 and sin25 were reduced by increasing the length of time analyzed, suggesting that IS60 values depend on the analyzed time series size (Fig. 2B).
Table 1.
Values of non-parametric variables for the three sine waves with period equal to 24, 24.5 and 8 h.
| Variable | T=24 | T=24.5 | T=8 |
|---|---|---|---|
| IS60 | 1 | 0.5517 | 1 |
| ISm | 1 | 0.5518 | 1 |
| IV60 | 0.0680 | 0.0658 | 0.5835 |
| IVm | 0.0233 | 0.0225 | 0.2033 |
| M10 | 1043.8 | 1049.7 | 709.6933 |
| L5 | 21.2004 | 20.361 | 160.3758 |
Fig. 2.
Calculation of fragmentation and the stability of the rhythm in sinusoids with different periods of simulated data. (A) IV measured profile for the three sinusoids with a period of 8.24 h and 24.5; (b) behavior of is 24.5 for two sinusoids of different lengths and 25 h in days.
Experimental data
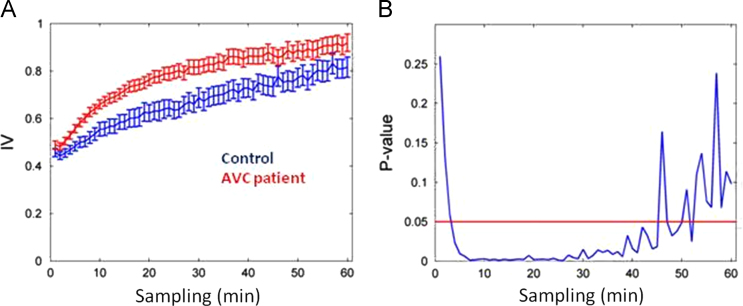
The results obtained using the Actiwatch showed that patients with cerebrovascular disease have reduced activity compared to the control group (Table 2). Analyzing IVm, we found that these patients׳ rhythm was more fragmented. On the other hand, when using IV60, no significant difference was found between groups (Student׳s t-Test). The IV profile was calculated for the control group and patients with cerebrovascular disease (Fig. 3A). In all calculated intervals, the mean IV was higher for the patient group. There were significant differences for different intervals using Student׳s t-Test, shown in Fig. 3B.
Table 2.
Values of non-parametric variables for the control group and patients with stroke.
| Control | AVE | p-Value | |
|---|---|---|---|
| IS60 | 0.6381 (0.0907) | 0.6182 (0.1442) | 0.5361 |
| ISm | 0.5267 (0.0822) | 0.4940 (0.1142) | 0.2119 |
| IV60 | 0.8162 (0.2090) | 0.9190 (0.2649) | 0.0983 |
| IVm | 0.6648 (0.1626) | 0.7834 (0.1769) | 0.0068 |
| 3.438e5 (1.098e5) | 2.466e5 (1.203e5) | 4.0341e−13 | |
| L5 | 10,805 (7769) | 10,564 (833.06) | 0.7894 |
Fig. 3.
Calculation of fragmentation of the circadian rhythm of activity and rest recorded at Actiwatch. (A) Calculation of profile IV data of the control group and patients with stroke; (B) level of statistic difference between the control groups. For each re-sampling values of the two groups IV and were calculated by two-tailed t-test value was obtained from p.
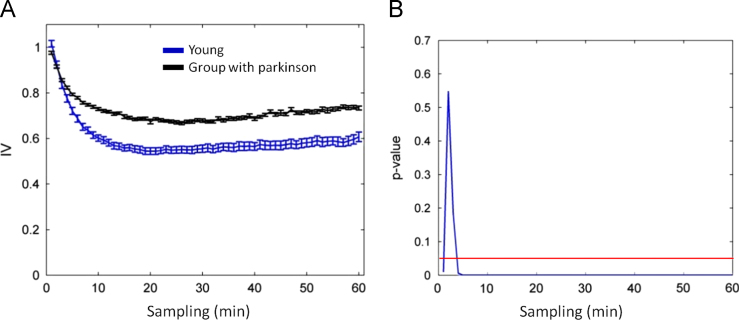
Analysis of the Tempatilumi data demonstrated that people with Parkinson׳s disease (PD) showed reduced activity compared to young individuals (Table 3). The rhythm of the oldest population was more fragmented when analyzing the following variables: IVm, IVerror, and IV60. As for synchronization, we found a tendency (p=0.0583) between groups, as the young individuals were more synchronized to zeitgeber׳s 24 h cycle. The IV profile was calculated for each group (Fig. 4A). In all calculated intervals, the mean IV was higher for patients with PD. There were significant differences for different intervals (Fig. 4B) (Table 4).
Table 3.
Values of non-parametric variables of the young and oldest group with Parkinson׳s.
| Young | Oldest +Parkinson | p-Value | |
|---|---|---|---|
| IS60 | 0.5498 (0.1287) | 0.4871 (0.1053) | 0.0647 |
| ISm | 0.4254 (0.1028) | 0.3688 (0.0812) | 0.0349 |
| IV60 | 0.6069 (0.6069) | 0.7336 (0.0435) | <0.0001 |
| IVm | 0.5970 (0.0683) | 0.7182 (0.0288) | <0.0001 |
| M10 | 76,148 (7015) | 68,800 (1011) | <0.0001 |
| L5 | 5781 (883.67) | 5936 (688.92) | 0.4891 |
Fig. 4.
Calculation of fragmentation of the circadian rhythm of activity and rest recorded at Tempatilumi. (A) Calculation of profile IV data of young and old with Parkinson׳s; (B) level of statistic difference between groups. For each resampling the IV values of the two groups and were calculated by two-tailed t test was obtained p value.
Table 4.
Values of non-parametric variables for the group of rats and marmosets.
| Marmoset | Rat | p-Value | |
|---|---|---|---|
| IS60 | 0.6111 (0.1529) | 0.4455 (0.1435) | 0.0781 |
| ISm | 0.5067 (0.1436) | 0.3529 (0.1061) | 0.0643 |
| IV60 | 0.8571 (0.3275) | 0.9834 (0.3259) | 0.5121 |
| IVm | 0.6951 (0.2052) | 0.9198 (0.1613) | 0.0628 |
| IVerror | 0.6694 (0.2052) | 0.8941 (0.1613) | 0.0628 |
| M10 | 5041 (1737.4) | 12,132 (5463.2) | <0.01 |
| L5 | 0.6656 (0.8381) | 823.433 (529.5) | <0.01 |
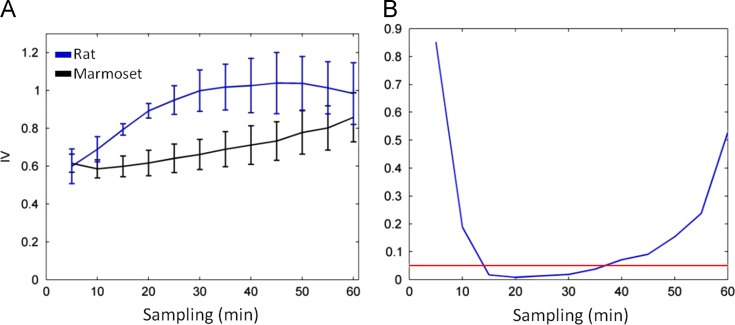
Analysis of the data obtained from animals using infrared sensor showed that rats׳ rhythm was more fragmented at intervals 15, 20, 25, 30, and 35 (Fig. 5A). Rats presented higher values for M10 and L5 when compared to marmosets.
Fig. 5.
Calculation of fragmentation of the circadian rhythm of activity and rest recorded with infrared sensor. (A) Calculation of rats and marmosets IV profile; (B) Level of statistical difference between groups. For each resampling the IV values of the two groups and were calculated by two-tailed t test was obtained p value.
Discussion
The main contribution of this study is the implementation of alternative methods of nonparametric variables analysis which aims to more precisely detect sleep–wake cycle fragmentation and synchronization. The statistical analysis of the simulated data showed its methodological ability to detect fragmentation in known intervals. In addition, the IS calculation, using different re-samplings, enables a higher sensitivity of this methodology. In regards to the time series size, we observed that it is important to be careful when using IS index.
It was not possible to detect rhythm fragmentation in patients with cerebrovascular disease using the classical IV calculation with a 60 min sampling. However, when using different sampling rates, it was observed that patient rhythm was more fragmented than in the control group. As in other studies [10], the use of variable IV60 was not efficient to detect differences in sleep fragmentation in both groups. We propose that by utilizing only the IV calculated for the 60 min interval, one may lose the sensitivity needed to determine rhythm fragmentation. The new method appears to be more sensitive to rhythm fragmentation. Moreover, by calculating IVm and IVerror, significant differences were observed between the groups, with the IV60 p-value approximately 14 times greater than that calculated for IVm and IVerror. This greater sensitivity shall encourage the use of this new method. Furthermore, to our knowledge there are no reports demonstrating that IV calculated by hourly sampled data is the best method to identify rhythm fragmentation.
The IV profile on the data collected with the Tempatilumi device showed a greater fragmentation at sampling intervals of 1–8 min. This pattern is similar to the one observed in the noise profile+sin24. This is likely due to the equipment׳s recording methodology, which measures acceleration in three axes, then repeats the procedure at 1 min and records the acceleration variation. This method ignores the movements which occur between one measurement and another. This should create a type of noise that is modulated by the circadian rhythm, such as the simulated data.
In the animal data, fragmentation calculated every hour showed no significant differences in rhythm between rats and marmosets. In addition, neither of new variables IVm identified a significant difference in fragmentation, only a tendency (both with p-value equal to 0.0628). However, in sampling intervals of 15–35 min, the rhythm fragmentation in rats was greater than that found in marmosets. This may be explained by the alternation in rats׳ sleep phases, which occur in periods of 15–35 min [1,2].
The simulated data analysis has shown the proposed method robustness. Noise analysis, even with different amplitudes, was not significantly different. The compound noise analysis showed that it is possible to identify a distinct peak at 30 min of a known interval. The pure sinusoid presented the lowest IV values and by increasing the modulated noise amplitude using sinusoid, there was an increase in IV.
Similarly to Van Someren et al., we have also found IV random data values next to two [10]. The method robustness was demonstrated with the simulated data analysis. Random data with different amplitudes showed high IV in all intervals, and no significant differences. This can be explained by the IV equation in which the denominator is the data population variance.
Pure sinusoid showed the lowest IV value, as there was a small variation between measurements. Ortiz-Tudela et al. have also found IV60 close to zero for sine wave [8]. IV values grew as we increased noise multiplied by the sinusoid. Ortiz-Tudela et al. calculated IV equal to zero for sine wave, which increased as noise was included [8].
Our study demonstrated that the calculation of the synchronization to the 24-h light–dark cycle (IS) was significantly related to the length of the time series analyzed. Simulated data showed that this relationship is greater as the free-running period approaches 1440 min. This finding can be applied for both simulated and experimental data. IS was calculated by dividing data into 1440 min intervals (light–dark cycle external period); therefore, to calculate the mean IS (ISm), it was applied interval divisors of 1440. Our data showed that in all studies, ISm value is more sensitive and can even present a significant difference when compared to IS60.
Our study proposes the use of a more sensitive method for circadian rhythm analysis that may improve the study of the rest–activity rhythm in humans. Traditional 60 min data analysis of IV calculation (IV60) in cerebrovascular disease patients was not able to detect significant differences between groups. The same results were obtained by many other studies that adopted the same method of analysis. With the implementation of the proposed method of analysis, it will be possible to increase the sensitivity of the circadian rhythm fragmentation and synchronization measurements.
Conclusions
The results of this study suggest new variables for circadian rhythm studies: mean IV for each sampling interval (IVm) and mean IS for sampling intervals divisors of 1440, between 1 and 60 min (ISm). In our knowledge this is the first study to propose a more sensitive method of detecting circadian rhythm alterations.
Competing interests
The authors declare no competing interests.
Acknowledgments
We thank CNPq – 305290/2009-6 and FAPERN – 20231195722003 for financial support.
References
- 1.Araujo J.F., Marques N. Circadian and ultradian rhythms of drinking behavior of albino rats maintained in constant darkness. Braz J Med Biol Res. 1996;29:1369–1372. [PubMed] [Google Scholar]
- 2.Araujo J.F., Marques N. Ultradian rhythms in albino rats during the light phase. Biol Rhythm Res. 1996;27:351–357. [Google Scholar]
- 3.Bromundt V., Köster M., Georgiev-Kill A., Opwis K., Wirz-Justice A., Stoppe G. Sleep–wake cycles and cognitive functioning in schizophrenia. Br J Psychiatry. 2011;198(4):269–276. doi: 10.1192/bjp.bp.110.078022. [DOI] [PubMed] [Google Scholar]
- 4.Carvalho-Bos S.S., Riemersma-van der Lek R.F., Waterhouse J., Reilly T., Van Someren E.J. Strong association of the rest–activity rhythm with well-being in demented elderly women. Am J Geriatr Psychiatry. 2007;15(2):92–100. doi: 10.1097/01.JGP.0000236584.03432.dc. [DOI] [PubMed] [Google Scholar]
- 5.Hatfield C.F., Herbert J., van Someren E.J., Hodges J.R., Hastings M.H. Disrupted daily activity/rest cycles in relation to daily cortisol rhythms of home-dwelling patients with early Alzheimer׳s dementia. Brain. 2004;127(Pt 5):1061–1074. doi: 10.1093/brain/awh129. [DOI] [PubMed] [Google Scholar]
- 6.Huang Y.L., Liu R.Y., Wang Q.S., Van Someren E.J., Xu H., Zhou J.N. Age-associated difference in circadian sleep–wake and rest–activity rhythms. Physiol Behav. 2002;76:597–603. doi: 10.1016/s0031-9384(02)00733-3. [DOI] [PubMed] [Google Scholar]
- 7.Oosterman J.M., van Someren E.J., Vogels R.L., Van Harten B., Scherder E.J. Fragmentation of the rest–activity rhythm correlates with age-related cognitive deficits. J Sleep Res. 2009;18(1):129–135. doi: 10.1111/j.1365-2869.2008.00704.x. [DOI] [PubMed] [Google Scholar]
- 8.Ortiz-Tudela E., Martinez-Nicolas A., Campos M., Rol M.A., Madrid J.A. A new integrated variable based on thermometry, actimetry and body position (TAP) to evaluate circadian system status in humans. PLoS Comput Biol. 2010;6:e1000996. doi: 10.1371/journal.pcbi.1000996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Swaab D.F., Fliers E., Partiman T.S. The suprachiasmatic nucleus of the human brain in relation to sex, age and senile dementia. Brain Res. 1985;342(1):37–44. doi: 10.1016/0006-8993(85)91350-2. [DOI] [PubMed] [Google Scholar]
- 10.Van Someren E.J., Hagebeuk E.E., Lijzenga C. Circadian rest–activity rhythm disturbances in Alzheimer׳s disease. Biol Psychiatry. 1996;40:259–270. doi: 10.1016/0006-3223(95)00370-3. [DOI] [PubMed] [Google Scholar]
- 11.Van Someren E.J., Swaab D.F., Colenda C.C., Cohen W., McCall W.V., Rosenquist P.B. Bright light therapy: improved sensitivity to its effects on rest–activity rhythms in Alzheimer patients by application of nonparametric methods. Chronobiol Int. 1999;16:505–518. doi: 10.3109/07420529908998724. [DOI] [PubMed] [Google Scholar]
- 12.Witting W., Kwa I.H., Eikelenboom P., Mirmiran M., Swaab D.F. Alterations in the circadian rest–activity rhythm in aging and Alzheimer׳s disease. Biol Psychiatry. 1990;27:563–572. doi: 10.1016/0006-3223(90)90523-5. [DOI] [PubMed] [Google Scholar]
- 13.Zhou J.N., Hofman M.A., Swaab D.F. VIP neurons in the human SCN in relation to sex, age, and Alzheimer׳s disease. Neurobiol Aging. 1995;16(4):571–576. doi: 10.1016/0197-4580(95)00043-e. [DOI] [PubMed] [Google Scholar]
- 14.Zorzona-Moreno M., Fuentes-Hernández S., Sánchez-Solis M., Rol M.Á., Larqué E., Madrid J.A. Assessment of circadian rhythms of both skin temperature and motor activity in infants during the first 6 months of life. Chronobiol Int. 2011;28(4):330–337. doi: 10.3109/07420528.2011.565895. [DOI] [PubMed] [Google Scholar]