Calculation of dose conversion factors for doses in the fingernails to organ doses at external gamma irradiation in air

Abstract

Absorbed doses to fingernails and organs were calculated for a set of homogenous external gamma-ray irradiation geometries in air. The doses were obtained by stochastic modeling of the ionizing particle transport (Monte Carlo method) for a mathematical human phantom with arms and hands placed loosely along the sides of the body. The resulting dose conversion factors for absorbed doses in fingernails can be used to assess the dose distribution and magnitude in practical dose reconstruction problems.

For purposes of estimating dose in a large population exposed to radiation in order to triage people for treatment of acute radiation syndrome, the calculated data for a range of energies having a width of from 0.05 to 3.5 MeV were used to convert absorbed doses in fingernails to corresponding doses in organs and the whole body as well as the effective dose. Doses were assessed based on assumed rates of radioactive fallout at different time periods following a nuclear explosion.

1. Introduction

In large-scale radiation incidents, there is a critical need to rapidly and reliably differentiate people who did or did not receive a clinically significant dose so that those with a significant dose can be triaged to receive immediate medical attention for radiation injury. A whole body dose of about 3.5 Gy has been estimated to be lethal, without medical treatment, to 50% of the population within 60 days (LD50₆₀). Therefore, to improve survival rates for very large populations potentially exposed in a radiation event, a reasonable threshold above which people should be triaged for medical care is generally set at a measured whole body dose of about 2 Gy (Swartz et al., 2014).

Current guidelines for methods of biodosimetry at the level of the individual are based on clinical signs and symptoms and assays based on changes in white blood cells (WBC). However, these biologically-based responses are not uniquely indicative of exposure to ionizing radiation and associated changes may not occur promptly enough to facilitate initial triage. So, especially in the early phase of a large-scale event, biodosimetry methods that are based on physical changes in the body, which occur nearly instantaneously with exposure, offer some especially useful advantages. Based on extensive research investigating the sensitivity of the physical response of nails to ionizing radiation, using electron paramagnetic resonance (EPR) spectroscopy to measure dose in fingernails and toenails has been proposed as a physically-based biodosimetry method to use in initial triage. More specifically, allowing for proper collection and storage of samples, and accounting for water content, mechanical stress and signal fading, EPR-based dosimetry in nails could in the foreseeable future provide a reliable dose assessment for an individual with a detection limit of the order 1–2 Gy (Reyes et al., 2008; Wilcox et al., 2010; He et al., 2014).

However, to correctly interpret the doses absorbed in nails and to measure the individual dose for purposes of treatment triage, it is also necessary to have prior knowledge of the ratio between the dose absorbed in fingernails and effective whole body or organ dose for a broad photon energy range and standard irradiation geometries. Such relations or dose conversion factors (DCF) can be calculated by Monte-Carlo methods using geometrical models of various itemization levels ranging from simple to very complex forms.

Monte-Carlo codes have previously been widely and successfully implemented for EPR-based dosimetry to relate the doses in tooth enamel or other materials of interest to effective organ-specific and whole body doses for external photon irradiation using both mathematical models (Takahashi et al., 2001) and voxel models (Ulanovsky, 2005). In the case of neutron irradiation, DCFs for tooth enamel were reported by Khailov (2010). Herve et al. (2007) calculated the relationships between the dose to the organs and the dose to teeth, bones and non-biological samples (such as mobile phones) located in the pockets of victims’ clothes, for different external exposures representative of accidental situations.

For external irradiation there is a set of well-known idealized irradiation geometries in a vacuum, which are commonly used to represent the actual conditions of exposure. Since nails are located on the top surface of the fingers, frontal irradiation of a hand with high energy photons may not create secondary electron equilibrium in nails with the result that the dose absorbed in nails could be much less than the dose in adjacent tissues. Therefore, to avoid mis-estimating the doses measured in nails, calculations have to be made in realistic conditions, in particular by taking into account the presence of air around the person exposed to radiation field.

One of the most frequently encountered scenarios in practical geometries of external irradiation is the geometry of gamma irradiation produced by fission products deposited on the ground surface. The intensity and energy spectra of the gamma radiation emitted by fission products is known to depend on time elapsed following the detonation and release of ²³⁵U fission products (French, 1965).

This paper aims to provide conversion factors for absorbed doses in fingernails related to doses to various organs (listed in Table 4) and to the whole body as well as the effective dose for several homogenous external gamma-ray geometries of irradiation in air as well as the geometry where irradiation could occur from a contaminated soil surface. Using data obtained for real fallout spectra, DCF were also calculated to estimate the feasibility of using fingernails to assess the effective and absorbed whole body doses in victims during triage in an area contaminated with gamma emitting radioactive materials.

Table 4.

Dose conversion coefficients for dose absorbed in the nail of the middle finger (left hand) to organ, whole body and effective dose at external gamma irradiation in air. Unit: Gy/Gy or Sv/Gy. The statistical uncertainties of the values are 6–9 %.

	50 keV
	AP	PA	RLAT	LLAT	ROT	Soil Surface
Dorgan/Dnail
Lung	0.83	0.71	6.40	0.28	0.69	0.54
Thymus	1.35	0.16	4.18	0.20	0.58	0.50
Heart	0.97	0.29	4.48	0.20	0.52	0.41
Liver	0.89	0.46	10.1	0.06	0.61	0.48
Pancreas	0.67	0.50	1.08	0.34	0.50	0.38
Stomach	1.10	0.30	1.16	0.46	0.59	0.48
Testes	1.43	0.22	3.00	0.15	0.59	0.75
Genitalia	1.34	0.25	3.18	0.16	0.58	0.70
Brain	0.44	0.36	10.1	0.49	0.59	0.40
Eyes	1.20	0.07	12.6	0.61	0.78	0.64
Thyroid	0.90	0.20	10.8	0.54	0.69	0.43
Ovaries	0.65	0.46	3.15	0.16	0.46	0.36
Breast	1.65	0.27	13.2	0.65	1.00	0.94
Skin	0.81	0.62	10.0	0.49	0.79	0.89
Uterus	0.78	0.39	2.75	0.14	0.46	0.39
Bladder	1.11	0.27	3.41	0.17	0.53	0.50
Kidney	0.27	0.97	4.88	0.24	0.59	0.51
Colon	0.71	0.45	1.13	0.30	0.49	0.41
Oesoph	0.39	0.39	4.08	0.24	0.40	0.28
Red Bone Marrow	0.36	0.54	5.11	0.25	0.47	0.16
Whole body	0.88	0.69	8.85	0.44	0.80	0.75
Effective dose	0.88	0.44	5.00	0.30	0.59	0.49

	250 keV
	AP	PA	RLAT	LLAT	ROT	Soil Surface
Dorgan/Dnail
Lung	0.91	0.98	11.3	0.47	0.94	0.79
Thymus	1.23	0.41	10.2	0.45	0.83	0.68
Heart	1.03	0.60	11.0	0.46	0.85	0.71
Liver	0.96	0.76	16.1	0.19	0.86	0.76
Pancreas	0.86	0.84	4.42	0.60	0.82	0.72
Stomach	1.10	0.61	4.23	0.69	0.85	0.73
Testes	1.23	0.53	7.85	0.35	0.80	0.84
Genitalia	1.19	0.56	8.11	0.36	0.81	0.84
Brain	0.68	0.67	17.2	0.77	0.95	0.70
Eyes	1.17	0.24	19.3	0.87	1.03	0.91
Thyroid	0.99	0.51	17.9	0.80	1.02	0.75
Ovaries	0.86	0.81	8.26	0.37	0.79	0.69
Breast	1.52	0.67	19.2	0.86	1.28	1.10
Skin	0.87	0.85	14.6	0.65	1.00	1.04
Uterus	0.94	0.75	7.86	0.36	0.78	0.78
Bladder	1.11	0.58	8.59	0.39	0.81	0.79
Kidney	0.52	1.16	9.89	0.44	0.85	0.75
Colon	0.89	0.80	4.42	0.57	0.81	0.74
Oesoph	0.66	0.84	11.0	0.53	0.83	0.67
Red Bone Marrow	0.70	0.97	12.1	0.54	0.91	0.93
Whole body	0.87	0.85	12.1	0.54	0.92	0.89
Effective dose	0.96	0.76	9.97	0.52	0.89	0.80

	670 keV
	AP	PA	RLAT	LLAT	ROT	Soil Surface
Dorgan/Dnail
Lung	0.91	1.02	7.02	0.54	0.99	0.85
Thymus	1.11	0.52	6.77	0.55	0.89	0.76
Heart	0.98	0.69	7.10	0.55	0.91	0.77
Liver	0.93	0.82	9.05	0.27	0.90	0.80
Pancreas	0.87	0.89	3.47	0.62	0.86	0.81
Stomach	1.02	0.71	3.50	0.72	0.89	0.77
Testes	1.12	0.70	5.86	0.47	0.90	0.83
Genitalia	1.08	0.71	5.84	0.47	0.89	0.91
Brain	0.75	0.77	9.73	0.79	1.02	0.74
Eyes	1.18	0.41	11.6	0.94	1.15	1.03
Thyroid	0.96	0.63	10.2	0.84	1.07	0.86
Ovaries	0.86	0.87	5.32	0.45	0.85	0.80
Breast	1.46	0.92	11.6	0.95	1.40	1.22
Skin	0.85	0.88	8.36	0.68	1.01	1.06
Uterus	0.90	0.81	5.36	0.44	0.84	0.80
Bladder	1.02	0.68	5.91	0.48	0.87	0.86
Kidney	0.61	1.11	6.42	0.52	0.90	0.76
Colon	0.88	0.85	3.54	0.61	0.86	0.82
Oesoph	0.72	0.88	6.99	0.60	0.90	0.72
Red Bone Marrow	0.72	0.99	7.18	0.58	0.94	0.95
Whole body	0.87	0.90	7.22	0.59	0.96	0.93
Effective dose	0.94	0.85	6.37	0.59	0.94	0.86

	1.25 MeV
	AP	PA	RLAT	LLAT	ROT	Soil Surface
Dorgan/Dnail
Lung	1.13	1.14	2.96	0.70	1.14	0.93
Thymus	1.29	0.67	2.93	0.72	1.05	0.81
Heart	1.17	0.83	3.04	0.72	1.07	0.81
Liver	1.13	0.95	3.58	0.42	1.04	0.87
Pancreas	1.05	0.99	1.69	0.78	0.99	0.90
Stomach	1.20	0.86	1.75	0.87	1.03	0.88
Testes	1.31	0.87	2.65	0.66	1.07	0.93
Genitalia	1.27	0.89	2.63	0.64	1.06	0.96
Brain	0.97	0.92	3.83	0.95	1.18	0.81
Eyes	1.59	0.61	4.62	1.14	1.39	1.22
Thyroid	1.16	0.77	4.02	0.98	1.21	0.92
Ovaries	1.05	0.98	2.41	0.58	0.99	0.82
Breast	1.79	1.20	4.84	1.19	1.66	1.30
Skin	0.92	0.88	3.03	0.75	1.02	1.00
Uterus	1.09	0.94	2.41	0.59	0.99	0.93
Bladder	1.21	0.83	2.61	0.65	1.02	0.90
Kidney	0.83	1.20	2.75	0.69	1.05	0.81
Colon	1.09	0.97	1.75	0.77	1.00	0.88
Oesoph	0.92	1.00	2.99	0.76	1.06	0.80
Red Bone Marrow	0.93	1.07	2.96	0.73	1.07	0.99
Whole body	1.08	1.02	3.00	0.74	1.11	0.99
Effective dose	1.14	0.98	2.75	0.75	1.09	0.93

	3.5 MeV
	AP	PA	RLAT	LLAT	ROT	Soil Surface
Dorgan/Dnail
Lung	1.40	1.43	2.31	1.44	1.56	1.14
Thymus	1.53	1.07	2.31	1.53	1.51	1.00
Heart	1.42	1.16	2.35	1.47	1.49	1.03
Liver	1.39	1.27	2.58	1.04	1.45	1.08
Pancreas	1.32	1.31	1.63	1.53	1.42	1.00
Stomach	1.44	1.19	1.68	1.64	1.45	1.07
Testes	1.54	1.23	2.19	1.43	1.52	1.26
Genitalia	1.50	1.23	2.16	1.37	1.49	1.34
Brain	1.29	1.27	2.71	1.73	1.60	1.01
Eyes	2.65	0.95	3.61	2.30	2.19	1.76
Thyroid	1.36	1.18	2.80	1.76	1.62	1.00
Ovaries	1.31	1.30	1.99	1.31	1.41	1.18
Breast	2.32	1.75	3.76	2.37	2.37	1.74
Skin	0.62	0.61	1.20	0.77	0.74	0.75
Uterus	1.33	1.25	2.06	1.30	1.41	1.17
Bladder	1.47	1.17	2.15	1.39	1.46	1.17
Kidney	1.15	1.48	2.21	1.39	1.47	1.07
Colon	1.35	1.29	1.68	1.51	1.42	1.19
Oesoph	1.21	1.28	2.28	1.49	1.46	1.02
Red Bone Marrow	1.20	1.34	2.26	1.44	1.46	1.21
Whole body	1.37	1.36	2.32	1.48	1.54	1.25
Effective dose	1.41	1.31	2.20	1.50	1.52	1.18

2. Methods of computation

2.1. Elemental composition and density of nails

The concentration of the radiation-induced radicals in nails obviously varies in direct proportion to the absorbed dose in nail keratin. For purposes of our investigation the elemental composition of nails (Table 1) was determined using the amino acid composition of nail keratin from Marshal (1980) as reported by Paschou (2011). Our calculations took into account nail water content of 18% relative to dry weight, according to methods reported by Venkat Rao (2010). Nail density value of 1.27 g/cm³ was taken from Dias et al. (2007).

Table 1.

Elemental composition of nails. Mass% - mass composition of each element in nail (water content - 18%) in mass %.

Element	C	O	N	H	S
Mass %	48.98	22.53	18.13	6.86	3.45

The term “absorbed doses to nails” used throughout this article refers to deposited energy per mass in fingernail volume elements filled with nail keratin (taking into account the water content of nails). The conversion from any directly measureable quantities at calibration (such as the dose in water or air kerma) to doses calculated for nails could be made using the ratios of appropriate mass energy absorption coefficients. For this purpose values of mass energy absorption coefficients (μ_en/ρ) for nail keratin were calculated as mass-weighted sums from the μ_en/ρ values for their atomic components taken from Hubbell (1982). The resulting energy dependence of μ_en/ρ for nails according to their elemental composition in Table 1 are presented in Table 2.

Table 2.

Mass energy absorption coefficients for nails calculated using data from Hubbell, (1982) and elemental composition given in Table 1 in units cm² g⁻¹ and relations between mass energy absorption coefficients for soft tissue, air, water and nail.

Energy, MeV	0.01	0.05	0.1	0.5	1	2	4	6	8	10
${(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{nail}}$	4.587	0.042	0.025	0.032	0.030	0.025	0.020	0.017	0.016	0.015
${(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{tissue}}/{(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{nail}}$	1.087	1.028	1.029	1.031	1.031	1.032	1.034	1.036	1.038	1.040
${(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{air}}/{(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{nail}}$	1.034	0.966	0.940	0.936	0.936	0.937	0.945	0.955	0.966	0.975
${(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{water}}/{(\frac{{\mathrm{\mu }}_{\text{en}}}{\mathrm{\rho }})}_{\text{nail}}$	1.078	0.996	1.029	1.041	1.041	1.042	1.044	1.047	1.050	1.053

The relations of μ_en/ρ values for soft tissue, air and water (taken directly from Hubbell [1982]) to the calculated μ_en/ρ values for nails are also given in Table 2 for ten photon energies from 0.01 to 10 MeV. They are seen to be almost constant for photons with energy more than 0.1 MeV. To make a fast conversion from the doses in tissue, air and water to the doses in keratin in the photon energy interval 0.1–10 MeV the dose conversion factors were calculated as ratios of the corresponding μ_en/ρ values integrated over this energy interval. This dose conversion factors values for tissue, air and water were calculated to be equal to 1.04, 0.95 and 1.05, respectively.

2.2. Phantom description

To calculate the nail doses and organ doses the hermaphrodite mathematical body phantom (Fig. 1a) was created on the basis of a standard mathematical model of an adult designed by Cristy and Eckerman (1997). The standard model does not contain hands and has its arms included in the trunk. In order to adapt it for the purposes of the present study, the trunk width of the original model was reduced and two arms with hands of 2.5 kg each on both sides of the phantom were added. The distance from the middle fingertip to the ground was about 74 cm.

Fig. 1.

(a) Geometrical model of the human body created on the base of mathematical phantom developed by Cristy and Eckerman (1997);

(b) Detailed image of the hand. Nail regions are shown in black. Nails are numbered as follows: 1=thumb, 2=index, 3=middle, 4=ring, 5 = pinkie.

Leg dimensions were also adjusted to correlate with the new trunk dimension and to preserve the overall weight of leg tissue and bones of the standard phantom. Most internal organs composed of soft tissue were retained in their original positions in the trunk. Scapulars and lungs were moved towards each other (scapulars by 2 cm, lungs by 1 cm) and six upper ribs widths of the original model were slightly reduced.

The geometrical model of the hand with five nail regions was composed from a number of anatomical regions of complicated shapes (Fig. 1b). The thumb was rotated 30° clockwise with respect to the other fingers. All five nail regions had the same thickness of 0.3 mm. Nail mass varied from 24.3 to 63.9 mg.

The overall sum of the volumes and weights of the phantom parts made of soft tissue and bones remained the same within 1.5 %. The sum of bone weights of arm, forearm and hand (of the created phantom) also remained equal within 3 % to the weight of the arm bone of the unmodified phantom. The soft tissue, lung tissue and bone elemental composition and density were also taken from Cristy and Eckerman (1997).

2.3. Geometry of irradiation and parameters of sources

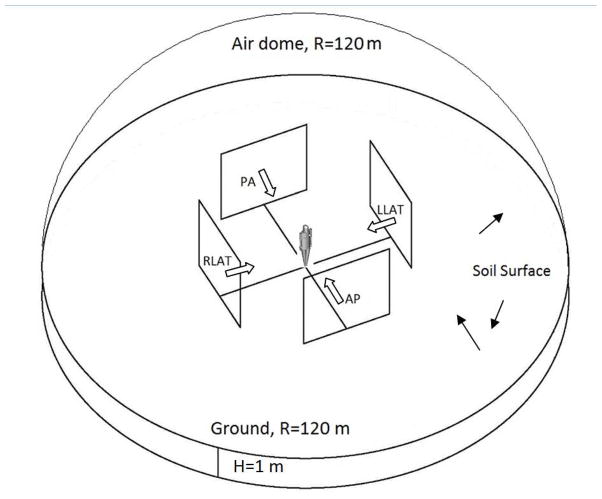
The geometry of irradiation is shown schematically in Fig. 2. The phantom was positioned on the homogeneous cylindrical ground layer with 1 m depth. An air hemisphere was situated above the phantom. The diameters of both the hemisphere and the ground layer were chosen to be 240 m. Soil composition and density were taken from a NCRP report on cesium (NCRP, 1977). Calculations for all irradiation geometries were conducted for eleven energies of the monoenergetic photons between 0.05 and 3.5 MeV.

Fig. 2.

The geometries of irradiation: AP (antero-posterial), PA (postero-anterial), LLAT (left-lateral), RLAT (right-lateral) and the irradiation by a contaminated soil surface. The scale of the presented objects is arbitrary.

Altogether five standard homogeneous unidirectional exposures in the presence of air and the irradiation from an ‘infinite’ soil surface were considered. Standard exposures included: AP (antero-posterial), PA (postero-anterial), LLAT (left-lateral), RLAT (right-lateral) and ROT (rotational). The first four geometries were defined by uniform sampling of unidirectional particles on a square source plane positioned perpendicular to the ground surface and parallel to the long axis of the phantom. The source plane dimensions for unidirectional irradiations (AP, PA and both LAT) were 4×4 m to provide a uniform irradiation of the phantom in air. The distance from the source to the center of the long axis of the phantom was chosen to 5 m for all four unidirectional irradiations, which was estimated to ensure electron equilibrium conditions in the vicinity of the hands with the air layer between the phantom and the source.

The results for AP, PA, LLAT and RLAT irradiation geometries were averaged to calculate the data for the rotational (ROT) geometry of irradiation.

To model the irradiation by a contaminated soil surface in an open terrain, a homogeneous, isotropic and monoenergetic plane source of 240 m diameter was simulated at zero ground depth. Preliminary calculations using these dimensions showed that this size was sufficient for the source to be representative of the ‘infinite’ plane source. At the same time such diameters of the source were adequate to achieve the required computational errors.

2.4. Dose calculation

Monte Carlo calculations of dose values were performed with MCNP 4b code in the PE (photon-electron) mode, where both photon and electron transports are taken into account (Briemeister, 1997). The cut-off energy for photons was 10 keV. To obtain the organ or tissue doses the deposited energy in volume elements (or ‘cells’) of interest were calculated using the standard pulse height tally with an asterisk (*F8), which was then divided by mass of the cells. The absorbed doses in nails were also determined by normalizing the deposited energy in the corresponding cells by their masses. The time of calculations was chosen based on the relative error of the dose to the nail of the fifth finger (pinkie), which did not usually exceed 7%.

Additionally, air kerma values at 1 m above the ground in 0.05–3.5 MeV photon energy interval were calculated for both unidirectional exposure in the presence of air and the irradiation from an ‘infinite’ soil surface. The calculated kerma values were used to present some of the nail dose values in terms of air kerma for reasons of convenience and better perception.

Since the radiation weighting factor for photons is unity, the calculated absorbed dose for organ or tissue is equal to the equivalent dose (ICRP, 1991). The effective dose (E) was determined as the sum of the weighted equivalent doses in all the tissues and organs of the body according to the expression: E = Σ_T w_T · H_T, where w_T is the tissue weighting factor (taken from ICRP, 1991) and H_T is equivalent dose in T-th tissue/organ. The calculated values of effective doses per unit air kerma agreed with the corresponding values presented in ICRP, 1997 within 10 % for all photon energies. This discrepancy between the results is not considerable and can be attributed to: (1) differences in irradiation geometries, namely, the presence of air and soil in our geometry and (2) modifications made to the standard body phantom.

Also, the whole body dose (D_body) was determined according to the expression:

D_body = Σ_j D_j · m_j/Σ_j m_j where D_j is dose and m_j is mass of j-th cell of the body.

DCF for doses in the fingernails to doses of interest were calculated as effective, whole body or organ dose divided by dose absorbed in fingernails.

To obtain the DCF for nail doses to effective dose and absorbed whole body or organ doses for real energy spectra expected from fallout, the source terms were taken from French, 1965. These source data (presented in Table 3) were normalized in intensity to correspond to the products of one ²³⁵U fission per cm² of ground surface and presented for four elapsed times following the detonation and release of the ²³⁵U fission products, i.e., 1.12 h, 23.8 h, 4.57 days and 9.82 days.

Table 3.

Fallout source terms for the gamma radiation for various elapsed times following the detonation (photons/sec per ²³⁵U fission) according to French, 1965.

Energy, MeV	Time after fission
	1.12 h	23.8 h	4.57 d	9.82 d
0.10	3.19E-07	5.12E-09	3.13E-09	2.11E-09
0.14	4.31E-06	7.50E-08	3.20E-08	1.77E-08
0.25	5.19E-06	1.82E-07	5.46E-08	1.88E-08
0.40	1.73E-05	1.85E-07	3.67E-08	1.56E-08
0.67	1.68E-05	5.73E-07	3.63E-08	1.68E-08
0.85	1.09E-05	6.81E-07	3.88E-08	1.88E-08
1.25	1.42E-05	1.33E-07	1.30E-08	3.00E-09
1.75	1.35E-05	7.04E-08	2.46E-08	2.21E-08
2.50	3.50E-06	4.70E-09	6.23E-10	5.24E-10
3.50	4.23E-06	8.99E-10	1.12E-09	1.03E-09

The resulting DCF for nail doses to the effective dose (F_E) and DCF for nail doses to the organ or whole body dose (F_D) for the typical fallout spectra arising from large-scale radiation accidents were calculated according to the equations:

$${\mathrm{F}}_{\mathrm{E}}={\sum }_{\mathrm{i}}({\mathrm{E}}_{\mathrm{i}}·{\mathrm{\phi }}_{\mathrm{i}})/{\sum }_{\mathrm{i}}({\mathrm{D}}_{{\text{nail}}_{\mathrm{i}}}·{\mathrm{\phi }}_{\mathrm{i}})\text{and}{\mathrm{F}}_{\mathrm{D}}={\sum }_{\mathrm{i}}({\mathrm{D}}_{\text{org}/{\text{body}}_{\mathrm{i}}}·{\mathrm{\phi }}_{\mathrm{i}})/{\sum }_{\mathrm{i}}({\mathrm{D}}_{{\text{nail}}_{\mathrm{i}}}·{\mathrm{\phi }}_{\mathrm{i}})$$

where E_i, D_org/_bodyi, D_naili are effective dose, dose to a given organ or whole body dose and nail dose respectively, per source photon/unit area for the i-th source energy (calculated for the geometry of irradiation by a contaminated soil surface); φ_i - source strength (number of photons/sec per ²³⁵U fission) for the i-th source energy.

The summations were made for the ten photon energies from 0.1 to 3.5 MeV using the source data presented in Table 3 and DCF for irradiation by a contaminated soil surface partially presented in Table 4.

3. Results and discussion

Fig. 3 shows the nail doses for the thumb and for the middle finger of the left hand in all six irradiation geometries as a function of photon energy. The data are given in the form of the ratio of the absorbed dose to the air kerma, in the unit of Gy/Gy. The nail doses for the thumb and for the middle finger are similar to each other in all considered irradiation geometries with the exception of PA geometry. For backward irradiation (PA geometry) the thumb, being shielded by the other fingers, receives less doses than the middle finger from photons with energies up to 1.25 MeV.

Fig. 3.

Nail doses (a) for the (a) 1-st (thumb) finger and (b) for the 3-rd (middle) finger of the left hand normalized by air kerma at different irradiation geometries. Unit: Gy/Gy.

For photons with energies 0.85–1.75 MeV the nail doses of the left hand are close to air kerma within 25 % in all irradiation geometries excluding the right-lateral geometry. In the considered energy range, the doses to nails of the left hand in the right-lateral geometry are considerably lower (e.g., four times lower for 1.25 MeV photons) than that in the left-lateral geometry, due to shielding by the trunk. Consequently, taking into account the mirror symmetry of the position of the hands, any significant difference between the nail doses of the left hand and the right hand may indicate that the exposure for the victim took place in a lateral orientation during irradiation.

Table 4 presents the numerical data of the DCF for dose absorbed in the middle finger nail of the left hand to organ (tissue) dose or effective dose. The values are given in the units Gy/Gy or Sv/Gy for five chosen photon energies. (Values for the other energies and for the other fingernails are not included here for the sake of space.)

The results of the simulations indicate that the differences between nail doses of the left hand and organ doses or effective dose can be very substantial in both lateral irradiations, especially for the photons with energies less than 0.67 MeV. These differences can obviously be explained by shielding of the fingernails of the left hand by the trunk at right-lateral irradiation and by shielding of organs by tissue and other organs with left-lateral irradiation. At backward and frontal irradiations the doses in nails and organ doses, whole body dose and effective dose tend to be more similar. For rotational irradiation geometry and for the geometry of irradiation by a contaminated soil surface, the differences between the nail doses and effective dose for the photons in the energy interval 0.25–1.25 MeV are usually less than 20 % due to a more uniform dose distribution. Starting with photon energies above 1.25 MeV the nail doses are less than the effective/whole body dose (with the exception of LLAT geometry) and these differences increase with photon energy.

The resultant data can be used to directly assess the protection quantity needed during irradiation by broad parallel beams incident in various directions and during irradiation coming from contaminated soil. The real radiation fields usually include a great range of photon energies. So, the integration over the photon spectrum should be carried out to assess the DCF for dose in nails to organ or effective dose in each situation encountered in practice for any photon spectrum of interest.

Table 5 displays the resulting DCF for the dose to the middle finger nail to effective dose and organ/whole body dose for real energy spectra expected from fallout for the 4 time periods following exposure. These data were obtained using previously calculated DCF for irradiation by a contaminated soil surface. The differences for the conversion factors for effective/whole body dose between different fingers were less than 4 %. Therefore, the data for the other fingers was not presented here for the sake of space, but dose based on the nails of the other fingers can be assumed to be fairly similar to the dose based on the middle fingernail.

Table 5.

Dose conversion coefficients for dose absorbed in the nail of the middle finger to organ, whole body and effective dose for the fallout gamma radiation for various elapsed times following the detonation and release of the 235U fission products. The statistical uncertainties of the values are 6–10 %.

Fallout age	FD, (Gy/Gy) or FE (Sv/Gy)
	1.12 h	23.8 h	4.57 d	9.82 d
Lung	0.99	0.91	0.93	0.96
Stomach	0.93	0.84	0.86	0.89
Breast	1.43	1.31	1.33	1.38
Colon	0.96	0.88	0.89	0.92
Red Bone Marrow	1.08	1.01	1.03	1.06
Whole body	1.05	0.99	1.00	1.03
Effective dose	0.97	0.92	0.92	0.95

The sensitivity of the data to fallout age (i.e., the time elapsed from time of exposure) is seen to be less than the error values. Overall, the conversion factors for effective dose vary from 0.89 to 1.01 (for all fingernails), suggesting that there would be less than a 6 % variation regardless of which nail or time period was used to estimate the effective dose. As a consequence, for the case of homogenous exposure on nails, the choice of finger does not apparently unduly influence the interpretation of measurements that would be available to make during the likely conditions of triage (where there may not be a choice of nails to sample). On the other hand, it follows from the data presented in Figure 3 for unidirectional exposures that the dose to the nail strongly depends on the geometry of irradiation. Therefore, in the case of suspected accidental unidirectional exposure (e.g., a radiation burst during an explosion) it may be necessary to measure nails from both hands to avoid incorrectly assessing whole body or organ dose based on nails.

4. Conclusions and Implications

A mathematical phantom representing a person with arms and hands placed loosely along the sides of the body was used to compute the DCF for doses absorbed in the fingernails to organ, whole body and effective doses for photon sources of various geometries. The photon sources included planar unidirectional (AP, PA, RLAT and LLAT), rotational (ROT) and soil surface geometries. The photon energies considered ranged from 50 keV to 3.5 MeV. Such an energy range is usually sufficient for interpolation of the values to arbitrary photon spectra.

Using Monte-Carlo calculations, the dose conversion factors were obtained for the dose absorbed in the fingernails converted to effective dose and to whole body dose as well as to different organ doses. The results show that in photon energy ranges of 0.25–2.5 MeV, most values of the DCF lie in 0.8–1.2 interval for rotational and soil surface irradiation geometries that would be frequently encountered in practical scenarios. Therefore, for the scenario of homogenous exposures that would be expected in the case of environmental contamination or protracted exposures, no correction is needed to evaluate an effective dose or a whole body dose from a dose in nails. However, in the case of unidirectional exposures (especially, right lateral for the left hand nails and vice versa) DCF can increase several-fold (the magnitude depending on photon energy) due to shielding by the body itself.

There are several important implications of the work presented in this article for emergency response decision makers and policy makers. In both large scale events and smaller radiological events, the conversion factors for estimating dose in nails and predicting whole body and effective exposure would be especially important to accurately triage people above the threshold to receive further evaluation or medical care. For those people above the threshold, the more refined information about dose to the organs, particularly to those most sensitive to acute radiation syndrome, as well as effective dose to the body would be helpful for medical care decision-making. Similarly information based on nails from both hands (or, although not discussed in this paper, to the nails on hands and feet) could provide evidence about the direction of the body relative to the source at the time of exposure and provide information about whether there is a homogeneous or heterogeneous exposure to the whole body, especially useful in small incidents where mishandling of radioactive sources could be expected to lead to very asymmetric exposures.

In our view, there are also important directions for simulation research on nail dosimetry to continue to investigate. First, during the time of exposure the position of massive body regions (trunk, and, possibly arms and legs) relative to the source have the potential to affect both the nail dose and organ/tissue doses. So it would be important to determine how much variation in dose to the nails might occur with different likely placements of the body such as standing, sitting or lying down at the time of exposure.

Second, in a catastrophic radiological event resulting in fallout, it is likely that the skin and clothing of victims will be contaminated by radioactive dust. Such external contamination deposited on fingernails could lead to a significant dose to nails prior to their being decontaminated that is not representative of the whole body exposure and therefore source and rate might act as confounding factors that should be modeled. Therefore, the assessment of the relative contribution to the nail dose from beta-emitting radioactive contaminants deposited on hands is very important and also worth future consideration.

Accordingly, future studies are being planned to investigate: (1) the influence of the body position and, possibly, of the specific placement of the hands and feet on nail doses, and (2) the potential contribution of beta-emitting radio nuclides deposited on the nails to the doses absorbed in fingernails.

HIGHLIGHTS.

• Elemental composition and density of nails were determined

• MIRD-type mathematical human phantom with arms and hands was created

• Organ doses and doses to nails were calculated for external photon exposure in air

• Effective dose and nail doses values are close for rotational and soil surface exposures