Abstract
Longitudinal designs are common in the field of athletic training. For example, in the Journal of Athletic Training from 2005 through 2010, authors of 52 of the 218 original research articles used longitudinal designs. In 50 of the 52 studies, a repeated-measures analysis of variance was used to analyze the data. A possible alternative to this approach is the hierarchical linear model, which has been readily accepted in other medical fields. In this short report, we demonstrate the use of the hierarchical linear model for analyzing data from a longitudinal study in athletic training. We discuss the relevant hypotheses, model assumptions, analysis procedures, and output from the HLM 7.0 software. We also examine the advantages and disadvantages of using the hierarchical linear model with repeated measures and repeated-measures analysis of variance for longitudinal data.
Key Words: longitudinal designs in athletic training, statistical analysis
Researchers in athletic training commonly use longitudinal designs. In fact, 1 of the current research priorities of the National Athletic Trainers' Association Research & Education Foundation is to fund work that uses “longitudinal studies of the epidemiology of conditions typically managed by athletic trainers, which will help establish a firm scientific foundation.”1 As the body of longitudinal studies increases in the field, ensuring that this type of data is being analyzed appropriately to make clinical decisions is very important. One option for analyzing this type of data is the hierarchical linear model (HLM), which is widely used in other fields. Therefore, the focus of our short report was to determine whether the HLM analysis can be used as an alternative to the repeated-measures analysis of variance. We discuss the advantages and disadvantages of each analysis.
LONGITUDINAL DESIGNS
Longitudinal designs, or designs in which the dependent variable is measured over time, are common in the field of athletic training. From 2005 through 2010, the Journal of Athletic Training published a total of 218 original research articles. In 52 (24%) of these studies, the authors used a longitudinal design.
The most common analysis for longitudinal designs is the univariate repeated-measures analysis of variance (RM ANOVA).2 Authors of 50 (96%) of the 52 studies in the Journal of Athletic Training involving a longitudinal design used the RM ANOVA to analyze the data. With RM ANOVA, 3 key assumptions should be met to ensure that the interpretation of the final results is valid: independence, normality of the dependent variable, and sphericity. If these assumptions are not met, the results may be biased.2
HIERARCHICAL LINEAR MODELING
A possible alternative to RM ANOVA is HLM with repeated observations. Hierarchical linear modeling is widely accepted in other fields, including medicine,3 health,4 and education.5 It is a specific name for a broader class of modeling called multilevel or random-effects models6 and mixed-effects designs.5 For this short report, we use the nomenclature associated with HLM.7 From 2005 through 2010 in the Journal of Athletic Training, HLM was not used in any of the analyses.
Hierarchical linear modeling allows the data to be structured in at least 2 levels. For longitudinal design, the first level is the repeated measure (time or condition) nested within the second level, which is the person-level data.7 The first level captures the within-subject variation, whereas the second level describes the between-subjects variability.8 This multilevel approach is not possible with the traditional RM ANOVA.
As with RM ANOVA, certain assumptions should be met for the HLM results to be considered valid. These assumptions consist of the following: level 1 error terms are independent and normally distributed with a mean of 0 and variance of σ2; level 1 predictors are independent of level 1 errors; level 2 errors are multivariate normal with a mean of 0 and variance of τ; and level 2 predictors are independent of level 2 errors.7 We will present these assumptions with a sample data set later in this article.
RESEARCH QUESTIONS
When using RM ANOVA, the following research questions are typically of interest: Does a difference exist in the dependent variable over time? Does a difference exist in the dependent variable across the conditions? Depending on condition, does a difference exist in the dependent variable over time? Depending on time, does a difference exist in the dependent variable across conditions? However, when using HLM, the following research questions can be answered: Do participants differ at a specific time point (on the dependent variable) in terms of condition? Do growth rates (slopes) differ in terms of condition? Do quadratic (or cubic) growth rates differ across participants? Do specific time points vary among individuals? Do growth rates vary among individuals?
Using the traditional RM ANOVA allows for comparisons of group means but not comparisons at the individual level. All athletes are not the same, so comparing averages may not be the most patient-centered analytical technique. In addition, the HLM allows for comparison of individual growth trajectories and comparisons between participants. For example, a research team may be interested in determining if the number of days missed from competition due to a specific injury varies among athletic trainers or among institutions.
ADVANTAGES OF HIERARCHICAL LINEAR MODELING
The major advantage of the HLM is the estimation of individual change over time.7 In addition, fewer assumptions need to be met using the HLM than RM ANOVA.7 Time can be treated as a fixed or random effect within the model.9 For example, time may be treated as random if the dependent variable was not measured at equally spaced time points. Specifically, in the data set used for analysis in this article, temperature was measured at baseline, 5 minutes, 15 minutes, 30 minutes, and every 15 minutes thereafter until 120 minutes; hence, we treated time as random. If temperature had been measured every 15 minutes throughout the study, then time could be treated as fixed. For the traditional RM ANOVA, the dependent variable should be measured in equal increments to increase the likelihood of meeting the sphericity assumption. This assumption can be challenging to meet in athletic training research, especially in studies that involve rates of injuries and healing time.
Another advantage is that the HLM can handle missing data at all levels except the highest level, which in this case is level 2. In a traditional RM ANOVA, no data can be missing. When collecting the same measures from the same people over time, it is common for some of them not to complete the study, necessitating the removal of these participants from the data set in the traditional RM ANOVA. This attrition can greatly affect the power and interpretability of the study.
METHODS
To serve as a detailed example, 1 author (C.C.C.) provided a data set presented in a previous publication10 that was analyzed using a traditional RM ANOVA for reanalysis using the HLM. This study had 2 conditions (placebo, treatment) with 10 time points per condition. Each participant completed both conditions, and the dependent variable was core temperature (°C). The research questions that were asked in the original study included the following: Did core temperature differ over time (from baseline to 120 minutes)? Did core temperature differ across the 2 conditions? Depending on condition, did core temperature differ over time? Depending on time, did core temperature differ across conditions?
By using the HLM, different research questions can be answered: Did participants differ at baseline core temperature in terms of condition? Did growth rates (slopes) differ in terms of condition? Did quadratic (and cubic) growth rates differ across participants? Did baseline core temperatures vary among individuals? Did growth rates vary among individuals? The HLM analysis was generated using the HLM 7.0 software (Scientific Software International, Inc, Skokie, IL).11 The level 1 model (repeated measures) assessed the within-subject variation, and the level 2 model described the between-subjects variation. This analysis included 120 level 1 units and 12 level 2 units (6 men, 6 women). A power analysis is important to complete before any study is conducted, but given the complexity, it was not presented in this article. For a more detailed description, refer to the study by Raudenbush and Xiao-Feng.12
In this analysis, the placebo condition was the referent group. The data were cubic rather than linear because they did not follow a linear trajectory. Instead, the data had 2 stationary points, sometimes referred to as a peak or a trough depending on whether the cubic term is positive or negative.9 To determine the best model fit, each coefficient (linear, quadratic, and then cubic) was added to the model. All terms were different (P < .05); therefore, the model for the analysis included both the quadratic and cubic parameters.
The most basic error structure, unstructured, was used for simplicity.9 Other error structures, such as compound or first-order auto-regressive symmetry, could have been used; however, using the default in the program simplifies the analysis for the reader. This specific analysis used restricted maximal likelihood as the method of estimation because the number of level 2 observations was small.7 We chose not to center the data to allow the intercept to represent the baseline measures for the participants.
Although not planned before the study, we added the person-level predictor of sex to the level 2 model after the analysis to further explain some of the variance we found. We performed the analysis with sex as a level 2 predictor because it may influence core temperature, both at baseline and as the tissue changes in temperature.
RESULTS
When using RM ANOVA, we found that the data were not normally distributed (P = .001) using the Shapiro-Wilk test. Sphericity also was violated for the main effects (time and condition) and the interaction (P = .001). These findings suggest that the results might have been biased if the traditional RM ANOVA was used. The assumption testing for the HLM was performed using the residuals from levels 1 and 2. A simple histogram can be generated for each level to check for normality. At level 1, 2 possible outliers appeared to be present. Through further investigation, we determined that including the outliers did not change the statistical results; therefore, the outliers were included in the final analysis of this short report. Using the HLM software, we performed hypothesis testing to check for equal variances at level 1. For this example data set, the data did not violate the assumption of homogeneity at level 1 (P > .50).
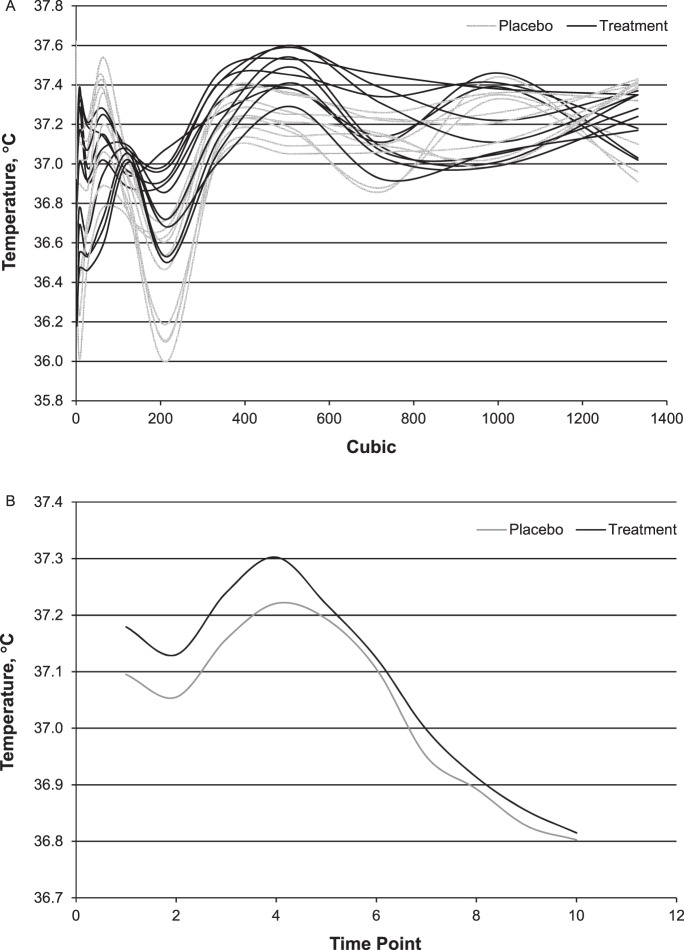
The results revealed no differences in baseline measures for the placebo and treatment conditions (β10 = 0.086, P = .09) with a reliability estimate of 0.922 (Table). We also found no differences in linear growth rates (β30 = −0.004, P = .94), mean quadratic growth rates (β50 = −0.002, P = .88), or mean cubic growth rates (β70 = 0.002, P = .85) across the 2 conditions. In other words, the linear growth trajectories for individuals did not vary between conditions, and this finding was supported by the reliability estimate of 0.942. The curvature of the slopes (quadratic, cubic) over time also did not vary between conditions (Figure).
Table.
Common Hierarchical Linear Model Output
| Variable |
Interpretation of Variable |
Coefficient |
Standard Error |
P Value |
| β00 | Mean baseline temperature for placebo | 37.04 | 0.067 | <.001a |
| β10 | Mean treatment effect on baseline temperature | 0.086 | 0.051 | .09 |
| β20 | Mean linear growth rate of placebo | 0.136 | 0.038 | .005a |
| β30 | Mean treatment effect on linear growth rate | −0.004 | 0.052 | .94 |
| β40 | Mean quadratic growth rate for placebo | −0.035 | 0.001 | <.001a |
| β50 | Mean treatment effect on quadratic growth rate | −0.002 | 0.014 | .88 |
| β60 | Mean cubic growth rate for placebo | 0.002 | 0.0007 | .009a |
| β70 | Mean treatment effect on cubic growth rate | 0.002 | 0.001 | .85 |
| τ00 | Person-level random effect associated with baseline temperature | NA | 0.038 | <.001a |
| τ11 | Person-level random effect associated with linear growth rate in the placebo condition | NA | 0.002 | <.001a |
| τ01, τ10 | Covariance of baseline and growth rate | NA | −0.003 | NA |
| δ2 | Error associated with level 1 | NA | 0.019 | NA |
Abbreviation: NA, not applicable.
Indicates a difference at an α level of .05.
Figure.
Individual growth trajectories compared with group means for both placebo and treatment groups using, A, hierarchical linear modeling for cubic growth rate and, B, repeated-measures analysis of variance for time.
As noted in the Table, we found variability among participants in the baseline temperature (τ00 = 0.038, P < .001) and linear growth rates (τ11 = 0.002, P < .001). With sex as a level 2 predictor, the analysis showed that sex did not interact with baseline temperature, condition, or the various growth trajectories (P > .05). Furthermore, including sex as a predictor explained only 2% of the variation at level 2 in the model.
DISCUSSION
These HLM results suggest that the growth trajectories were not different between the placebo and treatment conditions. Essentially, even with the treatment in place, the growth trajectory of the participant did not change, on average, when compared with the placebo condition. The findings from the HLM analysis are consistent with Cheatham et al,10 who noted no difference between conditions (placebo, treatment). However, in this analysis, we were able to fit a cubic model. We also modeled the individual trajectories, as seen in Figure A. As suggested by the findings, the trajectories are similar. Using RM ANOVA would produce the graph seen in Figure B. With the cubic model, researchers can model individual differences in the instantaneous slope (linear), rate of acceleration (quadratic), and rate at which the acceleration changes (cubic).
CONCLUSIONS
The goal of this short report was to demonstrate the HLM analysis as a possible alternative to the traditional RM ANOVA. The findings from the HLM analysis are consistent with the findings of Cheatham et al,10 who reported no difference between conditions (placebo, treatment). However, using the HLM analysis, we fit a cubic model, which represents the data more closely than a traditional group analysis. In addition, using the HLM analysis allowed for the variances to be decomposed to the within-subject variance, the between-subjects variance, and baseline and individual linear growth rates. By partitioning this variance, a clearer picture of the data for an individual can be seen, as demonstrated in the differences between graphs in the Figure. This creates a more patient-centered approach for data analysis and takes into account the fact that all patients are not the same. We also added a level 2 predictor to the model. This specific predictor, sex, did not explain a large portion of the variance in the slopes. However, including a level 2 predictor may be beneficial in other cases. These advantages suggest that the HLM analysis may be a valuable tool for researchers in athletic training, especially because the National Athletic Trainers' Association Research & Education Foundation has noted that 1 of its current research priorities is to fund work that uses “longitudinal studies of the epidemiology of conditions typically managed by athletic trainers, which will help establish a firm scientific foundation.”1
REFERENCES
- 1.Current research priorities. NATA Research & Education Foundation Web site. http://www.natafoundation.org/research/research-priorities/current-research-priorities. Accessed December 9, 2013. [Google Scholar]
- 2.McCall RB, Appelbaum MI. Bias in the analysis of repeated-measures designs: some alternative approaches. Child Dev. 1973;44(3):401–415. [Google Scholar]
- 3.Cornelius AE, Brewer BW, van Raalte JL. Applications of multilevel modeling in sport injury rehabilitation research. Int J Sport Exerc Psychol. 2007;5(4):387–405. [Google Scholar]
- 4.O'Connell AA, McCoach DB. Applications of hierarchical linear models for evaluations of health interventions: demystifying the methods and interpretations of multilevel models. Eval Health Prof. 2004;27(2):119–151. doi: 10.1177/0163278704264049. [DOI] [PubMed] [Google Scholar]
- 5.Singer JD., Using SAS PROC. MIXED to fit multilevel models, hierarchical models, and individual growth models. J Educ Behav Stat. 1998;23(4):323–355. [Google Scholar]
- 6.Ware JH. Linear models for the analysis of longitudinal studies. Am Stat. 1985;39(2):95–101. [Google Scholar]
- 7.Raudenbush SW, Bryk AS. Hierarchical Linear Models: Applications and Data Analysis Methods. 2nd ed. Thousand Oaks, CA: Sage Publications;; 2002. [Google Scholar]
- 8.Van Der Leeden R. Multilevel analysis of repeated measures data. Qual Quant. 1998;32(1):15–29. [Google Scholar]
- 9.Singer JD, Willett JB. Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence. New York, NY: Oxford University Press;; 2003. [Google Scholar]
- 10.Cheatham CC, Caine-Bish N, Blegen M, Potkanowicz ES, Glickman EL. Nicotine effects on thermoregulatory responses of men and women during acute cold exposure. Aviat Space Environ Med. 2004;75(7):589–595. [PubMed] [Google Scholar]
- 11.Hierarchical Linear & Nonlinear Modeling. Skokie, IL: Scientific Software International, Inc; 2004. (for Windows) computer program. Version 6. [Google Scholar]
- 12.Raudenbush SW, Xiao-Feng L. Effects of study duration, frequency of observation, and sample size on power in studies of group differences in polynomial change. Psychol Methods. 2001;6(4):387–401. [PubMed] [Google Scholar]