Are there dynamical effects in enzyme catalysis? Some thoughts concerning the enzymatic chemical step

Highlights

• •The possible role of enzymatic reaction dynamical effects is examined.
• •Solution reactions usefully inform the issue of dynamical effects in enzymes.
• •Division into regions containing and away from the transition state is important.
• •Motions in passage to/from the transition state need not lead to dynamical effects.
• •Transition State Theory is usually a reasonable description of enzyme kinetics.

Abstract

We offer some thoughts on the much debated issue of dynamical effects in enzyme catalysis, and more specifically on their potential role in the acceleration of the chemical step. Since the term ‘dynamics’ has been used with different meanings, we find it useful to first return to the Transition State Theory rate constant, its assumptions and the choices it involves, and detail the various sources of deviations from it due to dynamics (or not). We suggest that much can be learned about the key current questions for enzyme catalysis from prior extensive studies of dynamical and other effects in the case of reactions in solution. We analyze dynamical effects both in the neighborhood of the transition state and far from it, together with the situation when quantum nuclear motion is central to the reaction, and we illustrate our discussion with various examples of enzymatic reactions.

Introduction

Enzyme catalysis is a complex process involving a series of kinetic steps. In order to complete a full catalytic cycle, these steps include at the very least substrate binding in the enzymatic active site, the chemical reaction per se, and product release into the solvent. These steps do not differ in a fundamental way from those for a bimolecular reaction in solution, where the overall reaction process involves the diffusion of the reacting pair, the chemical reaction per se, and then the dissociation of the newly formed products. But of course enzymatic reactions are so important and of such great interest because they involve catalysis in a biological context. Since the basic reaction classes involved are the same [1–6], the natural question is then just what, at the microscopic level, is key for the reaction acceleration in the enzyme compared to the solution reaction? This is of course a question of long standing with assorted proposed answers [2–11]. In this contribution, we will be concerned only with a small portion of the general question, namely: are there special “dynamical” effects that are key for enzymatic catalysis reactions? Further, we concern ourselves exclusively with the chemical step in the catalysis.

It seems fair to say that there is a degree of confusion about the answer to this question. The question is of course by no means a simple one to answer. But in our view, a significant contributor to the confusion concerning the importance of dynamical effects (or lack thereof) in enzyme catalysis is simply the ambiguity of the terms ‘dynamical’ and ‘dynamics’: these are frequently interpreted and/or employed by different authors in quite different fashions. Of course, even a rate constant itself could be labeled as evidence of the existence of dynamics, but this is certainly far from what anyone would currently intend. In the following, we will not necessarily insist on any procrustean definition of dynamics, but will instead give assorted interpretations, with commentary and as much clarity as we can manage.

We will find it quite useful in this effort to spend considerable time on key reaction rate features and concepts that have been elucidated over the years for chemical reactions in solution. We think that this helps both to focus the issues and to highlight what might be different for reactions in enzymatic and solution environments. We hope that this perspective for the chemical step in enzymatic catalysis will add something useful to the by now extensive literature discussion on the general issue [10–24]. The present article, which is limited to the scope that we have indicated, makes no pretense of completeness vis a vis the topics discussed or the references to the literature. We would like to point in particular to the very recent issue on “Protein Motion in Catalysis” [21] for recent contributions of relevance.

Certainly there are dynamics everywhere if one views with a molecular level eye chemical reactions in solution or in enzymes from beginning to end. And there are differences in the typical time scales that occur in these systems. For example, a characteristic feature of enzymatic environments is the presence of a very broad spectrum of protein conformational motions, which occur on timescales ranging from picoseconds to milliseconds (see e.g. [25]). Solvation dynamics in water typically takes place in the femto- to picosecond (10⁻¹⁵–10⁻¹² s) range [26], but much longer time scales can occur in e.g. aqueous ionic solutions (with long-lived ion atmospheres) or in viscous liquids [27]. But are these dynamics relevant for the reaction rates? Possibly, but not necessarily; vide infra.

It is true that major, large amplitude conformational changes in the protein may occur during substrate binding and product release, i.e. before and after the chemical transformation. These include for example loop motions or the opening of lids which gate the active site entrance. But our exclusive focus in this article is the chemical transformation itself. Here it is expected that smaller and faster conformational changes may occur in the active site. These can affect the interaction between the protein active site and the substrate. One impact of this would be to change the electrostatic properties and the hydrogen-bond network of the active site in order to favor the electronic rearrangement associated with the bond-breaking and -forming processes. In the solution reaction, such roles are served by the solvent itself. But as noted above, certain solvents and especially proteins possess particularly slow dynamics and it is conceivable that these slower motions have a role to play in the reaction rates.

The repeated reference to “reaction rates” just made emphasizes an important distinction that has already arisen and will recur at a number of junctures within. Slow motions can and undoubtedly often occur in the process of a reaction mechanism yet their dynamics have little or no impact on the reaction rate. For example, in a solution reaction, a particular vibration occurring along the reaction pathway might be critical for the reaction to occur and its activation can make a contribution to the effective barrier for the reaction. But if the rate of that activation is not sufficiently slow, the dynamics of that vibration will not explicitly enter the reaction rate constant. (We will see an example of this in the section ‘Diffusion-influenced reactions’.)

The outline of the remainder of this contribution is as follows. The section ‘Transition State Theory’ is devoted to a discussion of Transition State Theory, its assumptions and some of its principal ingredients. Deviations from this theory – which serves as our reference throughout – which are due to events occurring in the neighborhood of the transition state are discussed in the section ‘Dynamical effects in the transition state neighborhood’, in a general theoretical context and then in terms of applications to solution and enzymatic reactions. The special case of quantum nuclear particle transfer reactions is dealt with in the section ‘Dynamics for reactions involving quantum nuclear motion’, where the issue of “promoting modes” – which has garnered considerable attention in an enzymatic catalytic context – is considered. The section ‘Dynamical effects away from the transition state neighborhood’ deals with deviations from Transition State Theory due to events occurring away from the transition state region with applications to solution and enzymatic reactions. The section Concluding Remarks summarizes our key points.

Transition State Theory

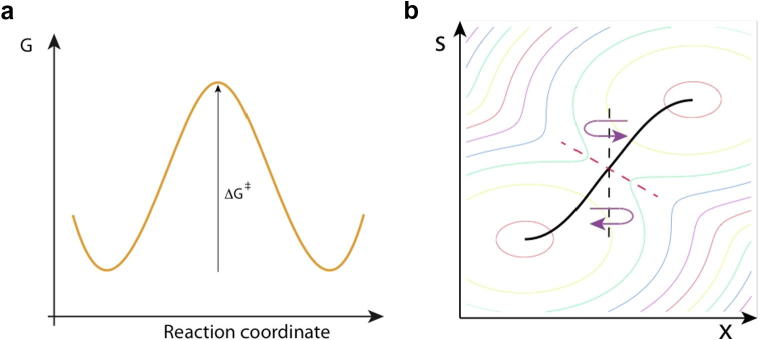
One quite useful and commonly employed reference – and the one given pride of place in our discussions – is Transition State Theory (TST), also known in former times as “Activated Complex Theory”. One definition of ‘dynamical effects’ for reactions is the departure of a reaction rate constant k from its TST value k_TST. The standard measure of this departure is the transmission coefficient κ, defined by the ratio k/k_TST. TST has been described in many different ways (not all of which are very compelling), especially in the older literature; but nowadays most would accept the ‘no recrossing rule’ version enunciated by E. Wigner in the 1930s [28], which we now present.

The TST rate constant for the forward reaction is given by the equilibrium average, normalized with respect to the reactants R, of the one-way flux across the transition state surface

$$k_{\text{TST}}=\langle J_{+}^{‡}{\rangle }_{\text{R}}$$ (2.1)

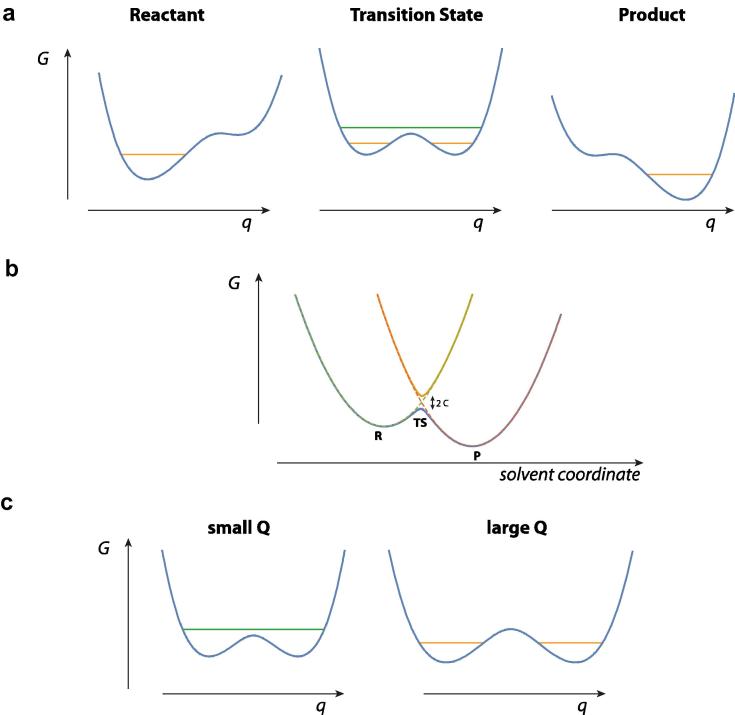
Fig. 1 for a collinear (gas phase!) atom transfer reaction provides a useful illustrative perspective for the terms to be defined. Here the brackets 〈(…)〉_R denote the above-mentioned equilibrium average and $J_{+}^{‡}$ is the one way flux

$$J_{+}^{‡}=\frac{p}{m}{\theta }_{+}(p)\delta (x-x^{‡})$$ (2.2)

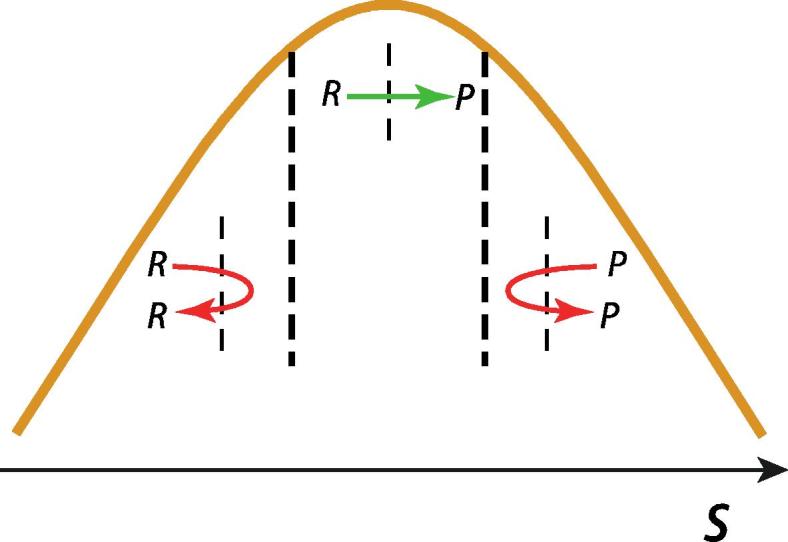
Here p and m are the momentum and mass associated with the reaction coordinate x at the transition state (TS), θ₊(p) is the step function assuring that only positive p values are included – corresponding to trajectories crossing the TS surface x = x^‡ in the direction from reactants R to products P – and the delta function δ(x–x^‡) restricts the reaction coordinate x to its TS surface value. The basic assumptions here are a description by classical mechanics for the nuclei, the idea that the rate constant for a system in chemical equilibrium is the same as in a non-equilibrium kinetics experiment, and that (to repeat) there is no recrossing of the TS surface x = x^‡, i.e. all trajectories crossing from the side of reactants to the side of the products continue on to become (stable) products (Figs. 1 and 2). The latter fundamental assumption of TST could legitimately be – and often is – termed a dynamical assumption, since it is an edict about the trajectories, but we will not insist on this in the present discussion. Note that, in the simple model illustration, both panels of Fig. 1 emphasize that the TS is really a surface (and not a point), and that there must be a distribution of trajectories that cross this surface, an aspect not always recalled.

Fig. 1.

Schematic energy diagrams for a collinear, symmetric, gas phase A + BC → AB + C reaction, with A = C, and all masses equal for simplicity. (a) Contour potential energy diagram with q₁ = the AB separation and q₂ = the BC separation. Surfaces associated with the reactant (R), product (P) and symmetric transition state (TS, ‡) are shown. Solid line indicates the minimum energy path (MEP). (b) Plot of the energy along the MEP. The reaction coordinate x is the relative translation of the reactants in the R region, the ABC antisymmetric stretch at the TS, and the relative translation of the products in the P region. The dashed curves indicate the transverse, non-reactive coordinates: the BC stretch in the R region, the symmetric ABC stretch at the TS, and the AB stretch in the P region.

Fig. 2.

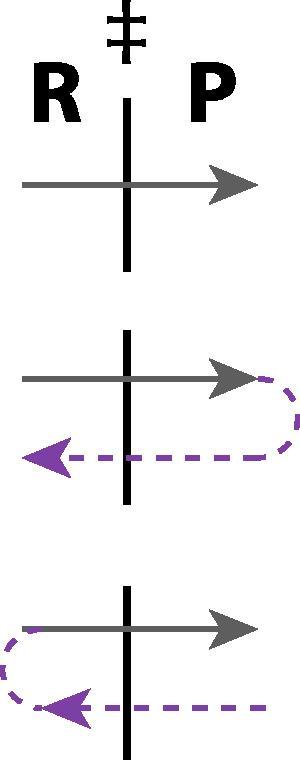
Crossing and recrossing trajectories at the TS surface. TST assumes that all trajectories are like the topmost trajectory, leading successfully from the side of reactants (R) to the side of products (P). The remaining two trajectory types are in violation of the TST no-recrossing assumption.

Equation (2.1) can readily be shown (e.g. [29]) to yield the familiar formulas associated with TST, such as

$$k_{\text{TST}}=\frac{k_{B}T}{h}\frac{Q^{‡}}{Q_{\text{R}}}\exp \left[-\mathrm{\Delta }{V}^{‡}/k_{B}T\right]=\frac{k_{B}T}{h}{({\text{C}}^0)}^{1-n}\exp \left[-\mathrm{\Delta }{G}^{‡}/k_{B}T\right]$$ (2.3)

involving TS and reactant partition functions Q^‡ and Q^R, the TS activation potential energy ΔV^‡ and free energy ΔG^‡, a reference concentration factor C⁰ to guarantee correct dimensions, and the famous Eyring prefactor involving the ratio of the thermal energy and Planck’s constant h. Despite assorted statements in the literature about the meaning of the latter factor, this factor does not represent any physical speed in the problem; indeed, the quantum factor h is canceled by an inverse h factor in the partition function ratio [29]. The activation free energy aspect in the simple model illustration Fig. 1 arises (primarily) from the differing distributions in the reactant and transition state transverse coordinates. In solution and enzymatic reactions to be discussed, the same basic structure of k_TST applies, but the coordinates differ.

An alternate form of Eq. (2.3) more convenient for our purposes is

$$k_{\text{TST}}=\frac{{\omega }_{\text{R}}}{2\pi }\exp \left[-\mathrm{\Delta }{G}^{‡}/k_{B}T\right]$$ (2.4)

Here ω_R is a collision frequency of the reactants for a bimolecular reaction (with appropriate units) and is a vibrational frequency in a reactant free energy well for a unimolecular reaction. In this way, the activation free energy ΔG^‡ refers to the same number of degrees of freedom in the TS and in the reactants [30].

In anticipation of our use of the forms Eqs. (2.3) and (2.4) for solution and enzymatic reactions, we note that the appearance of an activation free energy in Eqs. (2.3) and (2.4) emphasizes the point that it is now common for calculations of free energy to be made along some presumed reaction coordinate, especially in condensed phases. In general, and as is the case in Fig. 1, that reaction coordinate can change its character on the way from reactants to the TS and on to products; it may or may not include aspects of the environment of the basic reacting molecular system. Such free energy curves involve the assumption that at each point along that coordinate, all other degrees of freedom are equilibrated to it, a point to which we will return at several junctures. For the most part, it is only in the TS region that this assumption is relevant for a rate constant discussion.

Before proceeding, let us pause for an overview of TST. In the TST framework, the rate of the chemical step is determined by the average forward flux through the transition state surface – subject to the assumptions we have prescribed. This particular flux is proportional to the relative probability to be at the TS with respect to the reactant configurations when the system is equilibrated; this rests on the idea that e.g. the forward rate constant is the same in a non-equilibrium kinetics experiment and in equilibrium, even if the latter is usually unobserved. The rate constant is thus essentially determined by the free energy barrier between reactants and TS. The actual successful barrier passage is quite rapid, as we will see. The rate constant is small (and its inverse, the reaction time is large) because – for any barrier significantly higher than the thermal energy – it is very improbable for the system to be in a position to actually do that passage. Almost all of the trajectories originating from the reactants fail precisely because of that difficulty. Even though the calculation of this activation free energy undoubtedly presents a challenge, it should be appreciated just how simple the TST rate constant really is; one need not be concerned with the innumerable details of the complex activity of all the trajectories attempting the reaction. This is not at all to say that the microscopic details of reaching the TS region from the reactant and reaching the product from the TS region are not interesting – of course they are extremely interesting! But typically they are not relevant for the rate constant (but see the section ‘Concluding remarks’).

Dynamical effects in the transition state neighborhood

TST provides an approximate expression for the reaction rate constant, without any explicit accounting of dynamical effects. But it is easy to imagine that some dynamical effects might play a role here. The reacting fragments must be moved close together and correctly oriented, some bonds must be lengthened while others are shortened. In the environment of the reacting molecules, conformational changes need to tune the electrostatics to favor these processes. Such motions that take the reactants to the TS region span a variety of time scales. There can also be dynamics within the TS region itself. For example, large amplitude motions might be opposed by dynamic viscous environment forces. Charge transfers and redistributions might be opposed by sluggish motional rearrangement of polar and charged molecules in the environment.

As we will argue at several junctures, slower conformational rearrangements in solution and in enzymes need to occur first in order to bring the system to the TS region (and as remarked above, most trajectories fail in the attempt). The much more rapid events – bond-breaking and bond-making and charge transfer – occur subsequently, in the TS region. Both of these aspects can be the source of dynamical effects for the rate. In this section, we will focus on the latter, TS region.

A popular and widespread criterion for the presence of dynamical effects is the departure of the reaction rate constant from its TST value, conveniently measured by the transmission coefficient κ defined by the ratio k/k_TST, so that

$$k=k_{\text{TST}}\kappa$$ (3.1)

In the classical description of nuclear motion, this departure arises from TS surface recrossing (Fig. 2). Since those recrossing trajectories do not represent successful R to P transitions – as TST would have it, in fact they do not contribute to the rate constant, and so κ is reduced below unity. In this view, the more that κ is reduced, the greater are the dynamical effects on the rate. This is indeed (often) a reasonable viewpoint, and we will often adopt it. But we hasten to stress that all is not so straightforward. Here we single out two reasons for this. First and most importantly, κ depends via Eq. (3.1) on the TST rate constant and its definition. But this in turn depends upon the choice of reaction coordinate x in the TS neighborhood, and herein lies an element of choice. The transmission coefficient value could be unity (or very close to it) for one choice of x and be very small for another choice, with a corresponding difference in the assessment of the importance of dynamics. This issue is coupled to what is often called “Variational Transition State Theory”, as we will discuss within. The second (and more subtle) complicating feature is that it can happen that κ is reduced below unity, but no environmental dynamics is involved; instead the absence of dynamics is responsible for the depression of κ. As we will see in the section ‘A solution reaction example’, this is related to what can be termed “nonequilibrium” effects on a reaction rate, which are often – but not necessarily – related to dynamical effects. In addition, the existence and extent of nonequilibrium effects on the rate also depend on the reaction coordinate definition.

All the above discussion has assumed classical motion for the nuclei. This is clearly inappropriate for proton, hydride and hydrogen atom transfer reactions, and special discussions are required (section ‘Dynamics for reactions involving quantum nuclear motion’). We can however anticipate a bit and indicate that often the actual reaction coordinate is a classical environmental variable, so that our classical considerations above and below apply.

Theoretical descriptions of κ for reactions in condensed phases began with Kramers in 1940 [30–32], who adopted a Brownian motion view of the reaction with motion described by a Langevin equation involving a simple frictional force – ζv, where v = $\dot{x}$ is the velocity of the reaction coordinate and ζ is the friction constant. In modern terms, this frictional force arises from the interaction of the reaction system of interest with the surroundings. One impact of this force can be to impede the motion and alter the reaction coordinate momentum, e.g. reversing a trajectory crossing the TS from R to P, resulting in TS recrossing. Kramers’ result for κ is

$${\kappa }_{\text{KR}}={\left[{(\varsigma /2m{\omega }_b)}^2+1\right]}^{1/2}-(\varsigma /2m{\omega }_b)$$ (3.2)

where ω_b is the barrier frequency, the square root of the magnitude of the negative curvature of the free energy barrier at the TS divided by the reaction coordinate’s effective mass m. This shows that κ steadily diminishes from its TST value of unity as the friction increases. (There is another, small friction, regime result due to Kramers which we do not address here [31]). At a fundamental level, the friction constant ζ is proportional to the time integral of the time correlation function of the force F exerted on the reaction coordinate at the TS

$$\varsigma \propto {\displaystyle \underset{0}{\overset{\infty }{\int }}}\mathit{dt}\langle \mathit{FF}(t)\rangle$$ (3.3)

For solution reactions, ζ is often assumed to be proportional to the solution viscosity η, but this is neither fundamental nor always applicable.

Grote and Hynes (GH) generalized Kramers’ result [33] in order to take into account that the impact of the environment on the TS barrier recrossing should not depend on the friction constant ζ – which reflects the retarding power of the environment on long space and time scales – but rather on the time-dependent friction ζ(t) (whose time integrated area is ζ) exerted on the reaction system during the (often very) short space and time scales of the passage in the barrier neighborhood. This time scale is approximately given by ${\omega }_b^{-1}$, the inverse of the barrier frequency. For many modest to high barrier reactions, this can easily be just a few fs. The GH result for the transmission coefficient

$${\kappa }_{\text{GH}}={\left\{{\kappa }_{\text{GH}}+\left[\widehat{\varsigma }({\kappa }_{\text{GH}}{\omega }_b)/m{\omega }_b\right]\right\}}^{-1}$$ (3.4)

in which $\widehat{\zeta }\left({\omega }_b{\kappa }_{\text{GH}}\right)$ is the Laplace transform of ζ(t), is generally much closer to the TST prediction κ_TST = 1 than is κ_KR, i.e. it predicts smaller environmental dynamical effects on the rate – a closer, and often much closer, approach to the TST prediction – since it is usually difficult for the environment to exert a significant influence on short space and time scales. Sometimes the ratio κ_GH/κ_KR can be ∼ 10^{2 27}. κ_GH reduces to κ_KR when ω_b is small and the space and time scales determining the recrossing become long enough for the full frictional impact characterized by ζ to be felt by the reaction system. Since GH theory has been repeatedly found to accurately account for simulation results (including those of enzyme reactions [34,35]) and has proved useful for the interpretation of experiments [27], we employ this perspective in much of what follows. One of its lessons is that, as explained above, deviations from TST, while they exist, are not often very large; with a reasonable choice of reaction coordinate, TST is typically an excellent description of the reaction rate constant.

There can be many different types of environmental friction ζ(t) for the TS passage: from collisional friction to hydrodynamic friction when reacting particles must translate and or rotate significantly and displace environmental molecules; electrical polarization field (or “dielectric”) friction when charge transfer reactions occur in polar environments and the environment molecular dipoles are set in motion (this general type of friction will be of special interest to us here), ionic atmosphere friction when charge transfer reactions occur in mobile ionic environments and motion of those ions is involved, and so on. Associated with all these circumstances are different time scales and different coupling strengths for the environment-reaction system interaction.

Some special and important regimes can be distinguished in the GH theory perspective [36]. When the barrier frequency is sufficiently high and the reaction system-environment coupling is not too strong, there is no time for the friction ζ(t) to depart from its initial value during any recrossing events, and a “frozen environment” regime applies; the reaction proceeds without any dynamics in the environment (during the short time of the trajectories involved in the barrier passage). If the reaction system-environment coupling is instead strong, then no successful reaction can occur until environmental dynamics occurs, so that dynamics is critical; this has been termed the “polarization cage” limit [36].

A solution reaction example

The Cl⁻–MeCl’ S_N2 reaction in water [37] (with the prime included for convenience of discussion) illustrates the former, frozen environment limit of GH theory, as well as several other important issues introduced in our discussion. The barrier frequency is sufficiently high that recrossing events responsible for the κ value occur before any water motion in the TS neighborhood can take place and the initial value of the time dependent friction is sufficiently small that reaction can occur even without such solvent motion. A microscopic level description of this involves two key features. The first is the hydrogen (H)-bonding of the solvent waters with the TS structure (here taken as the symmetric Cl^δ—Me–Cl’^δ−); the equilibrium hydration pattern favors symmetric H-bonding of several waters to each of the two partially charged chlorines, but allows other, asymmetric configurations (as we will see). The second feature is the antisymmetric stretch character of the (selected) reaction coordinate, i.e. compression of the incipient Cl–Me bond forming neutral Cl–Me, and expansion of the breaking Me–Cl’ bond forming the departing chloride anion; this involves a rapid charge flow from the attaching chloride to the departing chloride in the presence of the “frozen” hydrating water molecules.

Fig. 3 indicates the recrossing patterns. RR recrossings occur when there is an asymmetric H-bonding hydration pattern favoring the R side of the TS, i.e. the charge localized on the left-hand side Cl (note though that the actual charge distribution is the symmetric TS one). This is unfavorable for formation of the product P, which has the negative charge localized on the right-hand side Cl’, and the trajectory heading towards P from R rapidly recrosses, contradicting the TST assumption. PP recrossings have an asymmetric H-bonding hydration pattern favoring the P side of the TS, i.e. the charge localized on the right-hand side Cl’; a trajectory apparently crossing in the R → P direction – and would be counted as successful in the TST view – in fact originated from the P side and rapidly recrosses to that side since the hydration pattern disfavors the R side. Finally, a symmetric H-bonding hydration pattern has no bias either way, and successful R → P trajectories occur, just as the TST assumption would have it. All of this – leading to the departure from TST and a transmission coefficient less than unity – involved no environmental dynamics at all. This is of course not always the case [27]; we discuss an enzyme reaction where dynamics are involved in the section ‘Beyond the frozen environment limit; environmental dynamics impact’ for example. The transmission coefficient κ ∼ 0.5, which is well predicted by GH theory, so that TST while not perfect, is not very far in numerical error.

Fig. 3.

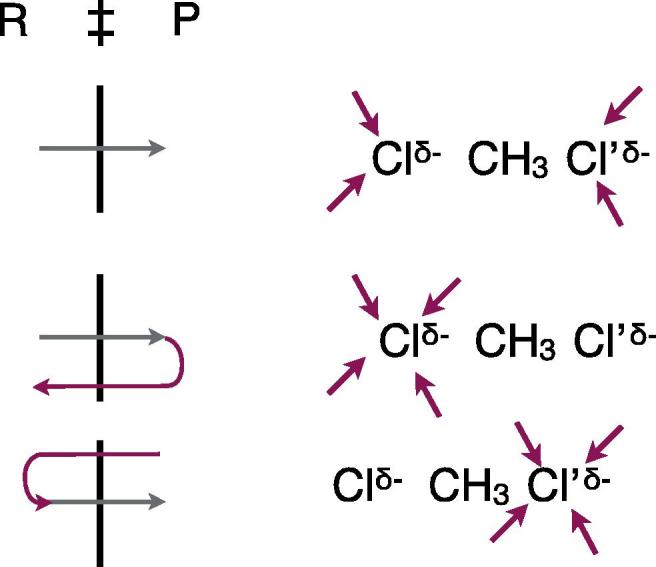
Trajectory types for the S_N2 reaction discussed in the text, together with their associated schematic water solvent hydrogen-bonding patterns of the transition state S_N2 solute. The trajectory patterns are those already shown in Fig. 2.

The preceding can be regarded as an instance of “nonequilibrium solvation”. What does this mean? The equilibrium free energy curve along a reaction coordinate, such as that in Fig. 4a and in numerous examples in the literature, assumes that the environment is always equilibrated at each point along the reaction coordinate. In our S_N2 example, this implies that the water solvent molecules are always equilibrated to the instantaneous charge distribution in the reacting solute. This is an “equilibrium solvation” assumption, and it is clearly violated in the events described in the preceding paragraph, with the nonequilibrium solvation consequence that k falls below k_TST: κ < 1. It follows that TST assumes equilibrium solvation. This issue is often a source of confusion, so it is worthwhile to be explicit here, using our S_N2 example. Fig. 5 qualitatively portrays the equilibrium distribution of water H-bonding configurations at the TS, i.e. when the reacting solute has the TS arrangement Cl^δ−–Me–Cl’^δ−. TST assumes that the entire equilibrium distribution leads to successful R → P transitions. But we have just seen that the flanking asymmetric portions of the distribution are not successful; only the central, sufficiently symmetric portion leads to successful trajectories. Thus the distribution of successful, reactive R → P trajectories is a nonequilibrium one.

Fig. 4.

Schematic free energy diagrams for the Cl + MeCl’ S_N2 reaction in aqueous solution. (a) Schematic free energy diagram, indicating the activation free energy ΔG^‡. (b) Contour diagram indicating a vertical TS surface (perpendicular to the antisymmetric stretch coordinate– which in the TS neighborhood is x) rotated to give a better TS surface with reduced recrossing; the latter involves a solvent coordinate contribution. Recrossing trajectories for the original surface are shown. The solid line is a schematic minimum free energy path. Ref. [38] may be consulted for the original discussion.

Fig. 5.

Schematic illustration of the equilibrium distribution of solvent water hydrogen-bonding configurations at the S_N2 reaction TS. (See also Fig. 3). The central panel (green arrow) represents the fraction leading to TS surface crossing satisfying the TST recrossing assumption. The flanking panels (red arrows) represent asymmetric water solvent configurations leading to recrossing trajectories of the labeled type, violating the TST assumption. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The discussion just given concerned the non-equilibrium aspects of the distribution in the TS region. Away from the TS region, i.e. between the reactants and the TS region, and the TS and the products region, there is a very significant deviation from the equilibrium assumption implicit in the calculation of free energy curves as in the schematic Fig. 4a [39]. But it is important to stress that the activation free energy factor ΔG^‡ between the TS and the reactions is correctly given in the exponential context of the TST rate constant Eqs. (2.3) and (2.4), modulo corrections arising from κ.

Another insight available from the S_N2 study [38] concerns the issue of the choice of the reaction coordinate. The discussion above involved the – in many ways quite natural – choice of the (unstable) antisymmetric stretch, here termed x with x = 0 at the TS, for the (ClMeCl')^−‡ system. But the analysis of the recrossing patterns discussed above revealed that these events could be quite closely associated with extra, comparatively small, barriers in x, not apparent in the equilibrium free energy curve. The locations and heights of these barriers depend on the degree of H-bonding hydration of the TS complex, which can be related to a solvent coordinate, here termed s. For example, RR recrossing trajectories arise from s-dependent barriers in x located slightly past the nominal TS surface x = 0 so that they are encountered by the trajectory coming from R and are reflected back to R. In an orthogonal x–s coordinate system, our original perspective x = 0 for the TS surface can be altered to a rotated surface lying along the peaks of these barriers to minimize the flux across the new surface [38]; Fig. 4b gives a qualitative impression of this. In this Variational Transition State Theory (VTST) perspective [40], there is no recrossing (or rather very little in the real system) and TST is exact (much improved in the real system).

We will encounter other applications of VTST later in this article, in an enzymatic context, since it can serve as a quite useful way to improve the description of a reaction coordinate and thus provide a better (lower) TST-type estimate of the rate constant. Indeed, the first simplistic choice of a reaction coordinate is often susceptible to improvement to capture the influence of several other motions on the reaction rate. Here we take the opportunity to address an issue sometimes stated in connection with GH theory, the claim that GH is equivalent to a form of VTST. We have just recounted a case where this is indeed true [38] (see also [41]). However, we definitely do not consider this to be generally true. We limit ourselves to very brief remarks here. Consider for example a reaction rate that depends strongly on dissipative aspects such as the viscosity or dielectric relaxation time of the environment. It is difficult to conceive how a momentum-independent configurational coordinate or set thereof would suffice to capture such effects. The interested reader may consult [42,43] for a recent discussion. In any event, as a practical matter, the explicit inclusion of more and more coordinates in a reaction coordinate ultimately would appear to become closer to a phone book description rather than to a useful chemical or biochemical perspective.

A frozen environment enzymatic reaction

An example of an enzymatic reaction illustrating the case when the coupling between the reacting system and the environment is not too strong is provided by another S_N2 process. This is the methyl transfer reaction from the cationic cofactor S-adenosyl-l-methionine (SAM) to the catecholate anion which is catalyzed by catechol O-methyl transferase (COMT) [34], and is an S_N2 reaction that formally proceeds from charged reactants to neutral products (see Fig. 6).

Fig. 6.

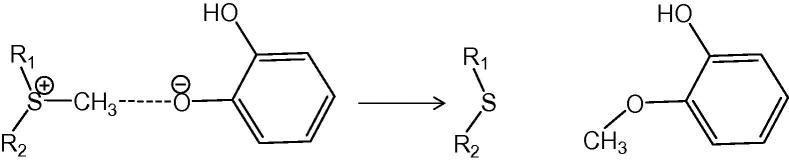
The S_N2 methyl transfer reaction catalyzed by the enzyme catechol O-methyl transferase.

With the choice of the antisymmetric S–C–O stretch as reaction coordinate, GH theory was shown in a simulation study to provide a transmission coefficient in excellent agreement with the value obtained from a GH theory limit frozen environment (FE) description (κ_GH = 0.89 ± 0.03 and κ_FE = 0.86 ± 0.02, respectively). Both values agreed with the estimation (κ_MD = 0.83 ± 0.03) obtained from rare-event trajectories initiated at the TS. Thus, there is a nonequilibrium environment effect but not a dynamical effect. On the other hand, Kramers theory clearly underestimated the transmission coefficient (κ_KR = 0.10), since it includes the full time integrated frictional effect, i.e. the full impact of environmental dynamics, which is not relevant on the short time scale in the TS region (inverse barrier frequency ∼ 30 fs).

These results were related to the concept of active site preorganization [3]: the protein structure provides a reaction site that is organized to favor the reaction [34]. In addition to an important reduction of the free energy barrier included in a TST perspective, this reduces the coupling of environmental motions with the reaction coordinate at the TS, since the environment suffers smaller changes during the TS, barrier top passage. The catalytic effect is traditionally assessed by comparison with the aqueous phase reaction. The scenario is substantially different for these two situations. In solution, water molecule dipoles must be reoriented at a free energy cost not paid in the enzyme. This reorientation is needed for the solvent waters to follow the charge flow taking place in the reaction and then environmental dynamics becomes important. This is reflected in the underestimated transmission coefficient obtained from the frozen environment approach in solution (κ_FE = 0.44 ± 0.09 and κ_MD = 0.62 ± 0.04, respectively). The solvent environment dynamics decreases the rate by about a factor of 2. The difference in the enzymatic and solution transmission coefficients and the associated lack of, or presence of, environmental dynamics is important for a detailed comprehension of the reaction microscopics, but is unimportant compared to the exponential impact of the difference in the enzyme and solution phase ΔG^‡ values, a feature captured by a TST treatment.

The results for the catechol catalytic S_N2 reaction involving a methyl transfer between a donor (S) and an acceptor (O) are of interest in connection with an issue that will occupy our attention in the section ‘Dynamics for reactions involving quantum nuclear motion’. Several authors [44,45] have proposed that protein motions could favor methyl transfer enzymatic reactions by compressing or compacting the donor–acceptor distance. The computational results do not find this to be important for this reaction: the average S–O distances at the TS in the enzyme and solution are almost equal; the transmission coefficient κ obtained using the antisymmetric S–C–O coordinate is quite high, and there is no signature of the symmetric S–C–O motion in the GH friction spectrum governing κ [34].

Beyond the frozen environment limit; environmental dynamics impact

If the reaction system-environment coupling is strong, then a polarization caging regime can hold, in which a trajectory recrosses the TS surface and cannot escape the TS region without environmental dynamics to annihilate this cage. This is obviously a nonequilibrium solvation situation, but in contrast to the frozen environment limit, κ will depend explicitly on those dynamics in a manner determined by the GH Eq. (3.4). For example, in a dynamic dielectric continuum model of the environment, κ is an explicit function of a certain dielectric relaxation time [36]. More generally, outside of the frozen environment regime, environmental dynamics will enter the rate to a degree described by the GH equation.

At this stage, an additional important point needs to be made explicit. The definition of the “environment” clearly depends on the definition of the reaction coordinate. In this entire section, the environment has been interpreted as e.g. the surrounding solvent. But it may also involve other degrees of freedom of the reaction system which are not explicitly included in the reaction coordinate; this is illustrated in the following.

The enzymatic reaction catalyzed by Chalcone Isomerase (CHI) provides an example of strong reacting system-environment coupling. CHI catalyzes the transformation of chalcones via an intramolecular Michael addition of a deprotonated hydroxyl group to the α,β-double bond, as shown in Fig. 7.

Fig. 7.

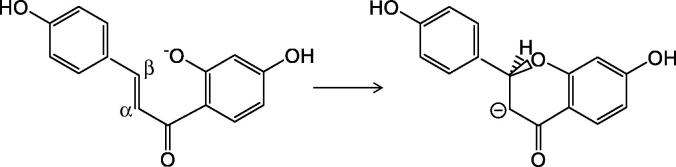
The intramolecular Michael addition reaction catalyzed by the enzyme Chalcone Isomerase.

In a computational study [35], this reaction was monitored using the O–C^β stretch as the reaction coordinate. The involvement of some environmental dynamics was signaled by the noticeable underestimation by the frozen environment approach of the enzymatic transmission coefficient with respect to the result obtained from the analysis of trajectories initiated at the TS (κ_FE = 0.56 and κ_MD = 0.87 ± 0.03, respectively). On the other hand, full GH theory is in excellent agreement, within standard deviation of the molecular dynamics estimation (κ_GH = 0.82 ± 0.02). Again, TST is quite a good description. In contrast, Kramers theory strongly overestimates the friction and the recrossings (κ_KR = 0.03). In addition, just as with the methyl transfer to catecholate reaction in the section ‘A frozen environment enzymatic reaction’, the transmission coefficient difference between the enzyme and aqueous solution reactions contributes in a negligible fashion to the catalytic enhancement, which is dominated by the activation free energy difference. This type of conclusion has been reached for other enzyme reactions as well [46].

An appealing aspect of GH theory is that it can also be used to determine the differing impacts of different coordinates on the transmission coefficient [47]. For this enzyme reaction, environmental motions strongly coupled to the O–C^β reaction coordinate were found to occur on the barrier crossing timescale; since their dynamics is thus relevant, the failure of the frozen environment approach is explained. Most of these dynamically coupled motions are in fact located in the reacting system and not in the protein environment. In particular, the hybridization change at the C^β atom due to the nucleophilic addition leads to an out-of-plane motion of the bonded hydrogen atom and the lengthening of the C^β–C^α bond. One could envisage including these aspects in a more complicated reaction coordinate, if desired. As for the protein environment, this dynamical coupling involves to some extent some active site residues. The changes suffered by the substrate propagate into the protein, which must accommodate to the hybridization-induced repositioning of the substrate phenyl rings.

“Heavy” enzymes

Schramm and coworkers have grown enzymes in which all the nitrogen, carbon and non-exchangeable hydrogen atoms are substituted by heavier isotopes (¹⁵N, ¹³C and ²H) [48]. The “heavy” version of enzymes usually shows modest reductions in the reaction rate constants. This has been analyzed in terms of the participation of vibrations in the reaction event (see e.g. the case of Purine Nucleoside Phosphorylase in [49]). According to this interpretation, the substitution by heavier isotopes lowers the frequency of protein motions, causing a slower, less efficient sampling of the complex pathways leading to barrier crossing, thus reducing the rate constant.

An alternate interpretation is possible using the TST/transmission coefficient framework Eq. (3.1). The changes induced by the isotopic substitution in the dynamics of the environment and in the spectral density of these “bath” modes can be satisfactorily incorporated into the calculation of the rate constant by considering the mass dependence of the transmission coefficient calculated via GH theory. Very briefly, an increase of the mass leads to a slower environment that increases the friction on the reaction coordinate in the TS region. This increased friction increases in turn the fraction of recrossing trajectories, thereby diminishing the transmission coefficient and the rate constant [50]. However, it should be recognized that other effects might also contribute to the change of the rate constant in the heavy enzyme: the vibrationally averaged C–D bond lengths are slightly shorter than those of the C–H groups, causing slight structural perturbations in the protein.

Some closing thoughts

In concluding this particular section, we give a few more thoughts, implied by the preceding but worth stating explicitly. In practice, a selected reaction coordinate is simply a reasonable choice, based for example on the lengths of the bonds to be broken and formed. It will never be a perfect reaction coordinate and it is not even certain that such a thing exists. But the resulting error due to (generally small) non-equilibrium effects – involving dynamics or not – due to the degrees of freedom which are not included in the approximate definition of the reaction coordinate and other events not incorporated will lead to a typically small to modest decrease in the actual rate constant with respect to the TST value [14,27,30]. This decrease can be included by correcting the TST expression with a recrossing transmission coefficient, which can often be theoretically described.

Dynamics for reactions involving quantum nuclear motion

As we remarked in the section ‘Transition State Theory’, standard TST is a classical theory for the rate constant; in particular, the reaction coordinate for the passage through the TS surface is described by classical nuclear motion. Reactions involving the transfer of a proton H⁺, hydride H⁻, or hydrogen atom H require a quantum treatment for the proper description of their nuclear motion [51–63]; this applies as well to aspects of proton-coupled electron transfer reactions [64–66]. The first two of these are charge transfers and usually have strong coupling to a polar environment; these will be our focus here, usually mainly the language for proton transfers, hereafter PTs. Our remarks also apply to the PT portion of proton-coupled electron transfers.

Proton transfer rate constants

Although other approaches are possible (see e.g. [51–53,60]), we will discuss these quantum transfer reactions from the perspective described in the group of one of us [54–58] that the rapid quantum nuclear motions can be quantized at fixed values of the remaining, slower and largely environmental coordinates, such that it is the latter that provide the reaction coordinate, which itself is classical. In a solution context, this is typically a solvent coordinate reflecting the solvent’s nuclear electrical polarization in interaction with the reacting solute system [54,55,57,58]. This coordinate can also be related to an energy gap coordinate associated with the different interaction of the solvent’s configuration with either of reactant and product configurations, especially with their different charge distributions (see Eq. (4.1) below). Related considerations can be used to define an environmental reaction coordinate for enzymatic reactions [59].

There are two PT regimes, the adiabatic and nonadiabatic (or tunneling) regimes, now discussed for a PT acid-base reaction of form

$$\text{AH}\cdots \text{B}\to {\text{A}}^{-}\cdots {\text{HB}}^{+}$$ (4.1)

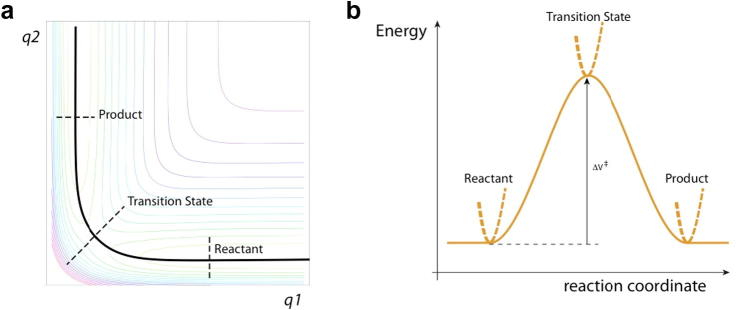
occurring in an H-bonded complex. The fundamental picture in either regime, characterized in Fig. 8, is that the quantum PT event itself is rapid compared to the reorganization of the environment which is necessary for the attempt of the transfer. Therefore, this reorganization must occur prior to the attempt, such that the environment (and other “slow” coordinates not including the proton) constitutes the reaction coordinate and determines the activation barrier (Fig. 8b.)

Fig. 8.

Schematic free energy (G) curves for the discussion of proton transfer reactions of type Eq. (4.1) in a polar environment, involving the proton coordinate q and the hydrogen-bond coordinate Q (a) proton potentials at different values of the environmental/solvent coordinate, with the proton vibrational levels shown (two different levels are shown for nonadiabatic tunneling and adiabatic cases at the transition state solvent coordinate value). (b) Free energy curves in the environmental/solvent coordinate; the reactant and product curves cross in the tunneling regime, but these are split by twice the proton coupling C to produce upper and lower curves in the adiabatic regimes. (c) Illustration of the aspect that the adiabatic regime is favored by small Q values (larger C), while the tunneling regime is favored by larger Q values (smaller C). The exponential behavior of C is especially important in the latter regime. See also e.g. [54,56].

In the adiabatic regime [54,57] the proton adiabatically follows the slower environmental coordinate (Fig. 8a) and at the transition state of the latter – reached from the reactants at a cost of ΔG^‡ (Fig. 8b) – the zero point energy (ZPE) level for the proton lies above the proton barrier in the proton coordinate q; this bound vibrational motion is in contrast to the common view of unstable, above the barrier classical, supposed reaction coordinate, motion of the proton. Quantum and kinetic isotope effects then enter via the difference ΔZPE^‡ of the ZPEs at the environmental reaction coordinate’s transition state s^‡ and reactant values. Beyond this, all of our previous remarks apply to this regime, with the classical environmental coordinate being the reaction coordinate. The rate constant is

$$k_{\text{AD}}=k_{\text{AD,TST}}\kappa =\frac{{\omega }_{\text{R}}}{2\pi }\exp \left[-\left(\mathrm{\Delta }{\text{ZPE}}^{‡}+\mathrm{\Delta }{G}^{‡}\right)/k_{B}T\right]\kappa$$ (4.2)

where ω_R is the frequency in the R well of the free energy curve Fig. 8b and κ is the transmission coefficient determined by any recrossing of the TS in the environmental coordinate s leading to a departure from TST (see also Eq. (2.4)). Evaluations of κ for adiabatic PT in this fashion indicate that GH theory provides an accurate description and that deviations for TST so defined are small [58].

In the nonadiabatic, tunneling regime [54–56,61], at the TS s^‡ of the environmental coordinate, the proton ZPE level lies below the barrier in the proton coordinate (Fig. 8a). For ease of discussion, we assume that both the first two levels lie below this barrier, and are separated by the tunneling splitting or coupling C(Q). This coupling is approximately an exponential function of the H-bond vibrational coordinate Q, the A–B separation; this reflects the overlap of the (nonadiabatic) proton wave functions localized in the R and P wells at s^‡; a schematic illustration of the important impact of Q on the PT potential and levels is given in Fig. 8c. In the tunneling regime, this coupling is small, so that the activation free energy ΔG^‡ is given by the intersection of the nonadiabatic (proton-localized) R and P curves (Fig. 8b). When s^‡ is reached, at the cost of ΔG^‡, a successful (incoherent) tunneling through the proton potential barrier (Fig. 8a) will occur with a probability proportional to 〈C²〉, where the brackets indicate an appropriate average over the Q motion, discussed further below. This defines a quantum tunneling transmission coefficient κ_Τ proportional to 〈C²〉. This is of course logically distinct from the transmission coefficient κ, which is – as per usual – associated with recrossing, here in the environmental coordinate, of the TS surface at s^‡. The rate constant is thus of the form

$$k_{\text{NA}}=k_{\text{NA,TST}}{\kappa }_T\kappa =\frac{{\omega }_{\text{R}}}{2\pi }\exp \left[-\mathrm{\Delta }{G}^{‡}/k_{B}T\right]{\kappa }_T\kappa$$ (4.3)

In contrast to the adiabatic case Eq. (4.2), no ZPE difference enters. The tunneling transmission coefficient reflects via the coupling factor 〈C²〉 the exponential sensitivity of the coupling to the Q motion: as Q decreases or the A–B “bond” is compressed, the transfer barrier is lowered, its width is diminished, with a consequence that the tunneling rate constant can increase dramatically. And, due to the well-known strong sensitivity of tunneling to the mass, it is also the principal source of a kinetic isotope effect (KIE), the ratio between the reaction rate constants for the transfer of a hydrogen and of a heavier isotope, e.g. deuterium.

We pause to remark that the nonadiabaticity here is of nuclear origin, i.e. the proton motion, due to the weak coupling 〈C²〉. The electronic motion governing the proton potentials in Fig. 8a is instead adiabatic, since electronic coupling in proton (and hydride) transfer systems is very strong (∼1 eV). Some tunneling rate formulas in the literature have an additional weak electronic coupling transmission coefficient factor, which is inappropriate [61].

Quantum tunneling considerations-“promoting” modes

The acceptance of frequent occurrence of tunneling in reactions, most especially in enzymatic reactions, is of fairly recent vintage. The tunneling transmission coefficient κ_Τ per se might be considered to automatically involve dynamical effects, since it involves the quantum crossing of a barrier via a probability flux. But this barrier is in the hydrogenic coordinate, not the reaction coordinate determining the reaction barrier height. We will not call tunneling a dynamical effect here, unless some explicit dynamics of the coordinate e.g. Q it depends on, is involved. Finally, it appears that the quantum motion regime most prevalent in enzymes is the tunneling regime rather than the adiabatic transfer regime. This may reflect – in a fashion similar to the more frequent occurrence of tunneling in intramolecular rather than intermolecular reactions in solution [55] – configuration restrictions in the enzyme active site [62].

As already emphasized, the strong sensitivity of the tunneling to the Q vibration is a characteristic feature of, and has played a featured role in, many discussions of tunneling reactions, with its origins in the Russian school [51–53], including older gas phase reactions [67]. In solution, intramolecular rather than intermolecular reactions are likely to exhibit tunneling due to geometric constraints on the donor–acceptor distance Q. The situation appears to be somewhat similar in enzymes, where the prevalence of tunneling or quantum adiabatic limits depends on the range of Q values attained in the TS region (itself defined via the environmental coordinate). In view of its special role, a coordinate such as Q is often termed a ‘promoting’ mode or vibration. More recently, it has received special attention in connection with proton and hydride transfer reactions in enzymes [10,68–71], one fairly general definition being a “vibration with some degree of motion along the reaction coordinate, coupled to a transient compression of the apparent barrier” [10].

Before proceeding, we need to make some important remarks concerning the nature of the average in 〈C²〉 within the tunneling transmission coefficient κ_Τ. This is typically assumed to be an equilibrium average, whether the Q motion is treated classically or quantum mechanically [54,72], i.e. the thermal average over the Q motion when the TS is reached in the environmental coordinate (and any other relevant coordinates). The Q coordinate – which can of course be coupled to other, protein, coordinates – can be important for the rate without the occurrence of dynamical effects. Examples of the latter effects – which would violate the equilibrium assumption – could include a dynamical dependence on vibrational activation (thus involving a vibrational activation time) or some kind of important frictional damping of Q or some protein coordinate strongly coupled to it, involving either mechanical or electrostatic impediments for the motion (thus involving a dynamical parameter such as a dielectric relaxation time).

Promoting modes in enzyme reactions

Protein motions involved in such promoting vibrations acting on the donor–acceptor distance (Q in our discussion) are often invoked to explain the observed temperature dependence of enzymatic KIEs. Strongly temperature-dependent KIEs are thought to be the signature of these promoting vibrations, the argument being that when the temperature is increased, smaller donor–acceptor distances become more easily accessible, which reduces the importance of tunneling and consequently decreases the KIE [73].

The effects of compressing motions on the reaction rate and KIEs have been also monitored through mutagenesis [74,75]. A common observation is that while KIEs are largely temperature-independent in wild type enzymes, they become temperature-dependent when the system is perturbed in mutants. It has thus been suggested that only the wild type enzyme is able to efficiently sample small donor–acceptor distances at all temperatures [76]. In contrast, mutants would be more rigid and their equilibrium donor–acceptor distance would be larger. This has for example been suggested for hyperthermophilic enzymes, whose optimum functioning temperature is higher than for their mesophilic counterparts. The increased rigidity in thermophiles would on the one hand increase their structural stability at high temperature, but on the other hand would also hinder the necessary donor–acceptor distance compression. This has been interpreted as supporting the importance of protein flexibility and activation of compression motions in the chemical step [77].

It is important to note, however, that these experimental observations do not necessarily imply the presence of dynamical effects contradicting any equilibrium assumption. After all, different probabilities of finding short donor–acceptor distances are included in the equilibrium distribution involved in the tunneling transmission coefficient; this is a point also strongly made elsewhere for enzymatic quantum transfers [46,78]. The demonstration of a dependence on some dynamical parameters indicating a nonequilibrium distribution would provide evidence of dynamical effects. It is also worth noting that alternative explanations for the temperature-dependence of KIEs are also possible which consider the conformational diversity of enzyme reactants and the shift caused by temperature in their relative populations [11].

On the theoretical side, the role of promoting vibrations in hydrogen tunneling in enzymes has received considerable attention. For example, Schwartz and coworkers have defined such vibrations as ‘non-equilibrium density fluctuations that propagate through specific structures within the protein’ [68]. These promoting motions are identified by following a Transition Path Sampling (TPS) approach (which however does not treat the hydrogen motion quantum mechanically) [79]. Promoting vibrations are identified in this approach by determining the degree of implication of protein motions in the reaction coordinate that crosses the transition state. Subpicosecond motions of some active site residues were found to be involved in the reaction coordinate, which demonstrates that protein motions are a constitutive part of the reaction coordinate. This computational process could be seen as equivalent to an optimization of the reaction coordinate in a VTST fashion by including protein and substrate degrees of freedom [80]. The general perspective concerning the reaction-environment coupling that we have stressed in the paragraph preceding the present one seems quite relevant here.

In a recent systematic study on the hydride transfer reaction catalyzed by E. coli DiHydroFolate Reductase (EcDHFR), Major and coworkers – using however a classical description for the hydride – compared the TS ensembles obtained using sampling techniques based on different a priori definitions of the reaction coordinate (e.g. Umbrella Sampling and the String-Method), with those resulting from unbiased trajectories generated by TPS [81]. Statistically significant but small differences were observed for average geometrical parameters obtained by the two approaches, although the relative free energies were found to be quite similar. The authors associated this small difference with the contrast between the TPS approach – which involves dynamical trajectories where non-equilibrium effects can be included – and the other sampling techniques – which are intrinsically equilibrium descriptions with remaining degrees of freedom relaxed at each reaction coordinate value.

It is certainly possible that the small difference between the results for the TS ensembles arise from an inadequate choice of reaction coordinate in the equilibrium sampling approach. In particular, it has been shown that in hydride transfer reactions, such as that occurring in DHFR, the reaction coordinate is not the fast motion of the transferred hydride (the q coordinate) but is rather the slow rearrangement of the active site electrostatic environment, along the lines of the section ‘Proton transfer rate constants’ discussion (see e.g. [14,59,62]). In this view, the difference in TS ensembles would not be due to dynamical effects.

Dynamical effects away from the transition state neighborhood

The perspective developed so far focuses on dynamical effects arising from events in the neighborhood of the reaction TS. There are possibilities of dynamical affects on rates due to motions occurring away from the TS region. One example is the case where vibrational activation is necessary to reach the TS region from the stable, low energy Reactant, and – in an aspect sometimes forgotten – vibrational deactivation is necessary from the TS region to reach the stable Product. Another would be if some important spatial coordinate – for example the separation between reactants or some angle – is crucial for bringing the reactants together or into the TS region for the reactant proper; that motion might be diffusive for example. These and related situations can be described by the Stable States Picture (SSP) for reactions formalism [82], here simplified to only the basic structure of its results. A simple model version of the situations just described is

$$\text{R}\underset{k_{RA}}{\overset{k_{RD}}{\leftrightharpoons }}{\text{R}}^{\ast }\underset{k_{f^{*}}}{\overset{k_{b^{*}}}{\leftrightharpoons }}{\text{P}}^{\ast }\underset{k_{PD}}{\overset{k_{PA}}{\leftrightharpoons }}\text{P}$$ (5.1)

involving stable reactant R and product P and (energetically or spatially) “activated” reactant R^* and product P^*. R^* and P^*, though activated, do not include the immediate TS region. If only the TS region were important for the overall reaction, then the forward rate constant would be just (k_RA/k_RD)k_f* = K_R.eqk_f* involving the equilibrium constant K_R.eq for R^* formation times the forward rate constant k_f* for the R^* to P^* reaction. This amounts to k_f,TSTκ, which we stress includes any correction to TST due to recrossing in the TS region; we will call this k_f,eq in the development below. The actual (for the model) forward rate constant in the formal R = P reaction follows from the well-known steady state approximation applied to the activated species as [82]

$$k_f=k_{f\text{,eq}}/\left[1+\left(k_{f\text{,eq}}/k_{\text{RA}}\right)+\left(k_{r\text{,eq}}/k_{\text{PA}}\right)\right]=k_{f\text{,eq}}/\left[1+\left(k_{f^{\ast }}/k_{\text{RD}}\right)+\left(k_{r^{\ast }}/k_{\text{PD}}\right)\right]$$ (5.2)

In the SSP, time correlation function expressions are given for all of these rate constants [82].

The second formulation on the second line of Eq. (5.2) here is perhaps the most easily apprehended. Here the equilibrium TS region rate constant is k_f,eq = K_R∗,eq k_f∗ with K_R∗,eq = k_RA/k_RD being the equilibrium constant for an equilibrium population of activated R^∗ compared to reactant R. (An analogous interpretation holds for k_r,eq). In order for k_f,eq to be the actual rate constant, the deactivation rate constants on both the reactant and product sides must be large compared to the TS region rate constants, i.e. k_f∗/k_RD ≪ 1 and k_r∗/k_PD ≪ 1. On the reactant side, this guarantees that equilibrium applies for the R^∗ population and on the product side it guarantees that P^∗ is rapidly deactivated before a reverse transition of P^∗ to R^∗ can occur. If the latter condition is satisfied but the former is not, then k_f becomes the R → R^∗ activation rate constant k_RA. If the former condition is satisfied but the latter is not, k_f depends on the P^∗ → P deactivation rate constant k_PD, becoming increasingly smaller as k_PD diminishes compared to k_r∗; the stable product P is increasingly difficult to form. An important point is that the activation and deactivation processes captured by the scheme Eq. (5.1) occur in the reaction, i.e. are events along a reaction path. But the dynamics of these activation and deactivation steps will only enter (via the relevant rate constants) when the conditions we specified (k_f∗/k_RD ≪ 1 and k_r∗ /k_PD ≪ 1) are violated. We now emphasize this key point by several examples.

Diffusion-influenced reactions

We can illustrate Eqs. (5.1) and (5.2) by the well-known example of diffusion-influenced reactions. Here R and P represent the separated reactants and products in solution, while R^∗ and P^∗ represent those species in a solvent cage. Then k_RA would be the diffusive rate constant k_Diff,R for the reactants to reach the caging region, k_PA is the diffusive rate constant for the caged products to be formed, and k_f,eq and k_r,eq are the forward and reverse rate constants for the caged reactants and products respectively. For example, if the reverse reaction can be completely ignored (e.g. if ΔG_rxn ≪ 0 for the caged species), then the first member of Eq. (5.2) reduces to the familiar textbook expression k_f = k_f,eq/[1 + (k_f,eq/k_Diff,R)], which predicts the rate constant to be the rate constant with an equilibrium spatial distribution, k_f,eq, when diffusion is rapid compared to reaction, and to be the diffusion-controlled rate constant k_Diff,R in the opposite limit. Certainly the reactant diffusion to a caged situation is a dynamical event along the reaction path. But its dynamics, e.g. time scale or rate constant, only enters when (k_f,eq/k_Diff,R) is not ≪1.

It is especially noteworthy that similar considerations apply to the influence of substrate binding dynamics on the rate constant using a Michaelis–Menten scheme of an enzymatic reaction. In that case R and R^∗ would represent the substrate in solution and in the active site, respectively [83].

Vibrationally activation/deactivation-influenced reactions

We can illustrate the application of our two equations to the general issue of vibrational activation and deactivation impacts on a reaction rate by exploiting the Cl⁻–MeCl’ S_N2 reaction in water system of the section ‘A solution reaction example’ again. In this reaction, the MeCl’ reactant must be activated to the fourth vibrationally excited state (v = 4) for the carbon–chlorine bond vibration, i.e. production of MeCl’^∗, and the activated product ClMe^∗ – with v = 4 in the produced Cl–Me bond – must be deactivated to generate the ground state ClMe product [39]. In this case, k_f,eq (equal to k_r,eq by symmetry) is the rate constant we discussed in the section ‘A solution reaction example’, k_RA (=k_PA) is the vibrational activation rate constant to produce the v = 4 level for the MeCl’ reactant (ClMe product). The corresponding rate constants for vibrational deactivation for the appropriate v = 4 level, respectively k_RD and its equal k_PD, are related to k_RA and k_PA via an equilibrium constant factor, e.g. K_R∗ = k_RA/k_RD which depends exponentially on the vibrational energy difference between the v = 0 and v = 4 levels.

The essentials of the important limits of the overall rate constant k_f have already been described in the paragraph below Eq. (5.2). Certainly the vibrational activation and deactivation steps are important, indeed essential components, along the reaction path for many reactions. But the dynamics of those steps, i.e. their rate constants and time scales, will only enter under the conditions specified in that paragraph. For the S_N2 reaction case, vibrational activation is certainly slow since the energy of four vibrational quanta must be provided by the environment, but the reaction is much slower. (k_f,eq/k_RA) (=k_r,eq/k_PA) is very small, indeed k_f,eq/k_RA ≪ 1; reaching the TS surface additionally requires other activation events, e.g. very considerable water solvent rearrangement [39], and the reaction rate constant is independent of any vibrational activation or deactivation time. Similar considerations will apply to assorted vibrations in enzymatic reactions as well.

Impact of conformational changes in enzymes

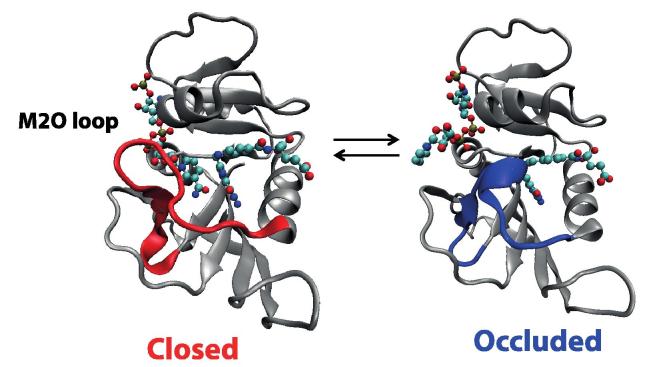
A particular example that can be analyzed from this perspective is that of E. coli DHFR, a case which has attracted considerable attention. In this enzyme, the M20 loop closes the active site, thus playing a critical role during the catalytic cycle of this enzyme [84,85] (Fig. 9). If the loop conformation were to change along the reaction path, conformational dynamics would be involved in the chemical step, but with different possible consequences for the rate.

Fig. 9.

Representation of E. coli DHFR showing two different configurations of the M20 loop: closed (in red) and occluded (in blue). Substrate and cofactor are shown using ball and sticks. According to X-ray crystallographic studies the M20 loop alternates between these two conformations during the catalytic cycle. The closed conformation appear in the Michaelis complex (E:NADPH:dihydrofolate) and the occluded conformation in the product of the chemical step (E:NADP:tetrahydrofolate). Instead, the N23PP-S148A mutant is unable to undergo the closed to occluded transformation because of the introduction of two proline residues that rigidify the loop. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

It was recently proposed that the reduction observed in the reaction rate constant of a mutant enzyme – designed to impair the dynamics of this loop – was the consequence of the suppression of millisecond time-scale motions that allow the enzyme to sample activated reactant conformations [86]. In the perspective of Eqs. (5.1) and (5.2), a reduced value for k_RA would result in a smaller rate constant k_f. This interpretation was confronted by subsequent experimental measurements that found the same temperature dependence of KIEs in the wild type and in the mutant; according to the authors, this ruled out the participation of conformational motions in the observed rate constants [87]. The main argument presented was that if conformational fluctuations were significantly different, then distinct donor–acceptor distances should be sampled in the wild type and mutant enzymes, and this would lead to a different dependence of KIEs with temperature. The same conclusion was reached after observation of the lack of any solvent viscosity effects on the EcDHFR rate constant [88].

Theoretical simulations of the hydride transfer step in the mutant and wild type versions of this enzyme based on hybrid QM/MM techniques were carried out to elucidate the consequences of mutations [89,90]. These studies showed that the observed reduction in the rate constant in the mutant could be explained by an increase in the free energy barrier associated with the chemical transformation. This activation free energy increase was interpreted as a consequence of a change in the enzyme’s average equilibrium properties by the mutations, which were shown to decrease the TS stabilization provided by the active site. This is an effect captured in calculations of the rate constant k_f∗ carried out from the activated reactants in the language of Eq. (5.1); the dynamics between different reactants conformers would not be required to explain the observed differences.

In a general perspective, the interplay between the chemical reaction coordinate and the protein conformational rearrangements can be effectively represented through a free energy landscape along – in a minimalist description – a reaction coordinate and an orthogonal conformational coordinate [46,89,91] This multidimensional, rugged free energy landscape can then include a series of possible conformations and TS geometries [92]. For example, a free energy surface for the enzyme adenylate kinase was defined in a two coordinate fashion via a conformational coordinate associated with the motion from the open to closed active site configuration and a collective reaction coordinate [91]. Different free energy barriers for the conformational transition were then investigated, via simulation, with simplified models. The mean first passage time τ over the chemical barrier – basically the inverse of the forward rate constant k_f – was examined and the results can be considered in the context of our discussion of Eqs. (5.1) and (5.2). The time τ was found to be independent of the conformational barrier, as long as this barrier was smaller than the chemical barrier (k_RA > k_f,eq). The authors found that it was only for unphysically low barriers for the chemical transformation the relaxation dynamics along the conformational coordinate could impact the reaction dynamics.

A similar analysis was carried out on a four-state model of an enzymatic chemical reaction including two enzyme-substrate complexes and two enzyme-product complexes [83]. The conformational coordinate drives the transformation from unproductive to productive enzyme-substrate complexes, while the chemical coordinate transforms the productive enzyme-reactant complex into the enzyme-product complex only for a limited subset of values of the conformational coordinate. Solution of the time-dependent probability distributions shows that the overall rate is dependent on conformational dynamics whose time scales are similar to or slower than that of the chemical step. In the limit of slow chemical rates, only the faster components of enzyme dynamics can be coupled to the reaction step per se. This is an effect similar to those we have discussed in the section ‘Dynamical effects in the transition state neighborhood’, and one that can be included through the calculation of the transmission coefficient to correct the TST value of the rate constant obtained along the chemical coordinate. In a GH theory description, these effects would show up as a generalized frictional influence. In some cases, they might also be included in a VTST approach (see the section ‘A solution reaction example’).

Conformational diversity

Protein motions – in addition to their possible implication in the fast crossing of the chemical barrier – can also be important in the transitions between different conformers that can lead to a slow modulation of that chemical barrier. Protein conformational changes are a constitutive part of the catalytic cycle, and numerous experimental studies, e.g. X-ray [93], NMR [94] and single-molecule experiments [95], have revealed that several conformational transitions occur during the full catalytic cycle. These conformational transitions not only drive the system forward along the catalytic cycle from one step to the next, from substrate binding to product release; they also lead at each step to an important conformational diversity. Hence, different conformations of the Michaelis–Menten complex may be accessible depending on the protein conformation, and the chemical barrier may change with the conformer due to the different interactions with the substrate.

A beautiful illustration of the kinetic disorder resulting from the situation just described has been provided by single-molecule experiments: these found slow fluctuations between states with different enzymatic activities, which could be analyzed in terms of multiple enzyme conformations contributing to the total reaction flux, each of them with different rate constants. There are two important limits. In the first, the protein conformational equilibrium is sampled rapidly with respect to the reaction time, and the dominant reaction pathway involves the lowest barrier conformer and the rate average constant can be described by TST. The TST free energy barrier includes a contribution due to the conformational rearrangement. In the second limit, the conversion between the different conformers is very slow, and the average rate constant is then a Boltzmann average of the rate constants obtained for the different conformers, with each of the individual rate constant determined in the framework of TST (with possible recrossing corrections à la section ‘Dynamical effects in the transition state neighborhood’). Outside of these limits, i.e. when conformational transitions occur on a timescale similar to that of the chemical step, a different scenario applies: now the protein conformational dynamics can play a role in the determination of the total reaction rate. While the details differ here, we trust that the reader will recognize the strong similarity of the conclusions recounted with the considerations that we have stressed throughout this article.

Concluding remarks

This contribution started with a question in its title: are there dynamical effects in enzyme catalysis? As anticipated in the Introduction, this is not a simple question and thus neither can the answer itself be simple. In order to reduce the complexity of the problem, we have restricted ourselves to the analysis of possible dynamical effects in the chemical step of the enzyme catalytic cycle. However, we have found it extremely useful for perspective to also examine reaction rates in solution, a field where considerable effort has been made during the last decades to elucidate the interplay between the chemical system and the environment, and where the ‘temperature’ of the scientific debate is now probably less than in the field of enzyme catalysis. This inclusion has also helped to differentiate between the different meanings of ‘dynamical effects’ used by various researchers in enzyme catalysis. This is a non-trivial issue, since clearly there is a real sense in which no reaction can occur without dynamics. We have tried to be precise in our own definition, confined to a dynamical impact on the reaction rate constant.

We have also found it useful to dissect the possible impact of those motions taking place in the vicinity of the transition state (TS) and those occurring away from the TS region. This spatial distinction is intimately related to the nature of the motion. Comparatively slow rearrangements in the enzyme and the environment need to occur first to bring the system to the TS region, where the chemical bond reorganization can then take place. These slower motions are certainly required for reaction to occur, but they may or may not have an impact on the reaction rate constant, i.e. a dynamical effect in the language that we use. In the TS region, comparatively fast motions of the environment (typically in the femto- to picosecond timescale) can be found during barrier crossing. The impact of these motions is usually a small decrease in the actual rate constant with respect to its Transition State Theory (TST) value, i.e. a transmission coefficient less than unity. It is important to emphasize that this effect’s origin can be either dynamical (motions occurring along the selected reaction coordinate) or not (the lack of an environmental response to the changes in the chemical system). The values of a TST rate constant, of the associated transmission coefficient which measure the actual rate constant’s departure from TST, and the underlying choice of reaction coordinate in the TS region are all dependent upon reasonable choices, which must always remain inexact to a degree in any real enzymatic catalysis.

Quantum mechanical effects for nuclear motion, of which there are several, were long ignored in many discussions of enzyme reactions. However, in recent years, enzymatic reactions involving quantum tunneling in proton, hydride or hydrogen-atom transfer processes – which we here simply term H-transfer reactions – have provided an important arena for discussion of possible dynamical effects. In particular, such reactions have focused considerable literature attention on the impact of environmental motions on the reaction rate constant. Tunneling clearly depends on the barrier along the hydrogenic coordinate, which, in turn, is extremely sensitive to the distance between the H-donor and -acceptor, often called the ‘promoting’ or ‘gating’ mode, and this distance can be coupled to various features of the enzyme. However, this dependence and coupling do not produce any dynamical effects on the reaction rate, provided that the donor–acceptor distance has an equilibrium distribution. The shifting of the equilibrium distribution of donor–acceptor distances as a result of a protein mutation or a temperature change could change the rate of tunneling in an H-transfer reaction or even change the quantum regime from tunneling to the quantum adiabatic regime (or vice versa); such shifting could explain some of the experimental observations without invoking dynamical effects.

Motions occurring away from the TS region, such as conformational changes in the protein, can have an impact on the rate constant. (An example could be protein conformation coupled to the H-donor–acceptor distance for tunneling reactions, as just discussed). We have shown that this effect can be rationalized within the framework of the Stable States Picture formalism. In a situation that does not differ in the essentials from e.g. diffusion-influenced reactions in solution, slow protein conformational changes taking place along the reaction pathway could, in principle, reduce the value of the observed rate constant to a degree dependent on the rate of those changes. However, computational simulations indicate that this scenario will only hold for enzymatic reactions with very low barriers for the chemical step, a conclusion consistent with simple rate law analysis.

At the risk of oversimplification, we conclude this contribution with an approximate, certainly not universal, but (we hope) useful answer to our question posed in its title. One could affirm that even if assorted molecular dynamics are without doubt essential ingredients of any reactive event, the impact of the rates of those dynamics appears typically not to be pronounced. As a result, reasonably accurate estimations of enzymatic rate constants can often (always assuming reasonably accurate force fields) be achieved using Transition State Theory, which in the terminology employed by most researchers, means that there are no important dynamical effects.