Functional Additive Mixed Models

Abstract

We propose an extensive framework for additive regression models for correlated functional responses, allowing for multiple partially nested or crossed functional random effects with flexible correlation structures for, e.g., spatial, temporal, or longitudinal functional data. Additionally, our framework includes linear and nonlinear effects of functional and scalar covariates that may vary smoothly over the index of the functional response. It accommodates densely or sparsely observed functional responses and predictors which may be observed with additional error and includes both spline-based and functional principal component-based terms. Estimation and inference in this framework is based on standard additive mixed models, allowing us to take advantage of established methods and robust, flexible algorithms. We provide easy-to-use open source software in the pffr() function for the R-package refund. Simulations show that the proposed method recovers relevant effects reliably, handles small sample sizes well and also scales to larger data sets. Applications with spatially and longitudinally observed functional data demonstrate the flexibility in modeling and interpretability of results of our approach.

In recent years, many scientific studies have collected functional data that exhibit correlation structures amenable to explicit modeling. Such structures may arise from a longitudinal study design (e.g. Goldsmith et al., 2012; Greven et al., 2010; Morris and Carroll, 2006), crossed designs (e.g. Aston et al., 2010), or spatial sampling of curves (e.g. Delicado et al., 2010; Giraldo et al., 2010; Gromenko et al., 2012; Nerini et al., 2010; Staicu et al., 2010). Simultaneously, regression for independent functional responses (e.g. Faraway, 1997) has made large advances, including both multiple scalar (e.g. Reiss et al., 2010) and multiple functional predictors in concurrent or more general relationships (e.g. Ivanescu et al., 2012). Our work is motivated by a longitudinal neuroimaging study containing repeated measurements of a functional proxy variable for neuronal health along 3 white matter tracts derived from diffusion tensor imaging (DTI). The goal of our analysis is to quantify the relationship of these function-valued proxy measures while accounting for the longitudinal correlation structure as well as the effects of patient characteristics like age and gender. This DTI study is an example of a longitudinal functional data set where models must account for the correlation structure of the data while including both scalar and functional covariates in the predictor.

To address these challenges, we propose conditional regression models for functional responses that accommodate general correlation structures via functional and scalar random effects as well as flexible linear or nonlinear effects of scalar and functional covariates. The major contributions of this paper thus consist in 1) developing a general inferential framework for additive mixed models for correlated functional responses that accommodates diverse correlation structures and flexible modeling of the mean structure extending Ivanescu et al. (2012), 2) unifying two previously separate strands of prior work, by subsuming both functional principal component- (FPC) and spline-based approaches, and 3) evaluating our implementation available in the the R-package refund (Crainiceanu et al., 2011) on real and simulated data.

Our goal is to describe and implement a framework that offers analysts of functional data similar flexibility in model specification to what is available in current implementations of (geo-)additive mixed models for scalar data. Specifically, we consider structured additive regression models of the general form

$$y_i\left(t\right)=\sum _{r=1}^R{f}_r({\mathcal{X}}_{ri},t)+{\epsilon }_i\left(t\right),$$ (1)

for functional responses y_i(t),i = 1,...,n, observed over a domain $\mathcal{I}$. Each term in the additive predictor is a function of a) the index t of the response and b) a subset ${\mathcal{X}}_r$ of the complete covariate set $\mathcal{X}$ including scalar and functional covariates and (partially) nested or crossed grouping factors. To make this more concrete, Table 1 shows the most important combinations of ${\mathcal{X}}_r$ and effect shapes available in our framework. We assume a white noise error process independent of $\mathcal{X}$, such that the ε_i(t) are independent and identically distributed (i.i.d.) Gaussian variables with mean zero and constant variance ${\sigma }_{\epsilon }^2$ across $\mathcal{I}$. Additionally, smooth and potentially correlated error curves can be included via curve-specific random effects to model (co-)variance along t and dependence between functional observations. We assume all effects in Table 1 to be smooth but unknown functions in the covariates, and this smoothness assumptions on all components of the predictor ensures smoothness of y_i(t) up to the white noise measurement error ε_i(t). Scalar random effects b_g are mean zero Gaussian variables with general covariance structure between the different levels of g. Functional random effects b_g(t) for a grouping variable g with M levels are modeled as realizations of a mean-zero Gaussian random process on $\{1,\dots ,M\}\times \mathcal{I}$ with a general covariance function K^b(m,m′,t,t′) = Cov(b_m(t),b_m′(t′)) that is smooth in t, where m,m′ denote different levels of g. Note that our model class and software admits multiple partially or completely nested or crossed grouping factors for both scalar and functional random effects, but different random effects b_g(t),b_g′(t) are assumed to be mutually independent. We assume integrability for the effects of functional covariates. Our implementation for functional effects such as $\int x_i\left(s\right)\beta (s,t)ds$ also accommodates varying integration ranges with fixed, potentially observation-specific integration limits l_i(t),u_i(t), similar to the historical functional model in Malfait and Ramsay (2003). Densely as well as sparsely observed functional responses and suitably preprocessed functional predictors with measurement error can be used in this framework. We approximate each term $f_r({\mathcal{X}}_r,t)$ by a linear combination of basis functions defined by the tensor product of marginal bases for ${\mathcal{X}}_r$ and t. Since basis dimensions have to be sufficiently large to ensure enough flexibility, maximum likelihood estimation of model (1) is likely to lead to substantial overfitting. The penalized likelihood approach described in Section 1.2 stabilizes estimates by suppressing variability not strongly supported by the data and finds a data-driven compromise between goodness of fit and simplicity of the fitted effects.

Table 1.

Forms of $f_r({\mathcal{X}}_r,t)$ depending on the covariates in ${\mathcal{X}}_r$ and linearity or smoothness in these covariates (rows), and on whether the effect is constant or varying over t (columns). For scalar categorical covariates, synthetic scalar covariates in effect or reference category coding are created. Note that effects can become interaction effects if ${\mathcal{X}}_r$ additionally contains such scalar categorical covariates. For example, we estimate group-specific effects of the functional covariates for MS patients and healthy controls in our DTI application.

${\mathcal{X}}_r$	$f_r({\mathcal{X}}_r,t)$ constant over t	$f_r({\mathcal{X}}_r,t)$ varying over t
∅ (no covariates)	scalar intercept α	functional intercept α(t)
functional covariate x(s)	linear functional effect ${\int }_{\mathcal{Y}}x\left(s\right)\beta \left(s\right)ds$	linear functional effect ${\int }_{\mathcal{Y}}x\left(s\right)\beta (s,t)ds$
	smooth functional effect ${\int }_{\mathcal{Y}}F(x\left(s\right),s)ds$	smooth functional effect ${\int }_{\mathcal{Y}}F(x\left(s\right),s,t)ds$
scalar covariate z	linear effect zδ	functional linear effect zδ(t)
	smooth effect γ(z)	smooth effect γ(z, t)
vector of scalar covariates z	interaction effect z1z2δ	functional interaction effect z1z2δ (t)
	varying coefficient z1δ(z2)	functional varying coefficient z1δ(z2, t)
	smooth effect γ(z)	smooth effect γ(z,t)
grouping variable g	random intercept bg	functional random intercept bg(t)
grouping variable g and scalar covariate z	random slope zbg	functional random slope zbg(t)

Most existing work on functional random effects has considered only special cases such as the functional random intercept model (Abramovich and Angelini, 2006; Di et al., 2009; Krafty et al., 2011), functional random intercept and slope model (Greven et al., 2010), a single level of random effects functions (Antoniadis and Sapatinas, 2007; Guo, 2002; Qin and Guo, 2006), or a two or three-level hierarchy (Baladandayuthapani et al., 2008; Bigelow and Dunson, 2007; Brumback and Rice, 1998; Li et al., 2007; Morris et al., 2003; Scarpa and Dunson, 2009; Staicu et al., 2010; Zhou et al., 2010). Aston et al. (2010) consider a general functional random effects structure under the assumption of a joint functional principal component (FPC) basis for all functional random effects in the model, which are estimated under a working independence assumption between curves. It is unclear, however, how well this approach works if the latent processes do not share the same eigenfunctions and how the correlation between functional observations affects FPC estimation. FPC estimation for correlated observations is a topic of ongoing research (c.f. Hörmann and Kokoszka, 2010, 2011; Panaretos and Tavakoli, 2013a,b). Morris and Carroll (2006); Morris et al. (2003); Zhu et al. (2011) propose a general Bayesian functional linear mixed model based on a wavelet transformation of (usually very spiky) data observed on an equidistant grid. The model proposed by Morris and Carroll (2006) includes correlation between different random effects and heterogeneous residual errors, which we do not. Our approach, on the other hand, is well suited to smooth underlying curves and allows a more general mean structure than previous functional linear mixed models; in particular we are able to estimate smooth nonlinear or linear effects of scalar and/or functional covariates within the same framework. In addition, we are able to handle data on non-equidistant or sparse grids.

To the best of our knowledge, our proposal is the first publicly available implementation that allows such a high level of flexibility for a functional regression model – prior work either limits the predictor to the effect of a single functional covariate and a functional intercept, such as the linmod function in package fda (Ramsay et al., 2011) for the R language (R Development Core Team, 2011) or to linear effects of scalar covariates, such as the fosr function for function-on-scalar regression (Reiss et al., 2010) in the R-package refund. Like the linear function-on-function regression approach in Ivanescu et al. (2012) we build on, both approaches are limited to independent functional responses. Morris and Carroll (2006) provide a closed source implementation for wavelet-based functional linear mixed models in WFMM (Herrick, 2013) that allows very general random effect and residual structures, but implement neither effects of functional covariates nor nonlinear effects of scalar covariates. The PACE package (Fang et al., 2013) for MATLAB implements FPC based regression models where the predictor is limited to the effect of a single functional or scalar covariate. Our proposal has some similarities with the regression models for independent or longitudinal scalar responses in Goldsmith et al. (2011, 2012), implemented in the pfr and lpfr functions in refund, since we also base inference on additive mixed models for scalar-on-scalar regression. However, the extension to functional responses and functional random effects with flexible correlation structure as well as the inclusion of FPC-based effects is non-trivial.

The paper is organized as follows: Section 1 develops our general approach and estimation framework for functional additive mixed models. Our method is evaluated in a simulation study and in an application to the motivating longitudinal DTI study in Section 2. Section 3 closes with a discussion and outlook.

1 Penalized regression for correlated functional data

Functional responses y_i(t) are observed on a grid of T_i points $t_i={(t_{i1},\dots ,t_{i{T}_i})}^{\mathsf{T}}$. To simplify notation, we assume identical grids $t_i\equiv t={(t_1,\dots ,t_T)}^{\mathsf{T}}$ for i = 1,...,n in the following, but note that functional responses observed on irregular and/or sparse grids are naturally accommodated in the rephrased model formulation given in (2). Then, model (1) can be expressed as

$$y_{il}=\sum _{r=1}^R{f}_r({\mathcal{X}}_{ri},t_l)+{\epsilon }_{il}$$ (2)

for i = 1,...,n and l = 1,...,T. The assumption of white noise errors translates to ${\epsilon }_{il}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }N(0,{\sigma }_{\epsilon }^2)$. The smoothness assumption on E(y_i(t)) is preserved implicitly by enforcing smoothness across $\mathcal{I}$ for all $f_r({\mathcal{X}}_r,t)$. To fit the model, we form $\mathit{y}={({\mathit{y}}_1^{\mathsf{T}},\dots ,{\mathit{y}}_{\mathit{n}}^{\mathsf{T}})}^{\mathsf{T}}$, an nT-vector that holds the concatenated function evaluation vectors ${\mathit{y}}_i={(y_{i1},\dots ,y_{iT})}^{\mathsf{T}}$. In the following, let ${\mathcal{X}}_r$ denote the vector or matrix containing rows of observations ${\mathcal{X}}_{ri}$. Let f(t) denote the vector of function evaluations of f for each entry in the vector t and let f(x,t) denote the vector of evaluations of f for each combination of rows in the vectors or matrices x,t. Let $1_d={(1,\dots ,1)}^{\mathsf{T}}$ denote a d-vector of ones. The row tensor product of an m × a matrix A and an m × b matrix B is defined as the m × ab matrix $\mathit{A}\odot \mathit{B}=(\mathit{A}\otimes 1_b^{\mathsf{T}})\cdot (1_a^{\mathsf{T}}\otimes \mathit{B})$, where · denotes element-wise multiplication.

1.1 Tensor product representation of effects

Each of the R terms in model (2) can be represented as a weighted sum of basis functions defined on the product space of the covariates in ${\mathcal{X}}_r$ and t, where each marginal basis is associated with a corresponding marginal penalty. A very versatile method to construct basis functions on such a joint space is given by the row tensor product of marginal bases evaluated on ${\mathcal{X}}_r$ and t (e.g. De Boor, 1978; Wood, 2006, ch. 4.1.8). Specifically, for each of the terms,

$$f_r(\underset{nT\times 1}{{\mathcal{X}}_{\mathit{r}}},\mathit{t})\approx (\underset{nT\times K_x}{{\Phi }_{\mathit{xr}}}\odot \underset{nT\times K_t}{{\Phi }_{\mathit{tr}}})\underset{K_x{K}_t\times 1}{{\theta }_r}={\Phi }_r{\theta }_r,$$ (3)

Φ_xr contains the evaluations of a suitable marginal basis for the covariate(s) in ${\mathcal{X}}_r$ and Φ_tr contains the evaluations of a marginal basis in t. The shape of the function is determined by the vector of coefficients θ_r. A corresponding penalty term can be defined by the Kronecker sum of the marginal penalty matrices P_xr and P_tr associated with each basis (Wood, 2006, ch. 4.1), i.e.

$$\mathrm{pen}({\theta }_r\mid {\lambda }_{tr}{,}_{xr})={\theta }_r^T({\lambda }_{xr}\underset{K_x\times K_x}{{\mathit{P}}_{\mathit{xr}}}\otimes {\mathit{I}}_{K_t}+{\lambda }_{tr}{\mathit{I}}_{K_x}\otimes \underset{K_t\times K_t}{{\mathit{P}}_{\mathit{tr}}}){\theta }_r={\theta }_r^T{\mathit{P}}_r({\lambda }_{tr},{\lambda }_{xr}){\theta }_r.$$ (4)

P_xr and P_tr are known and fixed positive (semi-)definite penalty matrices and λ_tr and λ_xr are positive smoothing parameters controlling the trade-off between goodness of fit and the smoothness of $f_r({\mathcal{X}}_r,t)$ in ${\mathcal{X}}_r$ and t, respectively. This flexible construction is valid for any combination of bases associated with quadratic penalties. Alternative constructions of the joint penalty such as a direct Kronecker product ${\lambda }_r({\mathit{P}}_{xr}\otimes {\mathit{P}}_{tr})$ associated with a single smoothing parameter λ_r are possible, see Wood (2006, ch. 4.1.8) for a discussion. Typically, K_x and K_t vary with r as well, but we drop the additional index for simplicity. In the following paragraphs, we will motivate and define Φ_xr, Φ_tr,P_tr and P_xr for the different types of terms available in our implementation. Effects that are constant over t are associated with Φ_tr = 1_nT and P_tr = 0, while users are free to choose any suitable marginal basis matrix Φ_tr and penalty P_tr for terms that vary over t.

Spline basis representation of effects of scalar covariates

For scalar covariates, index-varying effects are very similar to varying coefficient terms in models for scalar responses, c.f. Ivanescu et al. (2012). For the functional intercept α(t), Φ_xr = 1_nT and P_xr = 0. For effects like zδ and zδ(t) that are linear in a scalar covariate z, the marginal basis for the covariate direction reduces to ${\Phi }_{xr}=\mathit{z}\otimes 1_T$ where $\mathit{z}={(z_1,\dots ,z_{\mathit{n}})}^{\mathsf{T}}$, with penalty P_xr = 0. For nonlinear effects of scalar covariates like γ(z) or γ(z,t), Φ_xr is a suitable marginal spline basis matrix over z and P_xr is the associated penalty.

Spline basis representation of functional effects

For linear effects of functional covariates x(s), we model β(s,t) using tensor product splines with basis functions Φ_ks(s),k_s = 1,...,K_x, over $\mathcal{Y}$ and a spline basis defined over $\mathcal{I}$. We approximate the integral by numerical integration on the grid defined by the observation points s₁,...,s_H in $\mathcal{Y}$. The effect in (2) then is

$${\int }_{\mathcal{Y}}{x}_i\left(s\right)\beta (s,t_l)ds\approx \sum _{h=1}^H{w}_h{x}_i\left(s_h\right)\sum _{k_s=1}^{K_x}\sum _{k_t=1}^{K_t}{\Phi }_{k_s}\left(s_h\right){\Phi }_{k_t}\left(t_l\right){\theta }_{r,k_s,k_t}.$$

In the notation of (3), ${\Phi }_{\mathit{xr}}=\left[\mathit{x}\mathrm{diag}\left(\mathit{w}\right){\Phi }_s\right]\otimes 1_T\approx {\left[{\int }_{\mathcal{Y}}{x}_j\left(s\right){\Phi }_{k_s}\left(s\right)ds\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill k_s=1,\dots ,K_x\hfill \end{array}}\otimes 1_T$, where $\mathit{w}={(w_1,\dots ,w_H)}^{\mathsf{T}}$ contains the quadrature weights for a numerical integration scheme, $\mathit{x}={\left[x_i\left(s_h\right)\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill h=1,\dots ,H\hfill \end{array}}$ and ${\Phi }_s={\left[{\Phi }_{k_s}\left(s_h\right)\right]}_{\begin{array}{c}\hfill h=1,\dots ,H\hfill \\ \hfill k_s=1,\dots ,K_x\hfill \end{array}}$. P_xr in the tensor product penalty (4) is the penalty associated with the Φ_ks(s). We can extend this construction, which is equivalent to the one introduced in Ivanescu et al. (2012), to cover terms like ${\int }_{l_i\left(t\right)}^{{\mathit{u}}_i\left(t\right)}{x}_i\left(s\right)\beta (s,t)ds$ (e.g. Malfait and Ramsay, 2003) with fixed, potentially observation-specific integration limits $l_i\left(t\right),u_i\left(t\right)\in \mathcal{Y}$. This is achieved by defining suitable weight matrices w_i,l with zero entries for s_h < l_i(t_l) and s_h > u_i(t_l). Such effects will often be required for covariates and responses that are observed on the same time domain, where responses cannot be influenced by future covariate values. In the limit, this also includes the concurrent model with terms X(t)β(t).

Our framework also extends to non-linear function-on-function effects ${\int }_{\mathcal{Y}}F(x_i\left(s\right),s,t)ds$, which generalize the functional generalized additive model (McLean et al., 2012) from scalar to functional responses. They offer similar flexibility to purely nonparametric approaches like Febrero-Bande and Oviedo de la Fuente (2012); Ferraty et al. (2011); Ferraty and Vieu (2006), e.g. In our framework, such terms can be represented as

$${\int }_{\mathcal{Y}}F(x_i\left(s\right),s,t_l)ds\approx \sum _{h=1}^H{w}_h\sum _{k_s=1}^{K_x}\sum _{k_t=t}^{K_t}{\Phi }_{k_s}(x_i\left(s_h\right),s_h){\Phi }_{k_t}\left(t_l\right){\theta }_{k_s{k}_t}$$

with ${\Phi }_{\mathit{xr}}=\left[({\mathit{w}}^{\mathsf{T}}\otimes {\mathit{I}}_{\mathit{n}}){\Phi }_{\mathit{s}}\right]\otimes 1_T$ and ${\Phi }_{\mathit{s}}={\left[{\Phi }_{k_s}(x_i\left(s_h\right),s_h)\right]}_{\begin{array}{c}\hfill i=1,\dots ,n,h=1,\dots ,H\hfill \\ \hfill k_s=1,\dots K_x\hfill \end{array}}$, and P_xr the penalty associated with Φ_s. Basis functions Φ_ks(x(s),s) can be tensor product basis functions derived from marginal bases for x(s) and s or true bivariate basis functions.

FPC basis representation of functional effects

Consider a functional covariate expanded in the Karhunen-Loève expansion $x_i\left(s\right)={\sum }_k{\psi }_k\left(s\right){\xi }_{ik}$ with $\int {\psi }_k\left(s\right){\psi }_{k^{\prime }}\left(s\right)ds={\delta }_{k{k}^{\prime }}$; $\mathrm{E}\left({\xi }_{ik}\right)=0$; $\mathrm{Var}\left({\xi }_{jk}\right)={\zeta }_k$. Under the assumption that ${\int }_{\mathcal{Y}}{\sum }_{k>K_x}{\psi }_k\left(s\right){\xi }_{ik}\beta (s,t)ds\approx 0$ for some K_x, i.e., that all smaller modes of variation of x(s) only have a negligible effect on y(t), we can write

$${\int }_{\mathcal{Y}}{x}_i\left(s\right)\beta (s,t)ds\approx {\int }_{\mathcal{Y}}\sum _{k=1}^{K_x}{\psi }_k\left(s\right){\xi }_{ik}\beta (s,t)ds=\sum _{k=1}^{K_x}{\xi }_{ik}{\tilde{\beta }}_k\left(t\right)$$

with ${\tilde{\beta }}_k\left(t\right)={\int }_{\mathcal{Y}}{\psi }_k\left(s\right)\beta (s,t)ds$. Thus, a linear function-on-function effect can be represented as a sum of varying coefficient terms for the FPC loadings ξ_ik. This representation extends FPC regression approaches (e.g. Reiss and Ogden, 2007) from scalar to functional responses. In the notation of the general framework, ${\Phi }_{\mathit{xr}}={\left[{\xi }_{ik}\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill k=1,\dots ,K_x\hfill \end{array}}\otimes 1_T$ and P_xr = 0. For the t-direction, Φ_tr and the associated P_tr can be chosen freely. An implicit assumption here is that all β_k(t),k= 1,...,K_x have similar smoothness, as they are all associated with the same smoothing parameter.

This FPC-based approach may be advantageous for functional covariates observed on irregular or sparse grids – for such data, the spline-based method requires a preprocessing step (c.f. Goldsmith et al., 2011, 2012; James, 2002) to impute the incomplete trajectories on a dense and regular grid, whereas FPCs can be estimated directly from sparse data (Yao et al., 2005). Additionally, if the shapes of the ${\widehat{\psi }}_k\left(s\right)$ are meaningful to practitioners and K_x is small, the coefficient functions ${\tilde{\beta }}_k\left(t\right)$ may be easier to interpret than a coefficient surface β(s,t). On the other hand, since inference is performed conditional on the estimated FPCs ${\widehat{\psi }}_k\left(s\right)$ and associated loadings ${\widehat{\xi }}_{ik}$ coverage issues associated with these neglected sources of estimation variability (c.f. Goldsmith et al., 2013) and bias introduced by estimation error in the FPC analysis step may occur. Additionally, ${\int }_{\mathcal{Y}}{\sum }_{k>K_x}{\psi }_k\left(s\right){\xi }_{ik}\beta (s,t)ds\approx 0$ might be a strong assumption that is hard to check in applications, as is the choice of the discrete tuning parameter K_x.

As in the spline-based case, we can extend this to FPC-based nonlinear function-on-function effects. The proposal corresponds to an extension of the functional additive model by Müller and Yao (2008) from scalar to functional responses, with the effect of the functional covariate given by $f_r(x_i\left(s\right),t)={\sum }_{k=1}^{K_x^{\prime }}{F}_k({\widehat{\xi }}_{ik},t)$. In the notation of our general framework, ${\Phi }_{\mathit{xr}}=[{\Phi }_{{\xi }_1}\mid \dots \mid {\Phi }_{{\xi }_{K_x^{\prime }}}]$ where ${\Phi }_{{\xi }_k}={\left[{\Phi }_a\left({\widehat{\xi }}_{ik}\right)\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill a=1,\dots ,A\hfill \end{array}}\otimes 1_T$ for suitable spline basis functions Φ_a(·), such that $K_x=A{K}_x^{\prime }$. The marginal penalty is given by ${\mathit{P}}_{\mathit{xr}}={\mathit{I}}_{K_x^{\prime }}\otimes {\mathit{P}}_{\xi }$, where P_ξ is the penalty associated with the ${\Phi }_a\left({\widehat{\xi }}_{jk}\right)$. In t-direction, we are again free to choose any suitable basis Φ_tr and penalty P_tr. Further extensions to interaction effects of estimated FPC scores $f_r(x_i\left(s\right),t)={\sum }_{k=1}^{K_x^{\prime }}{\sum }_{k<k^{\prime }\le K_x^{\prime }}{F}_{k,k^{\prime }}({\widehat{\xi }}_{ik},{\widehat{\xi }}_{i{k}^{\prime },t})$ are also obvious in this framework.

Spline basis representation of functional random effects

Functional random effects b_g(t) are represented as smooth functions in t for each level 1,...,M of the grouping variable g. In the notation of equation (3), functional random intercepts are associated with a marginal basis ${\Phi }_{\mathit{xr}}={\left[{\delta }_{g\left(i\right)m}\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill m=1,\dots ,M\hfill \end{array}}\otimes 1_T$, where g(i) denotes the level of g for observation i. This yields an incidence matrix mapping the observations to the different levels of the grouping variable. For a functional random slope effect in a scalar covariate z, ${\Phi }_{\mathit{xr}}={\left[z_i{\delta }_{g\left(i\right)m}\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill m=1,\dots ,M\hfill \end{array}}\otimes 1_T$. In the notation of equation (4), the marginal penalty P_xr for functional random effects is a M × M precision matrix that defines the dependence structure between the levels of g. The quadratic penalty (4) is mathematically equivalent to the distributional assumption ${\theta }_r\sim N(0,{\sigma }_{\epsilon }^{-2}{\mathit{P}}_r{({\lambda }_{tr},{\lambda }_{xr})}^{-1})$ (Brum-back et al., 1999). Through the representation in (3), this induces a mean zero Gaussian process assumption b_g(t) ~ GP(0,K^b(g(i),g(i′),t,t′)), with covariance evaluated for all nT observations $K^b(g,g,t,t)={\sigma }_{\epsilon }^{-2}{\Phi }_r{\mathit{P}}_r{({\lambda }_{tr},{\lambda }_{xr})}^{-1}{\Phi }_r^{\mathsf{T}}$. The smoothing parameter λ_xr controls the relative contribution of the inter-unit variability relative to the common roughness of the functional random effects controlled by λ_tr.

If observations on different levels of the grouping factor are assumed independent, P_xr = I_M is simply the identity matrix. More generally, P_xr can represent any fixed dependence structure between levels of g: It can be a (partially improper) precision matrix of a random field with known correlation structure, implied, for example, by the spatial or temporal arrangement of the different levels of g, such as a Gaussian Markov random field (GMRF) on geographical regions for conditionally auto-regressive (CAR) model terms. Alternatively, (P_xr)⁻¹ can be defined using any valid correlation function based on – for example – spatial, temporal, or genetic distances between levels of g. If the grouping variable is simply the index of observations (i.e., g(i) = i), this construction yields smooth residual curves with potential for spatial or temporal autocorrelation. This innovative definition of functional random effects admits very flexible model specifications, since any combination of spline basis, smoothness penalty and between-subject correlation can be used for functional random effects. This allows, for example, for spatially correlated functional residuals with periodicity constraints for the Canadian Weather data (see Appendix C of the online supplement). Multiple (partially) nested or crossed random effects can be constructed in this way and are implemented in pffr().

FPC basis representation of functional random intercepts

For functional random intercepts without between-unit correlation, i.e., for $b_g\left(t\right)\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }GP(0,K^b(t,t^{\prime }))$, it can be advantageous to use the eigenfunctions of the covariance operator K^b(t,t′) as basis functions in t. Specifically, we use the Karhunen-Loève expansion of random processes to represent $b_g\left(t\right)\approx {\sum }_{k=1}^{K_t}{\eta }_k\left(t\right){\nu }_{gk}$ with κ_k,η_k(t) the ordered eigenvalues and -functions of K^b(t,t′), ν_gk the associated FPC loadings, and K_t a suitable truncation lag. The marginal basis for the t-direction is then ${\Phi }_{\mathit{tr}}=1_{\mathit{n}}\otimes [{\widehat{\eta }}_1\left(t\right)\mid \cdots \mid {\eta }_{K_t}\left(t\right)]$. Since E(ν_gk) = 0 and Var(ν_gk) = κ_k, a reasonable marginal penalty is ${\mathit{P}}_{\mathit{tr}}=\mathrm{diag}{({\widehat{\kappa }}_1,\dots ,{\widehat{\kappa }}_{K_t})}^{-1}$. This encourages relative contributions of the FPCs to the random effect curves that are roughly proportional to their estimated magnitudes ${\widehat{\kappa }}_k$. As for the spline-based functional random effects, ${\Phi }_{xr}={\left[{\delta }_{g\left(i\right)m}\right]}_{\begin{array}{c}\hfill i=1,\dots ,m\hfill \\ \hfill m=1,\dots ,M\hfill \end{array}}\otimes 1_T$ is an incidence matrix for the group levels, while P_xr = I_M.

In practice, η_k(t) and κ_k have to be estimated. An iterative procedure can be outlined as follows: (1) Use a fit without functional random effects under independence assumption to obtain working residuals $\mathit{E}={\left[{\epsilon }_{il}\right]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill l=1,\dots ,T\hfill \end{array}}$. (2) Compute the group-level means of residual curves $\stackrel{‒}{\mathit{E}}={\Delta }^{\mathsf{T}}\mathit{E}$ with $\Delta ={[{\delta }_{g\left(i\right)m}∕n_m]}_{\begin{array}{c}\hfill i=1,\dots ,n\hfill \\ \hfill m=1,\dots ,M\hfill \end{array}}$, where n_m is the number of observations for the m-th level of g. (3) Perform a (truncated) spectral decomposition of ${\widehat{\mathit{K}}}^b={\left[{\widehat{K}}^b(t_l,t_{l^{\prime }})\right]}_{l,,l^{\prime }=1,\dots ,T}$ to obtain ${\widehat{\eta }}_k\left(t\right)$, ${\widehat{\kappa }}_k$ for k = 1, ..., K_t. A suitable estimate for ${\widehat{\mathit{K}}}^b$ can be derived from smoothing the entries in the matrix $M^{-1}{\stackrel{‒}{\mathit{E}}}^{\mathsf{T}}\stackrel{‒}{\mathit{E}}$ (without the diagonal) as in Yao et al. (2005). This approach for estimating ${\widehat{\mathit{K}}}^b$ can only be used for random intercepts for a single grouping variable. Compared to spline-based functional random effects, FPC-based modeling holds the promise of using the optimal, most parsimonious basis to represent b_g(t). Computationally, it is expected to scale much better for large M, as the number of coefficients associated with a functional random effect is MK_t and K_t for FPCs will typically be much smaller than in a sufficiently flexible spline basis. On the other hand, the FPC approach requires a pilot estimate for ${\mathit{K}}^b$. The subsequent performance will be sensitive to the quality of the estimation of the FPCs and to the choice of K_t.

1.2 Mixed model representation

Using the tensor product representation introduced in the previous subsection for all terms, model (1) can be re-written as

$$\mathit{y}=\Phi \theta +∊;∊\sim N(0,{\sigma }_{\epsilon }^2{\mathit{I}}_{nT}),$$ (5)

where Φ = [Φ₁|...|Φ_R] contains the concatenated Φ_r associated with the different model terms and $\theta ={({\theta }_1^{\mathsf{T}},\dots ,{\theta }_R^{\mathsf{T}})}^{\mathsf{T}}$ the respective stacked coefficient vectors θ_r. To clear up notation, we assign a sequential index v = 1,...,V to the smoothing parameters λ_xr,λ_tr in (4), where V is the total number of smoothing parameters in the model. We pad ${\mathit{P}}_{\mathit{tr}}\otimes {\mathit{I}}_{{\mathit{K}}_x}$ and ${\mathit{I}}_{K_t}\otimes {\mathit{P}}_{\mathit{xr}}$ with rows and columns of zeros, denoting these matrices P̃_v1 and P̃_v2 such that the penalty ${\theta }_r^T({\lambda }_{tr}{\mathit{P}}_{tr}\otimes {\mathit{I}}_{K_x}+{\lambda }_{xr}{\mathit{I}}_{K^{\prime }}\otimes {\mathit{P}}_{xr}){\theta }_r={\lambda }_{v_1}{\theta }^T{\tilde{\mathit{P}}}_{v_1}\theta +{{\lambda }_v}_2{\theta }^T{\tilde{\mathit{P}}}_{v_2}\theta$ refers to the full coefficient vector θ. The penalized likelihood criterion to be minimized then becomes

$$\frac{1}{{\sigma }_{\epsilon }^2}{\Vert \mathit{y}-\Phi \theta \Vert }^2+\sum _{v=1}^V\frac{{\lambda }_v}{{\sigma }_{\epsilon }^2}{\theta }^T{\tilde{\mathit{P}}}_v\theta .$$ (6)

The total number of smoothing parameters is V ≤ 2R, as some terms are constant over t or ${\mathcal{X}}_r$ and the corresponding P̃_v are zero. Let ${\tau }_v=\frac{{\sigma }_{\epsilon }^2}{{\lambda }_v}$ and use similar arguments as in Ruppert et al. (2003, ch. 4.9) to obtain the solution $\widehat{\theta }$ of (6) as the best linear unbiased predictor in the linear mixed effects model (MEM)

$$\mathit{y}\sim N(\Phi \theta ,{\sigma }_{\epsilon }^2{\mathit{I}}_{nT});\theta \sim N\left(0,{\left(\sum _{v=1}^V{\tau }_v^{-1}{\tilde{\mathit{P}}}_v\right)}^{-}\right),$$ (7)

where S⁻ denotes the generalized inverse of S, and N(0,S⁻) is a partially improper Gaussian distribution with positive semi-definite covariance matrix S. The impropriety results from rank deficiencies in some of the P̃_v, since roughness penalties typically define a nullspace of maximally smooth functions. Numerical difficulties posed by the positive semi-definiteness are solved by another re-parameterization that separates the various model terms into their unpenalized and penalized components, i.e. into “fixed” effects and “random” effects with a proper distribution, respectively. These are well known issues in the literature on penalized regression splines described in detail e.g. in Ruppert et al. (2003, ch. 4.9),Wood (2006, ch. 6.6.1); recent developments for tensor product splines are in Wood et al. (2013).

One of the main advantages of formulating the penalized likelihood optimization as estimation in an MEM is that the smoothing parameters ${\lambda }_v=\frac{{\sigma }_{\epsilon }^2}{{\tau }_v}$ can be treated as variance component parameters and thus can be estimated using restricted maximum likelihood (REML). In particular, Reiss and Ogden (2009) and Wood (2011) have shown that smoothing parameter selection with REML is more stable and results in somewhat lower MSE than generalized cross-validation (GCV) and Krivobokova and Kauermann (2007) have shown that REML estimation of penalized splines is more robust to error correlation mis-specification than AIC-based criteria. A second advantage this approach offers is that the representation of our model class (1) results in a fit criterion (7) equivalent to that of conventional additive mixed models for scalar data. This means much of the powerful and versatile inference machinery developed for scalar linear and additive mixed models (AMMs) over the last years can be applied directly to the proposed model class of functional AMMs, due to their close structural similarity. Specifically, 1) pointwise, bias-corrected confidence bands (Marra and Wood, 2012; Nychka, 1988; Ruppert et al., 2003) are available for the functional effects, 2) tests for random effects as well as tests for constant or linear effects versus more general alternatives developed for scalar responses (Crainiceanu and Ruppert, 2004; Crainiceanu et al., 2005; Greven et al., 2008; Scheipl et al., 2008; Wood, 2013), and 3) model selection approaches that have recently been proposed for scalar-response AMMs (Greven and Kneib, 2010; Marra and Wood, 2011) are directly applicable to the proposed model class. Finally, the proposed approach accommodates a large variety of effects, at no increase in the level of complexity of the algorithm itself. The tensor product representation given in Section 1.1 combined with the MEM representation (7) allows for a unified framework for smoothness parameter selection and estimation of all model components in model (1), including functional random effects and FPC-based effects.

Implementation

The full framework for functional additive models we describe here is implemented in the pffr-function in the refund package for R. The underlying inference engine is the mgcv package (Wood, 2011) for generalized additive models which also supplies most of the functionality for constructing basis and penalty matrices. pffr offers a formula-based interface similar to the established formula syntax of mgcv and returns a rich model object whose fit can be summarized, plotted and compared with other model formulations without any programming effort by the user through convenient utility functions.

2 Empirical evaluation

The following section describes an extensive simulation study and results for the motivating application to a longitudinal DTI study. A fully reproducible example analysis of the well known Canadian Weather data showcasing the flexibility of pffr can be found in Section C of the online appendix.

2.1 Simulation study

Simulation setup

We simulate data with repeated measures structure for a model $y_{ij}\left(t\right)={\sum }_{r=1}^{\mathit{R}}{f}_r({\mathcal{X}}_{rij},t)+{\epsilon }_{ij}\left(t\right)$ for the following four scenarios to investigate the sensitivity of the estimates to varying model complexity, noise levels and number of observations:

1. Functional random intercept, functional random slope: $\sum f_r({\mathcal{X}}_{rij},t)=\alpha \left(t\right)+b_{i0}\left(t\right)+b_{i1}\left(t\right)u_{ij}$

2. Functional random intercept, functional covariate: $\sum f_r({\mathcal{X}}_{rij},t)=\alpha \left(t\right)+\int x_{1,ij}\left(s\right){\beta }_1(s,t)ds+b_{i0}\left(t\right)$

3. Functional random intercept, two functional covariates: $\sum f_r({\mathcal{X}}_{rij},t)=\alpha \left(t\right)+\int x_{1,ij}\left(s\right){\beta }_1(s,t)ds+\int x_{2,ij}\left(s\right){\beta }_2(s,t)ds+b_{i0}\left(t\right)$

4. Functional random intercept, functional covariate, smooth scalar covariate effect, varying coefficient term: $\sum f_r({\mathcal{X}}_{rij},t))=\alpha \left(t\right)+\int x_{1,ij}\left(s\right){\beta }_1(s,t)ds+{\gamma }_1(z_{1,ij},t)+{\delta }_2\left(t\right)z_{2,ij}+b_{i0}\left(t\right)$

Definitions of the various effect functions and descriptions of the data generating processes used for the covariates can be found in section B of the online supplement, along with unabridged simulation results and graphical displays of data and estimated effects for the replications with minimal, maximal and median error for each scenario.

For each of the four scenarios, we run 10 replications for each combination of the following settings, yielding 1920 model fits in total:

• – number of subjects: M ∈ {10,100}

• – mean number of observations per subject: n_i ∈ {3,20}. Subject labels i ∈ {1,...,M} are drawn from a multinomial distribution with probabilities $P(i=i^{\prime })\propto \sqrt{i^{\prime }}$ to generate unbalanced designs.

• – number of grid points for t: T ∈ {30,60}

• – relative importance of random effects: SNR_B ∈ {0.2,1,5}, where SNR_B is the ratio of the standard deviation of the additive predictor without random effects divided by the standard deviation of the random effect functions; e.g. for SNR_B = 5, the contribution of each functional random effect to the variability in y(t) is about 5 times smaller than that of the non-random effects.

• – signal-to-noise ratio: SNR_ε ∈ {1,5}, where SNR_ε is the ratio of the standard deviation of the additive predictor divided by the standard deviation of the residuals σ_ε.

Our results show that 10 replications for each combination are sufficient to derive precise estimates of effects of the setting parameters on estimation errors and computation times, c.f. Figures 1 and 2. Fits are obtained with the defaults in pffr(), i.e., cubic B-spline bases with 20 basis functions and first order difference penalty for the functional intercept, tensor products of cubic B-spline bases with five marginal basis functions for the tensor product terms, with first order difference penalties for the t- and s-directions and second order difference penalties for the covariate direction (if applicable). The smoothing parameters are REML estimates as returned by mgcv. The models for settings 1 to 4 include K = 120 to 1020 coefficients and 5 to 8 smoothing parameters.

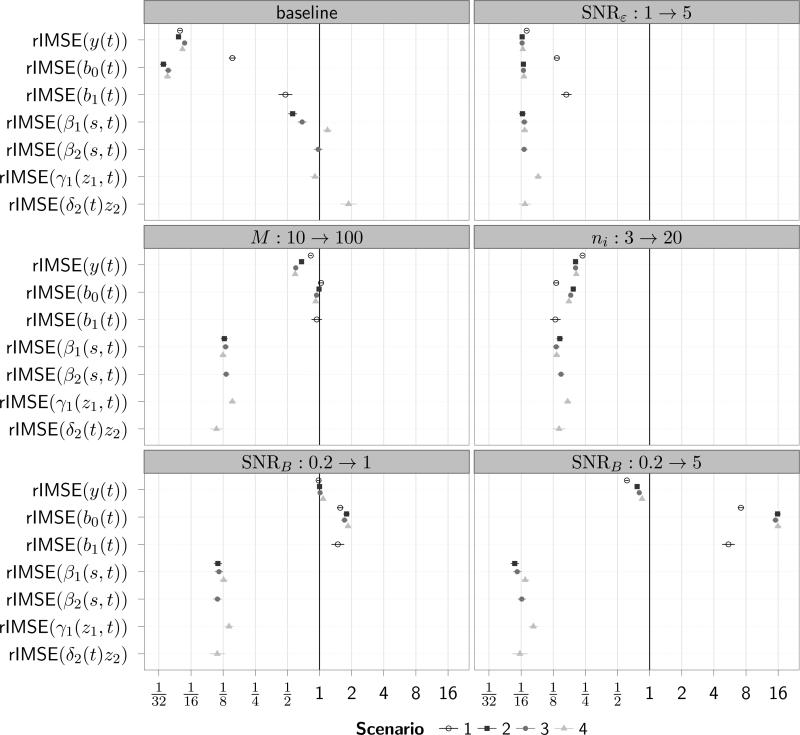
Figure 1.

Baseline levels and estimated multiplicative change in rIMSE for the 4 scenarios. The scenarios are depicted with different symbols, and the segments accompanying the symbols correspond to the estimated effect ± 2 standard errors. Effects other than b₀(t) only occur in a subset of scenarios. Horizontal axis on log₂.

Figure 2.

Computation times for scenarios 1 to 4 (from left to right). Vertical axis on log₁₀-scale. Horizontal axis for the various combinations of numbers of subjects M and average number of replications per subject n_i. Results for T = 30 in dark grey and in light grey for T = 60. Timings are wall-clock time taken on an 2.2 GHz AMD Opteron 6174.

Estimation error

We use the relative integrated mean squared error defined as $\mathrm{rIMSE}\left({\widehat{f}}_r({\mathcal{X}}_r,t)\right)=n^{-1}{\sum }_{i=1}^n\frac{\int {({\widehat{f}}_r({\mathcal{X}}_{ri},t)-f_r({\mathcal{X}}_{ri},t))}^{2}dt}{\int f_r{({\mathcal{X}}_{ri},t)}^{2}dt}$ to evaluate the accuracy of the estimates. Relative errors allow comparisons across different scenarios and noise levels regardless of the ranges of the true $f_r({\mathcal{X}}_r,t)$. Note that we evaluate the estimation accuracy of the effects on the scale of the response, not on the scale of the coefficient function itself to make errors directly comparable across effects. Detailed analysis of results (see Appendix B in the supplement) shows that there are no relevant interaction effects between the setting parameters M, n_i, T, SNR_B and SNR_ε on the observed errors within scenarios, so we fit log-linear models with main effects for the setting parameters in each scenario to observed rIMSE values and proceed to analyze the estimated effects. Figure 1 shows baseline levels and the estimated multiplicative effects of the simulation parameters on the rIMSEs. The effect of increasing the number of grid points T for y(t) from 30 to 60 is not shown, as it decreased relative errors for all quantities by a factor of about 0.7 to 0.5. Baseline rIMSE values (top left panel) are given for data with SNR_ε = 1, M = 10, n_i = 3, T = 30, SNR_B = 0.2. In this very noisy setting with small sample size and dominant random effects, covariate effect estimates are not very accurate, with relative errors mostly in the vicinity of one. Since the random effects are estimated with little error, however, the error for the responses in this difficult setting is small as well. Increasing SNR_ε from 1 to 5 (top right panel) decreases relative errors about 16-fold, with smaller 8-fold reductions for the random effects in scenario 1. Increasing the number of groups from M = 10 to M = 100 (second row, left panel) has no substantial effect on the overall estimation accuracy of the y_i(t). Estimation accuracy of the functional random effects is not improved either due to the commensurate increase in the number of parameters, while errors for the covariate effects decrease about 8-fold. An increase in the average number of observations per group from n_i = 3 to n_i = 20 (second row, right panel) results in a similar reduction of relative errors for the covariate effects, and also a marked four- to sixfold decrease in the errors for the response trajectories. A reduction of the relative contribution of the random effects to the linear predictor, i.e. increasing SNR_B from 0.2 to 1 [5] (bottom row, left [right] panel), improves the overall estimation accuracy of y(t) only slightly if at all [factor 0.7 to 0.8]. This overall improvement is due to the large reduction of errors for the covariate effects, which compensates for the observed deterioration of random effect estimates. While the errors for the former decrease about 8-fold [16-fold], the errors for the latter increase about 1.5- to twofold [five- to 16-fold].

Comparison to other approaches

Appendix C summarizes additional results for comparisons between spline-based and FPC-based terms implemented for function-on-function effects and functional random effects in pffr as well as the wavelet-based approach for functional linear mixed models of Morris and Carroll (2006) implemented in WFMM (Herrick, 2013).

Coverage

We also evaluate coverage of approximate point-wise empirical Bayes confidence intervals (CIs) (c.f. Wood, 2006, eq. (4.35)) with constraint correction (Marra and Wood, 2012) for a nominal level of 95%. For each fitted model, we record the proportion of point-wise intervals covering the true value of each quantity evaluated on a fine grid. Note that the coverages of neighboring grid points are not independent, but for the computationally intensive models we fit this is a feasible alternative to coverage estimates based on hundreds of replicates of each setting. CI coverage was consistently very close to the nominal level for ŷ(t) (Median_10% quantile−90% quantile : 0.95_{(0.92−0.97)}) and b̂₀(t) (0.95_(0.9−0.98)), while $\widehat{\alpha }\left(t\right)\left({0.97}_{(0.9-1)}\right)$ showed some overcoverage as well as a few replicates with coverage below 0.7 for small and noisy data. Coverage for functional random slopes b̂₁(t) was below nominal for small groups, but close to nominal for larger datasets (n_i = 3: 0.9_{(0.81−0.96)}; n_i = 20: 0.95_(0.9−0.99)). Similarly for ${\widehat{\beta }}_1(s,t)$ and ${\widehat{\beta }}_2(s,t)$, overall coverage was close to the nominal level (0.95_{(0.85−0.99)}), with systematic undercoverage in small and noisy data sets with dominating random effects. Both ${\widehat{\gamma }}_1(z_1,t)\left({0.99}_{(0.94-1)}\right)$ and ${\widehat{\delta }}_2\left(t\right)\left(1_{(0.75-1)}\right)$ had overcoverage, the latter with many outliers with observed coverages below 0.8.

Computation times

Figure 2 shows computation times on an 2.2 GHz AMD Opteron 6174 processor for the different scenarios and sample sizes. Especially for models with multiple random effects (scenario 1) computation times increase dramatically in M. Smaller models are fit rapidly, and even for the largest data sets with nT = 1.2 · 10⁵, computation times are not prohibitively long. Speed gains for REML inference on large data sets can be achieved by using the pffr()-option to use mgcv's bam() routine for estimating additive models on data sets that do not fit into memory, as in Section 2.2. Using GCV optimization (Wood, 2004) instead of REML-based inference in pffr() can yield up to 10-fold speedups especially for large data sets, but tends to be less stable.

Summary

Important effects that contribute relevantly to the predictor are estimated with good to excellent accuracy. Only a single replicate resulted in an rIMSE for y(t) greater than 0.1 – even in the most challenging data situations with few noisy observations and small group sizes, our approach is able to reproduce the true structure of the data well. Our results indicate that estimation accuracy of covariate effects is affected most strongly by changes in the noise levels SNR_ε and especially SNR_B, and less strongly by changes in the available number of observations M,n_i and T. The patterns of relative change in accuracy are identical for simple functional regression coefficients, index-varying smooth effects or effect surfaces for functional covariates. The estimation accuracy of the functional random effects is affected strongly by the relative importance of the random effects SNR_B and the group size n_i, and little by the number of groups M. FPC-based random effects seem to require a sufficiently large number of groups and low noise level to obtain usable FPC estimates. Spline-based approaches yielded superior results to FPC-based and wavelet-based approaches, but it should be noted that the data-generating process for the simulation study was spline-based itself. Overall, the observed coverage of the approximate pointwise CI was very close to the nominal level except for very small or noisy data.

2.2 Modeling spatial association of demyelination in a longitudinal MS study

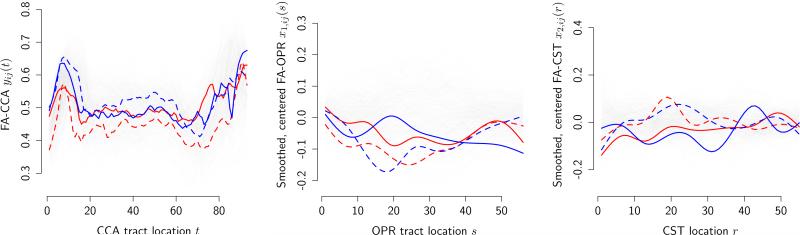
Our motivating tractography study comprises 162 MS patients and 42 healthy controls who are observed at one to eight visits, spread over up to four years, with 476 visits in total. MS damages white matter tracts (WMT) in the brain due to lesions, axonal damage and demyelination. Diffusion tensor imaging (DTI) is a magnetic resonance imaging technique that is able to resolve individual WMTs in the central nervous system (Basser et al., 2000), and is thus a very useful tool in monitoring disease progression in MS patients. At each visit, fractional anisotropy (FA) was determined via DTI along the corpus callosum (CCA, connecting the left and right hemispheres of the brain), the left corticospinal tract (CST, connecting the brain and the spinal cord), and the left optic radiation tract (OPR, connecting visual cortex and thalamus). FA is derived from the estimated diffusion tensor and is equal to zero if water diffuses perfectly isotropically (Brownian motion) and to one if it diffuses with perfectly organized movement of all molecules in one direction for a given voxel. It may be decreased in MS patients and thus serves as a marker of disease progression here. Tracts are registered within and between subjects using standard biological landmarks identified by an experienced neuroradiologist. Figure 3 displays registered tract profiles as functions of tract location; profiles corresponding to four different subjects at first visit are highlighted.

Figure 3.

From left to right: FA profiles along CCA, OPR and CST for MS patients (red) and controls (blue). Solid line: females; dashed: males. FA-OPR and FA-CST are de-trended and smoothed.

Various aspects of this complex tractography dataset have been explored in a sequence of papers including Goldsmith et al. (2011), Goldsmith et al. (2012), Staicu et al. (2011), Ivanescu et al. (2012). This study was first introduced by Greven et al. (2010), who modeled longitudinal variability in trajectories FPC-based, but could not take into account any covariate effects. Our goal here is to better understand the spatial course of the demyelination process via its FA proxy and investigate possible differences therein between MS and healthy subjects. Ivanescu et al. (2012) considered a similar question, but used only the first measurement of each subject since their approach is unable to handle the longitudinal structure of the data. We assume a functional linear dependence between the FA along the CCA and the two functional covariates – FA along the OPR and FA along the CTS – while adjusting for the effects of other relevant covariates such as gender, age at visit, and disease status. Specifically, if y_ij(t) is the FA profile at location t on the CCA tract observed at visit j for subject i, we assume that the conditional mean of y_ij(t), μ_ij(t), is

$${\mu }_{ij}\left(t\right)={\alpha }_{d_i}\left(t\right)+{\delta }_{g_i}\left(t\right)+\nu (u_{ij},t)+\int x_{1,ij}\left(s\right){\beta }_{1,d_i}(s,t)ds+\int x_{2,ij}\left(r\right){\beta }_{2,d_i}(r,t)dr$$ (8)

where x_1,ij(s) and x_2,ij(r) are the FA profiles at locations s and r along the OPR and CTS tracts, respectively, observed at the jth visit of the ith subject. Here d_i is the disease status of the subject, with d_i = 1 for MS patients, and d_i = 0 for healthy subjects; g_i indicates the gender: g_i = 1 for males and 0 for females; and u_ij is the age (in years) at the jth visit of the ith subject. Note that the effects of FA-OPR and FA-CST at the current visit are disease group-specific, with β₁,₀(s,t),β₂,₀(r,t) for controls and β₁,₁(s,t),β₂,₁(r,t) for MS patients. Neither age nor gender effects were found to differ between disease groups in the model-building process.

Effect estimates for a naïve model (8) along the lines of Ivanescu et al. (2012) under assumed independence with measures of uncertainty are provided in Appendix B, Figure 7 for completeness. Due to the inappropriate conditional independence assumption, this approach underestimates the variability of the estimates. We use our proposed functional additive mixed model to account for the within-subject correlation, which is the key advantage of our approach over available function-on-function regression methods. Specifically, a more appropriate model is

$$y_{ij}\left(t\right)={\mu }_{ij}\left(t\right)+b_{i0}\left(t\right)+{\epsilon }_{ijt},$$ (9)

where b_i0(t) are subject-specific functional random intercepts. Model (9) can be fit using the pffr() function in the refund package. Estimating (9) took about 17 hours on an 2 GHz AMD Opteron processor.

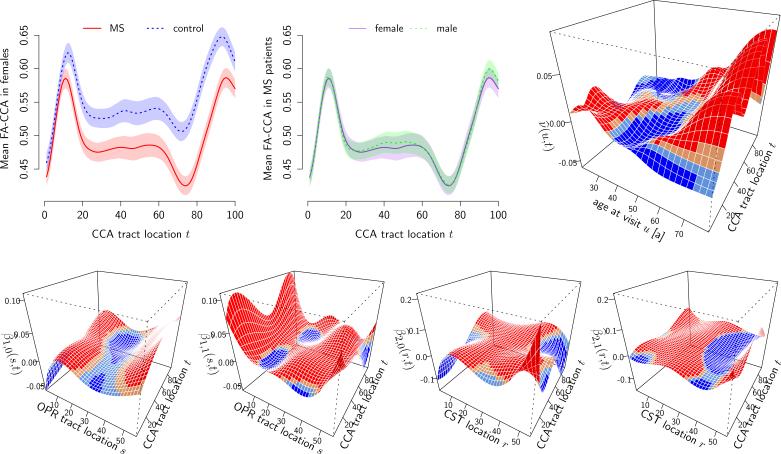
Figure 7.

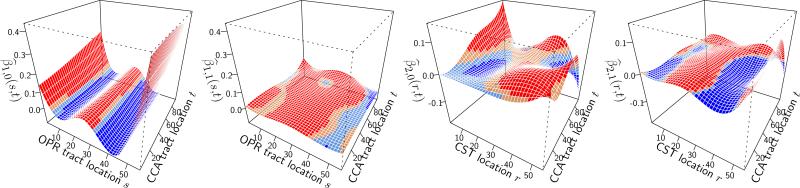
Estimated components of model (8) with ±2 pointwise standard errors, using Ivanescu et al. (2012). Coefficient surfaces are color-coded for sign and pointwise significance (95%): blue if sig. < 0, light blue if < 0, light red if > 0, red if sig. > 0. Top row, left to right: mean FA-CCA for healthy (blue, dotted) versus MS (red, solid) females; mean FA-CCA for female (purple, solid) and male (green, dotted) MS patients; estimated effect of age-at-visit $\widehat{\nu }(u,t)$. Bottom row, left to right: Estimated coefficient surfaces ${\widehat{\beta }}_{1,0}(s,t)$, ${\widehat{\beta }}_{1,1}(s,t)$, ${\widehat{\beta }}_{2,0}(r,t)$, ${\widehat{\beta }}_{2,1}(r,t)$.

Since there are subjects with a few missing locations along the tracts and since the FA measurements are observed with noise, we preprocess the functional covariates. (Note that missing values in the functional response are not an issue for our approach.) The FA profiles are first detrended by subtracting the disease group-specific mean function to make the estimated effects easily interpretable (see Appendix A.1). They are then smoothed, which also imputes missing values. For smoothing, we use functional principal component analysis (Di et al., 2009; Yao et al., 2005) for all tract-specific FA curves under a working independence assumption between profiles on the same subject. Since the observed FA-CCA profiles exhibit a lot of small scale structure at locations 5 − 20 and > 85, spline based functional random intercepts would require a very large basis to provide sufficient flexibility. Instead, we use the residual curves from model (8) fitted under an independence assumption to obtain an unsmoothed FPC-basis for the random intercepts, as described on page 10.

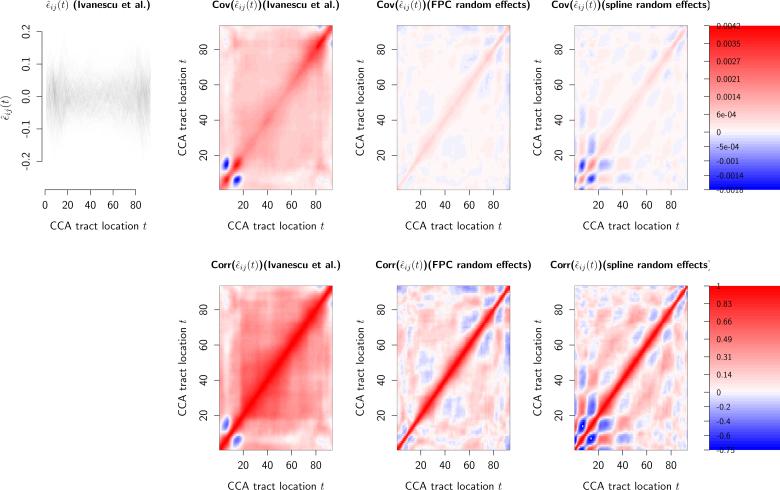
Figure 4 shows the estimated mean of the FA profiles along the CCA tract (anterior to posterior, i.e. front of the head to the back) for female subjects with and without MS (left panel) and for male and female MS patients (second from left). The estimated mean FA profiles have similar shapes, with a sharp increase in the rostrum/genu (front), a plateau in the middle section, followed by a decrease near the isthmus and a rapid increase towards the splenium (back). As expected, MS patients tend to have lower FA-CCA, especially in the posterior section from the rostral body to the splenium. The effect of gender seems to be negligible. The estimated age effect, $\widehat{\nu }(u_{ij},t)$, indicates that FA-CCA decreases almost linearly with age over the entire tract, particularly in the anterior part, but this effect is fairly small. Not accounting for the longitudinal data structure (c.f. Figure 7), differences between MS and healthy subjects would be found to be much larger and statistically significant along the entire tract. The corresponding estimate for the age effect seems implausible. Due to the misplaced independence assumption, the variability of the estimates shown in Figure 7 is underestimated, but should be approximately correct in Figures 4 and 5. The rightmost panels in Figure 8 give covariances and correlations for ε_ij(t) and show that the white-noise-error assumption is reasonable for model (9), but severely violated for (8). They also show that spline-based random intercepts are less successful in removing all structure from the residuals in this case, especially in the rostrum/genu.

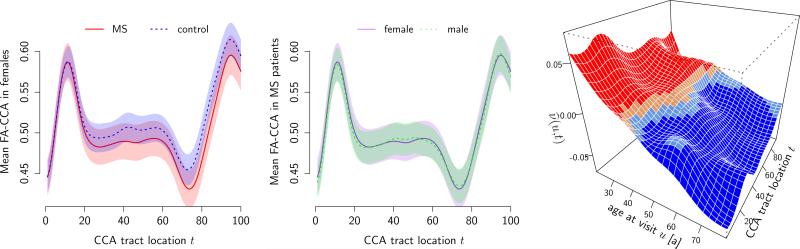
Figure 4.

Estimated components of model (9) with ±2 pointwise standard errors. Coefficient surfaces are color-coded for sign and approximate pointwise significance (95%): blue if sig. < 0, light blue if < 0, light red if > 0, red if sig. > 0. Left to right: mean FA-CCA for healthy (blue, dotted) versus MS (red, solid) females; mean FA-CCA for female (purple, solid) and male (green, dotted) MS patients; estimated smooth index-varying age effect $\widehat{\nu }(u,t)$.

Figure 5.

Left to right: Estimated coefficient surfaces ${\widehat{\beta }}_{1,0}(s,t)$, ${\widehat{\beta }}_{1,1}(s,t)$, ${\widehat{\beta }}_{2,0}(r,t)$, ${\widehat{\beta }}_{2,1}(r,t)$.

Figure 8.

Top row, left to right: Observed residuals ${\widehat{\epsilon }}_{ij}\left(t\right)$ for model (8); empirical covariance for ${\widehat{\epsilon }}_{ij}\left(t\right)$ for model (8); empirical covariance for ${\widehat{\epsilon }}_{ij}\left(t\right)$ for model (9) with FPC-based random intercepts; empirical covariance for ${\widehat{\epsilon }}_{ij}\left(t\right)$ for model (9) with spline-based random intercepts; legend for covariance values. Bottom row: Empirical correlations.

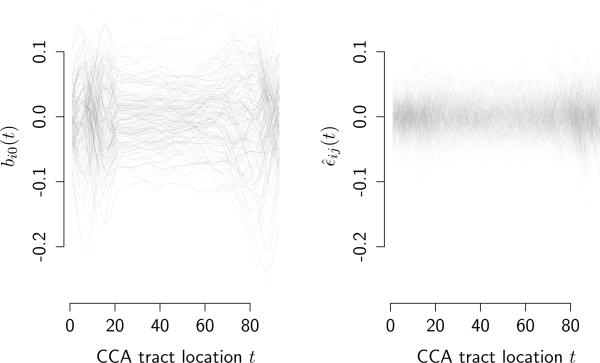
In healthy controls, FA values at the ends of the OPR tract (towards lateral geniculate nucleus and visual cortex, respectively) and in its middle section show a positive association with FA values along the entire CCA tract (see Figure 5). For the CTS tract, there is some indication of a positive association between FA values in the beginning of the CTS tract (medulla) and the end of the CCA (splenium) and between the end of the CTS tract (subcortical white matter) and the beginning of the CCA (rostrum/genu), the latter corresponding with spatial proximity. These patterns should be indicative of the normal ageing process, while the observed associations mostly vanish for MS patients or become much weaker. It should be noted, however, that simulation results indicate potentially low estimation accuracy of fixed effects in settings such as this one in which the random effects dominate the predictor. Figure 6 displays the predicted intercept curves b̂_i0(t) (left panel) and observed residuals ${\widehat{\epsilon }}_{ij}\left(t\right)=y_{ij}\left(t\right)-{\widehat{\mu }}_{ij}\left(t\right)-{\widehat{b}}_{i0}\left(t\right)$ (right panel). The large variation in the predicted functional intercepts reveals large inter-subject variability. By accounting for the between-subject variability the observed integrated root mean square error of the responses with the proposed method (0.027) reduces to half of its magnitude compared to Ivanescu et al. (2012) under an independence assumption (0.05). Model (9) explains about 90% of the observed variability, while (8) explains only about 63%.

Figure 6.

Predicted functional intercepts b̂_i0(t) and observed residuals ê_ij(t) for model (9).

In conclusion, using our flexible modeling framework for the FA profiles along the CCA tract shows that a large fraction of the variability in the data is captured by subject-specific random effects. Modeling the dependence on FA profiles at other well identified tracts, OPR and CTS, can provide new insights into the spatial association in normal ageing and disease processes. Interestingly, our results indicate that the associations between demyelination along the left CTS and left OPR tracts and the CCA tract are weaker for MS patients than for healthy controls. A possible interpretation of this finding could be that demyelination processes in MS patients are more strongly localized, consistent with the development of localized lesions during MS. By properly accounting for the longitudinal structure of the data the estimation uncertainty of all effects increases compared to model (8) under an independence assumption.

3 Discussion and Outlook

We propose a general framework for flexible additive regression models for correlated functional responses, allowing for multiple functional random effects with, for example, spatial, temporal, spatio-temporal or longitudinal (Section 2.2) correlation structures. Dependence structures can be modeled either implicitly by specifying smooth temporal, spatial or tempo-spatial effects or explicitly by including functional random effects with marginal between-unit correlation structures given by the precision matrices of Gaussian (Markov) random fields. Estimation and inference is performed by standard additive mixed model software, allowing us to take advantage of established robust and flexible algorithms. The approach is implemented as fully documented open-source software in the pffr()-function in the refund package (Crainiceanu et al., 2011) for R. Effects of functional covariates and functional random effects are available in both FPC- and spline-based variants and both scalar and functional covariates can have linear or more general smooth effects on the outcome trajectories, allowing analysts to choose the most suitable tools for the task at hand.

Simulation experiments show that the proposed method recovers relevant effects reliably and handles small group sizes and/or low numbers of replications well. Data sets of considerable size can be fit in acceptable time. Two applications demonstrate that our approach makes it possible to fit flexible models that do justice to complex data situations and yet still yield interpretable results that can help to understand the underlying processes.

This work opens up a number of interesting avenues for further research. A first direction concerns the covariance structure of the residuals. Since our present inference algorithms do not exploit the extreme sparsity of the design matrices for smooth observation-specific residual terms, estimating such terms dramatically increases computation time and memory requirements for large data sets. On the other hand, simply assuming i.i.d. errors ε_it will often be unrealistic since some degree of auto-correlation and heteroscedasticity over the index of the functional response is usually encountered in practice. We are currently investigating an iterative procedure similar to the approach in Reiss et al. (2010), where observed residuals from an initial model estimated under a working independence assumption are used to estimate a working covariance structure and the model is then re-estimated based on de-correlated data. If successful, such a marginal model specification could offer an efficient alternative to the conditional modeling approach outlined in the present paper. In a second direction, we are currently developing diagnostic measures to identify potential problems with low-rank functional covariates (c.f. Appendix A) as well as practical model-building strategies regarding the estimation of corresponding regression surfaces. A closely related avenue of inquiry are more in-depth comparisons of spline- and FPC-based approaches for modeling function-on-function terms as well as functional random effects in order to evaluate their relative strengths and weaknesses. The unifying framework implemented in pffr() will greatly facilitate such comparisons. In addition, we have begun implementing a dedicated toolbox for REML-based inference tailored to function-on-function regression. This effort is based on the computationally efficient array regression approach of Currie et al. (2006), which is expected to speed up inference for large scale problems and help to generalize the proposed methods for multidimensional functional responses and image regression.

A Identifiability

A.1 Imposing suitable identifiability constraints

Additive models for scalar responses ensure identifiability by imposing suitable constraints on the functions that make up the additive predictor ${\beta }_0+{\sum }_s{f}_s\left(x_s\right)$, such as a sum-to-zero constraint ${\sum }_{i=1}^n{f}_s\left(x_{si}\right)=0$ for each function f_s(x_s) (Wood, 2006). Otherwise, any constant could be added to one function and subtracted from the others without changing the fit criterion.

A similar issue arises in the context of our proposed model. For arbitrary functions ${\stackrel{‒}{\gamma }}_z\left(t\right),{\stackrel{‒}{b}}_g\left(t\right)$

$$\mathrm{E}\left(y_i\left(t\right)\right)=\alpha \left(t\right)+\gamma (z_i,t)+b_{g\left(i\right)}\left(t\right)=(\alpha \left(t\right)+{\stackrel{‒}{\gamma }}_z\left(t\right)+{\stackrel{‒}{b}}_g\left(t\right))+(\gamma (z_i,t)-{\stackrel{‒}{\gamma }}_z\left(t\right))+(b_{g\left(i\right)}\left(t\right)-{\stackrel{‒}{b}}_g\left(t\right))$$

obtains the same fit with two different parameterizations. To avoid this, we impose sum-to-zero constraints for each t so that $n^{-1}{\sum }_{i=1}^n{b}_{g\left(i\right)}\left(t\right)=n^{-1}{\sum }_{i=1}^n\gamma (z_i,t)=0\forall t$.

We also center covariate trajectories x_i(s) by subtracting the mean function $\stackrel{‒}{x}\left(s\right)=n^{-1}{\sum }_i{x}_i\left(s\right)$. If both the sum-to-zero constraints for each t are imposed and functional covariates are centered, all effects that vary over the index of the response are directly interpretable as deviations from the overall mean trajectory α(t). Standard sum-to-zero constraints implemented in mgcv, which would correspond to Σ_i,t γ(z_i,t) = 0, yield neither identifiable models nor effects that are interpretable like this. Implementationwise, we use the method described in Wood (2006, ch. 1.8.1) to absorb the sum-to-zero-for-each-t constraints into the design matrices of all effects varying over t, see section A in the online supplement for details and examples.

A.2 Limits on the identifiability of complex regression surfaces for low-rank functional covariates

For function-on-function-regression terms ${\int }_{\mathcal{Y}}x\left(s\right)\beta (s,t)ds$, identifiability of β(s,t) is guaranteed under conditions derived in He et al. (2003), Chiou et al. (2004) and Prchal and Sarda (2007), which are hard to verify empirically. In practice, an important quantity in this regard for the stability of spline-based estimates is the effective rank of the covariance operator of x(s), which can be defined as the number of eigenvalues that together account for at least 99.5% of the covariate's variability. If this effective rank is low, the kernel of the functional covariate's covariance operator is large. Scheipl and Greven (2012) have shown that spline-based regression surface estimates can be unstable if the kernel of the functional covariate's covariance operator overlaps the function space spanned by parameter vectors in the nullspace of the tensor product spline's roughness penalty. Based on theoretical considerations and simulation results (c.f. Scheipl and Greven, 2012), we recommend that practitioners check the effective rank of the observed covariance matrix of functional covariates and the amount of overlap between the kernel of the functional covariate's covariance operator and the nullspace of the associated roughness penalty. Utility functions to perform these checks and constructors for modified roughness penalties without nullspaces are included in refund.

B Supplementary Details for the DTI Data Analysis

C Supplementary Simulation Study Results

Comparison with FPC-based approaches

We fit models with an FPC-based function-on-function term (c.f. page 8) and models with FPC-based functional random intercepts (c.f. page 10) to each dataset generated for the second scenario. rIMSEs for the FPC-based function-on-function term were larger than those of the spline-based estimates by a mean factor of 1.5_(1.2−2.1), while computation time was about the same for M = 10 (1_(0.8−1.4)) and somewhat longer for M = 100 (1.3_(1.1−1.6)). Results for the FPC-based functional random intercept were more different from the spline-based option. Specifically, the FPC-based functional random intercept showed fairly little improvement for SNR_ε = 5 compared to SNR_ε = 1. For the latter, the FPC performance was fairly similar (M = 10: factor of 2.4_(1.3−9.4), M = 100: factor of 1.1_(1.0−1.5)), while it was much less precise for the former: 3.4_(1.1−17) for M = 100 and 17_(2.5−106) for M = 10. As expected, however, FPC-based functional random intercepts scaled much better than spline-based ones for larger datasets in terms of computation time due to their more compact optimal basis representation – for M = 100, the iterative FPC procedure was faster than spline-based random effect models by a factor of 0.3_(0.2−0.5). Also, our spline-based data generating process corresponding to five non-zero FPCs (c.f. Appendix B of the supplement) may be more difficult for FPC based approaches: previous simulation studies of FPC-based functional regression have typically used data generating processes with lower effective rank (e.g. Chen and Müller, 2012; Müller and Yao, 2008; Wu et al., 2010, with 2, 3, and 4 eigenfunctions, respectively) and simpler coefficient shapes.

Comparison with WFMM

We compare our approach to the available implementation of the wavelet-based functional linear mixed models of Morris and Carroll (2006) in WFMM (Herrick, 2013). We can only provide this comparison for scenario 1 as the other scenarios feature terms that are not available in WFMM, which can only fit random effect curves and functional linear effects z_ijβ(t) of scalar covariates z. Note that, differing from the results for pffr in the remainder of the article, these results are for balanced data, as the WFMM algorithm seems to fail whenever there are any subjects with 1 or 2 observations only, and 10 replicates per setting. We used the default hyper- and tuning parameters for WFMM, with 2000 iterations of burn-in followed by 10000 iterations of sampling. In general, the IMSEs for WFMM are about double to three times those of pffr. Specifically, the IMSE for y(t) is increased by a median factor of 2.5_(2.1−3.1) (IMSE(b₀(t): 2.3_(1.6−3.8), IMSE(b₁(t): 2.4_(1.5−4)). Note, however, that this comparison is not entirely fair to WFMM, as it is designed for spiky data e.g. from spectrometry (i.e., it assumes sparsity in a suitable wavelet domain), not the smooth functional data that we assume and correspondingly simulated here. Although WFMM is much slower (4- to 16-fold) than pffr for small and intermediate data sizes, its computation time increases much slower than pffr for larger data sets due to its efficient data representation in the wavelet domain and its very fast C++ implementation. Detailed results for this comparison are provided in Section B.6 of the online appendix.