A neural circuitry that emphasizes spinal feedback generates diverse behaviours of human locomotion

Abstract

Neural networks along the spinal cord contribute substantially to generating locomotion behaviours in humans and other legged animals. However, the neural circuitry involved in this spinal control remains unclear. We here propose a specific circuitry that emphasizes feedback integration over central pattern generation. The circuitry is based on neurophysiologically plausible muscle-reflex pathways that are organized in 10 spinal modules realizing limb functions essential to legged systems in stance and swing. These modules are combined with a supraspinal control layer that adjusts the desired foot placements and selects the leg that is to transition into swing control during double support. Using physics-based simulation, we test the proposed circuitry in a neuromuscular human model that includes neural transmission delays, musculotendon dynamics and compliant foot–ground contacts. We find that the control network is sufficient to compose steady and transitional 3-D locomotion behaviours including walking and running, acceleration and deceleration, slope and stair negotiation, turning, and deliberate obstacle avoidance. The results suggest feedback integration to be functionally more important than central pattern generation in human locomotion across behaviours. In addition, the proposed control architecture may serve as a guide in the search for the neurophysiological origin and circuitry of spinal control in humans.

Key points

• It is often assumed that central pattern generators, which generate rhythmic patterns without rhythmic inputs, play a key role in the spinal control of human locomotion.

• We propose a neural control model in which the spinal control generates muscle stimulations mainly through integrated reflex pathways with no central pattern generator.

• Using a physics-based neuromuscular human model, we show that this control network is sufficient to compose steady and transitional 3-D locomotion behaviours, including walking and running, acceleration and deceleration, slope and stair negotiation, turning, and deliberate obstacle avoidance.

• The results suggest feedback integration to be functionally more important than central pattern generation in human locomotion across behaviours.

• In addition, the proposed control architecture may serve as a guide in the search for the neurophysiological origin and circuitry of spinal control in humans.

Introduction

Humans show a range of locomotion behaviours from walking and running to stair and slope negotiation to turning and deliberate obstacle avoidance. Experimental evidence has established that neural networks along the spinal cord contribute substantially to generating these behaviours in humans and other legged animals (Grillner, 2006; Bizzi et al. 2008; Gerasimenko et al. 2008; Harkema et al. 2011); however, the specific neural circuitry involved in this spinal control remains unclear. The current main ideas about what this circuitry is composed of revolve around central pattern generators (CPGs) and muscle synergies. CPGs are mutually inhibiting neural circuits in the spinal cord (Guertin, 2009) that can produce rhythmic patterns of neural activity without rhythmic inputs (Ijspeert, 2008). Animal experiments have confirmed the existence of CPG networks in invertebrates (Orlovsky et al. 1999). They have also shown mammals performing locomotion-like rhythmic limb movements in the absence of both supraspinal and peripheral inputs (Brown, 1911; Grillner & Zangger, 1979; Rossignol et al. 2008), although their CPG network remains a black box (Guertin, 2009). Muscle synergies can be viewed as a generalization of CPGs, providing the flexibility to compose more than just rhythmic behaviour (Ijspeert, 2008). They are proposed control modules located in the spinal cord that activate a group of muscles in a fixed balance (Bizzi et al. 2008; Tresch & Jarc, 2009). Using computational factorization algorithms, several research groups have shown that only a handful of synergies would be required to explain the muscle activities found in different animals and humans for locomotion behaviours from swimming to balancing to walking (Tresch et al. 1999; Ivanenko et al. 2004; Cheung et al. 2005; Torres-Oviedo & Ting, 2007; Dominici et al. 2011). Recent physiological evidence supports the existence of synergies (Bizzi & Cheung, 2013), but similar to CPGs, the neural origin and circuitry of synergies remains debated (Tresch & Jarc, 2009; Kutch & Valero-Cuevas, 2012).

Using a physics-based neuromuscular human model, we here propose a specific neural circuitry to compose a range of locomotion behaviours. Most previous human model studies that propose a neural control architecture emphasize spinal pattern generation (Taga et al. 1991; Taga, 1998; Ogihara & Yamazaki, 2001; Hase et al. 2003; Paul et al. 2005; Kim et al. 2011). In these models, mutually inhibiting neurons (Matsuoka, 1985) are combined to a number of CPGs that generate spinal, oscillatory outputs at each joint of the lower limbs. Although the activity of the CPG models is altered in timing and amplitude by feedback from muscle, skin and joint sensors, as well as from the vestibular system (Hase et al. 2003; Paul et al. 2005; Kim et al. 2011), the functional importance of these sensory feedback pathways to generating locomotion behaviours is not explicitly addressed.

Here we show that sensory feedback integration, without spinal pattern generation, is sufficient to generate human locomotion across behaviours. We develop a three-dimensional human neuromuscular model that generalizes the muscle reflex circuitry of a previous sagittal plane model (Geyer & Herr, 2010). In particular, we replace the previous model's swing phase reflexes with a functionally more relevant reflex circuitry of swing leg placement (Desai & Geyer, 2012, 2013; Song et al. 2013), and integrate muscle reflexes for hip abduction and adduction (Song & Geyer, 2013). The resulting control is organized in 10, mainly independent, spinal feedback modules that realize limb functions essential to legged locomotion. In addition, we incorporate a higher layer, longer latency control that can alter some of the reflex gains. This supraspinal control adjusts the desired foot placements (Kajita et al. 2001; Yin et al. 2007) and selects the leg that is to transition into swing control during double support. Using computer optimization of the model's control parameters, we find that the control network is sufficient to compose steady and transitional 3-D locomotion behaviours including walking and running, acceleration and deceleration, slope and stair negotiation, turning, and deliberate obstacle avoidance. (Video S1 in the online Supporting information demonstrates these behaviours.) The results support the hypothesis that feedback integration is functionally more important than central pattern generation in human locomotion across behaviours. In addition, the proposed control architecture may serve as a guide in the search for the neurophysiological origin and circuitry of spinal control in humans.

Methods

We develop a human locomotion model which extends a previous sagittal plane model of the human neuromuscular system (Geyer & Herr, 2010) to a three-dimensional version with additional muscles and foot geometry (Fig.1) as well as with a neural control circuitry organized in 10 functional, spinal reflex modules (Fig.3) and a higher layer adjusting the foot placement (Fig.2).

Figure 1. 3-D neuromuscular human model walking over rough ground with height changes up to ±10 cm (snapshots every 600 ms).

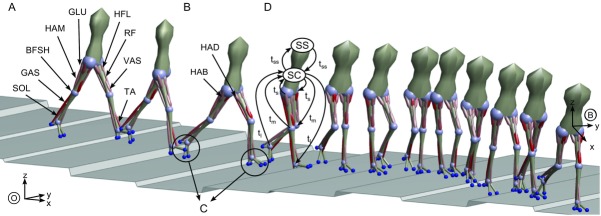
The model consists of 7 segments connected by 8 revolute joints and actuated by 11 muscles per leg. A, 9 muscles actuate the sagittal plane joints at the hip, knee and ankle. B, the hip is further actuated in the lateral plane by 2 muscles. C, each foot has 4 contact points generating continuous ground interaction forces when engaged. D, the neural circuitry of the spinal cord (SC) controlling the muscles is organized into 10 functional modules that are subject to long (t_l), medium (t_m), and short transmission delays (t_s). The communication between the spinal cord and the supraspinal system (SS) adjusting the foot placement is equally delayed (t_ss).

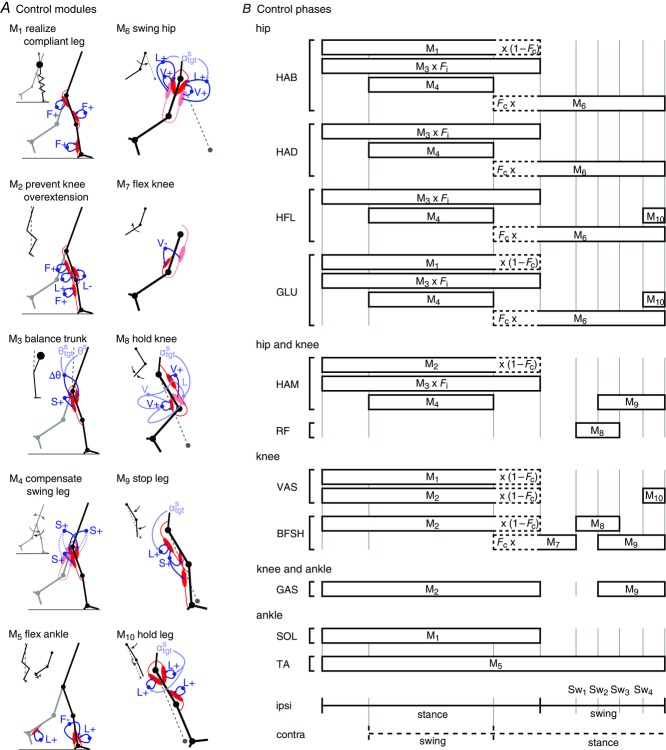
Figure 3. Reflex modules of the spinal control layer.

A, 10 reflex modules realize with decentralized feedback key functions of legged systems including compliant behaviour and trunk balance in stance (M₁ to M₅) and ground clearance and leg placement in swing (M₅ to M₁₀). B, schematic contribution of the modules to each muscle's stimulation throughout the gait cycle. The dotted portions indicate modules that are inhibited or excited during double support in proportion to the load F_c on the contralateral leg when transitioning from stance control to swing control. Sw₁ to Sw₄ trigger events within swing control (see text for details).

Figure 2. Neural control organization.

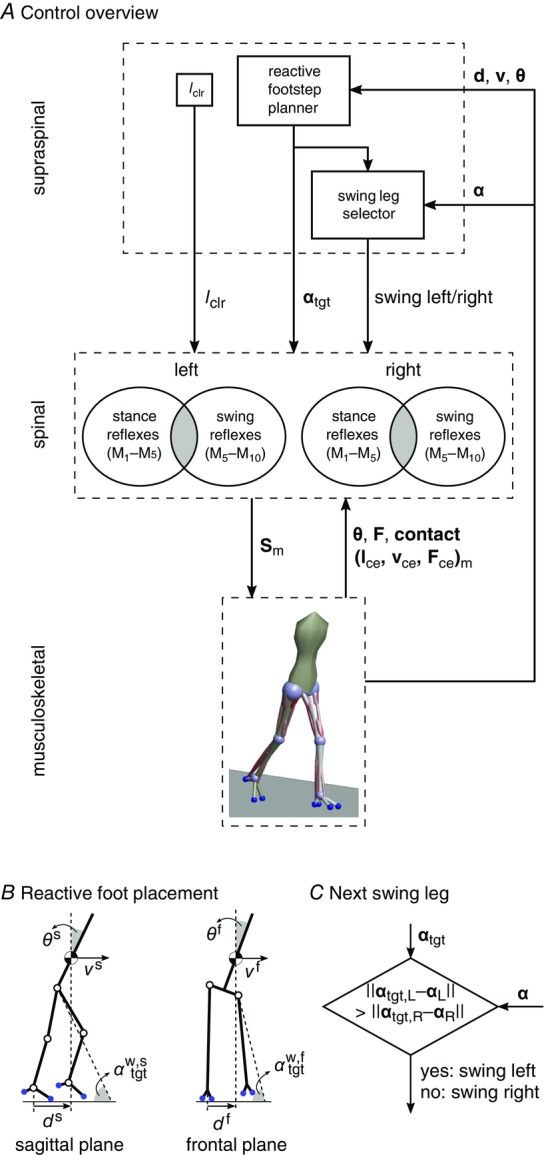
A, the control is organized in spinal and supraspinal layers. The spinal layer consists of 10 reflex modules, M₁ to M₁₀, for each leg which are active in stance or swing. The supraspinal layer adjusts the desired foot placements (α_tgt) and the desired minimum swing leg length (l_clr), and selects which leg should transition into swing control during double support. B, desired foot placement is calculated as target leg angles 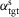and 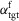for sagittal (s) and frontal (f) plane motions based on the velocity v^{s, f} of the COM and its distance to the stance leg ankle, d^{s, f}. C, in double support, swing control is initiated for the leg whose angle α is farther from the target.

Musculoskeletal mechanics

The model represents a 180 cm tall person weighing 80 kg with seven segments connected by eight internal degrees of freedom (DOFs) and actuated by 22 muscle tendon units (MTUs) (Fig.1). The segments include the trunk describing the whole upper body and the thighs, shanks and feet with geometric and inertial properties estimated from human data (Table 2, Appendix A). Revolute joints connect the segments with two DOFs at the hips (pitch and roll) and one DOF at the knees and ankles (pitch only). Each leg is actuated by 11 Hill-type MTUs. Nine MTUs actuate the three sagittal plane pitch joints (Fig.1A) modelling the lumped hip flexors (HFL), the glutei (GLU), the hamstrings (HAM), the rectus femoris (RF), the vastii (VAS), the short head of the biceps femoris (BFSH), the gastrocnemius (GAS), the soleus (SOL) and the tibialis anterior (TA). The remaining two MTUs, modelling the hip abductors (HAB) and adductors (HAD), actuate the hip roll joints (Fig.1B).

Muscle tendon units

The MTU model is detailed in Geyer & Herr (2010). Each MTU consists of a contractile element (CE) and series (SE) and parallel elasticities (PE). The MTU force F_m is calculated solving 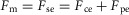, where the active CE exerts a force 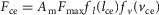with F_max being the maximum isometric force, 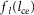and 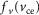being the force–length and force–velocity relationships, and A_m being the muscle activation. Muscle activation is generated by a first-order delay from muscle stimulation S_m, which is the output of the spinal control modules. The physiological differences between the MTUs are captured with four parameters including the maximum isometric force F_max, the maximum contraction velocity v_max of the CE, the optimal CE length l_opt, and the SE slack length l_slack. For each MTU, these properties are estimated from human data (Table 3, Appendix A).

Instantaneous moment arms

A muscle force F_m generates a torque 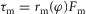at the joints the muscle spans, where 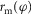is the instantaneous moment arm. All moment arms are matched to reported physiological data (Visser et al. 1990; Arnold et al. 2010; Geyer & Herr, 2010; McCullough et al. 2011), using either a constant value or a scaled cosine relationship (Table 4, Appendix A).

Foot–ground contacts

The musculoskeletal system interacts with the ground via four compliant contact models on each foot (Fig.1C). The contact points are located at the edges of the foot segment in the sagittal plane representing the heel as well as the ball and toe region of a human foot. In the frontal plane, the contact points are 10 cm apart at the ball and 5 cm apart at the heel. If a contact point touches the ground, ground reaction forces (GRFs) act on the foot segment at that point. The normal GRF is calculated as non-linear spring–damper force. The tangential GRF acts in either static or sliding mode, where static friction is modelled as non-linear spring–damper force, and sliding friction is proportional to the normal GRF (for details, see Song & Geyer, 2013).

Neural control circuitry

The neural circuitry of the human model is organized into spinal reflex modules combined with a supraspinal layer. The spinal modules realize individual limb functions essential to legged systems with decentralized feedback control. The supraspinal layer adjusts the desired foot placements and modulates some of the spinal reflexes (Fig.2A). The inputs to this hierarchical control structure include the muscle states such as the length, velocity or force of the contractile elements, joint states such as knee angle and angular velocity, the ground contact information, as well as the trunk's centre of mass (COM) position and velocity relative to the stance foot, and the leg angles and the global trunk lean. The outputs are the muscle stimulations 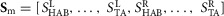of the left (L) and right leg (R) generated by the spinal reflex modules.

Reflex control modules

Each leg's muscles are controlled by 10 reflex modules M₁ to M₁₀ based on their functional role in stance (M₁ to M₅) or swing (M₅ to M₁₀) (Fig.2A). In addition, if a leg is selected by the supraspinal layer to switch from stance control to swing control during the transitional double support phase, some of the stance control modules can be inhibited (M₁ and M₂) and some of the swing control modules can be excited (M₆ and M₇) in proportion to contralateral leg loading. For most muscles, the resulting net stimulation is generated by several control modules that can be active simultaneously. We summarize here the function of each module and describe their implementation in Appendix B.

The stance control is taken from Geyer & Herr (2010) with modifications for some modules and an extension for lateral trunk balance (Fig.3). The first key function of the stance control is to robustly generate compliant leg behaviour. Module M₁ realizes compliant leg behaviour using positive force feedbacks (F⁺) of the leg extensors (GLU, VAS and SOL). As compliant behaviour of segmented legs is prone to buckling (Seyfarth et al. 2001), M₂ prevents knee hyperextension by positive force feedbacks of the biarticular knee flexors (HAM and GAS) throughout stance and by exciting the monoarticular knee flexor (BFSH) while reciprocally inhibiting the knee extensor (VAS) with muscle length feedbacks (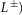 if the knee approaches hyperextension. The second key function of the stance control is to maintain trunk balance. M₃ is the main module realizing this behaviour by activating the hip antagonists in the sagittal (HFL, GLU and HAM) and frontal planes (HAB and HAD) based on an assumed vestibular or visual feedback of the trunk pitch (θ^s) and roll (θ^f) in the world frame. (S⁺ in the M₃ panel of Fig.3A indicates that HAM is co-stimulated in proportion to the stimulation of GLU.) The intensity of the M₃ output is modulated by sensory feedback of the load F_i on the ipsilateral leg to prevent it from slipping due to exaggerated hip torques. In addition, the module M₄ compensates for the moment induced on the trunk by the contralateral swing leg by co-stimulating the ipsilateral leg's antagonist hip muscles in the sagittal plane and agonist hip muscles in the frontal plane (S⁺).

The last spinal module active in stance control, M₅, is also active in swing control and serves a dual purpose. It uses muscle length feedback (L⁺) of the ankle flexor (TA) to generate foot ground clearance in swing and to prevent ankle hyperextension in stance. In stance control, this length feedback is inhibited reciprocally by negative force feedback (F⁻) from the ankle extensor (SOL) to reduce unnecessary antagonistic activation.

The main part of the swing control composed of modules M₆ to M₁₀ is adapted from Desai & Geyer (2013) (Fig.3). Its key functions are to generate sufficient ground clearance and to robustly place the leg into target angles in the sagittal and frontal planes. The desired minimum leg length, l_clr, for ground clearance and target angles 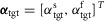are provided to the spinal layer by supraspinal inputs (Fig.2A). Throughout swing, module M₆ drives the hip muscles (HFL, GLU, HAB, and HAD) in proportion to the errors in leg angles 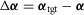to control swing leg placement. For the frontal plane, the error is provided as muscle length feedback (L⁻) from the hip abductor and adductor, HAB and HAD, interpreting the offset, l_off, in the length feedback signal 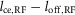as a means to adjust the target angle via γ-motoneuron stimulation (not shown in Fig.3A). A similar length feedback (L⁻) of the biarticular muscles spanning the hip and knee, HAM and RF, provides an estimate of the leg angle error in the sagittal plane (shown in Fig.3A).

The remaining swing leg modules control the knee to achieve ground clearance and return to leg extension when approaching the target angle (Fig.3A). Module M₇ uses velocity feedback from RF (estimating sagittal leg angular velocity 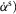to the monoarticular knee flexor BFSH to ensure initial knee flexion. Module M₈ uses length feedback of VAS (L⁺) to monitor leg length, again interpreting the length offset l_{off, VAS} as the desired minimum leg length l_clr which can be adjusted by γ-motoneuron activity. When VAS stretches past the offset (the leg shortens below l_clr) (Sw₁ in Fig.3B), M₈ deactivates M₇ and dampens the knee motion with positive velocity feedbacks (V⁺) of VAS on RF and of BFSH on itself, accounting for the fact that muscles can only pull. (BFSH is further modulated by feedback from RF to allow the knee to passively extend when α^s approaches its target). The sagittal leg angle, α^s, is monitored simultaneously with length feedbacks of HAM and RF. When α^s as measured by HAM passes a threshold close to the target value 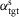(Sw₂), M₉ begins to use positive length feedback (L⁺) of HAM to decelerate the leg angular motion. At the same time, when α^s passes this target as measured by RF (Sw₃), M₈ is deactivated. Finally, once the leg starts to retract (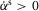, detected by velocity feedback of HAM; Sw₄), module M₁₀ engages and uses positive length feedbacks (L⁺) of the hip muscles (GLU and HFL) and the knee extensor (VAS) to extend the leg (VAS) and hold it close to the targeted angle (GLU and HFL).

If a leg is selected by the supraspinal layer to switch from stance control to swing control during the double support phase, the outputs of modules M₁ and M₂ for the hip and knee muscles are inhibited by proportional feedback of the contralateral leg force F_c to terminate stance (shown as a factor 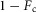in Fig.3B). (M₁ and M₂ remain unmodified for the ankle muscles to provide ankle push off.) At the same time, M₆ and M₇ are proportionally excited by the same contralateral force to initiate swing. The modulation with F_c guarantees that the transition from stance to swing control occurs only if the body weight transfers to the contralateral leg.

Supraspinal control layer

The supraspinal control layer adjusts the desired foot placements in swing. It selects the leg that is to transition into swing control in double support and provides to the spinal cord layer the desired minimum leg length l_clr for ground clearance and the desired foot placement in the form of target leg angles α_tgt in the sagittal and frontal planes (Fig.2A). Several approaches have been proposed to compute desired foot placements for dynamic balance in 3-D walking and running (Raibert & Tello, 1986; Kajita et al. 2001; Yin et al. 2007; Wu & Geyer, 2013). We adapt the heuristic approach of Yin et al. (2007) due to its simplicity. For instance, the desired leg angle of the left leg (L) in the sagittal plane (s) is calculated as 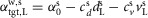, where 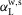is the angle that the sagittal hip-ankle line forms with the horizontal plane of the world frame w; 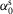, 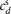and 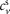are positive constants; an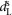d and 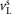are the time-delayed horizontal position and velocity of the COM relative to the ankle of the right foot (Fig.2B). Four different target angles are computed accounting for the sagittal and frontal planes of the left and right leg. The resulting target angle vector 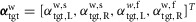is sent to the spinal layer in body frame coordinates,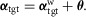

If the legs are in double support, the supraspinal layer additionally selects the leg whose control is to transition into swing based on the distance of the leg angles to their targets (Fig.2C). For each leg, the leg angle distance is cal-culated as 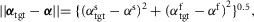and the next swing leg is chosen to be the one whose angle distance is larger, as the other leg is better positioned to balance the trunk in stance. Both the swing leg selection and the target angle vector α_tgt are updated continuously, allowing the supraspinal layer to react to disturbances throughout the gait cycle.

Neural transmission delays

All neural connections are time delayed to reflect physiological constraints on neural transmission speed (Meunier et al. 1990; Grey et al. 2001; Knikou & Rymer, 2002) (Fig.1D). The one-way delay between the supraspinal system and the spinal cord is set to 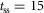ms. The delays projecting between the spinal cord and the areas of the hip, knee and ankle are set to short, medium and long delays with 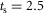ms, 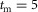ms, and 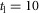ms. The total delay of a neural circuit results from the delays of its individual connections. For example, the delay of the positive force feedback of the ankle extensor SOL in module M₁ is 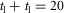ms, and the delay of the positive velocity feedback from RF to BFSH in module M₇ i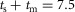s ms.

Implementation and behaviour optimization

We implement the neuromuscular model in the MATLAB Simulink/SimMechanics environment (R2013a) with the ode15s solver (max. step size of 10 ms, relative and absolute error tolerance of 1 × 10⁻³ and 1 × 10⁻⁴, respectively) and optimize the control parameters with the covariance matrix adaptation evolution strategy (Hansen, 2006) to test the versatility of the proposed neural control circuitry in generating locomotion behaviours. The circuitry has 82 control parameters (7 for the reactive foot placement, 40 for stance reflexes, 31 for swing reflexes, and 4 for the modulation in the control transition). The simulation runs at about real time on a modern desktop computer, and a typical optimization run with a population size of 16 parameter individuals evolving over 400 generations takes about 1 day.

A successful optimization run required proper initial parameters as solutions can get stuck in local minima. For energy-efficient walking (see next paragraph), we hand-tuned the initial parameters based on our intuition about walking from similar models (Song & Geyer, 2012). During this hand-tuning process, which involved about 10 optimization runs, we encountered different solutions in local minima with substantially higher energy cost and largely different joint kinematics and kinetics. Once we had found a suitable initial parameter set, the optimization consistently converged to solutions with similar kinematics, kinetics and energetic costs. With this initial parameter set, single optimization runs were sufficient to find most of the other target behaviours. Exceptions were some of the more complex behaviours, for which we chained several optimization runs. This process used the result of one optimization in the next (for example, we used the solution for fast walking to find speed transitions from fast to slow walking), which could take up to 1 week to compute.

The cost function has a similar structure for all investigated behaviours. It consists of three parts,

(1)

with the first two parts encouraging the model not to fall down first (eqn (1)a, falling distance x_fall) and then to achieve steady locomotion (eqn (1)b). The steadiness measure d_steady is the summed differences of the relative Cartesian positions of the segment edges at touchdown. Based on previous tests, the model is considered in steady locomotion if this sum is smaller than 10 cm for six consecutive steady steps (Song & Geyer, 2012). The last part (eqn (1)c) is task specific and encourages energy-efficient locomotion (energetic cost C_E) at a target velocity 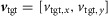, where the frontal plane target speed 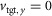, and v_avg is the average velocity over the last six steady steps. The constant 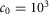ensures eqn (1)a > (1)b > (1)c. The energetic cost is calculated as 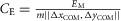, where E_M is the metabolic energy consumed by all muscles (Umberger et al. 2003), m is the body mass, and 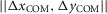is the distance travelled in the horizontal plane. The values of v_avg and C_E are calculated over the last six consecutive steps of steady walking.

Results

We first confirm that the proposed reflex circuitry reproduces human walking behaviour (Figs 4 and 5), then explore the contributions of the individual control modules (Figs 5 and 6), and finally show the versatility of the reflex circuitry in generating other locomotion behaviours by supraspinal modulation (Fig.7).

Figure 4. Kinematics and dynamics for walking at 1.2 m s⁻¹ in humans (grey traces) and the 3-D neuromuscular model (black traces) over a normalized gait cycle.

Stance lasts from 0% to about 60%. The panels show the roll, pitch and yaw of the trunk with respect to the world frame (A, compare Fig.1), the leg joint angles and torques (B), and the ground reaction forces in fore–aft (x), mediolateral (y), and vertical directions (z) (C). The grey areas (i–iv) highlight key differences between model and human data. Human data adapted from Rose et al. (2006) (angles), Eng & Winter (1995) (torques) and Damavandi et al. (2012) (GRFs). R, cross-correlation values (Wren et al. 2006).

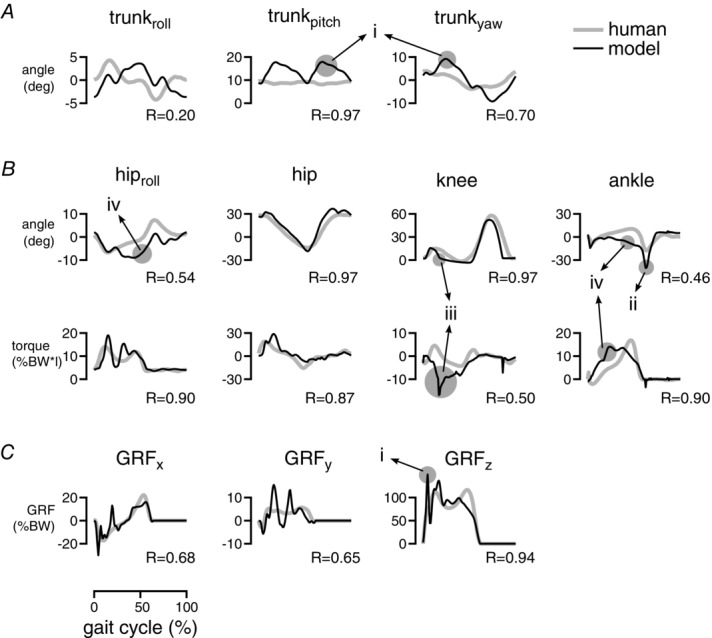
Figure 5. Comparison of muscle activations in normal walking.

A, human muscle activations for the 11 muscle groups of the model estimated from low-pass-filtered surface electromyograms (adapted from Perry & Burnfield, 2010). B, model-predicted muscle activations with coefficients of correlation (R) between model and human data. C, contributions of individual control modules M_i to the activation of selected muscles (S₀, prestimulation contribution). Net activation in B is the sum of the contributions and saturated within 0% and 100%. Shaded backgrounds indicate stance phase with double supports in a darker hue. Compared muscles: (i) gluteus medius, (ii) adductor magnus, (iii) adductor longus, (iv) gluteus maximus, (v) semimembranosus, (vi) vastus lateralis. R, cross-correlation value.

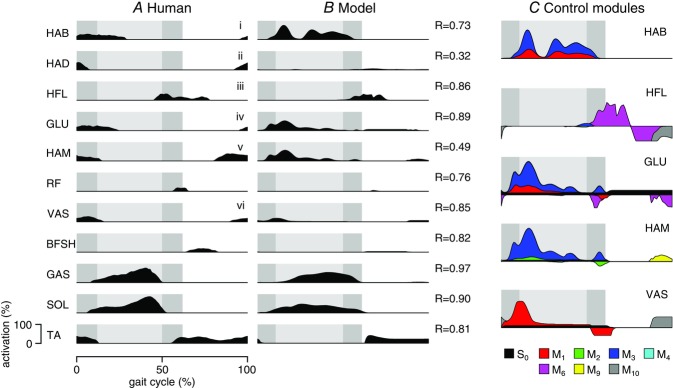
Figure 6. Peak contributions of spinal modules to individual muscle activations in steady (grey) and disturbed walking (black).

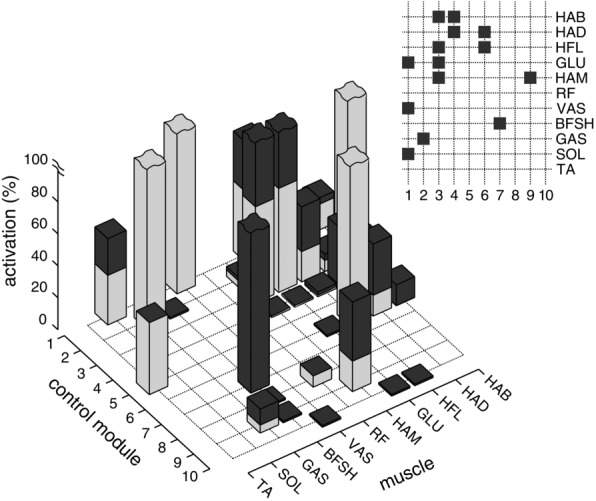
Control modules with peak increases of more than 20% are indicated in the grid.

Figure 7. Behaviour diversity.

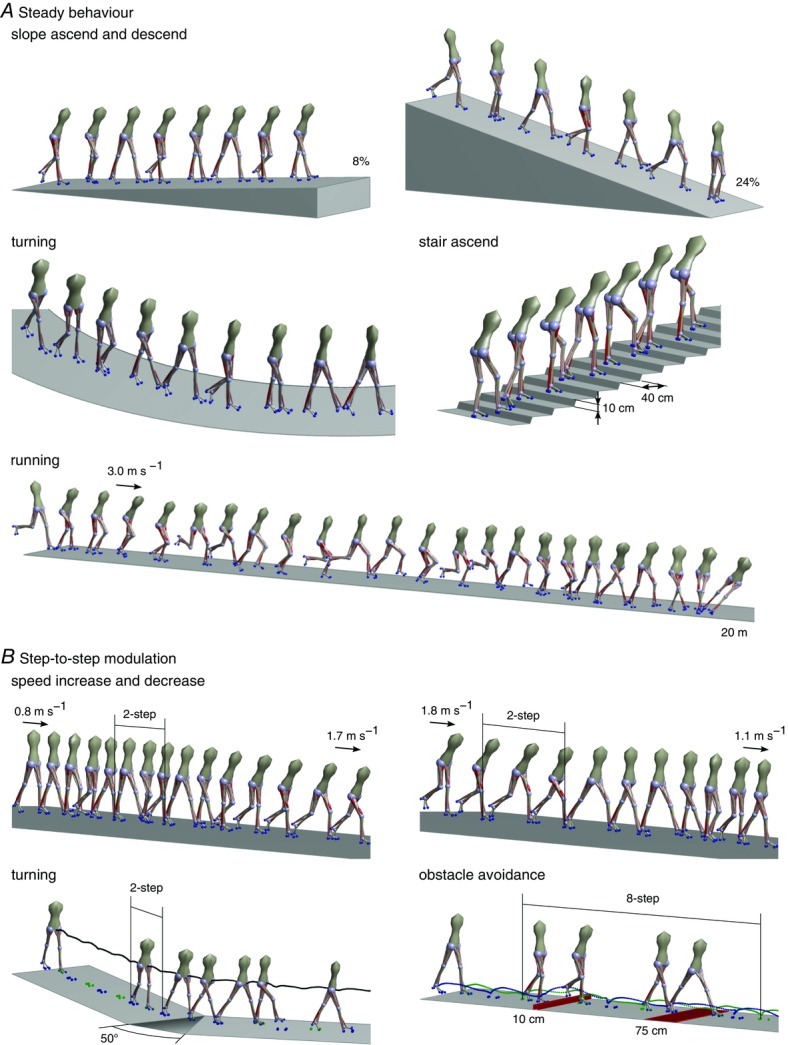
Snapshots of the human neuromuscular model during steady (A) and transitional behaviours (B) are shown.

Quality of walking behaviour

The reflex circuitry generates walking with overall human-like kinematics, dynamics and muscle activation patterns, although the energy optimization leads to a lower quality match than obtained in the previous work (Geyer & Herr, 2010). Figure4 shows the joint kinematics and dynamics and the GRFs obtained from optimizing the control parameters with the cost function (eqn (1)) for a normal human walking speed of 1.2 m s⁻¹. Some differences to the human walking patterns are introduced by the simplified structure of the skeletal model. For instance, the reduction of the entire upper body to a rigid segment neglects soft, force-buffering structures in the human trunk and leads to higher impact forces and larger trunk motions after heel strike (Fig.4 (i)). Also, the lack of a toe segment results in more plantar flexion in late stance (ii). These differences (i and ii) have also been observed in the previous, planar model (Geyer & Herr, 2010). However, the energy optimization introduces additional differences. The model now tends to straighten the knee early in stance (iii), known to generate more energy-efficient solutions in gait optimization (Ackermann & van den Bogert, 2010; Umberger, 2010). The early straightening induces less dorsiflexion at the ankle and excessive roll at the hip (iv). Both differences (iii) and (iv) are not observed when the model is optimized to match the reference kinematics instead of minimizing the energetic cost (not shown).

With the exception of HAD, the correlation coefficients between predicted and observed activation patterns lie within the range found in human experiments (average R = 0.40–0.81 for inter-subject comparison, Wren et al. 2006) (Fig.5A and B). Compared to the previous planar model, the energy optimization slightly reduces the quality of the match for the ankle muscles (SOL, GAS and TA; R ≥ 0.80). On the other hand, the functionally improved spinal circuitry leads to a better match for the hip flexor (HFL) throughout the gait cycle (R = 0.86), now generates VAS activity in stance preparation at the end of swing, and captures the overall activation patterns of the added muscles BFSH and RF, although the onset of RF activity is late by about 10% of the gait cycle. The largest difference between predicted and observed activity occurs for the added hip adductors (HAD, R = 0.32), whose exclusive action on the hip roll DOF in the model probably over-simplifies the action and control of hip adductors in humans.

While the quality of the fit improves by including, for instance, reference kinematics in the optimization goals, energy optimization provides a sufficient cost criterion to generate overall human locomotion behaviour without requiring reference data. It thus allows us to explore the behaviours that the spinal control circuitry can produce.

Contributions of spinal modules

The spinal modules combine to shape the activation patterns of individual muscles in ways that can obscure the interpretation of electromyograms (EMGs) in experiments (Fig.5C). Some modules contribute similarly to a muscle's activation. For instance, the modules for compliant stance leg behaviour (M₁) and trunk balance (M₃) contribute similar activation profiles for HAB, suggesting that a single peak of EMG activity in humans does not have to equal a single functionality. The peak can instead result from executing multiple functional goals at the same time. Other modules compete. The HAM activity in the late double support is nearly flat (Fig.5B), because the excitation provided by the balance module M₃ is suppressed by module M₂, which protects against knee hyperextension (Fig.5C). Thus, it can be misleading to equate flat muscle EMGs with the absence of control. Finally, the late swing activities of HAM and VAS provide an example in which apparently similar activation features across muscles are generated by different control modules (the stopping module M₉ for HAM and the leg-holding module M₁₀ for VAS).

Not all of the proposed control modules seem to contribute to steady walking, however. To test if they matter, we subject the neuromuscular model to disturbances. We train the model on rough terrain (40 m long track with random height changes up to ±10 cm during the middle 20 m portion; similar to Fig.1) with the cost function (eqn (1)), searching for energy-efficient walking that can tolerate disturbances. We find that the trained control is robust enough to let the model traverse randomly generated terrains (success rate >50% up to ±6 cm terrains) as well as withstand substantial horizontal pushes (Table 1) with a steady state gait that is slightly faster than before (1.4 m s⁻¹ vs. 1.2 m s⁻¹) and less energy optimal (metabolic cost of 6.2 J kg⁻¹ m⁻¹ vs. 5.0 J kg⁻¹ m⁻¹). Note that the model can be trained to walk on rougher terrain, but the resulting gait clearly deviates from normal locomotion and is not investigated here. We then subject the trained model to walking on flat and rough terrain and record the peak muscle activations that each module contributes.

Table 1.

Ground tolerance and push resistance for the neuromuscular controller trained on one ±10 cm terrain

A. Ground tolerance
Roughness (cm)	±0	±2	±4	±6	±8	±10
Survival rate (%)	100	90	80	55	15	0
B. Push resistance
Time (% gait cycle)	0	10	20	30	40
Forward (N s)	54	32	52	54	72
Backward (N s)	50	36	54	86	82
Medial (N s)	26	12	10	24	18
Lateral (N s)	12	8	10	32	50

Part A shows the survival rates on 20 randomly generated test terrains of different maximum step size, and part B the largest impulse (variable force, fixed time interval of 200 ms) that can be applied to the pelvis in different directions and times of the gait cycle.

The comparison shows that some swing leg modules which do not seem needed in steady walking become important when rejecting disturbances (Fig.6). At no instant in steady walking (grey bars) did the modules M₄, M₇ and M₁₀ contribute more than 2% of activation to any muscle. All three modules are related to swing leg control with M₇ supporting early knee flexion, M₁₀ holding the leg before stance, and M₄ compensating for moments induced on the trunk (Fig.3). Their negligible activities reveal that the optimization converged on an energy-efficient solution with a nearly passive knee in swing. Although this ballistic walking style (Mochon & McMahon, 1980) makes these modules seem unneeded, they become highly active in rough terrain (black bars), playing a major part in placing the swing leg (M₇, encountered peak activation of 100%) and stabilizing the trunk (M₄, 36% peak activation). Module M₁₀ is the exception. It does not meaningfully increase peak activity (1%), suggesting that the human stance preparation of hip and knee extensors (Perry & Burnfield, 2010) is not critical to gait robustness.

Behaviour diversity

The proposed spinal control modules are sufficient to generate a range of steady and unsteady locomotion behaviours observed in humans (Fig.7). Characteristic human locomotion behaviours range from walking and running to stair and slope negotiation to turning and deliberate obstacle avoidance. Optimization for different terrains with the cost function eqn (1) identifies control parameter sets that generate steady behaviours, including slope ascent (≤8%) and descent (≤24%) as well as stair ascent (10 cm risers with 40 cm treads). With different target speeds in eqn (1)c, the control network further generates walking at speeds ranging from 0.8 m s⁻¹ to 1.8 m s⁻¹ (not shown), which covers human slow and fast walking (Murray et al. 1984), and running steps at 3 m s⁻¹, although the model falls after about 20 m Fig.7A. In addition, using different constant parameter sets for the left and right leg (and replacing the velocity term in cost function in eqn (1)c with a cost term that seeks to maximize the change in trunk yaw), the control generates steady turning motions with the smallest radius of about 6.5 m. (The lack of yaw joints in the hips of the model probably prevents smaller radii as it has to slide about the stance foot to produce yaw motion. This shortcoming affects the performance of most behaviours. In humans, the internal yaw joints of the hips and trunk are used even in normal walking (Stokes et al. 1989). It is likely that adding these internal DOFs would help the model to achieve sharper turns, a larger range of walking speeds, and stable running (see below).)

To test whether the control architecture of the spinal modules produces unsteady locomotion behaviours, we allow the optimization to change the control parameter sets at heel strike between individual steps (Fig.7B). With two such step changes in the control parameters, the model can make large changes in walking speed from 0.8 m s⁻¹ to 1.7 m s⁻¹ and from 1.8 m s⁻¹ to 1.1 m s⁻¹, and change the walking direction with a maximum turning angle of 50 deg. In both cases, the speed and direction changes appear only after the steps with the control parameter changes, suggesting that earlier steps should not be overlooked in gait analysis when studying these behaviours. Expanding the control changes to multiple steps, the model can also avoid obstacles by increasing the foot ground clearance or the step size. For example, in the sequence shown in Fig.7B, the model approaches from steady walking, passes within eight steps of altered control a 10 cm high obstacle followed by a 75 cm wide obstacle, and then returns to steady walking.

Except for stair walking and running, all steady and unsteady behaviours have been generated without changing individual muscle reflex parameters in swing. It is sufficient to keep the swing reflex parameters used for energy-efficient walking, and to generate the different swing leg behaviours by altering the supraspinal commands of the desired minimum leg length, l_clr, and the desired target leg angle, α_tgt. (Note that since only the swing leg control is structured in a hierarchy with few supraspinal parameters, we always allowed the optimization to change all stance reflex parameters.) For instance, down slope walking was generated using the smallest desired leg length, l_clr = 75 cm, whereas normal walking used l_clr = 87 cm. Similarly, target angles ranged from 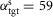deg in fast walking to 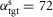deg for descending slopes. In contrast, for walking upstairs and running adjusting only l_clr and α_tgt was insufficient. For these behaviours the gains of the feedback pathways which stimulate HFL in M₆ needed to be largely increased, because a stronger hip swing is required to lift the thigh up in walking upstairs and to rapidly advance the leg in running. This additional adjustment suggests that the intensity of the swing should be part of the supraspinal control layer.

The optimization did not find a solution for walking down stairs (10 cm risers and 40 cm treads), pointing to a limitation of the current stance leg control. To lower the centre of mass down stairs, leg propulsion in late stance needs to be tempered, which could be achieved by lowering the feedback gains in module M₁ during the late stance phase. However, this gain adjustment will require organizing the stance control into a hierarchy with supraspinal modulation.

Changes in the optimized reflex gains for the different behaviours reveal several functional candidates for such a supraspinal modulation of the stance control. One candidate for supraspinal modulation is the target trunk lean, θ_tgt, in the balance module M₃. For instance, walking up stairs required a target trunk pitch of 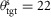deg as compared to 2–7 deg for all other behaviours. Including the target trunk lean in the supraspinal control layer seems a natural choice given that it is related to the vestibular and vision systems. Another candidate is the modulation of the force feedback gain of VAS, which tends to increase for walking behaviours with higher leg impacts (walking fast, down slope, or on rough terrain). The force feedback of VAS is part of module M₁ responsible for generating compliant leg behaviour. Changing the VAS gain will change the leg stiffness, a functional adaptation important to human locomotion (Ferris et al. 1998; Lipfert et al. 2012).

Discussion

We proposed a specific neural circuitry involved in the spinal control of human locomotion behaviours. The circuitry is organized in 10 muscle-reflex modules that realize limb functions essential to legged systems in stance and swing. We then implemented these modules in a three-dimensional human neuromuscular model in combination with a supraspinal control layer that adjusts the desired foot placements and adapts some of the reflex gains. Using optimization of the model's control parameters, we found in simulation that this circuitry suffices to generate steady behaviours from walking, turning and running to slope and stair negotiation, as well as unsteady behaviours such as large speed transitions and obstacle avoidance. The results suggest that, for human locomotion behaviours, the muscle synergies located in the spinal cord are composed more of sensory feedback circuits than of circuits stimulating muscles in a fixed pattern.

The role of sensory feedback in the activation and organization of muscle synergies remains debated. The analysis of muscle activity patterns in frog swimming and jumping before and after deafferentiation suggests that these behaviours are generated largely by centrally organized, fixed balance synergies (Cheung et al. 2005; Bizzi & Cheung, 2013). For humans, on the other hand, experiments with spinal-cord-injured patients demonstrate that sensory feedback integration is essential to the generation of locomotion behaviours (Sinkjær et al. 2000; Dietz, 2002; Harkema, 2008; Harkema et al. 2011). Our modelling results suggest how this sensory feedback integration may be organized in specific functional modules.

The proposed neural circuitry is not unique but plausible. The neurophysiological plausibility of some of the proposed reflex pathways is discussed in Geyer & Herr (2010). However, the human nervous system receives input from a vast sensory network, and the afferent pathways that we used to embed specific functions of legged locomotion can probably be replaced by alternative pathways transmitting similar information. Experimental methods which can either probe the proposed pathways or elicit characteristic mechanical or EMG responses (Sinkjær et al. 2000; Cronin et al. 2009; Hof & Duysens, 2013) will be necessary to test the specific modules.

One such method probing the spinal reflex network is epidural stimulation. Continuous epidural stimulation of the lumbosacral cord has been shown to restore standing and assisted stepping in patients with spinal cord injury (Harkema et al. 2011; Angeli et al. 2014). These experiments and computational models of transcutaneous electrical stimulation of the lumbar spine (Holsheimer, 2002; Capogrosso et al. 2013) indicate that epidural stimulation alters the physiological state of the injured spinal cord, primarily exciting afferent fibres and their corresponding neural circuits. The method has also been applied in experiments with unimpaired human subjects to elicit monosynaptic reflexes and study their modulation during locomotion (Minassian et al. 2007; Courtine et al. 2007). Figure8 compares the resulting modulation of the responses during walking in a number of leg muscles studied with epidural stimulation by Courtine et al. (2007) to the modulations predicted by our model when subjected to simulated epidural stimulation experiments. Although for several muscles deviations occur in phases of the gait cycle (initial stance and late swing for VAS and GAS), the modulations show similar patterns overall, supporting the plausibility of the proposed neural circuitry in walking. Further comparisons will be required to probe if this similarity extends to other locomotion behaviours, or if alternative control models can predict a similar response to epidural stimulation.

Figure 8. Muscle responses to epidural stimulation in walking.

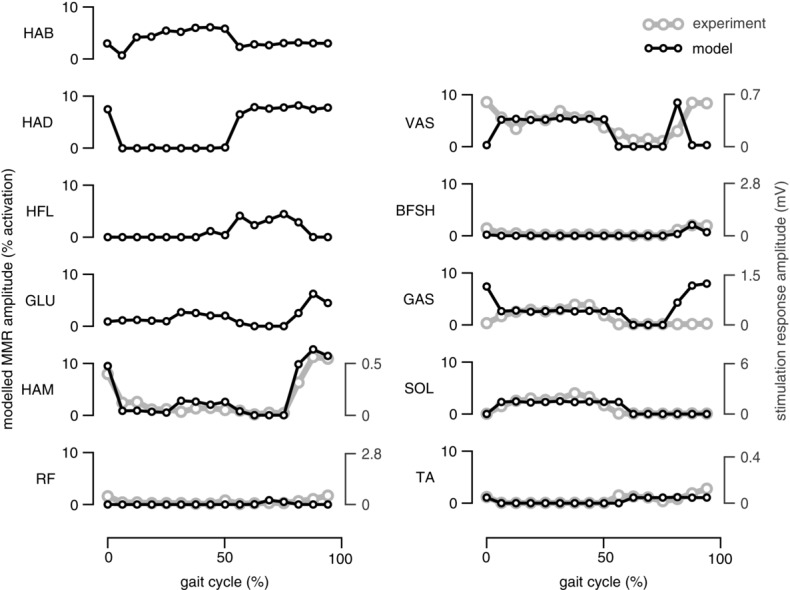
Model-predicted responses to epidural stimulation (black traces) are compared to human experimental data (grey traces) adapted from Courtine et al. (2007). In humans, changes in muscle EMG are observed for several leg muscles when electrical stimulation is applied transcutaneously to the lumbar spine. The peak-to-peak amplitude of these changes varies with the phase of the gait cycle in which the epidural stimulation is applied (divided into 16 phases, marked in open circles, no responses reported for the hip muscles). In the simulation, epidural stimulation is mimicked as 20 ms square-wave impulses simultaneously applied to all afferent pathways at the beginning of each phase of the gait cycle. The resulting peak-to-peak amplitude change in the muscle activations is shown.

Most of the alternative control models of human locomotion emphasize CPGs at the core of the spinal control circuitry (Taga et al. 1991; Taga, 1998; Ogihara & Yamazaki, 2001; Hase et al. 2003; Paul et al. 2005; Kim et al. 2011). From a theoretical standpoint, CPGs provide the advantage of a feedforward drive at the cost of being sensitive to external disturbances when compared to feedback control (Kuo, 2002). The sensory feedback network, on the other hand, shows large robustness to external disturbances (Table 1 and Figs1 and 6) but depends on the interaction with the mechanical environment to drive forward. One way to combine the advantages of both approaches is to understand CPGs as observers of feedback control rather than sole generators of limb motion. Kuo (2002) has shown that such an interpretation can improve the performance for systems subject to unexpected disturbances and sensory noise. Motivated by this idea, Dzeladini et al. (2014) combined the previously developed reflex model for planar locomotion (Geyer & Herr, 2010) with morphing central pattern generators that can learn to predict the sensory output generated by the reflex model. They found that the combined model can regulate walking speed by changing only a few CPG parameters, indicating how CPGs could function as an internal drive and speed control mechanism in a primarily reflex-based control network.

Glossary

BFSH

short head of biceps femoris

CE

contractile element

COM

centre of mass

CPG

central pattern generator

DOF

degree of freedom

EMG

electromyogram

GAS

gastrocnemius

GLU

glutei

GRF

ground reaction force

HAB

hip abductor

HAD

hip adductor

HAM

hamstring

HFL

hip flexor

MTU

muscle tendon unit

PE

parallel elasticity

RF

rectus femoris

SE

series elasticity

SOL

soleus

TA

tibialis anterior

VAS

vastii

Appendix A

Musculoskeletal parameters

The properties of the segments, muscles and musculoskeletal attachments are defined based on physiological data (Chandler et al. 1975; Yamaguchi et al. 1990; Visser et al. 1990; Günther & Ruder, 2003; Arnold et al. 2010; Geyer & Herr, 2010; McCullough et al. 2011) and shown in Tables 2, 3 and 4, respectively. The segment parameters include the dimension of the segment d_S, the distance of the joints d_J the segment is connected to, the position of the centre of mass d_G, the mass m_S, and the inertia around the principal axes 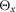, 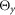and 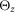. The values d_S, d_J and d_G are defined either as height (h), length (l) or width (w) as measured from the distal part of the segment for the human model standing straight up. The individual muscle parameters reported in Table 3 are the maximum isometric force F_max, the maximum contraction velocity v_max, the optimum fibre length l_opt, and the tendon slack length l_slack. The remaining muscle parameters common to all muscles are the same as in Geyer & Herr (2010). The moment arms of HAB, HAD, HFL, GLU, HAM_hip, HAM_knee, RF_hip and BFSH are assumed to be constant, 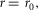leading to muscle length changes 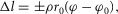where ρ accounts for the pennation angle of the MTU and φ₀ is the reference joint angle when the MTU is at its rest length 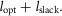For RF_knee, VAS, GAS_knee, GAS_ankle, SOL and TA variable moment arms 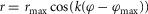are assumed with corresponding muscle length changes 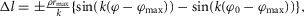where 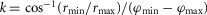is a scaling factor defined by the maximum and minimum moment arms, r_max and r_min, at corresponding angles, φ_max and φ_min. The joint angles are defined so that positive angles indicate extension of the pitch joints and abduction of the roll joints. The zero angle configuration corresponds to a pose of the human model where all the foot contact points lie on the ground plane, the shank, thigh and trunk segments are parallel to the ground plane, and the ankle and hip point backwards while the knee and head point forward. For example, when standing upright, the ankle joints are at 90 deg, the knee and hip pitch joints are at 180 deg, and the hip roll joints are at 0 deg.

Table 2.

Segment parameters

	Trunk	Thigh	Shank	Foot
dS (cm)	80 (h)	46 (h)	46 (h)	20 (l) 8 (h)
dJ (cm)	20 (w)	46 (h)	46 (h)	16 (l) 8 (h)
dG (cm)	35 (h)	28 (h)	28 (h)	14 (l) 7 (h)
mS (kg)	53.5	8.5	3.5	1.25
Θx (kg m2)	4.0	0.15	0.05	0.0007
Θy (kg m2)	2.5	0.15	0.05	0.005
Θz (kg m2)	1.0	0.03	0.003	0.005

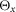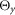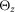d_S, the dimension of the segment; d_J, the distance of the joints the segment is connected to; d_G, the position of the centre of mass; m_S, the mass; , and , the inertia around the principal axes. h, height; l, length; w, width.

Table 3.

Muscle parameters

	HAB	HAD	HFL	GLU	HAM	RF	VAS	BFSH	GAS	SOL	TA
Fmax (kN)	3	4.5	2	1.5	3	1.2	6	0.35	1.5	4	0.8
vmax (lopt s−1)	12	12	12	12	12	12	12	12	12	6	12
lopt (cm)	9	10	11	11	10	8	8	12	5	4	6
lslack (cm)	7	18	10	13	31	35	23	10	40	26	24

F_max, maximum isometric force; v_max, the maximum contraction velocity of the CE; l_opt, the optimal CE length; l_slack, the SE slack length.

Table 4.

Musculoskeletal attachment parameters

	Hip						Knee					Ankle
	HAB	HAD	HFL	GLU	HAM	RF	HAM	RF	VAS	BFSH	GAS	GAS	SOL	TA
r0 (cm)	6	3	8	8	8	8	5	—	—	4	—	—	—	—
rmax (cm)	—	—	—	—	—	—	—	6	6	—	5	6	6	4
rmin (cm)	—	—	—	—	—	—	—	4	4	—	2	2	2	1
φmax (deg)	—	—	—	—	—	—	—	165	165	—	140	100	100	80
φmin (deg)	—	—	—	—	—	—	—	45	45	—	45	180	180	180
φ0 (deg)	10	15	160	120	150	170	180	125	120	160	165	80	90	110
ρ	0.7	1	0.5	0.5	0.5	0.3	0.5	0.5	0.6	0.7	0.7	0.7	0.5	0.7

r₀, constant moment arm; r_max and r_min, the maximum and minimum moment arms, with corresponding angles, ϕ_max and 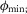ϕ₀, the reference joint angle when the MTU is at its rest length 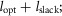rho, the pennation angle of the MTU.

Appendix B

Reflex control equations

Reflex pathways that are frequently used in the control network include force feedback (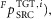 length feedback ( 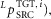velocity feedback ( 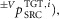proportional-derivative feedback ( 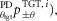and co-stimulation ( 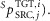The general structure of these pathways is shown in eqn (A1),

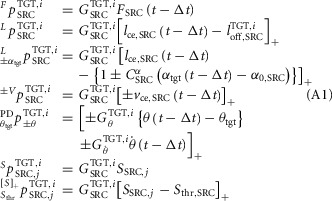where the left superscript indicates the type of the pathway, the right superscript specifies the target muscle (TGT) stimulated by the pathway and the control module (i) the pathway belongs to. The right subscript shows the signal origin as either the source muscle (SRC) or the trunk lean θ. In addition, for the length and co-stimulation pathways a left subscript indicates feedback modulation by either the swing-leg target angle (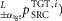 or the co-stimulation threshold ( 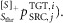The symbol [...]₊ indicates that only the positive values of the term in the bracket are used. With this notation system, the reflex pathways that generate the muscle stimulations are given below for each muscle individually:

HAB

HAD

HFL

GLU

where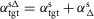

HAM

RF

VAS

BFSH

where 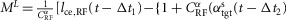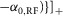and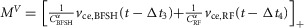

GAS

SOL

TA

where S_{TA, 5, st} is only active during stance (st).

The swing leg control trigger events (Sw₁–Sw₄, in Fig.3) are modelled as:

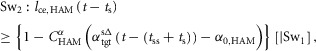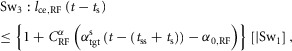where [|Sw₁] in Sw₂, for example, indicates that Sw₂ gets triggered only if Sw₁ is already triggered in the swing phase.

Additional information

Competing interests

None declared.

Author contributions

Both authors designed the research, drafted the article, and approved the final version of the manuscript. S.S. implemented the computational model and conducted the simulation studies.

Funding

This work was supported in part by the National Science Foundation (NSF) through the NSF Engineering Research Center (ERC) for Quality of Life Technology (EEC 0540865) and by the NIH through the NICHD National Center for Medical Rehabilitation Research (1R01HD075492).

Supporting information

The following supporting information is available in the online version of this article.