Diseased Region Detection of Longitudinal Knee Magnetic Resonance Imaging Data

Abstract

Magnetic resonance imaging (MRI) has become an important imaging technique for quantifying the spatial location and magnitude/direction of longitudinal cartilage morphology changes in patients with osteoarthritis (OA). Although several analytical methods, such as subregion-based analysis, have been developed to refine and improve quantitative cartilage analyses, they can be suboptimal due to two major issues: the lack of spatial correspondence across subjects and time and the spatial heterogeneity of cartilage progression across subjects. The aim of this paper is to present a statistical method for longitudinal cartilage quantification in OA patients, while addressing these two issues. The 3D knee image data is preprocessed to establish spatial correspondence across subjects and/or time. Then, a Gaussian hidden Markov model (GHMM) is proposed to deal with the spatial heterogeneity of cartilage progression across both time and OA subjects. To estimate unknown parameters in GHMM, we employ a pseudo-likelihood function and optimize it by using an expectation-maximization (EM) algorithm. The proposed model can effectively detect diseased regions in each OA subject and present a localized analysis of longitudinal cartilage thickness within each latent subpopulation. Our GHMM integrates the strengths of two standard statistical methods including the local subregion-based analysis and the ordered value approach. We use simulation studies and the Pfizer longitudinal knee MRI dataset to evaluate the finite sample performance of GHMM in the quantification of longitudinal cartilage morphology changes. Our results indicate that GHMM significantly outperforms several standard analytical methods.

I. Introduction

Osteoarthritis (OA) known as degenerative arthritis represents a group of mechanical abnormalities involving degradation of joints, including articular cartilage and subchondral bone. Symptoms include swelling, pain, discomfort, locking, and other problems in mobility and are often characterized by the progressive loss of joint cartilage [1]. Bone may be exposed and damaged without the protection of cartilage. Figure 1 shows the anatomy of the human knee and illustrates the cartilage loss. OA is the most common form of arthritis and a major cause of chronic disability in the United States [2]. It is estimated that more than 16% of all adults 45 years or older suffer from symptomatic OA of the knee [1]. Cartilage loss [3] is believed to be the dominating factor in OA. Studying cartilage morphological changes can help to understand OA progression and drug development.

Fig. 1.

Anatomy of human knee and illustration of cartilage loss. (left) A sagittal slice of a healthy knee. Bones are annotated in blue, femoral cartilage in purple and tibial cartilage in orange. (middle) A coronal slice of the same healthy knee. (right) A coronal slice of an OA knee with cartilage loss indicated by the red arrow.

In recent years, magnetic resonance imaging (MRI) has increasingly been used in OA diagnosis [4], [5], since MRI offers the distinct advantage of detecting signal and morphologic changes in articular cartilage in 3D. MRI is the most sensitive and accurate test for evaluating the articular cartilage noninvasively [6]. Particularly, MRI can demonstrate reactive bone edema or soft tissue swelling as well as small cartilage or bone fragments in the joint. However, little is known about the development of such cartilage lesions and their natural progression.

Recently, several large MRI databases have been acquired for OA research in order to help understand the progression of cartilage loss across OA subjects and to identify risk factors (such as genetics, dietary intake, and muscle weakness) associated with such loss [7]–[10]. For example, the Pfizer A9001140 is a longitudinal study, including baseline, 3-month, 6-month, 1-year and 2-year follow-up images of a single knee from 155 subjects [7], [8]; the Osteoarthritis Initiative (OAI) is another longitudinal cohort study of risk factors for incidence and progression of OA, where 4796 subjects with or at high risk of knee OA were recruited and image data was collected annually during 4 years of follow-up [9], [10]. Moreover, analyzing such large MRI datasets is necessary to establish knowledge about the expected pace of progression in knees with different exposure to risk factors for structural progression (e.g. radiographic joint space narrowing [JSN]). Such knowledge can then be used for the design of interventional trials.

Statistical analysis of cartilage thickness changes faces two major challenges. The first one is the lack of spatial correspondence across subjects and/or time. Observational studies have shown that cartilage loss in OA may not be uniform throughout the cartilage [11], and advanced statistical analysis methods are necessary to understand localized cartilage thinning. However, the localized analysis requires establishing spatial correspondence across time and subjects, and such analysis is challenging due to the small volume of cartilage in relation to the rest of the knee. The second challenge is the spatial heterogeneity of cartilage progression across subjects. Cartilage thinning may happen at different locations in different subjects, which is usually caused by biomechanical factors [12] or local risk factors [13]. Cartilage thinning at a particular location may only be consistent for a subset of the full subject population. Thus, treating all OA subjects equally and using all of them for standard statistical methods (such as voxel-wise analysis and region-of-interest analysis) would be problematic. In clinical practice, some non-surgical treatments for OA in the knee (e.g., corticosteroid injections) are most likely administered via injection and act globally [14] since the exact locations of lesions are unknown. Therefore, it is of great interest to propose some methods to detect such locations and refine these treatments.

Subregion-based analysis and the ordered value approach are two major statistical methods for quantifying cartilage thickness changes. Subregion-based analysis is one of the most popular approaches. Here, average thickness changes in defined anatomic subregions of the femorotibial joint are studied. In [15], the tibial cartilage was divided into a central area of the total subchondral bone area, and anterior, posterior, internal, and external subregions surrounding it. However, this approach is problematic due to the spatial heterogeneity of cartilage progression discussed above. In another region-wise statistical analysis method [16], a region partitioning process is performed by using a supervised machine learning framework on anatomically aligned medial tibial and medial femoral cartilage thickness maps, and then a point distribution model is used to establish spatial correspondence and a common coordinate system. However, their machine learning procedures are only implemented on the thickness maps at baseline. Buck et al. [17] proposed an ordered value approach by sorting subregional changes within each knee by ascending order to focus on the magnitude of the thickness irregardless of the location, in which subregion the change occurs in each subject. The ordered value approach was demonstrated to provide improved discrimination between healthy subjects and OA participants longitudinally [17]. The key advantage of the ordered value approach is to remove the link between the spatial location and the magnitude/direction of the change in cartilage thickness. But the ordered value approach still relies on subdivisions of the cartilage and the average thickness within each subregion. The subdivisions of the cartilage are purely geometric, and small local changes (that happen to a smaller region than the size of a subregion) can be difficult to recover, since they may be weakened by averaging over a large subregion. Therefore, to fully understand the spatial pattern of OA progression, it is necessary to pinpoint localized cartilage thickness changes.

The paper is organized as follows. Section II summarizes the image preprocessing pipeline and the key contributions in this paper. Section III introduces a novel Gaussian hidden Markov model (GHMM) and its related EM algorithm. In Section IV, simulation studies are performed to show the advantages of our proposed model in diseased regions detection. Section V applies GHMM to the 2D thickness maps derived from the 3D MRI data of the Pfizer Longitudinal Study (PLS-A9001140).

II. Image Preprocessing and Main Contributions

In this paper, the 3D knee MR images are preprocessed via a set of four image analysis steps including (I.1) segmentation, (I.2) 3D thickness map computation, (I.3) registration, and (I.4) thickness map projection. These four methods summarized in Fig. 2 can successfully establish spatial correspondence across subjects and/or time and therefore address the first challenge in statistical analysis of cartilage thickness changes.

Fig. 2.

Path diagram of the 3D knee MR image data preprocessing toolbox: ➀ extracting the joint region and obtaining the cartilage segmentation; ➁ computing the 3D cartilage thickness map; ➂ registering all thickness maps to a common atlas space; and ➃ projecting 3D thickness map onto a 2D plane.

The main contributions of this paper include (i) a statistical method based on GHMM to appropriately address the spatial heterogeneity of cartilage progression across OA subjects and quantify their longitudinal cartilage morphology changes and (ii) a systematic evaluation of our analysis method by using simulations and real data analysis. Moreover, we have developed companion software for GHMM and will release it to the public through http://www.nitrc.org/ and http://www.bios.unc.edu/research/bias.

The path diagram of GHMM is presented in Fig. 3. Specifically, a novel hidden Markov random field (HMRF) [18]–[27] is proposed to specifically discover the diseased regions for each OA subject and to integrate cartilage progression in different diseased regions with different change magnitudes/directions across OA subjects. Moreover, based on the correspondence established in the preprocessing step, our GHMM allows us to carry out a localized analysis of longitudinal cartilage thickness at each voxel. Therefore, GHMM integrates the strengths of both the local subregion-based analysis and the ordered value approach in a single framework.

Fig. 3.

Path diagrams of GHMM component. (a) Path diagram of GHMM for four different subjects (one normal control and three OA subjects). The change of the map thickness at pixel site k includes three parts in the proposed model, i.e., (i) the common dynamic change in both normal controls and OA subjects, (ii) the change caused by random effects and measurement errors, and (iii) the change caused by different diseased regions (moderately diseased region (yellow) and severely diseased region (red)). (b) Path diagram of GHMM for one subject at two neighboring pixel sites across time. Following the convention of path diagrams, observed variables are framed with rectangles whereas latent variables are framed with ellipses. Regression associations are depicted as (solid) one-headed arrows (parent=predictor, child=response); correlations between diagnosis result, the diseased region label and the observed thickness are described as (dotted-dashed) one-headed arrows; and the correlation of diseased region labels in the Potts model is shown as (solid) double-headed arrow. For easier interpretation, the following color-codes are used: exogenous variables (light red), endogenous variables (purple), continuous latent variables (blue), discrete latent variables (green), and measurement errors (yellow).

III. Background and Methods

A. Cartilage Segmentation

Cartilage segmentation in the knee has been investigated for several decades. Many segmentation approaches have been proposed, e.g., region growing methods [28], [29], watershed methods [30], live wire methods [31], active contour methods [32], [33], and graph cut methods [34]. However, all the aforementioned methods are semi-automatic, which precludes their applications to large image databases. Recently, several automatic methods have been proposed for cartilage segmentation, including pattern recognition methods [35], model-based segmentation method [36], and graph-based method [37]. However, the spatial interactions between neighboring pixels are neglected in [35]; the model-based segmentation method [36] is prone to local minima in the fitting process; the graph-based method [37] generally suffers from grid bias, also known as metrication errors.

Here we applied the automatic cartilage segmentation method [38], which is an extension of the multi-atlas segmentation approach initially proposed by us for cartilage segmentation in [39]. The main difference in these two cartilage segmentation approaches is how label-fusion is achieved once multiple segmentation candidates (from the multiple atlases) are available. In [39], a simple locally weighted label-fusion strategy was used, whereas in [38] the locally weighted label-fusion was compared to the baseline majority-voting approach and a more advanced non-local patch-based label fusion approach was also investigated. The latter approach turned out to be superior to the other two label-fusion strategies. In general, the segmentation method [38] has the following advantages. First, the method is fully automatic and requires no user interaction (besides quality control). Secondly, the method is robust as it benefits from multi-atlas-based strategies. Thirdly, both spatial and local appearance information are utilized in the segmentation. Local tissue classification is probabilistic (unlike [35]) and combined with the spatial prior to generate the final segmentation within a segmentation model. Furthermore, the segmentation model is convex and thus allows for the computation of global optimal solutions which cannot be guaranteed by active contour models, active shape models or active appearance models. The segmentation model also allows for the incorporation of spatial and temporal regularization.

The approach that we use for segmenting cartilage and to compute local thicknesses works in a three-dimensional (3D) space. Specifically, our segmentation produces a 3D label map for femoral and tibial cartilage. Given a segmentation, we compute thickness using a Laplace-equation approach [40] through which we define a top and a bottom of the structure and correspondence lines between them. Each point on such a correspondence line is then assigned the thickness value (distance between beginning and end of this line) resulting in a 3D distance map. It should be noted that, all the segmentations are performed for each subject independently and in their own untransformed coordinate systems to avoid any bias introduced by resampling the image. For the same reason, the thickness maps are computed in the native image spaces obtained from cartilage segmentations.

Once these measures have been computed, population comparisons require a common coordinate system for the statistical analysis across time-points and subjects, which requires an additional registration step to this common space. Note that this may cause slight local distortions (depending on the quality of the registration), but it will not change the actual thickness measures as they are computed in the native image spaces. Here, we have used an affine transformation followed by a B-Spline transform based on the bone segmentations for each cartilage thickness volume. Since we are dealing with sheet-like structures, which we have approximately axis-aligned in atlas space, we simply compute the local median values of this 3D thickness map in the axial directions, where thicknesses are approximately constant.

B. Gaussian Hidden Markov Model

We consider a longitudinal thickness map dataset with thickness data {y_ij(s_k) : k = 1, …, m} measured at time t_ij for j = 1, …, T_i and i = 1, …, n, where n is the total number of subjects, S₀ = {s₁, …, s_m} is the set of m pixels in a common template, denoted by , and T_i is the total number of time points for the i-th subject. Let x_i represent disease status of OA for each subject such that x_i = 0 and 1, respectively, represent normal control and patient with OA.

We introduce a latent partition of for each subject. Specifically, it is assumed that for the i–th subject, can be decomposed into the union of normal region R_i0, moderately diseased region R_i1, and severely diseased region R_i2, that is

$$\mathcal{S}=R_{i0}\cup R_{i1}\cup R_{i2}\text{and}{R}_{ic}\cap R_{i{c}^{\prime }}=\varnothing \text{for}c\ne c^{\prime }.$$

Here we also assume that normal controls are expected to be perfectly healthy, i.e. to not have any cartilage loss or lesions. Then, both R_i1 and R_i2 should be the empty set for normal controls. For OA patients, the size and location of R_i1 and R_i2 may vary across subjects and play a critical role in establishing spatial correspondences of diseased regions at different locations across subjects. Statistically, we introduce an unobserved random effect b_i(s_k) ∈ L = {0, 1, 2} to label R_i0, R_i1, and R_i2 at each pixel s_k of for the i–th subject. Thus, b_i(s_k)s are label configurations of three nonoverlapping regions {R_i0, R_i1, R_i2}. It is also possible to extend GHMM to the scenarios with more than two types of diseased regions.

Our Gaussian hidden Markov model consists of a spatial random effect model and a Potts model [20], [21], [23]. Spatial random effects models (SREM), also called hidden Markov models, are very useful for image segmentation and restoration in image analysis [18], [19], [22], [24]–[27].

We first propose SREM to model the conditional distribution of the observed thickness maps given two sets of random effects including b_i = {b_i(s_k) : s_k ∈ } and v_i = {v_i(s_k) : s_k ∈ }, where v_i(s_k) will be defined below. We present the path diagrams of SREM in Fig. 3. Given b_i and v_i, we propose a general spatial random effect model as

$$y_{ij}(s_k)={\mathit{w}}_{ij}^T\mathit{\beta }(s_k)={\mathit{w}}_{ij}^T{\mathit{v}}_i(s_k)+{\epsilon }_{ij}(s_k)+c(x_i,{\mathit{w}}_{ij},b_i(s_k),\overline{\mathit{\alpha }}),$$ (1)

where w_ij is a q_w × 1 vector of covariates (e.g., time, gender, or genetic marker) that usually includes an intercept 1, but is independent of disease status. Moreover, β(s_k) and v_i(s_k) are both q_w × 1 vectors of regression coefficients. It should be noted that, if w_ij only comprises an intercept 1 and time, β(s_k) represents both the average thickness at baseline and average thickness change rate at time point t_ij, while the two components in v_i(s_k) indicate the individual thickness difference relative to the average thickness at baseline and the individual difference of the thickness change rate relative to the average thickness change rate at time point t_ij respectively. The c(x_i, w_ij, b_i(s_k), ᾱ) is defined as

$$c(x_i,{\mathit{w}}_{ij},b_i(s_k),\overline{\mathit{\alpha }})=\{\begin{array}{cc}0,& x_i=0,\\ \sum _{l=1}^2{\mathit{w}}_{ij}^T\overline{\mathit{\alpha }}(l)\delta (b_i(s_k),l),& x_i\ne 0,\end{array}$$

where δ(·, ·) is the Kronecker function and ᾱ = (ᾱ(1)^T, ᾱ(2)^T)^T is a 2q_w × 1 vector of coefficients, in which ᾱ(1) and ᾱ(2) respectively characterizes the dynamic thickness differences in the diseased regions R_i1 and R_i2 in addition to the dynamic thickness changes at pixel s_k in normal regions. Thus, c(x_i, w_ij, b_i(s_k), ᾱ) equals zero for all pixels for normal controls and the pixels with b_i(s_k) = 0 for OA patients. For OA patients, pixels in different diseased regions may have different dynamic thickness changes. Throughout the paper, we assume w_ij = (1, t_ij)^T, β(s_k) = (β₁(s_k), β₂(s_k))^T and set q_w = 2 for simplicity. Generally, the time measurement t_ij in the first two terms of model (1) is not required to be the same as the one in the last item of model (1). In principle, age is used as t_ij in the first two terms of (1) to capture the average thickness changes across age, whereas time to diagnosis is used in the last term of (1) to character the relative thickness changes in the diseased regions caused by OA. However, neither the age nor time to diagnosis are available in this dataset. Instead, the scan date is the only time measurement in this dataset. Since the range of thickness changes is small compared to the thickness at baseline and the time range (2 years) is also small relative to the age of each subject (all subjects are middle aged [41]), it is reasonable to use the scan date as t_ij throughout the model (1). In this paper, for each subject, the fist scan date was set to 0 and the following scan dates were calculated in years, e.g., 0.5 means six months. Therefore, it is straightforward to consider some basis functions (such as spline or wavelet) for w_ij. Moreover, ε_ij(s_k)s are independent measurement errors across subjects, time, and pixels, following $N(0,{\sigma }_{s_k}^2)$.

Second, we model the random effects b_i and v_i as follows. First, it is assumed that b_i = (b_i(s₁), …, b_i(s_m))^T and v_i = {v_i(s_k) : k = 1, …, m} are mutually independent. Moreover, v_i(s_k) are assumed to be mutually independent across pixels and v_i(s_k) follows N(0, Σ_vsk) at pixel s_k. It is assumed that b_is are independent across subjects and each b_i follows a Potts model [20], [21], [23], whose Gibbs form is given by

$$p({\mathit{b}}_i\mid \tau )=exp\{-U({\mathit{b}}_i)\tau -logC(\tau )\},$$ (2)

where U(b_i) = −Σ_sk~sl δ(b_i(s_k), b_i(s_l)) and τ is introduced to encourage spatial smoothness in homogeneous regions. Moreover, C(τ) is the partition function such that p(b_i|τ) is a probability function. The notation “Σ_si~sj” means that s_i is a neighbor of s_j and each neighboring pair enters the summation only once. Throughout the paper, we only consider the closest 4 neighbors of each pixel.

To illustrate the key ideas of GHMM, we present two path-diagrams of GHMM in Figure 3(a) and (b). Model (1) has two key novelties compared with the subregion-based analysis and the ordered value approach. As shown in the subcomponents (i) and (ii) of Figure 3(a), the first novelty is that ${\mathit{w}}_{ij}^T\mathit{\beta }(s_k)$ allows us to utilize information in all normal regions R_i0 across all normal subjects and OA patients and then carry out a localized (or pixel-wise) analysis of longitudinal cartilage thickness at each pixel. As shown in the subcomponent (iii) of Figure 3(a), the second novelty is that the use of c(x_i, w_ij, b_i(s_k), ᾱ) and ᾱ allows us to integrate information in all diseased regions R_i1 ∪ R_i2 across all subjects together and then carry out a joint analysis in the union of all moderately diseased regions ${\cup }_{i=1}^n{R}_{i1}$ (or all severely diseased regions ${\cup }_{i=1}^n{R}_{i2}$) across all OA patients.

C. Estimation Procedure

Our next problem of interest is to estimate all unknown parameters, denoted as θ, and random effects. Here θ is a vector of all unknown parameters consisting of τ, β(s_k), ᾱ, ${\sigma }_{s_k}^2$, and the covariance matrices Σ_vsk for k = 1, …, m. We decompose the parameter θ into two parts: τ, and all others, denoted as θ̄. The maximum likelihood estimate (MLE) of θ̄ can be calculated by using the expectation-maximization (EM) algorithm [42], whereas τ can be estimated by using a pseudo-likelihood method [43] since the MLE of τ is generally difficult to compute due to the normalizing part of the probability function in (2).

To derive the EM algorithm, we need the complete-data log-likelihood function of GHMM as follows. Let y_i(s_k) = (y_i1(s_k), …, y_iTi (s_k))^T, W_i = (w_i1, …, w_iTi), c̄(x_i, W_i, b_i(s_k), ᾱ) = (c(x_i, w_i1, b_i(s_k), ᾱ), …, c(x_i, w_iTi, b_i(s_k), ᾱ))^T, ${\mathbf{\sum }}_{s_k,i}={\sigma }_{s_k}^2{\mathit{I}}_{T_i}$, where I_Ti is T_i × T_i identity matrix. Thus, the distribution of y_i(s_k) conditional on random effects is given by N(z_i(s_k), Σ_ski), where z_i(s_k) is given by ${\mathit{W}}_i^T(\mathit{\beta }(s_k)+{\mathit{v}}_i(s_k))+\overline{\mathit{c}}(x_i,{\mathit{W}}_i,b_i(s_k),\overline{\mathit{\alpha }})$. Thus, the complete-data log-likelihood function is given by

$$\begin{array}{l}log\stackrel{\sim }{L}(\mathit{\theta })\propto -\frac{1}{2}\sum _{i=1}^n\sum _{k=1}^{m}log\mid {\mathbf{\sum }}_{s_k,i}\mid -\frac{n}{2}\sum _{k=1}^{m}log\mid {\mathbf{\sum }}_{v_{s_k}}\mid \\ -\frac{1}{2}\sum _{i=1}^n\sum _{k=1}^m{\mathit{z}}_i^T(s_k){\mathbf{\sum }}_{s_k,i}^{-1}{\mathit{z}}_i(s_k)-\sum _{i=1}^{n_0}U({\mathit{b}}_i)\tau \\ -n_{0}logC(\tau )-\frac{1}{2}\sum _{i=1}^n\sum _{k=1}^m{\mathit{v}}_i^T(s_k){\mathbf{\sum }}_{v_{s_k}}^{-1}{\mathit{v}}_i(s_k),\end{array}$$ (3)

where n₀ = #{x_i : x_i ≠ 0} denotes the number of OA patients. Given the current estimate θ̃^(r) at iteration r, the value ${\stackrel{\sim }{\overline{\mathit{\theta }}}}^{(r+1)}$ is obtained via maximizing the following Q-function Q_θ̃^(r) (θ̄) ≐ E_θ̃^(r) [log L̃(θ)|y, x] with respect to θ̄:

$$\begin{array}{l}{Q}_{{\stackrel{\sim }{\theta }}^{(r)}}(\overline{\mathit{\theta }})\propto -\frac{1}{2}\sum _{i=1}^n\sum _{k=1}^{m}log\mid {\mathbf{\sum }}_{s_k,i}\mid -\frac{n}{2}\sum _{k=1}^{m}log\mid {\mathbf{\sum }}_{v_{s_k}}\mid \\ -\frac{1}{2}\sum _{i=1}^n\sum _{k=1}^{m}E\left[{\mathit{z}}_i^T(s_k){\mathbf{\sum }}_{s_k,i}^{-1}{\mathit{z}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\\ -\frac{1}{2}\sum _{i=1}^n\sum _{k=1}^{m}E\left[{\mathit{v}}_i^T(s_k){\mathbf{\sum }}_{v_{s_k}}^{-1}{\mathit{v}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right].\end{array}$$ (4)

We consider the E-step and M-step of the EM algorithm as follows.

E-step

In the E-step, we need to calculate four conditional expectations: E[v_i(s_k)δ(b_i(s_k), l)|y_i(s_k), x, θ̃^(r)], E[v_i(s_k)|y_i(s_k), x, θ̃^(r)], $E\left[{\mathit{v}}_i(s_k){\mathit{v}}_i^T(s_k)\mid {\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]$, and E[δ(b_i(s_k), l)|y_i(s_k), x, θ̃^(r)]. In order to calculate these conditional probabilities, the class labels b should be estimated first. Here we consider the maximum a posteriori on Markov random field (MRF-MAP) estimation, which is efficient and adopted in many existing papers, e.g., [23], [44], [45]. First, the conditional probability density function of y_i(s_k) given x_i and b_i(s_k) is derived as

$$f({\mathit{y}}_i(s_k)\mid x_i,b_i(s_k),{\stackrel{\sim }{\mathit{\theta }}}^{(r)})~\mathcal{N}({\mathit{\varpi }}_i(s_k),{\stackrel{\sim }{\mathbf{\Lambda }}}_{s_k,i}^{(r)}),$$ (5)

where ${\mathit{\varpi }}_i^{(r)}(s_k)={\mathit{W}}_i^T{\stackrel{\sim }{\mathit{\beta }}}^{(r)}(s_k)+\overline{\mathit{c}}(x_i,{\mathit{W}}_i,{\mathit{b}}_i(s_k),{\stackrel{\sim }{\overline{\mathit{\alpha }}}}^{(r)})$ and ${\stackrel{\sim }{\mathbf{\Lambda }}}_{s_k,i}^{(r)}={\mathit{W}}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i+{\mathbf{\sum }^{\sim }}_{s_k,i}^{(r)}$.

According to the MAP criterion, ${\stackrel{\sim }{\mathit{b}}}_i^{(r)}$ is defined as

$$\begin{array}{l}{\stackrel{\sim }{\mathit{b}}}_i^{(r)}=arg\underset{{\mathit{b}}_i}{max}\left\{\prod _{k=1}^{m}f({\mathit{y}}_i(s_k)\mid x_i,b_i(s_k),{\stackrel{\sim }{\mathit{\theta }}}^{(r)})p({\mathit{b}}_i\mid {\stackrel{\sim }{\tau }}^{(r)})\right\}\\ =arg\underset{{\mathit{b}}_i}{max}\{\frac{1}{2}\prod _{k=1}^m{[{\mathit{y}}_i(s_k)-{\mathit{\varpi }}_i^{(r)}(s_k)]}^T[{\mathit{W}}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i+{{\mathbf{\sum }^{\sim }}_{s_k,i}^{(r)}]}^{-1}[{\mathit{y}}_i(s_k)-{\mathit{\varpi }}_i^{(r)}(s_k)]+U({\mathit{b}}_i){\stackrel{\sim }{\tau }}^{(r)}\}.\end{array}$$ (6)

To obtain the optimal solution to (6), in this paper, we adopt the iterated conditional modes (ICM) algorithm [20], which which uses a greedy iterative strategy for minimization. Convergence is achieved after only a few iterations. As a result, the conditional expectation E[δ(b_i(s_k), l)|y_i(s_k), x, θ̃^(r)] can be calculated as

$$\frac{f({\mathit{y}}_i(s_k)\mid x_i,b_i(s_k)=l,{\stackrel{\sim }{\mathit{\theta }}}^{(r)})P(b_i(s_k)=l\mid {\stackrel{\sim }{\mathit{b}}}_i^{(r)},{\stackrel{\sim }{\mathit{\theta }}}^{(r)})}{{\displaystyle \sum _{l=0}^2}f({\mathit{y}}_i(s_k)\mid x_i,b_i(s_k)=l,{\stackrel{\sim }{\mathit{\theta }}}^{(r)})P(b_i(s_k)=l\mid {\stackrel{\sim }{\mathit{b}}}_i^{(r)},{\stackrel{\sim }{\mathit{\theta }}}^{(r)})},$$ (7)

where

$$P(b_i(s_k)=l\mid {\stackrel{\sim }{\mathit{b}}}_i^{(r)},{\stackrel{\sim }{\mathit{\theta }}}^{(r)})=exp\left\{{\stackrel{\sim }{\tau }}^{(r)}\sum _{s_j\in {\mathcal{N}}_k}\delta (l,{\stackrel{\sim }{b}}_i^{(r)}(s_j))-logC({\stackrel{\sim }{\tau }}^{(r)})\right\}.$$ (8)

Here is the set of sites neighboring s_k.

Given x_i and ${\stackrel{\sim }{b}}_i^{(r)}(s_k),{({\mathit{y}}_i^T(s_k),{\mathit{v}}_i^T(s_k))}^T$ is normally distributed as

$$\mathcal{N}\left(\left(\begin{array}{c}{\mathit{\varpi }}_i(s_k)\\ \mathbf{0}\end{array}\right),\left(\begin{array}{cc}{\mathit{W}}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i+{\mathbf{\sum }^{\sim }}_{s_k,i}^{(r)}& {\mathit{W}}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}\\ {\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i& {\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}\end{array}\right)\right).$$

Then, given y_i(s_k), x, and ${\stackrel{\sim }{b}}_i^{(r)}(s_k)$, we have

$$\begin{array}{l}E\left[{\mathit{v}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{b}}_i^{(r)}(s_k),{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]=\\ {\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i{({\mathit{W}}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i+{\mathbf{\sum }^{\sim }}_{s_k,i}^{(r)})}^{-1}({\mathit{y}}_i(s_k)-{\mathit{\varpi }}_i(s_k)),\\ E\left[{\mathit{v}}_i(s_k){\mathit{v}}_i^T(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{b}}_i^{(r)}(s_k),{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]=\\ {\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}-{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i{({\mathit{W}}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}{\mathit{W}}_i+{\mathbf{\sum }^{\sim }}_{s_k,i}^{(r)})}^{-1}{W}_i^T{\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r)}\\ +E\left[{\mathit{v}}_i^T(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{b}}_i^{(r)}(s_k),{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\\ +E\left[{\mathit{v}}_i^T(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{b}}_i^{(r)}(s_k),{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right].\end{array}$$

Finally, the desired expectations can be estimated as

$$\begin{array}{l}E\left[{\mathit{v}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]=\\ \sum _{l=0}^{2}E\left[{\mathit{v}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},b_i(s_k)=l,{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\\ \times P(b_i(s_k)=l|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}),\\ E\left[{\mathit{v}}_i(s_k)\delta (b_i(s_k),l)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]=\\ E\left[{\mathit{v}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},b_i(s_k)=l,{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\\ \times P(b_i(s_k)=l|{\mathit{y}}_i(s_k),x,{\stackrel{\sim }{\mathit{\theta }}}^{(r)}),\\ E\left[{\mathit{v}}_i(s_k){\mathit{v}}_i^T(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]=\\ \sum _{l=0}^{2}E\left[{\mathit{v}}_i(s_k){\mathit{v}}_i^T(s_k)|{\mathit{y}}_i(s_k),\mathit{x},b_i(s_k)=l,{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\\ \times P(b_i(s_k)=l\mid {\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}).\end{array}$$ (9)

M-step

Taking derivatives of (4) with respect to θ̄ and equating them to zeros, we find the updates of θ̄ as follows. For β(s_k) and ᾱ(l), we have

$$\begin{array}{l}{\stackrel{\sim }{\mathit{\beta }}}^{(r+1)}(s_k)={[\sum _{i=1}^n{\mathit{W}}_i{\mathbf{\sum }^{\sim }}_{s_k,i}^{{(r)}^{-1}}{\mathit{W}}_i^T]}^{-1}\sum _{i=1}^n{\mathit{W}}_i{\mathbf{\sum }^{\sim }}_{s_k,i}^{{(r)}^{-1}}\\ ({\mathit{y}}_i(s_k)-{\mathit{W}}_i^{T}E\left[{\mathit{v}}_i(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\\ -\delta (x_i,1){\mathit{W}}_i^T\sum _{l=1}^M{\stackrel{\sim }{\overline{\mathit{\alpha }}}}^{(r)}(l)E\left[\delta (b_i(s_k),l)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]),\end{array}$$ (10)

and

$$\begin{array}{l}{\stackrel{\sim }{\overline{\mathit{\alpha }}}}^{(r+1)}(l)=[\sum _{i=1}^{n_0}\sum _{k=1}^m{\mathit{W}}_i{\mathbf{\sum }^{\sim }}_{s_k,i}^{{(r)}^{-1}}{\mathit{W}}_i^T\\ {E[\delta (b_i(s_k),l)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}]]}^{-1}\\ \sum _{i=1}^{n_0}\sum _{k=1}^m{\mathit{W}}_i{\mathbf{\sum }^{\sim }}_{s_k,i}^{{(r)}^{-1}}\{{\mathit{y}}_i(s_k)-{\mathit{W}}_i^T{\stackrel{\sim }{\mathit{\beta }}}^{(r)}(s_k)\\ -{\mathit{W}}_i^{T}E\left[{\mathit{v}}_i(s_k)\delta (b_i(s_k),l)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right]\}.\end{array}$$ (11)

For the covariance matrix Σ_vsk, we have

$${\mathbf{\sum }^{\sim }}_{v_{s_k}}^{(r+1)}=\frac{1}{n}\sum _{i=1}^{n}E\left[{\mathit{v}}_i(s_k){\mathit{v}}_i^T(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right].$$ (12)

For ${\sigma }_{s_k}^2$ in Σ_{sk i},

$${\stackrel{\sim }{\sigma }}_{s_k}^{2^{(r+1)}}=\frac{1}{N}\sum _{i=1}^{n}E\left[{[{\mathit{z}}_i^{(r)}(s_k)]}^T{\mathit{z}}_i^{(r)}(s_k)|{\mathit{y}}_i(s_k),\mathit{x},{\stackrel{\sim }{\mathit{\theta }}}^{(r)}\right],$$ (13)

where $N={\sum }_{i=1}^n{T}_i,{\mathit{z}}_i^{(r)}(s_k)={\mathit{y}}_i(s_k)-{\mathit{W}}_i^T{\stackrel{\sim }{\mathit{\beta }}}^{(r)}(s_k)-\overline{\mathit{c}}(x_i,{\mathit{W}}_i,b_i(s_k),{\stackrel{\sim }{\overline{\mathit{\alpha }}}}^{(r)})-{\mathit{W}}_i^T{\mathit{v}}_i(s_k)$.

Since τ in model (2) is not the primary parameter of interest, we use an approximate, but computationally efficient method based on a pseudo-likelihood function. A key advantage of using the pseudo-likelihood function is its computational simplicity, since it does not involve the intractable partition function. The pseudo-likelihood at the r-th step is a simple product of the conditional likelihood

$$PL({\stackrel{\sim }{\mathit{b}}}^{(r)})=\prod _{i=1}^{n_0}\prod _{s_k\in \mathcal{S}-\partial \mathcal{S}}PL({\stackrel{\sim }{b}}_i^{(r)}(s_k)\mid {\stackrel{\sim }{\mathit{b}}}_i^{(r)}),$$ (14)

where ∂ denotes the set of points at the boundaries of , and $PL({\stackrel{\sim }{b}}_i^{(r)}(s_k)\mid {\stackrel{\sim }{\mathit{b}}}_i^{(r)})$ is given by

$$\frac{exp\left\{\tau {\sum }_{s_j\in {\mathcal{N}}_k}\delta ({\stackrel{\sim }{b}}_i^{(r)}(s_k),{\stackrel{\sim }{b}}_i^{(r)}(s_j))\right\}}{{\displaystyle \sum _{b(s_k)=1}^M}exp\left\{\tau {\displaystyle \sum _{s_j\in {\mathcal{N}}_k}}\delta ({\stackrel{\sim }{b}}_i^{(r)}(s_k),{\stackrel{\sim }{b}}_i^{(r)}(s_j))\right\}}.$$

Thus, the MPL estimate τ̃^(r+1) can be obtained by solving

$$\frac{\partial ln\mathit{PL}({\stackrel{\sim }{\mathit{b}}}^{(r)},\tau )}{\partial \tau }=0.$$ (15)

The E-step and M-step are repeated until the difference between log L(θ̃^(r+1)) and log L(θ̃^(r)) is smaller than a desired value (e.g., 10⁻⁴).

D. Inference Procedure

After all the parameters are estimated, we carry out formal statistical inference consisting of three different statistical tools below. First, we calculate the standard errors of computed MLEs, β̂(s_k), at each voxel s_k and $\widehat{\overline{\mathit{\alpha }}}$ in the moderately and severely diseased regions. As ${\mathit{w}}_{ij}^T\mathit{\beta }(s_k)$ captures the information in all normal regions R_i0 across all normal subjects and OA patients, we calculate the standard errors of β̂(s_k) via pixel-wise analysis of longitudinal cartilage thickness on all subjects with b̂_i(s_k) = 0, in which model (1) is simplified as follows:

$$y_{ij}(s_k)={\mathit{w}}_{ij}^T\mathit{\beta }(s_k)+{\mathit{w}}_{ij}^T{\mathit{v}}_i(s_k)+{\epsilon }_{ij}(s_k).$$ (16)

Thus, the estimated covariance matrix of β̂(s_k) can be approximated by

$${\left[\frac{1}{\stackrel{\sim }{n}(s_k)}\sum _{i=1}^{\stackrel{\sim }{n}(s_k)}{\mathit{W}}_i{({\mathit{W}}_i^T{\widehat{\mathbf{\sum }}}_{v_{s_k}}{\mathit{W}}_i+{\widehat{\mathbf{\sum }}}_{s_k,i})}^{-1}{\mathit{W}}_i^T\right]}^{-1},$$ (17)

where ñ(s_k) is the number of subjects with b̂_i(s_k) = 0 at voxel s_k. Then the standard errors can be estimated by the positive square root of the diagonal elements in (17).

On the other hand, the standard error of α is estimated based on data in the voxels of all diseased regions in all OA patients, since α captures the information in all diseased regions R_i1 ∪ R_i2 across all subjects together. Since the information of these diseased regions has to be estimated from the data, the standard errors associated with α̂ are the standard errors conditional on the given diseased regions across subjects. Moreover, the pixel-wise analysis is not suitable here, and thus it is impossible to obtain explicit expressions of the estimated standard errors. In order to tackle this problem, a resampling approach, wild bootstrap [46], is considered here. The idea of wild bootstrap is to leave the regressors at their sample value, but to resample the response variable based on the residuals values. This method proceeds as follows:

1. Fit the model with the original data and retain the fitted values ${\widehat{\mathit{y}}}_i(s_k)={\mathit{w}}_{ij}^T\widehat{\mathit{\beta }}(s_k)+c(x_i,{\mathit{w}}_{ij},{\widehat{b}}_i(s_k),\widehat{\overline{\mathit{\alpha }}})$ and the residuals ε̂_i(s_k) = y_i(s_k) − ŷ_i(s_k) for i = 1, …, n and k = 1, …, m;

2. Create synthetic response variables y_i(s_k)* = ŷ_i(s_k) + a_iε̂_i(s_k), where a_i is a random variable following standard normal distribution;

3. Refit the model using the synthetic response variables y_i(s_k)* and retain the estimates ${\widehat{\overline{\mathit{\alpha }}}}^{\ast }$;

4. Repeat Steps 1 and 2 independently B times to give B independent realizations of ${\widehat{\overline{\mathit{\alpha }}}}^{\ast }$, denoted by ${\widehat{\overline{\mathit{\alpha }}}}_1^{\ast },\dots ,{\widehat{\overline{\mathit{\alpha }}}}_B^{\ast }$;

5. The bootstrap covariance matrix of $\widehat{\overline{\mathit{\alpha }}}(l)$ is estimated by

   $$\frac{1}{B-1}\sum _{i=1}^B({\widehat{\overline{\mathit{\alpha }}}}_i^{\ast }(l)-\overline{{\widehat{\overline{\mathit{\alpha }}}}^{\ast }(l)}){({\widehat{\overline{\mathit{\alpha }}}}_i^{\ast }(l)-\overline{{\widehat{\overline{\mathit{\alpha }}}}^{\ast }(l)})}^T,$$ (18)

   where $\overline{{\widehat{\overline{\mathit{\alpha }}}}^{\ast }(l)}=B^{-1}{\sum }_{i=1}^B{\widehat{\overline{\mathit{\alpha }}}}_i^{\ast }(l)$ for l = 1, 2. The standard error of $\widehat{\overline{\mathit{\alpha }}}(l)$ can be estimated by the positive square root of the diagonal element of (18).

It has been shown that 50 to 100 bootstrap replications (B = 100 in this paper) are generally sufficient for standard error estimation [47].

Second, several hypothesis testing problems are quite interesting in real applications. Specifically, we are interested in testing (i) whether there is any cartilage progression across time at each pixel site in normal regions; (ii) whether there is any difference of cartilage thickness at baseline between normal regions and moderately (or severely) diseased regions; and (iii) whether there is any difference of cartilage progression across time between normal regions and moderately (or severely) diseased regions. They can written as

$$H_0(s_k):{\beta }_2(s_k)=0\text{v.s.}{H}_1(s_k):{\beta }_2(s_k)\ne 0;$$ (19)

$$H_0:{\overline{\alpha }}_1(1)=0\text{v.s.}{H}_1:{\overline{\alpha }}_1(1)\ne 0;$$ (20)

$$H_0:{\overline{\alpha }}_2(1)=0\text{v.s.}{H}_1:{\overline{\alpha }}_2(1)\ne 0;$$ (21)

$$H_0:{\overline{\alpha }}_1(2)=0\text{v.s.}{H}_1:{\overline{\alpha }}_1(2)\ne 0;$$ (22)

$$H_0:{\overline{\alpha }}_2(2)=0\text{v.s.}{H}_1:{\overline{\alpha }}_2(2)\ne 0,$$ (23)

where ᾱ_l′(l) is the l′^th component of ᾱ(l), l = 1, 2. A sequence of t tests can be used here. The standard errors of estimates β̂₂(s_k), k = 1, …, m, and $\widehat{\overline{\mathit{\alpha }}}(l)$, l = 1, 2 can be obtained as described above. The false discovery rate (FDR) adjustment method [48] is employed here to calculate the adjusted p-values corrected for the multiple comparison problem (19).

Third, after obtaining the diseased region labels across all pixel sites for each OA subject, we calculate the empirical probabilities of both the moderately diseased region and severely diseased region at each pixel across all OA subjects. The related formula is listed below:

$$\widehat{Pr}\{b(s_k)=l\}=\frac{\#\{i:{\widehat{b}}_i(s_k)=l\}}{n_0},l=1,2,$$ (24)

where #A denotes the number of the elements in set A.

IV. Simulation Studies

We examine the finite sample performance of GHMM for diseased region detection. We first fitted the model (1) to the femoral cartilage thickness data of all the normal controls derived from the 3D MRI data of the Pfizer Longitudinal Study (PLS-A9001140) and then we used the obtained parameter estimators of β(s_k), Σ_vsk, and ${\sigma }_{s_k}^2$ as their true values for simulations. Moreover, ᾱ(1) and ᾱ(2) were set (−0.17, −0.19)^T and (−0.26, −0.33)^T, respectively. The covariate vector w_i for each subject was generated according to the real data set analyzed in Section V. We generated 20 subjects from 3 groups of OA patients with 7 patients in group 1, 7 patients in group 2, and 6 patients in group 3. Without loss of generality, the location of all diseased regions is predetermined and does not vary for subjects in the same group, whereas it varies across groups. Fig. 4 presents different lesions that were manually designed and inserted into the thickness maps and the diseased regions associated with the three simulated groups.

Fig. 4.

Visualizations of simulated lesions in femoral cartilage sheets: normal region (blue); moderately diseased region (light blue); severely diseased region (orange).

We applied GHMM to detect the diseased regions in each subject. We randomly selected one subject from each group and presented its detection results in Fig. 5. For all selected subjects, the diseased regions can be successfully detected with few misclassifications in the results. To show the average detection performance among subjects in each group, the Jaccard index [49], Dice index [50], Rand index [51], and adjusted Rand index [52] were calculated to compare the detection results with the truth. Finally, we calculated the averages of all index values taken over all subjects in each subgroup. For all these indices, a higher index value indicates a more accurate detection result. Simulation results based on all the three groups are presented in Table I, where the related standard deviations are also shown in parentheses. For all these groups, the average of the four index values are all larger than 86 percent, and the related standard deviations are all less than 0.05. Figure 5 and Table I indicate that GHMM performs very well in diseased region detection of cartilage MRI data.

Fig. 5.

Diseased region detection for subjects from three groups: (a) subject with 5 time points in group 1; (b) subject with 3 time points in group 2; (c) subject with 4 time point in group 3. This is the simulated result and hence we have an imposed ground truth, which is shown in Fig. 4. In each group, the image with green background indicates the detection result, i.e., normal region (blue); moderately diseased region (light blue); severely diseased region (orange), the remaining ones are the observations for the time points, where the color bar for all the observations is presented on the right side of the fist raw in (a)–(c).

TABLE I.

Average detection performance among subjects in different groups

	Group 1	Group 2	Group 3
Jaccard index	0.8509 (0.0045)	0.9200 (0.0113)	0.8683 (0.0040)
Dice index	0.9142 (0.0026)	0.9583 (0.0078)	0.9295 (0.0023)
Rand index	0.9794 (0.0114)	0.9592 (0.0124)	0.9721 (0.0097)
Adjusted Rand index	0.9242 (0.0399)	0.8749 (0.0500)	0.8853 (0.0367)

V. Real Data Analysis

We consider the MRI dataset from the Pfizer longitudinal non-treatment study on osteoarthritis (PLS-A9001140). This dataset contains T1-weighted (3D SPGR) images from 155 subjects imaged at baseline, 3, 6, 12, and 24 months at a resolution of 1.00 × 0.31 × 0.31mm³. All the subjects are females. Some of them have missing scans and thus we have 706 MRIs in total. The Kellgren-Lawrence grades (KLG)¹ [53] were determined for all subjects from the baseline extended weight-bearing radiographs, classifying 81 subjects as normal control (KLG0), 1 subject as KLG1 (mild OA), 40 subjects as KLG2 (severe OA), and 33 subjects as KLG3 (severe OA). It seems that most of the OA patients in this dataset were selected to have predominantly medial OA.

We first computed the cartilage segmentations in the knee MRI data. We randomly chose two subjects with different KLG from the dataset, and presented the related 2D thickness maps for the chosen subjects at baseline in Fig. 6.

Fig. 6.

Local cartilage thickness (mm) for subjects with automatic segmentations at baseline with different KLGs: (top) femoral cartilage (FC) thickness map (left) and tibial cartilage (TC) thickness map (right) for subjects with KLG0; (bottom) femoral cartilage (FC) thickness map (left) and tibial cartilage (TC) thickness map (right) for subject with KLG3. The medial (M), lateral (L), anterior (A), and posterior (P) directions are annotated in the thickness map (top & left).

After extraction of the 2D thickness maps, we first applied the linear mixed model for voxel-based analysis to the thickness maps from the whole dataset and calculated the parameter estimation at each pixel site. The model is described as below

$$y_{ij}(s_k)={\mathit{w}}_{ij}^T{\mathit{\beta }}_0(s_k)+{\alpha }_1(s_k)\delta (x_i,1)+{\mathit{w}}_{ij}^T{\mathit{v}}_i(s_k)+{\epsilon }_{ij}(s_k),j=1,\dots ,T_i;i=1,\dots ,n,$$ (25)

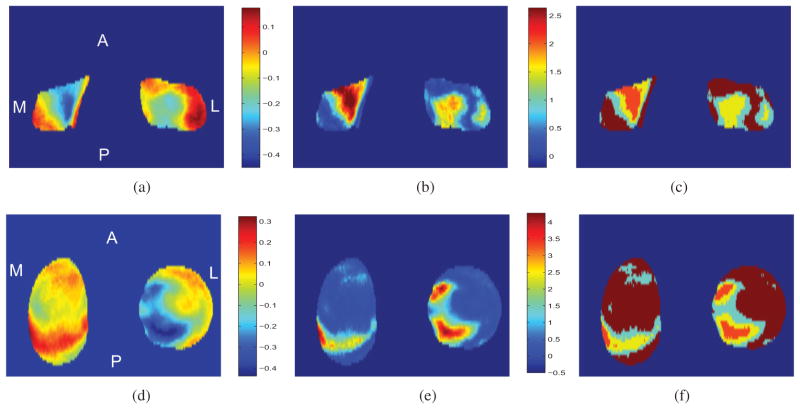
where w_ij, x_i, v_i(s_k) and ε_ij(s_k) are all defined the same as those in (1). Compared with GHMM, the reduced model (25) cannot handle the spatial heterogeneity of cartilage progression across subjects, and thus it can only capture the diseased regions at population level instead of individual level. The estimates of α₁(s_k) across all the pixels in both femoral and tibial cartilages are presented in Fig. 7(a) and (d). We carried out a sequence of t tests on the hypotheses H₀(s_k) : α₁(s_k) = 0 versus H₁(s_k) : α₁(s_k) ≠ 0 across all pixels to identify the regions with substantial differences between OA patients and normal controls. Figure 7(b) and (e) present the FDR adjusted − log₁₀(p)-value [48] at each pixel in both femoral and tibial cartilages. Based on the testing results, we are able to detect some significant subregions in the cartilage. Furthermore, for better visualization, we used the K-means clustering method [54] to cluster voxels into several sub-regions based on the FDR adjusted −log₁₀(p)-map. We chose clustering −log₁₀(p)-values, since the p-value indicates the statistical significance of the effect sizes. The clustering results are also presented in Fig. 7(c) and Fig. 7(f), where four subregions are discovered for both femoral and tibial cartilage. The mean values of FDR adjusted −log₁₀(p)-value for all the pixel sites in each cluster are also summarized in Table II. Table II reveals that the first three clusters are diseased regions, whereas the fourth one is a normal region. Such results are averages across all the subjects. Since the cartilage thinning happens at different locations for different subjects, the voxel-based analysis based on model (25) fails to capture the diseased regions for individual OA subjects.

Fig. 7.

Voxel-wise analysis based on linear mixed model (25): (a) estimates of α₁(s_k) in femoral cartilage; (b) FDR adjusted −log₁₀(p)-values in femoral cartilage; (c) clustering results based on FDR adjusted −log₁₀(p)-values in femoral cartilage: cluster 1 (light blue), cluster 2 (yellow), cluster 3 (orange), cluster 4 (dark red); (d) estimates of α₁(s_k) in tibial cartilage; (e) FDR adjusted −log₁₀(p)-values in tibial cartilage; and (f) clustering results based on FDR adjusted −log₁₀(p)-values in tibial cartilage: cluster 1 (light blue), cluster 2 (yellow), cluster 3 (orange), and cluster 4 (dark red).

TABLE II.

Mean values of FDR adjusted −log₁₀(p)-value for all the pixel locations in each cluster

Cartilage	Cluster 1	Cluster 2	Cluster 3	Cluster 4
femoral	1.2565	2.3616	3.8733	0.3111
tibial	1.5198	3.0583	5.0483	0.3491

As a comparison, we applied GHMM to the whole dataset. As an illustration, the estimates of β(s_k) across all the pixels in both femoral and tibial cartilages and their standard errors obtained via wild bootstrap are presented in Fig. 8(a)–(h). From Fig. 8(c)–(d) and (g)–(h), coefficients of most pixels show the range of cartilage thickness changes in normal regions similar to those in [17]. However, coefficients of some pixels show progression in normal regions. One of the reasons for these progressions may be that some regions may undergo tissue swelling, diluting, or even masking cartilage loss in adjacent pixels [15]. The FDR adjusted −log₁₀(p)-value for test (19) at each pixel is calculated in Fig. 8(i) and (j). The inference results of α, including estimation, standard error and −log₁₀(p)-value for tests (20)–(23), are presented in Table III as well. Fig. 8 and Table III reveal that (i) there is significant cartilage progression across time on only a few pixel sites in normal regions; (ii) the difference of cartilage progression across time between normal regions and moderately (or severely) diseased regions is highly significant with respect to their cartilage thickness at baseline; and (iii) both the difference of cartilage thickness at baseline and difference of cartilage progression across time between normal regions and severely diseased regions are larger than those between normal regions and moderately diseased regions. Then we chose two pixel sites from the femoral and tibial cartilages, respectively, and presented them in Fig. 9(a). Fig. 9(b)–(g) show the dynamic changes of cartilage thickness at two given pixel sites across time. We also included both the estimated curves and thickness changes of some chosen subjects. The estimated cartilage thicknesses at both two pixel sites follow a trend of decline across time for OA patients. Moreover, the estimated cartilage thickness in severely diseased regions decreases more quickly than that in moderately diseased regions. We randomly selected 3 subjects with different KLGs, i.e., 1 KLG1 subject, 1 KLG2 subject, and 1 KLG3 subject, and presented their diseased regions in Fig. 10. Fig. 11 presents the empirical probabilities of both moderately diseased region and severely diseased region. The locations of diseased regions change across subjects, and the detected diseased regions are more inclined to locate in some regions (e.g., center) of the cartilage. This indicates that the cartilage loss in OA may not be uniform throughout the cartilage, but OA may affect certain regions more frequently than others [11].

Fig. 8.

Inference results of β(s_k) based on GHMM: (a) estimates of β₁(s_k) in femoral cartilage; (b) standard errors of estimates β̂₁(s_k) in femoral cartilage; (c) estimates of β₂(s_k) in femoral cartilage; (d) standard errors of estimates β̂₂(s_k) in femoral cartilage; (e) estimates of β₁(s_k) in tibial cartilage; (f) standard errors of estimates β̂₁(s_k) in tibial cartilage; (g) estimates of β₂(s_k) in tibial cartilage; (h) standard errors of estimates β̂₂(s_k) in tibial cartilage; (i) FDR adjusted −log₁₀(p)-values for test (19) across all pixel sites in femoral cartilage; and (j) FDR adjusted −log₁₀(p)-values for test (19) across all pixel sites in tibial cartilage.

TABLE III.

Inference results of α̂ based on GHMM

	Femoral cartilage			Tibial cartilage
Parameter	Estimation	Standard Error	−log10(p)-value	Estimation	Standard Error	−log10(p)-value
ᾱ1(1)	−0.0104	0.0027	3.9721	−0.0256	0.0080	2.8562
ᾱ2(1)	−0.1374	0.0353	4.0128	−0.1534	0.0405	3.8111
ᾱ1(2)	−0.1253	0.0289	4.8366	−0.1387	0.0362	3.9018
ᾱ2(2)	−0.2619	0.0628	4.5107	−0.2328	0.0584	4.1733

Fig. 9.

Dynamic changes of cartilage thickness at randomly selected pixel sites across time: (a) two randomly selected pixel sites on femoral cartilage and tibial cartilage; (b) dynamic changes of cartilage thickness at s_k1 of subjects with b_i(s_k1) = 0 across time, i.e., estimated curve (solid line) and chosen subjects with b_i(s_k1) = 0 (dashed lines); (c) dynamic changes of cartilage thickness at s_k2 of subjects with b_i(s_k2) = 0 across time, i.e., estimated curve (solid line) and chosen subjects with b_i(s_k2) = 0 (dashed lines); (d) dynamic changes of cartilage thickness at s_k1 of OA patients with b_i(s_k1) = 1 across time, i.e., estimated curve (solid line) and chosen OA patients with b_i(s_k1) = 1 (dashed lines); (e) dynamic changes of cartilage thickness at s_k2 of OA patients with b_i(s_k2) = 1 across time, i.e., estimated curve (solid line) and chosen OA patients with b_i(s_k2) = 1 (dashed lines); (f) dynamic changes of cartilage thickness at s_k1 of OA patients with b_i(s_k1) = 2 across time, i.e., estimated curve (solid line) and chosen OA patients with b_i(s_k1) = 2 (dashed lines); and (g) dynamic changes of cartilage thickness at s_k2 of OA patients with b_i(s_k2) = 2 across time, i.e., estimated curve (solid line) and chosen OA patients with b_i(s_k2) = 2 (dashed lines).

Fig. 10.

Diseased region detection for subjects with different KLGs, including 1 KLG1, 1 KLG2, and 1 KLG3. Detection results of femoral cartilage thickness map (top) and tibial cartilage thickness map (bottom) for every subject are shown in each row, i.e., normal region (light blue); moderately diseased region (yellow); severely diseased region (orange).

Fig. 11.

Empirical probabilities of both moderately diseased region and severely diseased region based on estimated diseased region labels: (a) empirical probability of moderately diseased region in femoral cartilage; (b) empirical probability of severely diseased region in femoral cartilage; (c) empirical probability of moderately diseased region in tibial cartilage; and (d) empirical probability of severely diseased region in tibial cartilage.

Furthermore, we investigate whether there are some subgroups among patients and delineate their associated diseased region pattern in each subgroup. To achieve this, we used a clustering method to cluster all estimated maps {b̂_i}_i≥1 at the subject level. Since the number of informative pixels is much larger than the number of OA subjects, e.g., m = 4484 and n = 74 for tibial cartilage, we adopted a sparse k-means clustering method and its associated R package sparcl (http://www.icesi.edu.co/CRAN/web/packages/sparcl/) [55], which combines a Lasso-type penalty with the K-means clustering method to cluster observations. We applied sparcl to the estimated maps {b̂_i}_i≥1. Two subgroups were detected for the femoral cartilage, whereas three subgroups were identified for the tibial cartilage. The KLG information of subjects in each subgroup is presented in Table IV. Inspecting Table IV reveals that for the femoral cartilage case, the group membership of most patients is consistent with their KLG information. Specifically, most KLG2 subjects belong to Group 1, whereas most KLG3 subjects fall into Group 2. Similar to the procedures in voxel-based analysis, the diseased region pattern of each group in the average sense can also be calculated based on the detection results. For every group, the diseased-region detection results of two randomly chosen subjects and their related pattern are presented in Fig. A1, which can be found in Supplementary Materials. It reveals the spatial heterogeneity of cartilage progression across OA subjects.

TABLE IV.

KLG information of patients in each group

	Femoral cartilage
Group	KLG1	KLG2	KLG3	Total
1	0	36	8	44
2	1	4	25	30
	Tibial cartilage
Group	KLG1	KLG2	KLG3	Total
1	0	26	26	52
2	1	13	0	14
3	0	1	7	8

VI. Conclusion

We have developed a GHMM for longitudinal cartilage quantification in OA patients, while addressing these two issues: the lack of spatial correspondence across subjects and time and the spatial heterogeneity of cartilage progression across subjects. Our GHMM is designed to efficiently account for the spatial heterogeneity of cartilage progression across subjects. We have developed an efficient algorithm to estimate unknown parameters in the GHMM. The proposed model can effectively detect diseased regions in each OA subject and present a localized analysis of longitudinal cartilage thickness within each latent subpopulation. Our GHMM integrates the strengths of two standard statistical methods: the local subregion-based analysis and the ordered value approach. Simulation studies and real data analysis have demonstrated that GHMM can effectively detect diseased regions in localizing longitudinal cartilage thickness.

Several important issues need to be addressed in our future research. First, it is assumed that the disease effect b_i is an ordinal variable at each location and follows a Potts model. However, if the disease effect is strongly associated with the continuous loss of cartilage thickness, then it may be more reasonable to treat them as continuous variables. In this case, computational and theoretical challenges may arise. For example, we may need to introduce another hidden Markov model for continuous disease effects, and thus both the estimation and inference procedures have to be rederived. Second, we plan to apply GHMM to other knee MRI datasets, such as OAI, to investigate other clinical questions of interest. Third, it is interesting to extend GHMM to the group analysis of various neuroimaging data sets, such as the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database [56]. Most group analysis methods (e.g., Statistical Parametric Mapping (SPM)) assume the spatial homogeneity and spatial correspondence of effect regions across subjects, which may not be valid for many neuroimaging studies. For instance, in Alzheimer’s disease (AD) studies, quantifying patterns of structural change during early stages of AD is a major challenge. Brain atrophy in the early stages of AD may be relatively subtle and spatially distributed over different brain regions, and the patterns of atrophy have been found spatially heterogeneous [57]. Moreover, the error associated with structural measurements can vary throughout the brain and across subjects and time points. In this case, our GHMM can be used to capture complex morphological characteristics that distinguish AD from normal controls, furthermore to determine which patterns are most informative from a diagnostic perspective.