Abstract
Motion of the heart has complicated in vivo applications of cardiac diffusion MRI and diffusion tensor imaging (DTI), especially in small animals such as rats where ultra-high-performance gradient sets are currently not available. Even with velocity compensation via, for example, bipolar encoding pulses, the variable shot-to-shot residual motion-induced spin phase can still give rise to pronounced artifacts. This study presents diffusion-encoding schemes that are designed to compensate for higher-order motion components, including acceleration and jerk, which also have the desirable practical features of minimal TEs and high achievable b-values. The effectiveness of these schemes was verified numerically on a realistic beating heart phantom, and demonstrated empirically with in vivo cardiac diffusion MRI in rats. Compensation for acceleration, and lower motion components, was found to be both necessary and sufficient for obtaining diffusion-weighted images of acceptable quality and SNR, which yielded the first in vivo cardiac DTI demonstrated in the rat. These findings suggest that compensation for higher order motion, particularly acceleration, can be an effective alternative solution to high-performance gradient hardware for improving in vivo cardiac DTI.
Index Terms: cardiac imaging, magnetic resonance imaging, diffusion weighted imaging, heart, motion compensation and analysis, diffusion tensor imaging, animal models and imaging
I. Introduction
Cardiac diffusion tensor imaging (DTI) [1]–[3] is increasingly used for noninvasive or nondestructive characterization of myocardial microstructure and myofiber orientation in both normal and diseased hearts. DTI data of normal hearts have been incorporated into morphologically accurate computational modeling to better understand their electrophysiology [4], [5] and mechanics [6], [7]. In diseased hearts, alterations in the myocardial microstructure and fiber orientation have resulted in DTI-detectable changes. For example, while the average magnitude of diffusion increased, the fractional anisotropy (FA), which is a metric for the degree of diffusion anisotropy, was found to decrease in regions of myocardial infarction [8]–[10]. Fiber disarray, which is manifested by increased local heterogeneity of DTI directional parameters, has been reported in cases of myocardial infarction [11], [12] and heart failure [13], [14]. These studies demonstrate that DTI can be a useful alternative or adjunct to current MRI evaluations for providing unique imaging biomarkers for the diagnosis, staging and monitoring under therapy of cardiac diseases.
The ability to perform in vivo DTI for conducting longitudinal observations is highly desirable, especially for evaluating the progression of diseases. However, most cardiac DTI studies reported to date have been on ex vivo specimens [15]–[18], or arrested Langendorff perfused hearts [19]–[21], largely due to the technical challenges presented by the relatively large bulk motion of the beating heart for DTI, which quantifies the microscopic random translational motion of water. Nevertheless, in vivo diffusion MRI or DTI in humans has been shown feasible [22]–[24]. Techniques employed to reduce the effects of cardiac bulk motion for in vivo cardiac DTI in humans have included using bipolar diffusion-encoding gradient pulses [3], [25], [26], stimulated echoes (STEAM) over two cardiac cycles [27], [28] in conjunction with acquisition during quiescent phases of the cardiac cycle, or single-shot acquisition with navigator-based gating [29].
Due to their frequent use in preclinical research, the ability to perform in vivo cardiac DTI in small animals is also highly desirable. To date, although feasibility has been demonstrated for the mouse [12], [30], in vivo cardiac DTI remains elusive or at best sub-optimal for other small animal species such as the rat and rabbit, which are also important research models of cardiac diseases [31], [32]. The difficulty in extending the success of in vivo cardiac DTI in humans to small animals is likely related to the demands imposed by the unique physiology of the animals. For example, the heart rates in small animals are typically much higher than humans (~300 vs. ~60 bpm), and their hearts are constantly in motion, with relatively little quiescent phase. The impacts of the cardiac motion can be partially remedied by using very short duration pulses afforded by ultra-high performance gradients to achieve the necessary diffusion sensitization. Indeed, in vivo cardiac DTI in the mouse was reported [30] using bipolar diffusion encoding gradients with hardware that was capable of 1500 mT/m peak amplitude. However, the small inner diameters of ultra-high performance gradient sets (6 cm for the Bruker BGA-6S) preclude their deployment on larger animals, such as adult rats. Diffusion MRI or DTI using larger-diameter, relatively lower-performance gradient sets (those with 600 mT/m peak amplitude, for example) on the live rat heart has so far been unsatisfactory, even when bipolar diffusion pulses are used.
Diffusion-weighted images obtained as part of the current study have shown that different locations in the myocardium suffer varying degrees of signal dropout, depending on the diffusion encoding direction, cardiac cycle time point, and positioning of the animal. These clues suggest that bulk motion remains a source of complication even with the lower heart rate associated with the rat (compared to the mouse). To better understand the nature of the problem, and to develop effective solutions, a precise knowledge of the intricate interplay between the animal cardiac motion and diffusion sensitization is necessary.
The primary goals of this work are to design and evaluate the effectiveness of more robust motion-compensated gradient waveforms for in vivo diffusion encoding in small animals. Specifically, diffusion-encoding schemes capable of compensating for higher-order motion (acceleration and jerk) are presented. The effectiveness of the proposed methods is evaluated by both numerical simulation and experimental demonstration. Although the current work centers on the rat, the findings are expected to be applicable to other small animal species where physiologic motion and gradient performance are the limiting factors for in vivo cardiac diffusion MRI.
Underscoring the need for better motion compensation, a bSSFP sequence employing four pairs of bipolar encoding pulses to compensate for acceleration in a twice-refocused spin echo preparation was recently used to obtain diffusivity maps in humans [33]. In contrast, the current work presents a generalized strategy for achieving higher order (acceleration and beyond) motion compensation that is also suited for DTI and uses the minimum number of diffusion-encoding pulses for maximum diffusion weighting, which is important for applications in small animals with much faster heart rates.
II. Theory
A. Gradient Moment Nulling
Signal acquisition in MRI largely records the time-evolution of the spin phase that results from the interaction between the spin location and applied gradient waveform, commonly written as,
| (1) |
where γ is the gyromagnetic ratio, and G and r are the gradient waveform and spin displacement vectors, respectively. By performing a power series expansion on the displacement vector, the dependence of the spin phase on the individual motion components (such as position r0, velocity v0) and gradient moments (such as zeroth moment m0, first moment m1 and higher orders) can be explicitly described [34],
| (2) |
Having motion-induced spin phase in and of itself does not necessarily result in motion artifacts. Rather, it is the intra-voxel dispersion in highly heterogeneous motion [35] or shot-to-shot variation of the spin phase in a multi-shot acquisition (introduced by physiologic R-R fluctuation, for example) that gives rise to motion artifacts [36]. Due to the large gradient moments, and consequently spin phases, associated with the encoding pulses used, diffusion MRI is extremely prone to motion artifacts.
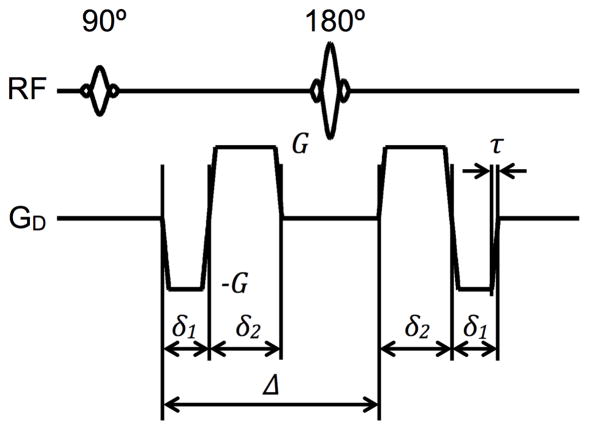
Since neither perfectly reproducible motion nor elimination of motion is practically feasible for in vivo imaging, an alternative approach is to employ gradient waveforms that have nulled moments, usually by incorporating additional gradient pulses that mathematically pose as constraining criteria of corresponding moments to compensate for the different motion components. Such gradient-moment nulling (GMN) methods [37]–[39] have long been used to eliminate the artifacts due to blood flow and pulsatile motion in the body. More recently, bipolar gradient pulses placed on either side of the spin echo refocusing RF pulse have been used for velocity compensation during diffusion-encoding in human cardiac DTI [26]. Although the general framework of GMN provides a mechanism to compensate for any number of motion terms, in practice most pulse sequences compensate for only the lowest components, such as velocity, which dominate physiologic motion.
B. Higher-order motion compensation
When lower order motion compensation is not sufficient, methodologies also exist to modify the waveforms to achieve higher order compensation. One approach is the binomial expansion method [38], which takes advantage of the properties of the gradient moment integral in (2) and successively adds inverted replicas of the gradient waveform immediately adjacent to the original waveforms for compensating progressively higher order motion. This method is the basis for using a pair of bipolar gradient pulses (as opposed to the conventionally used monopolar pulsed gradient) to compensate for velocity [26], and four pairs of bipolar pulses to compensate for acceleration [33]. (In the current work, compensation for a specific motion component (such as acceleration) implies concurrent compensation for lower-order components (position and velocity), unless otherwise specified.) Although elegant in its simplicity, GMN via binomial expansion of the gradient pulses has two practical limitations. First, for each successive order of motion compensation, the required number of gradient pulses is doubled, which has adverse implications for the TE and achievable diffusion-weighting b-value (when pulse duration is shortened to preserve the TE). Second, the method works only when the gradient timings (pulse widths and separations) are fixed, and does not apply to higher order motion compensation when, for example, extra timing delay between gradient waveform replicas is needed. There are several instances of timing changes in the gradient waveform when binomial expansion cannot be applied [38].
C. Novel Designs of Practical Higher Order Motion Compensated Diffusion Pulses
Since rapid inversions of the spin phase reduce the diffusion encoding b-value, to be practical, higher order motion compensated diffusion encoding gradient waveforms must utilize fewer but longer gradient pulses to simultaneously minimize the TE and maximize the level of diffusion encoding. In the present work, optimal motion-compensated spin-echo diffusion encoding waveforms consist of a minimum and equal number of gradient pulses placed on either side of the refocusing RF pulse. (The timing of the waveform need not be symmetrical about the RF pulse.) In order to null up to the second moment and achieve the desired b-value, diffusion-encoding waveforms that compensate for acceleration should consist of a minimum of four alternating pulses, as shown in Fig. 1a for equal-duration trapezoidal encoding pulses. A more straightforward approach could be to use binomial expansion, as detailed in the previous section, but six diffusion-encoding gradient pulses would be necessary to compensate up to acceleration, increasing the diffusion time required for a specific b-value. For the indicated timing variables in Fig. 1a and solving the system of analytical equations for nulling the zeroth, first, and second moments of the waveform, as formulated in (2), a novel expression that relates the gradient amplitudes can be obtained,
Fig. 1.
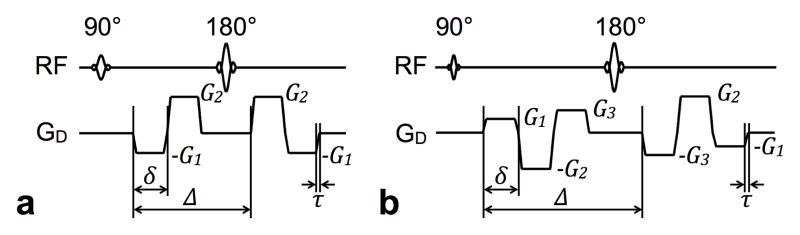
Spin-echo diffusion-encoding schemes for higher-order motion compensation. Gradient waveforms using practical trapezoidal pulses that compensate for acceleration (a) and jerk (b) are shown, with amplitude and timing labeling indicated for reference in the text.
| (3) |
where Δ is the separation between the leading edges of the first and third diffusion pulses and δ is the duration of a single diffusion pulse. Denoting the gradient ramp time with τ, the gradient amplitude and timing settings would correspond to a diffusion-encoding b-value of
| (4) |
Alternatively, to reach a desired b-value, the required gradient amplitudes can be obtained by,
| (5) |
| (6) |
Since the unequal G1 and G2 amplitudes mean that the spins are not completely refocused before the refocusing RF pulse, crusher gradient pulses, which would add to the minimum TE, are not needed.
Following the same design procedures, practical jerk-compensated diffusion-encoding schemes require six total gradient pulses, as shown in Fig. 1b. The required gradient pulse amplitude relationships are given by,
| (7) |
| (8) |
where G1, G2, and G3 are depicted in Fig. 1b. The corresponding b-value is specified by
| (9) |
Similarly, to achieve the desired b-value, the required gradient amplitudes were,
| (10) |
| (11) |
| (12) |
Since the gradient waveform has nulled zeroth moment at its halfway point, in other words the sum of G1, G2, and G3 is zero, crusher gradient pulses will be needed. Again, binomial expansion could be used to design a jerk-compensated sequence, but a total of ten diffusion-encoding gradient pulses would be necessary, increasing the diffusion time required for a specific b-value.
Although not investigated in the current study, the aforementioned methodology will also apply for designing diffusion gradient encoding waveforms that compensate for motion beyond jerk.
III. Methods
The effectiveness of the acceleration- and jerk-compensated diffusion encoding waveforms that were designed with the procedure in Part II was evaluated via both simulations on a numerical beating heart phantom and in live rats.
A. Numerical Testing
1) Realistic Numerical Beating Heart Phantom
To create a realistic beating heart model needed for subsequent motion sensitivity analysis, MRI was performed on a healthy, male Sprague-Dawley rat (350 g weight) using protocols approved by the University of Utah Institutional Animal Care and Use Committee in accordance to the Guide for the Care and Use of Laboratory Animals issued by the US National Institutes of Health (NIH Publication No. 85-23, rev. 1996). The animal was first anesthetized with 3.5% isoflurane in pure O2 (3.0 L/min). The animal’s vital signs, including heart and respiratory rate, blood oxygenation level, and rectal temperature, were continuously monitored and used to adjust the level of anesthesia when needed. A Bruker Biospec 70/30 instrument (Bruker Biospin, Billerica, MA) equipped with a 600 mT/m gradient set (BGA-12S) was used to acquire high-temporal resolution, short- and long-axis 2D FLASH-CINE images (7.73/2.8 ms TR/TE, 192 × 192 matrix size, 6.0 × 6.0 cm2 FOV, 3.0 mm slice thickness) in the mid-ventricular and four-chamber planes over the cardiac cycle (27 frames, 208 ms average R-R).
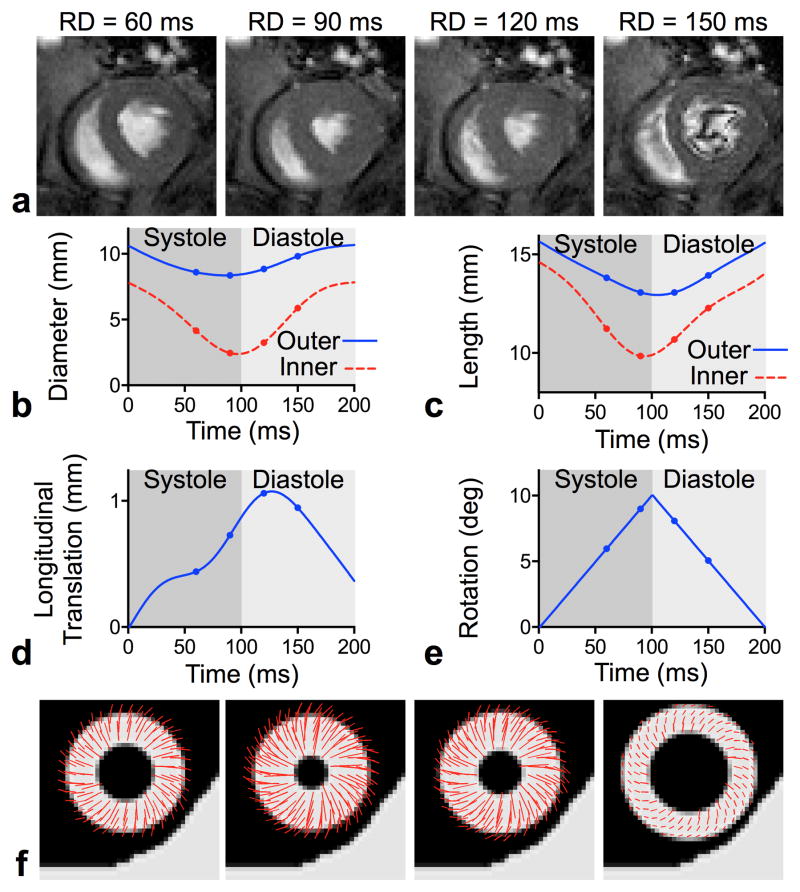
To create the numerical beating heart phantom, the inner and outer diameters and long-axis lengths of the left ventricular myocardium were measured frame-by-frame on the FLASH-CINE images (see Fig. 2), similar to the procedures described in [26]. In addition, the translation of the LV in the long-axis was measured by tracking the midpoint of the base and apex throughout the cardiac cycle in order to incorporate through-plane motion into the model. These measurements were smoothed using a 16th order Butterworth filter to reduce numerical artifacts arising from inconsistencies of manual ventricular wall tracking. To capture the torsional motion of the beating left ventricle, a rotational component – linearly increasing to 10° at end-systole and decreasing back to 0° at end-diastole – was imposed. The left ventricular diameters and lengths were used to define the major and minor axes of a prolate spheroid, while the longitudinal component shifted the center of the spheroid, allowing it to move through the imaging plane. The prolate spheroidal components, along with the rotational component, were then linearly interpolated over time and used to construct a 3D numerical motion phantom of the beating left ventricle, which allowed motion profiles at any given location in the numerical phantom, during an arbitrary time period of the cardiac cycle, to be computed. A static “chest wall” was added next to the beating heart to provide a stationary reference in the following motion sensitivity simulations. Subsequently, short-axis slices were simulated with the same in-plane resolution (0.35 × 0.35 mm2), slice thickness (3mm), and matrix size (128 × 128) as the in vivo experiments presented in a later section (see Section III.B).
Fig. 2.
Creation of the 3D numerical motion phantom. FLASH-cine images obtained at specified readout delays (RD) in the short- (a) and long- axis (not shown) from which the inner and outer diameters (b) and lengths (c) of the left ventricular myocardial walls were measured. From these measurements, along with components of longitudinal translation (d) and linear in-plane rotation (e), a prolate spheroid representing the left ventricle was created, with an added stationary object to simulate the chest wall. Displacement profiles with respect to the first frame of the CINE acquisition are superimposed on simulated short-axis slices of the numerical motion phantom in (f).
2) Gradient Waveform Motion Sensitivity Characterization
As a metric for evaluating the effectiveness of the gradient waveforms for motion compensation, images of the numerical motion phantom were generated via a two-step process that included first computing the spin phase induced by the diffusion-sensitive waveform, GD, in the presence of motion, followed by using the MRI signal equation to simulate artifacts due to motion. Without loss of generality, spin echo images, where each line of the k-space was obtained independently, were simulated. The spin echo acquisition, which was prone to shot-to-shot phase variation, was selected as a rigorous test of the proposed schemes and to isolate motion artifacts from other confounding issues, such as image distortion present in EPI.
To estimate the motion-induced spin phase for each voxel location (x, y) under the diffusion gradient waveform GD, (1) was modified to,
| (13) |
to account for the gradient waveform length T and the cardiac cycle time point. The latter was represented by the readout delay RD, or the time between the ECG R-wave and the start of the MRI readout pulse, which was done so waveforms of different lengths would yield similar LV images.
The computed motion-induced spin phase was then incorporated into standard MRI signal equation according to
| (14) |
where ρRD is the proton density at the specified RD during the cardiac cycle defined by the 3D motion phantom, Δt is the readout sampling period, Gx is the gradient amplitude of the readout pulse, τ is the phase encoding pulse duration, ΔGy is the phase encoding gradient step, and m and n are the readout and phase encoding indices, respectively.
Due to differences in their nature, motion artifacts due to intravoxel phase dispersion and shot-to-shot phase modulation in a multi-shot acquisition were simulated separately. Intravoxel phase dispersion was obtained by creating ρRD and ρRD maps at a higher spatial resolution, but cropping out the corresponding outer k-space before reconstructing the images, similar to what was done in [35]. Shot-to-shot variability of the spin phase was achieved by randomizing the RD in (13) and (14) with the specified Gaussian standard deviation around the nominal mean, to mimic the effects of physiologic fluctuations of the cardiac R-R interval or errors in identifying the R-wave due to a noisy ECG signal. Since the contribution of the imaging gradient pulses to the overall phase were two orders of magnitude less than the contribution from diffusion encoding, ρRD is assumed to be constant during a given readout and is recalculated and randomized for each phase encoding step when the diffusion encoding is repeated.
For simplicity, signal loss due to diffusion and T2 relaxation was excluded in all simulations.
3) Performance Evaluation
To assess the effectiveness of the proposed acceleration- and jerk-compensation schemes, images were generated via the aforementioned procedures and waveforms designed in Part II, and compared to those obtained using conventional non-compensated (mono-polar pulses) and velocity-compensated (bipolar pulses) diffusion waveforms. The diffusion-encoding waveforms were implemented with their shortest possible length T, as would be done in practice, to achieve the same b-value of 350 s/mm2 using 400 mT/m peak gradient amplitude and 280 μs gradient ramp time. These settings corresponded to an individual gradient pulse width δ of 2.88, 2.87, 3.76 and 3.76 ms, and separation time Δ of 5.4, 10.04, 11.83 and 16.15 ms for the uncompensated, velocity-, acceleration-, and jerk-compensated waveforms, respectively.
Three separate numerical experiments were conducted to compare the performances of the diffusion encoding waveforms in compensating for the effects of each of (a) intravoxel phase dispersion due to different motion profiles at different cardiac cycle points, (b) shot-to-shot phase variability at different cardiac cycle points, (c) shot-to-shot phase variability as a function of the degree of the variability for a given cardiac cycle point.
In the first experiment, images were obtained at arbitrarily selected RD values of 60, 90, 120 and 150 ms, which according to the motion profiles shown in Fig. 2, roughly corresponded to the cardiac cycle mid-systole, end-systole, beginning-diastole and end-diastole, respectively. No shot-to-shot variation was added, to simulate perfectly constant R-R interval and ideal gating. High-resolution ρRD and ρRD maps were generated at four-times the final image matrix size, or 512 × 512. Subsequently, 128 × 128 MR images were obtained from the corresponding central k-space.
In the second and third experiments, the spin phase within each voxel was considered constant to focus on the effects of shot-to-shot phase variation. To investigate the performance at different time points of the cardiac cycle, images (128 × 128 matrix size) were obtained for each diffusion-encoding waveform using the same nominal RD values as in the first experiment. Motion artifacts were introduced by adding to the nominal RD a small, random Gaussian-distributed variation of 5 ms standard deviation for each line of k-space. In contrast, the dependence of the performance on the degree of shot-to-shot variability was investigated by similarly generating images with the same nominal RD, 90 ms, but different standard deviations, 1.0, 2.0, 5.0, and 7.5 ms, which were equivalent to 0.50%, 1.00%, 2.50%, and 3.75% of the actual R-R interval, respectively.
The root mean squared error (RMSE) between the numerical motion phantom and each of the simulated images was calculated for comparison.
B. In Vivo Imaging in Rats
Imaging experiments were performed in vivo to demonstrate the effectiveness of the three motion compensation schemes. Four male Sprague-Dawley rats (285 g ± 35 g) were prepared similarly to that described in Section III.A.1. The acceleration- (24 ms TE) and jerk-compensated (33 ms TE) schemes were each incorporated into a standard spin-echo sequence and used to obtain diffusion-weighted images (1500 ms TR, 128 × 128 matrix size, 0.35 × 0.35 × 3.0 mm3 voxel size, 4.48 × 4.48 cm2 FOV, 1 signal average, 350 s/mm2 b-value, 280 μs ramp time, 400 mT/m maximum gradient amplitude) encoded in three perpendicular directions (slice, readout and phase-encoding axes) on the animals (295 bpm average heart rate) with dual cardiac and respiratory gating. A readout delay of 90 ms was selected to image the heart close to end-systole, which maximized the number of pixels obtained across the myocardium. The SNR was calculated in four quadrants of the LV myocardium and averaged for comparison between the acceleration- and jerk-compensated cases. Diffusion scans using monopolar (non-compensated, 13 ms TE) and bipolar (velocity compensated, 20 ms TE) encoding pulses were also acquired with the same acquisition parameters for comparison.
Because acceleration-compensation was found to provide the best tradeoff between motion sensitivity reduction and T2 relaxation loss, DTI was performed in the four rats utilizing acceleration-compensated diffusion scans with identical acquisition parameters as described above except that instead of 3 diffusion directions, an optimized set of 12 gradient directions [40] was used. This required an average total scan time of 50 minutes for each DTI data set.
To investigate the impact of varying levels of motion compensation on DTI parameter maps, DTI data was acquired in two of the rats using velocity- and jerk-compensated diffusion encoding (during the same scanning session as the acceleration-compensated acquisition) utilizing the same acquisition parameters and 12 diffusion-encoding directions previously described.
To test the inter-animal reproducibility of acceleration-compensated DTI, eight additional rats (275 g ± 16 g, 307 bpm average heart rate) were imaged with acceleration-compensated DTI for a total of n = 12 rats (including the previous experiments). Maps of DTI parameters, including myofiber helix angle, fractional anisotropy, and mean diffusivity, were derived from diffusion-weighted images via standard methods as described previously [41].
IV. Results
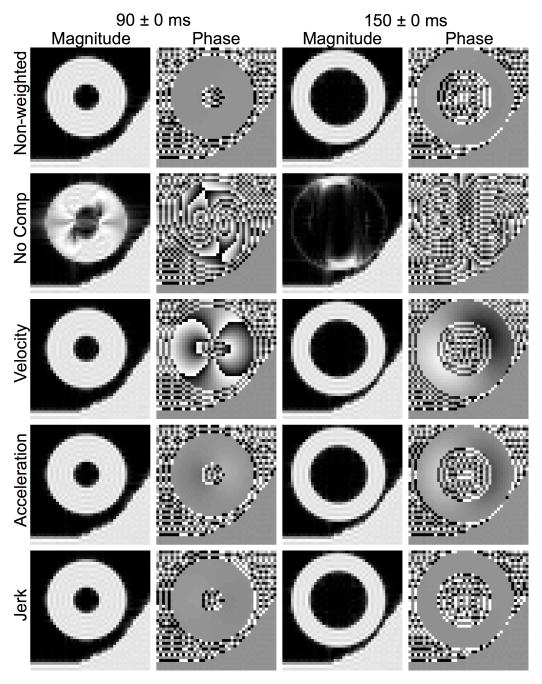
The results of the numerical experiment on the effectiveness of various degrees of motion compensation are presented in Figs. 3–5 and Tables I–III. Fig. 3 and Table I show the relative effectiveness of different degrees of motion compensation to intravoxel phase dispersion at different points of the cardiac cycle. Whereas the non-weighted case showed no signs of artifacts, the non-compensated case showed severe signal loss at all cardiac time points tested. These artifacts were largely consistent with the artifacts reported in [35]. The artifacts due to intravoxel phase dispersion were absent in the magnitude images produced from velocity-, acceleration-, and jerk-compensated diffusion encoding and the variation in image phase decreased with increasing motion compensation. The RMSE values reported in Table I are consistent with these observations, which suggest that the velocity-, acceleration-, and jerk-compensated diffusion encoding schemes sufficiently compensate for intravoxel phase dispersion for the defined motion model. The small differences between RMSE values for the velocity, acceleration, and jerk compensated cases are most likely due to the differences in diffusion encoding duration, T.
Fig. 3.
Effectiveness of intravoxel phase dispersion compensation at systole and diastole. Non-weighted and diffusion-weighted spin echo magnitude and phase images of the beating heart phantom were numerically obtained with varying degrees of compensation for intravoxel phase dispersion at the specified readout RD values representing different points of the cardiac cycle. Diffusion was encoded in the image readout (horizontal) axis.
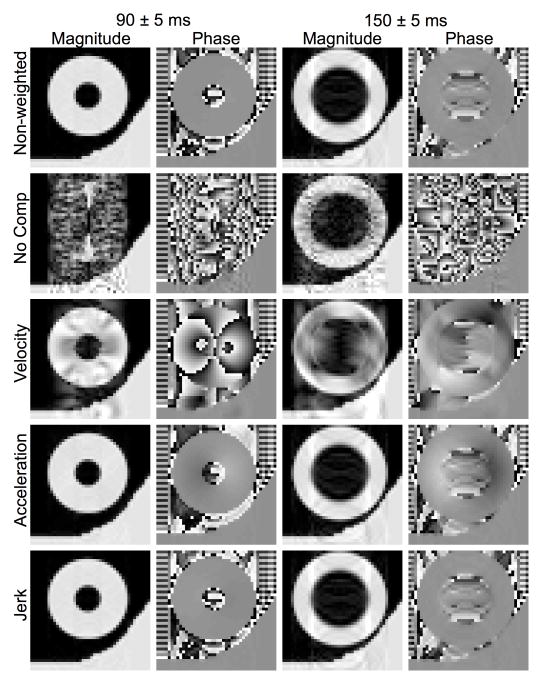
Fig. 5.
Effectiveness of motion compensation and cardiac cycle consistency. Magnitude and phase images were numerically obtained similarly as in Fig. 4, except with the same mean readout delay RD of 90 ms (end-systole) and varying degrees of gating consistency, represented by the specified standard deviation of the Gaussian distribution from which the shot-to-shot RD was randomly selected.
TABLE I.
Mean Error in the Presence of Intravoxel Phase Dispersion.
| RD | 60 ± 0 ms | 90 ± 0 ms | 120 ± 0 ms | 150 ± 0 ms |
|---|---|---|---|---|
| Scheme | ||||
| Non-weighted | 0.121 | 0.111 | 0.120 | 0.126 |
| No Comp | 0.793 | 0.309 | 0.453 | 0.826 |
| Velocity | 0.120 | 0.106 | 0.115 | 0.124 |
| Acceleration | 0.121 | 0.110 | 0.120 | 0.126 |
| Jerk | 0.121 | 0.111 | 0.120 | 0.126 |
Entries correspond to the root mean squared error between the numerical phantom magnitude and the simulated image magnitude from various diffusion encoding schemes.
TABLE III.
Mean Error in the Presence of Shot-to-Shot Phase Variation.
| RD | 90 ± 1 ms | 90 ± 2 ms | 90 ± 5 ms | 90 ± 7.5 ms |
|---|---|---|---|---|
| Scheme | ||||
| Non-weighted | 0.004 | 0.006 | 0.020 | 0.023 |
| No Comp | 0.342 | 0.546 | 0.613 | 0.637 |
| Velocity | 0.020 | 0.045 | 0.175 | 0.252 |
| Acceleration | 0.005 | 0.007 | 0.025 | 0.025 |
| Jerk | 0.004 | 0.006 | 0.020 | 0.022 |
Entries correspond to the root mean squared error between the numerical phantom magnitude and the simulated image magnitude from various diffusion encoding schemes.
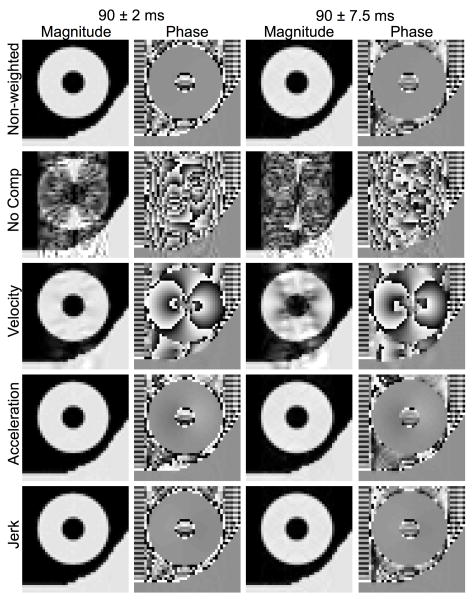
Fig. 4 shows the sensitivity of the different diffusion schemes to shot-to-shot phase variation at the same time points of the cardiac cycle. The non-weighted images at all points of the cardiac cycle were largely free of artifact, except for the minor localized hypointense areas most apparent in the RD = 150 ms (end-diastole) image that were likely caused by the small variation in the proton density between shots, unrelated to motion-induced spin phase inconsistency. In contrast, encoding diffusion without motion compensation yielded pronounced familiar ghosting and streaking artifacts associated with spin phase modulation along the image phase-encoding axis over the moving heart region, and not the static wall region. As expected, velocity compensation markedly improved the artifacts, but patches of signal loss and streaking and ghosting artifacts, signs of residual spin phase inconsistency, were still visible. Both uncompensated and velocity-compensated diffusion-weighted images showed differing severity of motion artifacts at different points of the cardiac cycle. For example, the uncompensated image at end-diastole showed the least amount of artifact, whereas velocity compensation appeared best at mid-diastole (see Table II), which suggests that different motion terms likely dominated the motion artifacts at different parts of the cardiac cycle. When acceleration-compensation was employed, the images obtained appeared nearly identical to those of the non-weighted images, indicating the effectiveness of motion compensation. The same applies to the jerk-compensated images, which were not noticeably better than acceleration-compensated images. The variation of image phase decreased with increasing motion compensation, with little difference between the acceleration- and jerk-compensated cases. Again, the RMSE values in Table II are consistent with these qualitative observations. The RMSE values of the acceleration- and jerk-compensated cases are similar to the non-weighted case, which suggests that the novel schemes sufficiently compensate for motion during diffusion encoding.
Fig. 4.
Effectiveness of motion compensation at systole and diastole. Non-weighted and diffusion-weighted spin echo magnitude and phase images were numerically obtained similarly as in Fig. 3, except with the RD’s randomized with a fixed 5 ms Gaussian-distributed standard deviation about the indicated means to simulate motion artifact due to shot-to-shot phase variations.
TABLE II.
Mean Error in the Presence of Shot-to-Shot Phase Variation.
| RD | 60 ± 5 ms | 90 ± 5 ms | 120 ± 5 ms | 150 ± 5 ms |
|---|---|---|---|---|
| Scheme | ||||
| Non-weighted | 0.080 | 0.020 | 0.058 | 0.071 |
| No Comp | 0.651 | 0.613 | 0.633 | 0.250 |
| Velocity | 0.299 | 0.175 | 0.135 | 0.374 |
| Acceleration | 0.076 | 0.025 | 0.073 | 0.067 |
| Jerk | 0.080 | 0.020 | 0.058 | 0.071 |
Entries correspond to the root mean squared error between the numerical phantom magnitude and the simulated image magnitude from various diffusion encoding schemes.
Fig. 5 shows the magnitude images numerically obtained for different motion compensation schemes at a fixed nominal mean RD (90 ms) but with different levels of RD variability, for testing the robustness of the schemes to R-R fluctuations. Compared to the non-weighted images, when a RD standard deviation of 2.0 ms was used, only the uncompensated image showed significant motion-induced ghosting and streaking artifacts. As the RD standard deviation increased, so did the artifacts seen in the uncompensated and velocity-compensated cases, albeit in the latter the severity of the artifacts was visibly reduced. In comparison, acceleration- and jerk-compensated images showed no visible artifact, even at the largest RD standard deviation (7.5 ms). Similar patterns were observed in results obtained for other points of the cardiac cycle, or mean RD values, (not shown). The phase images did not change substantially as the variation in RD increased. The RMSE values in Table III support the previous observations, where the error increased when variation in RD increased. Again, the acceleration- and jerk-compensated cases produced values close to the non-weighted case. Together, the findings in Figs. 3–5 and Tables I-III suggest that although velocity-only compensation may be sufficient when highly reproducible cardiac gating (within 1% of the R-R interval) is achievable, motion artifacts can be more reliably suppressed by employing higher order motion compensation.
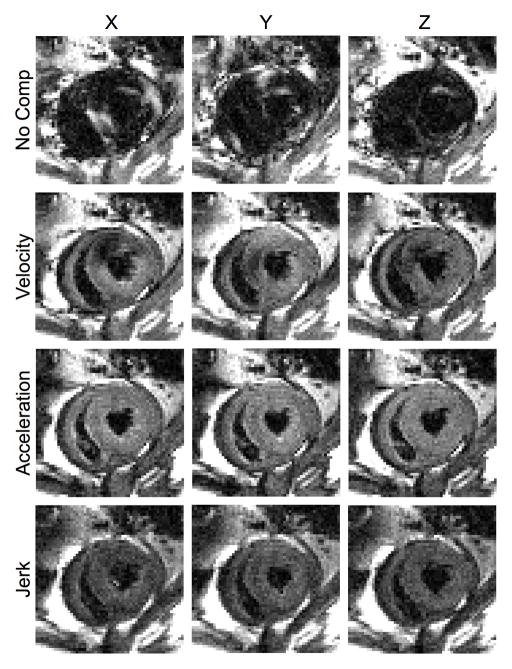
Fig. 6 shows representative diffusion-weighted images in three orthogonal encoding directions obtained with different levels of motion compensation on a live rat. The non-compensated results showed large patches of signal voids in the entire myocardium, similar to the effects of intravoxel phase dispersion seen in Fig. 3. In contrast, most of the myocardium was visible in the velocity-compensated images, although there were still regional areas of signal voids, possibly due to either, or the combination of, shot-to-shot phase variation (compare to Fig. 4) or residual intravoxel phase dispersion unaccounted by the simplistic motion model. The localized hypointense patches in the velocity-compensated images did not appear as symmetrical as they do in the simulation results in Figs. 3–5, which was likely due to the non-symmetry of the underlying cardiac kinematics [42]–[44] due to the positioning of the animal. When the animal is in the prone position, a higher degree of motion is likely to occur in the dorsal left ventricle away from the chest wall, which could result in more signal loss.
Fig. 6.
Diffusion-weighted images of the heart obtained on a live rat with various degrees of motion compensation. The images are obtained at the same cardiac short-axis location using diffusion encoding in the specified gradient axis and motion compensation scheme.
Both acceleration- and jerk-compensation yielded largely artifact-free images of the entire heart, again similar to Figs. 3–5. One notable difference between the numerical and in vivo images was in the jerk-compensated images, where the in vivo images showed visibly reduced intensity due to the prolonged TE necessary to accommodate the additional compensating and crusher gradient pulses. This observation was supported by the quantified SNRs of the in vivo acceleration and jerk-compensated images, which were 14.2, and 6.4, respectively. Consequently, acceleration compensation represented the optimal tradeoff between motion sensitivity reduction and T2 signal attenuation for practical imaging.
Finally, Fig. 7 shows myofiber helix angle, fractional anisotropy (FA), and mean diffusivity (MD) maps obtained from DTI using velocity-, acceleration-, and jerk-compensated diffusion-weighted scans on a live rat. The helix angle map obtained from acceleration-compensated diffusion encoding demonstrates the distinctive rotation from positive to negative helix angles from the endo- to epicardium [45]. Although the results need to be validated, to the authors’ knowledge, they are the first demonstrated DTI maps obtained in live rats. The transmural rotation of the helix angle is also apparent in the helix angle map derived from the jerk-compensated diffusion encoding. However, the lower SNR associated with the longer TE in the jerk-compensated case results in a noisier helix angle map and elevated FA, as expected [46]. The transmural rotation in velocity-compensated case is present in the ventral wall, but not in the dorsal wall where more motion is suspected. Fig. 8 shows DTI parameter maps obtained in four more rats using acceleration compensation. The average MD and FA values over the LV in the acceleration-compensated case in the 12 rat hearts were found to be 1.44 ± 0.08 × 10−3 mm2/s and 0.41 ± 0.05, respectively, which shows low inter-subject variability. These measurements are also in general agreement with values previously reported in Langendorff perfusion studies in the rat (1.01 ± 0.07 × 10−3 mm2/s and 0.34 ± 0.04) [47] and in vivo studies in the mouse (~1.2 × 10−3 mm2/s and ~0.29) [30], given the dissimilar experimental setup and species involved.
Fig. 7.
DTI images obtained on a live rat using velocity-, acceleration-, and jerk-compensated diffusion encoding in the same cardiac short-axis slice. The helix angle maps obtained from acceleration- and jerk-compensation exhibit the well-known transmural variation from positive to negative helix angles from the endo- to epicardium. However, the maps obtained from jerk-compensation are noisier due to the prolonged TE necessary to accommodate the additional moment nulling gradients. No smoothing was applied to these results.
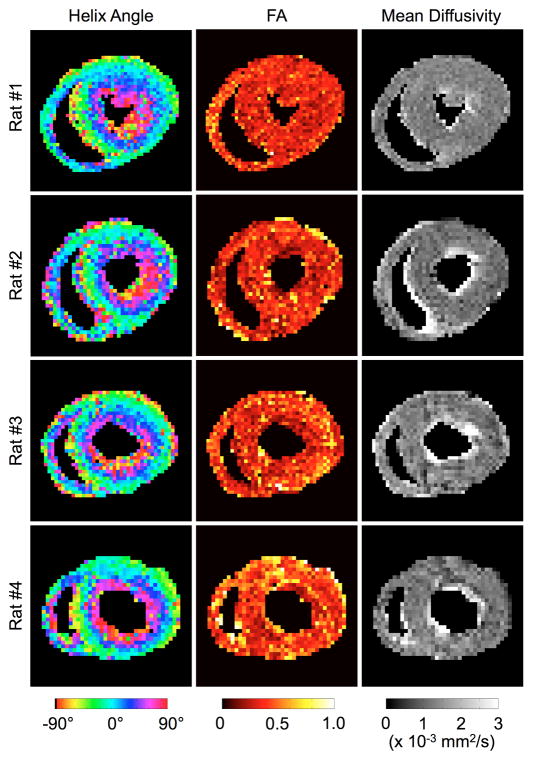
Fig. 8.
Unsmoothed DTI images obtained in four live rats. Again, the helix angle maps exhibit the distinctive counterclockwise transmural rotation of the myocardial fiber orientation. In contrast, fractional anisotropy and mean diffusivity maps show the scalar DTI properties to be relatively homogeneous in the short-axis slice.
V. Discussion
Results of the motion sensitivity analysis (Figs. 3–5) reveal that previous attempts of in vivo diffusion MRI or DTI in the rat heart likely have been complicated by insufficient motion compensation of the monopolar or bipolar diffusion encoding gradient waveforms used. Both numerical verification and live animal experimentation demonstrate the feasibility of encoding diffusion while simultaneously reducing the sensitivity to higher-order motion via the proposed moment-nulled gradient waveforms. Although waveforms that compensate for progressively higher-order motion are accompanied by lower achievable b-values and longer TE, acceleration compensation is shown to provide the necessary and sufficient combination of diffusion encoding, motion sensitivity reduction, and SNR preservation for practical diffusion MRI. Overall, these findings are highly promising and pave the way for longitudinal evaluation of myocardial remodeling associated with maturation, disease progression, and recovery in the rat.
The implementation adopted in the current study, by combining gradient pulses of identical duration but different amplitude in a spin echo setting, is not meant to be unique. While the principle of motion compensation by gradient moment nulling remains the same, there exist alternative ways motion-compensated diffusion encoding can be realized in practice, depending on the specific criteria desired. For example, acceleration-compensated diffusion encoding can also be carried out by gradient pulses with the same peak amplitude (either positive or negative polarity) but different durations, as shown in Fig. 9, with the required gradient durations related by,
Fig. 9.
Diagram of an alternative implementation of acceleration-compensated spin echo diffusion encoding using constant amplitude but variable width gradient pulses.
| (15) |
Under these timing conditions, the gradient waveform can achieve a b-value of
| (16) |
The expected main benefit of the implementation using peak-amplitude gradient pulses is its shorter TE, larger achievable b-value, or both. For instance, utilizing the 400 mT/m peak-amplitude gradients of the current study, the TE could be shortened by 2.45 ms for the same b-value of 350 s/mm2. Alternatively, the same 19.43 ms waveform length, T, would translate to an achievable b-value improvement of 66%, to 580 s/mm2.
Besides different gradient pulse specifications, the proposed diffusion encoding waveforms with higher-order motion compensation can also be alternatively implemented using different pulse sequences instead of spin echo, like the case of double-gated stimulated echo for acceleration compensation shown in Fig. 10. Because the same relationships specified in (3)–(6) also apply, and that the spins are not fully refocused prior to the magnetization restoring RF pulse, while there is the automatic 50% signal loss, the main advantage of the stimulated echo implementation is the increased achievable b-value. Indeed, using the same diffusion-encoding gradient pulse amplitudes and durations (δ), the longer pulse separation (Δ) afforded in the stimulated echo preparation would increase the b-value to 680 s/mm2, nearly double of the 350 s/mm2 attained in the current study via spin echo. Likewise, it is conceivable that the proposed higher-order motion compensation schemes could be adopted using, for example, echo-planar (EPI) acquisition to shorten the scan time.
Fig. 10.
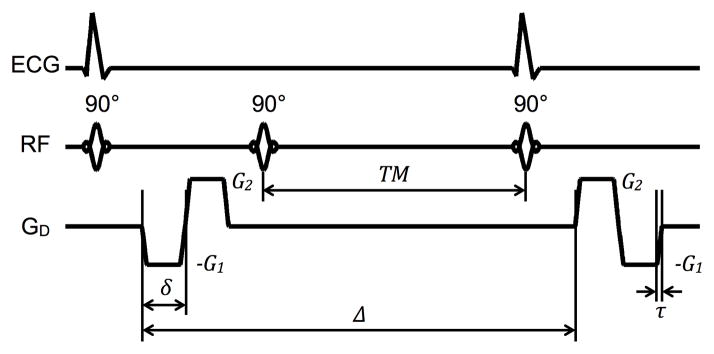
Diagram of an alternative implementation of acceleration-compensated, diffusion-weighted gradient pulses in a STEAM sequence for acquisition over two consecutive heartbeats.
Regardless of the means of implementation, the main potential pitfall of employing motion-compensated diffusion pulses in diffusion imaging or DTI is the reduced image SNR associated with the lengthened TE. Compensating for acceleration requires stronger, or longer duration, diffusion gradient pulses in order to achieve the same diffusion weighting b-value when compared to using uncompensated or velocity-compensated diffusion encoding pulses. This may be problematic when a sufficiently strong gradient set is unavailable or when imaging tissues with short T2 relaxation. Even though acceleration-compensation performed the best in the current study, there likely remains a significant noise contribution in the resulting parameter maps. Reconstruction methods [48] may be able to both speed acquisition and increase SNR. Finally, strong magnetic gradient pulses with alternating polarity, like those used here, are more prone to eddy current effects and concomitant magnetic fields. Phase errors from concomitant fields are easily eliminated by using a refocusing pulse, similar to the spin echo preparation used in the present study.
Logistical constraints restricted the current study to a single slice per animal. The long scan times resulting from the use of multi-shot spin echo acquisition also limited the study to one DTI set in the majority of the animals. Therefore, intra-subject repeatability was not directly evaluated. However, good repeatability is implied in the excellent inter-subject reproducibility observed in the tight standard deviations of global DTI parameters.
Lastly, it should be noted that, while the ability to compensate for higher-order motion in diffusion MR acquisitions is highly desirable and represents a significant step of advancement, it is only part of a nuanced approach required to accurately characterize the myocardial microstructure and fiber orientation via in vivo DTI. For example, tissue deformation, or strain, is known to skew MR diffusion measurements [49], [50], which require correcting [23], [27]. The impact on acceleration-compensated diffusion encoding remains to be investigated, but like the case of bipolar encoding gradient pulses [25], [26], the partial refocusing of spins that occurs during the proposed scheme is expected to at least partially reduce the errors caused by strain. Another potential physiology-induced complication that may need to be accounted for are the effects of perfusion on diffusion measurements [51]. Systematic examinations of these complicating factors are beyond the scope of the current study, but represent worthy areas of future research.
In conclusion, the present study employed the principles of gradient moment nulling and derived diffusion-encoding schemes that efficiently compensate for higher motion components, including acceleration and jerk. The effectiveness of the proposed diffusion-encoding schemes was evaluated via numerical verification on a realistic motion phantom of the rat heart, and empirical demonstration of cardiac diffusion MRI on live rats. Acceleration compensation was found to provide both the necessary and sufficient compromise among achievable b-value, motion sensitivity reduction, and SNR preservation for practical diffusion MRI in rats, for the given gradient hardware capabilities. The resulting sequence was used to demonstrate the first successful DTI myocardial fiber orientation and FA maps obtained in vivo in rats. These findings suggest that prospective compensation for acceleration, along with lower motion components, can be an effective alternative or adjunct to high-performance gradient hardware for improving in vivo cardiac DTI.
Acknowledgments
This research was supported in part by the National Institutes of Health grants R01 HL092055, S10 RR023017, and R01 NS08376.
Contributor Information
Christopher L. Welsh, Email: chris.welsh@utah.edu, Department of Bioengineering, University of Utah, Salt Lake City, UT 84112 USA
Edward V. R. DiBella, Email: Edward.DiBella@hsc.utah.edu, Department of Radiology, UCAIR, University of Utah, Salt Lake City, UT 84112 USA.
Edward W. Hsu, Email: edward.hsu@utah.edu, Department of Bioengineering, University of Utah, Salt Lake City, UT 84112 USA.
References
- 1.Tseng WI, Dou J, Reese TG, Wedeen VJ. Imaging myocardial fiber disarray and intramural strain hypokinesis in hypertrophic cardiomyopathy with MRI. J Magn Reson Imaging. 2006 Jan;23(1):1–8. doi: 10.1002/jmri.20473. [DOI] [PubMed] [Google Scholar]
- 2.Wu MT, Su MY, Huang YL, Chiou KR, Yang P, Pan HB, Reese TG, Wedeen VJ, Tseng WI. Sequential changes of myocardial microstructure in patients postmyocardial infarction by diffusion-tensor cardiac MR: correlation with left ventricular structure and function. Circ Cardiovasc Imaging. 2009 Jan;2(1):32–40. doi: 10.1161/CIRCIMAGING.108.778902. [DOI] [PubMed] [Google Scholar]
- 3.Toussaint N, Sermesant M, Stoeck CT, Kozerke S, Batchelor PG. In vivo human 3D cardiac fibre architecture: reconstruction using curvilinear interpolation of diffusion tensor images. Med Image Comput Comput Assist Interv. 2010 Jan;13:418–25. doi: 10.1007/978-3-642-15705-9_51. [DOI] [PubMed] [Google Scholar]
- 4.Plank G, Burton RAB, Hales P, Bishop M, Mansoori T, Bernabeu MO, Garny A, Prassl AJ, Bollensdorff C, Mason F, Mahmood F, Rodriguez B, Grau V, Schneider JE, Gavaghan D, Kohl P. Generation of histo-anatomically representative models of the individual heart: tools and application. Philos Trans A Math Phys Eng Sci. 2009 Jun;367(1896):2257–92. doi: 10.1098/rsta.2009.0056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vadakkumpadan F, Arevalo H, Ceritoglu C, Miller M, Trayanova N. Image-based estimation of ventricular fiber orientations for personalized modeling of cardiac electrophysiology. IEEE Trans Med Imaging. 2012 May;31(5):1051–60. doi: 10.1109/TMI.2012.2184799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Geerts L, Bovendeerd PHM, Nicolay K, Arts T. Characterization of the normal cardiac myofiber field in goat measured with MR-diffusion tensor imaging. Am J Physiol Heart Circ Physiol. 2002 Jul;283(1):H139–45. doi: 10.1152/ajpheart.00968.2001. [DOI] [PubMed] [Google Scholar]
- 7.Phatak NS, Maas SA, Veress AI, Pack NA, DiBella EVR, Weiss JA. Strain measurement in the left ventricle during systole with deformable image registration. Med Image Anal. 2009 Apr;13(2):354–61. doi: 10.1016/j.media.2008.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen J, Song SK, Liu W, McLean M, Allen JS, Tan J, Wickline SA, Yu X. Remodeling of cardiac fiber structure after infarction in rats quantified with diffusion tensor MRI. Am J Physiol Heart Circ Physiol. 2003 Sep;285(3):H946–54. doi: 10.1152/ajpheart.00889.2002. [DOI] [PubMed] [Google Scholar]
- 9.Wu MT, Tseng WI, Su MY, Liu CP, Chiou KR, Wedeen VJ, Reese TG, Yang CF. Diffusion tensor magnetic resonance imaging mapping the fiber architecture remodeling in human myocardium after infarction: correlation with viability and wall motion. Circulation. 2006 Sep;114(10):1036–45. doi: 10.1161/CIRCULATIONAHA.105.545863. [DOI] [PubMed] [Google Scholar]
- 10.Wu EX, Wu Y, Nicholls JM, Wang J, Liao S, Zhu S, Lau CPP, Tse HFF. MR diffusion tensor imaging study of postinfarct myocardium structural remodeling in a porcine model. Magn Reson Med. 2007 Oct;58(4):687–95. doi: 10.1002/mrm.21350. [DOI] [PubMed] [Google Scholar]
- 11.Strijkers GJ, Bouts A, Blankesteijn WM, Peeters THJM, Vilanova A, van Prooijen MC, Sanders HMHF, Heijman E, Nicolay K. Diffusion tensor imaging of left ventricular remodeling in response to myocardial infarction in the mouse. NMR Biomed. 2009 Feb;22(2):182–90. doi: 10.1002/nbm.1299. [DOI] [PubMed] [Google Scholar]
- 12.Mekkaoui C, Huang S, Dai G, Reese TG, Ruskin J, Hoffmann U, Jackowski MP, Sosnovik DE. Myocardial infarct delineation in vivo using diffusion tensor MRI and the tractographic propagation angle. J Cardiovasc Magn Reson. 2013;15(1):2. [Google Scholar]
- 13.Helm PA, Younes L, Beg MF, Ennis DB, Leclercq C, Faris OP, McVeigh E, Kass D, Miller MI, Winslow RL. Evidence of structural remodeling in the dyssynchronous failing heart. Circ Res. 2006 Jan;98(1):125–32. doi: 10.1161/01.RES.0000199396.30688.eb. [DOI] [PubMed] [Google Scholar]
- 14.Wang VY, Lam HI, Ennis DB, Cowan BR, Young AA, Nash MP. Modelling passive diastolic mechanics with quantitative MRI of cardiac structure and function. Med Image Anal. 2009 Oct;13(5):773–84. doi: 10.1016/j.media.2009.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hsu EW, Muzikant AL, Matulevicius SA, Penland RC, Henriquez CS. Magnetic resonance myocardial fiber-orientation mapping with direct histological correlation. Am J Physiol. 1998 May;274(5):H1627–34. doi: 10.1152/ajpheart.1998.274.5.H1627. [DOI] [PubMed] [Google Scholar]
- 16.Walker JC, Guccione JM, Jiang Y, Zhang P, Wallace AW, Hsu EW, Ratcliffe MB. Helical myofiber orientation after myocardial infarction and left ventricular surgical restoration in sheep. J Thorac Cardiovasc Surg. 2005 Feb;129:382–90. doi: 10.1016/j.jtcvs.2004.06.006. [DOI] [PubMed] [Google Scholar]
- 17.Jiang Y, Hsu EW. Accelerating MR diffusion tensor imaging via filtered reduced-encoding projection-reconstruction. Magn Reson Med. 2005 Jan;53(1):93–102. doi: 10.1002/mrm.20311. [DOI] [PubMed] [Google Scholar]
- 18.Wu Y, Zhang LJ, Zou C, Tse HF, Wu EX. Transmural heterogeneity of left ventricular myocardium remodeling in postinfarct porcine model revealed by MR diffusion tensor imaging. J Magn Reson Imaging. 2011 Jul;34(1):43–9. doi: 10.1002/jmri.22589. [DOI] [PubMed] [Google Scholar]
- 19.Garrido L, Wedeen VJ, Kwong KK, Spencer UM, Kantor HL. Anisotropy of water diffusion in the myocardium of the rat. Circ Res. 1994 May;74(5):789–793. doi: 10.1161/01.res.74.5.789. [DOI] [PubMed] [Google Scholar]
- 20.Scollan DF, Holmes A, Winslow R, Forder J. Histological validation of myocardial microstructure obtained from diffusion tensor magnetic resonance imaging. Am J Physiol. 1998 Dec;275(6):H2308–18. doi: 10.1152/ajpheart.1998.275.6.H2308. [DOI] [PubMed] [Google Scholar]
- 21.Hsu EW, Buckley DL, Bui JD, Blackband SJ, Forder JR. Two-component diffusion tensor MRI of isolated perfused hearts. Magn Reson Med. 2001 Jun;45(6):1039–45. doi: 10.1002/mrm.1138. [DOI] [PubMed] [Google Scholar]
- 22.Edelman RR, Gaa J, Wedeen VJ, Loh E, Hare JM, Prasad P, Li W. In vivo measurement of water diffusion in the human heart. Magn Reson Med. 1994 Sep;32(3):423–8. doi: 10.1002/mrm.1910320320. [DOI] [PubMed] [Google Scholar]
- 23.Reese TG, Weisskoff RM, Smith RN, Rosen BR, Dinsmore RE, Wedeen VJ. Imaging myocardial fiber architecture in vivo with magnetic resonance. Magn Reson Med. 1995;34(6):786–791. doi: 10.1002/mrm.1910340603. [DOI] [PubMed] [Google Scholar]
- 24.Tseng WI, Reese TG, Weisskoff RM, Brady TJ, Wedeen VJ. Myocardial fiber shortening in humans: initial results of MR imaging. Radiology. 2000 Jul;216(1):128–39. doi: 10.1148/radiology.216.1.r00jn39128. [DOI] [PubMed] [Google Scholar]
- 25.Dou J, Reese TG, Tseng WI, Wedeen VJ. Cardiac diffusion MRI without motion effects. Magn Reson Med. 2002 Jul;48(1):105–14. doi: 10.1002/mrm.10188. [DOI] [PubMed] [Google Scholar]
- 26.Gamper U, Boesiger P, Kozerke S. Diffusion imaging of the in vivo heart using spin echoes--considerations on bulk motion sensitivity. Magn Reson Med. 2007 Feb;57(2):331–7. doi: 10.1002/mrm.21127. [DOI] [PubMed] [Google Scholar]
- 27.Tseng WI, Reese TG, Weisskoff RM, Wedeen VJ. Cardiac diffusion tensor MRI in vivo without strain correction. Magn Reson Med. 1999;42:393–403. doi: 10.1002/(sici)1522-2594(199908)42:2<393::aid-mrm22>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 28.Dou J, Tseng WI, Reese TG, Wedeen VJ. Combined diffusion and strain MRI reveals structure and function of human myocardial laminar sheets in vivo. Magn Reson Med. 2003 Jul;50(1):107–13. doi: 10.1002/mrm.10482. [DOI] [PubMed] [Google Scholar]
- 29.Nielles-Vallespin S, Mekkaoui C, Gatehouse P, Reese TG, Keegan J, Ferreira PF, Collins S, Speier P, Feiweier T, de Silva R, Jackowski MP, Pennell DJ, Sosnovik DE, Firmin D. In vivo diffusion tensor MRI of the human heart: reproducibility of breath-hold and navigator-based approaches. Magn Reson Med. 2013 Sep;70(2):454–464. doi: 10.1002/mrm.24488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Huang S, Mekkaoui C, Chen HH, Wang R, Ngoy S, Liao R, Wedeen VJ, Dai G, Sosnovik DE. Serial diffusion tensor MRI and tractography of the mouse heart in-vivo: impact of ischemia on myocardial microstructure. J Cardiovasc Magn Reson. 2011;13(Suppl 1):O28. [Google Scholar]
- 31.Schumacher B, Pecher P, von Specht BU, Stegmann T. Induction of neoangiogenesis in ischemic myocardium by human growth factors: first clinical results of a new treatment of coronary heart disease. Circulation. 1998 Feb;97(7):645–650. doi: 10.1161/01.cir.97.7.645. [DOI] [PubMed] [Google Scholar]
- 32.Ravelli F, Allessie M. Effects of atrial dilatation on refractory period and vulnerability to atrial fibrillation in the isolated Langendorff-perfused rabbit heart. Circulation. 1997;96(5):1686–1695. doi: 10.1161/01.cir.96.5.1686. [DOI] [PubMed] [Google Scholar]
- 33.Nguyen C, Fan Z, Sharif B, He Y, Dharmakumar R, Berman DS, Li D. In vivo three-dimensional high resolution cardiac diffusion-weighted MRI: A motion compensated diffusion-prepared balanced steady-state free precession approach. Magn Reson Med. 2013 Nov; doi: 10.1002/mrm.25038. [DOI] [PubMed] [Google Scholar]
- 34.Simonetti OP, Wendt RE, Duerk JL. Significance of the point of expansion in interpretation of gradient moments and motion sensitivity. J Magn Reson Imaging. 1991;1(5):569–77. doi: 10.1002/jmri.1880010510. [DOI] [PubMed] [Google Scholar]
- 35.Wedeen VJ, Weisskoff RM, Poncelet BP. MRI signal void due to in-plane motion is all-or-none. Magn Reson Med. 1994 Jul;32(1):116–20. doi: 10.1002/mrm.1910320116. [DOI] [PubMed] [Google Scholar]
- 36.Trouard TP, Sabharwal Y, Altbach MI, Gmitro AF. Analysis and comparison of motion-correction techniques in diffusion-weighted imaging. J Magn Reson Imaging. 1996;6(6):925–35. doi: 10.1002/jmri.1880060614. [DOI] [PubMed] [Google Scholar]
- 37.Pattany PM, Phillips JJ, Chiu LC, Lipcamon JD, Duerk JL, McNally JM, Mohapatra SN. Motion artifact suppression technique (MAST) for MR imaging. J Comput Assist Tomogr. 1987;11(3):369–377. doi: 10.1097/00004728-198705000-00001. [DOI] [PubMed] [Google Scholar]
- 38.Keller PJ, Wehrli FW. Gradient Moment Nulling through the Nth Moment. Application of Binomial Expansion Coefficients to Gradient Amplitudes. J Magn Reson. 1988;78(1):145–149. [Google Scholar]
- 39.Pipe JG, Chenevert TL. A progressive gradient moment nulling design technique. Magn Reson Med. 1991 May;19(1):175–9. doi: 10.1002/mrm.1910190116. [DOI] [PubMed] [Google Scholar]
- 40.Jones DK, Horsfield MA, Simmons A. Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn Reson Med. 1999 Sep;42(3):515–25. [PubMed] [Google Scholar]
- 41.Jiang Y, Pandya K, Smithies O, Hsu EW. Three-dimensional diffusion tensor microscopy of fixed mouse hearts. Magn Reson Med. 2004 Sep;52(3):453–60. doi: 10.1002/mrm.20191. [DOI] [PubMed] [Google Scholar]
- 42.Oubel E, De Craene M, Hero AO, Pourmorteza A, Huguet M, Avegliano G, Bijnens BH, Frangi AF. Cardiac motion estimation by joint alignment of tagged MRI sequences. Med Image Anal. 2012 Jan;16(1):339–50. doi: 10.1016/j.media.2011.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Smal I, Carranza-Herrezuelo N, Klein S, Wielopolski P, Moelker A, Springeling T, Bernsen M, Niessen W, Meijering E. Reversible jump MCMC methods for fully automatic motion analysis in tagged MRI. Med Image Anal. 2012 Jan;16(1):301–24. doi: 10.1016/j.media.2011.08.006. [DOI] [PubMed] [Google Scholar]
- 44.Gomez AD, Merchant SS, Hsu EW. Accurate high-resolution measurements of 3-d tissue dynamics with registration-enhanced displacement encoded MRI. IEEE Trans Med Imaging. 2014 Jun;33(6):1350–62. doi: 10.1109/TMI.2014.2311755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Streeter DD, Spotnitz HM, Patel DP, Ross J, Sonnenblick EH. Fiber orientation in the canine left ventricle during diastole and systole. Circ Res. 1969 Mar;24(3):339–47. doi: 10.1161/01.res.24.3.339. [DOI] [PubMed] [Google Scholar]
- 46.Pierpaoli C, Basser PJ. Toward a Quantitative Assessment of Diffusion Anisotropy. Magn Reson Med. 1996;36:893–906. doi: 10.1002/mrm.1910360612. [DOI] [PubMed] [Google Scholar]
- 47.Hales PW, Schneider JE, Burton RAB, Wright BJ, Bollensdorff C, Kohl P. Histo-anatomical structure of the living isolated rat heart in two contraction states assessed by diffusion tensor MRI. Prog Biophys Mol Biol. 2012 Oct;110(2–3):319–30. doi: 10.1016/j.pbiomolbio.2012.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Welsh CL, Dibella EVR, Adluru G, Hsu EW. Model-based reconstruction of undersampled diffusion tensor k-space data. Magn Reson Med. 2013 Sep;70:429–440. doi: 10.1002/mrm.24486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fischer SE, Stuber M, Scheidegger MB, Boesiger P. Limitations of stimulated echo acquisition mode (STEAM) techniques in cardiac applications. Magn Reson Med. 1995 Jul;34(1):80–91. doi: 10.1002/mrm.1910340113. [DOI] [PubMed] [Google Scholar]
- 50.Reese TG, Wedeen VJ, Weisskoff RM. Measuring Diffusion in the Presence of Material Strain. J Magn Reson B. 1996 Sep;112(3):253–8. doi: 10.1006/jmrb.1996.0139. [DOI] [PubMed] [Google Scholar]
- 51.Callot V, Bennett E, Decking UKM, Balaban RS, Wen H. In vivo study of microcirculation in canine myocardium using the IVIM method. Magn Reson Med. 2003 Sep;50(3):531–40. doi: 10.1002/mrm.10568. [DOI] [PMC free article] [PubMed] [Google Scholar]