Methods to Quantify the Velocity Dependence of Common Gait Measurements from Automated Rodent Gait Analysis Devices

Abstract

Background

Walking slowly is a different biomechanical task than walking quickly, thus measures of gait will be different at different velocities, such as pre/post injury. It is necessary to determine if the difference in gait measures are from the experimental changes, or simply from traveling at different speeds.

New Method

Instead of limiting this effect, we have developed techniques to embrace the velocity dependence of gait measures. By translating the pawprints into a body coordinate frame we are able to measure location of paw placement in addition to the standard gait measures.

Results

At higher velocities rats have greater consistency of steps, place their forelimb initial contact more medially and anteriorly, and place their hindlimb toe off more medially and posteriorly. Interlimb phasing also becomes more consistent at higher velocities. Following a cervical spinal cord injury consistency is reduced and the velocity dependent behaviors are significantly different.

Comparison with Existing Method

Translating the coordinate frame improves the ability to measure changes in base of support following spinal cord injury. Employing a treadmill, or limiting analysis to a narrow velocity window does address the effects of velocity. We feel that measuring across all velocities is more appropriate than dictating that the animals match speeds.

Conclusions

Quantifying locomotion with automated gait analysis devices is a great way to evaluate the changes that experimental treatments provide. These new methods allow for a more appropriate way to address the confound of many gait measures being velocity dependent.

1.0 Introduction

Countless researchers use gait analysis to quantify behavioral changes in groups of animals, and a cottage industry exists to enable researchers to collect and process the locomotor data more quickly and accurately. The more popular automated gait analysis devices are the CatWalk (Noldus Inc, NE), DigiGait (Mouse Specifics Inc, MA), and TreadScan (Cleversys Inc, VA). We have used the CatWalk for many years to help us assess the effectiveness of therapies to restore locomotion following spinal cord injury in rats. But the more we compare our treatment groups to the pre-injury controls the more we realize we do not have a firm grasp on normal rodent locomotion. Our major concern comes from the confound of walking velocity. When walking slowly, one takes short strides infrequently, and long strides rapidly when walking fast. This simple fact that gait parameters have different values at different velocities has been known for quite some time (Heglund et al., 1974; Taylor, 1978, Hruska et al 1979) but this knowledge rarely makes its way to the users of automated gait analysis devices. A fair amount of researchers will look to limit the effects of velocity by employing a treadmill (Krizsan-Agbas et al., 2014, Redondo-Castro et al., 2013, Tom 2013) or by only analyzing data that falls in similar velocity windows (Bozkurt et al., 2011, Deumens et al., 2007). We struggled when we tried to apply that technique to our own data. Prior to injury our animals cross the walkway quickly, and one week after injury the animals are much slower. To limit the confounding effects of velocity we would need to match speeds. We could never determine if it was better to make our pre-injury animals walk slower, or excessively train our post injury animals to walk faster. So instead of limiting the effects of velocity, we have developed techniques that embrace the fact that locomotor measures change as velocity changes.

Our previous work examined how 3 common gait parameters, stride length, cycle time, and duty factor, change with increasing velocity, and how this behavior changes after spinal cord injury in rats (Neckel et al., 2013). Others have found similar velocity dependent measures of locomotion in healthy rats (Koopmans et al., 2007), mice (Batka et al., 2014) and velocity influences on coordination in cats (Frigon et al., 2014). Presented here is an expansion upon these themes, where we show the benefits of not just knowing the stride length or cycle time of a limb, but where that limb is in the context of the animals’ body. Yes, animals take longer strides when walking faster. What we show here is that rats move their limbs more medially and stretch farther when walking faster. We also offer a novel technique that quantifies the changes in coordination with increasing velocity. Taken together these findings have great implications on the current standard of rodent gait analysis and should be adopted by fellow researchers who use automated gait analysis devices in their own studies.

2.0 Material and methods

2.1 Animals and Study Design

Throughout the experiment animals were housed in the Georgetown University Division of Comparative Medicine and had unlimited access to food and water. The Georgetown University Animal Care and Use Committee approved all protocols. 74 adult female Sprague-Dawley rats were used (appx 5 weeks old, 160–220g range, 185±12g mean, Taconic Farms, Germantown, NY). These animals are part of our ongoing robotic gait training studies, and 46 of these animals were part of our previously reported work. Presented here for the first time is novel analysis of existing data.

Animals were pre-trained on the CatWalk XT9.1 gait analysis system on 3 non-consecutive days before pre-operative overground locomotion was recorded. Neither food deprivation nor food rewards were used as motivators, but a goal box (not the homecage) was located at one end of the walkway. Rats were allowed to transverse the walkway at their own self-selected walking speed and no time, velocity, or directional constraints were placed on the trials. Once several walking steps were recorded from each limb the trial was deemed complete (this could be accomplished from as few as 1 complete pass, or from several partial passes). Trotting or galloping steps were omitted.

All rats then received a right overhemisection injury at the C4–5 level (previously described in Bregman et al., 1993; Lynskey et al., 2006). Briefly, rats were anesthetized with 4% chloral hydrate (0.01 cc/g intraperitoneally), a partial C4/C5 laminectomy was done, and iridectomy scissors were used to create a lesions at C4–5. The lesion bilaterally ablates the dorsal corticospinal pathway, and unilaterally ablates the contralateral rubrospinal pathway. At the end of the study all lesion sites were reconstructed from serial cresyl violet sections and only the 61 animals with appropriate injuries were included in post-injury analysis.

The overground locomotion of all rats was re-assessed with the CatWalk 1 week after injury, with no re-training. A subset of 17 animals were then tested weekly for an additional 6 weeks starting on post-injury day 11 and ending on post-injury day 46 (hereafter referred to as weeks 2 through 7).

2.2 The Need for a New Coordinate Frame

As a rodent crosses the glass walkway of the CatWalk the pawprints reflect the light down towards the digital camera where they are recorded as a pixel array with values of time, position, and color. The time value is simply a measure of seconds from frame to frame in 9.983 msec intervals (in version XT9.1). The position is a grid with the x coordinate along the length of the glass walkway, and the y coordinate along the width of the glass. The resolution of this grid is user defined, user calibrated, and based on the distance of the camera from the glass plate. When the user labels a group of pixels as a pawprint, such as “right forelimb” the software recognizes the time when those pixels first surpass the color threshold (initial contact), when that group of pixels covers its widest area (max contact) and when those pixels are below the color threshold (toe off). The mean position of the group of pixels at max contact is used as the location of the footprint for the duration of stance phase. Once the user has labeled all the successive prints from all four limbs the software can calculate a myriad of gait measures from just that one crossing of the walkway. Figure 1A depicts one of our rats crossing the glass walkway of the CatWalk, and the user defined pawprints.

Fig 1. Benefits of Translating Footprints.

1A: the standard paw prints of a rat crossing the CatWalk (silhouettes for illustrative purposes). 1B: prints translated into a body coordinate frame with 1B1 and 1B2 from the same crossing as 1A. 1B3: all right hindlimb initial contacts from all rats in the cohort. 1B4: all right forelimb initial contacts divided into slow (blue), medium (yellow), and fast (red) velocity groups. 1C: Translation into a body coordinate frame increases the sensitivity of base of support measures, but not stride length (ANOVA, p<0.05).

Two of the more commonly reported gait measures are stride length and base of support. Stride length is the distance from one initial contact to the next. For animals traveling in straight lines this distance is along the direction of travel. For animals walking in circles the measure of stride length is more complex as it needs to be adjusted to accommodate the path of the animal. Base of support is the distance between the forelimb or hindlimb pairs. In a stationary animal, this distance is along the minor body axis. For animals walking in straight lines this distance is perpendicular to the direction of travel. Again, for animals walking in circles the measure of base of support is more complex as it needs to be adjusted to accommodate the path of the animal as well as the timing of the paw placement. The CatWalk software measures stride length as the distance between two successive pawprints and base of support as the difference between the average y position of the left and right limbs.

There is a difference between the space between labeled pixels on a computer grid and the paw placement of a walking rat. If all animals walked in straight lines that were perfectly parallel to the grid established by the CatWalk (world coordinate frame) the difference would be zero. Unfortunately, rats rarely walk in straight lines and to our knowledge are unaware of the world coordinate frame of the CatWalk (most CatWalk users are unaware of the world coordinate frame!) To remedy this we do not look at measures in the world coordinate frame, but in the body coordinate frame of the rat. This body coordinate frame has one axis along the major axis of the animal, the second axis along the minor axis of the animal, and the origin at the center of mass of the animal. Figure 1B depicts the same animal crossing as in 1A, but measured in the body coordinate frame.

In the body coordinate frame base of support is now the medial/distal placement of the paw. This measure is consistent even if the rat is walking in a non-straight line or a straight line that is not parallel to the edge of the glass plate (Fig 1B1). The measure of stride length is the anterior/posterior distance between the toe-off of one step to the initial contact of the next step. Again, these measures in the body coordinate frame of the animal are consistent with the changing position of the rat (Fig 1B2). With our body coordinate frame measures it is even possible to track the position of a paw print as it progresses through stance phase. The 4^th left hindlimb step from Fig 1A is seen in body coordinate frame in Fig 1B2 as it passes from initial contact (diamond) to max contact (triangle) through toe off (square). This measure also allows for an estimate of range of motion. A limb that cannot move can still make regular prints along the CatWalk as the whole body moves across the glass, and a stride length can be measured between successive prints. But if the limb is not moving relative to the body frame, is it a stride, or a measure of how far the other limbs have propelled the body frame?

For a rat traveling in an open field where it is free to travel in circles or zig-zags the need to translate to a body coordinate frame is rather apparent. But there is less of an obvious need to correct for the changes in path when the rats walking on the CatWalk are confined to such a narrow path anyway. When we compared our body coordinate frame measures to the standard CatWalk world coordinate frame measures we found no differences (ANOVA, p<.05). No statistical differences for measures of stride length or base of support pre or 1 week post SCI for any limb. Where the use of body coordinate frame measures becomes the better option is in its ability to assess the changes in gait measures pre/post SCI. With our body coordinate frame measures we were able to detect a significant increase in forelimb base of support following a C4/5 right over-hemisection injury. The world coordinate frame of the CatWalk is not sensitive enough to detect this difference in our animals (ANOVA, p=0.1626 Fig 1C1). Both coordinate frames are capable of measuring the decrease in stride length in all limbs following SCI (Fig 1C2).

2.3 How to Generate a Body Coordinate Frame

To convert a pawprint from the world coordinate frame of the gait analysis system to the body coordinate frame of the animal one needs to translate the origin to the center of mass and rotate the axis to the animals major axis, or body angle. Many of the latest software packages already estimate the center of mass and body angle but do not report them over time to the user. Our version of the CatWalk software did not provide either of these values, so we created our own estimates of body angle and center of mass from the data that the software did provide. We knew the position and time of successive pawprints, so we made the assumption that the limbs traveled in straight lines from one step to the next to give us an estimate of position during swing phase. The line segment between the forelimbs was considered the “shoulders” while the line segment between the hindlimbs was considered the “hips.” Additionally, the line segment from the midpoint of the “shoulders” to the midpoint of the “hips” was our estimate of the body axis, and the midpoint of this line segment was our center of mass. Because of the piecewise nature of the pawprint data, the final estimates were smoothed with a 5 point (±19.96msec) moving average filter.

A problem with using all four limbs to generate an estimate of body angle and center of mass is that the estimates are unreliable when pawprint data is absent. Generally speaking the first two forelimb prints as the animal enters the field of view and the last two hindlimb prints as the animal exits had to be discarded from analysis because at least 3 prints are needed to accurately define the body axis. Therefore we have more data in the standard CatWalk analysis than we do in our body coordinate frame analysis.

2.4 Further Benefits of Body Coordinate Frame Measures

Only one difference between our body coordinate frame measures and the standard world coordinate frame measures is hardly overwhelming proof that a change is needed. The real benefit to a body coordinate frame is not that it is slightly better in measuring base of support, but that it provides more information. Standard techniques can record the timing of initial contact, our technique captures timing and location of initial contact. Figure 1B3 shows the location of the right hindlimb initial contact of 74 healthy rats. From this body coordinate frame data measures of medial/lateral or anterior/posterior distribution can be made, and thus insight into consistency of paw placement pre/post injury and/or treatment can be made.

We also need to explain how velocity effects these parameters so we can accurately compare animals that may be traveling at different speeds. Figure 1B4 shows the initial contact placement of the right forelimb of our 74 healthy rats. Those steps that come from slow moving animals (<29cm/s) are colored blue, medium (29–36cm/s) yellow, and fast (>36cm/s) red. It should be noted that these velocities are not calculated from the time it takes to cross the entire glass walkway, but the smoothed mean stride velocity of all four limbs (11pt /±49.915msec moving average filter). This captures the slight variation in speed and path as the animals complete the passes across the walkway. When we apply the smallest ellipse that contains 95% of the data (almost as a target), visual inspection reveals that the area is reduced as the animals more faster, or the rats are more consistent with their steps, and the center of the ellipse moves anteriorly and medially, or the rats are reaching farther forward and reducing their base of support. This velocity dependence of paw placement is a measure unique to a body coordinate frame technique.

2.5 Velocity Dependence of Paw Placement

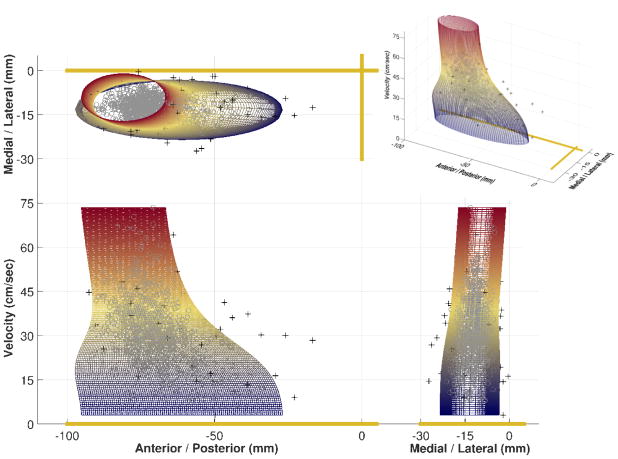
Instead of looking at ellipses at just 3 velocity ranges, we wanted to investigate how the paw placement changes across the whole spectrum of velocities. If we plot the paw placement in 2 dimensions of space (anterior-posterior and medial-lateral) we can plot in a third dimension of velocity. This creates a 3D cluster of data points. If paw placement was independent of velocity, then the cluster of data points would be uniformly and randomly distributed. If there was a velocity dependence of paw placement the cluster of data points would conform to a shape. Figure 2 shows the 908 right forelimb initial contacts from 74 healthy rats across all velocities and the smallest irregular elliptical cone that encloses 95% of the data. With the generation of such models, it is now possible to move beyond visual inspection and calculate exactly how a rat increases its consistency, reaches more anteriorly, and decreases its base of support with increasing velocity.

Fig 2. Right Forelimb Initial Contact Cone.

The smallest irregular elliptical cone that encloses 95% of the data shows that initial contact placement becomes more consistent, anterior, and medial as velocity increases. Black + - points outside of cone, gray o – points inside of cone. 908 points from 74 healthy rats.

2.6 How to Generate the Smallest Irregular Elliptical Cone

To begin, it is best to envision the irregular elliptical cone as a stack of ellipses. If there is no velocity dependence, the stack of ellipses would be random. If paw placement is velocity dependent then the shape and center location of the ellipses would change in a predictable manner as the stack gets higher. Our first step was to pass a narrow velocity window (4cm/s) up through the cluster of data points in 0.1cm/s increments. Whenever we had 5 or more data points in the window the smallest ellipse that encompassed at least 95% of the data in the anterior-posterior/medial-lateral plane was created at the level of the center of the velocity window. Only the first unique ellipse was retained as the window passed through. From this stack of ellipses we had a set of parameters such as center, area, and major axis over a range of velocities.

Our next step was to fit these parameters to a function of velocity. A 5 parameter logistic equation (5PL) was chosen for all ellipse parameters because it allowed us to assign physical limits to our model. If we removed the velocity dimension to the cluster of points, as if we were looking down on the cone, and fit a “master ellipse” that included 99% of the data, this would give us our limits to use in our 5PL. The area as a function of velocity could not exceed the area of the “master ellipse”, the center as a function of velocity could only exist within the “master ellipse”, and the major axis could not exceed the major axis of the “master ellipse”. Because neither rotation angle nor minor axis were good fits for initial contact or toe off placement of any healthy limb, they were excluded from the model. The final model for the irregular elliptical cone is given in equation 1A, where each function of velocity is a 5PL as in equation 1B.

$${\left(\frac{x-\mathit{xcenter}(z)}{\mathit{majoraxis}(z)}\right)}^2+{\left(\frac{y-\mathit{ycenter}(z)}{\frac{\mathit{area}(z)}{\pi +\mathit{majoraxis}(z)}}\right)}^2=1$$ 1A

$$f(z)=d_1+\frac{a_1-d_1}{{\left(1+{\left(\frac{z}{c_1}\right)}^{b_1}\right)}^{g_1}}$$ 1B

2.7 Limiting Effects of Velocity

Instead of embracing the effects that overground velocity has on gait measures, many researchers choose to limit the effects. Treadmill based gait analysis systems such as the DigiGait or TreadScan allow users to set the belt at a certain speed and hope that the animal matches it (and that animal never accelerates to the front of the belt nor slows down to the rear). Users of overground walkway devices like the CatWalk or MotoRater (TSE Systems, MO) tend to limit their analysis to data from passes that occurred within a 1 second window. We have previously shown that the choice of 1 second windows is not arbitrary, as healthy animals have different stride lengths, cycle times, and duty factor at “slow” velocities (6.5–7.5s window, or 17.33–20cm/s) than at “fast” velocities (2.5–3.5s, or 37.14–52cm/s) (Neckel 13).

Figure 3 shows that healthy animals have different paw placements when traveling across a wide spectrum of velocities. If we assume symmetry and combine the left limb placement with the right limbs we see that the initial contact cone of both limbs becomes more consistent, and moves anteriorly and medially as velocity is increased. Likewise, the toe off cone of both limbs becomes more consistent, moves posteriorly and medially. Basically, as the animals move faster they reduce their base of support, reach farther forward with their forelimbs and stretch farther back with their hindlimbs. In a body centered coordinate frame a stride length is the distance from initial contact to toe off, so these cones show where the increase in stride length with increasing velocity is happening.

Fig 3. Initial Contact/Toe Off Cones of Fore and Hindlimbs.

Rats have longer stride lengths at higher velocities, represented by a greater distance between initial contact and toe off cones. This increase in stride length is accommodated by placing the forepaw initial contact more anteriorly and the hindlimb toe off more posteriorly. Paw placement is more consistent at higher velocities, represented by a narrower cone. In efforts to minimize the effects of velocity it is possible to only analyze data from discrete windows. The choice of such window is not arbitrary as mean paw placement is different at different velocities. Slow -17.33–20, fast - 37.14–52cm/s. White values within bar graph are N’s. * p<0.05 ANOVA. Error bar ± 95% CI.

If we only analyzed steps that fit within a “fast” or “slow” 1 second window and reduced the paw placements of our animals to mean values, and then compared those means, we again see that the choice of windows is not arbitrary. Animals walking fast place their forelimb initial contact significantly farther ahead (ANOVA p<.001) and significantly reduce their base of support (ANOVA p<.001) when compared to slow walking animals. The location of forelimb toe off is also more posterior in fast walking rats (ANOVA p<.026). The hindlimbs do not significantly alter their initial contact but their toe off does occur more posteriorly at faster speeds (ANOVA p<.001). This is further confirmation that if one is looking to limit the effects of velocity on paw placement by selecting only steps of similar velocity, the choice of velocity window is important because rats place their paws in different locations when traveling at different speeds.

The cones on the bottom of Fig 3 are from all 1,808 forelimb and 1,810 hindlimb steps from 74 animals. The N values for the ANOVA comparisons are the animals that had taken at least 1 step within the velocity window. Only 18 animals took at least 1 forelimb step within both windows, and only 14 took at least 1 hindlimb step in both. We felt that an ANOVA with our previous velocity windows was more informative than searching for different 1 sec slow/fast windows that included more animals in both velocity windows for a more robust paired t test.

2.8 Temporal Aspects of Paw Placement Cones

Another advantage with using a body coordinate frame is the ability to know the position of the paws not just at initial contact and toe off but throughout the gait cycle. We investigated how the paw placement cones changed over the course of stance phase and from visual inspection concluded that they were uninteresting. The general shape of narrow tops and wide bases did not change, nor did the medial/lateral slant. As expected the anterior/posterior tilt in the forelimbs slowly shifted from the forward leaning initial contact to the more upright toe off, with the reverse seen in the hindlimbs. We also looked at the individual steps to see if the paths traced over stance phase in our 3D space (Ant-Post/Med-Lat/Velocity) are different at different velocities. Again, visual inspection revealed no noticeable differences. The behavior of more than 1,800 paws as they travel through space/time is more of a finite element analysis problem suited for a separate study.

2.9 Quantifying Differences Between Cones

Visual inspection has its limits of course, so it would be prudent to measure the difference between any 2 cones. Each cone is nothing more than a model and a collection of data points, thus giving us a set of residuals (shortest distance from point to surface of cone) and a sum-of-square error (SSE). As these cones are the smallest irregular volume that contains 95% of the data we considered any point within the cone to have a residual of 0. We also wanted our error measurement to differentiate between a cone with many points just outside the surface and a cone with 1 point very far from the surface so we weighted our SSE measure by the percentage of data points outside the surface. This weighted SSE value gives us an estimate of goodness of fit of a cone. But we are much more interested in how the cones of two groups differ, not how well their respective cones fit. If cone A is significantly different than cone B then putting data points A in model cone B would be a horrible fit resulting in a much higher SSE. And data points B in model cone A would also result in a much higher SSE. If cone A is not significantly different than cone B then switching the model cones/data points would only lead to a minor increase in SSE. We expressed this increase in SSE in relative terms $\frac{(\mathit{AinB}+\mathit{BinA})-(\mathit{AinA}+\mathit{BinB})}{(\mathit{AinA}+\mathit{BinB})}$. The next step was to determine a cut-off value to determine significance. We assumed that our healthy animals were symmetric, and that switching the R/L cones/points would give us the limit of our technique. The largest relative error was 0.244, found between the forelimb toe off cones. Any two cones whose relative error was greater than twice this amount, were considered significantly different.

2.10 Effects of Velocity on Coordination

Our focus so far has been on the individual limbs in the spatial domain, but it is equally important to investigate how the limbs work together in the temporal domain. The classic measure of limb phasing is the time difference between the initial contact of the reference limb and the target limb, expressed as a percent of the reference limb cycle time. Diagonal pairs of limbs are usually in phase (0.0 or 1.0) while R/L pairs tend to be out of phase (0.5). Traditionally the initial contact following the reference limb initial contact is taken, ensuring positive phasing. For this study in the case of diagonal pairs we chose the left forelimb initial contact which was closest in time to the right hindlimb reference limb, rendering some values negative.

As before, we wanted to see how this phasing changed across the spectrum of walking velocities. Figure 4 shows the 841 phasing pairs between the right hindlimb (reference limb) and the right forelimb from 74 healthy rats, plotted at the walking velocity of the reference limb step. We fitted this data with the smallest irregular 2 dimensional cone that enclosed 95% of the data. From visual inspection we can see that the animals are once again more consistent with their coordination as their walking velocity increases (95% of the data fits within a smaller range). However, it is difficult to tell if the center of this phase range shifts with increasing velocity. To get a more detailed measure of this phasing behavior a mathematical model was again employed.

Fig 4. Coordination Between Right Fore and Hindlimb Across all Velocities.

As velocity is increased the coordination becomes more consistent and shifts to the right. 841 phasing pairs from 74 healthy rats and the smallest irregular cone that encloses 95% of the data. Black + - pairs outside the cone, gray o – pairs inside the cone.

2.11 Creating the Smallest Irregular 2D Cone

As with our elliptical cones, it is best to envision these 2D cones as a stack of ranges. If there is no velocity dependence, the stack of ranges would be random. If limb phasing is velocity dependent then theses ranges would increase/decrease and the center would shift in a predictable manner as the stack gets higher. Our first step was to pass a narrow velocity window (4cm/s) up through the cluster of data points in 0.1cm/s increments. Whenever we had 9 or more data points in the window, we searched for the smallest 95% inter-quantile distance (0.0–0.95 through 0.05–1.0 in .001 increments). We chose this method because we were unsure if the distributions within the window were normal or not. Only the first unique range was retained for the stack as the window passed up through the velocity. From this stack of ranges we had a set of parameters such as minimum, mean, and maximum phase across the spectrum of walking velocities.

Our next step was to fit these parameters to a function of velocity. A 3 term Gaussian model was used because it allowed us to assign physical limits to our model. The foremost limit being that the maximum phase range, or width, of the cone could not exceed 1. We also wanted to ensure that the minimum edge (left edge) of the cone was never less than 10% lower than the minimum range of the stacks, and conversely that the maximum edge (right edge) was never more than 10% greater than the maximum range of the stacks. The 3 Gaussian terms were added to the minimum edge limit while the terms were subtracted from the maximum edge limit. In simpler terms, a 3 term Gaussian allowed for plenty of wiggle in the middle velocities without blowing up at the upper and lower extremes. The final model for the smallest irregular 2D cone that contains 95% of the data is given in equation 2.

$$\text{velocity}=min\text{or}max\text{edge}\text{limit}\pm {\mathrm{a}}_1{\mathrm{e}}^{-{\left(\frac{\text{phase}-{\mathrm{b}}_1}{{\mathrm{c}}_1}\right)}^2}\pm {\mathrm{a}}_2{\mathrm{e}}^{-{\left(\frac{\text{phase}-{\mathrm{b}}_2}{{\mathrm{c}}_2}\right)}^2}\pm {\mathrm{a}}_3{\mathrm{e}}^{-{\left(\frac{\text{phase}-{\mathrm{b}}_3}{{\mathrm{c}}_3}\right)}^2}$$ 2

2.12 Limiting Effects of Velocity on Phasing

The limb phasings relative to the right hindlimb reference limb across all velocities are shown in figure 5A. Unlike our paw placement data, the changes in limb phasing with increased velocity are less obvious. All limbs become more consistent with increasing speed. The left forelimb is generally in phase with the right hindlimb but shifts to a lower, even negative, phasing (meaning the left forelimb comes down slightly before the right hindlimb) with increasing speed. The right forelimb and left hindlimb are generally out of phase with the right hindlimb, with the right forelimb coming down slightly before the left hindlimb. Both of these limbs shift to a greater phasing with increasing velocity.

Fig 5. Limb Phasing Cones Reduced to Velocity Windows.

5A: The phasing cones of all 3 limbs in relation to the reference right hindlimb. 0 or 1 are “in phase” while 0.5 is “out of phase.” 5B: In efforts to minimize the effects of velocity it is possible to only analyze data from discrete windows. The choice of such window is not arbitrary as mean right fore/hindlimb phasing is different at different velocities. Slow - 17.33–20, fast -37.14–52cm/s. White values within bar graph are N’s. * p<0.05 ANOVA. Error bar ± 95% CI.

To limit the effects that velocity has on limb phasing one could only select data that falls within a select velocity window. When we take phasing data from the “slow” (17.33–20cm/s) or “fast” (37.14–52cm/s) velocity windows and reduced each animal’s pairings to mean values, and then compared those means, we again see that the choice of windows is not arbitrary. Animals walking slowly place their right forelimb down earlier in the gait cycle than fast walking rats do (Fig 5B ANOVA p<.028). Neither the phasing of the left forelimb nor the left hindlimb is significantly different at the different speeds. All three limb pairings express smaller 95% inter-quantile intervals at the higher speeds, further evidence for increased consistency at higher speeds. As we found with our preceding paw placement data, if one is looking to limit the effects of velocity on limb phasing by selecting only steps of similar velocity, the choice of that velocity window is important because rats coordinate their paws differently when traveling at different speeds.

The 2D cones of Fig 5A are from all right hindlimb pairings from 74 animals (870 left hindlimb, 841 right forelimb, 805 left forelimb). The N values for the ANOVA comparisons are the animals that had at least 1 limb pairing within the velocity window.

2.13 Quantifying Differences Between 2D Phase Cones

We again used measures of relative error to quantify the differences between any 2 2D phase cones (if cone A is not significantly different than cone B then switching the model cones/data points would only lead to a minor increase in SSE). For the 2D phase cones the cut-off value to determine significance was also 2 times the error found in the healthy symmetric animals. But this time we used the error associated with each pairing, not the largest error across all pairings (with the pairings being; diagonal pairs, ipsilateral limbs, contralateral hindlimbs). For example, if we assume that healthy animals are symmetric then the phasing between the left hindlimb and right forelimb should be no different than the phasing between the right hindlimb and left forelimb. When we take the data from our left hindlimb/right forelimb pairing and fit it to our right hindlimb/left forelimb 2D phase cone we get a relative increase in error of 0.0025, so any error above 0.005 was considered significant. For ease of interpretation, all errors reported are multiples of the cut-off error.

3.0 Results and Discussion

We had previously shown that rats have longer stride lengths at higher velocities, presented here is where in body space this is achieved. The initial contact of the forelimbs occurs more anteriorly, and the toe off of the hindlimbs is more posteriorly. In effect, the rats reach farther forward with the forelimbs and push farther behind with the hindlimbs. We presume that the toe off of the forelimbs does not move more posteriorly, nor the hindlimb initial contact more anteriorally, to limit the colliding of the two paws. The fact that the forelimbs move more medially at faster speeds could be a control strategy. If a wider base of support offers more stability, than a narrow base of support allows for quicker changes in direction, which may be preferred in a quickly moving rat. The minimal amount of hindlimb shifting in the medial/lateral direction may be due to the fact that they are trailing the forelimbs in forward walking. As the forelimbs steer the animal around the chosen path, the hindlimbs do not need to alter their base of support as much.

The main goal of this exercise is not to re-analyze how rats walk, but to show how velocity dependent locomotor behavior changes after neurological injury. Our laboratory uses a C4/5 right over-hemisection spinal cord injury which impairs the right limbs more than the left, and the forelimbs more than the hindlimbs. Just one week after injury these animals are able to cross the CatWalk, albeit with a very impaired gait. The untreated control animals contentiously recover over time, to a point where at 7 weeks they have no problems crossing the CatWalk. When we initially studied the stride length, cycle time, and duty factor of these animals we found that the right forelimb was initially very different from pre-injury but over time recovered. Conversely, the other limbs, specifically the left hindlimb were initially not very different from pre-injury but over time deviated and became more different from pre-injury. We interpreted this as the animals developing a compensatory technique where the less impaired limbs, with their greater control and broader range of motion were used in abnormal ways to enable the very impaired right forelimb to take more normal steps (Neckel 13).

3.1 Paw Placement Cones as a Measure of Recovery

We examined how the paw placement of our 17 untreated control animals changed over time. Figure 6 shows the initial contact cones of the forelimbs and the toe off cones of the hindlimbs for 1, 3, 5, and 7 weeks after injury. The pre injury cones from all 74 animals are included for comparison. From visual inspection the cones progress in agreement with our previous research. All limbs exhibit inconsistent placement 1 week following injury (represented by wider cones) but become more consistent with time (narrower cone). 1 week following injury the right forelimb lacks any distinct shape in the medial/lateral or anterior/posterior directions. However, as the weeks progress the right forelimb initial contact behaves more like a pre-injury limb. That cannot be said for the other limbs. The left forelimb initial contact moves much more anteriorly and slightly laterally while both hindlimb toe offs move more posteriorly.

Fig 6. Spontaneous Recovery of Paw Placement After SCI.

The other 3 limbs maintain differences or even deviate further away from pre-injured values to enable the more impaired right forelimb (blue) to take more normal steps. Dark cones are from the 74 pre-injured animals and the lighter cones are from a subset of 17 untreated injured rats tested on consecutive weeks. Forelimb cones are initial contact, hindlimb are toe-off. *~multiple of relative error, >2 significant.

For Fig 6 we calculated the relative error between that week post injury and the pre injury limb. The value shown is how many times greater the calculated relative error is than our 0.244 cutoff. With anything greater than 2 being significant. This quantitative measure of the difference between cones supports what was found with visual inspection. Over time the right forelimb becomes less different from pre injury whereas the other limbs diverge farther away from pre injury as the weeks progress. Our ongoing treatment studies look to enhance this recovery of right forelimb behavior while also reducing the abnormal behaviors that develop in the other limbs.

3.2 Phasing Cones as a Measure of Recovery

If the main goal of this exercise is to show how velocity dependent locomotor behavior changes after neurological injury, we also need to investigate how the 2D phasing cones change over time. Figure 7 shows the pre-injury baseline phasing from all 74 rats along with the cones from our 17 untreated control animals 1, 3, 5, and 7 weeks after C4/5 right over-hemisection injury. From visual inspection the cones progress in similar ways to our previous research. All limbs exhibit inconsistent phasing 1 week following injury (represented by wider cones) but become more consistent with time (narrower cone). 1 week following injury the right forelimb lacks any distinct shape. However, as the weeks progress the coordination between the right hindlimb and right forelimb behaves more like pre-injury limbs. That cannot be said for the left forelimb which begins uncoordinated, and does not improve over 7 weeks. The phasing of the left hindlimb is a little less easy to interrupt. The narrow cone is indicative of consistency, but the difference in shape reveals that it is still differently coordinated than pre-injury, even 7 weeks post injury.

Fig 7. Spontaneous Recovery of Coordination After SCI.

The less impaired left forelimb and left hindlimb maintain abnormal coordination 7 weeks post injury while the more impaired right forelimb exhibits pre-injury coordination values by 5 weeks post injury. Week 0 cones are from the 74 pre-injured animals and the lighter cones are from a subset of 17 untreated injured rats tested on consecutive weeks. *~multiple of relative error, >2 significant.

The calculated relative error between weekly and baseline 2D phase cones supports what was found with visual inspection. By 5 weeks post injury the right forelimb coordination is no longer significantly different from pre-injury. The same cannot be said of the left forelimb, as it begins different from pre-injury, and continues to divert away from pre-injury levels. The quantification of 2D phase cone differences confirms what we already knew, the left hindlimb is all over the place. This inconsistency and inability of all limbs to regain accurate coordination following injury is the target of our ongoing rehabilitation studies.

4.0 Conclusions

Automated gait analysis devices such as the CatWalk, DigiGait, and TreadScan are used by countless researchers to quickly assess the behavior of their animal models. We believe that quantifying locomotion is a great way to evaluate the changes that experimental treatments provide. We do not believe that the current methods employed by these devices and the researchers that use them are capable of capturing all the nuances of quadrupedal locomotion. Our previous work focused on how healthy rats change their stride length, cycle time, and duty factor with increasing velocity. With this work we wanted to show that the stride length alone is not enough. What is important is where in rat body space the paw is placed down to begin the stride and where it is lifted off to end the stride. By rotating the CatWalk data into the animals coordinate frame we were not only able to show this placement, but how this placement changes with increasing velocity. With our irregular elliptical cone technique we are able to quantify how healthy rats increase consistency, decrease base of support, and reach farther with increasing velocity. This novel finding has far reaching implications for the vast number of studies that compare groups of animals that may not travel at the same speed. The techniques we present here also enable us to quantify the changes in paw placement following injury and subsequent spontaneous recovery.

Many researchers prefer the measures of limb phasing as it reflects the coordination of the animal, showing how the limbs work together, not just how one limb behaves by itself. By applying our 2D phase cone technique we were able to quantify how rats also increase their consistency and alter their coordination patterns as they walk faster. The loss and subsequent spontaneous recovery of coordination following SCI can be measured through our techniques discussed here. Again, this is a novel finding with implications for any researcher using locomotion as a behavior measure.

Highlights.

• Gait measures are velocity dependent, a confounding factor when using automated gait analysis

• Instead of limiting this effect, measurement techniques that embrace the velocity dependence of gait are presented

• Rats move their paws more medially, stretch farther, and are more consistent as they move faster, not so after SCI