Measures of Agreement Between Many Raters for Ordinal Classifications

Abstract

Screening and diagnostic procedures often require a physician's subjective interpretation of a patient's test result using an ordered categorical scale to define the patient's disease severity. Due to wide variability observed between physicians’ ratings, many large-scale studies have been conducted to quantify agreement between multiple experts’ ordinal classifications in common diagnostic procedures such as mammography. However, very few statistical approaches are available to assess agreement in these large-scale settings. Existing summary measures of agreement rely on extensions of Cohen's kappa [1 - 5]. These are prone to prevalence and marginal distribution issues, become increasingly complex for more than three experts or are not easily implemented. Here we propose a model-based approach to assess agreement in large-scale studies based upon a framework of ordinal generalized linear mixed models. A summary measure of agreement is proposed for multiple experts assessing the same sample of patients’ test results according to an ordered categorical scale. This measure avoids some of the key flaws associated with Cohen's kappa and its extensions. Simulation studies are conducted to demonstrate the validity of the approach with comparison to commonly used agreement measures. The proposed methods are easily implemented using the software package R and are applied to two large-scale cancer agreement studies.

1. Introduction

Ordered categorical scales with three or more ordered categories are commonly used in screening and diagnostic tests to classify a patient's disease or health status, with higher scores often linked with increasing disease severity. Examples include the Gleason grading scale for categorizing severity of a patient's prostate cancer from biopsies [6,7] and the New York Heart Association functional four-point classification scale for categorizing a patient's level of heart failure [8]. Due to imperfect screening and diagnostic test procedures, classification of a patient's test result often involves some degree of subjective interpretation by an expert, and substantial variability between experts’ ratings has been observed in many widely used diagnostic and screening procedures, including mammography [9-11]. Consequently large-scale agreement studies involving many experts and ordinal classification scales are becoming increasingly common to assess levels of agreement and to investigate factors that may be linked with the observed variability between experts [9-13], providing a strong motivation to develop statistical approaches that can flexibly handle many raters. While some statistical methods exist to assess agreement between two experts using an ordinal classification scale, only a very limited number of approaches exist to assess agreement between ordinal classifications in larger-scale studies involving multiple (more than two or three) experts.

In this paper we explore a flexible approach to assess agreement between multiple experts classifying the same sample of patients’ test results according to an ordered categorical scale. Since diagnostic tests have such widespread use, an important advantage of our large-scale approach is the ability to generalize findings to experts and patients who typically use these diagnostic tests, if experts and subjects are randomly sampled from their populations.

Measures of agreement for ordinal classifications focus on quantifying levels of exact agreement between experts, i.e. where experts each assign an identical category to a patient's test result. Existing summary measures for assessing agreement between multiple raters when ordinal classifications are being examined include Fleiss’ kappa [3], Light's and Conger's kappa [4,5], Kraemer's kappa coefficient [14] and an AC2 statistic [15]. Many of these existing summary measures of agreement for ordinal classifications are either extensions of Cohen's kappa or are formulated as a Cohen's kappa-like statistic [3-5,16] and are prone to the same issues as the original Cohen's kappa, including sensitivity to marginal distributions of the experts and disease prevalence effects [16-18]. Model-based approaches for assessing agreement between multiple experts for ordinal classifications include log-linear models [19-21], latent class models [22], a marginal model generalized estimating equations method with Cohen's kappa-like formulated summary measures of agreement [16], a Bayesian approach with a nested random effect structure [23] and an exploratory graphical approach [24]. In practice, many of these procedures and measures are difficult to implement due to a lack of availability in statistical software packages, and/or become increasingly complex for more than three experts. Banerjee et al [25] provide a comprehensive list of agreement measures for nominal and ordinal classification data.

The proposed population-based approach utilizes the framework of ordinal generalized linear mixed models and generates a model-based summary measure of agreement for ordinal classifications based upon variance components for unobservable variables. Unlike most other available summary measures, our proposed agreement measure appropriately corrects for chance agreement in a different formulation from Cohen's kappa, and consequently is not influenced by the prevalence of the disease. Earlier work has demonstrated use of variance components in agreement studies for binary (for example, diseased versus not-diseased) classifications [26,27], and ordinal classifications [23,28,29], where the ordered nature of the classifications brings a unique set of challenges to the estimation and modeling process beyond those of binary classifications. Our methods can be extended to incorporate characteristics of experts and subjects that may potentially influence agreement. Unbalanced observations are allowed, where not every expert classifies every subject in the sample. Unique features of individual experts in the study can be examined, and the population-based nature of the approach ensures that conclusions can be drawn about agreement between typical experts and subjects from their respective underlying populations, not only about experts and subjects included in the study.

The paper is structured as follows. General concepts of agreement for ordered classifications in the population-based setting are defined in the next section. Section 3 describes the proposed model of agreement with details on estimation and fitting, and the proposed measure of agreement is presented in Section 4. Simulation studies demonstrating validity of the proposed approach are included in Section 5, with methods applied to two large-scale cancer agreement studies in Section 6. Section 7 presents a comparison to a logistic generalized linear mixed model while we conclude with a brief discussion in Section 8.

2. A Measure of Agreement in the Population-Based Setting

The primary goal of a population-based agreement study is to draw inference regarding levels of agreement between typical experts and patients in a specified setting such as a diagnostic or screening test. When experts and patients are randomly sampled from their respective populations, a well-defined measure of agreement describes how well one expert's classification of a subject agrees with what other experts would have reported (inter-rater reliability), after appropriately correcting for chance agreement [30]. For a single test result, agreement between two experts is defined where both experts classify the subject into the same category using an ordinal classification scale. In this setting, a natural measure of observed agreement, p₀, is the proportion of time two experts j and j′ (j ≠ j′) assign the ith subject to the same category (1). Since the two experts are randomly selected, classifications made by the jth and j′th experts on a subject are interchangeable, and thus any pair of ratings has a distribution that is invariant under permutations of the experts [25]. The raw observed agreement rate is the proportion of the total number of pairs of ratings which place subjects into the same category.

Chance agreement is the proportion of time experts agree in their classifications simply due to coincidence. The true measure of agreement expected by chance, p_c is the probability that an identical categorical rating is given to two randomly selected subjects i and i′ (i ≠ i′) by two randomly selected experts j and j′ (j ≠ j′) based upon an ordinal classification scale with C categories (1):

$$p_0=\sum _{c=1}^C\left[\mathrm{Pr}(Y_{ij}=c\cap Y_{i{j}^{\prime }}=c)\right]\text{and}{p}_c=\sum _{c=1}^C[pr(Y_{ij}=c)\times pr(Y_{i^{\prime }{j}^{\prime }}=c)]$$ (1)

These quantities of observed and chance agreement hold in general in the population-based setting and do not rely on any particular statistical model. An important link between p₀ and p_c and their minimum values in this setting is shown in Theorem One (proof in Appendix 1, Supplementary Materials):

Theorem 1

In the population-based setting, if the number of experts N in the population is not small, p₀ ≥ p_C ≥ 1/ C.

The lower bound 1/C is likely to be achieved when the disease status of subjects’ test results is not easily recognizable from the screening or diagnostic test, such that experts essentially randomly classify subject test results into one of the C categories (equivalent to the roll of a C-sided die).

3. Proposed Model of Agreement for Ordered Classifications

The class of ordinal generalized linear mixed models (GLMMs) [31-33] provides a natural and appealing framework for modeling agreement in large-scale studies between experts in the population-based setting since any number (at least three) of experts and subjects can be included without increasing the complexity of the model, in contrast to many other approaches, and each expert may rate some or all of the subjects [34]. Factors such as rater training or experience can be incorporated into the model to assess their impact on agreement between experts [16,35]. When experts and subjects included in the study are randomly sampled from their populations, results can be generalized to future users (both experts and subjects) of the diagnostic test under study.

We assume that subject i's true disease status as assigned by expert j is an unobserved continuous latent variable W_ij linked to the observed ordered classifications through a series of strictly monotonically increasing thresholds α₀,...,α_c dividing the real line into C+1 intervals, with α₀ = −∞ and α_c = +∞ [32,33,36]. The latent variable W_ij depends on unobserved subject and expert random effects and can be modeled using a linear random effects regression model. In its simplest form W_ij = β₀ + u_i + v_j + ε_ij where errors ε_ij are assumed N(0, σ²), β₀ is the intercept, and u_i and v_j are random effects for the ith subject and jth expert respectively, assumed to come from N(0, σ_u²) and N(0, σ_v²) distributions. The observed categorical classification Y_ij = c occurs if and only if α_c–1 ≤ W_ij < α_c, c=1,....,C. The absolute location β₀ and scale σ of the latent variable are not identifiable; to overcome this identifiability issue, wlog set β₀ = 0 and σ=1 [32]. Our set-up assumes that each of J experts (j=1,..., J) independently classifies each of I subjects’ test results (i=1,..., I) according to an ordered classification scale with C categories, c=1,...,C, yielding classifications Y_ij = c. The probability Pr(Y_ij = c) can be estimated using an ordinal generalized linear mixed model with a crossed random effects structure, appropriately accounting for dependency between classifications caused by the fact that the same sample of subjects is being classified by each expert. The ordinal GLMM with a probit link calculates the cumulative probability of a subject's test result being classified into category c or lower:

$${\Phi }^{-1}\left(\mathrm{Pr}(Y_{ij}\le c\mid u_j,v_j)\right)={\alpha }_c-(u_i+v_j)\text{or}\mathrm{Pr}(Y_{ij}\le c\mid u_i,v_j)=\mathrm{Pr}(W_{ij}<{\alpha }_c)=\Phi \left({\alpha }_c-(u_i+v_j)\right)$$ (2)

such that $\mathrm{Pr}(Y_{ij}=c\mid u_i,v_j)=\Phi ({\alpha }_c-(u_i+v_j))-\Phi ({\alpha }_{c-1}-(u_i+v_j))$, with W_ij distributed as N(0,1) and Φ the cumulative distribution function (cdf) of the standard normal distribution. While a choice of link functions are available for the ordinal GLMM, the probit link function is a natural and appealing choice due to the continuous latent disease status assumption underlying the model [36], and for ease of mathematics. In Section Seven we demonstrate that similar results are obtained using a logit link function, another common choice of link function for ordered GLMMs.

Natural heterogeneity amongst subjects’ test results is reflected in the subject random effect variance σ²_u. Subjects with clearly defined disease will have a higher positive random effect term u_i and be classified more often by experts into a higher disease category with stronger agreement between experts; more modest values of u_i are observed in test results with less clearly defined disease status. The experts’ random effect variance σ²_v is higher for a more heterogeneous group of experts; an expert who liberally (sparingly) assigns high disease categories has a higher positive (negative) value of v_j; experts who are not overly liberal or conservative in their ratings will have more modest values of v_j. The proposed model also allows for possible interactions between expert and subject random effect terms, as can be seen from an alternative derivation of the model (Appendix 2, Supplementary Materials).

Parameters of the ordered GLMM (2), $\theta =({\alpha }_1,\dots ,{\alpha }_{C-1},{\sigma }_u^2,{\sigma }_v^2)$, α_o = −∞ and α_C = +∞ provide valuable information about the agreement process under study, and are incorporated into the summary measure of agreement described in Section Four. Estimation of the parameter vector θ requires the marginal likelihood function of the corresponding ordinal GLMM, L(θ; y). Given the random effects u_i and v_j, and defining d_ijc = 1 if y_ij = c and 0 otherwise, the ordered classification of the ith subject by the jth expert y_ij is a multinomial variable with probability mass function:

$$\prod _{c=1}^C{\left[pr(Y_{ij}=c)\right]}^{d_{ijc}}=\prod _{c=1}^C{\left[\Phi ({\alpha }_c-(u_i+v_j))-\Phi ({\alpha }_{c-1}-(u_i+v_j))\right]}^{d_{ijc}}.$$

The marginal likelihood function is:

$$\begin{gathered} L(\theta ;Y)={\int }_{u,v}L(\theta ;u,v,y)dudv={\int }_{u,v}{f}_{Y\mid u,v}(y;u,v)f_u(u;{\sigma }_u^2)f_v(v;{\sigma }_v^2)dudv \\ ={\int }_u{\int }_v\left[\prod _{i=1}^I\prod _{j=1}^J\prod _{c=1}^C{[\Phi ({\alpha }_c-(u_i+v_j))-\Phi ({\alpha }_{c-1}-(u_i+v_j))]}^{d_{ijc}}\right]\left[\prod _{i=1}^I\frac{1}{\sqrt{2\pi {\sigma }_u^2}}{e}^{\frac{-u_i^2}{2{\sigma }_u^2}}\right]\left[\prod _{j=1}^J\frac{1}{\sqrt{2\pi {\sigma }_v^2}}{e}^{\frac{-v_j^2}{2{\sigma }_v^2}}\right]dudv \end{gathered}$$

This likelihood does not have a closed form due to the high-dimensionality of the crossed random effects structure, also restricting use of adaptive quadrature as a fitting procedure which becomes computationally infeasible as the number of random effects increases [36-38]. However, multivariate Laplacian maximum likelihood approximation [39] is an efficient and valid approach for estimating the parameter vector θ, and is implemented in the R package ordinal used here for estimation purposes.

The covariance matrix Σ of the parameter estimates $\widehat{\theta }$ is obtained as the inverse of the negative of the Hessian matrix H, where $H=\frac{{\partial }^{2}l(\theta ;u,v,y)}{\partial \theta \partial {\theta }^t}$ is the second-order derivative of the log-likelihood function l(θ; u, v, y) evaluated at the approximate maximum likelihood estimates of θ and is generated during the algorithmic multivariate Laplacian model-fitting process. The standard errors of $\widehat{\theta }$ are obtained by taking the square-roots of the diagonals of H at convergence as $se\left(\widehat{\theta }\right)=\sqrt{\mathrm{diag}[-{\left\{\mathrm{H}\left(\widehat{\theta }\right)\right\}}^{-1}]}$. In Section Five we demonstrate using simulation studies that this approach leads to unbiased estimators of the parameters of the ordered GLMM. In the next section, a summary measure of agreement is derived based upon this GLMM model.

4. Proposed Summary Measure of Agreement

4.1. A Model-Based Measure of Agreement

We propose a population-based summary measure of agreement κ_m based upon the ordinal GLMM model of agreement in Section Three. The proposed measure κ_m provides an overall assessment of chance-corrected agreement between many experts classifying the same sample of subjects’ test results using an ordered categorical scale. It is a linear transformation of observed (exact) agreement p₀ (4), corrected for chance agreement p_c (4) and scaled to lie between 0 and 1 to allow for easy interpretation in a manner similar to Cohen's kappa [40] and Scott's pi [41]:

$${\kappa }_m=\left(\frac{C}{C-1}\right)\ast {\int }_{-\infty }^{+\infty }\left\{\sum _{c=1}^C{\left[\Phi \left(\frac{{\Phi }^{-1}\left(\frac{c}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\Phi \left(\frac{{\Phi }^{-1}\left(\frac{c-1}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}^2\right\}\varphi \left(z\right)dz-\frac{1}{C-1},0\le {\kappa }_m\le 1$$ (3)

where $\rho ={\sigma }_u^2∕({\sigma }_u^2+{\sigma }_v^2+1)$ and z is a N(0,1) variable. Within the summation expression in (3) for category c = 1 the second term in brackets is set to 0, and the first term in brackets for category c = C is set to 1. A value of κ_m close to 0 is interpreted as little or no agreement, a value around 0.5 suggests a moderate amount of agreement, and a value of 1 as perfect agreement between the multiple experts, after correcting for chance agreement [40]. The forms of observed agreement p₀ (proof in Appendix 3, Supplementary Materials) and chance agreement p_c are:

$$p_0={\int }_{-\infty }^{+\infty }\left[\sum _{c=1}^C{\left[\Phi \left(\frac{{\alpha }_c^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\Phi \left(\frac{{\alpha }_{c-1}^{\ast }-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]}^2\right]\varphi \left(z\right)dz\text{and}{p}_c=\sum _{c=1}^C{\left[\Phi \left({\alpha }_c^{\ast }\right)-\Phi \left({\alpha }_{c-1}^{\ast }\right)\right]}^2$$ (4)

with standardized thresholds ${\alpha }_c^{\ast }={\alpha }_c∕\sqrt{{\sigma }_u^2+{\sigma }_v^2+1}$. As shown in Theorem 1, the minimum value that chance agreement can take in this population-based setting is p_c = 1/C and is obtained when the standardized thresholds (${\alpha }_0^{\ast },{\alpha }_1^{\ast }\dots ,{\alpha }_c^{\ast }$) take the values $(-\infty ,{\Phi }^{-1}\left(\frac{1}{C}\right),{\Phi }^{-1}\left(\frac{2}{C}\right),\dots ,{\Phi }^{-1}\left(\frac{C-1}{C}\right),+\infty )$. These values divide the real line into C segments, each having equal probability under the standard normal curve, minimizing differences within the squared brackets in the right-hand side expression in (4). The values are then incorporated in the expression for κ_m to appropriately minimize the effects of chance agreement on the statistic; consequently the value of κ_m is not influenced by prevalence of the disease, which here is indicated by the percent of observations falling into each of the C categories.

For any particular dataset, the estimate ${\widehat{\kappa }}_m$ is obtained from (3) using estimated random effects variances ${\widehat{\sigma }}_v^2$ and ${\widehat{\sigma }}_u^2$ from the fitted ordinal GLMM in (2). Estimates p̂₀ and p̂_c of observed and chance agreement respectively can be obtained from (4) using the estimated parameters from the fitted ordinal GLMM in (2). We describe κ_m in (3) as a function of parameter ρ (0 ≤ ρ ≤ 1), which itself is a natural measure of the variability amongst subjects’ test results, ${\sigma }_u^2$ relative to the overall variability present between classifications in a similar manner to the ICC (2) for multiple experts [16]. Values of ρ close to 0 suggest that variability between experts is greater relative to variability between the test results, while values of ρ closer to 1 suggest variability between test results is the dominating factor.

The variance of ${\widehat{\kappa }}_m$ is derived using the multivariate delta method based upon parameters in the GLMM model with crossed random effects, where expert and subject random effects are assumed independent, with $\mathrm{var}\left({\widehat{\sigma }}_u^2\right)=2{\left({\sigma }_u^2\right)}^2∕I$ and $\mathrm{var}\left({\widehat{\sigma }}_v^2\right)=2{\left({\sigma }_v^2\right)}^2∕J$. The variance of $\widehat{\rho }$ as a function of ${\sigma }_v^2$ and ${\sigma }_u^2$ is $\mathrm{var}\left(\widehat{\rho }\right)=\frac{2{\left({\sigma }_u^2\right)}^2{({\sigma }_v^2+1)}^2}{I{({\sigma }_u^2+{\sigma }_v^2+1)}^4}+\frac{2{\left({\sigma }_v^2\right)}^2{\left({\sigma }_u^2\right)}^2}{J{({\sigma }_u^2+{\sigma }_v^2+1)}^4}$. Since κ_m is a function of ρ, the delta method can be further applied leading to:

$$\begin{gathered} \mathrm{var}\left({\widehat{\kappa }}_m\right)={\left(\frac{C}{C-1}\right)}^2\ast \mathrm{var}\left(\widehat{\rho }\right)\ast {[{\int }_{-\infty }^{+\infty }\sum _{c=1}^{C}2\ast \left[\Phi \left(\frac{{\Phi }^{-1}\left(\frac{c}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)-\Phi \left(\frac{{\Phi }^{-1}\left(\frac{c-1}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\right]\ast \left[\varphi \left(\frac{{\Phi }^{-1}\left(\frac{c}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\Phi }^{-1}\left(\frac{c}{C}\right)-z\sqrt{\rho }}{2{(1-\rho )}^{3∕2}}\right) \\ -\varphi \left(\frac{{\Phi }^{-1}\left(\frac{c-1}{C}\right)-z\sqrt{\rho }}{\sqrt{1-\rho }}\right)\left(\frac{-z}{2\sqrt{\rho (1-\rho )}}+\frac{{\Phi }^{-1}\left(\frac{c-1}{C}\right)-z\sqrt{\rho }}{2{(1-\rho )}^{3∕2}}\right)\right]\varphi \left(z\right)dz]}^2. \end{gathered}$$

Functions in R to calculate the proposed measure ${\widehat{\kappa }}_m$ and variance $\mathrm{var}\left({\widehat{\kappa }}_m\right)$ for a dataset are available upon request from the first author {or in supplementary materials**}.

4.2. Cohen's Kappa with Model-Based Parameters

Many of the existing summary measures of agreement for multiple raters classifying subjects according to an ordinal scale are either extensions of Cohen's kappa [1-5] or take the form of Cohen's kappa κ = (p₀ – p_c)/(1– p_c) obtaining terms p₀ and p_c using a model-based technique [16]. For comparison with our proposed summary measure of agreement, it is informative for us to also calculate a model-based kappa formulated as a Cohen's kappa-like statistic using our ordinal GLMM quantities of observed and chance agreement p₀ and p_c. This measure will be referred to as κ_GLMM and can be estimated using the estimated parameters p̂₀ and p̂_c from the ordinal GLMM in (2):

$${\kappa }_{GLMM}=\frac{p_0-p_c}{1-p_c}.$$

4.3. Other Existing Summary Measures for Agreement

Existing measures that can be used to assess agreement between multiple raters in the ordinal classification setting include Fleiss’ kappa κ_F [3], Light's and Conger's kappa κ_LC [4,5] and Mielke et al's kappa κ_MB [42]. All of these measures are derivations or extensions of Cohen's kappa. These existing measures will be compared with the proposed measure κ_m in the following simulation studies and examples.

5. Simulation Studies

Performance of the ordinal GLMM (2) and proposed summary agreement measure (3) was investigated via extensive simulation studies. Sets of one thousand datasets were randomly generated based upon an ordinal GLMM with a crossed random effect structure with C=5 categories with a set of true parameter values $\theta =({\alpha }_1,\dots ,{\alpha }_{C-1},{\sigma }_u^2,{\sigma }_v^2)$, α_o = −∞ and α_C = +∞. For each dataset I subject random effects u_i and J expert random effects v_j were randomly generated from $N(0,{\sigma }_u^2)$ and $N(0,{\sigma }_v^2)$ respectively. The rmultinom function in R was used to randomly generate n = I*J (I ratings per expert) observations Y_ij based upon multivariate normal probabilities $\mathrm{Pr}(Y_{ij}=c\mid u_i,v_j)=\Phi ({\alpha }_c-(u_i+v_j))-\Phi ({\alpha }_{c-1}-(u_i+v_j))$. The clmm function in the R package ordinal [43] was used to fit the GLMM model for each dataset to obtain parameter estimates, and the proposed summary measures and their variances estimated. Four sets of simulations were conducted to investigate effects of varying rater and subject variances, numbers of subjects and experts included, and extreme or moderate disease prevalence (based upon probabilities of being classified in high or low disease categories). A fifth set of simulations was conducted to explore the robustness of the proposed approach and measure κ_m to the assumption of normally distributed random effects. In this fifth set of simulations, one thousand datasets were generated with non-normal subject random effects u_i, i = 1,....,I randomly sampled from a scaled and centered chi-squared distribution [44] with five degrees of freedom $({\chi }^2-5)∕\sqrt{2^{\ast }5∕10}$ which has a mean of 0 and the same variance, 10, as in two of the other sets of simulations; the expert random effects v_j, j=1,...,J were randomly sampled from a Uniform($-\sqrt{3},\sqrt{3}$) distribution yielding a mean of 0 and variance of 1, the same mean and variance as for all other sets of simulations. Conditional on the random effects u_i and v_j, the classifications Y_ij were assumed independent and generated according to probabilities based upon a multivariate normal distribution [44] in a similar manner to the first four sets of simulations. Simulation results, including the estimated means of the parameters and their standard errors (based upon the averages of the one thousand estimates) for the five simulation studies are presented in Table 1. Observed standard errors (calculated by taking the square-root of the variance of one thousand parameter estimates) are also presented.

Table (i).

Results from sets of five simulation studies, each based upon 1000 datasets simulated from an ordinal GLMM with five classification categories (C=5), with thresholds α₀ = −∞ and α₅ = +∞.

	Simulation Set #1			Simulation Set #2			Simulation Set #3			Simulation Set #4			Simulation Set #5
Parameter	Truth	Est. Mean	Est. S.E. (obs.)	Truth	Est. Mean	Est. S.E. (obs.)	Truth	Est. Mean	Est. S.E. (obs.)	Truth	Est. Mean	Est. S.E. (obs.)	Truth	Est. Mean	Est. S.E. (obs.)
n	500			500			5000			5000			5000
I	50			50			100			100			100
J	10			10			50			50			50
C	5			5			5			5			5
α 1	0	−0.001	0.340 (0.354)	0	0.022	0.565 (0.657)	0	0.007	0.173 (0.175)	0	0.018	0.349 (0.353)	0	0.239	0.352 (0.347)
α 2	1	0.995	0.344 (0.358)	1	1.020	0.570 (0.667)	1	1.009	0.174 (0.175)	1	1.018	0.349 (0.356)	1	1.243	0.353 (0.347)
α 3	2	2.003	0.354 (0.365)	2	2.024	0.578 (0.668)	2	2.009	0.176 (0.178)	2	2.020	0.350 (0.354)	2	2.239	0.355 (0.350)
α 4	3	3.022	0.382 (0.399)	3	3.019	0.590 (0.691)	3	3.011	0.180 (0.181)	3	3.021	0.352 (0.353)	3	3.234	0.357 (0.351)
Random effects ui	$\mathrm{N}(0,{\sigma }_u^2)$			$\mathrm{N}(0,{\sigma }_u^2)$			$\mathrm{N}(0,{\sigma }_u^2)$			$\mathrm{N}(0,{\sigma }_u^2)$			(χ2 – 5)
${\sigma }_u^2$	1	1.017	0.269 (0.279)	10	9.330	2.602 (3.936)	1	0.999	0.151 (0.141)	10	9.469	1.571 (1.485)	10	9.701	1.610 (1.692)
Random effects vj	$\mathrm{N}(0,{\sigma }_v^2)$			$\mathrm{N}(0,{\sigma }_v^2)$			$\mathrm{N}(0,{\sigma }_v^2)$			$\mathrm{N}(0,{\sigma }_v^2)$			Unif (–√3, √3)
${\sigma }_v^2$	1	0.939	0.450 (0.461)	1	0.985	0.487 (0.504)	1	0.985	0.204 (0.208)	1	0.993	0.208 (0.212)	1	1.000	0.210 (0.146)
ρ	0.333	0.346	0.063 (0.075)	0.833	0.816	0.044 (0.050)	0.333	0.335	0.038 (0.041)	0.833	0.824	0.025 (0.027)	0.833	0.826	0.025 (0.027)
var(ρ)	0.004	0.006		0.002	0.002		0.0015	0.0017		0.0006	0.0007		0.0006	0.0007
κ m	0.090	0.095	0.021 (0.025)	0.368	0.356	0.040 (0.055)	0.090	0.091	0.012 (0.013)	0.368	0.360	0.024 (0.029)	0.368	0.362	0.024 (0.029)
var(κm)	0.0005	0.0005 (0.0006)		0.002	0.002 (0.003)		0.0002	0.0002 (0.0002)		0.0006	0.0008 (0.0300)		0.0006	0.0006 (0.0009)

The simulation studies demonstrate that the ordinal package in R yielded essentially unbiased parameter GLMM estimates of the threshold parameters (${\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_4$) and variance components (${\widehat{\sigma }}_u^2,{\widehat{\sigma }}_v^2$) in both large and small sample sizes, and large (${\sigma }_u^2=10$) and small (${\sigma }_u^2=1$) random effects variances. In simulation set #2, the scenario with a large subject random effects variance (${\sigma }_u^2$) and smaller total sample size (n = I*J = 500), the observed variability of the one thousand estimates of ${\sigma }_u^2$ is slightly larger than expected, but this issue was not observed at the larger sample size of n = 5000. The proposed measure ${\widehat{\kappa }}_m$ and its variance were estimated essentially in an unbiased manner in all simulation settings. In the fifth set of simulations with non-normal random effects (simulation set #5), the ordinal GLMM thresholds ${\widehat{\alpha }}_1,\dots ,{\widehat{\alpha }}_4$ were estimated with more bias than in the sets of simulations with normally distributed random effects, although variance parameters were estimated on average with little or no bias. The proposed measure κ_m which is not reliant upon the estimated threshold values and its variance was estimated with essentially no bias. These results suggest that the proposed approach may be fairly robust to the normal random effects assumption and confirm results in earlier studies examining the impact of non-normal random effects in GLMMs [44,45], though further work is required to confirm these findings.

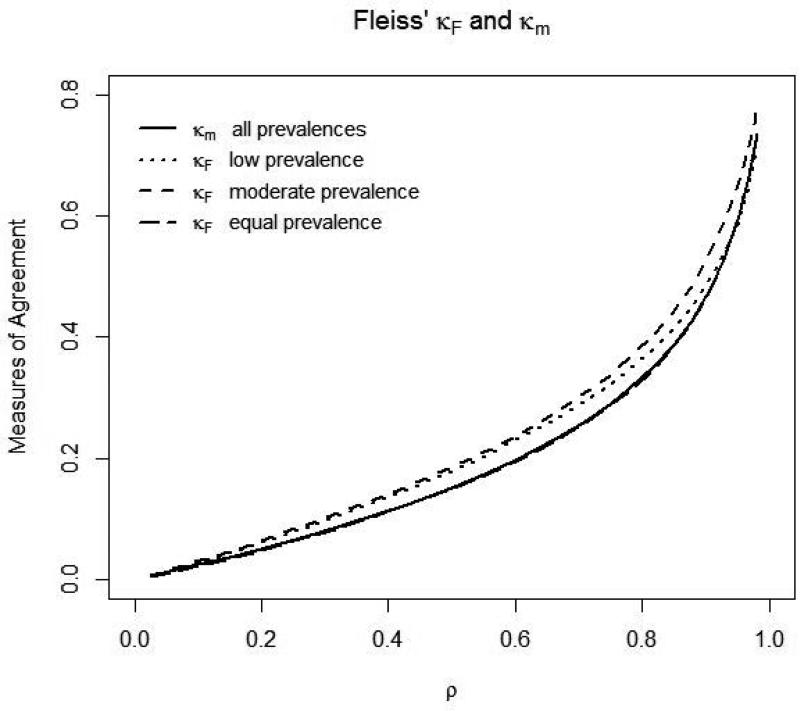
The behavior of the new measure of agreement κ_m was explored for a range of different settings including varying disease prevalence and ρ for an ordinal classification scale with five categories (C=5), with results presented in Figure 1. Comparisons were made with existing measures of agreement (Section 4.2) and a Cohen's kappa based upon GLMM parameters of agreement (Section 4.3). Figure 1 presents plots of the measures of agreement for increasing ρ and varying prevalence (extreme low or high, moderate, equal in each category as presented in Table 2). Fleiss’ kappa, Light and Conger's kappa and Cohen's kappa based upon GLMM parameters all yielded virtually identical average values so only Fleiss’ kappa κ_F is presented on the plots. True parameter values were used in the plots with the exception of κ_F, which was averaged over sets of 1000 simulated datasets. All agreement measures increased in value as ρ increased, and at a steeper rate as ρ approached 1. Thus, experts agree more often when there is a wider spread of test results (larger ${\sigma }_u^2$) relative to the variability between experts. All agreement measures took very similar values when disease prevalence (as indicated by the percent of observations in each category) was distributed evenly over the five categories. However, as disease prevalence became more extreme (either high or low), the proposed new measure of agreement κ_m remained unaffected, while the Cohen's kappa-based agreement measures (κ_GLMM, κ_F, and κ_LC), which are prone to prevalence effects, all increased in value.

Figure (i).

Plots of agreement measures, proposed κm and κF versus ρ for varying prevalence (extreme low or high, moderate, equal in each category; the percent of observations falling into each of the Ci categories, i=1,...,5 in each prevalence case are presented in Table 2) with σ2v set to 1 and σ2u increasing in value.

Table (ii).

Varying levels of disease prevalence examined in simulation studies and figures based upon an ordinal classification scale with C=5 categories.

	Percentage (%) of classifications in each category
Disease Prevalence	Category 1	Category 2	Category 3	Category 4	Category 5
Very low	80%	10%	3.4%	3.3%	3.3%
Moderately low	50%	26%	16%	6%	2%
Equal	20%	20%	20%	20%	20%
Moderately High	2%	6%	16%	26%	50%
Very High	3.3%	3.3%	3.4%	10%	80%

6. Examples: Two Cancer Agreement Studies

6.1. Prostate Cancer Agreement Study

Allsbrook et al [46] conducted a study of agreement between 10 urologic pathologists each independently interpreting the severity of prostate cancer of 46 patients’ biopsies using a condensed version of the Gleason Grading scale [7]. The scale had four categories defined as: category i) Gleason scores 2-4 (mild disease); category ii) Gleason scores 5-6; category iii) Gleason score 7; category iv) Gleason scores 8-9 (severe disease). Table 3(a) displays a subset of the ordinal classifications of the 46 patients’ test results by each of the 10 urologists. Tables 3(b) and (c) present the observed classifications of selected pairs of urologists. An ordinal GLMM (2) was then fitted to the full dataset incorporating the dependency between the classifications of the experts via the crossed random effects structure using the ordinal package in R, taking less than 1 minute of computational time. Parameter estimates and summary measures are presented in Table 4. As an indicator of disease prevalence, the estimated probabilities of being classified into each of the four categories over the ten experts are: (from mild to severe cancer) 6%, 31%, 28% and 36% respectively, thus there was a high probability of being categorized with a moderate to high degree of prostate cancer. Observed agreement (3) based upon the ordinal GLMM in (2) was estimated to be p̂₀ = 0.669. The proposed new agreement measure ${\widehat{\kappa }}_m=0.484$ (se = 0.035) indicated a moderate level of chance-corrected agreement between the ten urologists. This was substantially lower in value than Fleiss’ kappa ${\widehat{\kappa }}_F=0.569$, Conger's and Light's kappa, ${\widehat{\kappa }}_{LC}=0.570$, and Cohen's GLMM-based kappa estimated at ${\widehat{\kappa }}_{GLMM}=0.526$ (described in Sections 4.2 and 4.3), which may be attributed to the effects of high disease prevalence that Cohen's kappa measures are prone to as observed in Figure 1, while the proposed kappa is unaffected by disease prevalence. Mielke et al's kappa [42,47] which is based upon the probability that every one of the ten urologists classify a subject's test result into exactly the same category is estimated as 0.196; this kappa reflects the low chance that such classifications would occur very often in practice, and less so as the number of experts increases.

Table (iiia).

Table of classifications by individual raters for the Gleason Grading study [46]. Based upon an ordinal classification scale with C=4 categories; I=46 patient biopsies (cases); J=10 experts.

	Classifications by Individual Experts (J = 10)
	Expert
Case	1	2	3	4	5	6	7	8	9	10
1	2	2	2	2	2	2	2	2	2	2
2	2	3	4	3	3	3	2	3	3	3
3	4	4	4	4	4	3	4	4	3	4
4	4	4	4	4	4	4	4	3	4	4
5	2	2	2	2	2	2	1	2	2	2
6	3	3	3	3	3	3	3	3	3	3
7	2	3	3	2	3	3	2	2	2	2
8	3	3	3	3	3	4	2	3	3	3
9	3	3	4	3	4	4	4	3	3	4
10	3	3	4	3	3	4	3	3	3	3
⋮			⋮				⋮			⋮
41	3	3	4	3	3	4	4	3	3	4
42	2	2	3	2	2	2	2	2	2	2
43	2	2	2	2	2	5	2	2	2	2
44	4	4	4	4	4	4	4	4	4	4
45	3	3	3	3	3	3	4	3	3	3
46	3	3	3	3	3	3	3	3	2	3

Table (iii b and c).

Tables showing pairwise agreement between some randomly selected pairs of urologists classifying 46 slides [46] according to an ordinal scale based upon the Gleason grading scores with C=4 categories.

		Rater Three
	Category	1	2	3	4	Total
Rater One	1	1	5	0	0	6
	2	0	6	4	4	14
	3	0	0	5	5	10
	4	0	0	0	16	16
	Total	1	11	9	25	46

		Rater Six
	Category	1	2	3	4	Total
Rater Two	1	0	0	0	0	0
	2	2	13	0	0	15
	3	0	2	10	6	18
	4	0	0	3	10	13
	Total	2	15	13	16	46

Table (iv).

Results for the Gleason Grading Agreement Study [46] based upon an ordinal classification scale with C=4 categories; I=46 patient biopsies; J=10 urologists.

Parameter	Symbol	Estimate	S.E.	Z-value
Ordinal GLMM:
Thresholds: (α0 = –∞, α4 = +∞)
Between categories 1 and 2	α 1	−5.226	0.641	−8.154
Between categories 2 and 3	α 2	−1.258	0.522	−2.411
Between categories 3 and 4	α 3	1.549	0.521	2.971
Subject Random Effect variance	${\sigma }_u^2$	9.295	2.453
Rater Random Effect variance	${\sigma }_v^2$	0.358	0.200
Rho	ρ	0.873	0.027
GLMM-based Observed Agreement	p 0	0.669
Agreement Measures:
Model-based Kappa	κ m	0.484	0.035
Fleiss’ kappa	κ F	0.569	0.014
Light and Conger's kappa	κ LC	0.570
Mielke's et al kappa		0.196
Cohen's GLMM-based kappa	κ GLMM	0.526

The original analysis of agreement presented in Allsbrook et al's paper [46] compared Cohen's kappas (unweighted) for each pair of urologists, yielding 45 pairwise Cohen's kappas ranging between 0.31 – 0.79. This approach leads to complexities in interpretation with limited overall conclusions about the agreement between the ten urologists. In contrast, our proposed approach allows classifications of all ten urologists to be analyzed and interpreted in one unified approach. Characteristics of individual urologists can also be examined through their estimated random effect terms v̂_j, j=1,..., J if required.

6.2. Cervical Cancer Agreement Study

An early study was conducted by Holmquist et al [11] to examine the variability in the classifications of cervical cancer from histological slides and to assess the level of overall agreement among pathologists. Seven pathologists evaluated and classified 118 slides according to a five-category ordinal scale: (1) negative; (2) atypical squamous hyperplasia; (3) carcinoma in situ; (4) squamous carcinoma with early stromal invasion; and (5) invasive carcinoma. A table of individual classifications made by each pathologist is presented in Landis and Koch [40]. The original analysis presented in Holmquist et al [11] focused on examining the number of slides between each pair of pathologists that were rated as higher by one pathologist in the pair. Table Five presents the results from fitting the proposed ordinal GLMM model and summary measures and existing summary measures. Based upon all seven pathologists’ classifications, the observed probabilities of being rated in categories 1 (negative) to 5 (most severe cancer) were 27%, 17%, 52%, 3% and 1.7% respectively, indicating only a small proportion of slides indicated more severe disease. The variability in classifications between the patient slides (${\sigma }_u^2=4.13$) is large relative to the variability observed amongst the pathologists (${\sigma }_v^2=0.627$) yielding a moderately high value of ρ = 0.717. The model-based kappa ${\widehat{\kappa }}_m=0.266$ (se = 0.032), indicating only a low level of chance-corrected agreement between the seven pathologists. Each of the Cohen's kappa-based summary measures, Fleiss’ kappa, Conger's and Light's kappa and Cohen's GLMM-based kappa yielded slightly higher estimated chance-corrected agreement (${\widehat{\kappa }}_F=0.354$, ${\widehat{\kappa }}_{LC}=0.361$ and ${\widehat{\kappa }}_{GLMM}=0.296$ respectively). This may be attributed, in a similar manner to the Gleason Grading example in Section 6.1, to prevalence effects, where severe disease (categories 4 and 5) is very rarely observed for this sample of slides. Mielke et al's kappa [42,47] is very small at 0.127, demonstrating the unlikely scenario that all seven pathologists would assign an identical classification to any particular slide.

7. A Logistic Generalized Linear Mixed Model for Modeling Agreement

The generalized linear mixed model with a logistic link function is often a popular choice when modeling ordinal classifications. In this section we demonstrate that almost identical results are obtained for observed agreement p₀ whether a probit or logit link function is employed in the ordinal GLMM framework for modeling agreement.

The logistic function $\Psi ({\alpha }_c-(u_i+v_j))=1∕(1+e^{-({\alpha }_c-(u_i+v_j))})$ replaces the probit function Φ(·) in the logistic ordinal GLMM. Wlog we set β₀to 0 for identifiability purposes, with variance of the logistic distribution π²/3, and the logistic ordinal GLMM in terms of cumulative logits is:

$${\Psi }^{-1}\left(\mathrm{Pr}(Y_{ij}\le c\mid u_i,v_j)\right)=\log \left(\frac{\mathrm{Pr}(Y_{ij}\le c\mid u_i,v_j)}{1-\mathrm{Pr}(Y_{ij}\le c\mid u_i,v_j)}\right)={\alpha }_c-(u_i+v_j),c=1,\dots ,C$$

with the probability of the ith subject's test result being classified by expert j into category c as $\mathrm{Pr}(Y_{ij}=c\mid u_i,v_j)=\Psi ({\alpha }_c-(u_i+v_j))-\Psi ({\alpha }_{c-1}-(u_i+v_j))$. It is helpful to define a random variable Q with a logistic distribution with mean 0 and variance π² / 3, and density function $f_Q\left(q\right)=e^{-q}∕{(1+e^{-q})}^2$. Observed agreement p₀ is derived for the logistic ordinal GLMM as:

$$p_0=\sum _{c=1}^C\mathrm{Pr}[(Y_{ij}=c)\cap (Y_{i{j}^{\prime }}=c)]={\int }_{-\infty }^{+\infty }\left\{\sum _{c=1}^C{\left[F_{Q^{\ast }}\left(\frac{{\alpha }_c}{{\sigma }_u}-z\right)-F_{Q^{\ast }}\left(\frac{{\alpha }_{c-1}}{{\sigma }_u}-z\right)\right]}^2\right\}\varphi \left(z\right)dz$$

where $Q^{\ast }=(Q+v_j)∕{\sigma }_u$. The cdf $F_{Q^{\ast }}\left(q^{\ast }\right)$ takes the form [48]:

$$F_{Q^{\ast }}\left(q^{\ast }\right)=\mathrm{Pr}(Q^{\ast }\le q^{\ast })={\int }_{-\infty }^{+\infty }{e}^{-q}{(1+e^{-q})}^{-2}\Phi \left(\frac{q^{\ast }-q∕{\sigma }_u}{{\sigma }_v∕{\sigma }_u}\right)dq,\text{leading to}:$$

$$p_0={\int }_{-\infty }^{+\infty }\left\{\sum _{c=1}^C{\left[{\int }_{-\infty }^{+\infty }{e}^{-q}{(1-e^{-q})}^{-2}\Phi \left(\frac{{\alpha }_c-{\sigma }_{u}z-q}{{\sigma }_v}\right)dq-{\int }_{-\infty }^{+\infty }{e}^{-q}{(1-e^{-q})}^{-2}\Phi \left(\frac{{\alpha }_{c-1}-{\sigma }_{u}z-q}{{\sigma }_v}\right)dq\right]}^2\right\}\phi \left(z\right)dz$$

This expression is evaluated using the integrate function in R. Figure 2 demonstrates that almost identical values of observed agreement p₀ are obtained under the ordinal GLMM framework irrespective of choice of probit or logit link function. It is also interesting to note that for both choices of link function, as disease prevalence becomes more extreme (high or low), model-based observed agreement increases; and as subjects’ test results become more distinguishable from each other relative to the variability between experts (increasing ρ), observed agreement between experts also increases, though at a faster rate for prevalences that are more moderately spread over the C categories.

Figure(2).

Model-based observed agreement p0 for probit and logistic ordinal GLMMs versus increasing ρ and varying prevalence of disease for an ordinal classification scale with five categories (C=5).

8. Discussion

In this paper we describe a comprehensive framework and propose a chance-corrected summary measure in a population-based setting to examine agreement between multiple experts classifying a sample of subjects’ test results according to an ordered categorical scale. The proposed approach flexibly can accommodate large numbers of experts and subject test results without increasing complexity as the number of experts increases, while allowing for missing data. The proposed methods are easily implemented using the freely available software package R. Initial findings suggest the approach is fairly robust to non-normal random effects, though further work is needed in this area.

Limited alternative approaches exist to examine agreement in this large-scale setting with ordinal classifications, and many existing measures of agreement are prone to prevalence effects of the disease or condition under study. Due to a lack of available methods for studies involving ordinal classifications made by many experts, many agreement studies in the medical literature have instead elected to use approaches intended to assess agreement between just two experts at a time. For example, several pairwise Cohen's kappa statistics between all possible pairs of experts are often calculated, leading to complexities in interpretation and limited overall conclusions regarding the group of experts as a whole. Our approach allows agreement between all the experts to be assessed in one unified approach, lending power and efficiency to the study of agreement between the multiple experts when assumptions are met, and a simpler interpretation of results. If the experts and patients included in the study are randomly sampled from their respective populations, the results are generalizable to these populations of experts and patients, which is especially advantageous for widely used screening procedures. There is also the opportunity to examine the rating characteristics of individual experts through exploration of individual random effect components. In addition, our approach is not vulnerable to some of flaws observed when using Cohen's kappa, such as prevalence effects. Examining the effects of factors (such as rater training) that may play an influential role in the levels of agreement between experts, such as the levels of training and volume of tests read annually will be examined in a future paper.

In addition to measures of agreement, measures of association are also commonly used to compare the ordered categorical classifications of two or more experts. These measures incorporate valuable information regarding the extent of disagreement between experts, where disagreement arises when two experts assign a different classification to the same subject's test result. For example, stronger disagreement is implied when two experts’ classifications are three categories apart rather than one or two categories apart. A common measure of association is Cohen's weighted kappa [2,14,49] which employs a weighting scheme which assigns partial “credit” for classifications not in exact agreement, with larger weights (“credit”) assigned to pairs of classifications closer together. Extensions of Cohen's weighted kappa to more than two experts [50] has been described as problematic [42]. Gonin et al [51] describe a model-based approach using generalized estimating equations that generates a weighted kappa coefficient, including a fixed term for each expert, thus best-suited to a smaller number of experts. Extending the proposed population-based approach described in this paper for multiple experts to incorporate information about disagreement using measures of association is a topic for future research.

Due to the categorical nature of ordinal classifications, non-parametric rank-invariant approaches are preferred by some researchers [52-55], where rank invariant methods are not influenced by a relabeling of the ordinal classification scale [52-56]. Svensson et al [52,53] describe a non-parametric rank-invariant approach for evaluating the various components of disagreement in paired rank-invariant data. These approaches are currently restricted to assessing association and agreement between pairs of experts, so are better suited to studies with a smaller number of experts. Liu and Agresti [36] note that for parametric approaches, when the latent variable model holds, for example, where disease status is considered an unobserved latent variable, the estimated effects are invariant to the number of categories of the classification scale and their cutpoints, and when the model fits well, different studies employing different scales for the classifications should lead to similar conclusions.

Table (v).

Results for the Holmquist et al's [11] Carcinoma in situ of the uterine cervix Agreement Study based upon an ordinal classification scale with C=5 categories; I=118 patient slides; J=7 pathologists.

Parameter	Symbol	Estimate	S.E.	Z-value
Ordinal GLMM:
Thresholds: (α0 = –∞, α5 = +∞)
Between categories 1 and 2	α 1	−1.364	0.364	−3.747
Between categories 2 and 3	α 2	0.370	0.361	1.024
Between categories 3 and 4	α 3	2.856	0.376	7.605
Between categories 4 and 5	α 4	4.214	0.407	10.347
Subject Random Effect variance	${\sigma }_u^2$	4.130	0.684
Rater Random Effect variance	${\sigma }_v^2$	0.627	0.348
Rho	ρ	0.717	0.049
GLMM-based Observed Agreement	p 0	0.485
Agreement Measures:
Model-based Kappa	κ m	0.266	0.032
Fleiss’ kappa	κ F	0.354	0.012
Light and Conger's kappa	κ LC	0.361
Mielke's et al kappa		0.127
Cohen's GLMM-based kappa	κ GLMM	0.296