Methods to calibrate the absolute receive sensitivity of single-element, focused transducers

Abstract

Absolute pressure measurements of acoustic emissions by single-element, focused passive cavitation detectors would be facilitated by improved wideband receive calibration techniques. Here, calibration methods were developed to characterize the absolute, frequency-dependent receive sensitivity of a spherically focused, single-element transducer using pulse-echo and pitch-catch techniques. Validation of these calibration methods on a focused receiver were made by generating a pulse from a small diameter source at the focus of the transducer and comparing the absolute pressure measured by a calibrated hydrophone to that of the focused transducer using the receive sensitivities determined here.

1. Introduction

Beneficial bioeffects associated with acoustic cavitation have been investigated for a variety of ultrasound-enhanced treatments such as ablative therapy¹ and drug delivery applications.² Cavitation activity is commonly monitored during these applications by passively detecting acoustic emissions from cavitating bubbles using a single-element transducer, referred to as a passive cavitation detector (PCD). The spectral contents of the PCD-measured waveforms are typically analyzed to quantify specific bubble activity by temporally integrating the amplitude,³ squared amplitude,⁴ or decibel-scaled level^5,6 of the received signal within distinct frequency bands associated with cavitation. These are system-dependent measurements, influenced by the frequency response of the receiving electronics and PCD, leading to challenges in comparing results obtained using different measurement configurations.

Absolute measurements of cavitational emission levels can be made using a PCD of known receive sensitivity. A large number of methods are available for calibrating the receive sensitivity of small needle-type hydrophones.^7,8 However, receive calibration techniques are limited for focused single-element transducers commonly used as PCDs. One recently proposed calibration method for focused PCDs is a bistatic scattering substitution technique.⁹ However, this method requires a dedicated configuration, which may not be easily reproduced in all laboratories. Alternative calibration methods would facilitate a broader application of absolute PCD measurements for focused single-element receivers.

In the following, two substitution techniques for determining the wideband, absolute sensitivity of a single-element, spherically focused receiver are presented. These calibration techniques were implemented using measurements of pulsed acoustic fields in pitch-catch and pulse-echo configurations, within a standard scanning measurement system. The proposed calibration measurements were analyzed numerically and both techniques were experimentally validated.

2. Method

The frequency-dependent receive sensitivity of an acoustic transducer can generally be defined as $M(f)=V_{\text{open}}(f)/P(f)$, where $V_{\text{open}}(f)$ is the open-circuit voltage in response to receiving P(f), the average pressure across the transducer face measured in the free field at a given distance from a source. In order to measure $V_{\text{open}}(f)$ and the corresponding P(f) to accurately calibrate the receive sensitivity of a focused receiver as a PCD, two methods were developed here. The configuration of each method results in nominally constant-phase wavefronts across the receiver face, reducing phase cancellation effects by mimicking wavefronts emanating from a point source, such as a cavitating bubble, near the PCD focus.

In the first method, the open-circuit voltage $V_{\text{PCD},\text{open}}(f)$ of the PCD was measured in a confocal pitch-catch configuration using a focused source to transmit a broadband pulse to the PCD, as schematically shown for a representative transducer pair of unequal diameter, but equal focal length in Fig. 1(a). In the second method, the open-circuit voltage $V_{\text{PCD},\text{open}}(f)$ of the PCD was measured in a pulse-echo configuration consisting of the PCD, used both as a source and receiver, and a rigid planar reflector at its focus. This pulse-echo configuration can be modeled by an equivalent confocal pitch-catch configuration of two identical transducers, as representatively shown in Fig. 1(b). The reference pressure $P_{\mathrm{H}}(f)$ was approximated from planar measurements made using a calibrated hydrophone at the same distance from the source as the PCD or its image for the pitch-catch and pulse-echo configurations, respectively.

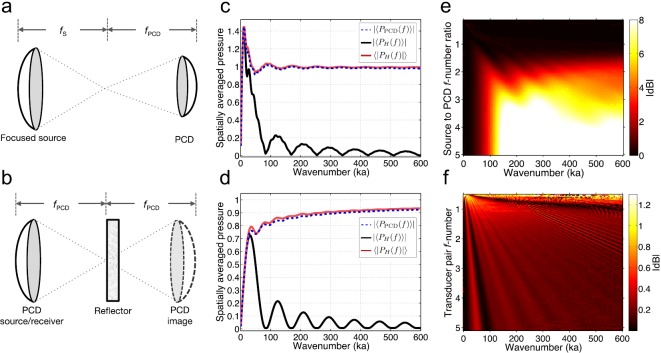
Fig. 1.

(Color online) (a) Representative configuration of the pitch-catch technique employing a confocal transducer pair of unequal geometry with source focal length $f_{\mathrm{S}}$ and PCD focal length $f_{\text{PCD}}$. (b) Corresponding configuration of the pulse-echo technique employing a reflector and image source. (c) Simulated pressure spatially averaged over a concave PCD surface, $\left|⟨P_{\text{PCD}}(f)⟩\right|$, pressure averaged over a planar hydrophone measurement surface, $\left|⟨P_{\mathrm{H}}(f)⟩\right|$, and pressure magnitude averaged over the same planar surface, $⟨\left|P_{\mathrm{H}}(f)\right|⟩$. Pressures are plotted normalized to the nominal surface pressure amplitude of the source as a function of ka for a pitch-catch transducer pair with respective f-numbers of 1.32 and 3.35. (d) Corresponding simulated, spatially averaged pressures for an equal-geometry pitch-catch transducer pair with f-number 3.35. (e) Decibel-scaled ratios of $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ to $\left|⟨P_{\text{PCD}}(f)⟩\right|$ for unequal transmit-receive transducer pairs representing the pitch-catch technique. (f) Corresponding pressure magnitude ratios for matched transducer pairs representing the pulse-echo technique.

The proposed calibration measurements were investigated numerically in matlab (Natick, MA) using an exact series solution to simulate the pressure field of a circular concave piston.¹⁰ First, the transmitted field was sampled over a concave surface corresponding to that of a confocally and coaxially aligned PCD. The surface pressure was spatially averaged and used to represent that received by a PCD as $\left|⟨P_{\text{PCD}}(f)⟩\right|$, where $⟨⟩$ represents spatial averaging over the surface. Second, the transverse plane at the same axial distance from the source was sampled over a circular diameter matching that of the PCD, using a step size in either azimuthal direction of approximately 1/2 of the smallest investigated wavelength. To represent potential hydrophone measurements, the spatial average of the pressure $\left|⟨P_{\mathrm{H}}(f)⟩\right|$ and pressure magnitude $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ were calculated.

Simulated pressures spatially averaged across a concave and corresponding planar surface are shown as a function of normalized frequency ka, relative to the wavenumber k in room temperature water and receiver radius a, in Fig. 1(c) for a confocal transmit-receive transducer pair with f-numbers 1.32 and 3.35, respectively. These dimensions matched those of the pair used later to implement the pitch-catch technique. Similarly, average pressure values are shown in Fig. 1(d) for an identical transducer pair with f-number 3.35, matching the geometry used later to implement the pulse-echo technique. In both cases, pressures averaged across the concave and planar surfaces were comparable at low ka values, but the amplitude of the average planar pressure $\left|⟨P_{\mathrm{H}}(f)⟩\right|$ diverged from the simulated PCD-measured pressure $\left|⟨P_{\text{PCD}}(f)⟩\right|$ before approaching an average pressure of zero at higher ka values. However, the average pressure magnitude $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ across the plane was approximately the same as the PCD-measured pressure $\left|⟨P_{\text{PCD}}(f)⟩\right|$ for all investigated ka values, consistent with the assumption of a nearly constant-phase wavefront across the PCD surface. Therefore, for both the pulse-echo and pitch-catch techniques, the hydrophone was used to map the transverse plane of the source and the average pressure magnitude $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ over the plane was used as the reference measurement for calibration.

To illustrate the potential calibration accuracy using this reference pressure, the absolute value of the dB-scaled ratio of $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ to $\left|⟨P_{\text{PCD}}(f)⟩\right|$ is shown for a variety of transmit-receive pairs of unequal and equal geometry in Figs. 1(e) and 1(f), respectively. The comparisons made in Fig. 1(e) are shown as a function of ka, for a receiver of radius a and f-number of 3.35, using a source with f-number 0.5–16.8 to represent potential transducer pairs for the pitch-catch technique. For transducer pairs consisting of a source of greater f-number than the receiver, $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ significantly exceeded $\left|⟨P_{\text{PCD}}(f)⟩\right|$ and this difference increased with increasing source f-numbers, especially at higher ka values. However, for transducer pairs consisting of a source with equivalent or smaller f-number than the PCD, the difference between measurements was no more than 0.45 dB over the range of investigated ka values.

The comparisons made in Fig. 1(f) are shown as a function of ka, employing simulated transducer pairs of equal geometry with a 4 mm radius and scaled focal lengths resulting in paired f-numbers of 0.5–5.1, representing potential PCD geometries for the pulse-echo technique. For the equal-geometry transducer pairs with an f-number less than 1, $\left|⟨P_{\text{PCD}}(f)⟩\right|$ was overestimated by $⟨\left|P_{\mathrm{H}}(f)\right|⟩$ by no more than 1.3 dB over the range of investigated ka values. However, the difference between measurements was less for transducer pairs with an f-number greater than 1, exceeding a difference of no more than 0.7 dB over the same ka range.

Acoustic measurements were made in a tank of degassed, deionized water. The receive sensitivity of the same spherically focused, single-element transducer (8.1 MHz center transmit frequency f₀, 8 mm diameter, 26.8 mm focal length; IMASONIC, Voray-sur-l'Ognon, France) was determined using both calibration methods over a frequency range of 1–20 MHz, corresponding to a ka range relative to the PCD of approximately 17–340. For the pitch-catch technique, a focused source (4.5 MHz f₀, 19 mm diameter, 25 mm focal length; UTX, Ithaca, NY) was confocally and coaxially aligned at a distance of 51.8 mm from the PCD and powered by a pulser-receiver (PR; 5052UAX50, Panametrics, Waltham, MA) to generate a broadband pulse. The time-dependent voltage generated by the PCD was digitized by an oscilloscope (Waverunner 6050A, LeCroy, Chestnut Ridge, NY). This and all subsequent time-domain voltage acquisitions were made by temporally averaging 100 consecutive, 20 μs long waveforms sampled at 100 MHz by the oscilloscope. PCD voltage measurements were repeated independently five times, reconstructing the entire pitch-catch configuration for each measurement. Absolute values of the fast Fourier transform (FFT) of each measurement were averaged and used as $V_{\text{PCD},\text{open}}(f)$ for the pitch-catch technique.

For the pulse-echo technique, the PCD was aligned with a flat, 51 mm thick × 51 mm circular-diameter aluminum plate at its focus. The PCD and PR were used in a pulse-echo mode and the reflected wave measured by the PCD was digitized by the oscilloscope. The frequency response of the PR on receive was characterized by amplifying a white noise signal provided by a function generator (34401A, Agilent, Santa Clara, CA) and comparing it in the frequency domain with the unamplified signal. Pulse-echo measurements were independently repeated five times, reconstructing the configuration for each measurement. After accounting for the frequency response of the PR on receive and the reflection coefficient of the plate, the absolute value of the FFT of each measurement was calculated and the average of the multiple trials was used as $V_{\text{PCD},\text{open}}(f)$ for the pulse-echo technique.

All reference measurements were made using a manufacturer-calibrated hydrophone (0.5 mm diameter; 1239, Precision Acoustics, Dorchester, Dorset, UK). The same sources used for PCD-voltage measurements, excited by the PR in the same manner, were used for the reference measurements for each calibration technique. For the pitch-catch technique, the PCD was substituted with the hydrophone and the acoustic field was mapped in the transverse plane at an axial distance of 51.8 mm from the source, equal to the sum of the focal lengths of the focused transducer pair. For the pulse-echo technique, the reflection plate was removed and the transverse plane of the PCD's transmit field was mapped at an axial distance of 53.6 mm, equal to twice its focal length. Both planes were sampled over an 8 mm circular diameter, matching the planar diameter of the PCD, with a 0.2 mm spatial resolution in either azimuthal direction by scanning the hydrophone across the plane using a three-dimensional stepper motor system (Velmex, Bloomfield, NY). Time-dependent voltages were digitized at each planar position by the oscilloscope. The spatial average of the absolute value of the FFT of the signal measured at each planar position was taken to determine the average open-circuit voltage $⟨\left|V_{\mathrm{H},\text{open}}(f)\right|⟩$ amplitude measured by the PCD. The average pressure amplitude measured by the hydrophone was calculated as $⟨\left|P_{\mathrm{H}}(f)\right|⟩=⟨\left|V_{\mathrm{H},\text{open}}(f)\right|⟩/M_{\mathrm{H}}(f)$, where $M_{\mathrm{H}}(f)$ is the hydrophone's receive sensitivity, provided by the manufacturer over the frequency range 1–20 MHz.

The frequency-dependent absolute receive sensitivity of the PCD was determined for both calibration methods as $M_{\text{PCD}}(f)=V_{\text{PCD},\text{open}}(f)/⟨\left|P_{\mathrm{H}}(f)\right|⟩$, the ratio of the corresponding open-circuit PCD voltage to the planar, hydrophone-measured average pressure amplitude. Frequency-dependent uncertainty, associated in part with alignment variations, was estimated from the coefficient of variation of repeated PCD voltage measurements. This uncertainty was propagated with the manufacturer-specified uncertainty for the hydrophone sensitivity to calculate the total, frequency-dependent uncertainty of the PCD's receive sensitivity. Uncertainties in measured pressures were estimated as the frequency-dependent pressures multiplied by the frequency-dependent receive sensitivity uncertainties of the hydrophone and PCD, respectively.

Validation measurements were conducted using a 2 mm diameter barrel-shaped transducer (1.4 MHz f₀; Sonometrics, London, Ontario, Canada) as a source, aligned coaxially with the hydrophone or PCD at a distance of 26.8 mm, the focal distance of the PCD, to mimic an approximate point radiator. The source was excited by the PR using four energy settings to generate broadband pulses of different amplitude. Using the PCD as a receiver, the voltage generated upon receiving each pulse was digitized by the oscilloscope and the open-circuit voltage $V_{\text{PCD},\text{open}}(f)$ of the PCD was calculated as the absolute value of the FFT of the acquired signal. Using the receive sensitivity $M_{\text{PCD}}(f)$ of the PCD determined from the pitch-catch and pulse-echo methods, the frequency-dependent pressure amplitude of each pulse measured by the PCD was calculated as $|P_{\text{PCD}}(f)|=V_{\text{PCD},\text{open}}(f)/M_{\text{PCD}}(f)$. The absolute, frequency-dependent pressure of the each pulse was determined using the hydrophone as in the calibration methods by scanning the transverse plane at the same distance, taking the average of the absolute value of the FFT of each signal, and taking the ratio of this voltage to the hydrophone sensitivity as $⟨\left|P_{\mathrm{H}}(f)\right|⟩=⟨\left|V_{\mathrm{H},\text{open}}(f)\right|⟩/M_{\mathrm{H}}(f)$. Measured pressures were compared as a function of frequency up to approximately 10 MHz, the approximate maximum useful radiating frequency of the Sonometrics source.

3. Results

Frequency-dependent voltage amplitudes measured by the PCD, with the corresponding average voltage amplitudes of the planar hydrophone measurements, are shown in Figs. 2(a) and 2(b) for the pulse-echo and pitch-catch techniques, respectively. Voltage measurements using the pulse-echo technique provided a calibration bandwidth of approximately 20 MHz, limited by the calibration bandwidth of the hydrophone. Although the signal-to-noise ratio (SNR) of measurements using the pitch-catch technique approached the noise floor within a narrower bandwidth, calibration was still feasible over a bandwidth of approximately 16 MHz.

Fig. 2.

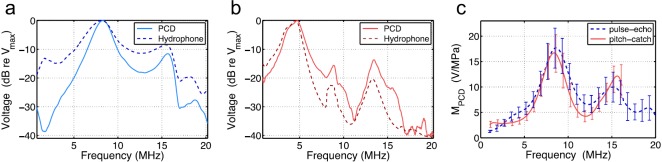
(Color online) (a) Measured voltages using the PCD and hydrophone as receivers for the pulse-echo technique. (b) Measured voltages using the PCD and hydrophone as receivers for the pitch-catch technique. (c) Frequency-dependent, absolute PCD receive sensitivities $M_{\text{PCD}}(f)$ determined using the pulse-echo and pitch-catch techniques, with error bars representing the uncertainty of the PCDs receive sensitivity.

The absolute receive sensitivity of the PCD determined using both techniques is shown as a function of frequency in Fig. 2(c) over the usable bandwidth for each method. Error bars shown indicate the calculated frequency-dependent uncertainty of the PCD's receive sensitivity for each calibration method. The frequency-averaged uncertainty in the PCD receive sensitivity for the pulse-echo and pitch-catch techniques was 23.4% and 23.2%, respectively. The contribution of uncertainty from the hydrophone measurements alone, based on values provided by the manufacturer, was on average 19.7% across its calibrated bandwidth. For comparison, the uncertainty contributed from repeated PCD voltage measurements over the bandwidth of each calibration was 12.6% and 12.2% for the pulse-echo and pitch-catch techniques, respectively.

Frequency-dependent pressures measured from the 2 mm validation source by the PCD, calculated using the receive sensitivities determined using the pulse-echo and pitch-catch techniques, are compared with corresponding hydrophone-measured pressures in Fig. 3(a) for a representative trial using the highest of the four voltage amplitudes employed to drive the validation source. Relatively good overall correspondence between the hydrophone- and PCD-measured pressures is seen, but considerable differences are evident near higher-frequency nulls, e.g., at approximately 8 MHz. Mapping the transmit field within these anomalous frequency ranges revealed asymmetric phase patterns, which caused significant destructive interference across the PCD surface. Since these aberrations were inherent to the transmit field of the source and not to the calibration or validation methods, the pressures associated with these null-producing frequencies were neglected for comparison purposes. Instead, for the four different transmit conditions, pressure values were sampled at frequencies associated with symmetric phase maps which more closely resembled those produced by a point radiator at the focus. The frequency bins sampled for further analysis are indicated by error bars in Fig. 3(a). Pressure values measured at these frequencies by the PCD using the pulse-echo and pitch-catch techniques are directly compared with corresponding hydrophone-measured pressures in Figs. 3(b) and 3(c), respectively. All error bars in Fig. 3 represent the dB-scaled, frequency-dependent calculated uncertainty of pressure measured by each respective receiver. The gray boxes in Figs. 3(b) and 3(c) represent the dB-scaled average uncertainty of the hydrophone plotted above and below the one-to-one line for comparison with the PCD-measured pressures.

Fig. 3.

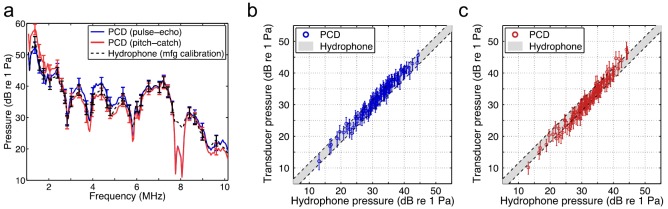
(Color online) (a) Representative frequency-dependent pressures measured by the hydrophone and PCD, with error bars representing their calculated uncertainty. (b) PCD-measured pressures and uncertainties using the receive sensitivity determined using the pulse-echo technique vs corresponding hydrophone-measured pressures. (c) PCD-measured pressures and uncertainties using the receive sensitivity determined using the pitch-catch technique vs corresponding hydrophone-measured pressures. Dashed lines in (b) and (c) indicate the average hydrophone uncertainty above and below the one-to-one line.

4. Discussion

Numerical and experimental results demonstrate that the wideband, absolute receive sensitivity of the spherically focused PCD employed here can be calibrated using a reference pressure approximated from planar hydrophone measurements, using either the pulse-echo or pitch-catch technique. Additionally, numerical results indicate that both techniques are appropriate to calibrate a variety of other PCD geometries. For the pulse-echo, relatively low error between the approximated reference pressure and the PCD-measured pressure can be maintained for the calibration of any PCD with an f-number greater than 0.5. To maintain relatively low error for the pitch-catch technique, care must be taken to use a focused source with an equivalent or smaller f-number than the PCD. Otherwise, the PCD diameter will exceed the transmit beamwidth and the pressure wave will arrive nonuniformly across its face, resulting in appreciable phase cancellation and associated measurement errors, especially at higher frequencies.

The bandwidth of any calibration is generally dependent on the combined, finite bandwidths of the transmit and receive sensitivities of the transducer pair used for measurements. Both transducer configurations used here resulted in relatively high SNR measurements over a broad bandwidth. Therefore, the PCD receive sensitivities were also determined over a broad bandwidth for both methods, including the pitch-catch technique, even though the source and PCD had different center frequencies of approximately 4.5 and 8.1 MHz, respectively. Considering the bandwidth and precision of measurements made here, both calibration methods were shown to produce approximately the same receive sensitivity for the PCD over a broad range of frequencies and were validated by comparison with hydrophone measurements over a range of frequencies and pressures. These results indicate that both techniques are suitable for calibrating the receive sensitivity of focused, single-element PCDs in order to make absolute pressure measurements.