A Simplified Spin and Gradient Echo (SAGE) Approach for Brain Tumor Perfusion Imaging

Abstract

Purpose

A simplified acquisition and analysis approach for spin- and gradient-echo (SAGE) based DSC-MRI data that is free of contrast agent T₁ leakage effects is proposed.

Methods

A five-echo SAGE sequence was used to acquire DSC-MRI data in rat C6 tumors (n=7). Non-linear fitting of all echoes was performed to obtain T₁-insensitive ΔR₂^* and ΔR₂ time series. The simplified approach, which includes two gradient echoes and one spin echo, was also used to analytically compute T₁-insensitive ΔR₂^*, using the two gradient echoes, and ΔR₂, using all three echoes. The blood flow, blood volume and vessel size values derived from each method were compared.

Results

In all cases, the five-echo and simplified SAGE ΔR₂^* and ΔR₂ were in excellent agreement and demonstrated significant T₁-leakage correction compared to the uncorrected single-echo data. The derived hemodynamic parameters for blood volume, blood flow and vessel size were not significantly different between the two methods.

Conclusions

The proposed simplified SAGE technique enables the acquisition of gradient and spin echo DSC-MRI data corrected for T₁ leakage effects, yields parameters that are in agreement with the five echo SAGE, and does not require non-linear fitting to extract ΔR₂^* and ΔR₂ time series.

Introduction

Unlike other tracer-based perfusion imaging modalities, dynamic susceptibility-contrast magnetic resonance imaging (DSC-MRI) is unique in its acquisition-dependent vessel size sensitivity. When acquired with spin echo (SE) sequences, the derived DSC parameters, including cerebral blood volume (CBV), cerebral blood flow (CBF), and mean transit time (MTT), are maximally sensitive to capillary-sized vascular structures, while gradient echo (GE) derived hemodynamic parameters are sensitive to vessels of all sizes (1). Although GE imaging is preferred for clinical practice due to its higher SNR, the addition of SE imaging may provide complementary information due to its microvascular sensitivity (2–5). Moreover, the combination of GE and SE imaging permits analysis of mean vessel diameter (mVD) (1,4,6–9). However, quantification of these parameters relies on the assumption that the contrast agent (CA) remains confined to the intravascular space, which may not be the case in tumors (10) or stroke (11).

In tumors, a compromised blood-brain barrier (BBB) leads to extravasation of small molecular weight Gd-based contrast agents (CA) and can severely reduce the reliability of the derived perfusion measures due to competing T₁ effects (10,12–14). The use of a preload CA dose can reduce, but not eliminate, the magnitude of T₁ leakage effects on DSC-MRI signals (15). In contrast, dual gradient echo sequences (16) provide a simple analytical method to obtain both T₁-insensitive ΔR₂^* measures and T₁-weighted signals for Dynamic Contrast Enhanced (DCE) MRI analysis (17). In a comparison with other leakage correction methods, dual-echo sequences were found to provide the most robust T₁-insensitive gradient-echo hemodynamic measures (14). However, no analogous method exists to obtain T₁-insensitive spin-echo hemodynamic measures. Towards this end, a combined spin- and gradient-echo (SAGE) EPI method was recently proposed to simultaneously obtain T₁-insensitive ΔR₂ and ΔR₂^* dynamic time-courses (4,18). This method relies upon the acquisition of multiple echoes (typically between 5 and 7 echoes) and non-linear fitting of each dynamic in order to compute the ΔR₂ and ΔR₂^* time courses. Here, we propose a simplified SAGE approach that utilizes a combined dual gradient-echo and spin-echo pulse sequence and an analytical solution for computing T₁-insensitive ΔR₂^* and ΔR₂ time series. As this approach only requires the acquisition and storage of three echoes and does not rely upon computationally demanding non-linear fitting algorithms, it could facilitate the more rapid clinical translation and adoption of SAGE-based DSC-MRI.

Theory

As described above, the simplified SAGE approach, which we will henceforth term sSAGE to delineate it from the original SAGE technique, relies upon the acquisition of two gradient echoes followed by a spin echo. To remove contrast-agent induced T₁ leakage effects from the GE and SE data, the MRI signal is expressed in terms of the combined dynamic T₁ and T₂ (=1/R₂) or T₂^* (=1/R₂^*) changes. In the case of the spin echo, the MRI signal at a given echo time, S_TE(t), and resulting ΔR₂, assuming exponential decay, are given by:

$$S_{TE}(t)=M_0\frac{sin\alpha \left(1-e^{-TR·R_1(t)}\right)}{1-cos\alpha ·e^{-TR·R_1(t)}}{e}^{-TE·R_2(t)}=M_0·f({\mathrm{T}}_1)·e^{-TE·R_2(t)}$$ [1]

$$\mathrm{\Delta }{R}_2(t)=R_2(t)-R_{2,\mathit{pre}}=\frac{1}{TE}\left(ln\left(\frac{S_{TE,\mathit{pre}}}{S_{TE}(t)}\right)+f({\mathrm{T}}_1)\right)$$ [2]

where f(T₁) describes the dynamic changes in the tissue T₁ due to contrast agent leakage, α is the flip angle, TR is the pulse sequence repetition time, TE is the echo time, M_o is the initial magnetization, and “pre” designates the mean signal prior to contrast arrival. The GE signal can be similarly derived using Eqs. [1] and [2], with T₂ and ΔR₂ replaced by T₂^* and ΔR₂^*.

While f(T1) is typically assumed to be negligible, this assumption is not valid in cases of compromised BBB. As previously shown (16), T₁ effects can be completely removed from ΔR₂^* through the use of a dual gradient echo sequence:

$$\mathrm{\Delta }{R}_2^{\ast }(t)=\frac{1}{{TE}_2-{TE}_1}\left(ln\left(\frac{S_{{TE}_2,\mathit{pre}}}{S_{{TE}_2}(t)}\right)-ln\left(\frac{S_{{TE}_1,\mathit{pre}}}{S_{{TE}_1}(t)}\right)\right)$$ [3]

where S_TE1 and S_TE2 are the gradient echo signals at each echo time. A dual-echo acquisition also has the advantage of providing a T₁-weighted signal extrapolated to TE=0 (16):

$$S_{TE=0}=S_{{TE}_1}·{\left(\frac{S_{{TE}_1}}{S_{{TE}_2}}\right)}^{\raisebox{1ex}{${TE}_1$}\!\left/ \!\raisebox{-1ex}{$({TE}_2-{TE}_1)$}\right.}$$ [4]

The main purpose of this study is to provide a similar analytical solution to eliminate T₁ effects from ΔR₂ time series, thus enabling simultaneous extraction of T₁-insensitive GE and SE DSC-MRI data. Using the signal extrapolated to TE=0 as f(T₁) in Eqs. [1] and [2], the T₁ leakage effects can be removed from spin echo signals using:

$$\mathrm{\Delta }{R}_2(t)=\frac{1}{{TE}_{SE}}\left(ln\left(\frac{S_{{TE}_{SE},\mathit{pre}}}{S_{{TE}_{SE}}(t)}\right)-ln\left(\frac{S_{TE=0,\mathit{pre}}}{S_{TE=0}(t)}\right)\right)$$ [5]

Methods

Animals Studies

All animal studies were performed in accordance with Vanderbilt University’s Institutional Animal Care and Use Committee (IACUC) protocols. For all procedures and imaging, the animals were immobilized in a stereotactic head holder. Anesthesia was induced using 3–5% isoflurane in air and maintained with 1–2.5% isoflurane in air. Body temperature was maintained at 38°C using forced warm air. The sSAGE and SAGE signal and SNR were compared in normal male Wistar rats (n = 3). For the tumor studies, male Wistar rats (Harlan Laboratories, Indianapolis, IN) were inoculated with 1×10⁵ C6 glioma cells (American Type Culture Collection, Manassas VA), respectively, at 1 mm anterior and 3 mm lateral to the bregma and 4 mm depth from the dural surface. Imaging was performed after 16 days (n = 7).

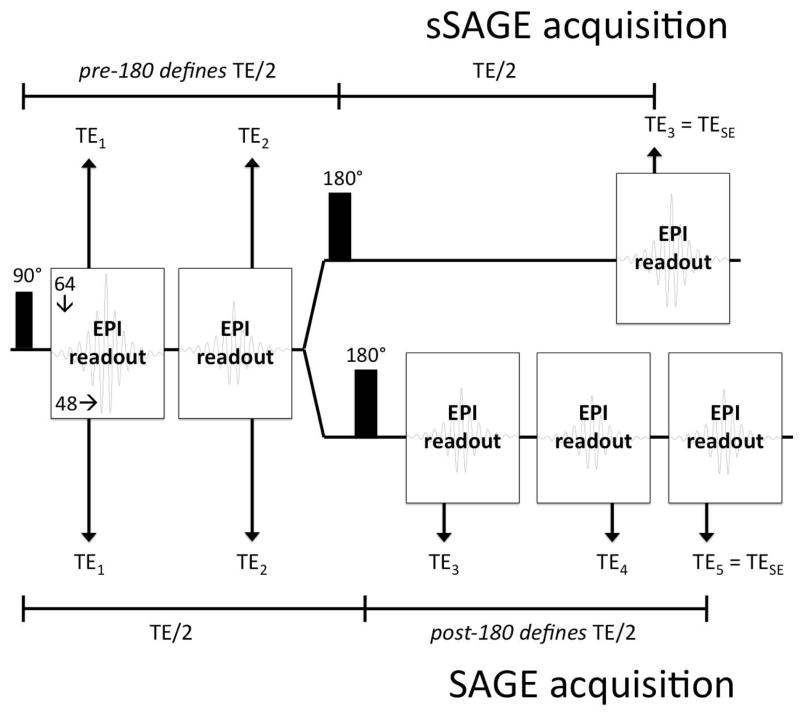
MRI was performed at 4.7T (Agilent, Santa Clara, CA). The sSAGE- and SAGE-EPI sequences, shown in Figure 1, were used to obtain three and five echoes, respectively. Both sequences incorporate two gradient echoes before a 180° pulse; the sSAGE sequence includes a single spin echo, while the SAGE sequence includes two asymmetric spin echoes and a final spin echo. For the sSAGE acquisition, the 180° pulse follows immediately after the 2^nd gradient echo, as the first TE/2 period determines the where the SE (TE₃) occurs. In the original SAGE acquisition, the SE (TE₅) is determined by the second TE/2 period, which depends on the number and length of the acquired asymmetric spin echoes. Partial Fourier encoding (48 of 64 lines acquired) was used to obtain acceptable echo times (Table 1; TE₁ – TE₃ = 8.6/35/86 ms for sSAGE; TE₁ – TE₅ = 8.6/35/56/82/96 ms for SAGE). As a result of the shorter final TE, the sSAGE sequence provided 10 slices in a 1 s TR, while the SAGE sequence provided 8 slices in the same TR. The partially sampled k-space data were reconstructed to full Fourier space using an iterative homodyne reconstruction algorithm (19,20) in Matlab (Mathworks, Inc.). Standard slice-selective sinc pulses were used for excitation and refocusing, with crusher gradients surrounding the refocusing pulse. A 64×64 acquisition matrix within a 36×36 mm² FOV was acquired with 1-mm thick slices. To obtain adequate temporal resolution for dynamic studies, a TR of 1 s was used for at least 5 minutes. After 80 s of baseline images, 0.4 mmol/kg gadopentetate dimeglumine (Gd-DTPA) was injected via jugular catheter.

Figure 1.

Pulse sequence diagram for the sSAGE (top) and SAGE (bottom) acquisitions with three and five echoes, respectively.

Table 1.

Comparison of TE, signal, and SNR for sSAGE and SAGE acquisitions in normal rat brain (n=3).

		TE1	TE2	TE3	TE4	TESE
TE (ms)	sSAGE	8.6	35	--	--	86
	SAGE	8.6	35	54	80	96
Signal (SD)	sSAGE	1.73 (0.04)	1.01 (0.05)	--	--	0.40 (0.01)
	SAGE	1.69 (0.05)	0.99 (0.05)	0.58 (0.02)	0.42 (0.01)	0.33 (0.01)
SNR (SD)	sSAGE	39.2 (0.6)	23.2 (0.4)	--	--	10.1 (0.2)
	SAGE	38.7 (0.4)	23.1 (0.7)	14.4 (0.4)	10.5 (0.2)	8.5 (0.2)

Post-processing and Analysis

The SAGE-derived ΔR₂ and ΔR₂^* time-courses were obtained using nonlinear least squares fits to a piecewise function (Eq. [5]) as previously described (18). Due to slice profile imperfections between the excitation and refocusing pulses (18), the signal intensities S^I₀ and S^II₀ were permitted to differ in the fitting.

$$S(\tau )=\{\begin{array}{cc}{S}_0^I·e^{-\tau ·R_2^{\ast }}& 0<\tau <TE/2\\ S_0^{II}·e^{-TE·(R_2^{\ast }-R_2)}·e^{-\tau ·(2·R_2-R_2^{\ast })}& TE/2<\tau <TE\end{array}$$ [6]

The baseline signals were averaged to obtain the pre-bolus signal, and the voxel-wise R₂, R₂^*, S^I₀, and S^II₀ were determined from Eq. [6]. The full four-parameter fit for ΔR₂^* and ΔR₂ was compared to a reduced fit with the ratio S^I₀/S^II₀ – a measure of the slice profile mismatch – held constant for the dynamic time course (4). Due to temporal inconsistencies observed with the full four-parameter fit (Supporting Figure S1), the reduced 3-parameter fit was used for all remaining data to obtain R₂(t), R₂^*(t) and S^I₀(t) (with S^II₀(t) replaced with S^I₀(t)/(S^I₀/S^II₀) in the fit function).

To avoid differences that may occur between multiple injections, the sSAGE data in tumor-bearing rats were obtained from the full SAGE datasets using only TE₁, TE₂, and TE₅. The 2^nd (gradient-echo) and 5^th echo (spin-echo) signals were used to determine the single-echo-based ΔR₂^* and ΔR₂ time series. The first two gradient echoes and the 5^th echo were used, along with Eqns. [3] and [5], to compute the T₁-insensitive sSAGE ΔR₂^* and ΔR₂ time series. The SAGE fits for R₂^*(t) and R₂(t) were used to determine the T₁-insensitive ΔR₂^* and ΔR₂ time series. The arterial input function (AIF) was selected from the T₁-insensitive ΔR₂^* time courses using an automated method (21) specifically adapted for use with multi-echo acquisitions (22). CBV was determined from the ratio of the scaled integrals of the tissue ΔR₂^* and ΔR₂ curves and the arterial input function curve. To avoid artifactually low CBV values that are often observed in single echo brain tumor data, negative ΔR₂^* and ΔR₂ values were not included in the integration. CBF was taken as the maximum of the tissue impulse response function determined from the circular singular value decomposition (SVD) of the AIF and tissue ΔR₂^* and ΔR₂ (23). For display purposes, CBV and CBF were normalized to 4% and 60 ml/100g/min in gray matter. Relative mVD maps were calculated from the ratio of the integrals of the single-echo, sSAGE and SAGE GE ΔR₂^* and SE ΔR₂ curves during bolus passage (1,6,7). Regions of interest (ROIs) were initially drawn from a fast spin echo (FSE) image at a long TE (80ms), and the tumor ROIs were further refined using a 15% enhancement threshold compared to the normal tissue ROIs. Group means were compared using a paired t-test with 5% and 1% significance levels.

Results

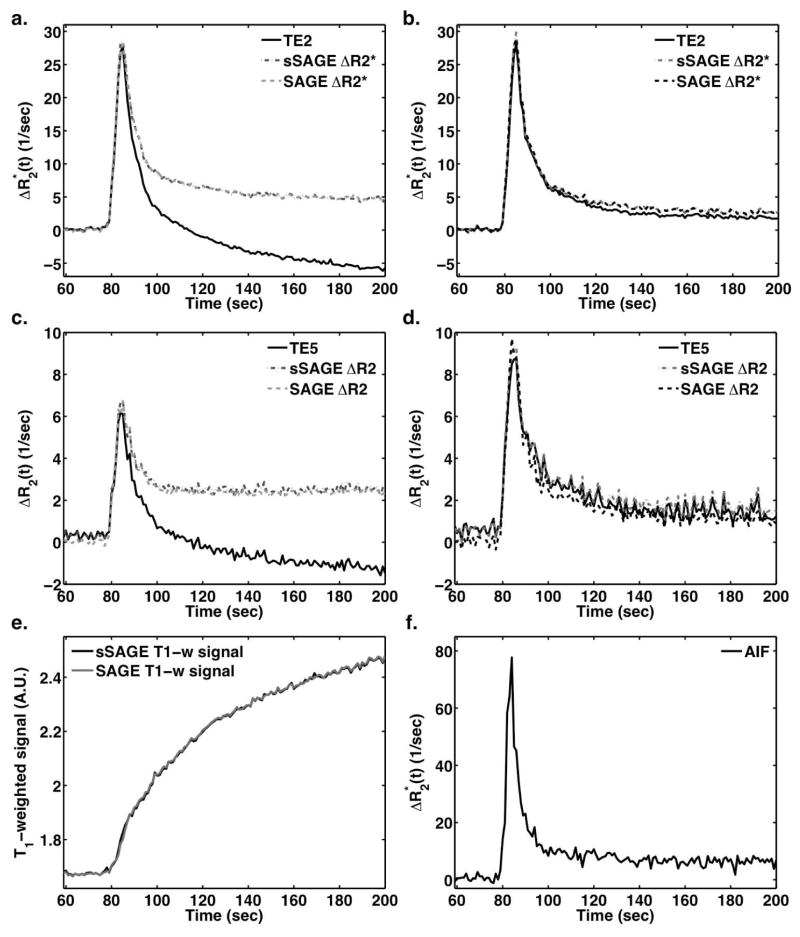
Figure 2 demonstrates representative examples of dynamic DSC data following Gd-DTPA injection in a C6 rat brain tumor ROI (a,c) and normal brain ROI (b,d). In tumor, Gd-DTPA extravasates out of the vasculature, leading to T₁-shortening effects that manifest as lower post-bolus ΔR₂^* and ΔR₂ for single echo data (TE₂ and TE₅, respectively). The SAGE (three-parameter fit) and sSAGE ΔR₂^* curves, both corrected for T₁ leakage effects, do not exhibit reduced post-bolus ΔR₂^* and are in close agreement. Similarly, the T₁-corrected sSAGE derived ΔR₂ curve matches well with the T₁-insensitive SAGE ΔR₂. In normal tissue (b,d), where CA does not typically extravasate, the various ΔR₂^* and ΔR₂ measures are similar. In the bottom left panel, the T₁-weighted signals in tumor derived from the two SAGE techniques are in good agreement.

Figure 2.

Dynamic ΔR₂^* (a,b) and ΔR₂ (c,d) curves for a tumor ROI (a,c) and normal ROI (b,d) following bolus injection of 0.4 mmol/kg Gd-DTPA. The sSAGE and SAGE-based T₁-weighted signals in a tumor ROI are also shown (e), along with the AIF used for DSC-MRI analysis (f).

Supporting Figure S1 compares dynamic SAGE and sSAGE ΔR₂^* and ΔR₂ obtained with the full four-parameter fit, a reduced three-parameter fit, and the sSAGE method. The four-parameter fit results in identical ΔR₂^* curves to sSAGE in both C6 tumor (a) and normal ROIs (b). However, ΔR₂ from the four-parameter fit is dramatically narrowed and reduced during bolus passage compared to sSAGE. Further analysis shows that this can be attributed to the large, incorrect change in the fitted S_II parameter during bolus passage (e,f). The T₁-weighted signals for the fitted S_I parameter are nearly identical to the T₁-weighted signal from sSAGE. To improve temporal stability, a reduced three-parameter fit without dynamic compensation for slice profile mismatch was compared to sSAGE in tumor (c,g) and normal brain (d,h), where the curves were in close agreement for ΔR₂^*, ΔR₂, and T₁-weighted signals.

The reduced SE TE (86 ms) of sSAGE provides higher SE signal and SNR compared to SAGE (SE TE = 96 ms) (Table 1). The two GE acquisitions for both sSAGE and SAGE have the same TEs and similar signals and SNR.

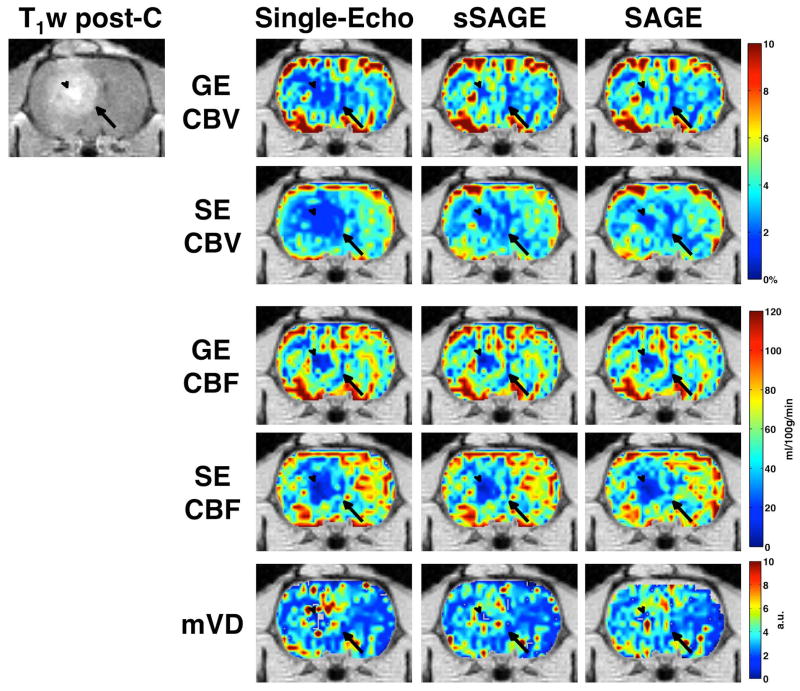
The CBV and CBF maps for gradient-echo and spin-echo are shown in Figure 3 for the single-echo (TE₂ and TE₅), sSAGE and SAGE. Both the gradient-echo and spin-echo CBV maps for single-echo are substantially underestimated in the tumor region, while the sSAGE- and SAGE-derived maps both exhibit similarly higher CBV. For CBF, the single echo, sSAGE, and SAGE-derived maps for gradient-echo and spin-echo are similar.

Figure 3.

GE (TE₂, sSAGE, and SAGE) CBV and CBF, SE (TE₅, sSAGE, and SAGE) CBV and CBF, and mVD in a tumor-bearing rat (T₁-weighted post-contrast image shows tumor edge, indicated by arrow, and necrotic core, indicated by arrowhead).

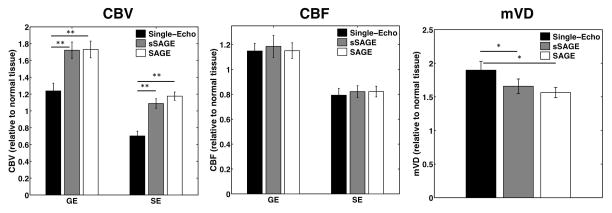
The bar plots in Figure 4 show the mean CBF, CBV, and mVD in tumor relative to normal tissue using the single-echo, sSAGE, and SAGE ΔR₂^* and ΔR₂ (n=7). The gradient-echo CBF in tumor was slightly higher than normal tissue, while the spin-echo CBF was slightly lower than normal tissue. None of the gradient-echo or spin-echo CBF measures were significantly different (p>0.05). T₁-leakage effects led to significantly reduced single-echo CBV for both gradient-echo and spin-echo compared to the sSAGE and SAGE measures. The single-echo CBV values were significantly different from the sSAGE and SAGE CBV (p<0.0005 for both GE and SE values), while the sSAGE and SAGE CBV were not significantly different from each other (p>0.05). All three mVD measures were similarly increased in tumors, and the sSAGE and SAGE measures were not significantly different (p>0.05). The single-echo measures were significantly different from the sSAGE and SAGE measures (p=0.0429 and p=0.0222, respectively).

Figure 4.

Bar plots showing mean GE and SE CBV and CBF and mVD relative to normal tissue for the single-echo, sSAGE, and SAGE methods (n=7). ^**p<0.01 and ^*p<0.05.

Discussion

The proposed simplified SAGE technique leverages the known insensitivity of dual-gradient echo DSC-MRI data to T₁ leakage effects and provides a simple, computationally efficient analytical solution for T₁-correction of SE data, thereby yielding T₁-insensitive GE and SE hemodynamic parameters, plus measures of vessel size. On a computer with a 2.4 GHz dual-core processor with 8 GB of RAM, the computation time for deriving the ΔR₂^* and ΔR₂ curves for a typical whole rat brain (approximately 1800 voxels with 200 repetitions) was 2 hours for SAGE and 16 seconds for sSAGE. Consequently, the proposed analytic approach is 450 times faster than the non-linear fitting procedure used for full SAGE data. In reality, all voxels can be analytically calculated simultaneously, and thus, sSAGE for the entire rat brain and all repetitions can be calculated in less than 1 second. Furthermore, the sSAGE method will prove especially advantageous for human DSC-MRI that has substantially more voxels.

A limitation of the proposed approach is its inability to correct for slice profile mismatch that can occur with spin echo sequences (18). While this is important for absolute quantification of T₂, it is less important for DSC measures that rely on assessing changes in R₂ to obtain CBF, CBV, and MTT. Moreover, current SAGE DSC implementations quantify slice profile mismatch during baseline, which is held constant during the dynamic time-course (4,24,25). Thus, the effects of slice profile mismatch are effectively subtracted when ΔR₂ and ΔR₂^* are obtained for DSC purposes. In addition, dynamically correcting for slice profile mismatch using a four-parameter fit can incorrectly assign temporal ΔR₂ changes during bolus passage to changes in the post-180 signal intensity S_II. This is avoided in the sSAGE method or can be effectively rectified by using a reduced three-parameter fit with constant slice profile mismatch S_I/S_II. Because the sSAGE sequence requires only three echoes, shorter SE TEs may be feasible, which improves the SE SNR and may increase slice coverage (or yield shorter TRs). In addition, the later echoes (such as the 3^rd and 4^th asymmetric spin-echoes in SAGE) tend to be more sensitive to signal voids due to high CA concentration (26) or susceptibility-induced edge artifacts, which can yield inaccurate fits (25). The method proposed herein does not depend on asymmetric spin-echoes, although this also makes the method more sensitive to potential errors in any of the three echoes. Of the hemodynamic parameters, CBF is especially sensitive to noise due to the deconvolution step, and thus, the higher SE SNR of the simplified approach may be advantageous to improve the overall reliability of the derived hemodynamic parameters.

Many methods exist to mitigate or correct leakage effects (historically focusing on T₁ effects) in single gradient echo data, including preload dose, sequence modifications, and model-based corrections (12–14). With the advent of dual-echo acquisitions, the T₁ effects can be eliminated from the DSC ΔR₂^* data, and the derived T₁-weighted signal can subsequently be used for DCE analysis (17). This study presents an analogous solution for spin-echo data by utilizing the dual gradient-echoes to quantifying the dynamic T₁ changes and then removing these effects from ΔR₂. With the exception of the previously published SAGE papers (4,24), no studies have considered the effects of CA leakage on spin echo data. In this study, SE CBF was not significantly different for single-echo, sSAGE, or SAGE, consistent with previous studies showing minor leakage effects on GE CBF. On the other hand, GE and SE CBV values were significantly underestimated by the single echoes compared to the T₁-insensitive measures (sSAGE and SAGE), further demonstrating the importance of leakage correction for CBV assessment. Interestingly, single echo mVD was significantly higher than the sSAGE and SAGE measures, which were not significantly different, indicating that T₁ leakage effects do not simply cancel out when computing the ratio of ΔR₂^* and ΔR₂. In most vessel-size sensitive measurement methods (8), CA leakage effects are mitigated by γ-variate fitting, and this is likely sufficient for T₁-predominant leakage effects (9).

For the purposes of this study, tumors that exhibited predominantly T₁-leakage effects were deliberately chosen, as the primary focus was removing T₁ leakage effects from spin- and gradient echo DSC-MRI data. However, other tumor types (in both rat and human brains) that exhibit a range of T₁ and T₂^*/T₂ leakage effects should yield similar curves between SAGE and sSAGE, as these techniques should exhibit similar sensitivity to T₂ and T₂^* leakage effects. As T₂ leakage effects would undoubtedly affect the ΔR₂ curves and derived hemodynamic parameters, obtaining quantitative measures of SE hemodynamics will require both removal of T₁ leakage effects and corrections for T₂ leakage effects. While multi-echo acquisitions remove T₁ leakage effects, unfortunately, no consensus currently exists on the best method to correct T₂^* and T₂ leakage effects (12–14,24). While this is outside the scope of this study, such topics will be the focus of future investigations.

In conclusion, T₁-insensitive GE and SE hemodynamic parameters can be obtained using a simplified spin-and gradient-echo sequence with three total echoes (two gradient-echoes and one spin-echo). The T₁-insensitive ΔR₂^* and ΔR₂ time courses can be calculated using the previously proposed dual-echo equation and the spin-echo correction presented here. As this method does not require time-consuming nonlinear fitting, it is an efficient and clinically feasible method. Moreover, the ΔR₂ curves from the sSAGE method match well with the reduced three-parameter SAGE fit, both of which are more accurate than the originally proposed four-parameter SAGE fit. In addition to T₁-insensitive CBF, CBV, and MTT with both GE (total vasculature) and SE (microvasculature) contrast, this sequence provides measures of mVD. Aside from the addition of the T₁-insensitive spin-echo hemodynamic parameters, the proposed approach may still be used to obtain ΔR₁ curves for DCE analysis, thereby providing simultaneous measures of perfusion and permeability (16,17).

Supplementary Material

Supp MaterialS1. Supporting Figure S1.

Dynamic ΔR₂^* and ΔR₂ (c,d) curves comparing the four-parameter SAGE fit (a,b) and the three-parameter SAGE fit (c,d) to sSAGE in tumor (a,c) and normal (b,d) ROIs. The four-parameter signals S_I and S_II (e,f) and the three-parameter signal S_I (g,h) are also compared to the sSAGE-based signal S_TE=0 in tumor (e,g) and normal (f,h) ROIs.