Radiofrequency Energy Deposition and Radiofrequency Power Requirements in Parallel Transmission with Increasing Distance from the Coil to the Sample

Abstract

Purpose

We investigated global specific absorption rate (SAR) and radiofrequency (RF) power requirements in parallel transmission as the distance between the transmit coils and the sample was increased.

Methods

We calculated ultimate intrinsic SAR (UISAR), which depends on object geometry and electrical properties but not on coil design, and we used it as the reference to compare the performance of various transmit arrays. We investigated the case of fixing coil size and increasing the number of coils while moving the array away from the sample, as well as the case of fixing coil number and scaling coil dimensions. We also investigated RF power requirements as a function of liftoff, and tracked local SAR distributions associated with global SAR optima.

Results

In all cases, the target excitation profile was achieved and global SAR (as well as associated maximum local SAR) decreased with lift-off, approaching UISAR, which was constant for all lift-offs. We observed a lift-off value that optimizes the balance between global SAR and power losses in coil conductors. We showed that, using parallel transmission, global SAR can decrease at ultra high fields for finite arrays with a sufficient number of transmit elements.

Conclusion

For parallel transmission, the distance between coils and object can be optimized to reduce SAR and minimize RF power requirements associated with homogeneous excitation.

INTRODUCTION

Parallel transmission with multiple radiofrequency (RF) coils (1,2) can enable homogeneous excitations at ultra high magnetic field strengths, while minimizing the specific absorption rate (SAR) over the entire volume of the sample (2,3). However, electric fields generated by transmit coils placed close to the body can in principle cause dangerous hotspots, even if average global SAR remains small over the duration of the RF excitation. On the other hand, increasing the distance of the transmit coils from the body could require higher RF power to achieve a given flip angle distribution, possibly resulting in increased global SAR. Furthermore, moving the transmit array away from the sample widens the area of overlap between individual coil sensitivities, which may compromise the performance of parallel transmission techniques.

SAR dependence on the orientation of coils with respect to the sample was studied by Katscher et al (4) for parallel transmission, by changing the relative orientation between two transmit coils placed at a fixed distance from the center of a spherical object. For a two-coil experimental setup, they found that the angular tolerance of the coil positions was typically ~20°–30° for a 10% increase in SAR compared with the lowest coil SAR in the optimal configuration. Moreover, several groups have studied parallel transmission performance as a function of the number of transmit array elements, field strength and coil arrangement around the object (3,5–7). These studies showed that there can be SAR benefits associated with using higher numbers of channels and, if possible, distributing the transmit elements uniformly around the region of interest.

In these studies (3–6), the distance between the coils and the sample was kept fixed. In some of our previous work, reported at an annual meeting of the International Society for Magnetic Resonance in Medicine, we evaluated the effect of the distance between the transmit array and the sample for a spherical geometry (7). However, until now the effect of changing the distance between the transmit elements and the sample in parallel transmission, for both cylindrical and spherical geometries, has not been explored comprehensively.

In this work, we used semianalytical full-wave electrodynamic simulations to investigate global and local SAR behavior of transmit arrays, and the corresponding RF power requirements, with respect to the distance between the transmit elements and the surface of a uniform spherical or cylindrical object, both at 3 Tesla (T) and at 7T. Ultimate intrinsic SAR (UISAR), which is defined as the lowest possible global SAR consistent with electrodynamics for a particular excitation profile, but independent of transmit coil design (3), was used as an absolute reference to compare the performance of various transmit array designs.

METHODS

Simulations

A dyadic Green’s function (DGF) formulation (8,9) was used to derive the full-wave electromagnetic (EM) fields inside a dielectric sphere / cylinder, generated by a complete basis of current modes, which were defined on a spherical / cylindrical surface concentric with the object. The current modes were used as transmit elements of a hypothetical infinite array and the corresponding transmit sensitivities (i.e., ${\mathrm{B}}_1^{+}$) and electric field covariance matrix were used to calculate the UISAR, in the case of fully parallel transmission using the theory and methods described in Lattanzi et al (3) and Lattanzi and Sodickson (9) for spherical and cylindrical geometries, respectively. The same basis set was used to model actual transmit array geometries, by appropriate weighted combinations of the current modes (9), and to calculate the corresponding minimum global SAR. We modeled arrays of circular loops and cylindrical window coils, for a spherical and a cylindrical object, respectively, assuming uniform current distribution within the coils’ conductors. Perfect decoupling among array elements during transmission was assumed, while electric field correlations inside the sample were calculated and included in the SAR optimization algorithm. For both the ultimate case and the case of finite arrays, we used an algorithm for parallel transmission pulse design (2,3), which aims at achieving a target flip angle distribution while minimizing global SAR. For the case of finite arrays, we estimated input average RF power requirements by adding the average RF power dissipated in the coils’ conductors to the average RF power deposited in the sample (i.e., the minimized global SAR) over the course of the RF pulse. The RF power dissipated in coils’ conductors was modeled as resistive power losses (i.e., Johnson noise), as described by Eq. [26] in Lattanzi and Sodickson (9). RF power losses in cables were not explicitly considered here, but their potential effects are described in the discussion.

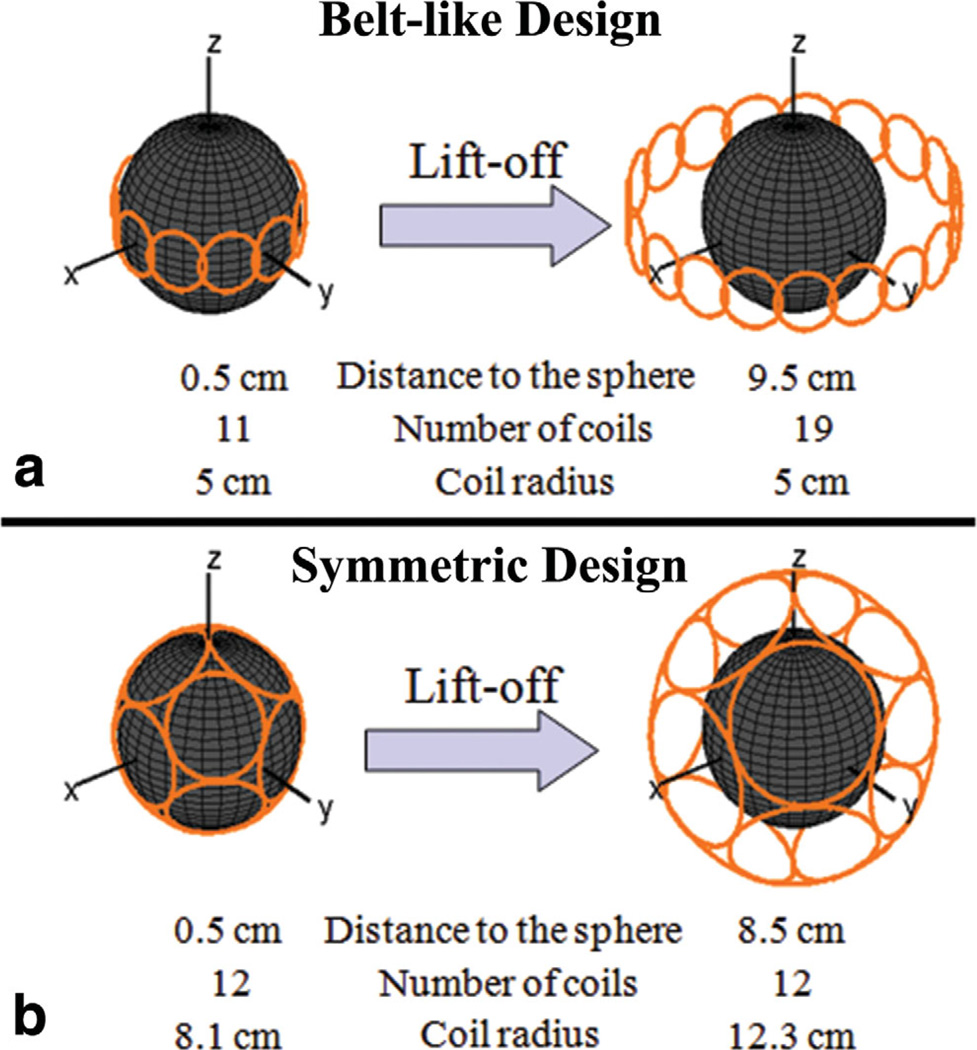
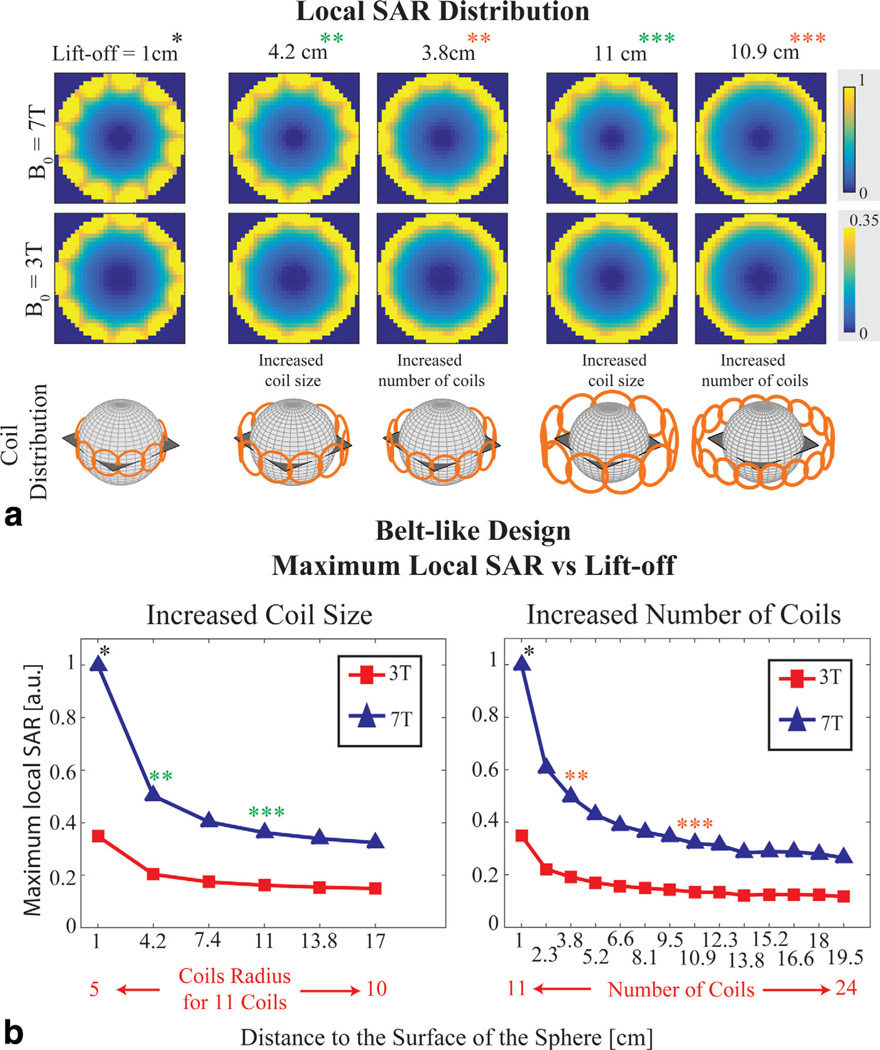
We investigated the effect on the minimum global SAR and RF power requirements of increasing the distance between the object surface and the center of the transmit coils. This could be achieved by increasing either the number or the size of the transmit coils in the arrays, and we simulated both cases. Figure 1 illustrates transmit array geometries associated with both lift-off strategies for the case of the sphere. In one approach, an increasing number of identical loop coils was arranged like a belt around the sphere equator, fixing coil radius to 5 cm (belt-like design, Figure 1a). The other approach used a transmit array with a fixed number of identical coils symmetrically packed around the sphere, and coil radius was scaled with respect to lift-off (symmetric design, Figure 1b). For both cases, we used a 15 cm radius uniform dielectric sphere with the following average brain tissue properties (10): relative permittivity ε_r = 63.1 / 51.9, electrical conductivity σ (S/m) = 0.46 / 0.55 for 3T / 7T. The smallest and largest number of coils used in the belt-like design was 11 (1 cm lift-off) and 24 (19.5 cm lift-off), respectively. The smallest and largest coil radius used in the symmetric design was 8.1 cm / 5.3 cm (0.5 cm lift-off) and 18.6 cm / 12.1 cm (20.5 cm lift-off) for 12- / 24-element transmit arrays.

Fig. 1.

Transmit array geometries for spherical simulations. a: Belt-like design in which coil size is kept constant and the number of coils is increased during lift-off. Coils were overlapped by 10% in all lift-off conditions. b: Symmetric design in which the number of coils is kept constant and coil radius is increased during lift-off.

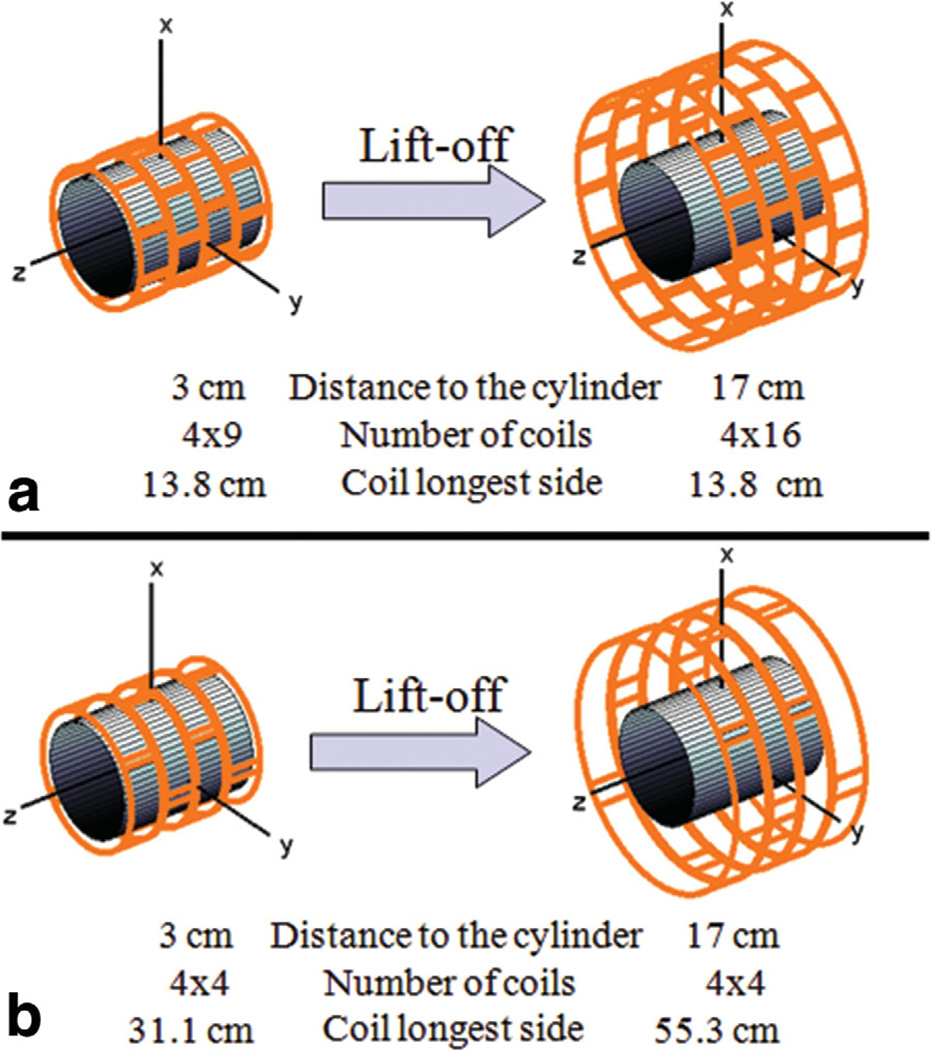
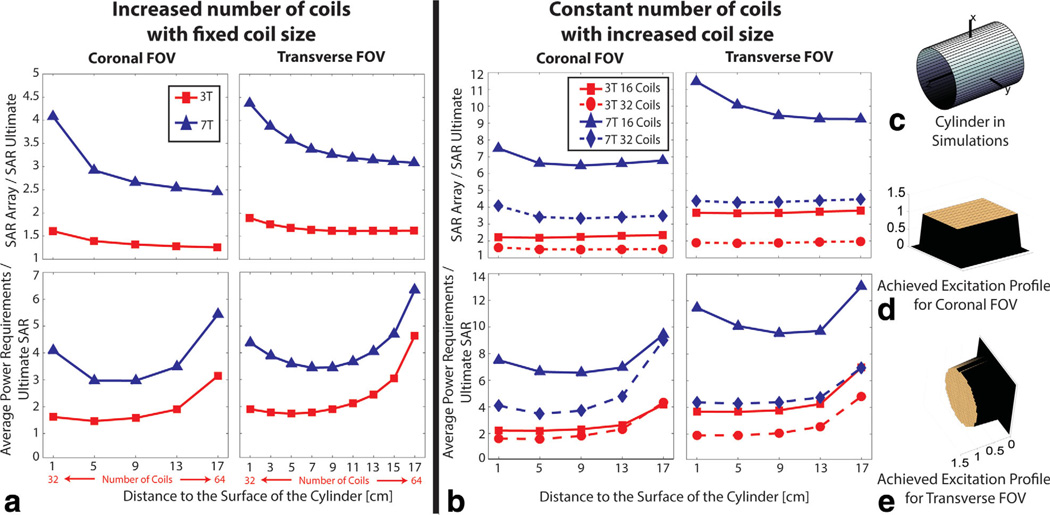
Similarly, for the case of the cylinder we used two approaches to account for increasing lift-off of the transmit array: (i) identical array elements (Fig. 2a) ranging from 32 (1 cm lift-off) to 64 (17 cm lift-off) and (ii) the same number of coils (Fig. 2b), either 16 or 32, with larger dimensions with increasing lift-off. Two different array configurations were used based on the orientation of the MR excitation plane. For transverse fields-of-view (FOVs), cylindrical window coils were densely distributed circumferentially, e.g., 32 elements were arranged in four staggered rows of eight coils each arranged around the circumference of the cylinder (Fig. 2a). Coils were instead densely distributed along the axial dimension for coronal FOVs, e.g., eight staggered rows of four coils each (not shown). The cylindrical object had radius = 15 cm, length = 40 cm and uniform electrical properties of canine skeletal muscle (11): ε_r = 50.2 / 45.3, σ (S/m) = 0.31 / 0.33 for 3T / 7T. In the case of the cylinder, we modeled the conductive copper shield of the MR scanner using radius = 34.3 cm and σ = 58 × 10⁶ S/m (9).

Fig. 2.

Transmit array geometries for cylindrical simulations. Coils were overlapped by 10% both in the circumferential and the axial direction, and every row was staggered by half of a coil angular width in the circumferential direction. a: Array design in which coil size is kept constant and the number of coils is increased during lift-off. b: Array design in which the number of coils is kept constant and coil size is increased during lift-off.

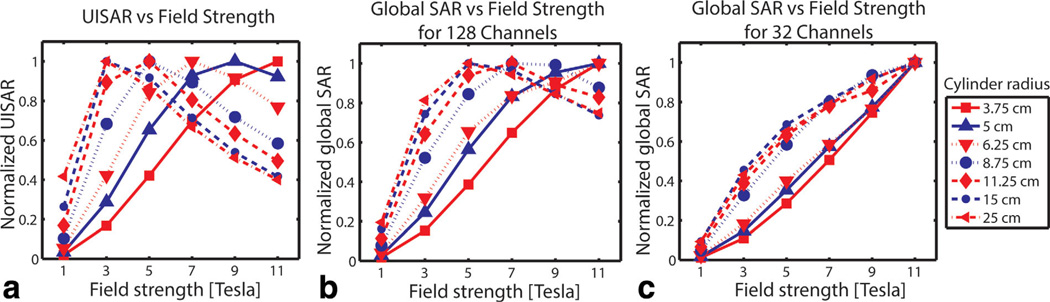
We also investigated UISAR as a function of main magnetic field strength, for various sizes of the cylinder (radius ranging between 3.75 cm and 25 cm) with constant 1 cm transmit array lift-off and compared the results with the correspondent minimum global SAR for a 32-element (4 rows × 8 column) and a 128-element (8 rows × 16 column) transmit array of cylindrical window coils.

The target excitation profile was a uniform flip angle distribution over the entire FOV in all cases. We used a 32 × 32 echo-planar imaging (EPI) excitation trajectory for the case of a transverse section through the center of the sphere, or 24 × 24 and 18 × 24 EPI excitation trajectories for the case of a transverse and a coronal section through the center of the cylinder, respectively. Calculations were performed in MATLAB (Mathworks, Natick, MA) for different lift-offs. Based on previous convergence studies (3,10), we used an expansion order l_max = 80 (see Eq. [4] of Lattanzi and Sodickson [9]) and expansion coefficients m = −90:Δ m:90 and n = −50: Δn:50 (see Eq. [27] of Lattanzi and Sodickson [9]) for the spherical and cylindrical case, respectively. The expansion coefficient n was varied with unit step (i.e., Δn = 1), whereas m, which in theory should be continuous, was varied with step Δm = 1/L, where L = 0.4 m was the FOV extension in the z direction. As a result, 13,122 and 14,746 current modes, equally divided in magnetic-type (divergence-free) and electric-type (curl-free), were used to calculate UISAR for the spherical and cylindrical case, respectively. Loop and cylindrical window coils were modeled using only magnetic-type current modes.

Experiments

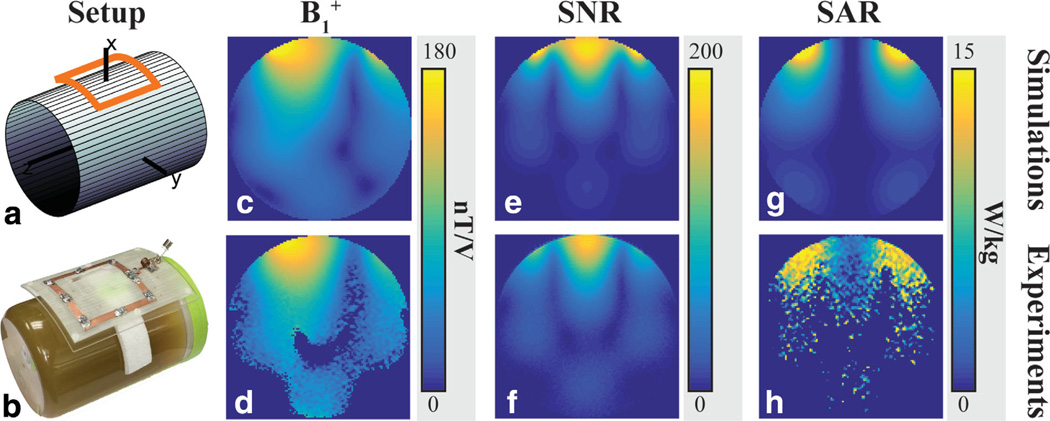
To validate our results, we compared simulated and experimental ${\mathrm{B}}_1^{+}$, signal-to-noise ratio (SNR) and SAR measurements for a single transmit/receive coil. Experiments were performed on a Siemens whole-body 7T Magnetom scanner (Erlangen, Germany) using a 10 × 10 cm cylindrical window coil and an acrylic cylindrical gel phantom, with radius = 8.25 cm and height = 21.6 cm (Fig. 7b). The transmit/receive coil was tuned to 297.2 MHz and matched to the gel phantom with S11 ~ −23 dB. The specific composition of the phantom was 17.1% sucrose (Domino Sugar, NY), 78.6% water, 4% gelatin (Kraft, Northfield, IL), 0.25% salt (99% Sigma-Aldrich) and 0.05% benzoic acid (Sigma-Aldrich) by weight. A commercial dielectric probe was used to measure the electric conductivity and relative permittivity of the phantom (Agilent 85070E dielectric probe kit; Agilent Technologies, Santa Clara, CA), which were σ= 0.45 S/m and ε_r = 71, respectively, The heat capacity, thermal conductivity, and density were 3622 (J/kg°C), 0.541 (W/m°C) and 1140 (kg/m³), respectively, as measured by a commercial thermal property probe (KD2 Pro, WA).

Fig. 7.

Comparison between simulation and experimental results for a cylindrical window coil. Phantom-coil setup in DGF simulations (a) and experiments (b) are shown with corresponding maps of ${\mathrm{B}}_1^{+}$ (c,d), SNR (e,f), and SAR (g,h) for an axial plane through the center of the coil. Good agreement was found between simulation and experiments, except for the regions away from the coil where experimental mapping techniques are not accurate due to limited EM field penetration.

An axial ${\mathrm{B}}_1^{+}$ map of the coil was acquired using a turbo fast low-angle shot based ${\mathrm{B}}_1^{+}$ mapping approach (12). Relevant imaging parameters were: field of view (FOV) = 180 × 180 mm², echo time (TE) = 2.16 ms, acquisition matrix = 128 × 128, pulse repetition time (TR) = 5 s, slice thickness = 10 mm. An image in SNR units was reconstructed using a spoiled axial GRE image, estimating the noise statistics from a noise-only acquisition (i.e., with zero transmit voltage) (13). GRE images were acquired using FOV = 180 × 180 mm², TE = 5 ms, acquisition matrix = 128 × 128, pulse TR = 5 s, slice thickness = 5 mm, flip angle = 10 degrees and bandwidth = 1002 Hz/pixel. RF heating produced by the coil was calculated from two multi-slice multi-TE GRE measurements, before and after 10 min and 20 s of RF heating, using the proton resonance frequency shift method with nonlinear least squares fitting (14). Parameters for these GRE measurements were TR = 317 ms, 12 TEs from 2.5 ms to 29.45 ms, voxel dimensions = 1.4 × 1.4 × 5 mm³, number of slices = 7 and acquisition time = 41 ms. The calculated temperature map was converted into SAR using

$$SAR=C\frac{\mathrm{\Delta }T}{\mathrm{\Delta }t}$$ [1]

where ΔT (°C) is the temperature change induced during time interval Δt (s) and C is the heat capacity, by assuming RF heating occurred at a short time in which the effect of thermal conduction can be neglected.

Experimental setup was simulated using our DGF framework (Fig. 7a). ${\mathrm{B}}_1^{+}$ and SAR spatial distribution were computed for the same FOV and voxel resolution. Power losses from coil plug to the port of the coil was compensated by reducing the simulated fields by 18%, which was obtained empirically comparing average simulated and experimental ${\mathrm{B}}_1^{+}$ maps and was on the range of previous findings (14). An intrinsic SNR map was calculated and then scaled to account for the specific pulse sequence parameters and system characteristics, as defined by Eq. [12] in Lattanzi et al (15), for comparison with the experimental SNR map.

RESULTS

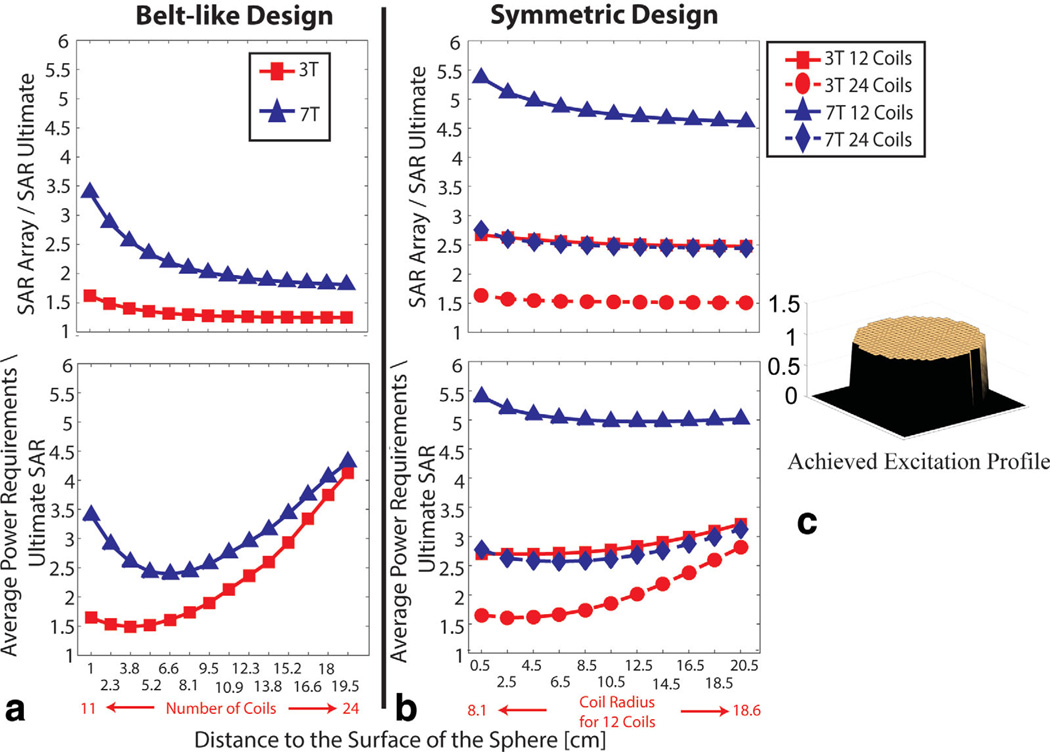
The parallel transmission pulse design algorithm (2,3) was capable of matching the uniform target flip angle distribution in all simulations, using any remaining degrees of freedom to minimize global SAR. Figure 3 shows minimum global SAR and RF power requirements as a function of the distance of the arrays from the surface of the sphere. Results are presented for 3T and 7T and for different coil designs (belt-like and symmetric). Minimum global SAR plots are normalized to the UISAR at the corresponding main magnetic field strength, which remained constant for all lift-offs. Note that, though minimization of global SAR does place certain constraints on local SAR everywhere, the resulting field distribution does not necessarily coincide with what would result from a specific minimization of local SAR in any given region of interest.

Fig. 3.

Minimum global SAR and RF power requirements of the transmit arrays versus lift-off. The reported values are associated with the excitation of a uniform flip angle distribution on a transverse plane through the center of a homogeneous sphere. Results are compared for the belt-like (a) and symmetric (b) array design. An optimal coil lift-off that minimizes the RF power requirements while achieving the target excitation profile with minimum SAR was observed for both lift-off strategies. SAR and power requirement plots are normalized by the UISAR at the corresponding magnetic field strength. Power requirements were calculated by adding the coil conductor losses into the minimum global RF power deposition. Achieved excitation profile from the designed RF pulses is shown in C.

Figure 3 shows that global SAR of the transmit arrays decreases and approaches its theoretical minimum (i.e., UISAR) as the transmit coils are moved further from the object in both belt-like and symmetric designs, at both 3T and 7T. However, for the same target ${\mathrm{B}}_1^{+}$ field distribution, the corresponding RF power requirements, which include coil conductor losses in addition to global SAR, at first decrease, but then increase with distance from the object. Both minimum global SAR and RF power requirements are always higher at 7T than at 3T. RF power requirements for the 24-element symmetric array are lower than for the 12-element symmetric array, but grow more rapidly with lift-off, because dissipation in the conductors increases more rapidly as coil size, therefore the total quantity of conductors, increases.

The spatial distributions of average local SAR for the duration of the excitation k-space (EPI-type) trajectory is shown for the transverse slice at the center of the sphere in Figure 4a for different lift-off values and strategies, in the case of the belt-like array design. Note that local SAR was not explicitly minimized by the algorithm, but was obtained from the contributions of the transmit coils using the optimal weighted combination that results in minimum global SAR (3). When the transmit elements are near the surface of the sphere (i.e., lift-off = 1 cm), the electric fields generated by the coils transfer more RF energy into the object and result in higher maximum local SAR values than when they are at a considerable distance from the object (i.e., lift-off = 10.9 cm). Figure 4b shows that maximum local SAR decreases with lift-off for both lift-off strategies (i.e., increasing either the coil radius while keeping the number of transmit elements constant or the number of coils).

Fig. 4.

Local SAR distribution (a) and maximum local SAR (b) associated with minimum global SAR in a homogeneous sphere versus lift-off. Maps in a show average local SAR over the entire pulse duration for a transverse plane through the center of the sphere, for both lift-off strategies (i.e., increasing either the size of the individual coils or the number of coils). Plots in b show the maximum SAR (from the average local SAR maps) for the belt-like array design for multiple lift-off values, at 3T and 7T. Data points corresponding to the maps in a are indicated with asterisks.

Figure 5 shows minimum global SAR, normalized by the corresponding UISAR, and average RF power requirements as a function of coil lift-off for the case of the cylindrical object, for both coronal and transverse excitation FOVs. Minimum global SAR approached UISAR for increasing lift-off when the number of transmit coils was changed based on the distance of the array from the object (Fig. 5a). When the number of elements was kept constant and their size increased, minimum global SAR did not monotonically decrease as a function of lift-off in all cases, although we observed only modest increases (Fig. 5b). Parallel MR transmission was more effective with a larger number of coils: lower global SAR and average RF power requirements could be achieved with the 32-element array compared with the 16-element array, for the same magnetic field strength and lift-off distance. Global SAR and average RF power requirements were always higher at 7T than 3T. Figure 5 shows that in the cylindrical case, as for the spherical geometry, there was an optimal coil lift-off that minimizes average RF power requirements.

Fig. 5.

Minimum global SAR and average RF power requirements of the transmit arrays versus lift-off. The reported values are associated with the excitation of a uniform flip angle distribution on coronal and transverse planes through the center of a homogeneous cylinder. Results are shown for the two different cylindrical array designs: increased number of coils with fixed coil size (a) and constant number of coils with increased coil size (b) as described in Figure 2. An optimal coil lift-off that minimizes the average RF power requirements while achieving the target excitation profile with minimum SAR was observed. SAR plots are normalized by the UISAR at the corresponding magnetic field strength. Representative achieved uniform excitation profiles from the designed RF pulses are shown in d and e for coronal and transverse FOV, respectively.

Figure 6a shows UISAR for the excitation of a uniform profile on a coronal FOV through the center of a homogeneous cylinder as a function of the main magnetic field strength. UISAR did not increase monotonically with field strength, but reached a maximum value and then started decreasing. The main magnetic field strength at which the reversal of the trend occurred depended on the size of the sample, as observed in previous work (3,16,17), and was lower for larger cylinder radius. For cylinder radius greater than or equal to 8.75 cm, UISAR decreased between 3T and 7T. Figure 6b shows a trend similar to that of UISAR for minimum global SAR in the case of a 128-element transmit array, with a fixed 1 cm lift-off and the size of the individual elements adjusted accordingly, suggesting that parallel MR transmission can effectively reduce global SAR at ultra-high field strength. However, Figure 6c shows that 32 coils—still a large number compared with most current experimental implementations of parallel transmission—may not be sufficient to achieve lower global SAR at higher magnetic field strength. Results similar to those displayed in Figure 6 were observed for the case of a transverse excitation FOV, but are not shown.

Fig. 6.

UISAR (a) and minimum global SAR for a 128-element (b) and a 32-element (c) transmit array associated with the excitation of a coronal FOV through the center of a homogeneous cylinder, as a function of the main magnetic field strength. Results are shown for six different radii of the cylindrical object, with a fixed 1 cm distance between the coil elements and the surface of the object. In each plot, every line (i.e., results for the same cylinder radius) is scaled by its own maximum value to limit the dynamic range and compare results between different cases more easily.

In Figure 7, simulation results for a single coil are compared with experiments. Our DGF framework enabled to model the experimental setup accurately (Figs. 7a and 7b) and, in fact, both the distribution and the magnitude of the coil’s ${\mathrm{B}}_1^{+}$ field were in good agreement (Figs. 7c and 7d). Note that regions of low SNR, where the flip angle mapping sequence is inherently not expected to produce accurate results, were masked in Figure 7d. SNR maps (Figs. 7e and 7f) also showed a good agreement between simulations and experiments. The magnitude and the location of high SAR regions estimated from experimental temperature measurements were simulated accurately (Figs. 7g and 7h), indicating that the coil’s electric field calculated using our DGF framework is correct. However, because heat diffusion was neglected in the conversion from temperature to SAR (Eq. [1]), the overall spatial distribution of SAR is slightly different between simulation (Fig. 7g) and experiment (Fig. 7h). Regions where low temperature change is expected, i.e. low SAR regions, were masked out in Figure 7h, because the temperature mapping method was not sensitive enough to capture the negligible heating at those locations.

DISCUSSION

Minimizing SAR while maintaining a homogenous excitation is one of the principal challenges associated with the use of ultra-high magnetic field strengths. Several RF pulse design strategies have been developed to address this (2,3,18–20). In this work, we investigated the role of array geometry (in particular, the effect of changing the number of transmit elements and their distance from the surface of the object) on the behavior of SAR and RF power requirements for parallel transmission.

We found that there are local and global SAR benefits in moving the transmit coils away from the object. Note that, although a reduction in magnetic field (i.e., ${\mathrm{B}}_1^{+}$) is expected in parallel with a reduction in electric field (i.e., SAR), the desired flip angle distribution was achieved in all lift-off cases. This result may be counterintuitive, but some observations about the degrees of freedom of the parallel transmission algorithm can provide insights. The algorithm we used aims at achieving a uniform flip angle distribution everywhere in the FOV and then uses the remaining degrees of freedom to minimize global SAR. When the transmit elements are close to the object, only a small number of transmit coils contribute significantly to excitation near any particular portion of the object surface, meaning that few degrees of freedom are then available to reduce SAR, which is already locally high because the electric field (like the magnetic field) is peaked near the coils. In other words, in the vicinity of close-fitting coils, the problem of designing uniform excitation reduces effectively to a few-coil problem. On the other hand, when the transmit elements are moved away from the object surface, not only are the fields less strongly peaked near the surface, but also more coils have substantial sensitivity in any given surface region and more coils can therefore contribute substantially to achieve the desired excitation profile. As a result, the optimization algorithm can rely less on individual elements and more on combinations of multiple elements, which provides the flexibility to create constructive and destructive interferences. In the case where coil size is kept constant with lift-off, additional degrees of freedom are available due to the larger number of elements in the transmit array.

A stringent global SAR constraint would likely lead also to low local SAR, which explains the similar reduction of maximum local SAR that we observed as a function of lift-off (Fig. 4). In fact, for maximum local SAR to increase while global SAR decreases, local SAR would have to decrease everywhere except at one position, or one particular region of the FOV. We expect this to be unlikely for uniform rotationally symmetric objects, as those considered in this work, but it cannot be excluded for the case of realistic human models with heterogeneous tissue properties, for which there could be local SAR hot spots, not necessarily near the surface, that are not reduced by moving out the transmit coils. Because our rapid DGF analytical calculations require simple geometries, this is an intrinsic limitation of this study that could be addressed in future work using numerical simulation techniques.

Note that the selection of a uniform target excitation profile across each FOV represents a strict constraint for RF pulse design and a limitation of the study. Different results might be obtained for different target excitation profiles or by not requiring the excited profile to conform precisely to the target profile (e.g., using regularization).

As the lift-off distance was increased, global SAR decreased monotonically and reached asymptotically a minimum value, which approached the UISAR more closely when the number of transmit coils was increased with lift-off compared with when the coil radius was increased while keeping coil number constant. On the other hand, we observed an optimum lift-off distance that minimizes average RF power requirements for both lift-off strategies (Figs. 3 and 5). For example, Figure 3a shows that a 5 cm lift-off at 7T could reduce average RF power requirements by 20% and global SAR by more than 30%, while still enabling a homogeneous excitation profile. Average RF power requirements were calculated as the sum of global SAR and power losses in the coil conductors divided by the RF pulse length. While the former decreases with lift-off, the latter increase because larger coil currents are required to achieve the same flip angle distribution from a greater distance. The optimal lift-off corresponds to the distance for which the balance between the two contributions shifts and coil losses dominate over global SAR. Note that RF power requirements could further increase if losses due to lumped elements in the coils and transmit chain cables are modeled. However, we found (results are not shown) that by adding hypothetical losses in the transmit chain electronics as large as six times the losses in the coil conductors, the behavior as a function of lift-off is maintained, although the optimum lift-off distance in Figures 3 and 5 becomes smaller.

Previous work by Lattanzi et al (3) calculated UISAR using a multipole expansion of the EM field inside a uniform sphere. In this work, we calculated UISAR with the DGF formalism, in which the net EM field inside the sphere is derived as a linear combination of the EM fields generated by a set of current modes defined on a surface concentric with the object. Our approach allowed us to investigate UISAR as a function of lift-off, by changing the radius of the surface on which the current distribution was defined. UISAR was found to be independent of lift-off, which is consistent with field equivalence principles of electromagnetic theory. In fact, according to the surface equivalence theorem (21), when an encircling surface on which currents are defined is altered (e.g., by moving it away from the sample), any given EM field distribution created by currents on the original surface can also be obtained with a suitably modified current distribution on the new surface (e.g., using a different combination of the current modes in the basis set). This principle certainly applies to the SAR-optimal EM field distribution and explains why UISAR, which is calculated with a complete basis of current modes, is radius-independent. Indeed, UISAR independence from coil lift-off is indicative of the completeness of the selected current basis and the convergence of the calculations. Note that, although a finite cylindrical surface is not inherently closed and is, therefore, not subject to the surface equivalence theorem, our simulations assumed an infinite cylinder along the axial direction (9,11) with the expansion coefficients spaced to ensure that periodic repetitions of the EM field do not impinge significantly upon the central volume of interest (i.e., we simulated a long enough cylinder that the equivalence theorem is likely to apply).

We showed in Figure 6a that under certain conditions the growth of UISAR with field strength flattened out and then reversed. This behavior depends on the object size and occurs at lower magnetic field strengths for larger cylinders. These findings are consistent with established electromagnetic principles, and similar results were observed in previous simulation work based on optimized RF excitations in uniform spherical objects (3) and in head models (17). We showed for the first time that global SAR can decrease at ultra-high field strength even for the case of finite arrays, if a sufficient number of transmit elements and a SAR-optimized parallel transmission pulse design are used (Fig. 6b).

Simulations were performed on uniform geometries with simplified coil structures, without lumped elements and decoupling circuitry. Despite these limitations, the DGF formulation can still provide useful physical insights for coil design (22,23) and allows rapid full-wave simulations (e.g., a few seconds for each time point of the EPI excitation trajectory) that enables investigation of a large number of parameters. Furthermore, calculation of UISAR involves combining the EM fields of thousands of distinct current modes and would not be practical with most existing numerical methods, such as the FDTD technique. However, new emerging methods enabling fast calculation of EM fields (24) can in principle be used as an additional approach for calculating UISAR in nonuniform objects. An additional limitation of the DGF approach is that although it fully accounts for overlapping EM fields (using superposition), it assumes that the transmit elements are perfectly decoupled. This in practice is difficult (but not impossible), because geometric decoupling works only for neighboring coils and decoupling of coils further away is usually accomplished with dedicated circuitry that could increase RF power requirements. Although a coupling matrix could be incorporated in our simulations, it would have to be derived from experimental calibration measurements or additional numerical simulations, because it cannot be calculated within the analytical DGF framework. However, as it was shown for the reciprocal case of parallel MR reception (25), the effect of coupling on array performance is expected to be minimal when the electric field covariance matrix is included in the parallel transmit optimization algorithm, as was the case for this study (2,3). In fact, because coil coupling can be described as a linear transformation model, mutual inductance couples electric fields between array elements in the same ratios that it couples ${\mathrm{B}}_1^{+}$, therefore any loss of distinctness in the transmit sensitivities is compensated for by information stored in the electric field correlations. Coupling between cables could induce additional RF power losses that would not be removed by the optimization algorithm, but we expect these to have a negligible effect on the trends shown in this study. Furthermore, note that our DGF framework assumes uniform current distribution within the coil conductors, whereas nonuniform cross-sectional current patterns, which are expected at high frequencies (26), could affect the balance of the results among different magnetic field strengths, especially for RF power requirements. However, we expect that the overall behavior of array performance as a function of lift-off would be maintained. Although a more rigorous prediction of RF power requirements would be possible, it would yet require building prototype coils matching the size of the elements for each simulated array and to experimentally calibrate their actual resistance, which is beyond the scope of this work.

Belt-like and symmetric coil arrangements were chosen to demonstrate the effect of lift-off in spherical simulations. In the cylindrical case, we chose to adjust the size or the number of coils only in one dimension during the lift-off. Although these choices do not necessarily represent coil design choices one would always make in practice, nor cover all possible coil configurations, they proved useful for the consistent comparative study of SAR at various lift-off distances.

There were a few notable differences between the spherical and cylindrical simulations. While in the case of the spherical object the conductive shield of the MR scanner was not modeled, in the case of the cylinder the EM field generated by the transmit coils accounted for the boundary conditions associated with the presence of the shield. However, we did not model RF power deposition associated with extra EM fields generated by eddy currents induced by the transmit coils in the shield. We are confident that adding such effects would not modify the overall trends for either minimum global SAR or RF power requirements, because in our simulations the array elements were always at least 2.3 cm away (i.e., for the largest lift-off) from the conductive shield, meaning that transmit efficiency was never significantly affected by the presence of the conductive layer, as it might be, for example, in the case of closely shielded array configurations (27).

We validated DGF simulations against experiments for a transmit/receive coil. In previous work, SNR values calculated using the same DGF framework were validated for a receive coil (28). Experimental verification of the accuracy of the electric field simulations can be performed using various approaches, such as electric field probes (29) or temperature change measurements (30). In this work, we used the latter to estimate local SAR, which is directly related to the square of the norm of the electric field inside the sample. We used a simplified approach, which neglects the thermal conduction during the course of RF heating, resulting in temperature diffusion errors. Although these errors do not compromise the overall validation of the simulation results, note that they could be mitigated either by decreasing the RF heating time and increasing RF power, therefore, capturing the initial slope of the heating regime, or by directly inverting the heat equation (31,32). We are confident that a similar agreement between experiments and simulations would be found also for the case of transmit arrays, given that in the DGF simulation framework the EM fields of the array elements are derived with the same equations as for the single coil and electric field correlations between array elements are calculated with an analytic formula. Further experimental validation for the case of parallel transmission would require building expensive transmit array prototypes and designing appropriate RF pulses and pulse sequences, which is beyond the scope of this study, whose principal aim was to provide physical insights into the benefits/drawbacks of moving the transmit elements away from the surface of the object.

CONCLUSIONS

In this work, we demonstrated that in parallel transmission there could be SAR benefits in moving RF transmit coils away from the subject and that a lift-off distance that optimizes the overall average RF power requirements could be found. While we confirmed that UISAR can decrease as a function of field strength in the case of cylindrical samples, we also showed that global SAR for finite arrays can decrease at ultra-high field strength if a sufficient number of transmit coils and a SAR-optimized parallel transmission pulse design are used.