Development of the Resolution Theory for Electrophoretic Exclusion

Abstract

Electrophoretic exclusion, a technique that differentiates species in bulk solution near a channel entrance, has been demonstrated on benchtop and microdevice designs. In these systems, separation occurs when the electrophoretic velocity of one species is greater than the opposing hydrodynamic flow, while the velocity of the other species is less than that flow. Although exclusion has been demonstrated in multiple systems for a range of analytes, a theoretical assessment of resolution has not been addressed. To compare the results of these calculations to traditional techniques, the performance is expressed in terms of smallest difference in electrophoretic mobilities that can be completely separated (R = 1.5). The calculations indicate that closest resolvable species (Δμ_min) differ by approximately 10⁻¹³ m²/Vs and peak capacity (n_c) is 1000. Published experimental data is compared to these calculated results.

1. INTRODUCTION

Separation science is a well-established suite of techniques for the analysis of complex samples, particularly for those which cannot be differentiated by spectroscopy, electrochemistry, or mass spectrometry. The broad field of chromatography [1–2] and the more closely related capillary electrophoresis [3] (among numerous others) are extremely successful for many applications, but they unavoidably result in diffusion and dilution over the course of their separation. In direct contrast, equilibrium gradient methods do not suffer this problem [4]. Isoelectric focusing (IEF), the best known example of an equilibrium gradient technique, employs a pH gradient with a constant electric field, separating species with respect to their pI’s [5–7]. Other more recent examples of equilibrium gradient techniques include counterflow electric field gradient focusing (EFGF) methods [8–14].

A successful separation is defined by generating adequate resolution. The resolving capabilities of the more common separations techniques, including chromatography [15–16], IEF [4], and CE [17], are well-established and experimentally confirmed. Capillary electrophoresis separations on a microchip in a spiral channel have proven to be very successful, with theoretical plates as high as 1,000,000 having been reported [18]. More recently, resolution equations for EFGF techniques have been developed. Tolley et al. described the resolution of electromobility focusing [19] and Kelly and Woolley described EFGF resolution by comparing the focusing effects near the zero-force point to that of a spring and invoked the mathematics of Hooke’s Law to describe the forces [10]. Ultimately, these theories described the properties of EFGF as it successfully increases sample concentration and separates species with similar electrophoretic mobilities.

Reducing dimensions to the microscale has the potential to improve EFGF devices. Gradient elution moving boundary electrophoresis (GEMBE), another equilibrium gradient technique, has been used to perform electrophoretic separations in short channels [20–22]. Ross developed a theoretical framework to describe the resolving capability of GEMBE and compared it to CE, showing that GEMBE works on the same time-scale and provides similar resolution as CE separations [23].

Electrophoretic exclusion, somewhat related to EFGF techniques, is a separation method first introduced by Polson et al. as an enrichment scheme [24] and exploits the counteracting forces of hydrodynamic flow and electrophoretic velocity. However, unlike EFGF techniques, the electric field remains constant in the channel, and a sharp local gradient is initiated right at the channel entrance. This gradient, when appropriately exploited, allows for a localized area of separation just outside of the channel entrance and effectively results in separation in bulk solution rather than within a channel. This difference, though it may seem subtle, allows for parallelization and is predicted, in this work, to positively affect the overall resolution capabilities.

The success of electrophoretic exclusion has been demonstrated experimentally using both mesoscale [24–27] and microscale [28] devices. The technique has proven to be applicable to a variety of analytes with various properties and sizes, including small molecules, polystyrene microspheres, and proteins. Additionally, studies have been conducted to model the physicality and actions of the electrode/solution/channel interface [29]. These highly detailed fluid flow and field based two- and three -dimensional analyses do not result in an ability to predict resolving power of this system; the interpretation with respect to traditional metrics is reduced to examining complex color plots or high vector-space summations of the interfacial space. Historically this has not found an audience willing to examine the details of the approach or compare the results to other separations strategies. A thorough study of the resolution capabilities of the technique from a traditional separations science point-of-view has yet to be conducted. Resolution and dynamic range of electrophoretic exclusion will be defined using common dimensionalities, materials, and electric potential magnitudes of contemporary devices, thereby developing a foundational framework to interrogate the resolving power of electrophoretic exclusion enabled by the localized microgradient that is initiated at the electrode/solution interface. By extension, since the interface can be parallelized or placed in series, a variety of new capabilities can be envisioned.

2. THEORY

For comparison to other electrophoretic techniques (traditional and gradient), resolution is described in terms of the closest electrophoretic mobilities of two species that can be fully differentiated. In electrophoretic exclusion, the complete separation of two species is defined as one species being fully excluded in the bulk solution reservoir, completely prevented from entering the channel, while the other species fully enters the channel, and is not excluded at all in the bulk solution.

In keeping with standard terminology, resolution, R, is defined as:

$$R=\frac{\mathrm{\Delta }X}{4\sigma }$$ (1)

For traditional techniques, ΔX is the distance between separated elements in a channel and σ is the standard deviation of the distribution of the elements. Both of these variables are easily defined within traditional separations, with ΔX and σ described in terms of distance or time. The interface under study here does not produce traditional concentration profiles, or peaks, and the distance between two separated species cannot be defined in a traditional sense. However, this interface does provide for separation of species and properties of the interface and the physicality of the target species allow for direct quantitative comparison to be made to other techniques.

To provide a basis for discussion, the principles of exclusion and conventions of the model are briefly outlined. This discussion will focus on the centerline of the channel and other factors, such as laminar flow and the resulting Taylor-Aris dispersion, are included. Flow is established inward, towards, and within a channel and an electric field is introduced within the channel itself only, introducing a gradient only at the entry region (Fig. 1A., interface zone). Electrophoretic exclusion occurs when the electrophoretic velocity (product of the electrophoretic mobility and the electric field) of a species is opposite to and greater than or equal to the fluid velocity into the channel. Under these conditions, the species is excluded from entering the capillary. Species with electrophoretic velocities smaller than the opposing fluid flow will instead flow through the channel. This narrative will explore the smallest difference in electrophoretic mobilities between two species that results in complete differentiation.

Figure 1.

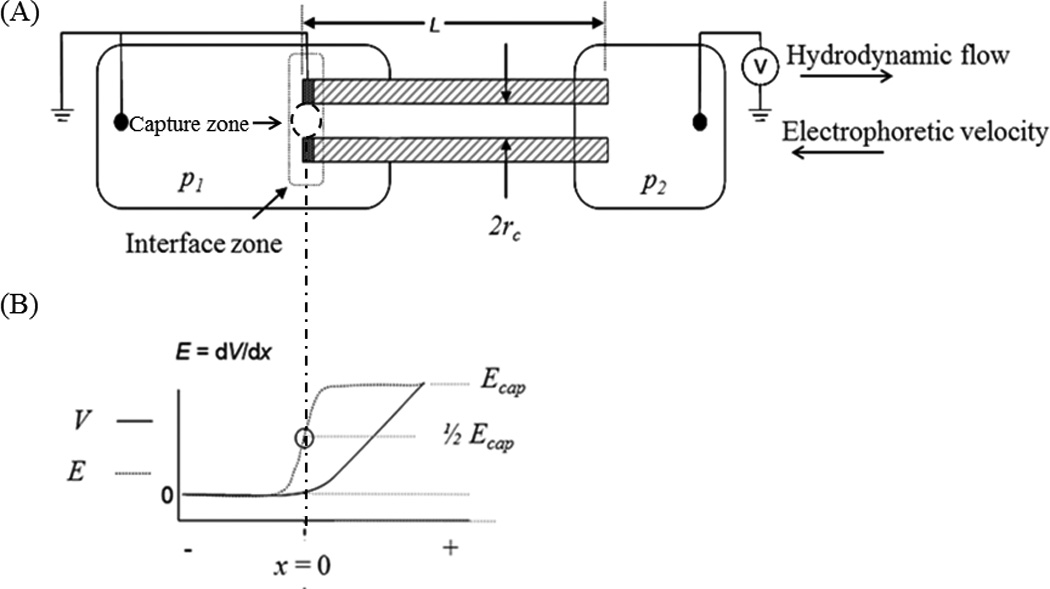
Device schematic and interface description. (A) Schematic of the device used to capture species of interest. A capillary (10 cm in length, 75 µm i.d.) with a sputtered electrode attached to two vials. The vial on the left is filled, at pressure 1 (p₁) with sample and the vial on the right, at pressure 2 (p₂) is filled with buffer. The capillary has a small window burned in it (~ 5 mm in length) where detection occurs. The interface zone, immediately outside the capillary entrance, and the capture zone, where exclusion occurs, are both identified. (B) Voltage and electric field near the channel entrance, where exclusion occurs.

For ease of discussion, visualizing the system, and adhering to existing experimental results that will be discussed later, a device description is included (Fig. 1A). The materials and details are not central to the theoretical approach, as it is a general model, but this is presented to aid in communication and establish physicality for later discussion. The device is composed of two reservoirs (p₁ and p₂) connected with a capillary. Bulk flow is from left to right through the system, driven by a pressure differential in the chambers. The end of the capillary (or channel) in reservoir 1 contains an integral electrode that is constructed by removing approximately 3 mm of polyimide coating from a capillary tip and then sputtering with 30 nm of Ti and 50 nm of Pt. Silver conductive epoxy is then used to physically connect the tip of the sputter-coated capillary to a 1 cm piece of Pt wire. Power can be applied to the wire and when potential is applied, the tip of the capillary acts as an electrode. As a result of the capillary tip electrode and the Pt wire in the reservoir, no potential field exists in the bulk of reservoir 1. A ground electrode is placed in reservoir 2. The area of interest, where exclusion occurs, is in reservoir 1, at the entry region or interface of the capillary (Figs. 1A & 1B).

2.1. Defining the interface

A successful exclusion experiment between two species is defined as one species being fully prevented from entering the channel and one completely entering the channel. Exclusion, therefore, occurs when the electrophoretic velocity of one species (v) out of a channel is greater than, or equal to, the opposing hydrodynamic flow velocity (u) into the channel:

$$v\ge -u$$ (2)

The calculated fluid flow velocity (u) through the system is given by:

$$u=\frac{\mathrm{\Delta }p{r}_c^2}{8Lɳ}$$ (3)

where Δp is the pressure difference between the two chambers, r_c is the radius of the capillary, L is the length of the capillary, and ɳ is the viscosity of the buffer. Electroosmosis is suppressed for the purposes of this model, but it can be added trivially without changing u, and could reduce Taylor-Aris dispersion.

Consider two arbitrarily closely related targets with electrophoretic mobilities μ₁ and μ₂ (ostensibly, one excluded, the other not), the average electrophoretic mobility (μ_ave) is:

$${\mathrm{\mu }}_{\mathit{\text{ave}}}=\frac{({\mathrm{\mu }}_1+{\mathrm{\mu }}_2)}{2}.$$ (4)

The electrophoretic velocity is the product of the electrophoretic mobility and the local electric field strength (E), so the average electrophoretic velocity (v_ave) of the target pair is:

$$v_{\mathit{\text{ave}}}={\mu }_{\mathit{\text{ave}}}E$$ (5)

2.2. Structure of flow and electric fields near/within the interface

In electrophoretic exclusion, due to electrode placement at the channel entrance, the electric field is initiated at the electrode-channel entrance interface. There is no field in the reservoir away from the capillary entrance. Within the body of the capillary, the electric field is constant and set at E_cap (Figs. 1A & 1B), and the gradient is approximated as linear between the bulk reservoir and capillary interior (penetration ~1/2 the capillary diameter into the reservoir) [27]. Immediately outside the capillary entrance, in the middle of the linear electric field gradient, where it is approximated that exclusion occurs, E = 1/2E_cap, v_ave is defined as the opposite of the bulk flow:

$$v_{\mathit{\text{ave}}}=-\frac{1}{2}{E}_{\mathit{\text{cap}}}{\mu }_{\mathit{\text{ave}}}$$ (6)

Assuming μ₁ is greater than μ₂, the species with μ₁ is completely excluded (effects of dispersion addressed below), while the species with μ₂ is not excluded, but allowed to travel past the interface and down the length of the capillary. Flow rate near the entrance is assumed to be constant over the length of the scale of the electric field gradient, a reasonable assumption given the recent quantitative assessments [27].

2.3. Steady state, fully developed concentration profile

It is important to note the structure of the fully developed concentration profile at long times across the interface. In broad terms, the final concentration profile is similar to that observed in isotachophoresis, GEMBE and the original works on “countercurrent electroconcentration” [30]. For the isotachophoretic profile, the field step and velocity gradient is induced by solution properties and dynamics rather than flow and externally applied fields, whereas the GEMBE profile has identical origins to the present technique (although less steep). It should be noted that initially, during the successful exclusion of a single analyte, the shape of the concentration profile starts as a bolus approximating Gaussian shape, not unlike a typical separation peak (of course, this bolus is eliminated by stirring [25], whereas the technique is still successful). The peak builds as more material is being excluded, increasing the diffusive flux on the bulk solution side of the peak until it exceeds the flow flux. This builds the concentration in the bulk buffer and, assuming a constrained volume as in this system, the concentration of the bulk solution reservoir will rise until the diffusive flux across the capillary side of the peak is greater than the resorting forces of the electric field. This steady state is established when the diffusive flux towards the capillary and the restorative forces from the electric field are equal, precisely the same construct used for calculating steady state peak width and resolution for gradient-based techniques.

The concentration profile for a fully excluded analyte is not well-defined by a single simple mathematical function since the flow and electric field about the entrance are not analytically solved (even at the centerline) [27]. It is therefore approximated by an error function (Fig. 2). While there may be some uncertainty introduced by this approximation, it will be minimal in that there will be a high concentration on one end and a low concentration on the other and some sigmoidal-like concentration profile will result. There are many choices in terms of fitting a sigmoidal-like function to this profile (it is most likely a hybrid function), where none are any more valuable than others at this point—other than to allow for translational assessments to accepted norms in separation science peak assessments. This form of the profile allows for simplified assessment of the width of the exclusion zone and is used successfully elsewhere for very similar purposes [23]. The use of an error function to represent the concentration profile across the interface indicates that the maximum concentration is in the reservoir and it decreases to zero in the channel (Fig. 2B). The steepness of the slope varies, depending on focusing and dispersive forces and defines the characteristic variance sought here.

Figure 2.

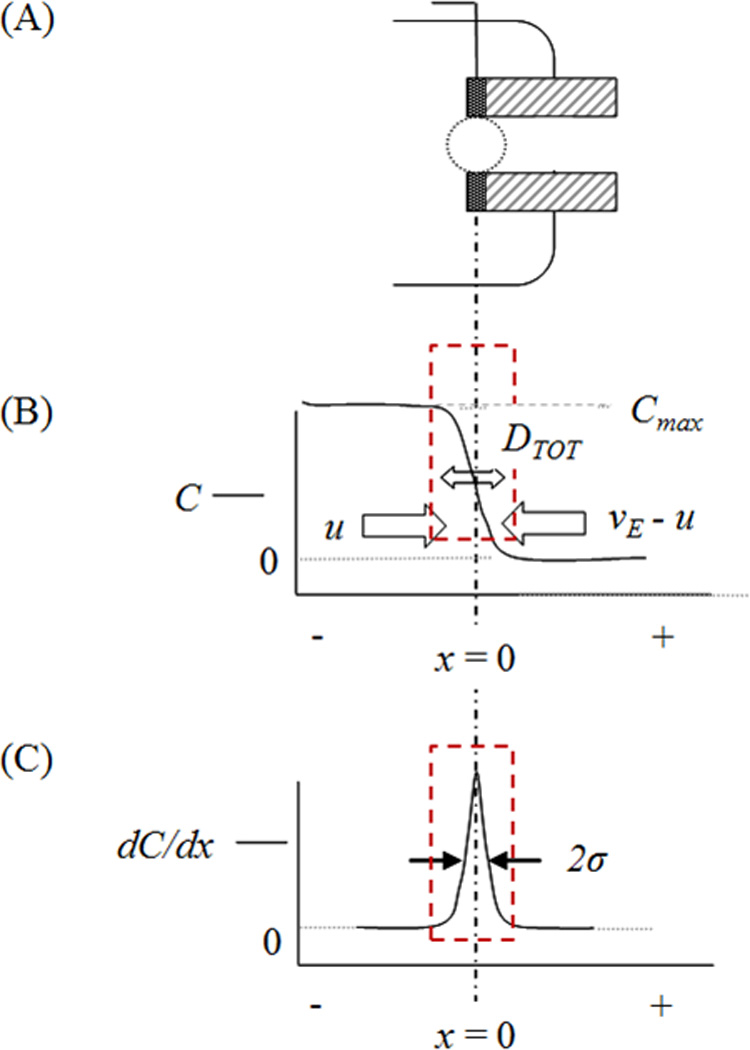
Development of the concentration profile at the interface. (A) The area of interest where exclusion occurs. (B) The concentration profile in the reservoir in the area of exclusion. Maximum concentration is in the reservoir, with concentration reaching zero in the channel. The shape of the concentration profile is modeled as an error function, as indicated with the red box. The focusing forces and dispersive forces affect the steepness of the gradient. (C) The first derivative of the concentration profile indicates that the largest change in concentration occurs at the channel entrance. The steeper the gradient, the narrower the peak of the first derivative.

Using the practice of Giddings, a steady state separation has a constant concentration profile with time (dc/dt = 0), where, in this case, the dispersion forces are equivalent and opposite to flow/electric field forces [31]. As mentioned above, the structure of this concentration profile at steady state can be approximated by an error function. The derivative of an error function is a Gaussian profile with a characteristic variance. This variance provides a standard means of comparison for steady state methods and is defined by including all dispersive forces (D_TOT) competing with the restorative forces and is equal to [4]:

$${\sigma }^2=\frac{D_{\mathit{\text{TOT}}}}{\mathit{\text{change in velocity with position}}}$$ (7)

The total dispersive forces cause band broadening, while focusing forces counteract them. D_TOT explicitly includes Taylor-Aris dispersion, along with diffusion (D_diff), where d is the diameter of the capillary : [32]

$$D_{\mathit{\text{TOT}}}=D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}$$ (8)

To understand the local velocity of the target species across this interfacial zone, the approach (and notation) given by Giddings [31] that states the overall transport (W) in the system is:

$$W=U+v,$$ (9)

where W is the overall component velocity, U is the drift velocity due to external fields (field-induced velocity), and v is the flow velocity. For electrophoretic exclusion, substitute, −u for v (eqn. 1) so that:

$$W=U-u$$ (10)

In this case, only U varies with x, so the equation can be rewritten as:

$$W=ax-u$$ (11)

where a is change in velocity (slope) with respect to x, describing the focusing effects (field gradient dE/dx at the entrance). In this case, a, is limited to only the entrance area of the channel, or the interfacial zone of the electrode and solution. Within the bulk reservoir, at negative values of x and outside the interface zone, the two target species move at an average velocity of u or less. The electrophoretic velocity of all species is less than the flow velocity due to small or nonexistent E. At exactly x = 0 (the capillary entrance/electrode solution interface, Fig. 2), the average velocity of the two species is zero because u is, set by definition, exactly offset by 1/2E_capμ_ave. This means that one species is moving backwards and one forward by an equal and opposite amount, again, by the definition of the interface. At x values well above zero (within the capillary, past the interfacial zone) the velocity is u + μE_cap.

The change in the electrophoretic velocity across the interface, a, is:

$$a={\mu }_{\mathit{\text{ave}}}dE/dx,$$ (12)

and therefore

$$W={\mu }_{\mathit{\text{ave}}}\frac{dE}{dx}x-\frac{1}{2}{\mu }_{\mathit{\text{ave}}}{E}_{\mathit{\text{cap}}}$$ (13)

The local slope of the electric field (dE/dx) can be approximated and linearized by the change in the field across the interface divided by the diameter of the entrance. Noting eqns. 7, 8 and 12, variance is:

$${\sigma }^2=\frac{D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}}{{\mathrm{\mu }}_{\mathit{\text{ave}}}\frac{dE}{dx}},$$ (14)

and standard deviation is equal to:

$$\sigma =\sqrt{\frac{D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}}{{\mathrm{\mu }}_{\mathit{\text{ave}}}\frac{dE}{dx}}},$$ (15)

resulting in a form very similar to other traditional gradient models, but with the local gradient at the entrance rather than the global gradient of standard techniques [10].

2.4. Determining the two closest resolvable species

Knowing the variance of the zones allows for the determination of the smallest difference between two electrophoretic mobilities that can be differentiated across the interface. To determine this difference, a spatial model is chosen that sets E_cap between adjacent capillary entrances as a direct function of the distance between the centerline of those capillaries (Fig. 3). This solves three problems: 1) it retains the advantages present in the local gradient at each capillary entrance, 2) it sets a physically meaningful construct reflective a of real experimental apparatus (something would enter one capillary and not the next – calculating the smallest difference that can be assessed), and 3) it provides a functional definition of ΔX that is easily conceptualized and tested.

Figure 3.

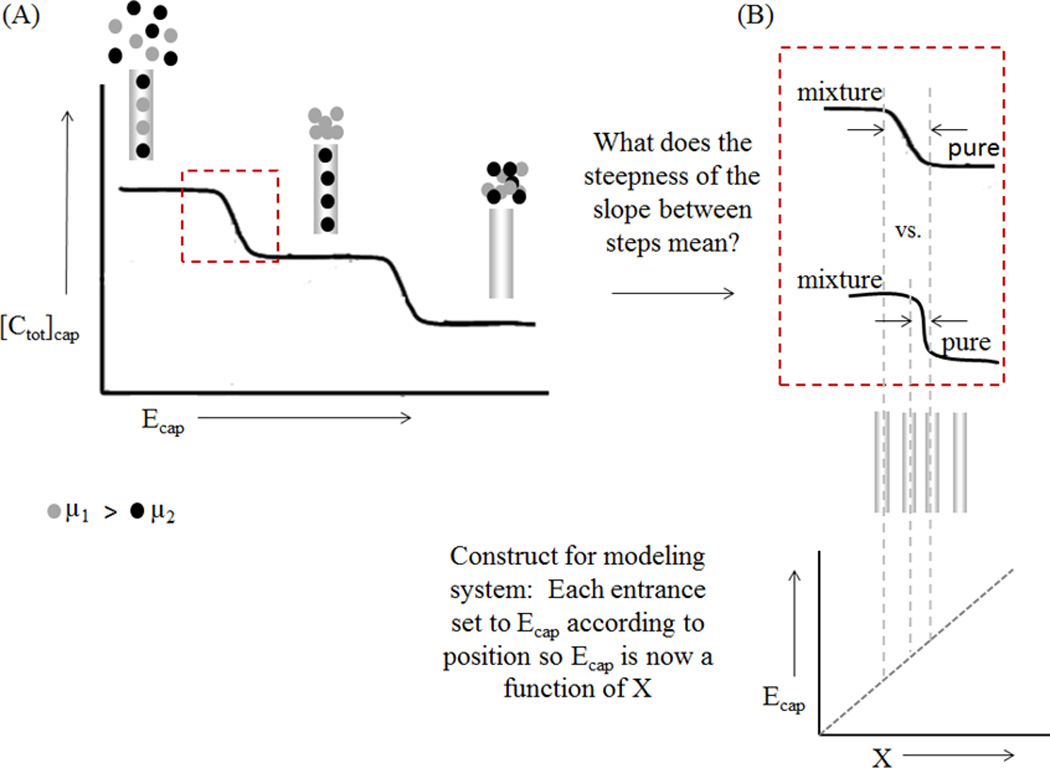
Using distance to determine the two closest resolvable species. A. Graph showing the total concentration inside the capillary for varying E_cap values. A large E_cap value corresponds to lower concentration inside the capillary due to exclusion. B. The transition between the channels entrances is related to the distance between the capillaries. The sharper the transition, the closer the capillaries can be.

A short description of the construct is presented as an example. Three channels are considered with three different E_cap values. One channel has a small enough E_cap that neither species will be excluded from the capillary entrance (Fig. 3A, left), allowing both species to flow through the capillary with the hydrodynamic flow (resulting in the highest total concentration in the channel). A second channel has an increased E_cap, such that the species with the larger mobility (represented with gray circles) is excluded (Fig. 3A, center), producing an increased concentration of that larger mobility species immediately outside of the capillary and complete passage of the other through the channel. In a third channel, E_cap is such that the species with the smaller mobility will also be completely excluded (Fig. 3A, right), and both species are completely prevented from entering the channel. In this case, the applied field is too large to achieve separation of the specified analytes.

Conceptually, the smaller the variance at a single entrance, the closer the capillary centers can be placed (in terms of ΔX and E_cap) and still achieve successful differentiation (Fig. 3B). The change in E_cap between the entrances defines ΔdE/dx, or the change in dE/dx, between two nearest neighbor channel entrances:

$$\mathrm{\Delta }X=\frac{\mathrm{\Delta }v}{\frac{du}{dx}}=\frac{\mathrm{\Delta }\mathrm{\mu }{E}_{\mathit{\text{ave}}}}{\frac{1}{2}{\mathrm{\mu }}_{\mathit{\text{ave}}}(\Delta \frac{dE}{dx})}$$ (16)

Note this differentiation is for only one of these ‘steps’ (Fig. 3) and resolution can be described by:

$$R=\frac{\mathrm{\Delta }X}{4\sigma }=\frac{\frac{\mathrm{\Delta }\mathrm{\mu }{E}_{\mathit{\text{ave}}}}{\frac{1}{2}{\mathrm{\mu }}_{\mathit{\text{ave}}}(\Delta \frac{dE}{dx})}}{4\sqrt{\frac{D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}}{{\mathrm{\mu }}_{\mathit{\text{ave}}}\frac{dE}{dx}}}}=\frac{\mathrm{\Delta }\mu E_{\mathit{\text{ave}}}\sqrt{\frac{dE}{dx}}}{2\sqrt{{\mu }_{\mathit{\text{ave}}}}\mathrm{\Delta }\frac{dE}{dx}\sqrt{D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}}}$$ (17)

The smallest change in electrophoretic mobilities is identified as the best resolution for the technique, so the resolution was solved for Δμ:

$$\mathrm{\Delta }\mu =\frac{R*2\sqrt{{\mu }_{\mathit{\text{ave}}}}\mathrm{\Delta }\frac{dE}{dx}\sqrt{D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}}}{E_{\mathit{\text{ave}}}\sqrt{\frac{dE}{dx}}}$$ (18)

If resolution is set to 1.5 (complete separation in traditional separations), Δμ becomes Δμ_min (the smallest change in mobilities that can be separated with adequate resolution) and is equal to:

$$\mathrm{\Delta }{\mu }_{\mathit{\text{min}}}=\frac{3\sqrt{{\mu }_{\mathit{\text{ave}}}}\mathrm{\Delta }\frac{dE}{dx}\sqrt{D_{\mathit{\text{diff}}}+\frac{u^2{d}^2}{192D_{\mathit{\text{diff}}}}}}{E_{\mathit{\text{ave}}}\sqrt{\frac{dE}{dx}}}$$ (19)

3. RESULTS AND DISCUSSION

According to this model and its theoretical assessment, the following factors influence resolution: capillary diameter, flow rate, average electrophoretic mobility, field strength (within the channel), and the difference in field strength between adjoining entrances. All other effects are controlled by adjusting these parameters.

3.1. Metric to compare to other techniques

There are no traditional chromatographic or electrophoretic peaks of a defined width separated by a specified time or space with this technique. To assess and compare the theoretical performance of this technique with others, the minimum difference in electrophoretic mobilities (Δμ_min) that can be resolved is used. This value is transferable and can give a raw measurement for direct comparison. Obviously, with this assessment the smaller value of Δμ_min, the better the resolution and peak capacity for the given technique, all other facts being held constant.

3.2. Capillary diameter and flow rate

The relationship between resolution and capillary diameter and flow rate are not algebraically simple (they are not trivially linear, exponential, or logarithmic relationships). To understand their relationship to resolution, they are assessed graphically (Fig. 4). Accordingly, Δμ_min is minimized for small diameters and low flow rates. The strongest effect is the reduction of Taylor-Aris dispersion, with an additional effect from an increased gradient at the capillary entrance. Since the smaller diameters positively influence resolution through two mechanisms, increased gradient and reduced dispersion, it dominates the relationship relative to flow. Resolution can be significantly increased by reducing channel diameters, by orders of magnitude, but at the cost of reduced volume flow rate. This is directly offset by the opportunity to operate this strategy with massively parallel interfaces, all with small diameter, high resolution interfaces, while attaining the desired bulk fluid transfer.

Figure 4.

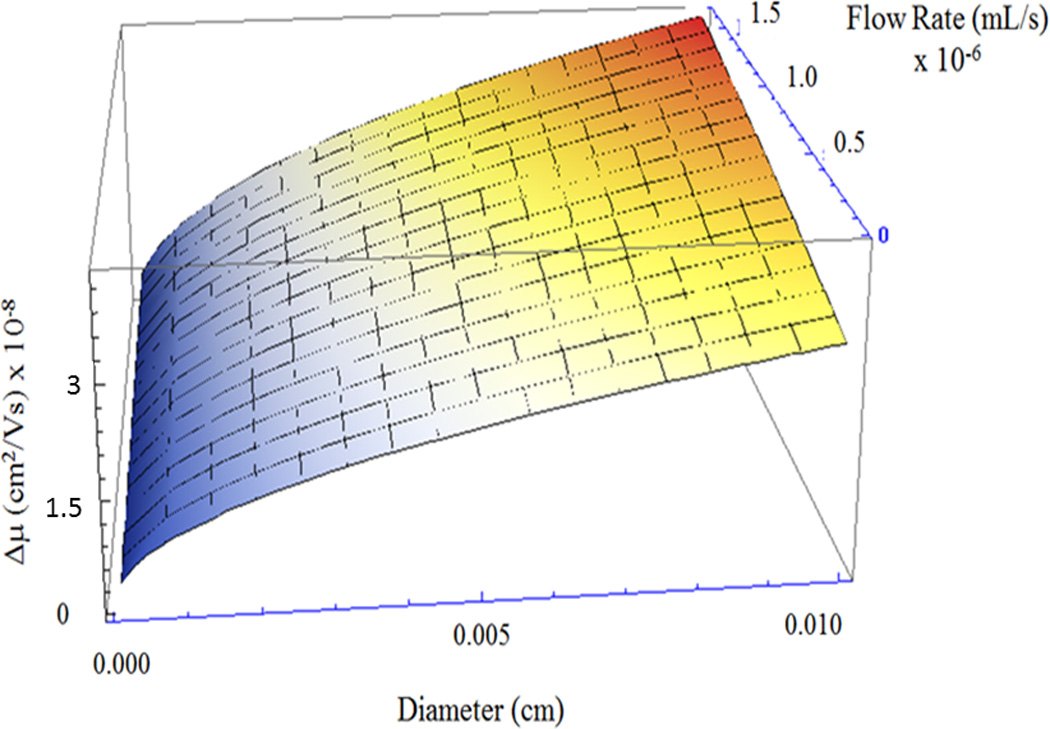
Resolution as a function of capillary diameter and flow rate. Resolution is described by Δμ_min (vertical axis) and decreases most notably with smaller capillary diameters (left edge of graph).

3.3. Smallest separable difference in electrophoretic mobilities

According to the calculations presented here, the smallest Δμ_min (R = 1.5) is ~ 10⁻¹³ m²/Vs. This occurs at the smallest common capillary diameter of 1 µm, a relatively low fluid velocity of 100 µm/s, and ΔdE/dx of 10⁵ V/m² (assuming a large diffusion coefficient of 6 × 10⁻⁸ m²/s, and a μ_ave of 5.0 × 10⁻⁹ m²/Vs). Driving these down to ultimate limits where assumed physics breakdown (200 nm channel diameter, 3 × 10⁵ V/m field, 50 µm/s flow velocity) gives ~ 10⁻¹⁴ m²/Vs. For more practical experimental conditions, where the capillary diameter is equal to 20 µm, the electric field is set at 5 × 10⁴ V/m, and a flow rate of 20 nL/min, Δμ_min is ~ 10⁻¹² m²/Vs. As a comparison, results are noted from the Jorgenson group [33–34]. According to the data presented in their impressive experimental studies, flow counterbalanced CE could separate species with electrokinetic mobilities as similar as 10⁻¹¹ m²/Vs in several hours [33], while an ultrahigh voltage CE study separated species with mobilities as close as 10⁻¹² m²/Vs in approximately 1 hour [34]. Additionally, Culbertson et al. performed a CE study using a spiral channel on a microchip to separate dichlorofluorescein from a contaminant that differed by as little as 10⁻¹⁰ m²/Vs in tens of seconds [18]. Comparison of the theory presented in this manuscript with the above-referenced experimental results, indicates the resolution of electrophoretic exclusion may be on par with some of the best CE performances.

Aside from traditional CE studies, there are several examples in the literature where species have been differentiated at an appropriate interface that allows direct comparison to these predictions, including GEMBE [23] and previous electrophoretic exclusion studies [26, 28]. To compare these studies, the variance of the concentration gradient at the entrance must be determined; however, it is difficult to quantitatively assess these data. GEMBE studies vary the flow rate as an integral element of the technique and introduce dispersion associated with the transport of the concentrated species to the detection element, along with an increase in measured dispersion from the detection element itself. The calculation and subtraction of these additional dispersion elements to estimate the experimental entrance dispersion are of little value since they are much larger. Nevertheless, GEMBE reports Δμ_min values on the order of 10⁻⁹ m²/Vs for short separation time (tens of seconds), and improved resolution with increased analysis time. In these GEMBE experiments, the detection window standard deviation is estimated to be 0.5 mm, which is noted to say that the initial width of the analyte boundary as it enters the capillary is negligible. According to the theory presented here, in fact, the standard deviation for the experimental conditions noted is approximately 15 µm, or about 3%, supporting their assertion that it is negligible.

Meighan et al. reported several electrophoretic exclusion data using a flow injection analysis on a benchtop device [25, 26]. These data can be assessed noting that the flow injection analysis mode also added Taylor-Aris dispersion and resulted in standard deviations measured at the detector of 1–2 mm, whereas the entrance contribution was about 40 µm according to the theory presented here. The calculated dispersion induced by the Taylor-Aris mechanism accounted for most (1.4 mm), if not all, of the standard deviation. The theoretical Δμ_min (R = 1.5) is approximately 10⁻¹¹ m²/Vs for the conditions reported and at least 10⁻⁹ m²/Vs was shown (data points for 1.5 kV and 1.7 kV, Figure 7 in Meighan et al., 2009). These previous studies were indirect and the dynamic strategies used are not especially helpful in clarifying exactly what resolution is possible with this overall strategy. Fortunately, direct observation of the local interface on a planar microfluidic chip is available and indicates very sharp concentration gradients [28] and the flow and electric field forces of the interface have been experimentally quantified [27]. The concentration gradients are shown to be less than 100 µm wide for small molecules (fluorescent dye). This was produced at an asymmetric interface not optimized for resolution, but does indicate that steep concentration gradients are observed consistent with these calculations. The experimentally quantified flow and electric field effects are consistent with the model presented here.

The presence of the parabolic flow profile at the entrance indicates some materials will travel some distance into the capillary or channel in the center before diffusing to lamina that arrests or reverses movement. An estimate of the resulting bolus (short time scale) or concentration profile (long time/steady state) location can be surmised by some rather simple logical statements. Three situations can be considered: species with electrophoretic velocity less that the average flow velocity (ν_EK < ν_ave), those with electrophoretic velocity greater than the maximum flow rate (equal to 2ν_ave for circular capillaries, ν_EK > 2ν_ave) and those in between (ν_ave < ν_EK < 2ν_ave). On average (assuming the targets sample all laminae within the channel), those with ν_EK < ν_ave will be transported out of the channel in the direction of flow and those with ν_EK > 2ν_ave will never enter the capillary/channel. The electrophoretic velocities in between will be trapped, but not outside the capillary/channel entrance.

One very rough estimate of maximum resolution would be to assess the minimum resolvable difference in ν_EK to be 2ν_ave − ν_ave and adjust the corresponding ν_EK for field strength to calculate minimum Δμ_min. However, this approach does not account for the fact that a species with electrophoretic mobility less than 2ν_ave will enter the capillary, but, on average, not exit in the flow direction. This species will form a bolus, initially, and eventually evolve into a concentration profile somewhere within the capillary/channel. How far into the channel is a function of the ratio of the specific electrophoretic velocity, the average flow velocity, the capillary/channel diameter, and the diffusion constant of the species.

If one assumes that a species is entrained in the center laminae moving at 2ν_ave − ν_EK, how long will it take to diffuse, on average, to a laminae (r) where its movement is arrested (local forces, flow & electric field effects, are equal) (Fig. 5)? The balance point of ν_{flow, r} and ν_EK is between the center (r = 0) and the wall (r = r_c). A reasonable position, for the purposes of this discussion, is r = r_c/2. Using a gross but common approximation that diffusion distance is approximately r_diffusion = (2Dt)^1/2 [D is the diffusion coefficient, t is time] resulting in r_c/2 = (2Dt)^1/2. Solving this for time: t_diffusion = r_c²/8D. Assuming a cylindrical capillary and using the Poiseuille equation [${\nu }_{\mathit{\text{max}}}=\frac{\mathrm{\Delta }p{r}_c^2}{4L\eta }$, where Δp: pressure differential, L: tube length, η: viscosity—all constant in this development], then the penetration (x_max) is less than $(\frac{\mathrm{\Delta }p{r}_c^2}{4L\eta }-\mu E)*\frac{r^2}{8D}$ or $\frac{\mathrm{\Delta }p{r}_c^4}{32DL\eta }-\frac{\mu E{r}_c^2}{8D}$ [μ: electrophoretic mobility, E: electric field]. For common published experimental systems (r_c = 38 µm diameter capillary, 10⁴ V/m electric field, D = 10⁻⁸ m²/s, L=0.1 m, Δp=100 Pa, η=0.89 cP), μ=10⁻⁹ m²/V s), the bolus location is calculated to be a few hundred microns inside the channel and is proportional to r_c² (for smaller diameters the penetration is much less). With the same conditions for a 10 µm diameter capillary the penetration average depth is less than 10 µm. None of this changes the smallest differences in resolving like species.

Figure 5.

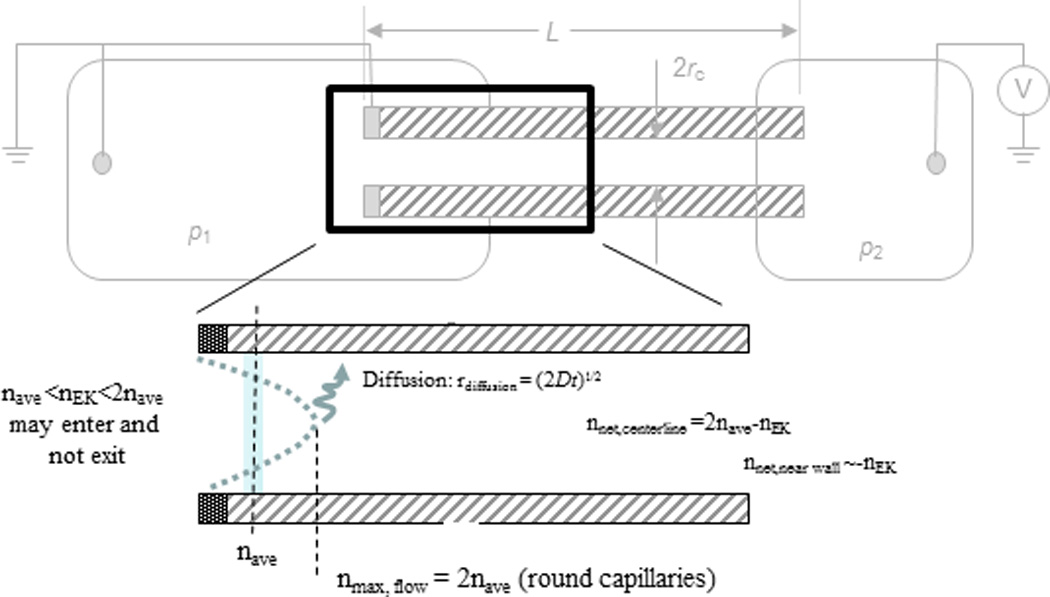
Laminar flow profile not only introduces dispersion, but it allows a bolus/concentration profile within the capillary for electrophoretic velocities between −ν_ave and −ν_max. The location of the concentration front/bolus is a function of capillary diameter, flow rate, electrophoretic velocity and diffusion. For typical experimental systems this front is located a few hundred microns within the capillary.

3.4. Peak capacity

Another measure of the quality of a separation process is peak capacity. Peak capacity is defined as the number of distinguishable peaks, or elements, that can be separated in a given space or time. Peak capacity is a valuable separations metric because it accounts for the total amount of differentiable elements, as opposed to just comparing between two species as in resolution assessments. In electrophoretic exclusion, peak capacity is the total number of species that can be differentiated in individual reservoirs, assuming R = 1.5. For this approach, it is an indication of how many elements could theoretically be designed into a device, whether it is in a parallel or serial format. A serial format would mimic standard electrophoretic experiments towards estimating how many useful fractions could be drawn that might represent a single species.

The calculated variance (σ) does not remain constant across the experimental space. To account for this variation, Δμ was calculated at both the lowest and highest reasonable electrophoretic mobility for an otherwise constant system. To calculate the peak capacity (n_c), several assumptions were made. First, it was determined that the range of electric fields that could successfully be used for separation were between 10 and 10⁵ V/m (this could be extended to 3 × 10⁵ V/m for a microdevice). A channel diameter of 1 µm was assumed and the ΔdE/dx between entrances was 10⁵ V/m² (noting this voltage difference can trivially be set by nearly any commercial power supply). Diffusion (D_diff) was set at 6 × 10⁻⁸ m²/s and hydrodynamic velocity ranged between 0.1 and 1 mm/s. Next, the smallest μ_ave (referred to as μ_min) was calculated using the lowest linear velocity and the largest electric field strength to be μ_min = 10⁻⁹ m²/Vs. The largest μ_ave (referred to as μ_max) was determined by using the highest linear velocity divided by the lowest electric field μ_max = 10⁻⁶ m²/Vs.

The smallest separable difference in mobilities between species at R = 1.5, Δμ_min, was calculated at both the μ_min and μ_max that was defined above. For Δμ_min at μ_min, Δμ_min was calculated using eqn. 18, which resulted in:

$$\mathrm{\Delta }{\mu }_{\mathit{\text{min}}{\mu }_{\mathit{\text{min}}}}={10}^{-14}{m}^2/Vs$$ (21)

Similarly, Δμ_min at μ_max was calculated, except the smallest electric field (1000 V/m) was used for E_ave, the largest flow velocity (1 mm/s) was used, and dE/dx was calculated as 1.0 × 10⁹ V/m²

$$\mathrm{\Delta }{\mu }_{\mathit{\text{min}}{\mu }_{\mathit{\text{max}}}}={10}^{-9}{m}^2/Vs$$ (22)

Finally, the total peak capacity was calculated by using the range of mobilities divided by the average Δμ_min:

$$n_c=\frac{{\mu }_{\mathit{\text{max}}}-{\mu }_{\mathit{\text{min}}}}{\raisebox{1ex}{$\mathrm{\Delta }{\mu }_{\mathit{\text{min}}{\mu }_{\mathit{\text{min}}}}+\mathrm{\Delta }{\mu }_{\mathit{\text{min}}{\mu }_{\mathit{\text{max}}}}$}\!\left/ \!\raisebox{-1ex}{$(2)$}\right.}=1000$$ (23)

These calculations indicate that electrophoretic exclusion can be used for the isolation of analytes in samples that contain a large number of species and whose species cover a large range of mobilities. A similar technique, electric field gradient focusing, suggested peak capacities of over 10,000 could be achieved [19], while capillary isoelectric focusing reported an experimental peak capacity of over 4000 [35].

Although the peak capacity for electrophoretic exclusion is already comparable to some of the better one dimensional separation techniques, it can be further improved by stacking separation steps, while varying the buffer pH, ionic strength, etc. (moving the effluent from a single element, changing the buffer and separating on a new element), which changes the electrophoretic mobilities of the species and allows them to be isolated in different locations. Electrophoretic exclusion is a dynamic technique that allows for adjustments to further improve its separation efficiency.

4. CONCLUDING REMARKS

To understand the applicability of a separations technique to various samples, the resolving capabilities of the technique must be understood. Here, the theoretical resolution of electrophoretic exclusion has been described, along with a brief analysis of previously published experimental data. Theoretically, results indicated that electrophoretic exclusion can separate species with very similar mobilities (Δμ_min ~ 10⁻¹³ m²/Vs), better even than experimental results reported for CE. The assessment of available experimental data indicated that electrophoretic exclusion is slightly less capable of resolving species than what was theoretically indicated, due to various dispersion forces, particularly on the mesoscale. However, when reducing the size scale to a microchip, the dispersive forces decreased, suggesting the possibility of better resolution. To further improve resolution, an optimized electrode and entrance flow field design can be created,[27] reducing the dispersive forces even further. With better resolution, more similar species can be differentiated and; therefore, more complex samples can be analyzed and separated. The engineering of an interface with high resolving capabilities can be used in designs that include several of these interfaces in series and parallel that can be envisioned for the complex sample analysis.

Abbreviations

ɳ

buffer viscosity

C_max

max concentration

D_diff

diffusion

D_TOT

all dispersive forces

E

electric field strength

E_cap

electric field within capillary

EFGF

electric field gradient focusing

GEMBE

gradient elution moving boundary electrophoresis

W

overall transport in the system

n_c

peak capacity

Δp

pressure difference

r_c

radius of capillary

R

resolution

U

drift velocity

ΔX

distance between separated elements

μ

electrophoretic mobility

ν_EK

electrophoretic velocity

Δμ_min

closest resolvable species

μ_ave

average electrophoretic mobility

μ_min

smallest average electrophoretic mobility

μ_max

largest average electrophoretic mobility

Δμ_minμmin

smallest difference in mobility at the smallest μ_ave

Δμ_minμmax

smallest separation difference in mobility at the largest μ_ave

u

hydrodynamic flow