Abstract
Purpose
Our goal is to develop an accurate, automated tool to characterize the optic nerve (ON) and cerebrospinal fluid (CSF) to better understand ON changes in disease.
Methods
Multi-atlas segmentation is used to localize the ON and sheath on T2-weighted MRI (0.6 mm3 resolution). A sum of Gaussian distributions is fit to coronal slice-wise intensities to extract six descriptive parameters, and a regression forest is used to map the model space to radii. The model is validated for consistency using tenfold cross-validation and for accuracy using a high resolution (0.4 mm2 reconstructed to 0.15 mm2) in vivo sequence. We evaluated this model on 6 controls and 6 patients with multiple sclerosis (MS) and a history of optic neuritis.
Results
In simulation, the model was found to have an explanatory R-squared for both ON and sheath radii greater than 0.95. The accuracy of the method was within the measurement error on the highest possible in vivo resolution. Comparing healthy controls and patients with MS, significant structural differences were found near the ON head and the chiasm, and structural trends agreed with the literature.
Conclusion
This is a first demonstration that the ON can be exclusively, quantitatively measured and separated from the surrounding CSF using MRI.
Keywords: Optic Nerve, Multiple Sclerosis, Magnetic Resonance Imaging, Segmentation, Non-convex Optimization, Multi-Atlas
Introduction
Optic neuritis, from demyelination, is a sudden inflammation of the optic nerve (ON) and is marked by pain upon eye movement, and visual symptoms such as a decrease in visual acuity, color vision, contrast and visual field defects (1). Demyelination optic neuritis is closely linked with multiple sclerosis (MS) and many patients who present with optic neuritis will develop MS within 15 years (2). The optic nerve treatment trial showed that the majority of patients, but not all, recover vision after an episode of unilateral optic neuritis (3). Despite this, there is no current radiological biomarker of the ON that is well suited to predicting the visual outcome or even the eventual development of MS or can adequately characterize tissue evolution (axonal loss, atrophy) after an event of optic neuritis. Furthermore, therapeutic interventions can potentially help preserve and/or restore visual function if administered before ON axons are lost, i.e., during the ‘neuroplasticity’ window (4–6). It would be beneficial to understand the relationship between ON damage and diseases of the central nervous system, such as MS. However, characterization along the length of the ON still remains challenging. Visually, high-resolution MRI methods have been developed to provide an appreciation of the ON in health (Figure 1A) and in disease (Figure 1B). The zoomed, coronal reformatted images in Figure 1A and B also show that in patients with remote optic neuritis (Figure 1B inset), tissue atrophy is noted compared to the healthy nerve (Figure 1A inset). However, quantification of the degree of atrophy and even the distribution of expected, normal and healthy optic nerve sizes has not been well characterized. Therefore, the goal of this work is to develop an automated tool to measure the size of the ON and the surrounding cerebrospinal fluid (CSF) independently for estimating normal population variation and comparison among patient populations.
Figure 1.
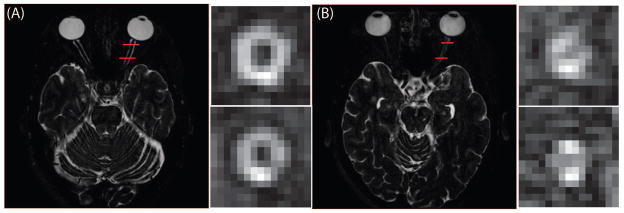
An example of a healthy nerve (A) and an atrophied nerve (B) from the multi-atlas segmentation atlas subjects. In the coronal view, ON atrophy is apparent. Quantification of these structural difference is the target of the presented algorithm.
Early works used scanning-laser-tomography which only provided information about the optic disk (7). Optical coherence tomography (OCT) is an important biomarker for visual pathologies; yet, OCT only captures the retinal nerve fiber layer at the back of the retina (8). In fact, from OCT we understand the magnitude of axonal loss in optic neuritis (9) and the relationship with visual loss (10,11). We further hypothesize that gaining information about ON damage along the entire length of the nerve will give insight to “normal” areas of the nerve, and areas that are either at risk or already undergoing atrophy. Thus, 3D imaging techniques may offer a better platform for understanding disease pathology along the length of the ON but high-resolution imaging of the entire ON is challenging due to the small size and propensity for artifacts that arise from eye movement and orbital fat. Thus, data derived from MR and CT are largely used to identify lesions qualitatively sense (i.e., absence or presence enhancement) or marked with limited quantitative measures (i.e., single-slice cross-sectional area).
Manual segmentation with “computer assistance” has been and remains the de facto standard process to quantitatively characterize the ON using MRI. Hickman et al. used contouring to identify ON cross-sections in a longitudinal analysis and revealed patterns consistent with acute inflammation followed by long-term atrophy (12,13). Combined conventional and magnetization transfer (MT) imaging studies using manual contouring of the ON volume have shown that ON degeneration is associated with persistent functional deficits (14) and that in acute optic neuritis, MT MRI is more sensitive than measures of atrophy in detecting disease-related changes (15). The use of fuzzy clustering algorithms has been proposed to differentiate healthy tissue and tumors (16). These studies have focused on ROIs consisting of the whole ON rather than capturing the cross-sectional variation along the entire tract. Shen et al. suggest limiting consideration to a single ON cross-section to limit resource requirements (17). Meanwhile, work toward automating segmentation of the ON has developed in the context of radiation therapy (18). Early “atlas–based” techniques (19,20) were mildly successful for segmenting the ON (21). To improve sensitivity and specificity, Bekes et al. (22) proposed a geometric method for semi-automatic ON segmentation, but indicated qualitative disagreements with expertly drawn labels. MRI has recently provided images whereby estimates of the ON and the surrounding CSF using manual observers have been accurate (23,24); we seek to automate this process. Segmentation of optic pathway gliomas has been attempted using a probabilistic tissue model (25). Recent efforts have also attempted to automatically segment the ON in MRI but did not isolate the nerve from the surrounding CSF or study the application in patients with expected ON atrophy (26). Recently, we have proposed multi-atlas segmentation pipelines for both CT (27) and MRI (28). The surrounding CSF is not differentiable from the nerve on CT, which is why we choose to focus this effort on high-resolution MRI, which when using a heavily T2-weighted, fat-saturated acquisition can visualize the dark optic nerve and surrounding CSF clearly (Figure 1). We therefore, propose an MRI–based analysis pipeline that 1) segments both the ON and CSF sheath together from the surrounding tissue, and 2) separates the nerve and CSF into two classes using intensity value information couched in a novel model of ON architecture. Importantly, this model takes into account the orientation of the optic nerve which may be oblique to the actual imaging plane.
Methods
MRI Acquisition and Summary of Analysis Approach
All MRI studies were performed with approval of the Vanderbilt Institutional Review Board and signed informed consent was obtained prior to data acquisition. Six healthy volunteers and 6 patients with multiple sclerosis concomitant with a noted clinical history of at least unilateral optic neuritis were enrolled in the study. Of the six patients one was male, ages ranged from 25 to 34 with an average age of 31. Controls consisted of 2 males while ages ranged from 22 to 33 with an average age of 29. Anatomical T2-weighted VISTA scans were obtained on a 3T Philips Achieva (Philips Medical Systems, Best, The Netherlands) using a 2 channel body coil for transmission and an 8 channel head coil for reception. After tri-planar localization, we acquired the T2-weighted volume in the axial plane. The VISTA sequence parameters were: 3D FSE (TR/TE/α = 4000ms/404ms/90°), FOV= 180 × 180 × 42mm3, nominal resolution = 0.6 × 0.6 × 0.6mm3, SENSE factor = 2, fat saturation = SPIR, and total scan time = 5:20. It should be noted that the TE is long due to the nature of the asymmetrically sampled k-space pattern of the VISTA (SPACE on Siemens, and CUBE on GE) acquisition but does provide excellent tissue:CSF contrast. We reformatted the data into the coronal plane and propose a model to fit the ON and surrounding CSF in the reformatted plane. The model is initialized using the result of a previously described multi-atlas segmentation protocol (28). We then fit the model to the ON using a conjugate gradient descent non-convex optimization method. A graphic outline of our proposed pipeline can be seen in Figure 2.
Figure 2.
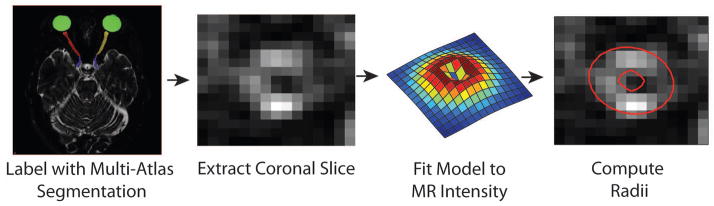
The proposed algorithm for ON radii extraction. Multi-Atlas segmentation is used to locate the ON and sheath as a single labeled object. Using this result, we use the fact that the data are acquired isotropically to switch to a coronal plane where the proposed model is fit. The parameters are found through this model fitting, and then fed into a nonlinear regression tree to extract the underlying radii.
Proposed Model
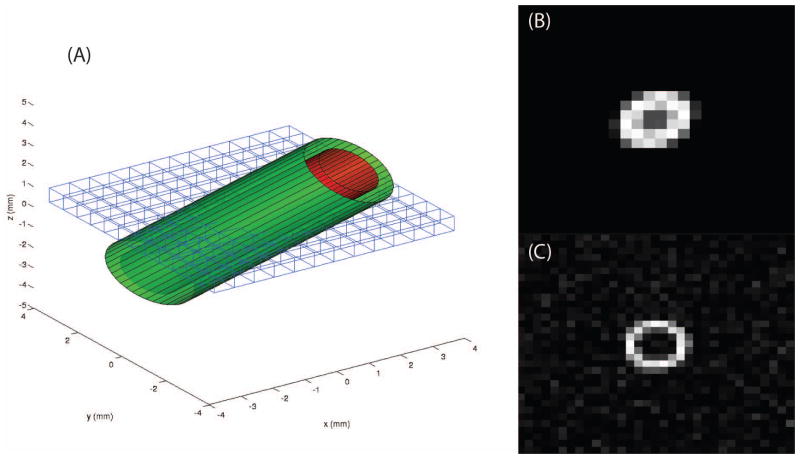
To first approximation, the ON can be thought of as a cylinder (~2–4 mm diameter) inside a cylindrical sheath (~3–6 mm diameter), which is imaged at an oblique angle. On T2-weighted MRI, CSF is brighter than nerve tissue such that the outer cylinder is white and the inner cylinder dark. Even using high-resolution methods as those proposed here with isotropic resolution ~0.6 mm, there are only a handful of voxels that span the ON (4–7) which are significantly partial volumed such that the resulting images appear to be blurred elliptical annuli (Figure 3).
Figure 3.
Some examples of the model used to generate synthetic images. (A) shows a rendering of the model and how the imaging plane crosses the tubular structure creating an elliptical structure in the image. (B) illustrates an example synthetic image with no noise added and slight off axis rotation. (C) presents an example synthetic image which is on axis (with Rician noise).
We propose a difference of two Gaussians model to fit the intensity values of the ON and CSF sheath in the coronal plane.
| [1] |
where N(μ⃑, Σxy)is a bivariate normal distribution with mean vector μ⃑ = [μx μy] and covariance matrix Σxy:
| [2] |
I0 is an intensity scaling factor, eβ is a scaling factor to control the relative height of the inner Gaussian. Formulating the scaling factor as an exponential constrains the scaling term from becoming negative and forces the model to be a sum of Gaussians (rather than a difference) during optimization. σ2 scales the covariance matrix to change the relative width of the inner Gaussian. The covariance matrix is comprised of the following components:
| [3] |
σx and σy control the width of the model in the x and y direction respectively. 2/(1 + e−ρ) − 1 is a correlation term which allows for ellipticity in the model. This is necessary due to the fact that the ON is not always perpendicular to the imaging plane and thus appears elliptical (Figure 3A) and heavily partial volumed (Figure 3B) compared to the true coronal (Figure 3C). This term is formulated as a sigmoid function such that the correlation is constrained in the range (−1,1), which improves stability during optimization.
In summary, the complete model is composed of eight terms: Θ = [σx, σy, σ2, I0, μx, μy, β, ρ]. Model error is defined as the sum of squared error between the model and the observed image in Equation [4]. Equation [5] is the derivative of the sum of squared error with respect to the set of parameters Θ.
| [4] |
| [5] |
For clarity, the partial derivatives for each parameter are shown in equations [6] through [11] and can then be used in Equation [5]. The derivatives for σy and μy are omitted as they are a direct substitutions into equations [6] and [9], respectively.
| [6] |
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
Initialization
The center of the model is initialized at the centroid of the previously described multi-atlas segmentation labels in the coronal plane (28). To initialize σx and σy, profiles are taken superiorly and inferiorly across the image and two local peaks around the center of the ON labels are identified and used to estimate the spread in x and y as half the distance between the two peaks. If this fails, both parameters default to an initialization of 2. ρ is initialized by similarly finding intensity peaks along the two diagonals and measuring the width between the two peaks along each diagonal. ρ is then initialized as the difference between these two distances. We initialize σ2 to the experimentally found value of 0.6. β is initialized such that the scaling term eβ = 0.5. Finally I0 is found such that the maximum value of the model is equal to the maximum value of the input image.
Optimization
For every coronal slice that contained ON labels from the initial multi-atlas segmentation, the difference of Gaussian model is fit using an iterative conjugate gradient descent (29). The input to the conjugate gradient descent algorithm is a patch which is 9×9 mm (15×15 voxels) centered at the centroid of the multi-atlas label. The non-linear optimization routine is a custom implementation in MATLAB R2013a (The MathWorks, Inc., Natick, MA, USA). Specific implementation details follow:
The patch is first normalized to the range [0,1]. The gradient is computed and its negative is used as the initial descent direction. The descent step size is found using a line search (iterative bracket search using cubic interpolation and bisection every fifth iteration). The line search is run for a total of 25 iterations. The step is taken and the conjugate direction is then chosen as the descent direction. Every eight iterations (because there are eight input parameters) the descent direction is reset to the negative gradient direction. Also, if the chosen direction is found to be an ascent direction, the direction is reset to the negative gradient. Convergence criteria: the magnitude of the gradient is less than 10−6; the change in the cost function is less than 10−12 between iterations. (Note that small gradients and non-decreasing function values indicate proximity to function extrema.) Divergence criteria: algorithm exceeds 70 iterations; function values become increasing or undefined. If a divergence criteria is reached the algorithm is restarted (only once) using the last iteration as the initialization of the second attempt. This resets the search direction to the gradient descent direction, which can allow the optimization to bypass local minima.
Calibration
Synthetic data was generated to calibrate model parameters to the radius of the ON and surrounding CSF in physical space. A model of two concentric tubes was constructed (Figure 3) and a Monte Carlo simulation is used to simulate partial volume effects. The test images simulate 0.6 mm isotropic voxels, which cover an area 30 mm by 30 mm (50×50 voxels). The model is rotated independently along x and y ranging from zero to 60 degrees rotation in 7.5 degree steps. The inner radius is varied from 0.4 mm to 3 mm in 0.1 mm steps and the outer radius varies from 0.5 mm to 4 mm in 0.1 mm steps. The CSF thickness is constrained to be at least 0.20 mm. Twenty five levels of Rician noise (30) were simulated which were experimentally determined to be visually similar to those observed in ON images we have acquired. These combinations produced a training set of 1,250,964 images. Six model parameters [σx, σy, σ2, I0, β, ρ] are correlated to surrounding CSF and ON radius measurements through a random forest regression (31). The centroids are omitted as they are assumed to depend on field of view placement only.
Validation
To validate that the results obtained from the automatic segmentation match manual measurements, we acquired a higher resolution scan of a healthy control. We acquired a short-inversion time inversion recovery (STIR) scan with TR/TI/TE = 5000ms/200ms/33ms and 2 signal averages at 0.5 × 0.5mm2 with 2 mm slice thickness. The image was reconstructed at 0.15 × 0.15 mm2 for the measurements. This image was then down sampled to 0.6 mm isotropic and smoothed with a 5×5 voxel Gaussian filter with standard deviation of 0.25 voxels. Our algorithm is then applied to the down sampled version to obtain an automatic measurement which can be compared to manual measurements made on the higher resolution scans.
Clinical Application
A small pilot study was conducted to evaluate the viability of this tool in differentiating diseased and healthy ONs. Six controls were chosen at random from a population of 47 and six patients with MS who have a concomitant clinical history of at least one unilateral optic neuritis event. We chose the MS patients who demonstrated poorest visual performance as determined by the adjusted 1.25% binocular contrast visual acuity. These patients were chosen from a pool of 32 MS patients. Each patient and control data set was acquired as in the methods. Using the outlined analysis approach and relying on multi-atlas segmentation for initialization (28) to locate the centroids of the ONs in the coronal plane and determine whether or not a slice contained ON tissue, we calculated the ON radii at every coronal slice. The slice-wise measurements were interpolated to be the same length as the longest observed ON. The nature of the ONs allows for them to be present in a different number of slices from volume to volume. Interpolation more closely aligns corresponding parts of the ON across subjects. A three-element moving window median filter is also applied across slices to reduce noise in the measurements.
Results
Calibration
Synthetic data was utilized to calibrate the model parameters of the radii of two concentric tubes using Monte Carlo simulation to examine the impact of partial volume effects. Tenfold cross validation was performed on a random forest regression using fifteen trees. Fifteen was found experimentally to be the point of diminishing returns (R2 improved by less than 0.01) with more trees and increased training time. The mean R2 of the predicted versus actual result of the testing set is 0.959 for the outer radius (CSF) and 0.958 for the inner radius (ON). The data density plots of these calibration results can be seen in Figure 4. These plots show the correlation between the predicted and true underlying radius of the model. Finally, another forest of fifteen trees was built using all of the training data to be used on clinical data.
Figure 4.
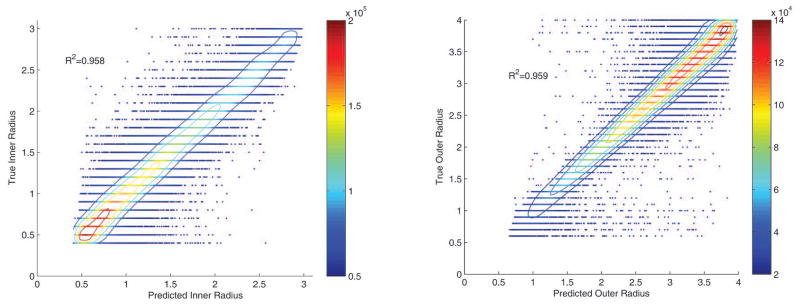
Calibration results for the random forest regression for the inner and outer radii from one fold of a tenfold cross validation on the 1.2 million synthetic images. The color scale represents data density calculated within a circle of radius 0.1. A five element 2-D moving window median filter was applied for smoothing. The isocontours show lines of constant data density. Note that data density is higher near the lower end for the inner radius and at the higher end for the outer radius, this is due to the width constraint on the synthetic images.
Validation
Validation proceeded by comparing manual measurement of the radii on high-resolution STIR acquisitions compared to the lower-resolution T2-weighted VISTA acquisition that was automatically segmented. Using the lower-resolution data, the automatic segmentation calculated the underlying inner radius (ON) to be 1.67 mm and the underlying outer radius (CSF) to be 2.93 mm. Using the STIR data (Figure 5, left panel) Manual measurements were taken along the visually determined approximate major and minor axes for the inner and outer radii. Manually, the inner radius was measured at 1.61 mm and 1.86 mm and the outer radius was measured at 2.85 mm and 3.26 mm indicating close agreement with the automated approach. Details of the measurements can be seen in Figure 5 right panels.
Figure 5.
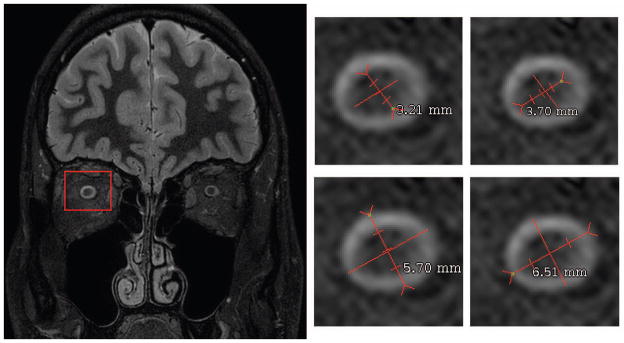
The test volume slice used for validation is shown. The four images show the four measurements of inner and outer optic nerve diameter. This image was then down sampled and smoothed to match current in vivo imaging, and the proposed automatic measurement algorithm was applied. The automatic segmentation found the inner radius to be 1.673 mm and the outer radius to be 2.929 mm.
Clinical Application
We compared the average distribution of inner (ON) and outer (CSF) radii across a small cohort of healthy controls and MS patients with clinical history of optic neuritis. The distributions over slices of the two cohorts (healthy volunteers, dotted solid lines and MS patients, dotted lines) along the length of the ON and separated into outer (CSF) radius (top curves) and ON radius (bottom lines) are shown in Figure 6. Statistically the profiles differ closest to the globe and chiasm and remain relatively similar across healthy volunteers and patients in the middle segments. The shaded areas indicate regions in which the radii of the two populations are statistically different using a one-sample t-test at p<0.05. It is important to note that the regions where the outer radii differ are similar to the where the inner radii differ. The inner radii have statistical difference only on slices nearer to the globe.
Figure 6.
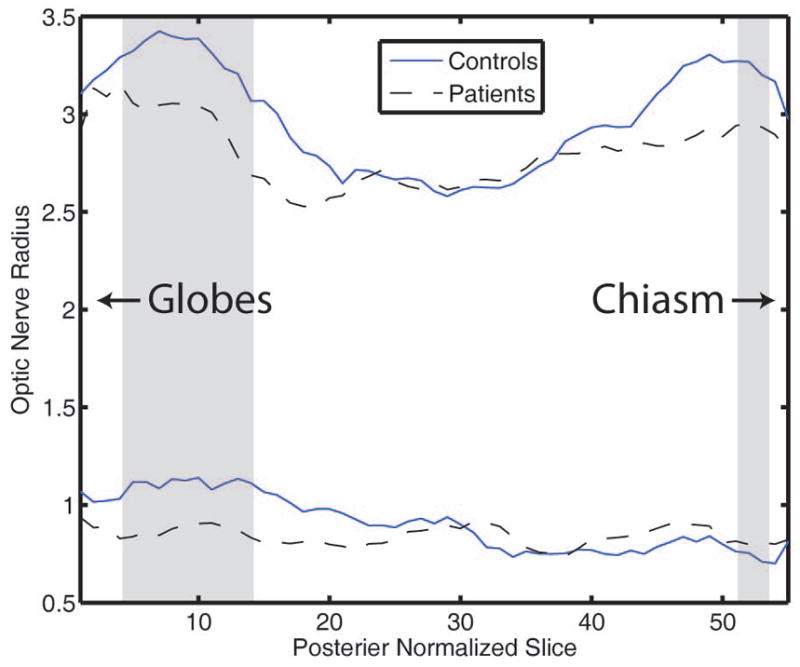
Mean inner and outer optic nerve radii for the two six person sample populations tested interpolated to the same length as the longest sample. The shaded regions indicate where the outer radii are statistically different with p<0.05
Comparison with state-of-the-art clustering approach
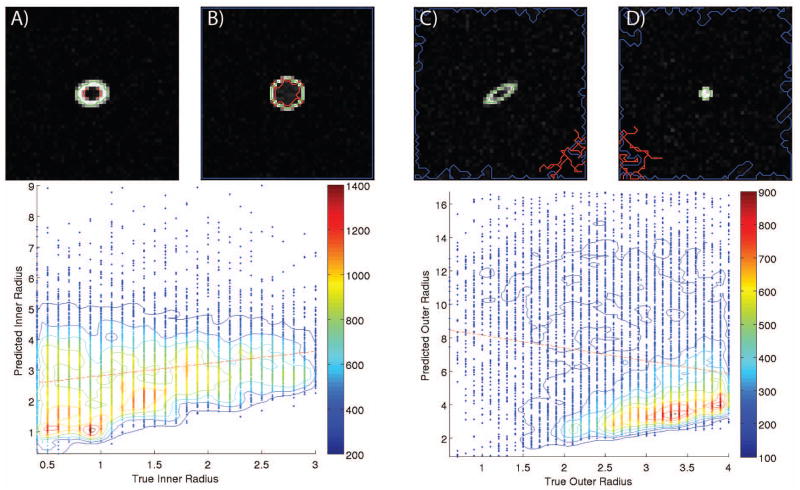
The proposed model is quite complex and the nature of this problem justifies a complex solution. To demonstrate this we have attempted to utilize a commonly utilized method, k-means clustering, to evaluate how a simpler solution will perform. Multi-dimensional k-means clustering is performed using the intensity values and the distance from the centroid with 1000 replicates on 10,000 simulated images which are randomly chosen from the 1.25 million simulated images used in the calibration section. To extract the radii the average distance from the centroid for the largest group of pixels for each class is used. The radii are then taken as the two smallest values as the largest value should be for the background class. The results of this evaluation can be seen in Figure 7. Total error is calculated as the sum of the inner and outer radii errors in quadrature. The two images with the least total error are shown in Figure 7A and 7B. Note that these images have no noise, high contrast and large radii. The two images with the highest total error are shown in Figure 7C and D. Note that these images have noise, obliqueness and 7D has a very small diameter. For both of these images one of the classes was found in the background which is why the radius measurements are so far off. The data density plots below these sample images show the results for all 10,000 images. The red line represents a line of best fit, which has a negative slope for the outer radius. The slope for the best fit line for the inner radius is 0.39 and −0.78 for the outer radius. The inner and outer radius measurements have correlation coefficients of 0.23 and −0.17 respectively.
Figure 7.
Results of evaluation of a simple k-means algorithm using intensity values and the distance from the centroid on 10,000 simulated images. (A) and (B) show the two best results, predicted radii from the k-means algorithm most closely matched the true underlying radii used to generate the image. The colored lines outline the pixels which were used for each radius measurement. In these images, the third (blue) class followed the edge of the image. (C) and (D) show the two worst results. The data density plots below show the results for all 10,000 simulated images for the inner and outer radius with a red line of best fit to the data. The color scale represents data density calculated within a circle of radius 0.1. A five element 2-D moving window median filter was applied for smoothing. The isocontours show lines of constant data density. Note the scales on the y-axes.
Discussion and Conclusions
This is a first demonstration that the ON can be automatically and quantitatively measured and separated from the surrounding CSF in vivo using MRI. In simulation, the model was found to have an explanatory R-squared for both ON and CSF radii of greater than 0.95. The accuracy of the method was within the measurement error on the highest possible in vivo acquisition (Figure 5). In the pilot study, significant structural differences were found near the ON head and the chiasm. Structurally, this is not surprising, as OCT has shown axonal loss near the ON head, which we identify as being an area of diminished ON radii. Very few studies have shown atrophy of the nerve proximal to the chiasm, which lends weight to the need for a high-resolution imaging method to survey the entire nerve.
Our results are in agreement with previous studies on optic nerve and surrounding CSF radii. Geeraerts et al. showed correlation between optic nerve sheath diameter and intracranial pressure (32). Their measurements of ON diameter and ON sheath diameter were taken 3mm posterior to the globe. They found a threshold of ON sheath diameter of 5.8 mm to differentiate between those with raised intracranial pressure and subjects without. They also found a mean ON diameter of 2.65mm. We replicated these measurements on the left and right eyes of our six subjects and six controls, yielding a total of 24 ON diameter measurements and 24 ON sheath diameter measurements. We found a consistently larger distribution for ON sheath diameter with a mean of 6.58mm with standard deviation of 0.64mm. A mean ON diameter of 2.42mm with a standard deviation of 0.32 mm agrees well with their measurements. A good explanation for this discrepancy in measurement which was noted during our replication process is that taking measurements in this area very near the globe yields inconsistent results due to a prevalence of motion artifacts from ocular movement.
Yiannakas et al. measured the cross sectional area of the anterior portion of the ON and a posterior portion of the ON, split 9mm posterior to the globe. They found that the posterior portion of the ON was smaller than the anterior portion (24). As can be seen in Figure 6 this agrees with our results although the actual distribution of the ON radii along the length of the nerve appears to be more complex. They reported a mean cross sectional area in the anterior portion of the ON as 11.6 ± 2.2 mm2 and a mean cross sectional area in the posterior portion as 8.5 ± 1.7 mm2. Using the assumption that the ON is a tubular structure these cross sectional areas correspond to a range of radii of 1.73–2.10 for the anterior portion and 1.47–1.80 for the posterior portion. These numbers are close to our measurements but it is also important to note that measurements were made using both coronal and coronal-oblique slices and were found to have the same mean cross sectional area for both the anterior and posterior region to within 1/100th. To evaluate the validity of this finding we measure the average angle of the ON relative to a coronal slice for left and right ONs in our six patients and six controls. We found a mean angle of 30° ranging from 10° to 49°. Using the cosine of the mean angle of 30° we can calculate that the radius and diameter measurements should be reduced by about 14% which indicates that the cross sectional area should be reduced by more than 26% which is larger than their reported error.
There are a number of possible future directions that could lead to improved resolution and accuracy of the measurements. If the method were to be used on a different imaging resolution the model-physical space mapping would need to be recalibrated using an appropriate simulation framework. The current approach assumes that slices are independent which is a simplified framework and as such the measurements tend to be noisy across the length of the ON for an individual participant. In this work, we utilized a median filter to smooth this noise but constraining the model along the length of the nerve could address some of these issues and increase accuracy. More careful inter-slice analysis could improve model estimation and result in more accurate segmentation. The proposed method does account for bending of the ON but cannot deal with highly complex bends. Our testing (section Methods, subsection Calibration) included bending of up to 60 degrees off axis from the imaging plane. If the ON were to bend perpendicular to the imaging plane the model would no longer fit or had multi-angle or nonlinear bending between slices. The curvature of the nerve could be better accounted for in the interpolation step along the entire length of the ON. The interpolation step currently assumes even samples along the length of every nerve which is not the case. If the curvature of the ON were characterized it would be possible to better align each measurement which may reveal new ways to differentiate patient populations. Future work will improve upon these techniques to better understand ON shape and size and how these vary among populations.
All tools used and developed in this work are available in open source from their respective authors. The tools that implement the ON specific components of analysis are based on the Java Image Science Toolkit (JIST)(33) and Non-Local STAPLE (34). The ON/sheath characterization code is primarily written in MATLAB (The MathWorks, Inc., Natick, Massachusetts, United States) and bundled into an automated program (i.e., “spider”(35)) that combines these tools using PyXNAT(36) for XNAT(37) and is available in open source through the NITRC project MASIMATLAB (http://www.nitrc.org/projects/masimatlab).
Acknowledgments
Research reported in this publication was supported by the National Eye Institute of the National Institutes of Health under Award Numbers R21EY024036, R01EY023240 and by the National Institutes of Health under Award Numbers 1T32EB014841 and 5T32EY007135. Additionally, one investigator received grant support from NIH/NIBIB K01EB009210 (SAS). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This project was supported by VICTR VR3029. The project described was supported by the National Center for Research Resources, Grant UL1 RR024975-01, and is now at the National Center for Advancing Translational Sciences, Grant 2 UL1 TR000445-06. This work was also supported by Capes: Coordination for the Improvement of Higher Education Personnel. This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, TN. Research to Prevent Blindness provided one investigator with a Physician Scientist Award and an unrestricted grant to the Vanderbilt Eye Institute.
References
- 1.Richa C. The Neuro-Ophthalmology Survival Guide. Optometry-Journal of the American Optometric Association. 2010;81(9):423–424. [Google Scholar]
- 2.Group ONS. Multiple sclerosis risk after optic neuritis: final optic neuritis treatment trial follow-up. Archives of neurology. 2008;65(6):727. doi: 10.1001/archneur.65.6.727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Group ONS. Visual function 15 years after optic neuritis: a final follow-up report from the Optic Neuritis Treatment Trial. Ophthalmology. 2008;115(6):1079. doi: 10.1016/j.ophtha.2007.08.004. [DOI] [PubMed] [Google Scholar]
- 4.Beck RW, Cleary PA, Anderson MM, Jr, Keltner JL, Shults WT, Kaufman DI, Buckley EG, Corbett JJ, Kupersmith MJ, Miller NR, et al. A randomized, controlled trial of corticosteroids in the treatment of acute optic neuritis. The Optic Neuritis Study Group. The New England journal of medicine. 1992;326(9):581–588. doi: 10.1056/NEJM199202273260901. [DOI] [PubMed] [Google Scholar]
- 5.Minen MT, Karceski S. Multiple sclerosis and disease-modifying therapies. Neurology. 2011;77(4):e26. doi: 10.1212/WNL.0b013e318229e6ca. [DOI] [PubMed] [Google Scholar]
- 6.Zhang K, Zhang L, Weinreb RN. Ophthalmic drug discovery: novel targets and mechanisms for retinal diseases and glaucoma. Nature reviews Drug discovery. 2012;11(7):541–559. doi: 10.1038/nrd3745. [DOI] [PubMed] [Google Scholar]
- 7.Chrástek R, Wolf M, Donath K, Niemann H, Paulus D, Hothorn T, Lausen B, Lämmer R, Mardin CY, Michelson G. Automated segmentation of the optic nerve head for diagnosis of glaucoma. Medical Image Analysis. 2005;9(4):297–314. doi: 10.1016/j.media.2004.12.004. [DOI] [PubMed] [Google Scholar]
- 8.Medeiros FA, Zangwill LM, Bowd C, Vessani RM, Susanna R, Jr, Weinreb RN. Evaluation of retinal nerve fiber layer, optic nerve head, and macular thickness measurements for glaucoma detection using optical coherence tomography. American journal of ophthalmology. 2005;139(1):44–55. doi: 10.1016/j.ajo.2004.08.069. [DOI] [PubMed] [Google Scholar]
- 9.Trip SA, Schlottmann PG, Jones SJ, Altmann DR, Garway-Heath DF, Thompson AJ, Plant GT, Miller DH. Retinal nerve fiber layer axonal loss and visual dysfunction in optic neuritis. Annals of neurology. 2005;58(3):383–391. doi: 10.1002/ana.20575. [DOI] [PubMed] [Google Scholar]
- 10.Costello F, Coupland S, Hodge W, Lorello GR, Koroluk J, Pan YI, Freedman MS, Zackon DH, Kardon RH. Quantifying axonal loss after optic neuritis with optical coherence tomography. Annals of neurology. 2006;59(6):963–969. doi: 10.1002/ana.20851. [DOI] [PubMed] [Google Scholar]
- 11.Costello F. Evaluating the Use of Optical Coherence Tomography in Optic Neuritis. Multiple Sclerosis International 2011. 2011 doi: 10.1155/2011/148394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hickman SJ, Toosy AT, Jones SJ, Altmann DR, Miszkiel KA, MacManus DG, Barker GJ, Plant GT, Thompson AJ, Miller DH. A serial MRI study following optic nerve mean area in acute optic neuritis. Brain : a journal of neurology. 2004;127(Pt 11):2498–2505. doi: 10.1093/brain/awh284. [DOI] [PubMed] [Google Scholar]
- 13.Hickman SJ, Brierley CM, Brex PA, MacManus DG, Scolding NJ, Compston DA, Miller DH. Continuing optic nerve atrophy following optic neuritis: a serial MRI study. Mult Scler. 2002;8(4):339–342. doi: 10.1191/1352458502ms809oa. [DOI] [PubMed] [Google Scholar]
- 14.Inglese M, Ghezzi A, Bianchi S, Gerevini S, Sormani MP, Martinelli V, Comi G, Filippi M. Irreversible disability and tissue loss in multiple sclerosis: a conventional and magnetization transfer magnetic resonance imaging study of the optic nerves. Arch Neurol. 2002;59(2):250–255. doi: 10.1001/archneur.59.2.250. [DOI] [PubMed] [Google Scholar]
- 15.Melzi L, Rocca MA, Marzoli SB, Falini A, Vezzulli P, Ghezzi A, Brancato R, Comi G, Scotti G, Filippi M. A longitudinal conventional and magnetization transfer magnetic resonance imaging study of optic neuritis. Mult Scler. 2007;13(2):265–268. doi: 10.1177/1352458506071212. [DOI] [PubMed] [Google Scholar]
- 16.Yang M-S, Hu Y-J, Lin KC-R, Lin CC-L. Segmentation techniques for tissue differentiation in MRI of ophthalmology using fuzzy clustering algorithms. Magnetic Resonance Imaging. 2002;20(2):173–179. doi: 10.1016/s0730-725x(02)00477-0. [DOI] [PubMed] [Google Scholar]
- 17.Shen S, Fong KS, Wong HB, Looi A, Chan LL, Rootman J, Seah LL. Normative measurements of the Chinese extraocular musculature by high-field magnetic resonance imaging. Investigative ophthalmology & visual science. 2010;51(2):631–636. doi: 10.1167/iovs.09-3614. [DOI] [PubMed] [Google Scholar]
- 18.Noble JH, Dawant BM. An atlas-navigated optimal medial axis and deformable model algorithm (NOMAD) for the segmentation of the optic nerves and chiasm in MR and CT images. Medical image analysis. 2011;15(6):877–884. doi: 10.1016/j.media.2011.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.D’Haese P-F, Duay V, Li R, d’Aische AdB, Merchant TE, Cmelak AJ, Donnelly EF, Niermann KJ, Macq B, Dawant BM. Automatic segmentation of brain structures for radiation therapy planning. 2003:517–526. [Google Scholar]
- 20.Isambert A, Dhermain F, Bidault F, Commowick O, Bondiau PY, Malandain G, Lefkopoulos D. Evaluation of an atlas-based automatic segmentation software for the delineation of brain organs at risk in a radiation therapy clinical context. Radiotherapy and oncology : journal of the European Society for Therapeutic Radiology and Oncology. 2008;87(1):93–99. doi: 10.1016/j.radonc.2007.11.030. [DOI] [PubMed] [Google Scholar]
- 21.Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology. 1945;26(3):297–302. [Google Scholar]
- 22.Bekes G, Mate E, Nyul LG, Kuba A, Fidrich M. Geometrical model-based segmentation of the organs of sight on CT images. Medical physics. 2008;35(2):735–743. doi: 10.1118/1.2826557. [DOI] [PubMed] [Google Scholar]
- 23.Steinborn M, Fiegler J, Kraus V, Denne C, Hapfelmeier A, Wurzinger L, Hahn H. High resolution ultrasound and magnetic resonance imaging of the optic nerve and the optic nerve sheath: anatomic correlation and clinical importance. Ultraschall in der Medizin-European Journal of Ultrasound. 2011;32(06):608–613. doi: 10.1055/s-0029-1245822. [DOI] [PubMed] [Google Scholar]
- 24.Yiannakas MC, Wheeler-Kingshott CA, Berry AM, Chappell K, Henderson A, Kolappan M, Miller DH, Tozer DJ. A method for measuring the cross sectional area of the anterior portion of the optic nerve in vivo using a fast 3D MRI sequence. Journal of Magnetic Resonance Imaging. 2010;31(6):1486–1491. doi: 10.1002/jmri.22202. [DOI] [PubMed] [Google Scholar]
- 25.Weizman L, Ben Sira L, Joskowicz L, Constantini S, Precel R, Shofty B, Ben Bashat D. Automatic segmentation, internal classification, and follow-up of optic pathway gliomas in MRI. Medical image analysis. 2012;16(1):177–188. doi: 10.1016/j.media.2011.07.001. [DOI] [PubMed] [Google Scholar]
- 26.Yiannakas MC, Toosy AT, Raftopoulos RE, Kapoor R, Miller DH, Wheeler-Kingshott CA. MRI Acquisition and Analysis Protocol for In Vivo Intraorbital Optic Nerve Segmentation at 3T. Investigative ophthalmology & visual science. 2013;54(6):4235–4240. doi: 10.1167/iovs.13-12357. [DOI] [PubMed] [Google Scholar]
- 27.Panda S, Asman AJ, DeLisi MP, Mawn LA, Galloway RL, Landman BA. Robust optic nerve segmentation on clinically acquired CT. International Society for Optics and Photonics. 2014:90341G–90310. doi: 10.1117/12.2043715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Panda S, Asman AJ, Khare SP, Thompson L, Mawn LA, Smith SA, Landman BA. Evaluation of multiatlas label fusion for in vivo magnetic resonance imaging orbital segmentation. Journal of Medical Imaging. 2014;1(2):024002–024002. doi: 10.1117/1.JMI.1.2.024002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nocedal J, Wright SJ. Conjugate gradient methods. Springer; 2006. [Google Scholar]
- 30.Gudbjartsson H, Patz S. The Rician distribution of noisy MRI data. Magnetic Resonance in Medicine. 1995;34(6):910–914. doi: 10.1002/mrm.1910340618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Breiman L, Friedman J, Stone CJ, Olshen RA. Classification and regression trees. CRC press; 1984. [Google Scholar]
- 32.Geeraerts T, Newcombe VF, Coles JP, Abate MG, Perkes IE, Hutchinson PJ, Outtrim JG, Chatfield DA, Menon DK. Use of T2-weighted magnetic resonance imaging of the optic nerve sheath to detect raised intracranial pressure. Critical Care. 2008;12(5):R114. doi: 10.1186/cc7006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lucas BC, Bogovic JA, Carass A, Bazin PL, Prince JL, Pham DL, Landman BA. The Java Image Science Toolkit (JIST) for rapid prototyping and publishing of neuroimaging software. Neuroinformatics. 2010;8(1):5–17. doi: 10.1007/s12021-009-9061-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Asman AJ, Landman BA. Non-local statistical label fusion for multi-atlas segmentation. Med Image Anal. 2013;17(2):194–208. doi: 10.1016/j.media.2012.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gao Y, Burns SS, Lauzon CB, Fong AE, James TA, Lubar JF, Thatcher RW, Twillie DA, Wirt MD, Zola MA, Logan BW, Anderson AW, Landman BA. Integration of XNAT/PACS, DICOM, and Research Software for Automated Multi-modal Image Analysis. Proceedings of SPIE 2013;8674. doi: 10.1117/12.2007621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schwartz Y, Barbot A, Thyreau B, Frouin V, Varoquaux G, Siram A, Marcus DS, Poline JB. PyXNAT: XNAT in Python. Frontiers in neuroinformatics. 2012;6:12. doi: 10.3389/fninf.2012.00012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Marcus DS, Olsen TR, Ramaratnam M, Buckner RL. The Extensible Neuroimaging Archive Toolkit: an informatics platform for managing, exploring, and sharing neuroimaging data. Neuroinformatics. 2007;5(1):11–34. doi: 10.1385/ni:5:1:11. [DOI] [PubMed] [Google Scholar]