Enhancing K-space Quantitative Susceptibility Mapping by Enforcing Consistency on the Cone Data (CCD) with Structural Priors

Abstract

Purpose

The inversion from the magnetic field to the magnetic susceptibility distribution is ill-posed because the dipole kernel, which relates the magnetic susceptibility to the magnetic field, has zeroes at a pair of cone surfaces in the k-space, leading to streaking artifacts on the reconstructed quantitative susceptibility maps (QSM). A method to impose consistency on the cone data (CCD) with structural priors is proposed in order to improve the solutions of k-space methods.

Method

The information in the cone region is recovered by enforcing structural consistency with structural prior, while information in the non-cone trust region is enforced in order to be consistent with the magnetic field measurements in k-space. This CCD method was evaluated by comparing the initial results of existing QSM algorithms to the QSM results after CCD enhancement with respect to the COSMOS results in simulation, phantom, and in vivo human brain.

Results

The proposed method demonstrated suppression of streaking artifacts and the resulting QSM showed better agreement with reference standard QSM compared with other k-space based methods.

Conclusion

By enforcing consistency with structural priors in the cone region, the missing data in the cone can be recovered and the streaking artifacts in QSM can be suppressed.

INTRODUCTION

Quantitative Susceptibility Mapping (QSM) provides an MRI contrast mechanism capable of mapping the underlying tissue magnetic susceptibility, making QSM a useful tool for scientific and clinical studies. The mapping requires solving a magnetic field-to-source inverse problem through a dipole deconvolution, which has attracted significant interests and has led to the design of fast and accurate deconvolution algorithms. Given the nature of MRI data, which is acquired in k-space and displayed in image space, there are naturally k-space and image space methods used to solve this inverse problem.

Compared to image-space based methods (1–8), which are generally computationally expensive and slow, the k-space based methods are easier to implement and faster to calculate. Most existing k-space based methods focus on constraining the energy of the solution by means such as variations of truncated singular value decomposition (9–13), early termination in iterative solution reconstruction (11), or filter use to interpolate the missing data (11,14). Although it is desirable to lower the energy of errors in the reconstruction, these energy constraints do not discriminate error energy from signal energy and often improperly underestimate the strength of the signal.

In this paper, we present an enhancement method that aims to recover the signal energy of the solutions of k-space methods by incorporating sophisticate prior information related to the underlying susceptibility distribution. We showed that this enhancement method, which is applicable to any existing QSM algorithm, is effective in suppressing streaking artifacts and retains quantitative accuracy in numerical simulation, phantom experiment, and in vivo data when compared with reference standards.

THEORY

The relationship between a magnetic field f and a scalar susceptibility distribution χ may be expressed as:

$$f=F^{-1}DF\chi ,$$ (1)

where F and F⁻¹ are the forward and backward Fourier transforms, respectively. $D=\mathit{diag}(1/3-k_z^2/k^2)$ is a diagonal matrix representing the dipole kernel in k-space, with k being the k-space coordinate and k_z being its projection along the direction of the B₀ field. D may be regarded as a sampling density function that undersamples Fχ because D has zeroes at a pair of opposing conical surfaces at $k_z^2/k^2=1/3$ (15–16). From the undersampled data, χ can be recovered: χ^* = F⁻¹D⁺Ff, where D⁺ is the Moore-Penrose pseudoinverse of D. Although there is a loss of information on the cones in Fχ^*, two observations suggest that a full recovery of χ is possible. First, the number of non-zero unknowns in χ, i.e. unknowns that are not equal to zero, may be drastically reduced by applying a sparsifying operator, such as a gradient operator ∇, which changes the number of unknowns to the number of edge elements in χ. Second, a large portion of k-space is faithfully reconstructed in the trusted region, or non-cone region $T:\mid 1/3-k_z^2/k^2\mid >th$ (th is a threshold value). Indeed, if the locations of the edges are known, it is proven that an accurate solution of χ is available (17).

Solving exclusively for the edge elements using a conjugate gradient algorithm

Here, we provide a method for improving the accuracy of k-space methods solutions using these two observations. According to the first observation, the susceptibility distribution χ may be succinctly expressed in a sparsified domain:

$$\begin{array}{c}\nabla \chi =U\omega ,or\\ \chi ={\nabla }^{+}U\omega ,\end{array}$$ (2)

where U is a diagonal matrix having non-zero elements at locations corresponding to edge elements, and ω represents unknown strengths at those locations. According to the second observation, such a susceptibility distribution should be consistent with the faithfully reconstructed data in the trusted region:

$$TF{\chi }_0=TF{\nabla }^{+}U\omega ,$$ (3)

where T is a binary mask, taking a value of one in the trusted region and zero otherwise, χ₀ is an initial result from any QSM method, F is the Fourier transformation, and ∇⁺ denotes the Moore-Penrose pseudoinverse of ∇. Eq.3 can be used to determine ω, and an edge matched susceptibility map can be recovered using χ_em = ∇⁺Uω. Since the missing data in the cone region is largely recovered from structural priors, we term this method Consistency on the Cone Data (CCD) with structural priors.

The normal equation of Eq.3 can be solved by using the conjugate gradient algorithm (CG) method. There are three favorable properties of using CG to solve Eq.3.

First, ω will only have nonzero elements at the edge locations dictated by U, effectively reducing the number of unknowns. This is because in the conjugate gradient algorithm, the candidate solution ω⁽ⁱ⁾ at the ith iteration is repeatedly updated from the previous iteration by adding a new search direction, where the new search direction is obtained from the Krylov subspace K_r(A, b) = span{b, Ab, A²b, …, Aⁱ⁻¹b}, with A = (TF∇⁺U)^HTF∇⁺U = U∇^+HF⁻¹TTF∇⁺U, and b = (TF∇⁺U)^HTFχ₀ = U∇^+HF⁻¹TTFχ₀. It is noted that the Krylov subspace K_r(A, b) is actually spanned by the columns of U. Because U is diagonal and is the leading matrix for both A and b, zero diagonal elements in U will lead to zeros in ω.

Second, the number of iterations needed for full convergence is bounded by the number of non-zero elements in U. This is because A is a semi-positive definite, so the number of iterations needed for convergence is the number of distinct eigenvalues of A (18), which is bounded by the rank of A, which is smaller than the rank of U.

Third, even when the iterations are terminated before full convergence is reached, the solution may still be acceptable. This is because early termination of the conjugate gradient algorithm provides an implicit regularization (19).

METHODS

The phantom experimental data and in vivo datasets were downloaded from the online QSM repository (http://weill.cornell.edu/mri/QSM/Online.zip). The associated parameters for preparation and imaging are briefly described below.

Numerical Simulation

A numerical brain phantom with a size of 256 × 256 × 98 was created based on an actual brain QSM. Constant susceptibility values are assigned to each of the different grey matter regions, which were manually segmented. These regions include the globus pallidus, caudate nucleus, putamen, thalamus, cortical grey matter, cerebrospinal fluid, and white matter, and their values were 0.19, 0.09, 0.09, 0.07, 0.04, 0, and −0.05 ppm respectively. After this, the magnetic field inhomogeneity was calculated according to Eq.1 and the field was converted to phase at 11 evenly spaced TE, with a first TE=2.6ms and a TE spacing of 2.6ms. T2*-decay was not simulated. The signal intensities varied from 1 to 1.6 arbitrary unit (a.u.) in the parenchyma, and the noise standard deviation was 0.02 (a.u.) in the real and imaginary parts, leading to a signal-to-noise ratio (SNR) above 50 for all voxels.

Gadolinium Phantom Experiments

There were five balloons filled with gadolinium solution (Magnevist, Berlex Labrotories, Wayne, NJ) inside the 2% agarose gel phantom. The prepared susceptibility values of the gadolinium balloons were 0.05, 0.1, 0.2, 0.4 and 0.8 ppm. The MR imaging was performed at a 3T scanner (HDx, GE healthcare, Waukesha, WI) using a multi-echo gradient echo sequence. Other imaging parameters were: TE/ΔTE/#TE/TR/FA/BW = 5ms/5ms/8/70ms/15°/480Hz/pixel, matrix size = 130×130×86, and voxel size =1×1×1 mm³. This phantom was scanned in 12 different orientations to obtain a reference standard using Calculation Of Susceptibility through Multiple Orientation Sampling (15). The first orientation was chosen as the reference orientation and subsequent scans were registered to it using FMRIB’s Linear Image Registration Tool (FLIRT) (20–21). The rotational angles ranged from 40° to 140°.

In vivo Human Brain Imaging

This human study was approved by our Institutional Review Board. One healthy subject volunteered for scanning at the same 3T scanner that was used to scan the phantom. The imaging parameters were: TE/ΔTE/#TE/TR/FA/BW = 5ms/5ms10/55ms/15°/260Hz/pixel, matrix size = 256×256×146, voxel size =.9375×.9375×1 mm³, and parallel imaging with a speed up factor of two. Similar to the phantom experiment, a reference standard using COSMOS was obtained by scanning this subject in five different orientations with respect to the B0 field. The first orientation was chosen as the reference orientation and subsequent scans were registered to it using FLIRT. The rotational angles ranged from 16° to 35°.

CCD Implementation

The field map was estimated from the multi-echo datasets using a nonlinear fitting algorithm followed by a magnitude image guided spatial phase unwrapping to resolve ambiguities caused by the limited dynamic range (1/ΔTE) (22), where the magnitude image was obtained by taking the square root of the sum of the squares of all the echoes. After that, Projection onto Dipole Field was used for background field removal (23). To apply CCD, an initial QSM, χ₀, was obtained from one of the existing QSM algorithms (2,6–7,9,11). U was determined by applying the gradient operator to the magnitude image and truncating the y% of voxels with the lowest gradient values. ω was then solved from Eq.3, where CG iterations started with zero as the initial solution and terminated when either the energy of the residual was smaller than 1% of the energy of measurement or when the number of iterations exceeded 40.

To account for potential error in the edge prior U, the edge matched QSM, χ_em, was combined with the original QSM χ₀ in k-space:

$$\begin{array}{l}{\chi }^{\ast }=F^{-1}\left[\frac{1}{\frac{\alpha }{D}+D}\left(\frac{\alpha }{D}F{\chi }_{em}+DF{\chi }_0\right)\right]\\ =F^{-1}\left[\frac{1}{\alpha +D^2}(\alpha F{\chi }_{em}+D^{2}F{\chi }_0)\right]\end{array}$$ (4)

where α is a parameter controlling the weights. This way, the final solution χ^* is a weighted sum of χ_em and χ₀, such that in the conical surface, the weight for χ₀ is at the minimum (equal to 0), and the weight for χ_em is at the maximum (equal to 1). When the weight for χ₀ is at the maximum in the trusted region, the weight for χ_em is at the minimum.

Validation, Comparison, and Influence of Parameter Selection

The effectiveness of the CCD method was evaluated on simulated and experimental data by comparing QSM solutions before and after CCD enhancement. Four QSM reconstruction methods, two of which were k-space based and two of which were image-space, were used in total. Truncated k-space division (TKD)(9) and LSQR (11) were the two k-space based methods used. Note that in the LSQR QSM method, the normal equation of Eq.1 is solved using the LSQR solver proposed in Paige and Saunders (24). Compressed sensing compensated (CSC) inversion (2) and Morphology Enabled Dipole Inversion (MEDI) (6–7) were the two image-space methods used. The various parameters employed in these methods were either chosen from their respective original studies or set to the optimal values suggested by another previous work through exhaustive search (25). Accuracy was evaluated by calculating the normalized root mean square error (RMSE) with respect to the truth in numerical simulation and COSMOS results in phantom and in vivo imaging, respectively. Linear regression was also performed with respect to truth, prepared susceptibility, and COSMOS results in numerical simulation, phantom experiment, and in vivo imaging, respectively. In the human brain, only grey matter was included for both RMSE calculation and regression analysis to avoid anisotropic susceptibility in the white matter, and the grey matter was segmented by applying a threshold (χ = 0) on COSMOS QSM. The slopes and coefficients of determination (R²) from the regression analysis were recorded. All the calculations were performed on a personal laptop equipped with Intel i7 quad-core 2.4GHz CPU and 8 gigabytes of memory. The reconstruction time, RMSE, slope and R² were recorded for all the methods.

In validation and comparison, th = 0.15, y% = 0 and α = 0.1 were used throughout the experiments. We further tested the influence of the parameters by adjusting th from 0.0 to 0.65, y from 0 to 90, and α from 0 to 1 with equidistance.

RESULT

Numerical Simulation

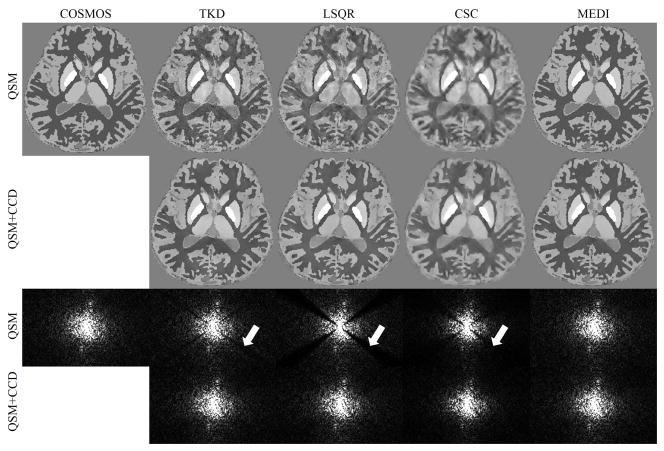
The ground truth, TKD, LSQR, CSC, and MEDI reconstructions and the CCD enhanced results of the numerical phantom in image space and k-space are shown in Fig. 1 and supporting figure s1 (supporting figures can be found in the Supporting Material). The TKD and LSQR results appeared to be noisy in the axial plane compared to the ground truth, but the noise was suppressed with CCD (arrows in Fig. 1). The results of CSC and MEDI before and after CCD enhancement appeared similar. In the k-space view, there was substantial reduction of signal energy near the cone region in TKD, LSQR, and CSC, and the energy was markedly recovered with the CCD enhancement. The k-space views of the MEDI solution and the CCD enhanced MEDI solution were visually identical.

Figure 1.

A comparison between QSM reconstructions before and after CCD enhancement in a numerical simulation. The first row shows the COSMOS results and the solutions of QSM algorithms. The CCD enhanced results are shown in the second row. The third and fourth rows show the sagittal k-space view of the corresponding results in the first and second row. The arrows indicate the signal variation near the conical surfaces.

Gadolinium Phantom

The COSMOS, TKD, LSQR, CSC, MEDI reconstructed phantom QSM, as well as the results after CCD enhancement, are shown in image space and k-space in Fig. 2 and supporting figure s2. There were substantial streaking artifacts in the TKD and LSQR reconstructions, and the streaking was markedly suppressed with CCD. In the k-space view, the signal energy near the conical surface appeared to be amplified in TKD and suppressed in LSQR (arrows in Fig. 2). With CCD enhancement, the signal energy was consistent over the entire k-space. CCD also suppressed the streaking artifacts seen on the CSC result. The MEDI result and the corresponding CCD enhanced result appeared visually identical in both image-space and k-space.

Figure 2.

A comparison between QSM reconstructions before and after CCD enhancement in a gadolinium phantom. The first row shows the COSMOS results and the solutions of QSM algorithms. The CCD enhanced results are shown in the second row. The third and fourth rows show the sagittal k-space view of the corresponding results in the first and second row. The arrows indicate the signal variation near the conical surfaces.

In vivo Human Brain

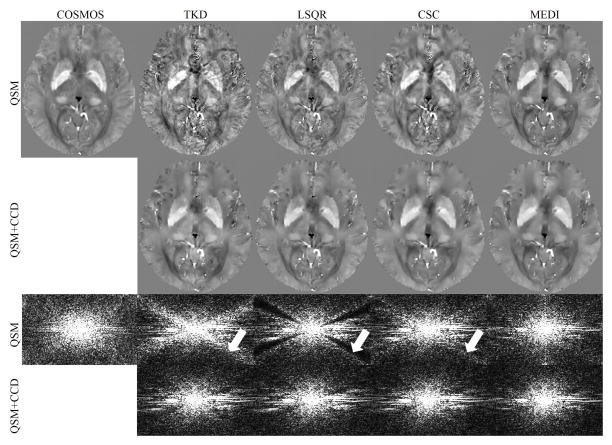
The COSMOS, TKD, LSQR, CSC, and MEDI reconstructed in vivo brain QSM and the CCD enhanced results are shown in image space and k-space in Fig. 3 and supporting figure s3. The TKD, LSQR, and CSC results appeared to be noisy in the axial plane compared to the COSMOS results, and the noise was suppressed with CCD. In MEDI, the result appeared to be smoothed with CCD. There was a loss of cortical details across all the methods. In the k-space view, the signal energy near the conical surfaces appeared to be amplified in TKD and CSC and suppressed in LSQR (arrows in Fig. 3), but the signal energy consistency was improved after CCD enhancement.

Figure 3.

A comparison between QSM reconstructions before and after CCD enhancement in a human brain scan. The first row shows the COSMOS results and the solutions of QSM algorithms. The CCD enhanced results are shown in the second row. The third and fourth rows show the sagittal k-space view of the corresponding results in the first and second row. The arrows indicate the signal variation near the conical surfaces.

Table 1 summarizes the reconstruction time and accuracy of the above results. CCD consistently reduced RMSE for all the methods except for MEDI in simulation, and improved R² for k-space based methods. Regarding the calculation time, although CCD took longer than k-space based methods, it was only about 10% of the overall CSC calculation time and 30% of the overall MEDI calculation time in experimental data. The axial, sagittal, and coronal views of the above results are included in supporting figures, where the suppression of streaking artifacts can be better assessed.

Table 1.

Accuracy and calculation time of the results.

Simulated Brain
	TKD	TKD+CCD	LSQR	LSQR+CCD	CSC	CSC+CCD	MEDI	MEDI+CCD
Slope	0.9	0.92	0.79	0.87	0.68	0.72	0.99	0.94
R2	0.89	0.94	0.82	0.93	0.74	0.83	0.99	0.97
RMSE(%)	1.6	1.15	2.03	1.28	2.46	2.06	0.43	0.79
Time(s)	2	2+137	59	59+137	1515	1515+137	203	203+137
Gadolinium Phantom
	TKD	TKD+CCD	LSQR	LSQR+CCD	CSC	CSC+CCD	MEDI	MEDI+CCD
Slope	0.77	0.81	0.69	0.78	0.6	0.61	0.82	0.81
R2	0.39	0.57	0.42	0.55	0.55	0.6	0.56	0.58
RMSE(%)	5.69	4.16	4.94	4.27	3.86	3.65	4.31	4.13
Time(s)	1	1+53	30	30+53	544	544+53	174	174+53
In vivo Brain
	TKD	TKD+CCD	LSQR	LSQR+CCD	CSC	CSC+CCD	MEDI	MEDI+CCD
Slope	1.1	1.02	0.95	0.93	1.05	0.95	1.05	0.93
R2	0.32	0.48	0.46	0.53	0.4	0.51	0.54	0.55
RMSE(%)	4.9	3.25	3.15	2.7	3.88	2.84	2.92	2.58
Time(s)	2	2+289	189	189+289	2431	2431+289	946	946+289

Influence of parameter selection

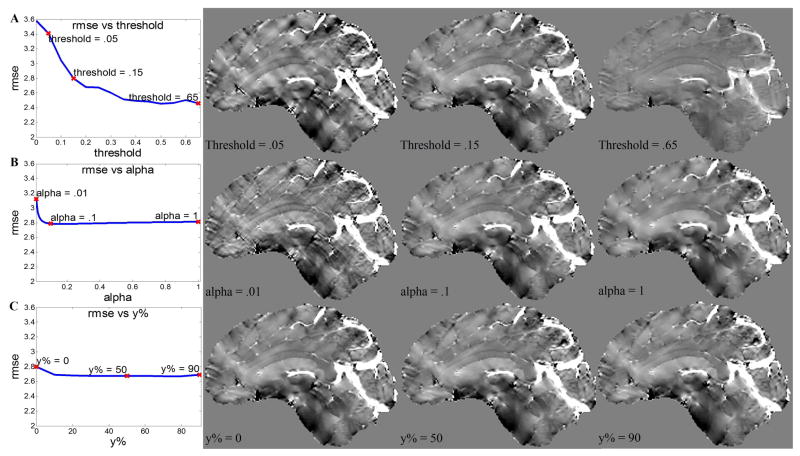
When th increased from 0 to 0.65, the RMSE showed a decreasing trend. Most of the reduction in RMSE was achieved before th reached 0.2. After that, the RMSE decreased slowly, but the susceptibility signal became underestimated, as shown in Fig. 4A.

Figure 4.

Influence of the parameters on the CCD enhanced brain QSM. A) The change of RMSE and image quality over a range of threshold values. B) The change of RMSE and image quality over a range of alpha values. C) The change of RMSE and image quality over a range of y%.

There was a similar trend between α and RMSE. Most of the reduction in RMSE was achieved before alpha reached 0.2. After that, the RMSE almost stopped decreasing, but the image became over-smoothed, as shown in Fig. 4B.

The RMSE did not show great dependence on the choice of y%, especially in the range of 10% to 80%. This is consistent with the image quality as shown in Fig. 4C.

DISCUSSION

In this paper, we presented a consistency on the cone data (CCD) enhancement method to reduce streaking artifacts on QSM by incorporating structural prior. Compared to the initial QSM, the CCD enhancement demonstrated improved quantitative agreement with ground truth and markedly improved image quality for k-space QSM methods, with a moderate computational time.

The CCD enhanced solutions outperform the other k-space based methods because CCD better accounts for the loss of information in dipole inversion. Fundamentally, CCD attempts to enforce consistency by data fitting with all available known information, which has three components: 1) the measured magnetic field, 2) the noise properties of the magnetic field, and 3) the structural information about the susceptibility. Correspondingly, CCD forces consistency across the three components. The data fitting is forced to be consistent with measured MRI data in the trusted region according to the dipole model and noise characteristics, and the susceptibility in the cone region (untrusted region) needs to be consistent with structural information. This way, the loss of information in the original dipole inversion problem is recovered by the introduction of the structural consistency.

In this process, the parameter th controls the size of the non-trusted region. In the non-trusted region, the SNR of the field map may be low, which is expected because the dipole kernel suppresses signal, but not noise, in the cone region. th therefore provides an effective means to exclude data with low SNR. The parameter α controls the contribution of the edge matched QSM χ_em in the final QSM. When α = 0, the final QSM coincides with the initial QSM χ₀ and often has streaking artifacts in k-space based methods. When α = ∞, the final QSM coincides with χ_em. In practice, it is very often that some edges on the susceptibility map are not captured by the prior U, so a large α tends to lead to over-smoothing. In this study, we empirically determined α = 0.1 is able to remove streaking without over-smoothing.

Although CCD improved the k-space based methods to achieve image qualities similar to some state-of-the-art image-space based methods, CCD is different from current image-space based methods in two major ways. 1) Constraints are applied differently. In CCD, the gradient support may be regarded as a hard constraint, i.e., χ_em is strictly spanned by the gradient support. In contrast, the regularization employed in image-space based methods may be regarded as a soft constraint, as the strength of the constraint is dependent on the regularization parameter. 2) The computational burden is lower. CCD only requires solving a single linear optimization problem using conjugate gradient algorithm, and this conjugate gradient algorithm may be further accelerated by applying preconditioning to facilitate convergence (3). CSC and MEDI need to solve nonlinear optimizations. This generally involves solving a series of linear optimization problems, which is much more time consuming. Therefore, combining k-space based methods and CCD may be a time-efficient way to achieve image quality comparable to some image-space based methods.

We also noticed that in the conjugate gradient algorithm that only a few iterations are needed to converge to a good solution, which helps to avoid long calculation times. This may be attributed to the properties of the Krylov subspace that dictate the iterative updates. When solving Ax = b using CG, b may be expressed as a linear combination of eigenvectors v_i of A: b = Σα_iv_i, so $A^{n}b=\mathrm{\sum }{\alpha }_i{\lambda }_i^n{v}_i$. Therefore, directions corresponding to larger eigenvalues of A are preferentially searched for at earlier stages, improving the efficiency of the search. By modeling the susceptibility in the gradient domain where uniform regions have small values in U, the conjugate gradient algorithm visits search directions that tend to introduce variations in uniform regions at a later point. Therefore, early termination actually helped with the solution. This may also explain why the final QSM is not sensitive to the choice of y%, as the small values in U have little contribution when the iteration is terminated.

Conjugate gradient algorithm has been widely applied in numerical optimization and included in many QSM algorithms. The original LSQR method published by Paige and Saunders is a variation of the conjugate gradient algorithm that may have better numerical stability. However, the LSQR QSM method enforces data consistency only through the dipole model, which has low eigenvalues in the cone region, leading to low energy in the reconstruction as well. CG has also been employed in other image space based QSM methods as a subroutine to solve the regularized minimization problem (5–7).

The CCD method may be further extended to remove non-local image artifacts due to undersampling, such as in dynamic spiral or radial MRI. For example, in the temporal resolution acceleration with constrained evolution reconstruction (TRACER) algorithm for spiral MRI(26), only the first frame is fully sampled, and later frames use the first frame as the reference for reconstruction. So for TRACER, it may be possible for a CCD-like method to reconstruct the contrast changes in later frames using the edge information from the first frame. It is also possible to apply this method to dynamic CT data, such as in the prior image constrained compressed sensing (27) method for reconstructing dynamic CT. A CCD-like method might be able to utilize this prior data for reconstructing undersampled dynamic CT to reduce the ionizing radiation to patients.

It should be noted that here, we used a simple dipole model to account for measured magnetic fields in the human brain, where more sophisticated models, such as tensor (28), may be needed. The mismatch between model and data may explain the suboptimal performances (e.g. low R²) of different methods in the human brain. In addition, the success of the CCD method hinges on the quality of the structural information. If the reference image for deriving U is overly smooth, the final reconstruction may also be over-smoothed. However, MRI is an excellent technique for depicting tissue structures. In addition to using the magnitude as the reference image, phase images may be used as well, as phase and susceptibility are strongly correlated in the Laplacian domain: ${\nabla }^{2}f=\frac{1}{3}{\nabla }^2\chi -\frac{{\partial }^2}{\partial z^2}\chi$, where $\frac{{\partial }^2}{\partial z^2}$ is the second order partial differential operator along the direction of the main magnetic field. The structural priors may be further improved by combining the magnitude and phase images (8).

CONCLUSION

We presented a CCD enhancement method to remove streaking artifacts on quantitative susceptibility images by enforcing consistency with known structural information in the dipole cone region. The CCD method is applicable to any existing QSM algorithms. It has been verified in simulation, experimental phantom, and in vivo brain imaging and has been shown to improve the image qualities of k-space based methods.

Supplementary Material

Supp Material

Supporting figure s1. Axial, sagittal, and coronal views of the results in simulation. The first column shows the QSM results, and the second column shows the CCD enhanced results. Third and fourth columns show the corresponding k-space view of the first and second columns.

Supporting figure s2. Axial, sagittal, and coronal views of the results in phantom. The first column shows the QSM results, and the second column shows the CCD enhanced results. Third and fourth columns show the corresponding k-space view of the first and second columns.

Supporting figure s3. Axial, sagittal, and coronal views of the results in in vivo brain. The first column shows the QSM results, and the second column shows the CCD enhanced results. Third and fourth columns show the corresponding k-space view of the first and second columns.