Local integration accounts for weak selectivity of mouse neocortical parvalbumin interneurons

SUMMARY

Dissecting the functional roles of excitatory and inhibitory neurons in cortical circuits is a fundamental goal in neuroscience. Of particular interest are their roles in emergent cortical computations such as binocular integration in primary visual cortex (V1). We measured the binocular response selectivity of genetically-defined subpopulations of excitatory and inhibitory neurons. Parvalbumin (PV+) interneurons received strong inputs from both eyes, but lacked selectivity for binocular disparity. Because broad selectivity could result from heterogeneous synaptic input from neighboring neurons, we examined how individual PV+ interneuron selectivity compared to that of the local neuronal network, which is primarily composed of excitatory neurons. PV+ neurons showed functional similarity to neighboring neuronal populations over spatial distances resembling measurements of synaptic connectivity. On the other hand, excitatory neurons expressing CaMKIIα displayed no such functional similarity with the neighboring population. Our findings suggest that broad selectivity of PV+ interneurons results from nonspecific integration within local networks.

INTRODUCTION

Inhibitory interneurons constitute a minority of cortical cells (~20 percent) (DeFelipe, 2002) and are highly diverse in morphology and molecular composition (DeFelipe et al., 2013; Markram et al., 2004). One particular interneuron subtype, parvalbumin expressing neurons (PV+), account for 35–40 percent of interneurons in mouse neocortex (Gonchar et al., 2007). Their prevalence has made them an ideal target by which to examine the functional connectivity among neocortical excitatory and inhibitory cells. Connectivity measurements from paired intracellular recordings in vitro reveal that PV+ interneurons are densely connected to neighboring excitatory pyramidal neurons, whereas excitatory pyramidal cells are weakly connected to one another (Holmgren et al., 2003; Levy and Reyes, 2012; Oswald et al., 2009; Packer and Yuste, 2011; Shepherd and Svoboda, 2005). While these studies in vitro have demonstrated distinct connectivity patterns, the functional consequences of these patterns are less clear.

If PV+ interneurons indiscriminately pool inputs from neighboring neurons with diverse selectivity, they should exhibit broader response selectivity than nearby excitatory neurons. Evidence from two-photon imaging and targeted-extracellular recordings in vivo in mouse V1 has revealed that inhibitory neurons, and in particular PV+ interneurons, exhibit weaker orientation selectivity (Kerlin et al., 2010; Hofer et al., 2011; Atallah et al., 2012; Wilson et al., 2012; Runyan and Sur, 2013). Such broad selectivity is proposed to result from nearby presynaptic neurons displaying heterogeneous orientation preferences (Dräger, 1975; Sohya et al., 2007; Kerlin et al., 2010; Bock et al., 2011; Runyan and Sur, 2013). It is unclear whether inhibitory neurons are broadly selective for other functional properties, or whether broad selectivity is restricted to orientation selectivity which first emerges in subcortical structures.

An emergent functional property in mammalian V1 is binocularity, which provides information about the depth of objects in the environment. The different vantage points of the two eyes create spatial offsets — or disparities — between retinal images, helping to generate a three-dimensional representation of the visual world (Barlow and Blakemore, 1967; Blakemore, 1969; Hubel and Wiesel, 1973; Joshua, 1970; Nikara and Bishop, 1968; Pettigrew et al., 1968). Individual V1 neurons in primates, carnivores, and rodents are selective for such binocular disparity (Hubel and Wiesel, 1962; Ohzawa and Freeman, 1986; Pettigrew et al., 1968; Poggio and Fischer, 1977; Poggio et al., 1988; Scholl et al., 2013a), whereby visually-evoked responses are strongly modulated by binocular stimulation, relative to monocular stimulation alone. Because this response property emerges in mouse V1, we have an opportunity to use genetic and imaging tools to explore differences in excitatory and inhibitory neurons within the cortical circuit.

The binocular response properties of interneurons in mouse V1 might arise from similar circuits as those proposed for orientation selectivity, but there are several reasons why binocularity may be distinct. First, mice lack a functional organization – or map - for orientation selectivity, but there could nonetheless be an organization for binocular disparity as described in carnivores (Kara and Boyd, 2009). Second, substantial orientation selectivity exists at subcortical structures in the mouse (Marshel et al., 2012; Piscopo et al., 2013; Scholl et al., 2013c) which likely originates from the retina (Zhao et al., 2013a). In contrast, the convergence of ocular inputs and formation of disparity selectivity is considered an emergent cortical computation. Third, inhibitory neurons in the visual cortex have been shown to possess precise fine scale connectivity (Yoshimura and Callaway, 2005), dependent on inhibitory cell type and direct coupling of pyramidal-inhibitory cell pairs. Although fine-scale connectivity of PV+ interneurons might be masked by broad orientation tuning, it is still possible that fine-scale connectivity underlies other functional properties, such as binocular disparity selectivity. Finally, evidence suggests that the circuits for orientation selectivity and binocularity are unrelated (Chino et al., 1994; LeVay and Voigt, 1988; Smith et al., 1997; Cumming, 2002; Read and Cumming, 2004). To uncover the functional organization for binocularity in excitatory and inhibitory neurons, we measured the disparity selectivity of cortical neurons using two-photon calcium imaging in vivo in the binocular zone of mouse V1. Either PV+ inhibitory interneurons or CaMKIIα-expressing excitatory neurons were tagged with a red fluorescent protein to enable visual identification. PV+ inhibitory neurons received stronger input from each eye than did PV− neurons, but, surprisingly, PV+ neurons exhibited weaker disparity selectivity. While we found no organization for disparity preference in mouse V1, we have uncovered a strong relationship between individual PV+ cell selectivity and the neighboring network: PV+ ocular dominance and disparity selectivity biases match the local population. Our findings suggest that broad selectivity of PV+ interneurons results from pooling across neighboring cells with heterogeneous functional responses with a spatial length constant less than 100 microns. The similarity in spatial length constants for disparity and ocular dominance suggests that the PV+ responses result from a circuitry pattern in which PV+ interneurons receive inputs from nearby cells without regard to functional selectivity, whereas excitatory neurons receive functionally-specific inputs.

RESULTS

Binocular integration in PV+ and PV− cells of mouse V1 binocular zone

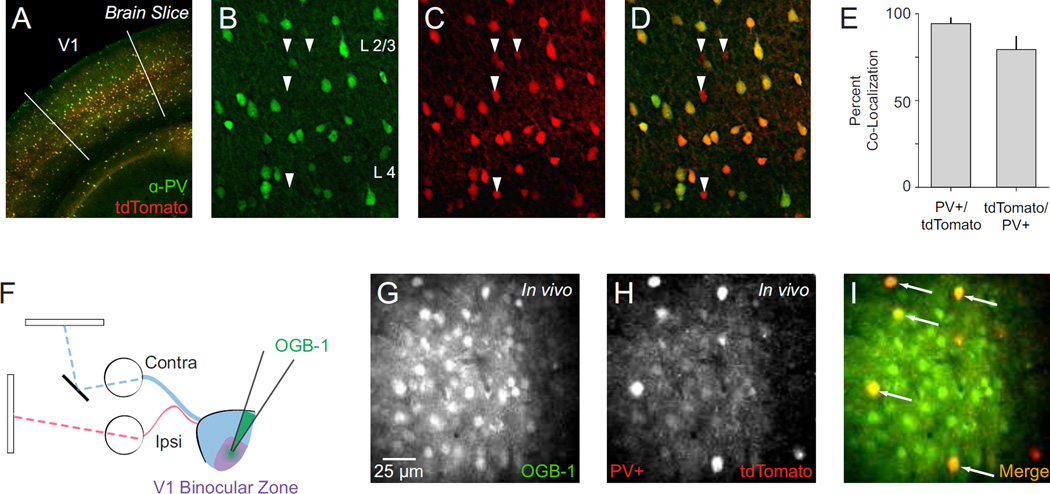
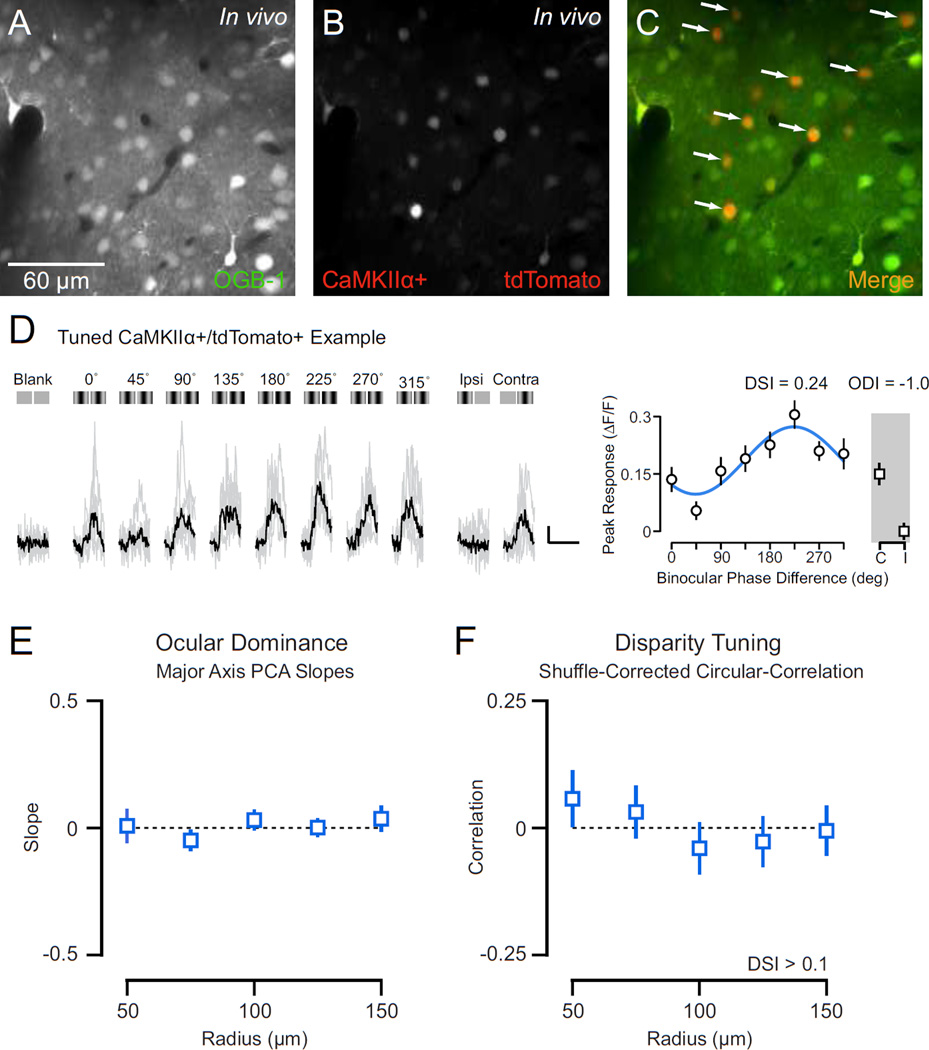
We used two-photon calcium imaging in vivo to measure the binocular disparity tuning of inhibitory parvalbumin expressing interneurons in V1 of anesthetized mice. PV+ interneurons were selectively labeled with the red fluorescent protein tdTomato using PV-Cre knock-in mouse crosses (Supp. Fig. 1). Broad co-localization of tdTomato and endogenous PV in V1 was established using post hoc immunostaining (1274 of 1613 PV+ expressed tdTomato: 79.4 ± 7.8% s.d.; 1274 of 1354 tdTomato cells expressed PV: 94.3 ± 3.6% s.d., n = 3 animals; Fig. 1AE). In each experiment, the binocular zone of V1 was identified using extracellular recordings and a mirror was placed in front of the contralateral eye for dichoptic stimulus presentation (Scholl et al., 2013a, Fig. 1F). Neurons were bulk loaded with the cell-permeable Oregon Green BAPTA-1 AM (OGB-1, see Methods) (Garaschuk et al., 2006; Golshani and Portera-Cailliau, 2008; Kerr and Greenberg, 2005; Stosiek et al., 2003), resulting in a stained volume of approximately 150–450 microns in diameter (Fig. 1G, Supp. Fig. 2A). Fluorescence collected from two-photon excitation (925 nm) was split into red and green channels (see Methods), enabling PV+ and PV− neuron activity to be clearly monitored (Fig. 1G–H, Supp. Fig. 2A–B). Neurons co-labeled with OGB-1 and tdTomato (Fig. 1I, Supp. Fig. 2C, white arrows) were designated PV+ and those containing only OGB-1, a mixture of excitatory and remaining inhibitory neurons, were designated PV−.

Figure 1. Characterization of PV-Cre knock-in mouse and two-photon in vivo imaging of PV+ interneurons.

(A) Representative PV-Cre;Ai14 mouse cortex stained for parvalbumin (PV) with V1 delineated. (B–D) Maximal projections showing co-localization of PV and tdTomato in cortical layers 2–4. In these panels all PV+ neurons are tdTomato+. Arrows indicate tdTomato+/PV− neurons. (E) Summary data on PV-tdTomato co-localization in V1. Counts obtained from cortical layers 2–5. (F) Dichoptic stimulus presentation used to evoke calcium responses. OGB-1 bulk loaded in mouse V1 binocular zone. (G) Two-photon image of OGB-1 In vivo. (H) Same as in (G) for tdTomato. (I) Merged OGB-1 and tdTomato signals. Cells with co-localized fluorescence (putative PV+ interneurons) appear yellow (arrows).

To measure binocular disparity selectivity and monocular responses in individual neurons, we randomly presented dichoptic vertical drifting gratings in both monocular and binocular conditions while recording changes in calcium fluorescence (ΔF/F) at multiple depths (6–15 focal planes) ranging from 150 to 460 microns below the pial surface. Binocular disparity was probed by varying the contralateral stimulus spatial phase, generating eight binocular disparities (0–315 deg phase difference). Across all animals (n = 6, P40 – P60) we identified a total of 338 PV+ neurons, of which 115 (34%) were visually responsive for monocular stimuli and 236 (70%) were visually responsive for binocular stimuli. We identified 3,982 tdTomato⁻ (PV−) neurons, of which 944 (24%) were visually responsive for monocular stimuli and 2001 (50%) were responsive for binocular stimuli.

The observed differences in the number of neurons responsive to monocular and binocular stimuli were in part due to the chosen stimulus parameters. To probe adequately the binocular disparities, a single orientation (90° or 270° orientation) and spatial frequency (0.02 or 0.03 cpd) was used in each experiment. Mouse V1 neurons exhibit a ‘salt and pepper’ pattern of orientation preferences and a wide range of spatial frequency selectivities (Niell and Stryker, 2008; Ohki et al., 2005), so monocular stimuli would be unlikely to stimulate all potential visually-responsive neurons (e.g., those tuned for horizontal gratings). The visual response criterion used (see Methods) required neurons to have significant responses for at least one monocular and binocular stimulus; in some neurons, binocular responses were evident despite a lack of monocular responses.

Binocular selectivity in mouse V1

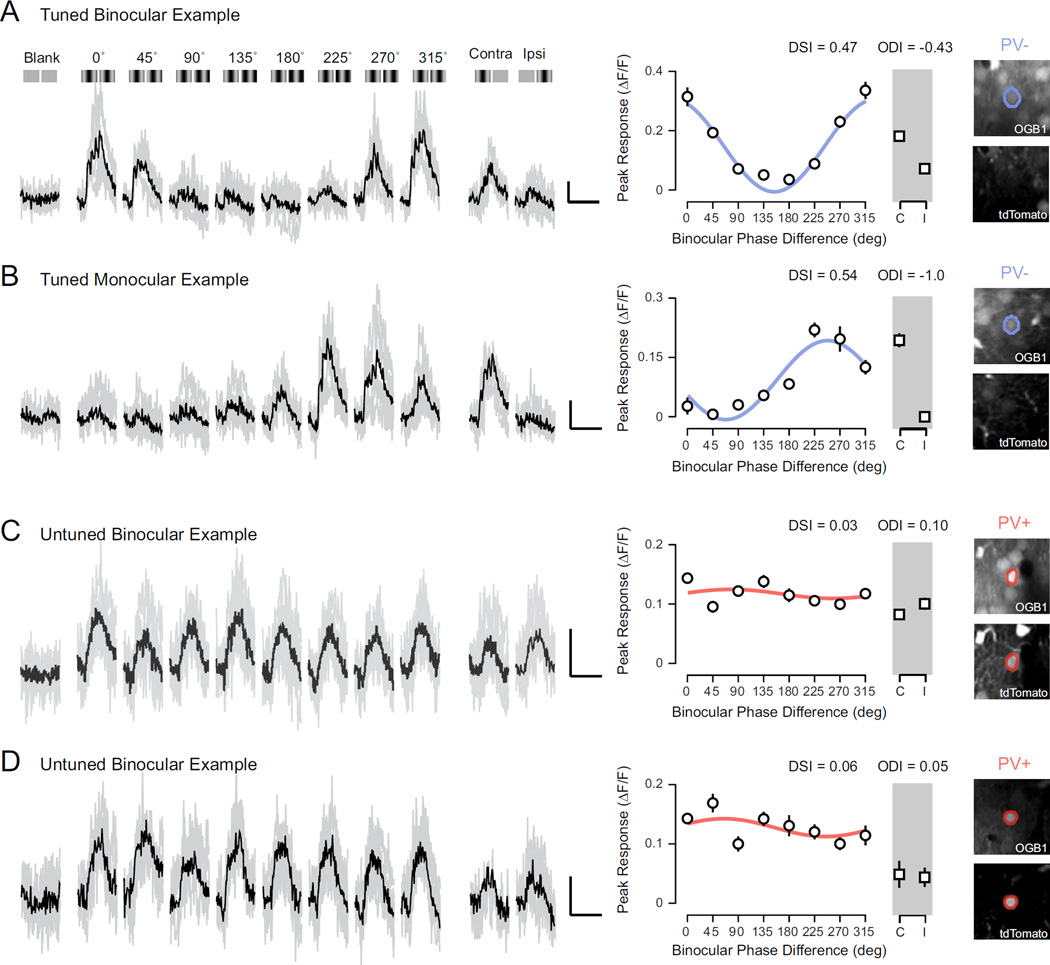
Calcium signals from mouse V1 cells are strongly modulated by binocular disparities, compared to stimulation of either eye alone or blank (mean luminance) trials, in accord with previous reports of spiking activity (Scholl et al., 2013a). For example, in one representative neuron, fluorescence changes evoked by preferred disparity (135° phase difference, ~40% ΔF/F, relative to gray screen stimulation) were much larger compared to monocular stimulation of either eye (contra: ~18% ΔF/F, ipsi: ~10% ΔF/F), while the null disparity (315° phase difference) evoked little change (~10% ΔF/F) (Fig. 2A). We constructed tuning curves from calcium responses evoked for each binocular stimulus as well as for stimulation of each eye alone (Fig. 2A, right). From these tuning curves we computed two metrics: an ocular dominance index (ODI), to compare monocular response from both eyes, where -1 indicates responses exclusively to contralateral stimulation and 1 indicates those exclusive to ipsilateral stimulation (Dräger, 1975; Gordon and Stryker, 1996; Hanover et al., 1999; Priebe, 2008), and the disparity selectivity index (DSI), to quantify the degree of response modulation by binocular stimuli, where 0 indicates no selectivity and 1 indicates high selectivity (Scholl et al., 2013a; 2013b). For the example neuron shown in figure 2A, these metrics describe a binocular, contralaterally biased neuron with robust disparity tuning (ODI = −0.43, DSI = 0.47). We also observed many monocular neurons with strong disparity selectivity, as shown in another example (Fig. 2B; ODI = −1.0, DSI = 0.54).

Figure 2. Functional two-photon imaging of binocular disparity selectivity.

(A) Example calcium responses in a binocular PV− neuron evoked by a range of binocular disparities (0–315 deg), monocular stimulation of each eye, and a mean luminance screen. Individual traces shown in gray and trial-average mean shown in black. Illustration of each stimulus shown above traces. Scale bar indicates 10% change in fluorescence (ΔF/F) and 2 sec duration. Mean ΔF/F and standard error shown in a tuning curve. Tuning curve shown is fit with a cosine function. Two-photon images (right) show fluorescence from OGB-1 (top) and tdTomato (bottom). Note lack of tdTomato. (B) Same as in (A) for a tuned monocular PVneuron. (C–D) Same as in (A) for binocular PV+ interneurons. Note fluorescence signature for both OGB-1 and tdTomato (right).

The responses of PV− neurons were generally modulated by binocular disparities. (Fig. 2A–B, blue). In contrast, PV+ interneurons, while activated by the binocular stimuli, exhibited weak disparity selectivity (Fig. 2C–D, red). Such weak disparity selectivity might be expected for neurons that receive input from only one eye, but we observed this lack of disparity selectivity in PV+ neurons responsive to both eyes alone (Fig. 2C–D).

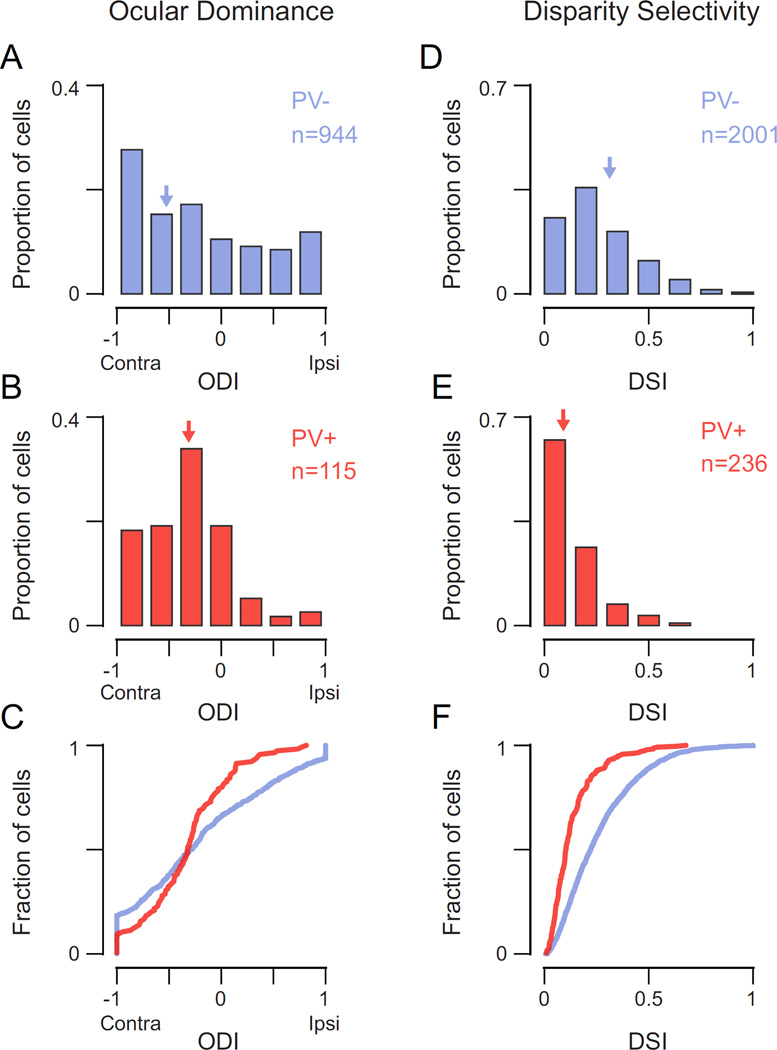
To quantify these observations, we systematically measured ocular dominance and disparity selectivity across our sample recorded neuron populations. A larger proportion of PV+ cells were activated by monocular stimulation of either eye than were PV− cells (64% and 45% respectively, −0.5 < ODI < 0.5), but both populations exhibited a bias for the contralateral eye (Fig. 3A–C) (Yazaki-Sugiyama et al., 2009; Kameyama et al., 2010; Kuhlman et al., 2013; Zhao et al., 2013b). To compare the degree of monocularity in these cell classes, we calculated the absolute value of ODI, or monocularity index (MI). An MI of 0 indicates equal responses to stimulation of each eye, and an MI of 1 indicates response to stimulation of only one eye. PV+ interneurons were significantly more binocular than PV− neurons (MI PV+: median = 0.36, mean = 0.41 ± 0.29 s.d.; MI PV−: median = 0.57, mean = 0.58 ± 0.32 s.d.; p = 0.01, Mann-Whitney test). We consistently observed this difference in monocularity between PV− and PV+ neurons, whether the neurons were grouped together (Fig 3A–C), or analyzed separately for each animal (mean PV− MI = 0.58 ± 0.04 s.d., mean PV+ MI = 0.43 ± 0.08 s.d., n = 6). A similar difference in monocularity was also reported by Kameyama et al. (2010), though they examined all layer 2/3 inhibitory neurons rather than just PV+ neurons. Because PV+ neurons comprise a significant portion of the layer 2/3 inhibitory neurons, it is likely that their dataset was dominated by PV+ neurons.

Figure 3. PV+ interneurons are more binocular but lack disparity selectivity compared to PV− neurons.

(A) Distribution of ocular dominance index (ODI) for PV− neurons (blue). Arrows indicate median value. (B) Same as in (A) for PV+ interneurons (red). (C) Cumulative distribution of ODI for both populations. (D) Distribution of disparity selectivity index (DSI) for PV− neurons (blue). (E) Same as in (D) for PV+ interneurons (red). (F) Cumulative distribution of DSI for both populations.

The pronounced binocularity of PV+ interneurons was coupled with weak binocular disparity selectivity (Fig. 3D–F; PV− DSI: median = 0.26, mean = 0.26 ± 0.17 s.d.; PV+ DSI: median = 0.09, mean = 0.12 ± 0.10 s.d.; p = 0.0001, Mann-Whitney test). Despite receiving more binocular input and disparity selectivity resulting from convergence of right and left eye inputs, PV+ neurons provide fewer signals related to the depth of objects in the world. In summary, PV+ neurons are more binocular by measures of ocular dominance yet exhibit broader disparity selectivity than do PV− neurons.

The relationship between ocular dominance and disparity selectivity is not well understood (Chino et al., 1994; LeVay and Voigt, 1988; Cumming, 2002; Read and Cumming, 2004; Smith et al., 1997), though it has been shown that increased binocularity is associated with greater disparity selectivity (Scholl et al., 2013a; 2013b; Smith et al., 1997). We examined this relationship by comparing monocularity and disparity selectivity and found no relationship between these measures in PV+ neurons (mean slope = 0.04 ± 0.02 s.e., Bootstrapped PCA). There is a weak correlation in PV− neurons (mean slope = 0.16 ± 0.03 s.e., see Methods), but the direction of the relationship was positive, indicating that more monocular neurons are associated with greater disparity selectivity, and the slope accounts for little variance (r² = 0.08). Since calcium signals reflect spiking activity (Stosiek et al., 2003), our finding of little relationship between these quantities is not unexpected (Chino et al., 1994; LeVay and Voigt, 1988; Read and Cumming, 2004; Smith et al., 1997).

Potential signal contamination of PV+ cell calcium responses

It is possible that the differences between PV+ and PV− neurons are confounded by tdTomato fluorescence labeling of these inhibitory neurons. If strong tdTomato fluorescence had contaminated OGB-1 signals, we might expect that baseline fluorescence would be larger, culminating in weaker ΔF/F OGB-1 responses. We therefore compared the ΔF/F of PV+ and PV− neurons with comparable disparity selectivity (DSI < 0.1). PV+ interneurons exhibited greater response amplitudes than PV− neurons (all binocular stimuli: PV+ median ΔF/F = 6.2%, PV− median ΔF/F = 4.3%, p < 0.001, Mann-Whitney test; best binocular stimulus: PV+ median ΔF/F = 8.7%, PV− median ΔF/F = 6.6%, p < 0.001, Mann-Whitney test). Because neurons labeled with tdTomato do not have weaker responses, it is unlikely that contamination from the red channel affects our measurements of selectivity. Another factor that might lead to weaker selectivity is out-of-focus fluorescence from the neuropil leaking into PV+ cell calcium responses. To determine whether neuropil activity contaminated our results, we examined the selectivity of individual neurons relative to the neuropil in surrounding locations. PV+ cells with low and high tdTomato expression exhibited distinct ocular dominance and disparity tuning compared to nearby patches of neuropil (Supp. Fig. 3A–B). We also observed a large fraction of PV+ cells with no evoked activity (28%) relative to nearby patches of active neuropil (Supp. Fig. 3C). Therefore, is does not appear that neuropil activity is driving the differences in selectivity we observe between PV+ and PV− neurons.

A functional organization of binocularity

For PV+ interneurons, the combination of increased binocularity and broad disparity selectivity is puzzling, since binocularity is more likely to be associated with greater disparity selectivity (Scholl et al., 2013a; 2013b; Smith et al., 1997). One potential explanation for these seemingly disparate results is that PV+ cells receive synaptic inputs from a heterogeneous population of presynaptic neurons with a variety of stimulus preferences (Kerlin et al., 2010; Bock et al., 2011; Runyan and Sur, 2013).

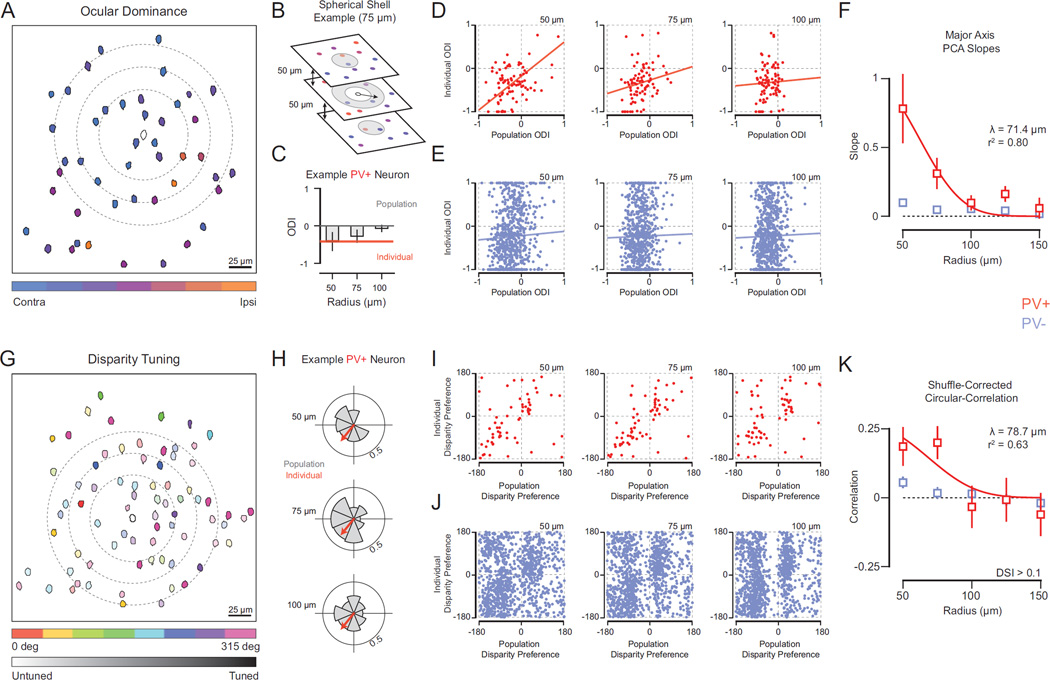
Pooling inputs from nearby neurons with distinct eye preferences might produce responses to stimulation of either eye (e.g., binocularity). Further, if the same neighboring neurons exhibited diverse disparity preferences, then the aggregate input to a target neuron would lack disparity selectivity. While this could account for PV+ neuron selectivity, a distinct connectivity rule would be necessary to account for PV− neuron selectivity. We therefore measured the degree to which functional selectivity of individual neurons is related to their neighbors. We first found mouse V1 neurons exhibit a heterogeneous ‘salt-and-pepper’ organization of ocular dominance (Fig. 4A), similar to previous reports (Mrsic-Flogel et al., 2007). Such heterogeneous organization is also found for disparity preference (Fig. 4G). To measure this spatial heterogeneity explicitly, we measured the correlation between distance and binocular response similarity, finding no relationship (monocularity (MI): Bootstrapped PCA slope = 0.01, p = 1; disparity: circular-linear correlation = 0, p = 1, for cells with DSI > 0.1).

Figure 4. Spatial relationship of PV+ interneuron functional properties and local population aggregate.

(A) Map of ocular dominance in V1 at single focal plane (depth = 420 µm). Cell masks colorcoded based on eye preference or ocular dominance index (ODI). Example PV+ interneuron in center (mask outline). Rings (dashed line) depict subset of radii tested (50 – 100 µm). (B) Example volume (radius = 75 µm) to generate local PV− neuron population. Neurons within boundary (gray shading) comprise this population. Note that at the individual PV+ interneuron’s focal location, volume is shown as ring because the inner sphere volume (radius = 50 µm) is excluded. For distances greater than 50 µm (a sphere), we restricted regions to avoid drawing from the same local population at different distances (spherical shells). (C) Example PV+ interneuron ODI (orange) and population average ODI at different radii (gray) (50 – 100 µm). (D) Plots of individual PV+ interneuron ODI and local population average (red) at different radii. Linear fits depict major axis PCA slope and y-intercept computed from Bootstrapped PCA. (E) Same as (D) for PV− neurons (blue). (F) Spatial dependence of relationship between individual cell and local populations. PV+ interneuron (red) and PV− neuron (blue) Bootstrapped PCA across radii. Spatial length constant (λ) computed from an exponential fit (red line). (G) Map of binocular disparity selectivity at single focal plane (depth = 400 µm). Cell masks color-coded based on disparity preference (0–315 deg). Color hue indicates disparity selectivity index (DSI). Example PV+ interneuron is shown in the center (mask outline). Rings (dashed line) depict subset of radii tested (50–100 µm). (H) Disparity selectivity in individual neurons are decomposed into polar vectors with an amplitude (DSI) and angle (disparity preference). Shown is an example PV+ interneuron disparity vector (orange arrow) and polar histogram of surrounding PV− vectors (gray) at three different distances (50 – 100 µm). (I) Plots of individual PV+ interneuron disparity preference and population average disparity preference for different radii (red). (J) Same as (i) for PV− neurons (blue). The observed biases in population average disparity preferences are due to non-uniform distributions of disparity preference within individual animals. However, because the exact position of the stimulation monitors and eye positions are different for each experiment, we do have an interpretation for these biases across subjects. (K) Spatial dependence of relationship between individual cell and local populations. PV+ interneuron (red) and PV− (blue) neuron shuffled-corrected circular-correlations shown across radii. Spatial length constant (λ) computed from an exponential fit (red line).

Integrating signals from heterogeneous populations of nearby neurons could give rise to the binocular selectivity of PV+ neurons. If so, the variation in selectivity observed in PV+ neurons should be related to local population variations. We therefore measured the relationship between individual neuron’s selectivity and the neighboring PV− neuron aggregate. For each PV+ and PV− neuron, we measured the ODI, then defined a spherical volume around that cell’s location to encapsulate a population of PV− cells (Fig. 4A,B dashed lines; see Methods). These spherical volumes extended both across 2-dimensional images we measured at each depth as well as across depth. We gauged the relationship between individual neurons and spatial distance over which integration occurs by increasing the radii (50 – 150 µm) defining each of PV-population (75 µm example shown in Fig. 4B, see Methods) and computing the average selectivity within these volumes.

PV+ interneuron ocular dominance closely matched the local aggregate ocular dominance within 50 microns, both for individual example cells (Fig. 4C) and across our population (mean slope = 0.78 ± 0.25 s.e., n = 86, Bootstrapped PCA; Fig. 4D, left). This relationship is consistent with the idea that PV+ interneurons integrate inputs from nearby cells. As we increased the distance separating PV+ cells and neighboring populations, the similarity between individual ODI and the population average systematically decreased (Fig. 4D,F). This relationship was only significant for the nearest PV− populations (50–75 µm, p < 0.01), in comparison to measurements from shuffled populations of PV− cells (see Methods). From these data (Fig. 4F), we then extracted a spatial length constant (λ) describing the functional relationship of PV+ interneurons within the local network, yielding λ of 71.4 microns (r² = 0.80).

One potential consideration with these data is that because neurons in the same focal plane were imaged simultaneously, shared signal correlation might contribute to any spatial relationship we uncovered. We therefore examined the spatial relationship of ocular dominance while excluding surrounding neurons within the same focal plane from local populations. Under this constraint, PV+ interneurons still strongly matched population averages for smaller radii (Supp. Fig. 4A). PV+ interneurons within the same focal plane also exhibited a distance-dependent relationship with population averages (Supp. Fig. 4B). A second consideration is that out-of-focus fluorescence signals from surrounding neuropil might contaminate the relationship between PV+ interneurons and local populations. To address this concern we performed our local integration analysis on neuropil patches: cell-sized areas with only out-of-focus OGB-1 fluorescence present (Supp. Fig. 5A). Here we found no relationship between individual neuropil patches and local population averages (n = 480 patches, Supp. Fig. 5B–E).

In contrast to PV+ interneurons, the individual ODI of PV− neurons and local population averages were generally unrelated (Fig. 4E). A weak, but significant, relationship was evident for neighbors with 50 microns (mean slope = 0.10 ± 0.02, n = 717, Bootstrapped PCA, p < 0.01). Across all other distances, the ODI of PV− neurons showed no significant relationship with population aggregates and no spatial dependence (p > 0.5) (Fig. 4F). Limiting our analysis to PV− cells with a similar ODI as PV+ neurons (−0.5 < ODI < 0) did not reveal a spatial dependence (Supp. Fig. 6A–B), and these measurements were indistinguishable from shuffled populations (p > 0.10).

Since PV− neurons are comprised of both excitatory and non-PV inhibitory cell subtypes, we sought to determine whether properties of PV− neurons (Fig. 4F, Supp. Fig. 4B) reflected those of excitatory neurons. To identify excitatory neurons, we infected wild-type adult mice with a recombinant adeno-associated virus (rAAV) supporting the expression of a nuclear-localized tdTomato red fluorescent protein from a truncated CaMKIIα promoter (Kalderon, 1984; Dittgen, 2004). Injections were made in the V1 binocular zone using a diluted virus to reduce the density of labeled cells (see Methods). We then loaded OGB-1 to measure binocular responses in individual tdTomato+ and nearby tdTomato- neurons (Fig. 5A–C). Individual excitatory neurons exhibited robust calcium responses to monocular (n = 285) and binocular (n = 306) visual stimuli, as observed in an example cell (Fig. 5D). From these data we examined the relationship between individual excitatory neuron ocular dominance and local population aggregate OD. Here, surrounding populations were comprised of both tdTomato+ and tdTomato- neurons. Like PV− neurons, the ocular dominance of individual excitatory neurons did not reflect the population average even at the shortest distance measured (radius = 50 µm; mean PCA slope = 0.01 ± 0.07 s.e., n = 50; Fig. 5E). Therefore, in contrast to PV+ interneurons, the ocular dominance of V1 excitatory neurons is not related to heterogeneity within local cortical networks.

Figure 5. Spatial relationship of excitatory neuron functional properties and local population aggregate.

(A) Two-photon image of OGB-1 in vivo. (B) Same as in (A) for tdTomato. (C) Merge of OGB-1 and tdTomato. Cells with co-localized fluorescence (putative CamKIIα+ excitatory neurons) appear yellow (arrows). (D) Example calcium responses in a tdTomato+/CamKIIα+ excitatory neuron evoked by a range of binocular disparities (0–315 deg), monocular stimulation of each eye, and a mean luminance screen. Individual traces shown in gray and trial-average mean shown in black. Illustration of each stimulus shown above traces. Scale bar indicates 10% change in fluorescence (ΔF/F) and 2 sec duration. Mean ΔF/F and standard error shown in a tuning curve. Tuning curve shown is fit with a cosine function. (E) Spatial dependence of relationship between individual excitatory neuron ocular dominance and local populations. Shown is mean Bootstrapped PCA slope and standard error across radii. (F) Spatial dependence of relationship between individual excitatory neuron disparity preference and local populations. Shown are shuffled-corrected circular-correlations across radii.

We next asked whether this functional space constant for PV+ interneurons exists for other receptive field properties. Given the ‘salt and pepper’ organization of disparity preference (Fig. 4G) we performed the same volumetric population analysis as for ODI. We decomposed each cell’s disparity selectivity into a polar vector with an angular direction (disparity preference) and normalized amplitude (DSI). An example PV+ interneuron vector and polar distribution of neighboring PV− neurons is shown for three distances (50 µm sphere and two spherical shells of radii 75 µm and 100 µm, Fig. 4H). To calculate the population bias we computed a vector average (see Methods). Our analyses excluded individual PV+ and PV− neurons with little response modulation to binocular disparities (DSI < 0.1). Despite the weak disparity selectivity of PV+ interneurons, their individual angular biases are similar to that of nearby populations (Fig. 4I). To quantify the relationship between individual PV+ disparity vector angle and population vector angles we computed a shuffle-corrected circular-correlation coefficient (Batschelet, 1981, see Methods). PV+ interneuron disparity preference was significantly correlated with populations composed of the nearest neighbors (radius = 50 µm; r = 0.19 ± 0.07 s.e., n = 63). PV+ interneurons also exhibited spatial dependence in their correlation to population vector angles (Fig. 4K). The exponential fit to these data resulted in a similar λ as for ODI (λ = 78.7 microns) albeit capturing less variance (r² = 0.63).

For PV− neurons, we found little relationship between population biases and the disparity preference of individual cells (Fig. 4J–K). A shuffled-corrected circular-correlation was only significant for the nearest neighboring neurons (radius = 50 µm; r = 0.05 ± 0.02, n = 1090). This lack of a relationship between individual PV− neurons and local populations was more evident when restricting our analysis to cells with disparity tuning comparable to PV+ interneurons (0.1 < DSI < 0.2, Supp. Fig. 6C–D). Similar to PV− neurons, the disparity preference of individual excitatory neurons expressing CaMKIIα also did not reflect nearby population averages and exhibited no significant spatial-relationship (Fig. 5F). Overall, we found that individual variations in PV+ interneuron ocular dominance and disparity preference closely match average selectivity bias of nearby neurons, whereas excitatory neurons, which constitute the majority of our PVrecords, exhibit selectivity unrelated to local network biases.

DISCUSSION

Parvalbumin-expressing (PV+) inhibitory interneurons exhibit a distinct ocular dominance profile, disparity selectivity, and functional organization from the remaining neuronal population. PV+ neurons are less monocular than excitatory neurons (Yazaki-Sugiyama et al., 2009; Kameyama et al., 2010; Kuhlman et al., 2013; Zhao et al., 2013b) and yet are only weakly selective for binocular disparity. The weak selectivity of individual PV+ interneurons is consistent with the aggregate selectivity of neighboring neuronal populations, but only within a 100 micron radius. We did not find any relationship between the selectivity of excitatory neurons and their local population. The functional space constant of PV+ interneurons reveals a connectivity with neighboring cells, potentially reflecting a generalized function of this cell type across neocortical circuits.

Spatial integration of PV+ interneurons

The binocular responses we observed in PV+ interneurons are similar to the weakly-tuned responses that these neurons exhibit for orientation and direction selectivity (Hofer et al., 2011; Kerlin et al., 2010; Runyan and Sur, 2013). Because this selectivity differs from that of excitatory neurons, PV+ cells might play a specific role in cortical circuitry, integrating sensory drive to modulate cortical response gain without affecting individual cell tuning properties (Atallah et al., 2012), potentially through divisive inhibition (Wilson et al., 2012). Our measurements of binocular disparity in PV+ neurons reveal a similar lack of selectivity, but also demonstrate an organization of their synaptic inputs that accounts for this weak selectivity.

Consistent with our observations, local cortical networks have been considered to be a factor in defining PV+ neuron orientation selectivity. Global population biases from large cortical regions have been shown to match the orientation preference of individual PV+ interneurons (Kerlin et al., 2010; Runyan and Sur, 2013). Although the similarity in orientation preference between individual PV+ cells and surrounding populations has been examined for nearby neighboring neurons (Runyan and Sur, 2013), we have been able to characterize the relationship between PV+ selectivity and comparably sized local populations of PV− neurons. Our analysis reveals that PV+ interneurons integrate inputs over a limited cortical area, less than 100 microns. Cortical heterogeneity beyond this distance appears to be unrelated to PV+ selectivity. All of these studies indicate that local spatial integration is a general principal of PV+ neuron connectivity.

Cortical wiring of excitatory and inhibitory cells

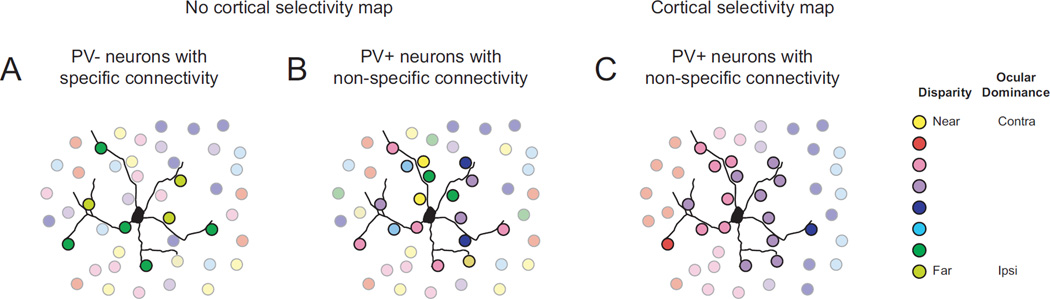
Our functional analysis of spatial integration in PV+ interneurons, in corroboration with previous studies using paired recordings in vitro, suggests that PV+ interneurons integrate synaptic inputs from nearby neurons without regard for the functional selectivity of those inputs (Holmgren et al., 2003; Levy and Reyes, 2012; Oswald et al., 2009; Packer and Yuste, 2011; Shepherd and Svoboda, 2005). Excitatory neurons integrate inputs within a similar cortical distance, but with a lower connection probability. One critical feature appearing to guide connection probability is whether excitatory neurons share functional selectivity (Ko et al., 2013; 2011). Whereas the cortical pattern of connectivity for excitatory neurons is built upon functional specificity, PV+ interneuron connectivity appears to be built upon a lack of specificity (Bock et al., 2011). These differential connectivity patterns suggest different wiring rules for excitatory and inhibitory cells (Fig. 6A–B).

Figure 6. Differential connectivity patterns for excitatory and inhibitory cells.

(A) Excitatory neurons (PV−) are connected to neighboring neurons of similar functional selectivity in a ‘salt-and-pepper’ network. Colors represent disparity or eye preference. (B) Inhibitory neurons (PV+) connect broadly to nearby neurons, regardless of functional selectivity, in a ‘salt-and-pepper’ network. (C) Inhibitory neurons (PV+) in a functionally organized neocortical circuit could follow the same wiring rule as in (B), but it would result in functionally selective PV+ neurons.

Not only was the functional spatial length constant (λ) for ocular dominance and binocular disparity preference comparable (71.5 µm and 78.7 µm, respectively), but these values are similar to estimates of spatial dependence of synaptic connection probability from slice physiology. Levy & Reyes (2012) recover a λ of 92 µm for the probability of an excitatory pyramidal cell synapsing onto a PV+ interneuron in the auditory cortex. They also determine that the inverse connection has an almost identical λ (90 µm). This second measurement has been derived by another group in somatosensory and frontal cortex (Packer and Yuste, 2011), but they reported a slightly higher value (124 µm) and did not measure synaptic connectivity of excitatory neurons onto PV+ interneurons.

The link between our functional λ and that measured in slice suggests PV+ cells pool the overall activity of local populations (Fig. 6B), which could act as a gain control on responses of postsynaptic targets. Because mouse V1 lacks functional organization beyond retinotopy, PV+ interneurons only provide a signal reflecting the population activity for a spatial location. In contrast, orientation selectivity and disparity selectivity are spatially organized across V1 in carnivores (Hubel and Wiesel, 1963; Kara and Boyd, 2009; Nauhaus et al., 2012a; Ohki et al., 2005; 2006), PV+ cells should also be selective for orientation and disparity (Fig. 6C). The same could be expected for PV+ interneurons in primate V1, at least for orientation selectivity and spatial frequency (Bosking et al., 1997; Essen and Zeki, 1978; Hubel and Wiesel, 1963; Nauhaus et al., 2012b). In fact, PV+ interneurons within mouse primary auditory cortex, which is organized tonotopically, exhibit a similar tuning bandwidth as PV− cells (Moore & Wehr, 2013), an expected outcome if cortical PV+ cells follow this simple wiring rule. PV+ neuron selectivity in primates and carnivores may depend on their location within the cortical map. For example, PV+ neurons located near pinwheels centers may be less selective, and may contribute to excitatory neuron responses in a manner distinct from PV+ interneurons within iso-orientation domains (Schummers et al., 2002). In this way, the same spatial connectivity rule for PV+ cells could result in diverse functional properties in the mammalian neocortex.

METHODS

All procedures were approved by The University of Texas at Austin Institutional Animal Care and Use Committee.

Transgenic Mouse Construction

PV-Cre knock-in mice were generated using an IRES targeting construct to insert the Cre recombinase coding sequence into the 3′ UTR of the mouse PV gene (Supp.Fig. 1A). The construct also contained a PGK1-NeoR positive selection cassette flanked by frt sites within the homologous arms and an RNAPII-DTA negative selection cassette following the 3’ homologous arm. The targeting construct was electroporated into hybrid C57BL/6J-129/SV stem cells, with correct recombinants selected with G418 and screened by Southern blot. Founders were crossed to ROSA26-FLP deleter mice to excise the NeoR cassette. F1 progeny were backcrossed repeatedly to C57BL/6J to reproduce the C57BL/6J genetic background. C57BL/6J content of the resulting mice was confirmed by microsatellite testing (Charles River Laboratory). To generate experimental animals, homozygous PV-Cre mice were crossed to ROSA26-tdTomato Cre-reporter mice (Ai14) (Madisen et al., 2010), selectively labeling PV+ interneurons with tdTomato in the hemizygous PV-Cre;Ai14 progeny.

rAAV Infection

rAAV:CamKIIα-nls-tdTomato was assembled using a helper-free system (Stratagene) as serotype 2/1 (rep/cap) and purified on sequential cesium chloride gradients as previously described (Grieger, 2006). Viral titer was at least 10¹¹ particles/µl, diluted (1/20 – 1/50 in buffer solution) prior to cortical injection to reduce labeled neuron density. Surgery was performed on adult C57/BL6 mice under isoflurane anesthesia (1 – 2 % in O₂). Small craniotomies were performed in three separate locations over the V1 binocular zone using an F/G dental drill bit. A fine glass injection pipette (5–10 um tip diameter) containing diluted viral suspension was inserted through the resulting opening using a stereotaxic manipulator. 300 nL of virus was injected in the cortical region of interest using an electronic pump (Nanoject II, Drummond). The pipette was left in place for 10–15 minutes to allow virus to disperse. After the procedure, the micropipette was removed and the incision sutured. Two-photon imaging experiments were performed 3 weeks following injection.

Immunohistochemical Analysis of PV-Cre Neurons

Brains of PV-Cre;Ai14 animals were perfused and post-fixed overnight with 4% paraformaldehyde. Non-consecutive 50 µm sections were incubated for 24 h with mouse anti-PV monoclonal antibodies (PV 235, Swant; diluted 1:1000). tdTomato expressing neurons in 4 independent fields of view within V1 were examined for the presence of PV staining on a fluorescence microscope (Axioscope, Carl Zeiss). Image z-stacks were captured using an Apotome attachment and evaluated for co-localization of red and green signals using ImageJ. Most (94.3%) PV+ neurons expressed tdTomato, whereas ~80% tdTomato neurons were PV+ (total = 1274/1613 cells, n = 3 mice). This discrepancy could be explained by developmental changes in the level of PV expression across neurons of the cortex or by differences in the sensitivities of the two detection methods. Similar variations have been observed in other PV-Cre transgenic mouse lines, especially among layer 5 cortical neurons (Madisen et al., 2010). Despite the potential for developmental and other caveats, staining overlap within cortical layers 2–3, where imaging took place, was notably higher (not shown).

Physiology

Physiological procedures for mouse recordings were based on those previously described (Scholl et al., 2013a). Experiments were conducted using adult animals (P40 – P60). Mice were anesthetized with intraperitoneal injections of 1000 mg/kg urethane (n = 6 transgenic animals, n = 2 AAV-infected animals) and 10 mg/kg chlorprothixene. Brain edema was prevented by intraperitoneal injection of 10 mg/kg dexamethasone. Animals were warmed with a thermostatically controlled heat lamp to maintain body temperature at 37°C. A tracheotomy was performed. The head was placed in a mouse adaptor (Stoelting) and a craniotomy and durotomy were preformed over visual cortex. Eyes were kept moist with a thin layer of silicone oil. V1 and binocular zone were located and mapped by multi-unit extracellular recordings with tungsten electrodes (1 mΩ, Micro Probes). The V1/V2 boundary was identified by the characteristic gradient in receptive locations (Dräger, 1975; Métin et al., 1988). Eye drift under urethane anesthesia is typically small and results in a change in eye position of less than 2 degrees per hour (Sarnaik et al., 2014).

Dye Loading and Two-Photon Imaging In Vivo

Bulk loading of a calcium sensitive dye under continuous visual guidance followed previous protocols (Garaschuk et al., 2006; Golshani and Portera-Cailliau, 2008; Kerr and Greenberg, 2005; Stosiek et al., 2003). A cortical region with central receptive fields in the V1 binocular zone was mapped with extracellular methods prior to loading. Dye solution contained 0.8 mM Oregon Green 488 BAPTA-1 AM (OGB-1, Invitrogen) dissolved in DMSO (Sigma-Aldrich) with 20% pluronic acid (Sigma-Aldrich) and mixed in a salt solution (150 mM NaCl, 2.5 mM KCl, 10 mM HEPES, pH 7.4, all Sigma-Aldrich). Either 40–80 µM Alexa Fluor 594 (Invitrogen) or 125 µM Sulforhodamine 101 (Sigma-Aldrich) was also included for visualization during and immediately after loading. Patch pipettes (tip diameter 2–5 µm, King Precision Glass) containing this solution were inserted into the cortex to a depth of 250–400 µm below the surface with 1.5% agarose (in saline) placed on top the brain. The solution was carefully pressure injected (100–350 mbar) over 10–15 minutes to cause the least amount of tissue damage. OGB-1 is weakly fluorescent before cellular-internalization, so the amount of dye injected was inferred through the red dye visualized through the two-photon microscope. To ensure full loading we waited 1 hr before adding a glass coverslip for imaging. Metal springs were fastened on the attached head plate to place pressure on the glass coverslip and reduce brain pulsations. Fluorescence was collected with a custom-built two-photon resonant mirror scanning microscope and a mode-locked (925 nm) Chameleon Ultra Ti:Sapphire laser (Coherent). Excitation light was focused by a 40× water objective (0.8 numerical aperture, Nikon). Collected light was split into red and green channels with a dichroic prior to the photo-multiplier tubes (PMTs). Images were obtained with custom software (Labview, National Instruments). A square region of cortex 300 µm wide was imaged at 256×455 pixels with a frame rate of 30 Hz. A rotatable objective was used to image normal to the cortical surface. In all experiments multiple focal planes, separated by 20–25 µm, were used to collect data, starting around 150 µm below the cortical surface. Before each experiment neuron drift was measured over a 2–3 min period. If drift occurred then glass coverslip and agarose were readjusted to ensure no drift during stimulus protocol (7–10 minutes each focal plane).

Stimulus Presentation

Visual stimuli were generated by a Macintosh computer (Apple) using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) for Matlab (Mathworks) and presented dichoptically using a Sony video monitors (GDM-F520) placed 38 cm from the animal’s eyes. The video monitors had a non-interlaced refresh rate of 100Hz and a spatial resolution of 1024×768 pixels, which subtended 40×30 cm (58×46 deg). The video monitors had a mean luminance of 40 cd/cm². Square-wave drifting gratings (38 deg diameter, 0.02–0.04 spatial frequency, 100% contrast, 2–4 Hz temporal frequency) were presented for 1.5–2 sec. Stimulus duration was typical for measurements in V1 of mouse (Gao et al., 2010; Niell and Stryker, 2008), as neurons in mouse V1 show stronger response adaptation. Square-wave gratings were used during all experiments. Each stimulus was followed by a 3 sec blank (mean luminance) period. Spontaneous activity was measured during blank (mean luminance) periods interleaved with binocular and monocular drifting grating stimuli, all presented in a pseudorandom sequence. Binocular phase differences (disparities) ranged 0–315 deg. During imaging sessions, each stimulation protocol was repeated 6–7 times at each focal plane. The microscope objective and photomultiplier tubes were shielded from stray light and the video monitors.

Data Imaging Analysis

Images were analyzed with custom Matlab software (Mathworks). Cells were identified by hand from structure images based on size, shape, and brightness. Cell masks were generated automatically following previous methods(Nauhaus et al., 2012a). Glia were easily avoided due to their different morphology from both OGB-1 filled neurons and PV+ interneurons labeled with tdTomato. PV+ interneurons were identified by selecting OGB-1 filled neurons with co-localized tdTomato fluorescence. Time courses for individual neurons were extracted by summing pixel intensity values within cell masks in each frame. Responses (F_t) to each stimulus presentation were normalized by the response to the gray screen (F_o) immediately before the stimulus came on:

$$\mathrm{\Delta }F/F=(F_t-F_o)/F_o$$

For each stimulus, the mean change in fluorescence (ΔF/F) was calculated in a 0.5 sec window, centered around the global average peak calculated by averaging responses to all stimulus conditions and trials. Visually responsive cells were identified if at least one monocular and one binocular stimulus response had:

$$({\mu }_{\mathit{\text{stimulus}}}-{\mu }_{\mathit{\text{blank}}})/({\sigma }_{\mathit{\text{stimulus}}}+{\sigma }_{\mathit{\text{blank}}})\ge 1$$

Here μ_stimulus refers to the mean stimulus evoked response, μ_blank refers to the mean spontaneous activity, σ_stimulus is the stimulus evoked response standard error, and σ_blank spontaneous activity standard error. Additionally, identified responses to each monocular and binocular stimulus were required to be larger than neuropil activity (>95% confidence interval). These requirements yielded clear visual responses that were verified by eye before subsequent analysis.

Mean changes in fluorescence from visually responsive neurons were used to generate tuning curves for binocular disparity. Tuning curves were fit with a cosine-wave function for illustration:

$$R(\varphi )=(e^{(i(\varphi -{\varphi }_{\mathit{\text{pref}}}))}-e^{(-i(\varphi -{\varphi }_{\mathit{\text{pref}}}))})\frac{\alpha }{2i+\mathit{\text{spont}}}$$

Here α is the modulation amplitude, ϕ are the binocular phase differences presented, ψ is the disparity phase preference, and y is the fit. To measure ocular dominance we used a standard metric (Dräger, 1975; Gordon and Stryker, 1996; Hanover et al., 1999):

$$ODI=\frac{R_{\mathit{\text{ipsi}}}-R_{\mathit{\text{contra}}}}{R_{\mathit{\text{contra}}}+R_{\mathit{\text{ipsi}}}}$$

Here R_contra and R_ipsi represent calcium responses from the contralateral and ipsilateral eyes, respectively. To measure monocularity, we took the absolute value of ODI, resulting in a nonsymmetric metric of binocularity where 0 is binocular and 1 is monocular. Disparity selectivity was quantified using a normalized vector strength (Ringach et al., 2002; Scholl et al., 2013a; 2013b; Swindale, 1998):

$$DSI=\frac{\sqrt{{\left(\sum _{\varphi }{R}_{\varphi }\text{sin}\varphi \right)}^2+{\left(\sum _{\varphi }{R}_{\varphi }\text{cos}\varphi \right)}^2}}{\sum _{\varphi }{R}_{\varphi }}$$

Here R_ϕ is the response to each binocular phase (ϕ) presented.

Local Network Analysis

Within each imaging session, the total number of visually responsive PV+ and PV− (monocular and binocular) were identified along with their spatial location and depth. Spatial positions in x–y were converted from pixels into microns. At each neuron’s 3-dimensional spatial location, spherical volumes were projected outwards to determine different local populations of PV− cells to average. Local populations for each neuron were drawn from 5 distances: 50,75,100,125, and 150 µm. For a distance of 50 µm we used a spherical volume. For distances greater than 50 µm, we restricted regions to avoid drawing from the same local population at different distances (spherical shells). Each sphere’s volume was calculated by:

$${\mathit{\text{Vol}}}_j=\frac{4}{3}\pi (r_j^3-r_{j-1}^3),$$

where j indicates the specific radius. In this way, the radius was a sphere and all larger radii were hollowed-shells. This was done to sample from each PV− neuron only once. There was ~2-fold increase in volume with each subsequent radius (for example: Vol_50µm = 1.67×10⁵ µm³ and Vol_75µm = 3.96×10⁵ µm³) Individual cells were only used for analysis if at least 50 microns from the image edges. This restriction was applied to all individual cells (PV+, PV−, and CaMKIIα+). It ensured that for all cells, we could accurately measure the local population average for the smallest distance tested (50 microns). At least 3 cells were required to generate a local population within a given volume, otherwise that individual cell was excluded from further analysis.

For ocular dominance, the individual cell’s ODI was compared to the population average ODI:

$$OD{I}_{\mathit{\text{pop}}}=\sum ^{n}OD{I}_n$$

The relationship between individual ODI and population average ODI was quantified with a Bootstrapped PCA (see below).

For binocular disparity, tuning of each cell was converted into a polar vector, where the amplitude was defined by the DSI and the angle was defined by the disparity preference (ψ). The relationship between disparity preference difference and distance (in microns) for pairs of cells was quantified by computing a circular-linear correlation coefficient (Zar, 1999; Berens, 2009). Population vectors were computed with a vector average:

$$v_{\mathit{\text{pop}}}=\frac{1}{n}\sum ^n{R}_n{e}^{i{\psi }_n},$$

where R_n is the DSI and ψ_n is the disparity preference of each PV− neuron (n) in the population. A Bootstrapped PCA (see below) was used to quantify the relationship between an individual cell’s DSI and the population vector amplitude.

To quantify the relationship between an individual neuron’s response selectivity and the local population, we used a principle component analysis (PCA; Sokal and Rohlf, 1995) to calculate the major-axis slope:

$$s_x=\frac{\sum _{i=1:n}\left({(x_i-\overline{x})}^2\right)}{n-1}$$

$$s_y=\frac{\sum _{i=1:n}\left({(y_i-\overline{y})}^2\right)}{n-1}$$

$$s_{xy}=\frac{\sum _{i=1:n}((x_i-\overline{x})\times (y_i-\overline{y}))}{n-1}$$

$$D=\sqrt{{(s_x+s_y)}^2-4\times (s_x\times s_y-{\left(s_{xy}\right)}^2)}$$

$${\lambda }_1=\frac{(s_x+s_y+D)}{2}$$

$${\mathit{\text{slope}}}_{\mathit{\text{major axis}}}=\frac{s_{xy}}{({\lambda }_1-s_x)}$$

Here s_x and s_y are the variance or sums of squares of x and y, respectively, and s_xy is the covariance between x and y. The random, independent measurements are indicated by x and y. The diagonal of variance-covariance matrix (D) used to compute the first (major-axis) eigenvector (λ₁). Eigenvectors measure variability along the major (λ₁) or minor (λ₁) axis. The major-axis slope is calculated from s_x, s_xy, and λ₁. To compute standard error on the major-axis slope, a Bootstrapped PCA was performed by sampling with replacement from the data (Sokal and Rohlf, 1995). Mean PCA slopes were computed against a distribution of PCA slopes computed from shuffled PV− cell populations. To calculate the PCA slope for shuffled population, we randomly shuffled PV− cell positions for a given imaging session and repeated the analysis above. Significance was measured by comparing the true mean PCA slopes measured against the distribution of PCA slopes computed from shuffled populations.

The relationship between individual cell’s disparity preference and the population vector angle quantified by computing a circular-correlation coefficient (Batschelet, 1981):

$$\mathit{\text{corr}}=\frac{1}{N}\sqrt{{(\sum \text{cos}({\psi }_n-{\zeta }_n\left)\right)}^2+{(\sum \text{sin}({\psi }_n-{\zeta }_n\left)\right)}^2},$$

where ψ is the individual cell’s disparity preference, ζ is the population vector angle, and N is the total number of neurons (n). Circular-correlations were subtracted by a shuffle-corrected circular-correlation to remove inherent biases in the data. Shuffle corrections were computed by randomly shuffling positions of PV− cells for a given imaging session and repeating the analysis above. Standard error on shuffled-corrected PCA was computed by Bootstrapping and sampling with replacement (Sokal and Rohlf, 1995).

To quantify the spatial dependence of PV+ interneurons we fit our data (PCA or shuffle-corrected circular-correlation) with an exponential:

$$y=a{e}^{-r/\lambda },$$

where a is the amplitude, r is the spherical radius in microns, and λ is the spatial length constant.