Hierarchical clustering method to improve transrectal ultrasound-guided diffuse optical tomography for prostate cancer imaging

Abstract

The inclusion of anatomical prior information in reconstruction algorithms can improve the quality of reconstructed images in near-infrared diffuse optical tomography (DOT). Prior literature on possible locations of human prostate cancer from trans-rectal ultrasound (TRUS), however, is limited, and has led to biased reconstructed DOT images. In this work, we propose a hierarchical clustering method (HCM) to improve the accuracy of image reconstruction with limited prior information. HCM reconstructs DOT images in three steps: After the initial step of reconstructing the human prostate, we divide the prostate region into geometric clusters to search for anomalies in finer clusters. The geometric segmentation is continued within found anomalies for improved reconstruction. We demonstrated this hierarchical clustering method using computer simulations and laboratory phantom experiments. Computer simulations were performed using combined TRUS/DOT probe geometry with a multi-layered model; experimental demonstration was performed with a single-layer, tissue-simulating phantom. In computer simulations, two hidden absorbers without prior location information were reconstructed with a recovery rate of 100% in their locations and 95% in their optical properties. In experiments, a hidden absorber without prior location information was reconstructed with a recovery rate of 100% in its location and 83% in its optical property.

1. Introduction

Prostate cancer is one of the leading causes of cancer deaths in men in the United States. (1) Conventional methods for diagnosing prostate cancer include the PSA (prostate specific antigen) blood test (2) and DRE (digital rectal examination). If the PSA level and/or DRE are suspicious, then in most cases the patient undergoes trans-rectal ultrasound (TRUS) guided biopsy. This is due to the fact that a PSA level could be misleading. PSA can be expressed high due to benign prostatic hyperplasia. (BPH) (3). On the other hand, men with a low PSA level (below 4.0 ng/ml) can still have prostate cancer (4). Despite recent advances in ultrasound, the grayscale-based ultrasound imaging has an accuracy only 50–60%; diagnosis accuracy can be even less in trans-rectal ultrasound (5). This is why TRUS has been used only for guiding a needle biopsy, not for detection of prostate cancer. In recent years, researchers have made great advances in using magnetic resonance imaging (MRI) and magnetic resonance spectroscopy (MRS) to detect prostate cancer and/or to guide needle biopsy (6,7). Given MRI and MRS cost, bulkiness, requirement for body confinement, and limited accessibility to the general public, it is highly desirable to have a portable, office-based imaging tool available to clinicians for improved detection or screening of prostate cancer as well as for active surveillance to determine an optimal treatment time.

For the past two decades, diffuse optical tomography (DOT) with near-infrared (NIR) light has been a popular non-invasive imaging modality using non-ionizing radiation to provide functional maps about the tissue under study. Since cancer tissues are more vasculature than the surrounding tissue, hemoglobin-based absorption in tumors provides optical contrast in DOT. When imaged at multiple wavelengths, DOT is capable of measuring chromophore concentrations such as oxy-hemoglobin, deoxy-hemoglobin, and water. Usage of DOT for breast cancer detection and diagnosis has been extensively studied for nearly 20 years (8, 9). However, investigations on detection of prostate cancer using DOT have been relatively limited compared to those done for breast cancer detection. A previous ex-vivo study (10) reported differences in water content between normal and cancer human prostate tissues. A recent review paper (11) has provided a comprehensive summary of optical properties of human prostate cancer tissue at selective wavelengths. Specifically, several reports given in references (12–15) show that light scattering of prostate cancer tissue is higher than that of normal prostate tissue. Trans-rectal DOT has been also reported by several recent studies (16–18) as a possible imaging tool for prostate cancer detection and diagnosis.

DOT instrumentation can be divided into three categories based on the principle of operation: 1) time-resolved systems (19–21), 2) frequency-domain systems (22), and 3) continuous wave (CW) systems (23, 24). Measurements are made in transmission geometry, reflection geometry, or both. A time-resolved system relies on photon counting or gated imaging, which provides photons’ time of flight through the tissue. However, these systems are costly in comparison with CW systems. A frequency-domain system modulates laser light typically in the radio frequency range (100 MHz) and measures the amplitude and phase shift of the detected signal. A CW system is the simplest, fastest, and most cost-effective system in data collection; it can also be made at a video rate for imaging. However, CW systems measure only the intensity of reflected/transmitted light, so they cannot separate the absorption property from the scattering effect of the tissue (25).

In order for trans-rectal DOT to be able to provide excellent reconstructed images for prostate cancer detection, we have to acknowledge our obstacles in order to find appropriate solutions. One main obstacle is closely associated with the location of measurements: the human rectum, where we have a limited space (allowing a limited number of optodes to be implemented); furthermore, only reflectance geometry of DOT can be utilized. Given the nature of light scattering in tissues, DOT suffers from poor spatial resolution. Measurements taken using reflectance geometry do not normally achieve the excellent spatial resolution that is more commonly obtained in those taken by transmission geometry. One way to improve the spatial resolution is to couple DOT with other imaging techniques such as MRI and ultrasound. In particular, a combined TRUS and DOT probe for imaging prostate cancer has been studied previously (26), utilizing the anatomical information from ultrasound to reduce the number of unknowns in the DOT image reconstruction. As shown by Xu et al. (26), each anatomical region was considered to be homogenous; uniform optical properties were reconstructed in each respective region. While the combined TRUS-DOT method improves accuracy of reconstructed DOT images, it relies highly on the ability of TRUS to locate the prostate cancer lesion. Given the fact that TRUS has a low prostate cancer detection accuracy and that each region is assumed to be homogenous, the reconstructed DOT images of prostate cancer could be erroneous.

In order to limit the dependency of DOT image reconstruction on TRUS sensitivity, we have developed a hybrid reconstruction technique by combining a piecewise cluster reconstruction approach with hard prior anatomy of prostate available from TRUS. Our method utilizes a hierarchical scheme of clustering where we define a cluster as a group of nodes/voxels within a predefined volume. By utilizing hierarchical clustering, a region of interest (ROI, i.e., the prostate) can be transformed into a partially heterogeneous medium, within which we can search and further reconstruct potential cancer lesions. The inverse problem of DOT is solved in multiple steps by changing cluster sizes within the image domain. Multi-step reconstruction in DOT has been reported earlier (27) for breast cancer detection based on a frequency-domain study. It is understood according to reference (27) that the size and location of the absorber were partially or roughly estimated in the first step of reconstruction, after which more steps were utilized to further improve the quality of reconstructed images. In the TRUS-DOT scenario, however, a rough reconstruction of the first step is futile to effectively detect prostate cancer due to the multi-layer tissue compositions, reflectance measurement geometry, limitation in the number of measurements, and particularly the inability of ultrasound to identify prostate cancer lesion or lesions. Thus, to improve the effectiveness and accuracy of prostate cancer imaging, we considered piecewise division of the image domain in DOT, assuming that the domain consists of disjoint sub domains with different optical properties.

Specifically, in our work, we performed the piecewise division of the image domain for a human prostate in the inverse calculation. By doing so, we were able to combine the piecewise division with hard-prior anatomic information for DOT image reconstruction. In this paper we present detailed procedures of our proposed method and validate it by showing its performance with the following computer simulations: 1) one anomaly at a depth of 1 cm to 3 cm below the measurement surface, 2) two anomalies at 1 cm and at 2 cm, respectively, 3) variable background absorption from 0.005 to 0.015 mm⁻¹), 4) variable noise percentage from 0% to 3%. By the end, we will also validate the performance of the proposed method by laboratory experimental results.

2. Methods

2.1 Forward and inverse methods in DOT

Light transport in biological tissues can be modeled by the diffusion approximation (DE) to the radiative transport equation (RTE), assuming that light scattering has great effects on light propagation in tissue. In the frequency domain, the diffusion equation is given by (28, 29)

$$-\nabla D(\overrightarrow{r})\nabla \mathrm{\Phi }(\overrightarrow{r},\omega )+({\mu }_a(\overrightarrow{r})+i\omega /c)\mathrm{\Phi }(\overrightarrow{r},\omega )=Q_o(\overrightarrow{r},\omega )$$ (1)

where Φ(r⃗,ω) is the photon density at the position r⃗, ω is the modulation frequency of light (in our study we use CW domain, so ω =0), Q_o(r⃗,ω )represents the isotropic source, c is the speed of light in the medium and μ_a is the absorption coefficient; finally, D(r⃗) is the optical diffusion coefficient which is defined as

$$D(\overrightarrow{r})=1/3[{\mu }_a(\overrightarrow{r})+{\mu }_s^{\prime }(\overrightarrow{r})],$$ (2)

where ${\mu }_s^{\prime }(\overrightarrow{r})$ is the reduced scattering coefficient and is defined as ${\mu }_s^{\prime }(\overrightarrow{r})={\mu }_s(\overrightarrow{r})(1-g)$. Here μ_s(r⃗) is the scattering coefficient and g is the anisotropic factor. Equation (1) can be solved using the finite element method (FEM) and applying Robin-type (30) (known as type III or mixed) boundary condition to model the refractive index mismatch at the boundary.

For a CW system, measurements are only amplitudes of light intensities and are used to estimate the spatial distribution of the product of μ_a(r⃗) and μ_s′(r⃗), namely, μ_eff(r⃗) = μ_a(r⃗) μ_s′(r⃗), or the distribution of μ_a(r⃗) if μ_s′(r⃗) is known and homogeneous. It is known that μ_eff(r⃗) values of prostate cancer are different from those of normal prostate tissues (11, 16, 26). Based on previous knowledge learned from breast cancer detection and diagnosis with DOT (8, 9), we started this study with an assumption that light absorption μ_a(r⃗) is the major source for optical contrast between cancerous and normal prostate tissues, while changes in μ_s′(r⃗) induced by prostate cancer are much less significant. Accordingly, the aim of the DOT reconstruction in this paper is to recover the light absorption property, μ_a(r⃗), from NIR measurements taken on the boundaries. The objective function, Ω for this procedure can be written as

$$\mathrm{\Omega }{=}_{D,{\mu }_a}^{min}\{{\Vert y-F(D,{\mu }_a)\Vert }^2+\lambda {\Vert (D,{\mu }_a)-(D,{\mu }_{a0})\Vert }^2\}$$ (3)

where y is a matrix to express all the measured data, F is the forward-calculation operator (or matrix) that generates diffusion-based light propagation responses,|| . ||₂ is the L2 norm, λ is the regularization parameter and μ_a0 is the initial estimate of light absorption coefficient. Note that variables D, μ_a and μ_a0 are simplified notations for D(r⃗), μ_a(r⃗), and μ_a0(r⃗), respectively. By minimizing Eq. (3), which is achieved by setting the first derivative of Eq. (3) with respect to μ_a as zero following a Taylor series, and ignoring the 2^nd and higher order terms, we arrive at the updated equation:

$$(J^{T}J+\lambda I)(\delta {\mu }_a)=J^T[y-F({\mu }_a)]+\lambda [(D,{\mu }_a)-(\mathrm{D},{\mu }_{a0})]$$ (4)

where J is the Jacobian matrix, I is the identity matrix, and δμ_a (δμ_a =μ_a –μ_a0 ) is a spatial distribution matrix of changes in μ_a with respect to the initial given value. Note that μ_a0 is only the initial estimate at the first iteration. After the first iteration, μ_a0 is basically the previous estimate. Now Eq. (4) becomes Eq. (5) after we replace μ_a – μ_a0 by δμ_a,

$$(J^{T}J+2\lambda I)(\delta {\mu }_a)=J^T(y-F({\mu }_a)).$$ (5)

As mentioned earlier, we consider changes only in μ_a here, because our DOT measurement utilizes CW NIR light with an assumption that variation in light scattering across the medium is minimal. Specifically, we utilized a uniform distribution of μ_s′(r⃗)=10 cm⁻¹ across different prostate tissue regions in all simulation examples to be shown in Section 3. Then, we will have further discussion on how to remove or modify this assumption in Section 4.

2.2 Hierarchical clustering

In our hierarchical clustering method (HCM), the reduction of a parameter space is realized by segmenting the medium or region of interest (ROI) into several geometric units or clusters. We assumed that each of the geometric clusters was homogeneous and had the same optical property. In this way, the medium or image domain could be partially heterogeneous since the domain may contain several geometric clusters. During the DOT image reconstruction process, a value of μ_a from each cluster was updated using Eqs. (3) to (5). Since the size of each cluster was user-defined, the smallest could be a single FEM mesh node and the largest could be the entire domain region—similar to that used in the regular reconstruction method without any spatial prior. Specifically, the nodes in the mesh were tagged and separated into clusters, as indicated by c₁, c₂…c_j with respect to each cluster. The Jacobian matrix in Eq. (5) was then modified to be J* as given by (27):

$$J\ast =JC,$$ (6)

where matrix C had the size of NN×NC (number of nodes × number of clusters). The elements of matrix C were given as follows:

$$C(i,j)=\left\{\begin{array}{ll}1\hfill & ifi\in c_j\hfill \\ 0\hfill & \mathit{else}\hfill \end{array}\right\},$$ (7)

where i marks the number of nodes and j labels the number of clusters. By the end of each iteration, the solution vector of δμ_a was mapped back to each node using Eq. (8),

$$\delta {\mu }_a=C(\delta {\mu }_a^{\ast })$$ (8)

where δμ_a^* is the vector with optical properties in respective geometric clusters solved from Eq. (5). The function of matrix C is to transform the initial image domain into a new image domain where the inverse procedure is performed with cluster-based geometric structures. Matrix C is a mediator or operator that converts the regular geometry to and from cluster-based geometry for the reconstructed object. So, technically no inversion or transpose of C is directly involved.

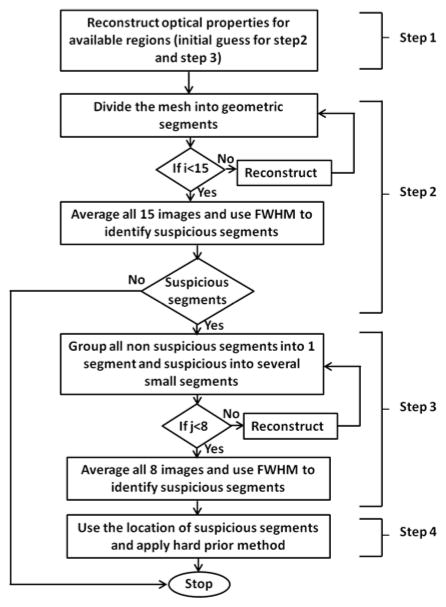
Initially, we started with reconstructing two ROIs, such as background and an anomaly; the background mesh was geometrically segmented in a heterogeneous fashion. For multiple ROIs, we hierarchically implemented the proposed method by segmenting the region which was more prone to cancer, while utilizing available prior information. Specifically, we implemented the proposed method in four steps, as shown in Fig. 1. To image prostate cancer through trans-rectal DOT imaging, four types of tissues were examined: rectum wall, peri-prostate tissue, prostate and tumor. Each of these tissues have their own optical properties. When being imaged without any prior anatomic information, different types of tissues are highly likely to be mixed among one another because their optical contrasts are relatively subtle, and it is difficult to distinctly separate them. Thus, in our HCM methodology, it is critical for us to achieve an improved spatial resolution for prostate imaging.

Fig. 1.

Methodology showing steps through a flow chart showing HCM

In Step 1, we performed the reconstruction based on prostate anatomic images offered by TRUS and the assumption of a homogeneous prostate. With such prior spatial information, the reconstructed μ_a values in both background and prostate regions (as two ROIs) should be reasonably accurate with respect to the actual values, assuming that the sizes of the prostate tumors are much smaller than the size of the prostate. Then, the reconstructed μ_a values in available ROIs would serve as the initial guess in Step 2 and Step 3.

Step 2 of HCM was dedicated to finding the probable locations of anomalies (i.e., prostate tumors). To achieve this, we geometrically divided the prostate region into several clusters, so the prostate tissue became a heterogeneous medium. However, without prior knowledge of suspicious locations, dividing the prostate into several clusters or elements may result in a mixing of suspicious tissue with normal prostate tissue and vice versa. In order to prevent mixing, we took a hierarchical approach to cluster the prostate volume with different unit volume sizes iteratively to minimize the mixing effect of cancer and normal tissues within a cluster.

Specifically, we chose the initial volume of a cluster to be 1 × 1 × 1 cm³ in each of the x, y and z dimensions. Then, we varied the volume of the cluster by increasing the length of the cluster in each dimension iteratively. For example, an increase in length of 0.5 cm in only x direction gave rise to a unit volume of 1.5 × 1 × 1 cm³, followed by the same length increase in only y or only z direction. In this way, we can generate eight different unit volumes in three x, y, z directions, by increasing the linear length in only one dimension (x, y, z), or in two dimensions (xy, yz, xz), or in three dimensions (xyz) and the initial size. The procedure is given as follows: (1) reconstruct an initial μ_a image with a starting base unit size (i.e., 1×1×1 cm³), (2) save the reconstructed image, and go back and change the unit volume size (e.g., 1.5 × 1 ×1 cm³ or 1.5× 1.5 ×1 cm³ or 1.5 × 1.5 × 1.5 cm³) and reconstruct the image again (Step 2 in Fig. 1). To be more comprehensive, we next increase our base unit volume from 1 × 1 × 1 cm³ to 1.5 × 1.5 × 1.5 cm³, for the latter of which the same length interval (0.5 cm) is applied to increase the base unit (e.g., 2 × 1.5 × 1.5 cm³, 2 × 2 × 1.5 cm³, or 2 × 2 × 2 cm³). In this way, we are able to generate another set of eight reconstructed images with varied base unit volumes resulting in an overall 15 (i=15) images (resulting from 15 combinations) by the end of Step 2. (3) We average all of the reconstructed μ_a images to obtain the final image. (4) Next, we search for suspicious clusters that have high μ_a values with respect to the background, as an indication of cancer. The location of suspicious clusters was selected using full width half maximum (FWHM) of the updated μ_a values within the prostate region. If no suspicious cluster is identified, we conclude that the prostate has a low probability of having cancer.

In Step 3, if some suspicious clusters in Step 2 are seen, we then group all the non-suspicious clusters as one new single cluster and subdivide the suspicious clusters into further smaller clusters. Now, the initial unit volume size used within the suspicious regions in Step 3 is set to be 0.5 × 0.5 × 0.5 cm³. The procedure explained in Step 2 is repeated here with a length variation of 0.25 cm in any one of three dimensions. Similar to Step 2, the final reconstructed image of Step 3 is an average of the eight images (j=8) obtained by varying the unit volume in eight different fashions. FWHM of the μ_a values is still used to localize suspicious regions for further inspection with an improved spatial resolution.

In Steps 2 and 3, we utilized a region-specific regularization parameter to favor the reconstruction in the prostate region using a hierarchical approach. The underlying rationale of this approach was previously reported in (31) where the regularization parameter controls the level of optical property updates at each iteration. A larger regularization parameter gives rise to a subtle update, while a smaller regularization parameter offers a steeper update with a broader solution range. In our case, a smaller regularization value applied to the prostate region allowed us to focus only on the prostate and to accurately update the reconstructed optical properties of the prostate. Finally, in Step 4, we repeated the reconstruction process using the suspicious regions identified in Step 3 as a hard prior anatomy or as given cancer regions, with a uniform initial guess as used in Step 1.

In principle, selections of regularization parameters and stopping criterion play a key role in any iteration-based reconstruction techniques. In HCM, we empirically determined the regularization parameters and the stopping criteria. For Step 1, the regularization parameter was 10 and the stopping criterion was when the change in projection error was less than 2% of that in the previous iteration. For Step 2, the regularization parameter was 0.1, and the stopping criterion was when the change in projection error was less than 20% of the previous iteration. The reason for this criterion at Step 2 was that the value of the regularization parameter was small so that the noise began to dominate the reconstructed images. For Step 3, we further decreased the regularization parameter to 0.001 while keeping the same stopping criterion as that in Step 2.

3. Simulation and experiment results

3.1 Trans-rectal DOT image reconstruction by HCM with limited prior information

To validate HCM, a simulated TRUS-DOT probe was used having 16 co-located or bifurcated optodes that served as both sources and detectors [see Fig. 2(a)]. We performed computer simulations by considering a FEM mesh, which was anatomically similar to a TRUS image of a human prostate [see Fig. 2(b)]. It consisted of four ROIs, such as prostate (sky blue region), peri-prostate tissue (blue region), rectum wall (green) and prostatic tumor (anomaly) [see Fig. 2(c)]. The mesh used in this study was an unstructured tetrahedral mesh with 28,174 nodes and 156,191 elements. The thickness of the rectum wall was set to be 5 mm with a curvature radius of 50 mm. The following optical property (i.e., absorption coefficient) distributions were used: 0.01 mm⁻¹ for rectum wall, 0.002 mm⁻¹ for surrounding tissue, 0.006 mm⁻¹ for prostate, and 0.02 mm⁻¹ for anomaly (16, 26). An anomaly was created at 1-cm depth from the rectum wall to test HCM. The CW mode was utilized in the simulations; 1% random noise was added to the data to mimic the instrument noise.

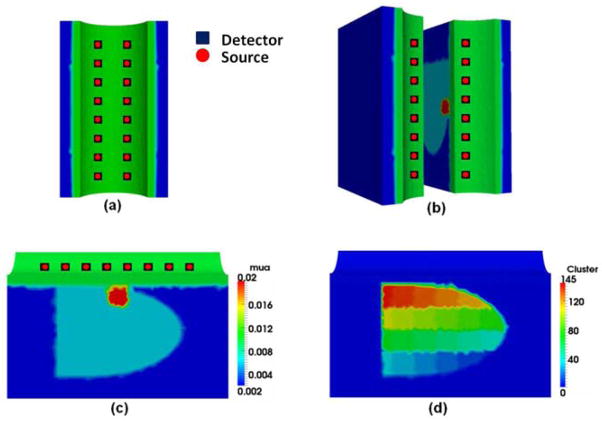
Fig. 2.

(a) Probe geometry used in this study; each optode is bifurcated to serve as a source and detector. (b) Mesh (elements not highlighted) has been rotated and sliced vertically into two halves to show the simulation geometry. (c) A slice from the mesh cut along the longitudinal direction, showing simulated rectum wall (green), surrounding tissue (blue), and prostate (sky blue). An anomaly has been created at 1-cm depth from the rectum wall. (d) Image reconstruction is in progress showing clusters within the prostate region.

Simulated DOT data was computed using the diffusion forward model with FEM; NIRFAST (32) was used to perform the forward calculation. The procedure given in Section 2 was used to reconstruct images from all simulated data. Specifically, Step-1 reconstruction was done using an initial guess of μ_a=0.01 mm⁻¹ to recover the optical properties of the rectum wall, prostate, and surrounding tissue. Then the reconstructed data from Step 1 served as the initial guess for Steps 2 and 3. Next, the prostate region was divided into several clusters [see Figure 2(d)], which had tissue volumes of 1.00 to 8 cm³. As noted earlier, the final image obtained after Step 2 was an average of over 15 independent reconstructions. In Step 3, the suspicious region identified (using FWHM) in Step 2 was further divided into smaller clusters (0.125 – 0.42 cm³ in volume). The final image of Step 3 was an average over eight image reconstructions. FWHM was again used to find the suspicious regions, which were treated as individual regions and entered as the hard prior anatomy for finer reconstruction in Step 4.

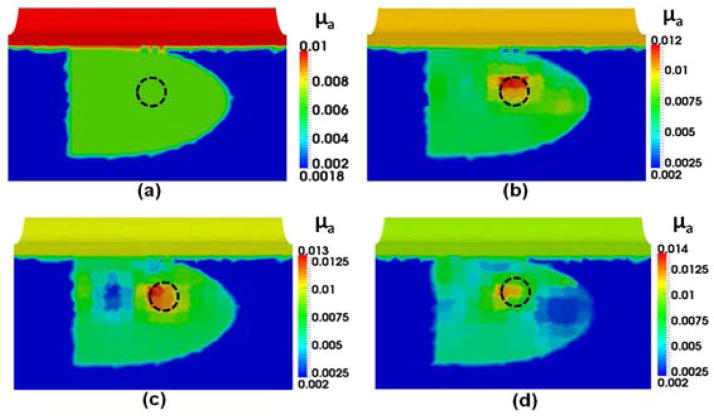
Panels in Fig. 3 provide overall steps involved in HCM to perform DOT image reconstructions. As shown in Fig. 3(a), an anomaly was embedded at 1-cm depth from the surface of the rectum. Figure 3(b) demonstrates the result after Step 1 showing that the reconstructed image is biased with the known priori information of the prostate, peri-prostate tissue and rectum wall. As seen in Fig. 3(c), Step 2 of HCM is able to determine a probable location of the anomaly inside the prostate without prior anatomical information. Figures 3(d) and 3(e) result from Steps 3 and 4 of HCM and clearly depict the location of the simulated tumor. After Step 3, while the optical properties in the anomaly region are not completely uniform, we can locate the absorber accurately inside the prostate. Finally by Step 4, the reconstructed μ_a value of the anomaly has been improved. For comparison, Fig. 3(f) illustrates a recovered μ_a image using the given spatial prior information on the anomaly location. Moreover, Table 1 shows that HCM resulted in a recovery rate of 95% for the embedded target, without using any spatial prior information.

Fig. 3.

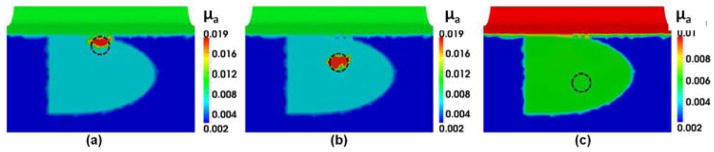
Reconstructed μ_a values in mm⁻¹ using different reconstruction steps for (a) an anomaly located within a simulated prostate. The dotted circles indicate the real locations of the anomaly. Reconstructed images (b) after Step 1 of HCM, (c) after Step 2 of HCM, (d) after Step 3 of HCM, (e) after Step 4 of HCM; (f) reconstructed image for the same case using a known hard prior anatomy/condition for the inclusion.

Table 1.

Comparison of reconstructed μ_a values by HCM with and without prior anatomical information

Tissue type	μa (mm−1)
	without prior information (%)	with prior information (%)
Peri-prostate	0.002 (100)	0.002 (100)
Rectum wall	0.01 (100)	0.01 (100)
Prostate	0.006 (100)	0.006 (100)
Anomaly	0.019 (95)	0.02 (100)

3.2 Investigation of HCM on depth sensitivity

In order to test depth sensitivity of HCM, an anomaly was created at depths of 1 cm, 2 cm and 3 cm from the surface of the rectum wall. Reconstructed images from all three locations were compared as shown in Fig. 4. The dotted circles in Fig. 4 indicate the actual location of the targeted anomaly. Figures 4(a) and 4(b) are the reconstructed images after Step 4 using HCM with anomaly placed at 1-cm and 2-cm depths, respectively; Figure 4(c) is the reconstructed image after Step 2 using HCM with anomaly placed at 3-cm depth. The algorithm was stopped after Step 2 in this case because of its inability to find any absorbers. Figure 4(c) demonstrates that HCM is incapable of recovering the anomaly at a 3-cm depth because of the severe decrease in measurement sensitivity with increasing depth, the number of optodes used, and the absorption coefficient of the prostate. For quantitative comparison, Table 2 lists the actual and recovered optical property and their recovery percentage rate for the reconstructed absorber at the three respective depths. This simulation-based summary table implies that HCM has the ability to reconstruct an absorbing-anomaly within a human prostate at a depth of 2 cm with a possible recovery rate of 95% if 16 bifurcated optodes are used. Whether the detection sensitivity may go deeper than 2 cm in practice remains to be seen since it also depends highly on the number of optodes, the power of light sources, and the type of detectors used for the measurement.

Fig. 4.

Reconstructed μ_a values in mm⁻¹ of the anomaly created in increasing depths. Panels (a), (b) and 4(c) show the reconstructed images of an anomaly located at 1 cm, 2 cm, and 3 cm, respectively. Dotted circles show the actual location of the anomaly.

Table 2.

comparison of reconstructed μ_a value of the target at different depths using HCM

Depth	Target (mm−1)	Reconstructed (mm−1)	% recovered of μa
1cm	0.02	0.019	95
2cm	0.02	0.019	95
3cm	0.02	---	---

3.3 Trans-rectal DOT image reconstruction by HCM with two absorbers

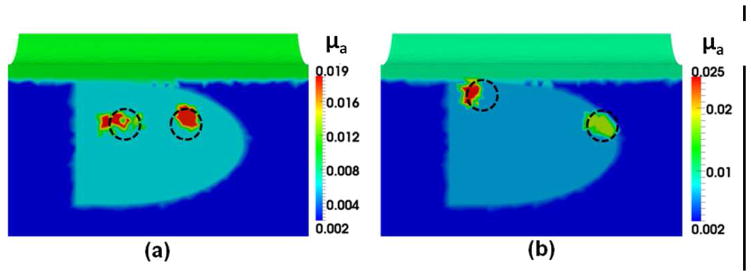
The capability of differentiating two absorbers by HCM is important in prostate cancer imaging because of the existence of multifocal cancer regions. Moreover, the results from Section 3.2 indicate that HCM is not able to detect an anomaly at a depth of 3 cm. So within the depth limit, we investigated whether HCM was able to reconstruct two absorbers in this sub-section. For this purpose, we performed the simulations with two cases. In Case 1, two anomalies of 1-cm diameter were created at the depth of 2 cm from the surface. The two anomalies were separated by 2 cm, as shown by dotted circles in Fig. 5(a). This test was useful in understanding the minimum separation between two absorbers that is required to recover them as two separable absorbers in reconstructed images. This test also allowed us to estimate the recovery of off-centered absorbers. This estimation is important because the sensitivity of DOT is often higher in the center of the image domain due to the number of overlapping measurements. In Case 2, the absorbers were created at the depths of 1 cm and 2 cm, respectively, as drawn by dotted circles in Fig. 5(b). The separation between the two absorbers was increased to 4 cm. Figures 5(a) and 5(b) also show the reconstructed images after Step 4 using HCM, demonstrating that the locations of the anomalies were successfully recovered.

Fig. 5.

This figure shows (a) the two anomalies separated by 2 cm and created at a depth of 2 cm, and (b) the two anomalies separated by 4 cm and located at depths of 1 cm and 2 cm. Dotted circles show the actual locations of the anomalies.

3.4 Investigation of HCM on effects of different background (prostate region) contrast

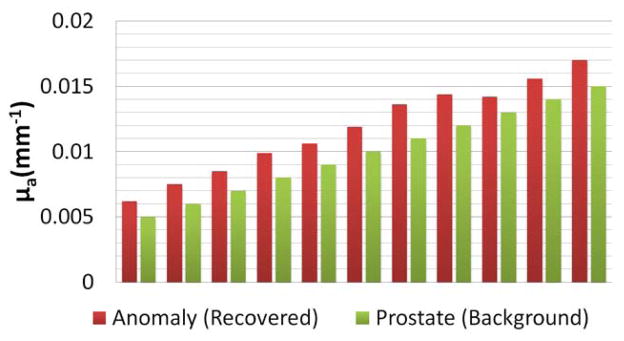
Further investigation of HCM on variation of background absorption in the prostate region is helpful for us to understand and estimate effects of the background optical properties on the reconstructed DOT images. As explained in Section 2, in Step 2 of HCM, the overall area of the anomaly was identified by selecting the full width at half maxima (FWHM) of the recovered optical properties. If the recovered optical properties were not much higher than that of the background, no probable anomaly would be identified, which is similar to the case shown Fig. 4(c). So, the background absorption or contrast plays an important role in achieving high-quality DOT images of prostate cancer. To estimate effects of the background optical properties, we performed 11 simulations, as listed and shown in Fig. 6, by varying the optical properties or μ_a values of the prostate (i.e., background tissue) from 0.005 to 0.015 mm⁻¹. The absorption coefficients for the surrounding tissue and the rectum wall were fixed; the anomaly contrast was set to be three times greater than the background (0.015 to 0.045 mm⁻¹) in all the simulations. The reconstructed results were plotted by comparing the recovered optical properties to the background in Fig. 6, which shows the recovered contrast from the background after Step 2 using HCM. We also calculated a recovery rate (RR) based on the recovered absorption (RA) versus expected absorption (EA) as expressed by RR = (RA/EA)*100. Specifically, our calculations gave rise to an averaged RR of 40% over all 11 simulations. This 40% recovery rate of the expected contrast indicates that variations in background optical properties would still allow us to locate the probable location of an anomaly in Step 2 as long as the absorption contrast between the anomaly and background is 3 times greater.

Fig. 6.

Comparison of absorption coefficients between the recovered anomaly and the prostate background after Step 2.

The reason why we stopped at Step 2 was that this stage was very crucial for the success of our algorithm. If we succeeded to obtain enough contrast in absorption with respect to the background in this step, we would be able to identify the region of interest for possible cancer lesions. Further steps (i.e., Steps 3 and 4) will allow us to refine the size, location, and optical properties to achieve final reconstructed images with high quality. If our algorithm failed to recover a reasonable amount of contrast in Step 2, then the algorithm would fail to give rise to correct results. Indeed, this is the major difference between our approach and those approaches of previous researchers (16, 26).

3.5 Investigation of HCM on effects of different noise levels

To further understand and support HCM, we performed another simulation with an anomaly placed at 2 cm below the surface of the rectum wall; the reconstructed images by HCM were generated while varying the noise levels at 1, 2 and 3% of measured signals. For comparison, we also reconstructed an image, as shown in Fig. 7(a), without any anomaly and with 1% noise added to the simulated data. Specifically, Fig. 7(a) was obtained after all the clusters were updated illustrating a uniform distribution within the prostate region. On the other hand, Figures 7(b), 7(c), and 7(d) are the reconstructed images after Step 2 with 1%, 2% and 3% noise levels added to the data, respectively. From this set of figures, it is evident that HCM is robust if the noise level is restricted to no more than 1%. Figure 7(c) is slightly corrupted due to 2% noise while Fig. 7(d) is heavily corrupted due to 3% noise.

Fig. 7.

This figure shows (a) the reconstructed image with 1% noise added to the data and without any anomalies, while (b), (c), and (d) show the reconstructed images with 1%, 2%, and 3% noise levels, respectively.

3.6 Experimental demonstration

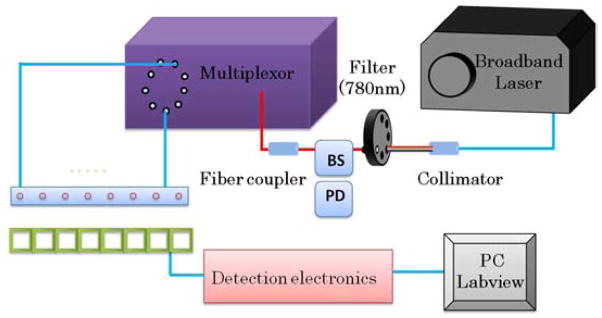
For demonstrating HCM experimentally, we utilized a CW DOT setup as depicted in Fig. 8. A broadband pulsed laser source (SC-450, Fianium Inc., Eugene, Oregon) with a maximal output power of 40 mW (as measured at the tip of an optical fiber) was utilized as the illumination source. Several photodiodes (OPT 101, Burr-Brown Corp., Tucson, Arizona) were implemented for diffuse light detection. Although our laser had a repetition rate of 20 MHz due to the limited response speed of the photodiodes, we still considered our system a CW system. As shown in Fig. 8, the laser output from the source was collimated and fed through a filter wheel where a desired wavelength of 780 nm was selected. In order to calibrate light fluctuations from the laser source, a beam splitter (BS) was utilized, and a small portion of the beam was fed into another photodiode (PD) for further calibration. The larger portion of the light was coupled into another optical fiber and fed into a multiplexor. The multiplexor, as controlled by a computer, was connected to eight silica optical fibers of 600 μm in diameter for light illuminations in sequence to eight locations on an optode probe.

Fig. 8.

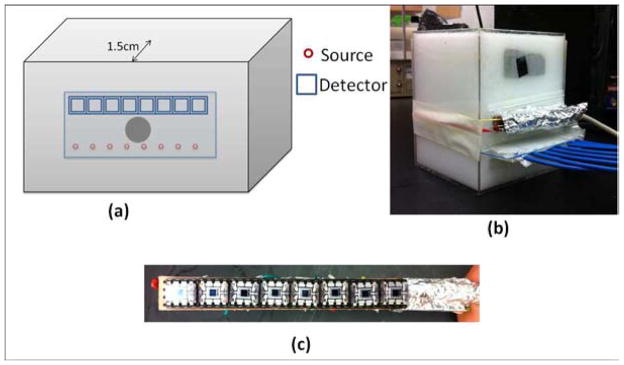
Instrumentation and probe setup utilized for laboratory phantom experiment. Eight sources and detectors were used for light delivery and detection. BS: beam splitter; PD: photodiode.

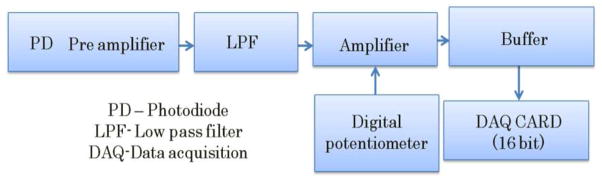
For the detection electronics (see Fig. 9), the detected light was collected and converted to electrical signals by the photodiodes. An analog low pass filter (LPF) was employed to filter out unwanted higher frequencies. Next, the electrical signals were amplified using an operational amplifier in the inverting mode. The operational amplifier’s gain was controlled by changing the resistance of a feedback resistor. A digital potentiometer was utilized such that the gain was controlled from the computer. Then, the electrical signal was further fed into a buffer amplifier which itself was an operational amplifier in a non-inverting mode with unity gain. Finally, we utilized a National Instruments DAQ card with a 16-bit resolution to convert analog signals into a digital format to be transferred to and stored in the computer. The entire instrument control and data collection including light source switching, multiplexer sequencing, electrical gain selection, and data acquisition were computer-driven using LabVIEW software.

Fig. 9.

Flow chart depicting various stages of detection electronics utilized in proposed instrumentation.

Although we demonstrated our HCM using a multilayered model in computer simulations, we utilized a single-layer phantom for experimental demonstration. We preferred a single-layer phantom because it could serve the need or confirm HCM with a relatively simple tissue phantom. Using a single-layered phantom with an absorber embedded inside, we skipped Step 1 in HCM and directly started the reconstruction from Step 2. The reason for skipping Step 1 was that it involved inducing the prior information; for this particular case, we did not use any prior information. The phantom setup is depicted in Fig. 10(a) with a photograph of the actual setup shown in Fig. 10(b). A homogeneous liquid tissue-mimicking phantom was prepared by filling a 15 × 10 × 10 cm³ container with 1% intralipid solution [see Fig. 10(b)]. An appropriate amount of India ink was added to the solution to make the absorption coefficient of the solution to be 0.01 mm⁻¹. This solution served as a homogeneous background medium with an approximate μ_s′ value of 1 mm⁻¹ and μ_a value of 0.01 mm⁻¹. Two optode arrays consisting of eight source fibers and eight photodiodes were placed on one side surface of the container in such a dimension that both source-to-source and detector-to-detector intervals were 1 cm between center to center and the distance between the source array and detector array was 2 cm. A spherical 1-cm-diameter absorber with μ_a = 0.03 mm⁻¹ was made and placed within the phantom solution 1.5 cm from the source-detector array surface. The lateral dimension of the photodiode array from end to end was ~8 cm, as illustrated in Fig. 10(c), with an active detection area of 0.23 × 0.23 cm².

Fig. 10.

(a) Experimental setup used in this study. The probe was placed on one side of the tank to avoid contact with the intralipid solution. An absorber was placed 1.5 cm from the probe side of the tank. (b) Photograph showing the experimental setup. (c) Photograph showing the photodiode array.

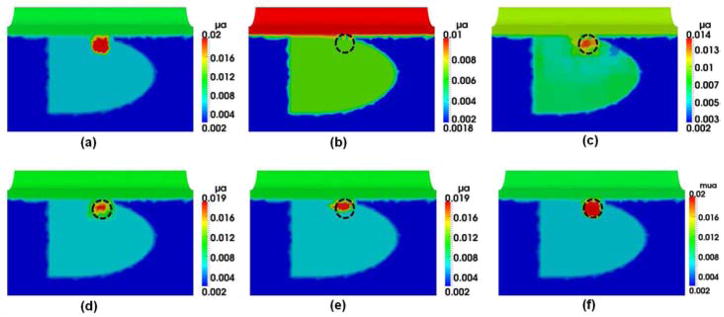
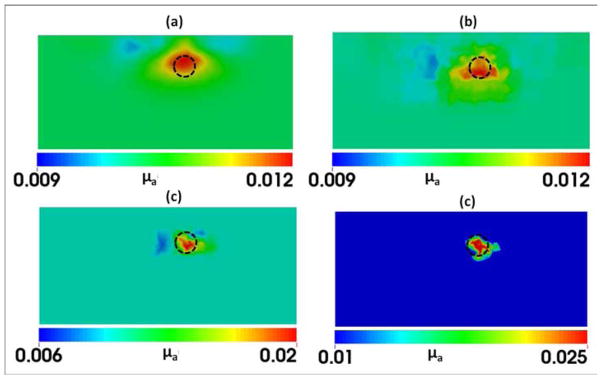
Panels in Fig. 11 provide overall comparisons among the reconstructed images that were obtained using the experimental setup given in Figs. 8–10. Figure 11(a) demonstrates the result obtained from the regular iterative DOT reconstruction technique. While this figure shows relatively good reconstruction in both location and size for the embedded absorber, we see very poor recovery in absorption contrast for the reconstructed object: the reconstructed value of μ_a was 0.012 mm⁻¹ while the expected value was 0.03 mm⁻¹. As seen in Fig. 11(b), Step 2 of HCM is able to determine the probable location of the absorber; Figs. 11(c) and 11(d) show the gradual improvement in the contrast recovery. By the end, both location and absorption contrast of the embedded absorber were reconstructed and greatly improved to meet the expected values. Moreover, Table 3 shows that HCM resulted in a recovery rate of 83% for the embedded target without using any spatial prior information.

Fig. 11.

Reconstructed μ_a values in mm⁻¹ using (a) regular DOT iterative reconstruction and HCM after (b) Step 2, (c) Step 3, and (d) Step 4. The dashed circles indicate the actual location of the 1-cm absorber with a depth of 1.5 cm below the measurement surface.

Table 3.

comparison of reconstructed μ_a value between regular DOT reconstruction and HCM for experimental data

	Target (mm−1)	Recovered (mm−1)	Recovery Percentage
DOT reconstruction	0.03	0.0115	38.3%
HCM	0.03	0.025	83.3%

4. Discussion

4.1 Investigation and confirmation of HCM by simulations and phantom experiments

In this work, we have investigated the feasibility of TRUS-guided DOT imaging of human prostate cancer through computer simulations and laboratory phantom experiments. While a trans-rectal DOT-only probe can possibly image cancer lesions within a human prostate without ultrasound guidance, reconstructed DOT images suffer from lack of anatomical landmarks and poor spatial resolution as well as a possible mixing of optical contrasts among the prostate gland, its surrounding tissues, and cancer lesions. In general, the spatial resolution of DOT imaging can be improved by increasing the number of optode channels; however, this is not a viable solution in our case because of the limited space available on a trans-rectal probe. Unlike previous work reported by references (16, 26), which required anatomic images of prostate cancer, we proposed and investigated a DOT-based HCM to image prostate cancer by utilizing anatomic images of the prostate, not the images of prostate cancer. While anatomic images of the prostate are readily available by routine clinical TRUS facility, they do not have a good ability to detect or image prostate cancer.

While the combined TRUS-DOT method can improve accuracy of reconstructed DOT images, the problem is not completely solved since TRUS-DOT highly relies on the ability of TRUS to locate the prostate cancer lesion. Given the fact that TRUS has low signature for prostate cancer, and that each region is assumed to be homogenous, the reconstructed DOT images could be erroneous. Thus, we further targeted the problem by (1) utilizing the available prior information on the locations of prostate, peri-prostate tissue and rectum wall and then (2) dividing the probable location of a prostate tumor or tumors into several clusters. This latter step made the prostate partially heterogeneous. The dimensions of the clusters were iteratively changed to limit the mixing of normal tissue with cancerous tissue and vice versa. Our HCM approach was implemented in four steps: The location of the absorber was identified in Steps 2 and 3, and the optical properties were reconstructed in Step 4. The figures shown in Section 3.1 demonstrate excellent reconstruction results when HCM was used. Table 1 also reports that the recovered optical properties of the target and surrounding tissues were matched well with the expected values. Furthermore, the reconstructed images shown in Section 3.2 reveal the depth sensitivity of HCM; however due to the exponential decay of measurement sensitivity with depth, our method can only reconstruct an anomaly located not deeper than 3 cm in depth. The depth limitation is a problem to be solved in future research.

Moreover, Section 3.3 illustrates the ability of HCM to recover up to two anomalies located inside the prostate. The optical properties were overestimated when the two absorbers were sited at different depths. This overestimation resulted from the fact that the measurement sensitivity is biased toward more superficial nodes than those of deeper nodes. In Section 3.4, HCM has been investigated using 11 simulation-based cases studying the effects of background absorption of the prostate tissue. The results indicate that a recovery rate of 40% for the target contrast could be achieved in all cases after Step 2 in HCM. Achieving a good contrast in a suspicious ROI after Step 2 is very crucial for the success of our algorithm. With a well localized target contrast after Step 2, further steps would allow us to refine the size, location, and optical properties to achieve final reconstructed images with high quality. Last, Section 3.5 shows that noise can have a significant impact on the image quality, while Section 3.6 confirms the performance of HCM by performing an actual experiment with a liquid tissue phantom. We demonstrated that a hidden absorber without prior location information was reconstructed with a recovery rate of 100% in its location and 83% in its optical property. Overall, the results indicate that both location and absorption contrast of the embedded absorber could be well reconstructed to meet the expected values when HCM was utilized.

4.2 Potential usefulness of HCM for prostate cancer detection and diagnosis

The current diagnostic method for high-grade prostate cancer is based on needle biopsy, which has three major deficiencies: (1) Needle biopsy may miss cancers that are present and have high-grade lesions, (2) it can underestimate the severity of cancer that a biopsy misses, and (3) it may find only low-grade cancers that likely do not cause problems. Because of the uncertainty and ambiguous conclusions from needle biopsy results, current prostate cancer patients are either undertreated or overtreated. Undertreatments cost lives; overtreatments cause unnecessary impotence or incontinence or both. It is, therefore, imperative to develop a diagnostic imaging technique that can accurately differentiate aggressive cancer lesions from low-risk ones, and which is compatible with existing clinical protocol.

While the current development of HCM is not yet tested in the clinical settings by human prostate specimen measurements, it can be readily available for clinical investigations since the results from both computer simulations and laboratory experiments are supportive for HCM. The feasibility of implementing a TRUS-coupled DOT probe has been demonstrated by (26). By combining such a TRUS-DOT optical probe with HCM, we may be able to develop a portable, diagnostic imaging device for early screening and diagnosis of prostate cancer. Further testing with human prostate measurements and optimal refinements are the planned next steps in order to make this technology clinically useful in detection and diagnosis of prostate cancer.

4.3 Limitation of the method and future work

While the reported results for HCM are promising for improved detection of prostate cancer, we need to recognize a few weaknesses of this study in order to either improve them in the near future or understand the limitation of the method. First, although HCM recovered well the absorption properties of imaged targets with a recovering rate of 95% in simulated results and of 83% in experimental results, excellent recovery in the target’s shape was not achieved. This may be partially due to the fact that the reconstructed images were defined by the FWHM in Steps 2 and 3 of HCM. Also, we believe that the inability to recover the target’s shape resulted from the reflectance geometry of the probe setup (see Fig. 2) and the limited number of channels available for the measurements. It is known that a reduced number of source-detector channels would reduce image sensitivity and spatial resolution of DOT. The method proposed by (33) and (34) could afford better results in recovering the shape of an anomaly when using circular or cylindrical probe geometries. This is because such geometries allow light to penetrate or pass through more tissue volumes under study, as compared to reflection geometries. Thus, while our HCM approach is simpler to implement than that given by (28), we are not able to recover the imaged object’s shape, partially due to the limited space (i.e., a human rectum) available to accommodate a fixed number of light sources/detectors, which are set in reflectance geometry for data acquisition. Under the same argument, we expect that the best spatial resolution of DOT-derived prostate cancer images reconstructed by HCM would be in an order of 5–8 mm.

Second, in Section 2.1 we stated the assumption of this study that variation in light scattering across the prostate and its surrounding tissues is minimal. This assumption was made due to the fact that CW-based DOT measurements cannot provide enough independent data quantities to uniquely solve both light scattering and absorption coefficients of the imaged objects. With this assumption, we were able to implement and validate HCM by achieving DOT reconstruction of absorption coefficients of simulated prostate cancer using both simulation and experimental data. We acknowledge that the assumption of constant light scattering across human prostate tissues may not be accurate, resulting in two negative impacts on our conclusion: (1) There exist variations in light scattering within the prostate tissue, which may create a large noise level to diminish the optical contrast between cancerous and normal prostate tissues. (2) Prostate cancer may result in light scattering changes, which may indeed be useful as an optical contrast for DOT but is ignored in the current HCM approach. In order to know whether or not these two negative impacts relate to HCM, it is necessary to perform human prostate specimen ex vivo and in vivo measurements with histology analysis confirmation, which is the next step in our research plan. Our expectation is that variations in light scattering within the prostate tissue are not large enough to diminish the optical contrast between cancerous and normal prostate tissues based on previous reports on both breast cancer (8, 9, 35) and prostate cancer studies (11, 16). If the variations in light scattering does affect DOT reconstruction results, we plan to modify Step 1 of HCM by utilizing a global algorithm to find both absorption and scattering from CW data. Further development to solve this problem will be reported for our future work.

It is noteworthy to point out that if prostate cancer does give rise to light-scattering changes, they may help enhance the optical contrast for DOT as long as cancer tissues yield an increase in light scattering with respect to the normal prostate tissues, which seems to be the case according to limited reports (12–15). The rationale of increases in light scattering within prostate cancer tissues is that cancer cells have enlarged nuclei with a higher and irregular cell density, both of which result in a significant increase in light scattering. As mentioned in Section 2.1, CW-based DOT are sensitive only to μ_eff(r ) = μ_a(r )μ_s′(r⃗) ; an increase in μ_s′(r⃗) due to prostate cancer is mathematically equivalent to an increase in optical contrast for reconstructed DOT images, and thus our HCM will still function well or even better with an increase in contrast in μ_eff(r ). Further experimental confirmation from human prostate specimens is underway in our research activities.

Conclusion

In this work we reported a method which improves the image reconstruction in the absence of prior information on cancer location in prostate cancer imaging with diffuse optical tomography. We believe that our hierarchical clustering method is able to produce good results for experimental data and represents a significant step towards future realization of this method for clinical applications. Upon further validation by liquid phantoms, HCM is ready to be applied to prostate cancer imaging by DOT; HCM will be particularly useful for cases where prior location information of several cancers is not clearly available. In a more general sense, this research is a springboard for translating DOT for cancer detection in clinics.