A Mixture Dose–Response Model for Identifying High-Dimensional Drug Interaction Effects on Myopathy Using Electronic Medical Record Databases

Abstract

Interactions between multiple drugs may yield excessive risk of adverse effects. This increased risk is not uniform for all combinations, although some combinations may have constant adverse effect risks. We developed a statistical model using medical record data to identify drug combinations that induce myopathy risk. Such combinations are revealed using a novel mixture model, comprised of a constant risk model and a dose–response risk model. The dose represents the number of drug combinations. Using an empirical Bayes estimation method, we successfully identified high-dimensional (two to six) drug combinations that are associated with excessive myopathy risk at significantly low local false-discovery rates. From the curve of a dose–response model and high-dimensional drug interaction data, we observed that myopathy risk increases as the drug interaction dimension increases. This is the first time that such a dose–response relationship for high-dimensional drug interactions was observed and extracted from the medical record database.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ Drug–drug interactions (DDIs) are a major cause of adverse drug reactions (ADEs) and represent a severe detriment to public health. In the United States alone, DDIs associate with an estimated annual 195,000 hospitalizations and 74,000 emergency room visits. • WHAT QUESTION DID THIS STUDY ADDRESS? ☑ Current computational methods for high-dimensional drug interactions have their own intrinsic limitations, including the lack of a false-positive control, and lack of a functional relationship between high-dimensional drug interactions and ADE frequency. To address these two concerns, in this study we proposed a novel approach, a mixture dose–response model and an empirical Bayes method. • WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ A mixture dose–response model was developed to investigate high-dimensional drug interactions using health databases. A mixture model framework provides local false discovery rate (LFDR) estimates for all high-dimensional drug interactions. The application of this mixture model was exemplified by high-dimensional drug interaction analysis of myopathy risk, using medical record data. Our model accurately identified 2-way to 6-way drug interactions that increased myopathy risk, with their associated LFDR. • HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ Our current statistical model establishes the feasibility to investigate high-dimensional drug interactions with a local false discovery rate estimation. These generated drug interaction signals shall be further validated in molecular pharmacology experiments or clinical studies.

Postapproval adverse drug effects (ADEs) are a major global health concern, costing $75 billion per year1 and causing more than 2 million injuries, hospitalizations, and deaths.2 Drug–drug interactions (DDIs), a major cause of ADEs, thus represent a severe detriment to public health. Based on statistics released recently by the National Health Statistics Report,3,4 and the results of pharmaco-epidemiology studies,5 DDIs in the United States alone are associated with an estimated annual 195,000 hospitalizations and 74,000 emergency room visits.6 With increasing use of polypharmacy,7 the incidence of DDIs is very likely to increase in the coming years.

Traditional pharmacovigilance studies have focused on associating single drugs with single ADEs.8 Pioneering work by DuMouchel using an empirical Bayes (EB) method was a groundbreaking contribution to pharmacovigilance research.9 More recent successful studies have significantly expanded the dimension of associations. For example, Duke et al. investigated drug interactions, using a local medical records database at Indiana University10 to successfully identify multiple, novel drug interaction pairs that significantly increased myopathy risk above a mere additive risk from the two drugs taken alone. In another example of multiple drug-ADE discovery, Tatonetti et al. further expanded association analysis between drugs or drug interactions and adverse events to assess all drugs and ADEs.11 Using the US Food and Drug Administration (FDA)’s Adverse Event Reporting System (FAERS) as a training set, and Stanford’s electronic medical records as a validation set, they identified 47 associations of drugs and drug interaction effects. To detect associations between any combinations of drugs and any combinations of adverse events, they implemented an association rule mining approach based on the FAERS database, claiming that 67% of associations were clinically validated by domain experts.12 Moreover, the computational efficiency of association rule mining was recently further improved by Xiang et al.13

Despite the above-described successes, current computational methods for high-dimensional drug interactions have their own intrinsic limitations, including the lack of a false-positive control, and a lack of functional relationship between high-dimensional drug interactions and ADE frequency. To address these two concerns, in this study we employed a novel approach, a mixture dose–response model combined with an empirical Bayes method for ADE estimation and inference. Please note that the dose here does not refer to the traditional drug dose. Instead, the dose refers to the number of different drugs coadministrated by the patients.

Myopathy, a muscle pathology that can progress to rhabdomyolysis (i.e., a rapid destruction of skeleton muscle),14 is an appropriate example to demonstrate the application of a high-dimensional drug interaction model. Among 7 million FDA spontaneous ADE case reports from 2001–2010, around 100,000 of these concerned myopathy.15 Among 1,634 FDA-approved drugs, 75 drug labels now list myopathy as a potential side effect,16 including the important drug class of statins (lipid-lowering medications), which have a reported myopathy frequency of 5%.17 Considering that more than 18% of Americans over the age of 45 (i.e., 127 million) took statins in 2012, the potential annual number of US myopathy cases could reach 1.15 million. To further investigate this statin–myopathy association, we recently identified six novel drug interaction pairs that significantly increased myopathy risk above a mere additive risk from two single drugs taken separately, using a local medical records database at Indiana University.10

METHODS

Indiana Network for Patient Care data (INPC)

The Indiana Network for Patient Care (INPC) is a health information exchange data repository containing medical records for over 15 million patients throughout the state of Indiana. The Common Data Model (CDM) is a derivation of the INPC containing coded prescription medications, diagnoses, and observational data for 2.2 million patients between 2004 and 2009. The CDM contains over 60 million drug dispensing events, 140 million patient diagnoses, and 360 million clinical observations (e.g., laboratory results, diagnose codes, medications). These data were anonymized and architected specifically for research on adverse drug reactions through collaboration with the Observational Medical Outcomes Partnership project.18

Myopathy definition

Myopathy has a number of potential clinical manifestations.14 This phenotype is mapped to the INPC CDM condition concept ids (Supplementary Table S3). The same myopathy terms are also used in the FDA Adverse Event Reporting System (FAERS) to define the cases.

Cohort study design and statistical data analysis of drug interactions and myopathy in the INPC CDM

Myopathy events and drug exposure

Among patients having a myopathy event, the drug–condition relationship is anchored by its date in the database. For our analysis, any drug exposure occurring within a 1-month window before the diagnosis of myopathy was considered a positive exposure. For a hypothesized drug pair (drug1, drug2), if only one drug was administered in the drug exposure window, it was defined as a single drug exposure; if both drugs were administered within a specific window, it was defined as a two-drug exposure; if neither drug was administered within the 1-month window, it was defined as nonexposure.

New myopathy event definition

Two types of new events were defined. The first type was the first event. However, patients whose first myopathy event was within the first 6 months of the database were excluded; we could not rule out additional myopathy events prior to the starting date of the database (01/01/2004). The second event type included any follow-up myopathy event whose corresponding drug exposure was more than 6 months after the previous myopathy event. In other words, the second type of new myopathy event required a “washout” period (i.e., no drug exposure) of more than 6 months.

Case and control selections

All patients who experienced new myopathy events were selected as cases. Patients who did not experience myopathy served as negative controls.

Drug exposure in the controls

For a control patient, an index time was randomly selected from the new myopathy event times from the cases. Anchored by this index time, a 1-month drug exposure window was defined. Then exposure to a single test drug, two drugs, or neither drug was defined in the same manner as for the cases.

Statistical model

Model specification

A finite mixture density of regression models can be expressed as:

1

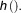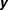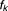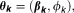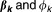where denotes the vector of all parameters for the mixture density The response variable is and are the covariates, where represent the number of comedications. The component-specific distribution is assumed to be univariate and belong to the exponential family.19 The component-specific parameters are given by where are the regression coefficient and dispersion parameter, respectively. Furthermore, the weights needed to satisfy

To prevent overfitting and identification problems related to finite mixture models, we further assumed that:

To simplify the mixture model, we assumed that the component-specific densities were from the same parametric family for each component, i.e.,.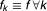

Mixture model of logistic regression

For each drug combination, the number of times that particular combinations appeared in case and control populations were considered outcomes for subsequent analysis. Let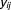 and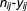 be the outcomes, corresponding to the case and control populations, for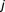th component in-way drug combination. Since the outcome clearly follows a binomial distribution, a generalized linear model approach was needed. In fact, we used a two-component mixture of logistic regression. Each outcome could be attributed to either of two groups: fixed curve or dose–response curve. Then the probability distribution function of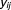 can be expressed in Eq. 2:

4

Let covariate be the number of comedications, the probability under the fixed curve model is constant as the number of comedications increased:

5

and the probability under the dose–response curve model will be increased as the number of comedications increased:

6

Thus, the probability distribution function of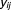 given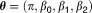 can be expressed as:

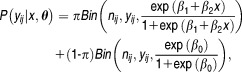7

and the log-likelihood function is given by:

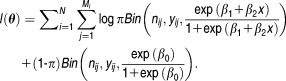8

To find the maximum-likelihood estimates, we used an Expectation-Maximization (EM)20 algorithm by defining

Since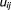 is unobservable, it is treated as a missing value, and the complete data are defined as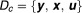. Then the complete data log-likelihood is:

10

Eq. 8 is a mixture of binomial regression equations fitted through the R package “mixtools.”21

Estimation

Much literature is available on estimating mixture models using both frequentist and Bayesian paradigms. An important characteristic of the estimation method is that the number of components must be fixed a priori or simultaneously estimated. The approach we considered in this work was based on the most popular EM algorithm.20

E-Step:

At theth iteration, we need to calculate

11

where in Eq. 7, is the maximum likelihood estimator obtained in iteration.

M-Step:

We replace the missing value by in the complete log-likelihood function Eq. 7. Then we maximize the function:

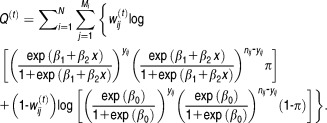12

Regular approaches can be used to obtain the maximum likelihood estimator of parameters in Eq. 9. Starting with proper initial estimates of the parameters, we iterate between E-step and M-step until convergence is achieved.

lFDR computation

The false-discovery rate (FDR) can be considered a by-product of the proposed mixture model. For the two-group model, we defined the “Bayesian FDR” for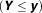 as:

13

However, these tail areas are not very natural for Bayesian FDR estimation. Eq. 10 can be defined as a general rejection region, consisting of infinitesimally “local” regions. Efron et al.22,23 defined the local false discovery rate (LFDR) as:

14

And in our analysis, Eq. 11 can be written as:

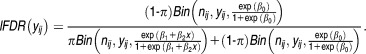15

RESULTS

Data prescreening analysis

It is computationally challenging to investigate the effect of all possible combinations of drugs in the database. Consequently, in this study we limited our focus to a finite number of drugs and their high-dimensional drug interactions. In particular, we emphasize the statistical aspects of high-dimensional drug interaction evidence, not the computational challenge. The subsequent article in this journal24 will address the computational challenges. To that end, the top 20 most frequently distributed drugs (Supplementary Table S1) were selected and all possible two, three, four, five, and six drug combinations were considered and their frequencies determined in case–control populations. For each drug combination, myopathy frequencies were computed. Figure 1 illustrates the distribution of these proportions, showing that some drug combinations elevated myopathy risk upon increased coadministration of other drugs, while myopathy risk stayed constant for many other drug combinations, even with increased numbers of co-committed drugs. This observation strongly motivated us to model myopathy risk using a mixture of two dose–response models. The dose means the number of co-committed drugs. One model followed a classical dose–response curve, while the other model was constant (see Methods section for model specification).

Figure 1.

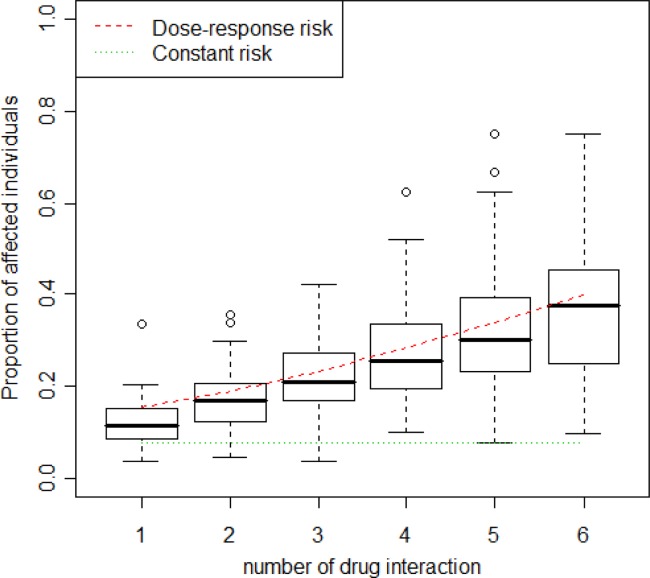
Distribution of the proportion of affected individuals over different drug combinations. Fitted regressions for two groups are fitted on these boxplots.

Result from mixture logistic model

To estimate regression parameters (Supplementary Table S2), we used the EM algorithm described in the Methods section. Specifically, we found that the mixing proportion π, the proportion of high-dimensional drug interactions associated with a constant myopathy risk, was 0.093. The mixture logistic model suggested that some drug interactions follow a dose–response curve. The mixture model is plotted in Figure 1.

Dose–response high-dimensional drug interaction effects on myopathy and their local false discovery rate estimates

Another important observation of the high-dimensional drug interaction dose–response mixture logistic model was that myopathy risk increases as the dimension of drug interaction increases. The estimated maximum myopathy risk, around 40% for high-dimensional drug interactions in our dose range, is a novel observation.

The best feature of our proposed mixture model scheme was its estimation of the LFDRs for all drug combinations, regardless of their dimensionality. Tables 1 2 3 4 5 show the minus log 10 transferred LFDRs for the top 10 drug combinations. It is clear that our model can provide accurate LFDR estimates across various dimensional DDIs. In fact, all the reported top 10 drug interactions from two-way to six-way drug interactions all had LFDRs of less than 5%. We further evaluated the top-ranked drug interaction signals using the Side Effect Resource (SIDER) database (sideeffects.embl.de), finding that all the top 10 drug interactions, from two-way to six-way, contained drugs with myopathy risks previously reported in the SIDER database. These findings strongly confirmed that our high-dimensional drug interactions present true myopathy risks previously associated with single drugs.

Table 1.

Top 2 drug combinations showing increased risk, based on LFDR values

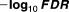
Drug_1	Drug_2	Sample size		Risk
Oxycodone	Acetaminophen	9,384	260.824	0.186
Alprazolam	Acetaminophen	6,092	207.978	0.200
Hydrocodone	Duloxetine	2,582	203.956	0.298
Oxycodone	Duloxetine	1,958	190.879	0.339
Tramadol	Duloxetine	1,812	190.109	0.355
Hydrocodone	Oxycodone	4,726	171.270	0.205
Hydrocodone	Alprazolam	5,296	167.413	0.194
Oxycodone	Alprazolam	2,949	166.647	0.249
Tramadol	Acetaminophen	5,981	147.900	0.179
Zolpidem	Acetaminophen	3,695	142.290	0.209

Bold represents drug combinations reported for myopathy in SIDER 2.

Table 2.

Top 3 drug combinations showing increased risk, based on LFDR values

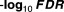
Drug_1	Drug_2	Drug_3	Sample size		Risk
Acetaminophen	Duloxetine	Hydrocodone	2,439	231.392	0.309
Acetaminophen	Oxycodone	Hydrocodone	4,627	169.796	0.207
Acetaminophen	Alprazolam	Hydrocodone	4,983	162.596	0.199
Acetaminophen	Duloxetine	Oxycodone	1,169	140.429	0.352
Acetaminophen	Hydrocodone	Zolpidem	2,821	116.481	0.214
Acetaminophen	Alprazolam	Oxycodone	1,892	115.488	0.249
Acetaminophen	Hydrocodone	Tramadol	3,323	108.268	0.199
Acetaminophen	Duloxetine	Tramadol	768	95.622	0.359
Duloxetine	Oxycodone	Hydrocodone	692	84.164	0.354
Acetaminophen	Alprazolam	Duloxetine	785	81.757	0.324

Bold represents drug combinations reported for myopathy in SIDER 2.

Table 3.

Top 4 drug combinations showing increased risk, based on LFDR values

Drug_1	Drug_2	Drug_3	Drug_4	Sample size		Risk
Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	679	91.808	0.358
Acetaminophen	Alprazolam	Oxycodone	Hydrocodone	1,179	79.761	0.260
Acetaminophen	Alprazolam	Duloxetine	Hydrocodone	618	72.642	0.332
Acetaminophen	Duloxetine	Hydrocodone	Tramadol	499	71.420	0.369
Acetaminophen	Duloxetine	Hydrocodone	Zolpidem	533	63.601	0.334
Acetaminophen	Oxycodone	Hydrocodone	Zolpidem	666	59.200	0.290
Acetaminophen	Alprazolam	Duloxetine	Oxycodone	322	47.981	0.376
Acetaminophen	Alprazolam	Hydrocodone	Zolpidem	757	47.840	0.252
Acetaminophen	Oxycodone	Hydrocodone	Tramadol	800	47.201	0.246
Acetaminophen	Duloxetine	Oxycodone	Tramadol	255	45.131	0.416

Bold represents drug combinations reported for myopathy in SIDER 2.

Table 4.

Top 5 drug combinations showing increased risk, based on LFDR values

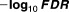
Drug_1	Drug_2	Drug_3	Drug_4	Drug_5	Sample size		Risk
Acetaminophen	Alprazolam	Duloxetine	Oxycodone	Hydrocodone	209	36.591	0.397
Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	Tramadol	174	32.136	0.408
Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	Zolpidem	171	31.777	0.409
Acetaminophen	Alprazolam	Oxycodone	Hydrocodone	Zolpidem	221	30.884	0.353
Acetaminophen	Alprazolam	Duloxetine	Hydrocodone	Zolpidem	174	27.374	0.374
Acetaminophen	Duloxetine	Hydrocodone	Zolpidem	Tramadol	114	24.160	0.439
Acetaminophen	Oxycodone	Hydrocodone	Zolpidem	Tramadol	139	22.126	0.374
Acetaminophen	Alprazolam	Duloxetine	Oxycodone	Zolpidem	99	20.777	0.434
Simvastatin	Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	112	18.894	0.384
Acetaminophen	Alprazolam	Oxycodone	Hydrocodone	Tramadol	235	17.745	0.272

Bold represents drug combinations reported for myopathy in SIDER 2.

Table 5.

Top 6 drug combinations showing increased risk, based on LFDR values

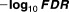
Drug_1	Drug_2	Drug_3	Drug_4	Drug_5	Drug_6	Sample size		Risk
Acetaminophen	Alprazolam	Duloxetine	Oxycodone	Hydrocodone	Zolpidem	66	17.699	0.485
Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	Zolpidem	Tramadol	42	14.013	0.548
Acetaminophen	Alprazolam	Oxycodone	Hydrocodone	Zolpidem	Tramadol	57	13.030	0.439
Acetaminophen	Alprazolam	Duloxetine	Oxycodone	Hydrocodone	Tramadol	53	10.150	0.396
Acetaminophen	Alprazolam	Duloxetine	Oxycodone	Zolpidem	Tramadol	24	10.115	0.625
Simvastatin	Acetaminophen	Alprazolam	Duloxetine	Oxycodone	Hydrocodone	36	9.692	0.472
Acetaminophen	Alprazolam	Duloxetine	Hydrocodone	Zolpidem	Tramadol	41	9.666	0.439
Alprazolam	Duloxetine	Oxycodone	Hydrocodone	Zolpidem	Tramadol	18	7.607	0.611
Simvastatin	Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	Zolpidem	34	7.345	0.412
Acetaminophen	Duloxetine	Oxycodone	Hydrocodone	Zolpidem	Fluoxetine	32	6.811	0.406

Bold drugs are reported for myopathy in SIDER 2.

Examples of high-dimensional drug interactions

Many instances were found that the increased number of co-committed drugs led to increased myopathy risk. For example, the myopathy risk is 0.20 for duloxetine, 0.12 for hydrocodone, and 0.16 for oxycodone. Then the myopathy risk for taking duloxetine and hydrocodone together is 0.30, duloxetine and oxycodone together is 0.34, hydrocodone and oxycodone together is 0.21. If all three drugs are taken together, their myopathy risk becomes 0.35. Thus, their myopathy risk increases as the number of drug combination increases (Figure 2).

Figure 2.

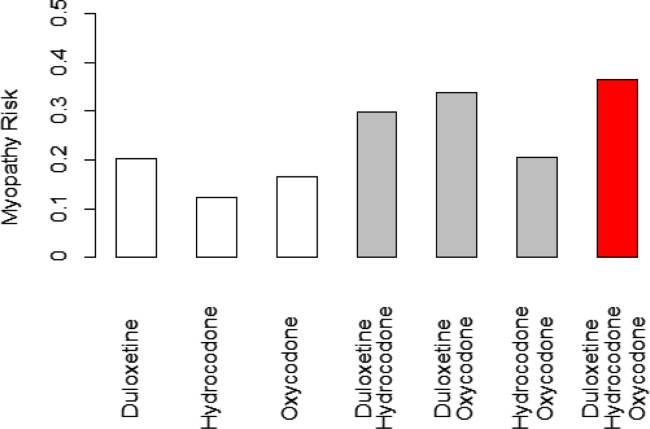
The risks of a single drug, 2-drug combination, and 3-drug combination of duloxetine, hydrocodone, and oxycodone.

DISCUSSION

In this study, a mixture dose–response model was developed to model high-dimensional drug interactions. We used myopathy as the ADE to exemplify a common pathology found in electronic medical records databases. This mixture model framework could accurately estimate the FDR of high-dimensional drug interactions, significantly improving the utility of our mixture model. The dose–response component of our mixture model suggested that the maximum myopathy risk was close to 40%. By using a complementary algorithm for high-dimensional drug interactions, we determined the effects of drug interactions on myopathy risk.

One limitation of our current statistical model is that it can accommodate only a finite number of drugs and their higher-order drug interactions. However, we were still able to analyze the top 20 drugs with the highest frequencies. In order to expand the analysis to all drugs, more sophisticated computational algorithms are needed. A second limitation is that the current model does not account for confounding variables. Like many other pharmacovigilance data analyses, our proposed associations between ADEs and high-dimensional drug interactions need further molecular experimental validation, and using a more stringent pharmacoepidemiological study design and alternative databases. Third, the common data model-derived database from Indiana Patient Care Data contains only the structured diagnosis and medications. We cannot go back and verify the accuracy of the myopathy definition. Hence, the potential misclassification of the ADE is another limitation. Finally, our model cannot provide a directionality of different drugs in a drug combination. This problem will be addressed in the subsequent article in this journal.24 Despite these limitations, we believe our approach has high potential for determining adverse drug effects (not only myopathy) associated with the combination of a large number of drugs that might be coprescribed for patients suffering from specific conditions (e.g., diabetes, hypertension, etc.).

Author Contributions

L.L., P.Z., L.D., L.W., M.L., L.C., C.-W.C., H.-Y.W., S.K., and L.S. wrote paper; L.L., P.Z., and L.D. designed research; L.L., P.Z., and L.D. performed research; P.Z. and L.D. analyzed data.

Conflict of Interest

The authors declare no conflicts of interest.

Supporting Information

Additional Supporting Information may be found in the online version of this article.