Graphic Mining of High-Order Drug Interactions and Their Directional Effects on Myopathy Using Electronic Medical Records

Abstract

We propose to study a novel pharmacovigilance problem for mining directional effects of high-order drug interactions on an adverse drug event (ADE). Our goal is to estimate each individual risk of adding a new drug to an existing drug combination. In this proof-of-concept study, we analyzed a large electronic medical records database and extracted myopathy-relevant case control drug co-occurrence data. We applied frequent itemset mining to discover frequent drug combinations within the extracted data, evaluated directional drug interactions related to these combinations, and identified directional drug interactions with large effect sizes. Furthermore, we developed a novel visualization method to organize multiple directional drug interaction effects depicted as a tree, to generate an intuitive graphical and visual representation of our data-mining results. This translational bioinformatics approach yields promising results, adds valuable and complementary information to the existing pharmacovigilance literature, and has the potential to impact clinical practice.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC? ☑ Drug–drug interactions (DDIs) are a major cause of adverse drug reactions (ADEs). Most traditional pharmacovigilance studies focused on examining single-drug–single-ADE associations. Most DDI studies examined two-way DDI on ADEs, while some studied high-order drug interactions. • WHAT QUESTION DID THE STUDY ADDRESS? ☑ No study has examined the relationships between high-order DDIs. We proposed a novel pharmacovigilance problem for mining directional effects of high-order ADE-associated drug interactions, and developed a graphical mining approach to efficient discovery and effective visualization of the directional DDI patterns with large effect sizes. • WHAT THIS STUDY ADDS TO OUR KNOWLEDGE ☑ Using the directional search method, we identified major contributing drugs in high-dimensional drug interaction signals that are associated with myopathy risk. • HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY AND THERAPEUTICS ☑ This is a newly proposed research problem that has never been studied before, and the identified directional DDI patterns have high potential to aid clinical decisions.

Drug–drug interactions (DDIs), a major cause of adverse drug effects (ADEs), are a serious global health concern, and a severe detriment to public health.1 A recent review2,3 indicated an annual estimate of 74,000 emergency room visits and 195,000 hospitalizations in the US associated with DDIs. While traditional pharmacovigilance studies have focused on examining single-drug–single-ADE associations,4–7 recent studies have started to analyze the DDI effects on ADEs.8–11 For example, Duke et al. analyzed a local medical records database at Indiana University and identified five drug pairs that significantly increased the risk of myopathy (a common muscle pathology) when compared to the expected additive myopathy risk from taking either of the drugs alone.9 Likewise, Tatonetti et al. developed a novel algorithm for revealing latent ADE signals from the US Food and Drug Administration (FDA)’s spontaneous adverse event reporting system (AERS), successfully identifying 171 novel drug pairs for eight ADEs.10

Similar to the reports mentioned above,8–10 most published DDI studies merely examine two-way DDIs on ADEs. While revealing previously unknown high-order DDI effects from the AERS or other electronic medical records data is an underexplored area, it is becoming an emerging topic attracting recent attention.2,12–15 For example, Harpaz et al. applied Association Rule Mining (ARM) to the FDA’s AERS data for discovering detrimental associations of multiple drugs to multiple ADEs.12 To overcome the computational challenge faced by ARM, Xiang et al. proposed an efficient algorithm that used Unified Medical Language System (UMLS) mapping, and frequent closed itemset mining and filtering for discovering multidrug interactions from the AERS, successfully identifying numerous multidrug combinations associated with ADEs.15

To estimate the significance of an identified drug interaction effect, the existing studies typically calculate the overall effect of the drug combination on the ADE. Let (D₁, D₂) be a drug pair with an interaction effect on the ADE. We hypothesize that the increased risk of taking D₂ for patients who are already taking D₁ is often different from the increased risk of taking D₁ for patients who are already taking D₂, although the overall D₁-by-D₂ interaction effect is the same in these two cases. We sought to discover such directional effects, providing valuable information to pharmacovigilance studies with the potential to offer useful guidance to clinical practice.

To the best of our knowledge, no studies have been performed to examine these types of directional interaction effects. To bridge the gap, we propose a novel approach for graphic mining of high-order drug interactions and their directional effects on an ADE. For example, to estimate the directional effect from drug combination (D₁, D₂, …, D_n-1) to drug combination (D₁, D₂, …, D_n-1, D_n), we wanted to calculate the altered ADE risk of adding D_n to the existing drug combination (D₁, D₂, …, D_n-1). For high-order drug interaction studies, there are many different paths from the baseline (i.e., taking none of the drugs in the studied n-drug combination) to taking a n-drug combination, making this directional analysis especially useful in understanding the ADE risk introduced by each single step of these paths.

To demonstrate the proposed method, we perform a data-mining task on a local medical records database. Myopathy, a muscle pathology that can progress to rhabdomyolysis (i.e., a rapid destruction of skeleton muscle),8 is an ADE9,16 with relatively high frequency (e.g., around 4% in our database). It is also a known side effect for close to 80 FDA-approved drugs. Therefore, in this article we focus on analyzing myopathy-related data, in order to demonstrate application of the proposed novel methods for revealing high-order drug interactions and their directional effects.

Standard association measures, such as relative ratios, proportional ratios, odds ratios (ORs), and information components13 can all be used to quantify the specific directional effect on an ADE from one drug combination to another. We demonstrate our approach by using ORs to measure the directional effect. While it is not complicated to obtain the OR, examination of high-order DDI effects on myopathy faces major computational challenges due to the combinational escalation. A relevant issue is that the number of subjects taking all drugs in a high-order drug combination decreases dramatically as the order of the drug combination increases. There could be no or very few subjects taking those high-order drug combinations, making the OR estimation impossible or imprecise. To overcome both issues, we employed frequent itemset mining algorithm, which has been adopted in prior ARM-based DDI studies.12,15

Frequent itemset mining aims to find the itemsets that occur in at least a certain portion of the database, where the portion threshold is specified by a number called "minimum support." By making use of frequent itemset mining, we could filter out all the infrequent drug combinations to achieve the following two goals: 1) a greatly reduced computational time, and 2) a reliably estimated OR, given sufficient support, enabling nonzero or large enough cell sizes in the corresponding contingency tables for calculating the OR. Furthermore, we propose to use a graphical visualization method to plot relevant directional DDI effects in a tree. There are many different paths of adding individual drugs to reach a high-order drug combination. Given a high-order drug combination, our graphical visualization shows the ADE risk introduced by each single step along specific paths, and provides an intuitive and aggregated representation of all relevant results. It has the potential to guide the domain experts to identify interesting and meaningful directional DDI patterns related to myopathy.

METHODS

Our experiments were performed in accordance with our protocol titled "Drug Safety and Efficacy Study Using Electronic Medical Records," approved by the Indiana University Institutional Review Board (IRB).

Indiana Patient Care Data (INPC)

The Indiana Network for Patient Care (INPC) is a health information exchange data repository containing medical records of over 15 million patients throughout the state of Indiana. The Common Data Model (CDM, Version 4) is a derivation of the INPC containing coded prescription medications, diagnoses, and observational data on 2.2 million patients between 2004 and 2009. The CDM contains over 60 million drug-dispensing events, 140 million patient diagnoses, and 360 million clinical observations such as laboratory values. These data have been anonymized and architected specifically for research on adverse drug reactions through collaboration with the Observational Medical Outcomes Partnership project.17

Data description and preprocessing

We analyzed a case–control dataset extracted from INPC CDM based on the myopathy-related cohort study design previously described in Duke et al.9 Incidences of all myopathy symptoms were recorded. The study data consisted of 125,275 case events and 6,263,399 control events. Any event belonging to either group had one or more drugs taken in the corresponding 1-month event window (Supplemental Figure 1). Around 50 control events were randomly selected and included to match the event window of each case event. Given a patient, any follow-up myopathy event was included as a new case event if and only if there is a washout period (i.e., 6 months of no drug exposure) after the previous myopathy event. We preprocessed the raw data and converted it to a binary matrix such that each row represented an event and each column denoted a drug. The resulting dataset was an n-by-m matrix, including n events and m drugs. For a row, its nonzero entries indicated all the drugs taken by the corresponding subject during the event window. Each row associated with either a myopathy event (i.e., case) or a nonmyopathy event (i.e., control). Supplemental Figure 1 shows a schematic representation of an example timeline and the corresponding event-drug matrix.

Measuring directional drug interaction effects

Generally, the OR, also called the cross-products ratio, is a measurement of correlation between an exposure (with/without target drug) and an outcome (with/without target ADE). In this study we used ORs, coupled with their 95% confidence interval,18 to measure the size of a directional drug interaction effect. The OR for a directional drug interaction from drug combination (D₁, D₂, …, D_n-1) to drug combination (D₁, D₂, …, D_n-1, D_n) was defined as the ratio of the following two odds: 1) the odds that myopathy occurs when a patient takes D_n together with drug combination (D₁, D₂, …, D_n-1); and 2) the odds that myopathy occurs when a patient takes (D₁, D₂, …, D_n-1) but not D_n. Table 1 shows the definition of the OR. It is easy to observe that OR values range from 0 to infinity. For a specific value, OR = 1 means that the myopathy risk is not affected by the status of whether or not the target drug is taken; OR >1 means that taking the target drug tends to increase the myopathy risk; and OR <1 means that taking the target drug decreases the myopathy risk.

Table 1.

Contingency table for examining directional effects from taking drug combination (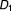,,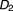 …,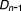) to taking drug combination (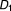,,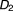 …,,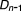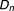), where 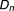is a newly added drug to be co-committed with the existing drug combination (,, …,)

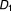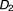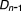	With myopathy	Without myopathy	Total
With (D1, D2, …, Dn-1, Dn)	a	b	a+b
With (D1, D2, …, Dn-1) and without Dn	c	d	c+d
Total	a+c	b+d	a+b+c+d

The odds ratio (OR) of the myopathy risk associated with adding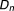 to (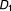,,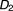 …,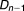) is defined as OR = (a×d)/(b×c).

Mining frequent itemsets

Our task was to identify directional DDIs with large OR values. It is straightforward to compute the ORs for all possible one-way directional drug effects (i.e., from no drug to one drug). However, we faced a major combinatorial escalation challenge for estimating the effects of high-order DDIs. The number of all possible n-drug combinations increases exponentially with regard to n. In practice, not all these possible n-drug combinations could exist in our database. Furthermore, the OR estimate of any rare n-drug combination could be statistically underpowered, due to its small a and b values in the contingency table (Table 4).

Table 4.

Odd ratios (ORs) of the myopathy risk associated with taking D₃ on top of D₁ and D₂: Top 10 findings for N_take ≥ MinSup, where N_take is the number of events where all three drugs were co-committed during the event window

D1	D2	D3	OR	LCI	UCI	Ntake	Ranking
							MinSup = 200	MinSup = 1,000
Ethinyl-Estradiol	Estradiol	Tramadol	10.96	8.60	13.96	481	1
Ethinyl-Estradiol	Estradiol	Oxycodone	10.53	7.65	14.49	272	2
Ethinyl-Estradiol	Estradiol	Cymbalta	10.51	8.65	12.78	813	3
Ethinyl-Estradiol	Loestrin	Cymbalta	9.64	6.75	13.78	242	4
Estradiol	Loestrin	Cymbalta	9.64	6.75	13.78	242	5
Ethinyl-Estradiol	Estradiol	Acetaminophen	7.87	6.40	9.67	871	6
Hydrocodone	Loestrin	Acetaminophen	7.37	0.98	55.76	203	7
Topamax	Butalbital	Acetaminophen	7.30	0.98	54.32	317	8
Ethinyl-Estradiol	Drospirenone	Cymbalta	7.12	4.55	11.15	212	9
Estradiol	Drospirenone	Cymbalta	7.12	4.55	11.15	212	10
Phenylephrine	Chlorpheniramine	Hydrocodone	6.77	4.84	9.47	1,046		1
Hydrocodone	Warfarin	Acetaminophen	5.67	0.77	41.67	1,168		2
Hydrocodone	Acetaminophen	Tizanidine	4.99	4.49	5.55	1,553		3
Hydrocodone	Loratadine	Acetaminophen	4.54	2.68	7.71	1,077		4
Hydrocodone	Pioglitazone	Acetaminophen	4.42	1.07	18.24	1,061		5
Ethinyl-Estradiol	Estradiol	Alprazolam	4.41	3.49	5.58	1,008		6
Hydrocodone	Celebrex	Acetaminophen	4.32	1.34	13.91	1,308		7
Hydrocodone	Hydrochlorothiazide	Acetaminophen	3.75	1.51	9.28	1,362		8
Hydrocodone	Acetaminophen	Topamax	3.70	3.26	4.20	1,142		9
Hydrocodone	Bupropion	Acetaminophen	3.49	1.68	7.26	1,362		10

Drugs reported for myopathy in SIDER 2 are shown in bold. LCI and UCI indicate the lower and upper limits of the confidence interval, respectively.

To address the above challenges, we proposed to focus our analyses only on the “frequent” drug combinations. Given a combination, we defined its “support” as the number of its occurrences in our data (i.e., number of rows containing this combination). We set a minimum support threshold MinSup, and regarded a drug combination "frequent" if its support is ≥ MinSup. In our study, we only estimated ORs for directional effects related to frequent drug combinations, greatly reducing computational costs and yielding well-powered OR estimates.

To identify frequent drug combinations, we apply the classical Apriori algorithm for mining frequent itemsets in a transactional database19–21 (see Algorithm1 below). We used a k-itemset to denote an itemset containing k elements, and used a k-subset to denote a subset containing k elements.

Algorithm 1 (mining frequent itemsets)

Input: (1) D, a collection of drug combinations (i.e., the binary event-drug matrix); (2) MinSup, a user-specified minimum support.

Output: F, a set of all frequent itemsets (i.e., frequent drug combinations)

1. 1. C₁ = the set of all 1-itemsets; k = 1; F = empty set;

2. 2. while C_k is not empty

3. 3. Count supports for all itemsets in C_k by a pass over D;

4. 4. F_k = {x | x and the support of C_k ≥ MinSup};

5. 5. C_k+1 = {x | x is a (k+1)-itemset such that any of its k-subsets ∈ F_k};

6. 6. F = F ∪ F_k; k = k + 1;

7. 7. return F;

Briefly, after initialization in Step 1, we computed frequent itemsets in passes. At pass k, we found all frequent k-itemsets (i.e., all the k-drug combinations with support ≥ MinSup; see Steps 2, 3). Let F_k be the set of all frequent k-itemsets. In Step 5, F_k is used to generate C_k+1, the candidate itemsets for whom support is counted in the (k+1)-th pass. The key idea is that an itemset x can be pruned from C_k+1 if any of its k-subsets does not belong to F_k because any subset of a frequent itemset must also be frequent. This iterative procedure terminates either when k reaches the total number of items or when C_k is empty.

Identifying and visualizing directional drug interactions with large ORs

Given a minimum support threshold MinSup, we applied Algorithm1 to identify all the frequent drug combinations. For each frequent drug combination (D₁, D₂, …, D_n-1,D_n), we computed the OR for each of the following directional drug interactions: 1) from (D₂, …, D_n-1,D_n) to (D, D₂, …, D_n-1,D_n), 2) from (D₁, D₃, …, D_n-1,D_n) to (D₁, D,D₃, …, D_n-1,D_n), …, and (n) from (D₁, D₂, …, D_n-1) to (D₁, D₂, …, D_n-1,D_n). Using "D3: Data-Driven Documents" (http://d3js.org/), a JavaScript library, we implemented a directional DDI tree visualization to present the resulting ORs in an intuitive and organized fashion (see Figures 3). The value shown on each tree node indicates the directional DDI effect on myopathy, which is the OR of the myopathy risk associated with taking the drug shown on the current node on top of all the other drugs shown on the path from the root to the current node. We also report a few top findings of directional drug interactions with highest ORs.

Figure 3.

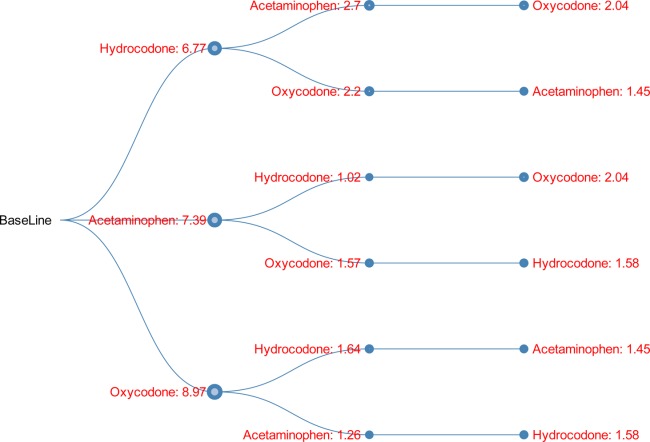
Directional DDI tree for 3-drug combination (hydrocodone, acetaminophen, oxycodone). The value shown on each node indicates the OR of the myopathy risk associated with taking the current drug on top of all the other drugs from the root to the current node. The node size is proportional to the OR. Green indicates OR <1, and red indicates OR >1.

RESULTS

Data processing

We extracted myopathy-related data from the Common Data Model, a derivation of the INPC. After preprocessing, we obtained a n-by-m binary event-drug matrix, including n = 6,388,674 events and m = 212 drugs. The nonzero entries of a row indicate all the drugs taken during the event window. Each row was associated with a myopathy event (i.e., case) or a nonmyopathy event (i.e., control). This approach yielded 125,275 cases and 6,263,399 controls.

Mining frequent drug combinations

To enable possible and precise estimates of directional drug interactions, we computed the directional interaction effects only for all the frequent drug combinations, i.e., those whose support was ≥ MinSup (a user-specified minimum support). Given a combination, we defined its "support" as the number of its occurrences in our data. In this proof-of-concept study, our analysis was focused on one-way, two-way, and three-way drug combinations. Thus, given a specific MinSup, our first task was to identify all frequent one-way, two-way, and three-way drug combinations. We implemented our method using R, and performed the experiments on a Linux Xeon 64-bit dual CPU workstation. We compared the performance of Algorithm1 to that of a naïve method (i.e., computing the supports for all possible combinations and then selecting the frequent ones). It took us 312.9 hours to finish the computation using the naïve method and only 6.5 hours for MinSup = 1,000 (or 36.4 hours for MinSup = 200) using Algorithm 1.

Identifying directional drug interactions

We estimated the directional drug interactions of frequent 1-drug, 2-drug, and 3-drug combinations for MinSup = 200 and MinSup = 1,000, respectively. Shown in Table 2 are the top 10 findings for single-drug experiments. For MinSup = 200, the OR values ranged from 23.38 for the highest-ranking drug (tizanidine) to 10.36 for the tenth highest-ranking drug (quinine). For MinSup = 1,000, three of the previous top 10 findings (i.e., cyclobenzaprine, naloxone, and quinine) did not meet the minimum support requirement, and three new drugs (i.e., chlorzoxazone, tramadol, orphenadrine) were included in the top 10 list with OR values ranging from 9.78 to 9.18.

Table 2.

Odd ratios (ORs) of the myopathy risk associated with taking D₁: Top 10 findings for N_take ≥ MinSup, where N_take is the number of events where the drug was committed during the event window

D1	OR	LCI	UCI	Ntake	Ranking
					MinSup = 200	MinSup = 1,000
Tizanidine	23.38	22.37	24.44	9,345	1	1
Fentanyl	19.69	18.33	21.15	3,738	2	2
Methadone	15.32	14.11	16.63	3,207	3	3
Morphine	13.51	12.38	14.75	3,005	4	4
Tegaserod	11.60	10.34	13.01	1,911	5	5
Hydroxychloroquine	11.28	10.59	12.02	6,466	6	6
Cyclobenzaprine	11.16	8.22	15.17	274	7
Naloxone	10.69	8.67	13.17	608	8
Transdermal-Patch	10.38	9.79	11.01	7,969	9	7
Quinine	10.36	8.35	12.87	577	10
Chlorzoxazone	9.78	8.60	11.12	1,702		8
Tramadol	9.25	8.97	9.54	32,327		9
Orphenadrine	9.18	7.97	10.58	1,465		10

Drugs reported for myopathy in SIDER 2 are shown in bold. LCI and UCI indicate the lower and upper limits of the confidence interval, respectively.

Shown in Table 3 are the top 10 findings for the two drug combination experiments. For MinSup = 200, the directional interaction from taking ethinyl-estradiol alone to taking both ethinyl-estradiol and tizanidine (i.e., taking tizanidine on top of ethinyl-estradiol) made the top one in the list, with an effect size of OR = 24.68. This indicates that in the population of patients taking ethinyl-estradiol, the addition of tizanidine was associated with an increased myopathy risk of OR = 24.68. For MinSup = 200, the OR values of the top 10 findings ranged from 24.68 (i.e., the directional effect from (ethinyl-estradiol) to (ethinyl-estradiol, tizanidine)) to 15.84 (i.e., the directional effect from (dextromethorphan] to (dextromethorphan, acetaminophen)). For MinSup = 1,000, the OR values of the top 10 findings ranged from 14.01 (i.e., the directional effect from (ethinyl-estradiol) to (ethinyl-estradiol, tramadol)) to 6.93 (i.e., the directional effect from (estradiol) to (estradiol, hydrocodone)).

Table 3.

Odd ratios (ORs) of the myopathy risk associated with taking D₂ on top of D₁: Top 10 findings for N_take ≥ MinSup, where N_take is the number of events where both drugs were co-committed during the event window

D1	D2	OR	LCI	UCI	Ntake	Ranking
						MinSup = 200	MinSup = 1,000
Ethinyl-Estradiol	Tizanidine	24.68	20.04	30.39	431	1
Bupropion	Tizanidine	24.01	19.43	29.66	367	2
Singulair	Tizanidine	22.64	18.56	27.62	411	3
Loratadine	Tizanidine	19.33	14.75	25.33	217	4
Quetiapine	Tizanidine	18.01	14.07	23.05	269	5
Phenylephrine	Acetaminophen	17.91	12.39	25.90	208	6
Estradiol	Tizanidine	17.80	14.15	22.39	350	7
Risperdal	Acetaminophen	16.32	12.29	21.66	267	8
Hydrochlorothiazide	Tizanidine	15.94	12.48	20.35	296	9
Dextromethorphan	Acetaminophen	15.84	12.66	19.83	446	10
Ethinyl-Estradiol	Tramadol	14.01	12.12	16.19	1,249		1
Loratadine	Acetaminophen	10.09	8.88	11.45	1,379		2
Estradiol	Cymbalta	9.06	7.82	10.50	1,312		3
Ethinyl-Estradiol	Cymbalta	8.96	7.82	10.26	1,924		4
Ethinyl-Estradiol	Acetaminophen	8.83	7.75	10.07	2,134		5
Loratadine	Hydrocodone	8.58	7.50	9.81	1,262		6
Estradiol	Acetaminophen	8.36	7.27	9.62	1,555		7
Phenylephrine	Hydrocodone	7.64	5.97	9.77	2,791		8
Loratadine	Alprazolam	7.49	6.51	8.62	1,190		9
Estradiol	Hydrocodone	6.93	5.93	8.10	1,365		10

Drugs reported for myopathy in SIDER 2 are shown in bold. LCI and UCI indicate the lower and upper limits of the confidence interval, respectively.

Shown in Table 4 are the top 10 findings for our three drug combination experiments. For MinSup = 200, the top 10 OR values ranged from 10.96 (i.e., the directional effect from (ethinyl-estradiol, estradiol) to (ethinyl-estradiol, estradiol, tramadol)) to 7.12 (i.e., the directional effect from (estradiol, drospirenone) to (estradiol, drospirenone, cymbalta)). For MinSup = 1,000, the top 10 OR values ranged from 6.77 (i.e., directional effect from (phenylephrine, chlorpheniramine) to (phenylephrine, chlorpheniramine, hydrocodone)) to 3.49 (i.e., the directional effect from (hydrocodone, bupropion] to (hydrocodone, bupropion, acetaminophen)).

Visualizing directional drug interactions

Given a high-order drug combination (D₁, D₂, …, D_n) with a sufficient support, we were interested in an overall picture of all individual directional drug interactions traversing different paths from baseline to (D₁, D₂, …, D_n). Here, the baseline event indicated an event where none of (D₁, D₂, …, D_n) were taken during the event window. To achieve this goal, we implemented a directional DDI tree visualization to present the resulting ORs in an intuitive and organized fashion (see Figures 3).

Shown in Figure 1 is a visualization of an example 3-drug combination: (ethinyl-estradiol, estradiol, tramadol). For example, given the path ("baseline" → "ethinyl-estradiol: 0.92" → "estradiol: 1.19" → "tramadol: 10.96"), we have the following observations. First, the OR of myopathy associated with taking ethinyl-estradiol was 0.92, indicating a decreased risk. Second, the OR of myopathy associated with taking estradiol on top of ethinyl-estradiol was 1.19, indicating a slightly increased risk. Third, the OR of myopathy associated with taking tramadol on top of ethinyl-estradiol and estradiol was 10.96, indicating a significantly increased risk. Note that this OR is the top finding in the experiment of MinSup = 200 shown in Table 4. Such visualization has the potential to provide valuable information and guidance in clinical practice. For a patient who is currently taking ethinyl-estradiol and estradiol, a doctor may want to be careful on prescribing the additional drug tramadol, since this could significantly increase the myopathy risk with OR = 10.96.

Figure 1.

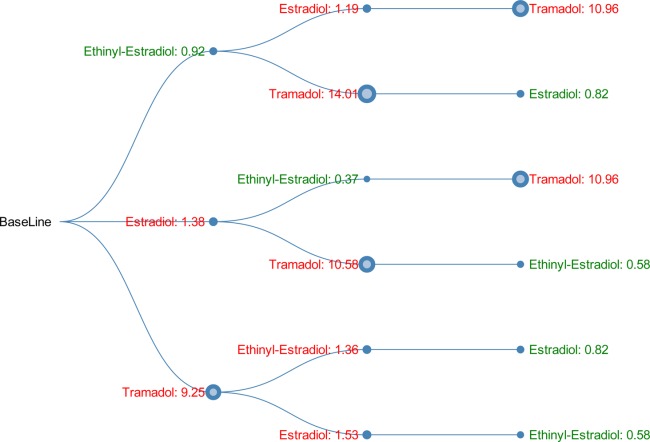
Directional DDI tree for 3-drug combination (ethinyl-estradiol, estradiol, tramadol). The value shown on each node indicates the OR of the myopathy risk associated with taking the current drug on top of all the other drugs from the root to the current node. The node size is proportional to the OR. Green indicates OR <1, and red indicates OR >1.

Shown in Figure 2 is the DDI tree visualization for another 3-drug combination: (hydrocodone, acetaminophen, tizanidine). Given the path “baseline” → "hydrocodone: 6.77" → "acetaminophen: 2.7" → "tizanidine: 4.99", we know that 1) adding hydrocodone to the baseline increased myopathy risk with OR = 6.77; 2) adding acetaminophen to hydrocodone further increased myopathy risk with OR = 2.7; and 3) adding tizanidine to the existing 2-drug combination (hydrocodone, acetaminophen) further increased myopathy risk with OR = 6.77 (i.e., the third top finding in the MinSup = 1,000 result shown in Table 4).

Figure 2.

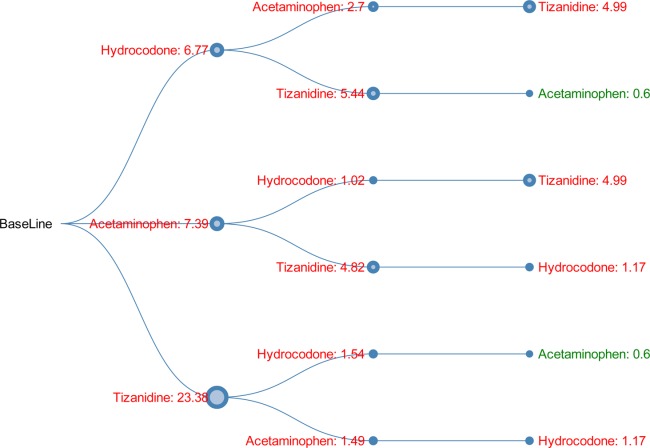
Directional DDI tree for 3-drug combination (hydrocodone, acetaminophen, tizanidine). The value shown on each node indicates the OR of the myopathy risk associated with taking the current drug on top of all the other drugs from the root to the current node. The node size is proportional to the OR. Green indicates OR <1, and red indicates OR >1.

Shown in Figure 3 is the DDI tree visualization for another 3-drug combination (hydrocodone, acetaminophen, oxycodone). This combination has been ranked in the second place in the list of top 3-drug combinations showing increased risk based on false-discovery rate (FDR) values, reported in the companion article.16 In this example, no matter which path was taken from the baseline to the 3-drug combination, each single step always increased myopathy risk to various degrees of effect size.

DISCUSSION

Previous pharmacovigilance studies examined ADEs, including single-drug–single-ADE associations,4–7 two-way DDI effects,8–10 and recently multidrug–multi-ADE associations.2,12–15 For DDI effects, the existing studies typically evaluated the overall effect of the drug combination on the ADE.2,8–10,12–15 In this study we proposed and studied a new pharmacovigilance problem, i.e., estimation of the directional DDI effect on an ADE when co-committing a new drug with an existing drug combination. We strongly believe that the solution to this problem can precisely estimate the ADE risk of any prescribed new drug while taking into consideration all the drugs a patient has already been taking.

To that end, we employed the Apriori algorithm to efficiently identify frequent drug combinations from an electronic medical records database, evaluated all the directional drug interaction effects associated only with those frequent drug combinations, to reveal the top directional interactions with the largest effect sizes measured by ORs. Our empirical studies, performed using myopathy-relevant data extracted from the INPC database, yielded promising results. We also devised a novel visualization method to plot all the directional DDI effects in a tree to provide an intuitive representation of our data-mining results to help us identify interesting and meaningful directional DDI patterns related to specific ADEs.

In a previous two-way DDI study, Duke et al. analyzed the same data and identified five drug pairs that significantly increased the risk of myopathy, as compared to the expected additive myopathy risk from taking either drug alone.9 For example, one of the five drug pairs was "loratadine and simvastatin." Although we knew the overall myopathy risk associated with this drug pair is significantly increased (compared to the baseline), we were not sure about the directional effects of adding one drug to another. This current work can help provide such useful information. In our analysis, we found the following OR values for myopathy risk: 1) OR = 1.71 for simvastatin alone; 2) OR = 2.59 for loratadine alone; 3) OR = 5.11 for adding loratadine on top of simvastatin; and 4) OR = 3.47 for adding simvastatin on top of loratadine. This information is complementary to the overall effect, and can help further dissect the overall effect.

In the top findings of the current work, shown in Tables 2 3 4, we replicated a few drugs reported for myopathy in the SIDER 2 database (sideeffects.embl.de), including fentanyl, hydroxychloroquine, and tramadol. In addition, we also reported many novel findings that warrant further investigation. For example, in Figure 2, taking hydrocodone alone has an increased myopathy risk with OR = 6.77, and taking tizanidine alone has an increased myopathy risk with OR = 23.38. The increased risk (OR = 1.54) of taking hydrocodone for patients who are already taking tizanidine is much lower than the increased risk (OR = 5.44) of taking tizanidine for patients who are already taking hydrocodone. Of note, since the problem we investigated in this work is new, we expect these analyses could yield novel findings with the potential to further our understanding of single drug effects or multiple drug interactions on a specific ADE(s).

In a companion article16 submitted to the same journal, we proposed a mixture dose–response model for high-order drug interaction effects on myopathy, validating the model using the same data. Based on FDR values, (acetaminophen, oxycodone) and (hydrocodone, oxycodone) were respectively ranked as the No. 1 and No. 6 findings in the top 2-drug combinations showing increased risk, and (hydrocodone, acetaminophen, oxycodone) was ranked as No. 2 in the top 3-drug combinations showing increased risk. This work could provide additional detailed information to the above two findings. For example, Figure 3 shows all the directional DDI effects associated with these three drugs. From those, one can understand the individual myopathy risk introduced by each single step.

The scope of this work is twofold: 1) to inform of the drug combinations that potentially induce myopathy, and 2) to introduce a method for calculating directional DDIs. We have included the identified top 100 DDI signals in Supplemental Table 1 and published the software package on the web (http://www.iu.edu/∼shenlab/tools/dditree/). We believe this is the first proof-of-concept study examining and visualizing directional DDI effects for high-order drug interactions. Based on our initial analyses and findings, there are many future directions to pursue: 1) study higher order interactions (including >3 drugs); 2) examine directional effects for adding >1 drugs to an existing drug combination; 3) include confounding variables in the model and algorithm design; 4) integrate this approach with other methods (e.g., the mixture dose–response model) to form a unified framework for better understanding the molecular and other underlying mechanisms; and 5) apply this method to study directional DDI effects on other ADEs. In the long run, we aim to further improve this translational bioinformatics method to generate a variety of visual atlases of directional DDI effects for different ADEs, providing valuable and complementary information to existing pharmacovigilance knowledge, to potentially impact clinical practice.

Conflict of Interest

The authors have no conflict of interest to disclose.

Author Contributions

L.S. and L.D. wrote the article; L.S., S.K.Q. and L.L. designed the research; L.S., L.D., A.C. and L.L. performed the research; L.S., L.D., A.C., L.C., H.W. and P.Z. analyzed the data; L.S. contributed new reagents/analytical tools.

Supporting Information

Additional Supporting Information may be found in the online version of this article.