A double barrier memristive device

Abstract

We present a quantum mechanical memristive Nb/Al/Al₂O₃/Nb_xO_y/Au device which consists of an ultra-thin memristive layer (Nb_xO_y) sandwiched between an Al₂O₃ tunnel barrier and a Schottky-like contact. A highly uniform current distribution for the LRS (low resistance state) and HRS (high resistance state) for areas ranging between 70 μm² and 2300 μm² were obtained, which indicates a non-filamentary based resistive switching mechanism. In a detailed experimental and theoretical analysis we show evidence that resistive switching originates from oxygen diffusion and modifications of the local electronic interface states within the Nb_xO_y layer, which influences the interface properties of the Au (Schottky) contact and of the Al₂O₃ tunneling barrier, respectively. The presented device might offer several benefits like an intrinsic current compliance, improved retention and no need for an electric forming procedure, which is especially attractive for possible applications in highly dense random access memories or neuromorphic mixed signal circuits.

Memristive devices have emerged as promising candidates in the field of non-volatile data storage for future information technology where the device resistance depends on the history of the applied voltage¹,²,³,⁴. Due to their simple two terminal capacitor-like layer sequence (metal-insulator-metal), highly scalable crossbar arrays and multilevel memory structures have been proposed where memristive devices might overcome technical and physical scaling limits of modern semiconductor devices⁵,⁶,⁷. Their binary and analog properties qualify them as promising building blocks for in-situ-computing⁸. Apart from memory and logic applications, the use of memristive devices as artificial synapses in neuromorphic circuits is intensively discussed, focusing on bio-inspired artificial neuronal networks⁹,¹⁰. In general, today’s research on memristive devices and networks is characterized by numerous elegant system concepts for novel memories, programmable logic units and neuromorphic circuits limited only by a lack of reliable devices and a thorough understanding of the involved switching mechanisms. Nevertheless, the steady progress in memristive device performance in recent years could close the gap between promising computing concepts and the hardware realizations in the near future.

Although the underlying physical mechanism is often unclear, the majority of memristive devices involve the random creation of one or more conductive filaments, resulting in a poor switching reproducibility and a high device-to-device variability⁶,¹¹,¹²,¹³. Moreover, most memristive devices require an initial and individual electrical forming step, additionally complicating their use in crossbar architectures and complex mixed-signal circuits.

Interface-based devices may overcome these restrictions, because uniform interface effects lead to a homogeneous change in resistance, avoiding the randomness generated by electroforming or filament growth¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰. Most of the investigated interfacial devices are oxide-metal junctions, where the resistive switching mechanism results from changes at a Schottky-like contact¹⁵,²¹. A less common approach uses junctions consisting of a tunnel barrier and a memristive layer, where the change in resistance results from a varying electron tunneling probability¹⁷,¹⁸,²²,²³. To explain the not completely understood resistance change in interface-based devices, two rather different models are usually considered: The first model is related to the concept of charge injection, where traps within the memristive layer or at the metal interface are charged and discharged, resulting in a high- and low-resistances state, respectively¹⁴,²⁴,²⁵,²⁶,²⁷,²⁸. In the second model, the applied electric field is sufficient to move ions within the memristive layer, leading to a change in interfacial properties and consequently changing the overall device resistance. Besides interface effects, contributions from the memristive layer itself (e.g. local chemical bounds, oxide phases, doping, local heating effects and so on) may affect or oppose the resistive switching, making a thorough analysis of the underlying mechanism more complicated. Therefore, scaling down the thickness of the memristive layer to the length scale of a single electron wave may provide an opportunity to avoid the stated contributions of the memristive layer, while the use of a second barrier might restrict switching effects to interfacial contributions and to derive a physical model of the resistance switching mechanisms.

Here, a double barrier device with an ultra-thin memristive layer sandwiched between a tunnel barrier and a Schottky-like contact is presented. The layer sequence of the device is Al/Al₂O₃/Nb_xO_y/Au, with a thickness of 1.3 nm for the Al₂O₃ tunnel barrier and 2.5 nm for the Nb_xO_y layer. In order to get a deeper understanding of the particular interfacial contributions to the observed switching characteristics, single barrier devices were fabricated, i.e. an Al/Al₂O₃/Nb_xO_y/Nb tunnel junction excluding the Schottky contact and an Nb/Nb_xO_y/Au Schottky contact without the tunneling barrier. Based on the experimental results an equivalent circuit model was developed, which shows evidence that the Nb_xO_y layer may act as an ionic/electronic (mixed) conductor, where the switching mechanism is related to mobile ions within the Nb_xO_y. This might offer several benefits. For example, the properties of the Al₂O₃ tunnel barrier could define the lower resistance boundary (i.e. the LRS) of the junction. In particular, amorphous Al₂O₃ is known to be a “good” tunnel barrier (i.e., elastic electron tunnelling dominates the transport) where the barrier thickness can be effectively controlled during growth²⁹. The tunnel barrier thickness acts as a current limiter and represents an essential design parameter as will be explained in detail. The tunnel barrier and the gold electrode define chemical barriers for the ionic species, confining them within the Nb_xO_y. A saturation of the ion density (number of ions per area) at either interface will define the LRS and HRS. No current compliance is needed, due to the self-limited ion assembly at either interface. The finite activation energies of the ionic species will lead to a frozen (memory) resistance state in case of zero bias and will therefore improve the data retention compared to a purely electronic switching mechanism, which face a voltage-time dilemma³⁰.

Results

Device structure

Figure 1 shows the cross-section of the double barrier Al/Al₂O₃/Nb_xO_y/Au memristive device. The thickness of the Al₂O₃ tunnel barrier is 1.3 nm and that of the Nb_xO_y layer 2.5 nm. In general, two rather different physical mechanisms may describe the memristive characteristics of this double barrier device. In Fig. 1(a), Nb_xO_y acts as a trapping layer for electrons, where localized electronic states within the Nb_xO_y layer are filled or emptied depending on the applied bias voltage polarity. Therefore, the amount of charge within this layer depends on the history of the applied bias voltage, where charged traps and discharged traps will represent the high- and low-resistances state, respectively. The first charge trapping model, originally used to describe resistive switching in metal-insulator-metal (MIM) Al/SiO (20 nm–300 nm)/Au junctions, was developed from Simmons and Verderber³¹.

Figure 1. Two models to describe the memristive double barrier tunnel junctions.

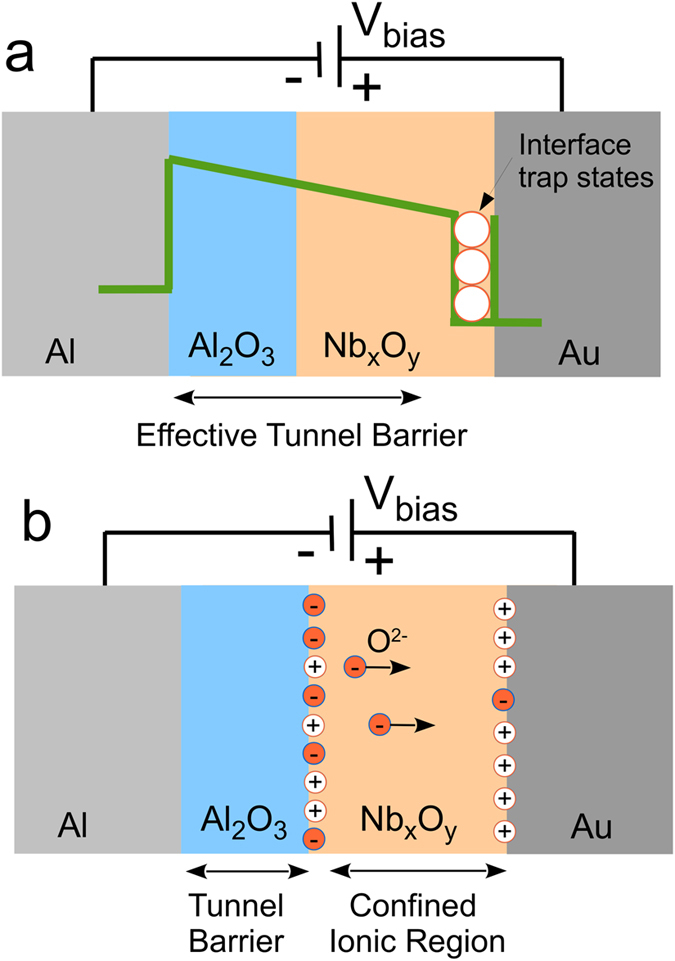
(a) Simplified cross-sectional view of the memristive tunnel junctions. Here, trap states within the Nb_xO_y are assumed. The filling and emptying of traps by injected electrons varies the amount of charge in the Nb_xO_y layer and therefore the resistance. (b) An alternative model to (a). Under forward bias voltages V_bias oxygen ions (orange circles) can move inside the Nb_xO_y layer, where their diffusion region is confined by the Al₂O₃ layer and the Nb_xO_y/Au interface. Both, the model in (a) as well as the model in (b) describe the memristive I–V characteristics.

In contrast to the charge injection model of Fig. 1(a), Nb_xO_y acts as an ionic/electronic (mixed) conductor in the model shown in Fig. 1(b). Here, Nb_xO_y represents a solid state electrolyte, while Al₂O₃ serves as a tunnel barrier. By applying a bias voltage, oxygen ions (within the Nb_xO_y) drift towards the tunnel barrier or Au interface in dependence on their charge and mobility. The redistribution of the ionic species will affect essential interfacial parameters (e. g. density of states, local barrier height, barrier thickness and so on) at the Al₂O₃/Nb_xO_y and the Nb_xO_y/Au (Schottky) interface simultaneously. By applying an opposite bias, the original ion distribution should be obtained. As a consequence, the electronic transport, i.e. the device resistance, will be altered in accordance to the local ion distribution leading to memristive I–V characteristics. We would like to emphasize that the charge injection and the mobile ion model (Fig. 1(a,b)) will be discussed below with respect to the experimental findings.

Resistive switching behaviour

A representative current-voltage (I–V) characteristic of the double barrier memristive device is depicted in Fig. 2(a). Neither an initial forming procedure nor a current compliance was used. Instead, a linear voltage sweep was applied to the Au electrode, while the current was measured simultaneously. In particular, the voltage was ramped linearly from 0 V to 2.8 V in order to set the device from the high resistance state (HRS) to the low resistance state (LRS), as marked by arrows in Fig. 2(a). To set the device resistance back to the initial HRS the voltage was ramped linearly from 2.8 V to −2 V and afterwards increased to 0 V. As a result, a pinched hysteresis loop of a bipolar memristive device was obtained. The fluctuations for small currents under negative bias indicate the current resolution of our set-up rather than physically relevant mechanisms. The most apparent feature of the memristive hysteresis is the asymmetry between positive and negative bias, which can be attributed to the Schottky-like Nb_xO_y/Au contact. Moreover, an important feature of our double barrier memristive device is the gradual resistance change rather than abrupt resistance jumps. An abrupt jump in the device resistance during voltage sweeps may indicate a filamentary-driven resistance switching effect, while gradual changes may result from homogeneously changed interface properties¹⁴,¹⁶. This suggestion is supported by the R × A vs. A plot shown in Fig. 2(b). For junctions with areas ranging from 70 μm² to 2300 μm², R × A for the high and low resistance states is independent of the device area, which suggests a homogeneous switching mechanism.

Figure 2. Resistive switching characteristics of the memristive double barrier device.

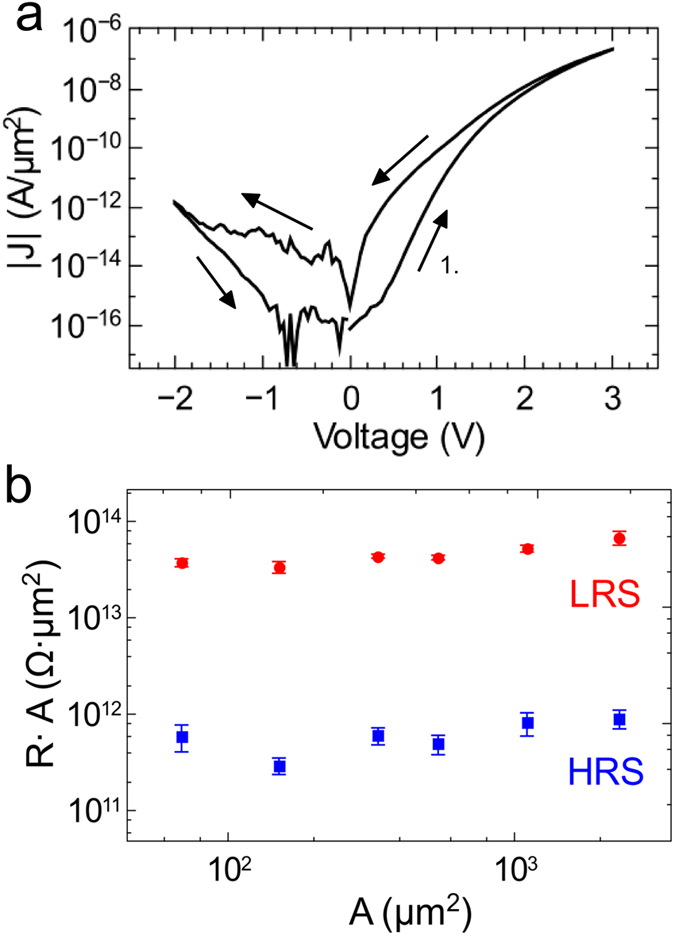
(a) Absolute current density |J| as function of the applied bias voltage. (b) The area-resistance product vs. junction-area curve of the double barrier device measured at 0.5 V indicates a homogeneous area dependent charge transport. The error bars are obtained from 5 cells of each area. Junction areas were confirmed with optical microscopy.

Interface barrier contributions

For interface-based memristive behavior, the charge transport through the tunneling barrier has to be dominated by elastic tunneling rather than trap induced tunneling or interfacial trap states within the Al₂O₃ barrier. This requires a nearly defect free, highly stable, and electrically high-quality tunnel barrier. Additionally, it requires that the memristive behavior originates from changes in the Nb_xO_y layer, while the Al₂O₃ layer is stable under a changed contact resistance at the Nb_xO_y interface. In particular, Al₂O₃ ranks among the best tunnel barriers for this purpose. In the field of superconductivity, Al₂O₃ is intensively used as a tunnel barrier in Josephson junctions, where the Nb/Al/Al₂O₃ technology is the prevailing technology²⁹. Moreover, the sputtered Nb_xO_y has been found to be amorphous by using X-ray diffraction measurements. Therefore, the Al₂O₃ can be assumed to be of higher quality than the Nb_xO_y.

To get a deeper understanding of the transport mechanism, two additional devices were investigated to separate the particular interfacial contributions. Therefore, Al/Al₂O₃/NbO_x tunnel junctions excluding the Schottky contact, as well as Nb/Nb_xO_y/Au Schottky contacts without the tunnel barrier were prepared, as shown in Fig. 3. Here, Nb is used as the electrode to keep the difference in work function between the electrode and Nb_xO_y layer low. The obtained I–V curves are compared in Fig. 3(a,b). While memristive behavior is clearly visible for the Nb/Nb_xO_y/Au contact, no change in the device resistance behavior was observed for Al/Al₂O₃/Nb_xO_y tunnel junctions (Fig. 3(a)). This indicates that the Nb_xO_y/Au Schottky-like interface contributes to the resistive switching observed in the double-barrier device. Memristive devices with oxide-metal Schottky contacts have been studied extensively, and the origin of the resistive switching is supposed to be the modulation of the Schottky barrier height¹⁵. Nonetheless, the aforementioned observations indicate that the two interfaces Al₂O₃/Nb_xO_y and Nb_xO_y/Au cannot be treated as separate entities and involve a very strong mutual interdependence. However, the following analysis considers the influence of both interfaces individually, while taking into account that both mechanisms should be treated simultaneously.

Figure 3. Interface contributions.

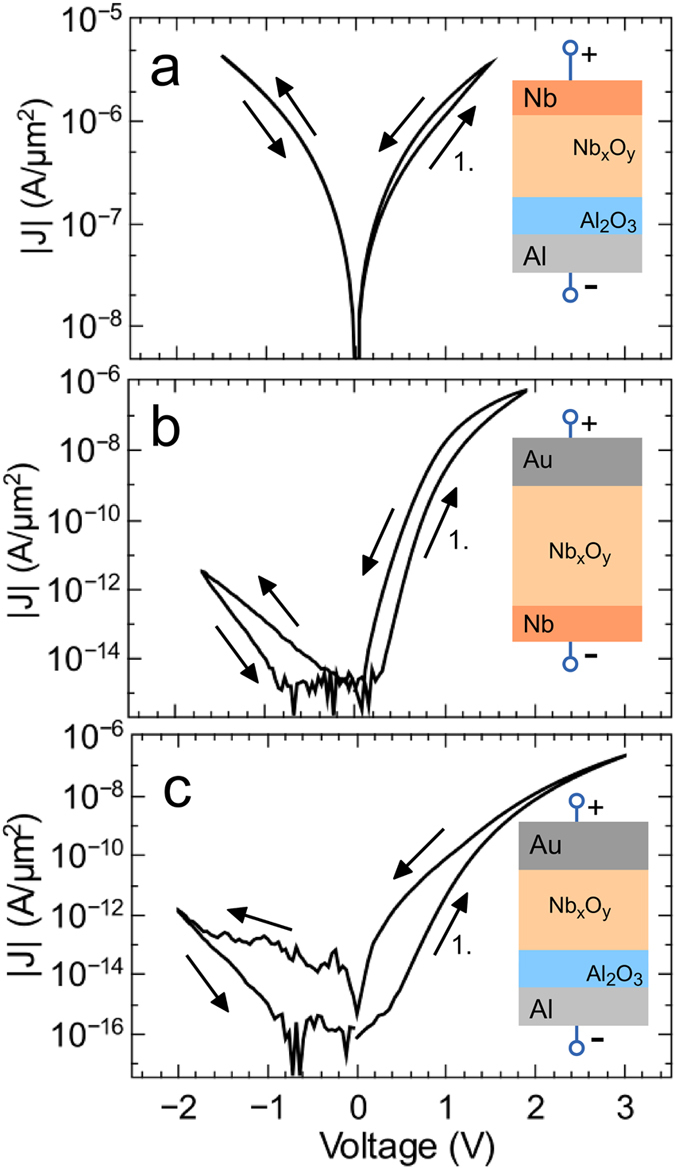
Absolute current density |J| versus applied bias voltage of (a) an Al/Al₂O₃/Nb_xO_y tunnel junction, (b) an Nb/Nb_xO_y/Au Schottky contact and (c) for comparison the Al/Al₂O₃/Nb_xO_y/Au double barrier device. Insets: Simplified cross-sectional view of the devices.

In order to study the influence of the Schottky interface, the thermionic emission theory was employed to get information from I–V data (cf. Fig. 4(b)). In this theory, a Schottky contact is described by a set of analytical expressions, where the Schottky diode current for forward bias voltages is defined as³²,³³

Figure 4. Schematic of the electronic band structure variations.

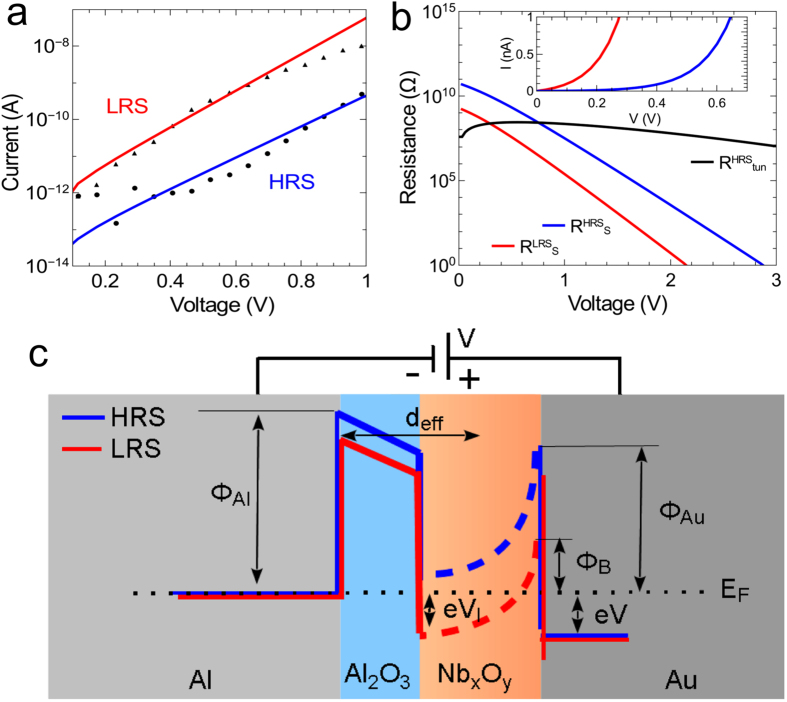
(a) I–V characteristics of the LRS and HRS branch of the double barrier device in the reverse voltage regime of the Schottky contact (device area is normalized to 1 μm²). Solid lines are data fits according to Equation 1 to extract the Schottky barrier height ϕ_B. (b) Comparison between the Schottky contact resistance at the LRS and HRS branch and the tunnelling resistance. Inset: Shift of the diode forward current onset. (c) Schematic electronic band diagram of the double barrier structure for the LRS (red line) and HRS (blue line). During the transition from the HRS to LRS, moving oxygen ions cause an decrease of the interfacial potential V_I by a down shift of the interfacial band in Nb_xO_y (dashed line). Further, the effective barrier tunnel width d_eff and the apparent barrier heights ϕ_Al, and ϕ_Au of ,respectively, the Al electrode, and Au contact are decreased.

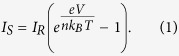Where k_B and T are the Boltzmann constant and temperature, respectively, while n is the ideality factor which describes the derivation from the ideal current. The reverse current I_Ris given by

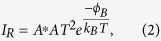where ϕ_B is the Schottky barrier height, A the junction area, and A^* the effective Richardson constant, which is 1.20173 10⁶ Am⁻²K⁻². The reverse current is dominated by the lowering of the Schottky barrier. If, however, the apparent barrier height ϕ_B at the Schottky interface is reasonably smaller than the conductive band gap of the insulator, the reverse current decreases gradually with the applied negative bias and it follows from Equations 1, 2 that³²

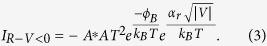Here, α_r denotes a device dependent parameter which is used to describe the experimentally observed reverse voltage dependence. By using ϕ_B and n as fit parameters, Equation 1 is fitted in the low forward bias voltage regime (V < 1 V) to the LRS and HRS branches of the measured I–V curve. The resulting fit curves are shown in Fig. 4(a). The apparent Schottky barrier height decreases from 0.62 eV to 0.54 eV and the ideality factor from 4.1 to 3.5 when the device resistance is decreased. In particular, the decrease of the ideality factor with increasing forward current suggests surface effects at the Nb_xO_y/Au interface, which could be the reason for the observed lowering of the apparent Schottky barrier height²⁰,¹⁹ in agreement with recent findings¹⁵.

Besides the Schottky interface, contributions arising from the tunnelling barrier have to be taken into account to better understand the charge transport in the device. The internal electrical field distribution is of particular interest, since this determines the effective interfacial potentials within the Nb_xO_y layer. Figure 4(b) compares the contact resistance of the Schottky interface for the HRS (blue line) and LRS (red line) to the tunneling resistance of the Al₂O₃ layer. For the calculation of the tunnelling resistance, we used the tunneling current formula from Simmons³⁴:

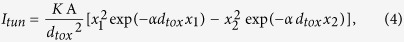where 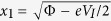, , 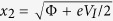K = 6.32 10¹⁰ V/s, Φ is the apparent barrier height of the tunnelling oxide (Φ = (ϕ_Al + ϕ_NbO)/2 = 3.1 eV), A the normalized device area (A = 1 μm²), and 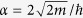(m: free electron mass; ћ Planck’s constant divided by 2π). V_I is the resulting voltage across the Al₂O₃ tunnel barrier and d_tox is the thickness of the Al₂O₃ layer (d_tox = 1.3 nm). As a result, most of the applied voltage drops across the Schottky barrier for bias voltages below 0.5 V (LRS) and 1.0 V (HRS), while the tunnelling resistance of the Al₂O₃ layer is getting more important for voltages above 0.5 V (LRS) and 1.0 V (HRS). The inset in Fig. 4(b) shows the state dependent diode forward voltages, V_HRS = 0.65 V and V_LRS = 0.255 V, at a forward current of 1 nA. Thus, the electron transport at low voltages is limited by the Schottky barrier and at higher voltages by the tunnelling barrier. Figure 4(b) shows a comparison for a constant tunnelling distance. However, due to the small thickness of the Al₂O₃ and the Nb_xO_y layer, the properties of both interfaces, Al₂O₃/Nb_xO_y and Nb_xO_y/Au cannot be considered independent. Any change in the electronic distribution within the Nb_xO_y layer will affect both interfaces simultaneously. Thus, the device can be only described by taking the properties of both interfaces into account, since both interfaces are interwoven via the Nb_xO_y layer. Our experimental data indicates a homogeneous area-dependent charge transport mechanism. This might be especially important in the case where mobile oxygen-ions are involved in the resistance switching process, as described in the model in Fig. 1(b). A variation of the oxygen concentration in the Nb_xO_y solid state electrolyte layer affects interfacial properties of both the Al₂O₃/Nb_xO_y as well as the Nb_xO_y/Au boundary. The macroscopically measured memristive I–V curve of a junction is a result of a delicate superposition of electronic and ionic effects at both interfaces. One obvious possibility is the change of the effective tunnelling thickness in accordance to the oxygen concentration at the Al₂O₃/Nb_xO_y contact:

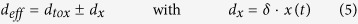Here, δ denotes the maximum variation of the effective distance and x(t) is the state variable of the memristive process, which ranges between 0 and 1. Figure 4(c) shows a schematic electronic band diagram for the double barrier device, which assumes an effective tunneling distance and a varying Schottky barrier height. In particular, the HRS (blue line) and LRS (red line) band profiles are shown, which differ due to the changed contact resistance at the Nb_xO_y/Au interface. This leads to a variation of the band structure, which itself influences the tunnelling process.

Device model

Although the fabricated devices and electrical characterizations fit the scenario described above, the experimental results can be explained by both models, i.e. charging and discharging of interfacial trap states and mobile oxygen ions. Moreover, by considering the local electric field and possible distribution of ions with respect to the electron tunneling transport, the electrical properties of the device and their interdependencies are not obvious at all and require a closer look from a theoretical point of view. Therefore, equivalent circuit models for the devices are often developed, which provides a more thorough understanding of the device functionality³⁵,³⁶,³⁷,³⁸,³⁹,⁴⁰,⁴¹.

Figure 5(a) shows the equivalent circuit which was used to model the scenario from Fig. 1(a), where both, mobile oxygen ions and interfacial trap states, are responsible for the observed resistive switching mechanism. The calculated I–V curve shown in Fig. 5(b) contains the main experimental recorded characteristics, such as an asymmetric pinched hysteresis, a high resistance at small voltages and the current saturation at higher voltages. In contrast, Fig. 5(c) shows the simulated I–V curve for a constant effective tunneling distance d_eff. In agreement with our experimental findings (cf. Fig. 3(b,c)) this decoupling of the particular interfacial interactions reduces the width of the memristive hysteresis, indicating that mobile oxygen-ions are involved in the resistance switching process and that the two interfaces cannot be treat separately.

Figure 5. Device model.

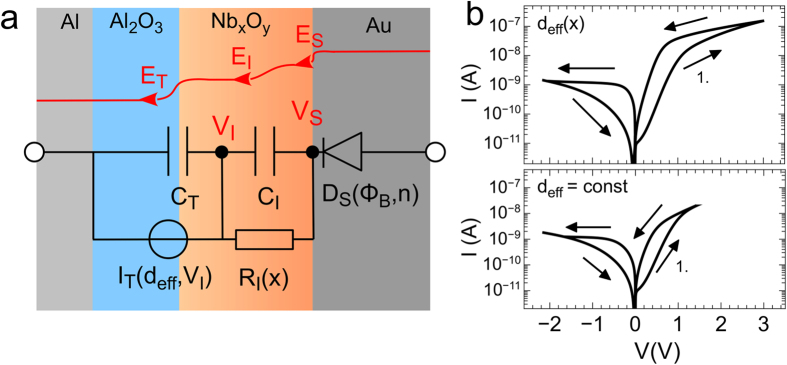
(a) Equivalent circuit model of a double barrier memristive device. The tunnelling current is defined by a current source supplying the current according to Equation 4. The Schottky barrier is taken into account as a diode according to Equation 1. The capacitance of the tunnelling barrier is C_T, while C_I represents the capacitance of the Nb_xO_y layer. The oxygen-ion migration, which changes the interfacial potential V_I, is expressed in the model as a variable resistance R_I(x) parallel to the Nb_xO_y layer capacitance C_I. The local electrical field strength E_S, E_I, and E_T due to the applied voltage are indicated as a red line. (b) Calculated I–V curve for a variable tunneling distance and (c) for a constant tunneling distance.

For the device model, the capacitances of the Nb_xO_y/Au interface C_I and the tunnelling barrier C_T are modelled in a capacitive divider. The values of C_I and C_T have been estimated from capacitance measurements. Therefore, devices with an Nb_xO_y layer thickness ranging from 1 nm to 20 nm were fabricated and the total capacitance was measured. By using a linear regression and extrapolating to 0 nm Nb_xO_y, the values C_T = 2.07 × 10⁻¹⁴ F/μm² and C_I = 1.74 × 10⁻¹⁴ F/μm² were found. The electron tunnelling is implemented in the model by a voltage driven current source, which depends on the effective tunnelling distance d_eff (see Equation 5) and the interfacial potential V_I. The potential change of the Nb_xO_y resistance is taken into account by the resistance R_I(x), which depends on the memristive state variable x(t). Additionally, the Schottky contact resistance is accounted for by using a Schottky diode D_S described by Equations 1, 2, 3. This diode defines the potential V_S(ϕ_B, n), which is a function of the memristive state dependent Schottky barrier height (ϕ^HRS_B = 0.62 eV and ϕ^LRS_B = 0.54 eV) and the ideality factors (n^HRS = 4.1 and n^LRS = 3.5). At negative bias voltages, the Schottky contact induced potential V_S(ϕ_B, n) is strongly influenced by the reverse current (cf. Equation 3), so that we assume a state variable dependent reset of ϕ_B according to ϕ_B = x/x_maxϕ^LRS_B + (1 − x/x_max) ϕ^HRS_B, where x_max is the maximal value of x during the set process and x varied between 0 and 1. For the set process we are using ϕ^HRS_B and ϕ^LRS_B estimated from Fig. 4(a).

The interfacial potential V_I is used as the reference potential of the equivalent circuit, so that the total capacitance of the device is C_tot = C_T + C_I (since they are in parallel according to the reference potential) and V_I thus reads

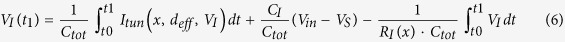where V_in is the external applied bias voltage. Hence, the specific value of the interfacial potential V_I modulates the tunnelling current and is responsible for the electron injection and the local field strength. The profile of the electrical field is sketched in Fig. 5(a) (red curve). Here, E_T, E_I, and E_S are, respectively, the local electrical field strengths at the tunnelling barrier, across the Nb_xO_y layer, and at the Schottky contact at the Au interface. While E_T depends on the effective tunnelling distance according to E_T = V_I/d_eff, we assume that the Nb_xO_y layer thickness d_NbO defines the region E_I = (V_I − V_S)/d_NbO. In addition, E_I depends on the Schottky potential V_S. For our device model we assume that mobile oxygen ions are involved in the resistance switching mechanisms by calculating the memristive state variable x(t) using the simple one-dimensional voltage driven memristor model of Ref. 4,

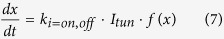where k_on = 35 × 10² (As)⁻¹ and k_off = 37 × 10⁴ (As)⁻¹ are constants for positive and negative bias voltages, while f(x) is the window function defined in Ref. 42. Therefore, the resistance change within the Nb_xO_y layer can be calculated by 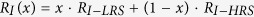, where R_I-HRS = 7 MΩ and R_I-LRS = 6 MΩ are the interface resistances for the HRS and LRS, respectively and x changes between 0 and 1.

Discussion

The most important feature of our device is the double barrier separated by the ultra-thin solid state electrolyte Nb_xO_y, which restricts the resistive switching to interface effects. The use of homogenous, interface effects as the origin of memristive switching avoids the formation of active current paths (conductive filaments) through the device. This avoids the drawbacks of initial electroforming steps and allows the targeted development of memristive devices by a controlled modification of interfacial potentials. Therefore, the interplay between electron tunneling, oxygen ion diffusion inside the Nb_xO_y layer, and interfacial state variations at the Schottky contact must be balanced by the local electrical fields.

Figure 6 shows the calculated electric field strengths for positive bias voltages across the tunneling barrier E_T, the interfacial layer of the double barrier device E_I, and the Schottky contact E_S. At low bias voltages the electrical field across the interfacial layer (Fig. 6(b)) and the tunneling layer (Fig. 6(c)) is nearly zero, since the current is blocked by the Schottky contact (Fig. 6(a)). In other words, the Schottky diode defines a threshold voltage for our device, which has to be exceeded to change the resistance of the device. This can be seen from the inset of Fig. 6(a), which shows the change of the effective tunneling distance as a function of the applied external voltage. Here, the resulting electrical field across the Nb_xO_y layer is too small to affect either ion diffusion or electron injections in the reverse diode regime. It is worth to mention that the device threshold additionally depends on the particular resistance state of the device, as marked by blue and red dotted lines in Fig. 6(a–c) for the HRS and LRS, respectively. This opens the possibility to adjust the device threshold by the memristive state of the device, which may be of interest in neuromorphic circuits to emulate threshold dependent plasticity processes, or for ultra dense packet crossbar memory arrays to suppress sneak-path leakage currents⁴³.

Figure 6. Local electrical field strengths.

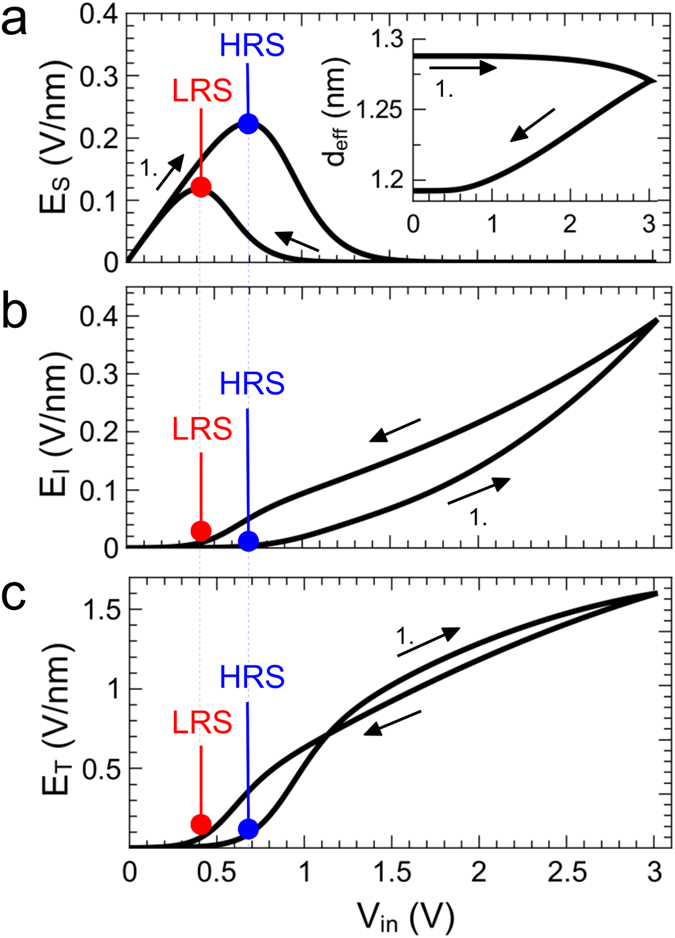
Calculated electrical fields across the Schottky contact E_S, the Nb_yO_x layer E_I (b), and across the tunnelling barrier E_T (b) during a positive voltage sweep. The onset current of the Schottky diode for the LRS and HRS are marked in red and blue, respectively. The black arrows show the direction of the voltage sweep. Inset: Corresponding change in effective tunneling distance.

If the applied bias voltage is increased in the forward regime of the Schottky diode D_S, the electric field E_T increases exponentially. While E_T saturates at higher voltages, E_I shows no saturation effects. Moreover, E_I exhibits memristive behavior in a way that the field strength with increasing voltage is always smaller than on the way back, while E_T decreases and crosses itself at 1.1 V, when the external voltage is ramped back to zero (cf. Fig. 5(c)). Regarding the device model shown in Fig. 5(a), we can explain the observed saturation from the interplay between the effective tunneling distance and the interfacial potential V_I. In particular, the increase of the tunneling current stems from the decrease of the tunneling resistance due to the reduced effective tunneling distance (cf. inset Fig. 5(a)). Since the interfacial potential V_I is increasing according to Equation 6 with a rising tunnelling current I_tun and a decreasing Schottky contact voltage V_S, the field strength E_I is increasing too, according to E_I = (V_I − V_S)/d_NbO. However, since E_T is decreasing with an increasing V_I, the tunneling interface acts as an intrinsic current compliance. Thus, no external current compliance has to be set, as it is typically the case for filamentary based memristive devices to protect the device from a dielectric breakdown. It is worth to mention that thin insulating layers as tunneling barriers have been used already to incorporate memristive cells into high density cross-type array structures⁴⁴. Due to their non-linear I–V characteristic, tunneling barriers act as access devices, where an intrinsic current compliance improves the device endurance by suppressing a too high device current during voltage application.

However, by referring to the two initially described microscopic models of trap charging and discharging (Fig. 1(a)) versus mobile ions (or oxygen vacancies, Fig. 1(b)), the inner field strength E_I is in the order of 10⁻¹ V/nm and consequently allows filling and emptying of traps as well as the drift of oxygen-ions within the Nb_xO_y layer as realistic scenarios. While the developed equivalent circuit models shows evidence that oxygen-ion diffusion are involved in the switching mechanisms, the impact of interfacial trap states cannot be ruled out. A closer look at the retention characteristic might be helpful to gain further insight. In Fig. 7 the retention characteristic of the memristive double barrier device is compared to the retention characteristic of the single Schottky barrier memristive device presented in Fig. 3(b). For the retention time measurements the devices were first set to their LRS by ramping the bias voltage to 2.9 V and 2.0 V for the memristive double barrier device and memristive Schottky contact, respectively. Afterwards the resistance was recorded by applying voltage pulses of 0.5 V for 2 s every 60 s and measuring the current. The double barrier device shows an increase in resistance in the first 500 s (black data points in Fig. 7), while afterwards the resistance increase is significantly less pronounced and shows an R_on/R_off ratio of more than one order of magnitude after one day. In contrast to the retention characteristic of the double barrier memristive device, the Schottky barrier device exhibited virtually no increase in the device resistance up to 700 s (gray data points in Fig. 7) but increased drastically afterwards. Hence, the introduction of the Al₂O₃ barrier led to a significantly improved retention characteristic.

Figure 7. Retention characteristics.

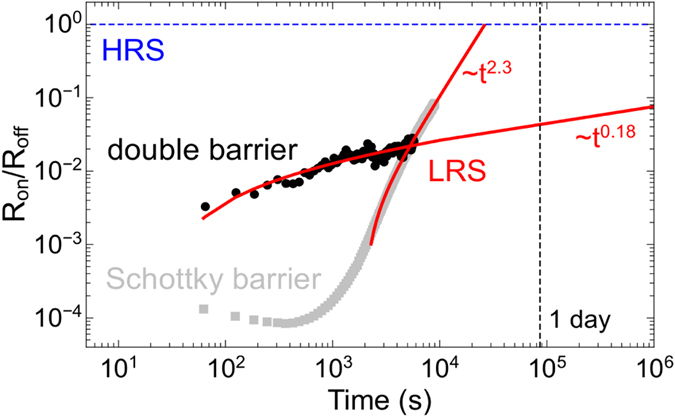
Time dependence of the LRS (data points) compared to the HRS (blue dashed line) for the Nb_xO_y/Au Schottky contact of Fig. 2(a) (gray data points) and the double barrier device (black data points). For the readout of the resistance state read pulses of 0.5 V every 60 s were applied. Red lines are data fits used to extrapolate retention times. Inset: retention characteristic for the double barrier device within the first 500s.

These obviously different retention behaviours can be quantitatively determined by fitting the experimental data to a t^β power law (red lines in Fig. 7), a procedure typically used to characterise high k-dielectrics⁴⁴. While the resistance ratio R_on/R_off of the Schottky barrier device follows a power law of the form t^3.56, the double barrier device follows for the first 600 s a t^0.65 power law and then changes to t^0.18. Although we cannot give a final explanation for the long retention time in case of the double barrier device, possibly both initially referred effects (cf. Fig. 1) are essential to explain the observed retention characteristics. However, from our investigation, the following picture seems to be the most likely: Right after switching the device resistance to the low resistance state, previously emptied traps are filled by electronic charge carriers, leading to an increase in resistance. After approximately 100 s this mechanism fades out and is followed by a second, independent, ionic driven process. During switching, oxygen vacancies are pushed towards the Au interface and lower the contact resistance. The further increase towards the high resistance state can be explained by a partial back-diffusion of oxygen vacancies, leading nevertheless to a considerably longer retention time in comparison to the Schottky barrier device. Nonetheless, further investigations are necessary to clarify the relevance of electronic and ionic effects in ultrathin double barrier devices.

For possible applications of the presented device, we see interesting possibilities in the field of neuromorphic computing⁹,¹⁰, where high resistances are desired in order to reduce the overall power consumption of the whole system. Moreover, the extremely high resistance at low voltages (<1V) make our device in particular interesting for crossbar-architectures, since it requires no selector device⁴³, as already mentioned above. However, we would like to mention that the scalability of the device is restricted by the relative high device resistances, which results from the Au (Schottky) contact. Here, the use of other electrode materials might lead to lower resistances without affecting the presented double barrier device mechanism.

In conclusion, a double barrier memristive device was realized with a highly uniform current distribution for the high and low resistance states, which indicates a non-filamentary based resistive switching mechanism. We have shown evidence that the use of an ultra-thin Nb_xO_y solid state electrolyte layer of 2.5 nm sandwiched between an Au (Schottky) contact and an Al₂O₃ tunneling barrier restricts the resistive switching mechanism to interfacial effects where both barriers are involved. This may lead to the observed drastically improved retention characteristic compared to the single barrier Schottky contact devices and may be based on confined oxygen ion diffusion within the sandwiched Nb_xO_y layer. An equivalent circuit model of the device was developed, which confirms our experimental findings and shows evidence that mobile oxygen-ions are involved in the resistance switching process. In order to come to a quantitative description of the resistance switching process, further investigation is necessary to study the influence of the second claimed scenario of charged traps within the Nb_xO_y layer. However, we showed that the controlled modification of interfacial potentials allows the development of homogenous resistive switching mechanisms, which is essential for a wider application of memristive devices in future digital and complex analog memory circuits.

Methods

Sample preparation

Memristive tunneling junctions were fabricated on 4-inch Si wafers with 400 nm of SiO₂ (thermally oxidized) using a standard optical lithography process. The junctions are arranged in 1 mm × 1 mm cells across the wafer, containing 6 different contact sizes ranging from 70 μm² to 2300 μm². The devices were fabricated using the following procedure: First of all, the multilayer (including top- and bottom-electrode) is deposited without breaking the vacuum using DC magnetron sputtering. The Al₂O₃ tunnel barrier was fabricated by depositing Al which was afterwards partially oxidized in-situ, the Nb_xO_y layer was deposited by reactive sputtering in an O₂/Ar-atmosphere. Following the subsequent lift-off, the junction area was defined by etching the top electrode using wet etching (potassium iodide, for Au) and dry etching (reactive ion etching with SF₆, for Nb). The etched parts were then covered with thermally evaporated SiO to insulate the bottom electrode from the subsequently deposited Nb-wiring to contact the top electrode.

I–V measurements

All measurements were performed using an Agilent E5260 source measurement unit. Current-voltage measurements (I–V curves) were obtained by sweeping the applied voltage and measuring the device current simultaneously.

Capacitance measurements

In order to determine the layer capacitance for the Al₂O₃ tunneling barrier and Nb_xO_y solid state electrolyte, capacitance measurements were done using a precision HP4284A LCR meter. The measurements were performed at room temperature using a bias voltage of 0.5 V and a sinusoidal signal of 0.3 V (peak-to-peak) at 50 kHz. To determine the capacities of the Al₂O₃ and Nb_xO_y-layers, 5 samples with Nb_xO_y thicknesses ranging from 1 to 20 nm were fabricated. For each of these samples, the capacity was measured for all contact areas (70 μm² to 2300 μm²). From each contact size, about 20 devices were measured. The spread in capacity for each area was typically in the order of few percents (which already includes the device-specific variance). To calculate the total capacitance for each sample, the slope of the C vs. area plot was taken, which always showed perfect area dependence and a negligible linear offset.

Additional Information

How to cite this article: Hansen, M. et al. A double barrier memristive device. Sci. Rep. 5, 13753; doi: 10.1038/srep13753 (2015).