Abstract
Objectives
This article presented four anthropometric theories (univariate, bivariate/probability distribution, multivariate, and shape-based methods) for protective equipment design decisions.
Background
While the significance of anthropometric information for product design is well recognized, designers continue to face challenges in selecting efficient anthropometric data processing methods and translating the acquired information into effective product designs.
Methods
For this study, 100 farm tractor operators, 3,718 respirator users, 951 firefighters, and 816 civilian workers participated in four studies on the design of tractor roll-over protective structures (ROPS), respirator test panels, fire truck cabs, and fall-arrest harnesses, respectively. Their anthropometry and participant-equipment interfaces were evaluated.
Results
Study 1 showed a need to extend the 90-cm vertical clearance for tractor ROPS in the current industrial standards to 98.3 to 101.3 cm. Study 2 indicated that current respirator test panel would have excluded 10% of the male firefighter population; a systematic adjustment to the boundaries of test panel cells was suggested. Study 3 provided 24 principal component analysis-based firefighter body models to facilitate fire truck cab design. Study 4 developed an improved gender-based fall-arrest harness sizing scheme to supplant the current unisex system.
Conclusions
This article presented four anthropometric approaches and a six-step design paradigm for ROPS, respirator test panel, fire truck cab, and fall-arrest harness applications, which demonstrated anthropometric theories and practices for defining protective equipment fit and sizing schemes.
Applications
The study provided a basis for equipment designers, standards writers, and industry manufacturers to advance anthropometric applications for product design and improve product efficacy.
Keywords: tractor, respirator, fire truck, harness, shape, size
INTRODUCTION
Protective equipment (PE) provides the last line of defense to workers who perform their professional duties in areas where hazards cannot be completely eliminated or control technologies cannot be cost-effectively implemented. PEs include but are not limited to respirators, tractor roll-over protective structure (ROPS) frames, vehicle cab workspace protective volumes, fall-arrest harnesses, heat-resistant bunker gear, chemical-resistant clothing, gloves, and hard hats. Key users of such PEs are firefighters, health care professionals, coal miners, agricultural workers, professional drivers, construction workers, and industrial laborers. One of the greatest challenges in designing effective PE is quantification of PE fit to specific worker populations. Poor fit of respirator units can result in serious health effects in firefighting, coal mining, hazardous waste cleanup, and other workplace conditions due to exposure to environmental hazards. An improperly conformed fall-arrest harness would not provide adequate protection to workers who work at height and could increase the risk of suspension trauma after a successful fall arrest (Hsiao, Turner, Whisler, & Zwiener, 2012). Insufficient protective volumes for vehicle rollover protection would not provide satisfactory mitigation of driver injury risks.
Proper evaluation of PE fit involves analysis of human body characteristics (i.e., size and shape), assessment of human-PE interfaces, accurate determination of PE sizing schemes, and effective selection of PE size. As the PE design process must consider the large variation in dimensions and configurations from person to person and from population to population, adequate methods are needed to report various body segment dimensions and their variants.
The State of Anthropometric Science
In the past, variances in body dimensions and configurations were typically reported as means and standard deviations for various body segments (Roebuck, Kroemer, & Thomson, 1975). This approach was successful in delivering general, broad parameters for protective equipment sizing but was deficient in generating the detailed fit information needed for workplace and protective equipment design. Often, anthropometry data are published in tabulated forms by parameters and percentiles. Some design applications are of the “design for extremes” paradigm (e.g., door dimensions, chair seat height, and guardrail height) and typically utilize a single parameter. In other PE design applications, multiple parameters are used because multiple body measurements are relevant to the function of the products (e.g., two dimensions for shoe sizing and multiple dimensions for fall-arrest harness sizing). The greater the number of involved dimensions, the more complex the product design process becomes. Many designers and human factors practitioners have noticed the inadequacy of standard anthropometry tables for designs involving bivariate or multivariate applications.
In the 1980s, the concept of multivariate accommodation was introduced into the field of anthropometry. The intent was to remove known noisy variables and to reduce data sets to a more manageable size while better addressing equipment accommodation (Bittner, Glenn, Harris, Iavecchia, & Wherry, 1987; Meindl, Zehner, & Hudson, 1993). Principal component analysis (PCA) has been the premier method of variable reduction and has been effective in increasing body size accommodation in tractor cab and cockpit designs (Hsiao et al., 2005; Robinson, Robinette, & Zehner, 1992); it however was found lacking when applied to body dimensions, which showed poor intercorrelation, such as facial dimensions (Hudson, Zehner, & Meindl, 1998).
While PCA represents a significant step forward in anthropometric size-and-shape quantification, it is still a discrete approach. It is a combination and contrast of multiple linear measurements and does not necessarily describe the true shape of an individual or a population. Recently, three-dimensional (3D) scanning and shape-quantification technologies have made the assessment of 3D anthropometric information for product design a much more feasible undertaking. For instance, Elliptic Fourier Analysis–based shape-expression methods have already resulted in improved PE fit quantification and PE design. A notable example of this is in fall-arrest harness sizing design (Hsiao, Friess, Bradtmiller, & Rohlf, 2009).
The State of Anthropometry in PE Design Practice
While literature has shown considerable growth of anthropometry databases and tabulation over the past few decades, systematic theories and examples of transferring anthropometric data into product design practices remain conspicuously absent. Often, practitioners have used tabulated data without considering age, gender, race/ethnicity, or occupational composition. Some designers have used nonadditive percentile data to derive anthropometric information. Others even mistakenly relied on “common sense,” “average person data,” and “individual data” in design practices (Pheasant & Haslegrave, 2006). With the emergence of 3D scanning technologies, many organizations have moved forward to establish 3D digital human databases during the recent years. Despite these advancements, procedures for utilizing anthropometric information from data to inform product design remain underdeveloped.
Scientists have debated the adequacy of both traditional linear anthropometry and 3D anthropometry for product design applications. Some have strong opinions on the use of percentiles in traditional linear anthropometry as it describes product accommodation. Others are skeptical about the practicality of 3D anthropometric information for product design. An organized presentation on anthropometric procedures by examples for product design would be beneficial to anthropometry scientists, engineers, and anthropometry data end-users as a whole; the procedures would include defining critical body dimensions for design applications, determination of the appropriate target demographic, selecting the adequate percentage of the population to be accommodated, obtaining the suitable reference materials, using appropriate computations to define the needed dimensions, and ascertaining necessary product adjustments for product safety and efficacy.
The Charges
This article presents a series of studies from traditional univariate and bivariate methods to emerging 3D anthropometric procedures (human body size-and-shape quantification, human-PE interface assessment, and PE sizing scheme determination), using ROPS, respirator test panels, fire truck cab accommodations, and fall-arrest harness designs as examples to improve the understanding of general anthropometric principles and specific procedures. Each of the studies employs a six-step paradigm for anthropometric design (Hsiao & Halperin 1998): (1) determining the body dimensions that are of essential importance (e.g., seating height for cab, hand width for gloves, etc.), (2) determining the population to be considered (e.g., sex, age, occupation, etc.), (3) selecting the percentage of the population to be accommodated (e.g., for safety, cost-benefit ratio, etc.), (4) obtaining the necessary reference materials and data to determine the appropriate statistics, (5) computing the specific dimensions, and (6) adjusting as necessary for clothing and other gear. These studies offer both robust theories for product ergonomics and practical usage of anthropometric data in protective equipment design.
STUDY 1: DESIGN WITH UNIVARIATE CONSIDERATION—TRACTOR ROLL-OVER PROTECTIVE STRUCTURES
Background
In some product design applications, the extreme value of a single anthropometric measurement of a user population plays the primary role in design decision. An example is to specify the vertical clearance for farm tractor roll-over protective structures to mitigate tractor roll-over–related fatalities and injuries. Farm tractor-related fatalities and injuries represent one of the most serious causes of occupational losses and suffering in the U.S. agricultural community. On average, 218 tractor fatalities occur annually with about half of these deaths due to tractor overturns (Myers et al., 1998). In addition, some 8,000 tractor-related lost-time injuries occur annually; about 54% of these tractor-related injuries are associated with overturn events (Cole, Myers, & Westneat, 2006). These injuries and fatalities are preventable and can be curtailed by well-accommodated ROPS and proper use of a seat belt. ROPS or tractor operator protective space envelopes were first specified in the 1950s with a height of 90 cm. The current SAE (Society of Automotive Engineers) J2194 standard maintains that the minimum vertical clearance for a tractor cab is 90 cm (ASAE, 2000). With the change of workforce and population body dimensions over the past decades, an update of the standard for product design is warranted, which may affect more than 6 million agriculture workers who operate farm tractors.
The update can be developed by following the six-step anthropometric procedure discussed in the Introduction section. First, the essential dimension for defining the minimum vertical clearance for a tractor cab or protective frame is sitting height. Second, the population to be considered is U.S. agricultural workers; the use of agricultural worker anthropometric data instead of general population data for this case is imperative because agricultural workers were reported shorter in height by an average of 2.5 cm compared to other occupational groups (Hsiao, Long, & Snyder, 2002). Third, the percentage of the population to be accommodated is 95% of the male population, balancing both safety and cost-effectiveness for industry manufacturers; this will cover almost all females as well. Fourth, reference points have been established for X (mean sitting height) at 90.8 cm and S (standard deviation) at 8.15 cm based on the data of male farm worker group (N = 843) in the NHANES III database (Hsiao et al, 2002). The Z value (a coefficient whose value varies with the percentage of population to be covered) for Z95 is 1.645. Therefore, sitting height95 is 90.8 + 1.645 × 8.15 = 104.2 cm. Finally, it may be necessary for some design applications to add an adjustment for the height for shoes (2.5 cm), headgear (5.0 cm), or SAE J154 seat suspension travel and maximum vertical adjustment (8 cm) (Das & Grady, 1983; Hertzberg, 1972; SAE International, 1992). In this ROPS application, no adjustment is needed (adding 8 cm for seat suspension travel and maximum vertical adjustment would be necessary if a full cab enclosure is proposed). Consequently, when using the NHANES III database, the sitting height used to determine the minimum vertical clearance for the ROPS is 104.2 cm, which is 14.2 cm taller than what is specified in the current SAE J2194 standard. The research goals are twofold: determine if this design specification is valid and provide justification for revision of the SAE J2194 standard.
Objectives
This study (1) experimentally defined the minimum vertical clearance for farm tractor ROPS and (2) evaluated the effect of ROPS vertical clearance on tractor operators’ use of retractable ROPS.
METHOD
Participants
In this study, 88 male and 12 female agriculture workers from farming communities in West Virginia participated. They were distributed between 18 and 76 years of age. All participants had driven tractors and 73% of them operated tractors on a regular basis. Their average height was 177.4 cm (SD = 6.5) with a mass of 87.8 kg (SD = 17.5) for males and 165.9 cm (SD = 6.6) with a mass of 72.6 kg (SD = 19.6) for females.
Independent Variable
The independent variable was the participants’ usage of ROPS during normal operation of tractors with three possible responses: ROPS folded, ROPS deployed, and no ROPS on the tractor.
Dependent Variables
The dependent variables include participants’ sitting height, shoulder width (bideltoid breadth), stature, and body weight.
Devices
An anthropometer (GPM, Switzerland) and a Toledo scale (Mettler-Toledo Inc., Worthington, OH) were used.
Procedures
Upon arrival, the participants viewed a PowerPoint™ presentation, which described the study. Each participant had the opportunity to ask questions before signing an informed consent form and filling out a short questionnaire related to the use of ROPS. The participant was then taken to a dressing room, where he or she changed clothing—bike shorts for men and bike shorts with halter top for women. The participant sat on a stool and looked straight ahead with shoulders relaxed. They lined up their feet with the premarked footprints on a platform. The platform was adjustable through a hydraulic control such that the participant’s knee angle was kept at 90 degrees. Sitting height, shoulder width, and stature measurements were taken using the GPM anthropometer and entered into a laptop computer. Body weight was then measured, using the Toledo scale.
RESULTS
The mean sitting height (and SD) of the male participants in this study were 92.5 cm (and 3.5 cm) with a normal distribution (Shapiro-Wilk W = .982, p = .267). Sitting height is the essential dimension for determining ROPS or cab vertical clearance. Since it is desirable for ROPS clearance to accommodate at least 95% of the male farm worker population (which would protect almost all female workers), the sitting height design value calculated from this sample would be 92.5 + 1.645 × 3.5 = 98.3 cm. Furthermore, the mean sitting height for male and female participants combined in this study was 91.8 cm (SD = 3.93 cm); the current SAE J2194 standard ROPS clearance specification of 90 cm (ASAE, 2000) would accommodate only about 32% of the farm tractor operators based on the calculation of z score = (90 – 91.8)/3.93 = −0.46.
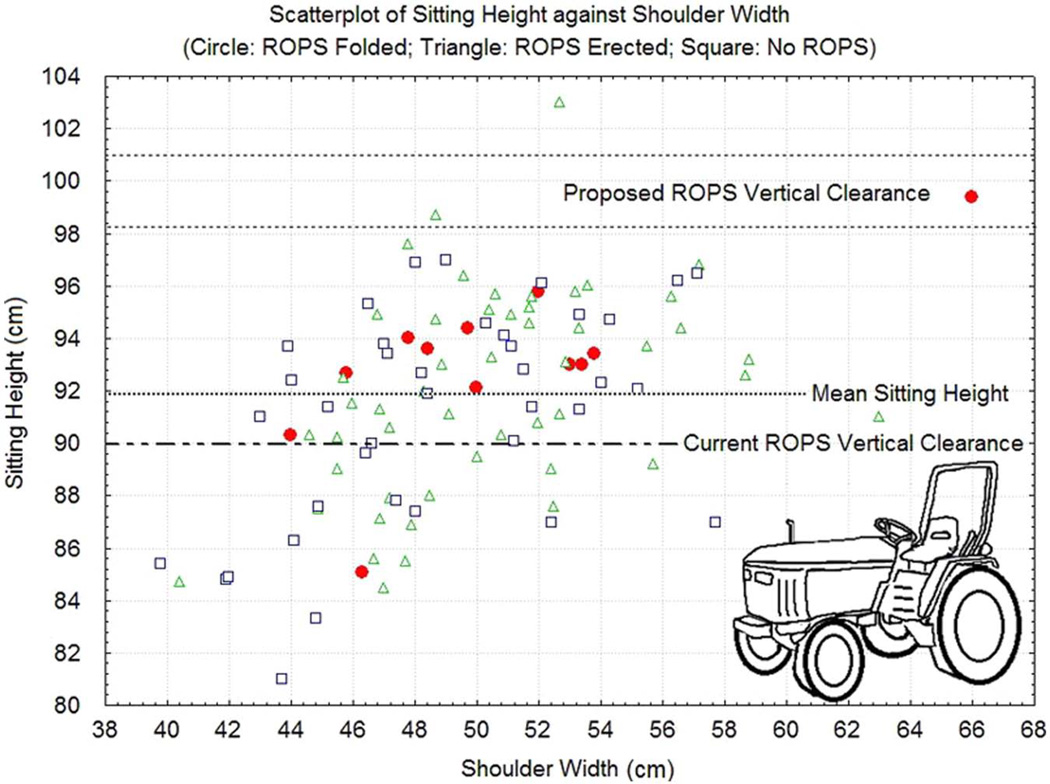
In all, 38 participants used tractors without a ROPS. Of the participants, 19% (n = 12) who had operated a tractor with a ROPS (n = 62) had at some time folded it away during operation. While some participants may just prefer to fold it away, others may have a reason for doing so (e.g., impediment or discomfort) based on their sitting height. In fact, the number of participants who kept ROPS deployed or did not have ROPS on their tractors were both evenly divided (50% vs. 50%) at the mean sitting height (91.8 cm), while 83.3% of the individuals who folded away their ROPS had a sitting height greater than 91.8 cm, which is significantly different from the former two combined, χ2(1) = 50.32, p < .001. In addition, 91.7% of those participants who folded away the ROPS had a sitting height over 90 cm, which is the clearance specification of current SAE J2194 standard for ROPS (Figure 1).
Figure 1.
The number of participants who kept roll-over protective structures (ROPS) erected (triangles) or did not have ROPS on their tractors (squares) were both evenly divided (50% vs. 50%) at the mean sitting height (91.8 mm), while 83.3% of the individuals who folded away the ROPS (circles/solid dots) had a sitting height greater than 91.8 cm. Eleven out of 12 (91.7%) of those participants who folded away the ROPS (circles/solid dots) have a sitting height greater than the clearance specification (90 cm) of current SAE J2194 standard for ROPS. Shoulder width did not have an association with the decision of folding away a ROPS.
This result warrants a revisit of the specification for ROPS clearance. While ROPS is not directly above the seat and thus the “clearance” shortage may not directly represent immediate injury potential, the association between the “short head-ROPS vertical distance” and “folding ROPS away” is significant, as demonstrated previously. Workers are not likely to be protected if they fold the ROPS away; extending the ROPS clearance is worth considering if the proportion of users who choose to retract their ROPS is to be reduced. It is understandable that a tall ROPS may interfere with farm works, such as in entering a low-clearance barn or orchard; foldable (two or three folds) and auto-deployable ROPS (with the deployed height set greater than current standard ROPS) may ease the problem.
DISCUSSION
The stature, weight, and sitting height from this study were compared to those of agricultural workers in the NHANES III literature (Hsiao et al., 2002). The average stature, weight, and sitting height of farm worker participants from West Virginia were greater than those of the national averages that were reported in NHANES III (p < .05). In this study, the average stature was 177.4 cm (SD = 6.5), weight 87.8 kg (SD = 17.5), and sitting height 92.5 cm (SD = 3.5) for males and 165.9 cm (SD = 6.6), 72.6 kg (SD = 19.6), and 86.7 cm (SD = 3.4) for females. In the NHANES III data set, the average stature was 173.3 cm (SD = 16.1), weight 80.5 kg (SD = 31.5), and sitting height 90.8 cm (SD = 8.15) for males and 159.2 cm (SD = 31.5), 68.7 kg (SD = 26.5), and 83.7 cm (SD = 8.9) for females. However, with a significantly larger standard deviation in the NHANES III data set, the estimated minimum ROPS clearance from the seat reference point from the NHANES III (104.2 cm) is larger than that from this study (98.3 cm). This leads directly to step 3 of the anthropometry procedure in determining percentage of population to be covered. The percentage of population to be covered requires careful balancing of cost and safety. When using the NHANES III data set for ROPS design specification, the percentage of population to be covered could be specified as 90% of the male population rather than 95% due to the large standard deviation of sitting height in the NHANES III data set. The estimated ROPS vertical clearance in that case would be sitting height90 = 90.8 + 1.285 × 8.15 = 101.3 cm.
CONCLUSION (STUDY 1)
This study presented both a traditional descriptive statistical approach for defining protective equipment clearance requirements and a six-step procedure for utilizing anthropometric data to develop improved protective design practices. The vertical clearance for agricultural tractor ROPS in the current SAE International J2194 standard (90 cm) is too short with respect to the 95th percentile sitting height of male farm tractor operators in this study (98.3 cm) and the 90th percentile sitting height of male farmers in the 1994 National Health and Nutrition Examination Survey III database (101.3 cm). A modification of standard for ROPS and introduction of auto-deploying folding ROPS (two or three folds) are desirable.
STUDY 2: DESIGN WITH BIVARIATE CONSIDERATION—RESPIRATOR TEST PANEL DESIGN AND FIREFIGHTER MASK SIZING
Background
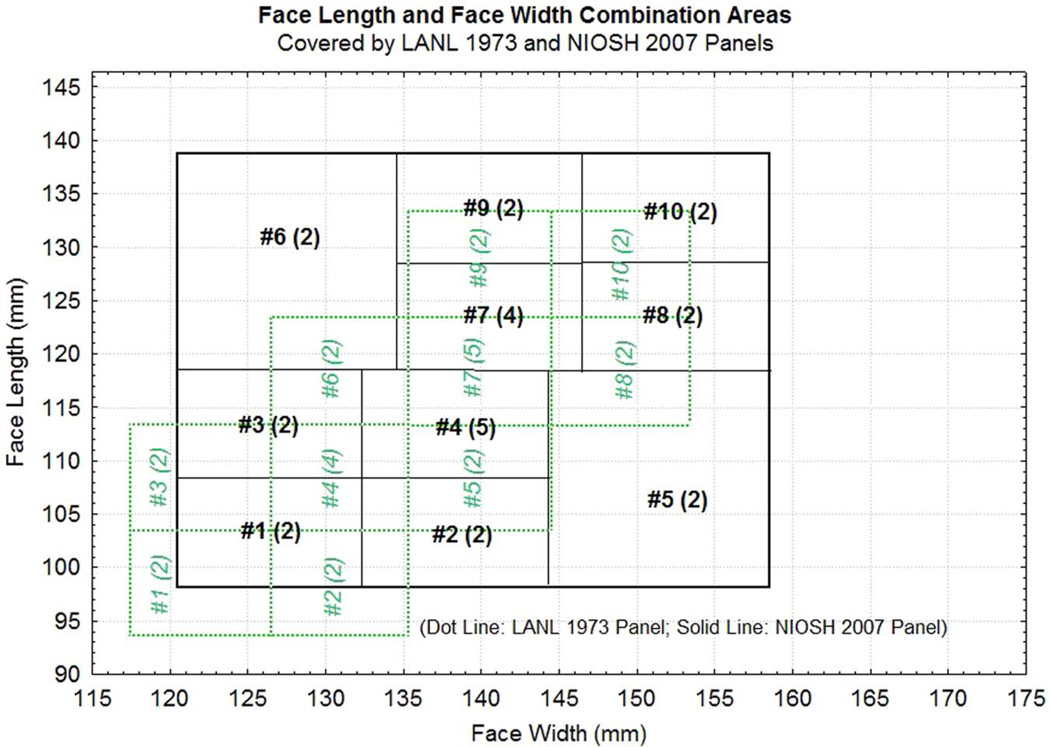
In some protective equipment development and testing applications, the design decision may involve multiple measurements but can be simplified to two critical dimensions. Full-face-piece respirators and their test panel design fall into this category. Most respirator users are familiar with typical respirator sizing schemes and respirator test panels that rely on the measurements of menton-nasal root depression length (face length) and bizygomatic breadth (face width). There are one to three sizes of respirators depending on brand names, and the respirator test panel contains 10 test panel cells that are made of 25 test models of a series of face length and width combinations. Respirators are certified for passing at least 95% of test panel models (i.e., 24 of 25 panel models). Before the most recent National Institute for Occupational Safety and Health (NIOSH) release on facial dimensions of an updated respirator test panel for the American industrial workers (Zhuang, Bradtmiller, & Shaffer, 2007), respirator tests relied on the test panel developed by the Los Alamos National Laboratory (LANL) for NIOSH in 1973. The LANL study was conducted in 1967 and 1968 via a survey of U.S. Air Force (USAF) servicemen and women (Hack et al., 1973; Hack & McConville, 1978). The upper limit of the LANL panel was defined by the weighted mean value of the male population plus two standard deviations and the lower limit was defined by the weighted mean value of the female population minus two standard deviations with round offs. The resulting range was 93.5 mm to 133.5 mm for face length and 117.5 mm to 153.5 mm for face width. Based on a 10 mm increment in face length and a 9 mm increment in face width, the range combination resulted in 16 cells. Because six cells contained very low percentages of the population (<0.1%–1.8%), they were excluded from the proposed panel, leaving a 10-cell panel representing about 91% of the total population. Twenty-five subjects were selected for the panel size as the practical limit of expense and time to perform tests. The number of subjects for each cell was determined based on the percentage of the USAF survey populations for that particular cell. Thus, the test panel is usually referred to as the 25-member panel for testing of respirators (Figure 2).
Figure 2.
Los Alamos National Laboratory (LANL) and National Institute for Occupational Safety and Health (NIOSH) full-face-piece panels based on face length and face width are shown. The dotted lines define LANL panel boundaries and the solid lines outline the NIOSH 2007 panel borders. The cells are numbered 1 to 10, and the numbers in parentheses indicate the number of models/participants to be sampled from each cell. When the participant’s face length or face width fall on cell boundaries, the participant is placed in the higher number cells with larger face dimensions.
NIOSH recognized the difficulties inherent in using old military data from the 1973 LANL panel to handle the great diversity in face size in today’s civilian population. A recent NIOSH survey of 3,997 respirator users reported that the LANL full-face-piece panel excluded more than 15% of the current U.S. population (Zhuang, Guan, Hsiao, & Bradtmiller, 2004). Subsequently, NIOSH proposed a new panel system with 10 cells; the number of panel models remained at 25. This panel system has boundary limits of 98.5 mm to 138.5 mm for face length and 120.5 mm to 158.5 mm for face width, which is significantly different from the LANL panel (Figure 2). The 10 mm increment in face length is the same as that of the LANL panel. The 12 mm increment in face width is larger than that of the LANL panel (9 mm). These limits and increments were first based on the male mean plus two standard deviations (SDs) and the female mean minus two SDs. Cell boundaries were then adjusted so that the population can be distributed among cells as uniformly as possible while maintaining that each cell has at least two models and that at least 95% of the population was included in the panel (Zhuang et al., 2007). The panel size of 25 members/models is for testing one-size-fits-all respirators. For two-size systems such as small-medium and medium-large, the small-medium is tested on members from Cells 1 through 6 and medium-large is tested with members from Cells 5 through 10. The total number of models becomes 29 for two-size systems. For three-size systems such as small, medium, and large, they are tested with models from Cells 1 through 4 for small, Cells 4 through 7 for medium, and Cells 7 through 10 for large, respectively. The total number of models becomes 34 for three-size systems.
Objectives
There are an estimated 3.3 million respirator users in the private sector in the United States (Bureau of Labor Statistics, 2002). There are also an estimated 1.1 million firefighters who use respirators on the job (National Fire Protection Association, 2006). Firefighters are a subset of respirator users who are constantly exposed to various known and unknown hazardous particles and gases. Their full-face-piece respirators (masks) commonly have three sizes. The goals of this study are to (1) evaluate the ability of LANL 1973 and NIOSH 2007 full-face-piece panels to accommodate 95% of the current firefighter population and (2) gauge the need for revised firefighter respirator test panels and respirator/mask sizing schemes for improving firefighter protection.
Following the six-step anthropometric procedures, the essential dimensions for this study are face length and face width, the population to be considered is firefighters, and the percentage of the population to be accommodated is 95%. The study also addresses the next three steps of bivariate anthropometric procedures: data processing, computation, and adjustments.
METHODS
Participants
The study used a stratified sampling plan (3-age × 3-race/ethnicity × 2-gender combinations) to collect firefighter facial anthropometric data in four U.S. regions (Rockville, MD; Philadelphia, PA; Phoenix, AZ; and Fort Worth, TX). It took into account the geographic density of racial/ethnic distributions calculated from the U.S. Census 2000 (Hsiao, 2008). A total of 951 firefighters participated in the study to analyze face length and width measurements via 3D face scans. In addition, face length and width measurements of 2,767 non-firefighter respirator users were retrieved from a NIOSH database (Zhuang et al., 2004) for comparison.
Independent Variables
The independent variables are firefighter face length and face width.
Dependent Variables
The dependent variables are the count and percentage of firefighter facial dimensions contained in each cell of the LANL 1973 and NIOSH 2007 full-face-piece panels.
Devices
The Cyberware Model PX 4206 head-and-face scanner (Monterey, CA) was used to collect 3D head and face scans of firefighters. Data extraction software, Integrate, was used to extract the facial landmark locations, which were marked with 3-mm diameter stickers. The landmark location data were then exported to a Microsoft Excel file to calculate the face length and width dimensions.
Procedure
The facial measurement was part of a national firefighter anthropometry survey (Hsiao, 2008). Upon arrival, the participants viewed a PowerPoint presentation, which described the study. Each participant had the opportunity to ask questions before signing an informed consent form and filling out a short questionnaire related to the use of fire apparatus and protective equipment. The firefighter was seated in a head-and-face scanner and an investigator placed 10 stickers to indicate anatomical locations of their face. These landmarks are visible in the scans and allow for semi-automated extraction of head and face measurements. Firefighters with long hair were asked to wear a hair cap in order to gain an accurate measurement of the firefighter’s actual head and face. After the scans were saved to the computer, the stickers were removed from the firefighter’s face, and the firefighter was dismissed.
DATA ANALYSIS
Only the face length and width data extracted from the scans were used in this analysis; they were fit into the 10 cells of the LANL 1973 and NIOSH 2007 full-face-piece panels. The count and percentage in each cell were then calculated. The total counts and percentage of acceptance define the ability of the panels to represent the face structure of the current firefighter population.
RESULTS
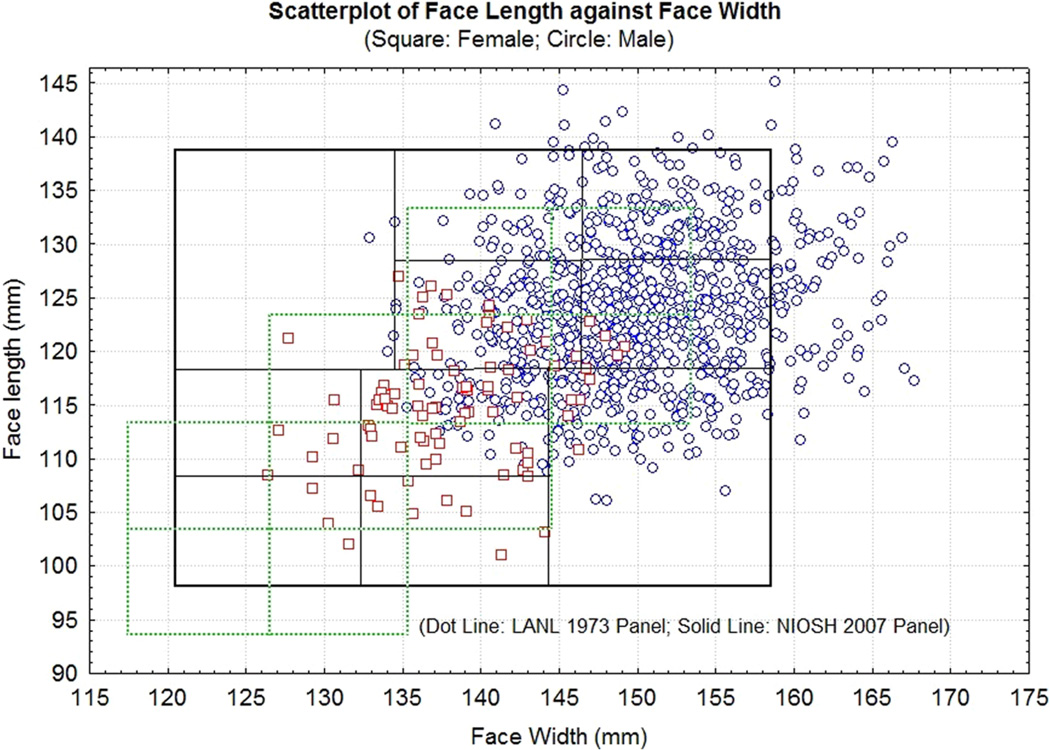
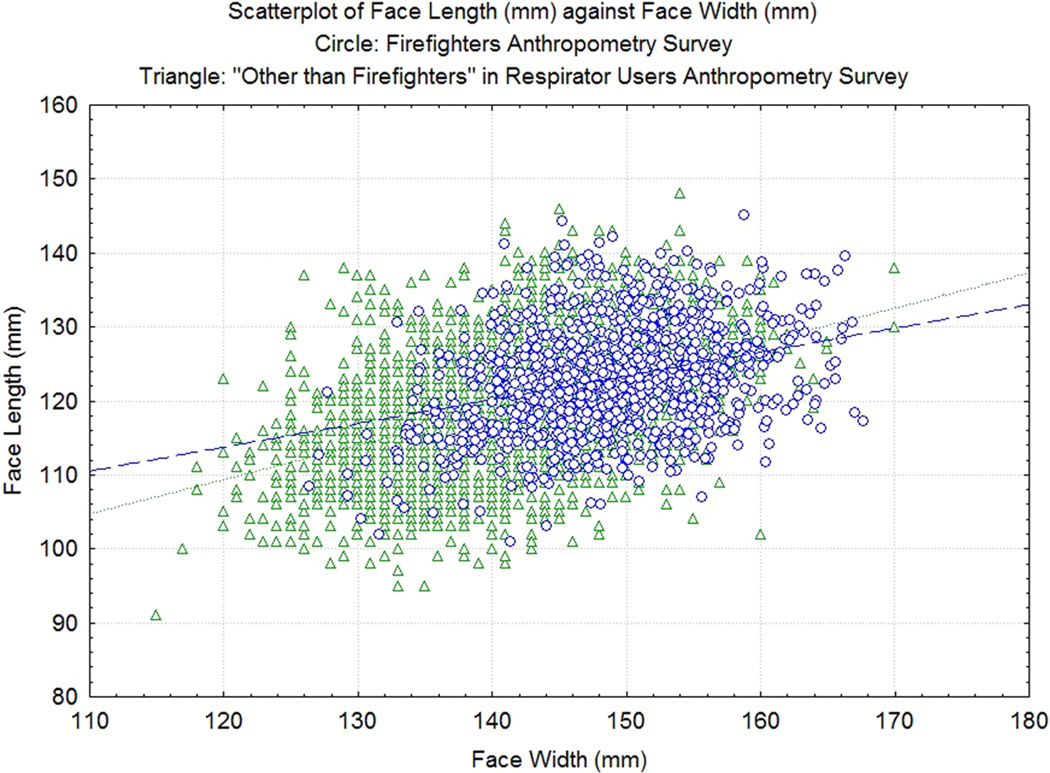
Figure 3 shows the distributions of face dimensions with respect to both the LANL 1973 and NIOSH 2007 panels. The squares represent female participants and circles denote male participants. Only 2 women (2.3% of female participants) and no men were covered in Cells 1 through 3 of the LANL panel. About 93.2% of female participants were covered under Cells 4 through 9. About 60% of male firefighters were covered under Cells 7 through 10. The LANL panel would have excluded 39% of the male firefighter population and 4.5% of the female firefighter population, or 35.9% (unweighted) of the total firefighter population. For the NIOSH 2007 panel, 94.3% of the 88 female firefighters fit in Cells 1 through 5 and 7 while 88.6% of male firefighters fit in Cell 4 and 5 and 7 through 10. The NIOSH 2007 panel would have excluded none of the female firefighter population and 10% of the male firefighter population, mainly those with a wider face. On average, the male and female firefighters appear to have larger face length and face width than those of the USAF airmen and airwomen and U.S. civilian respirator users.
Figure 3.
The distributions of firefighter face dimensions fitting to both the Los Alamos National Laboratory (LANL) 1973 and National Institute for Occupational Safety and Health (NIOSH) 2007 panels. The squares represent females and circles denote males. The dotted lines define LANL panel boundaries and the solid lines outline the NIOSH 2007 panel borders.
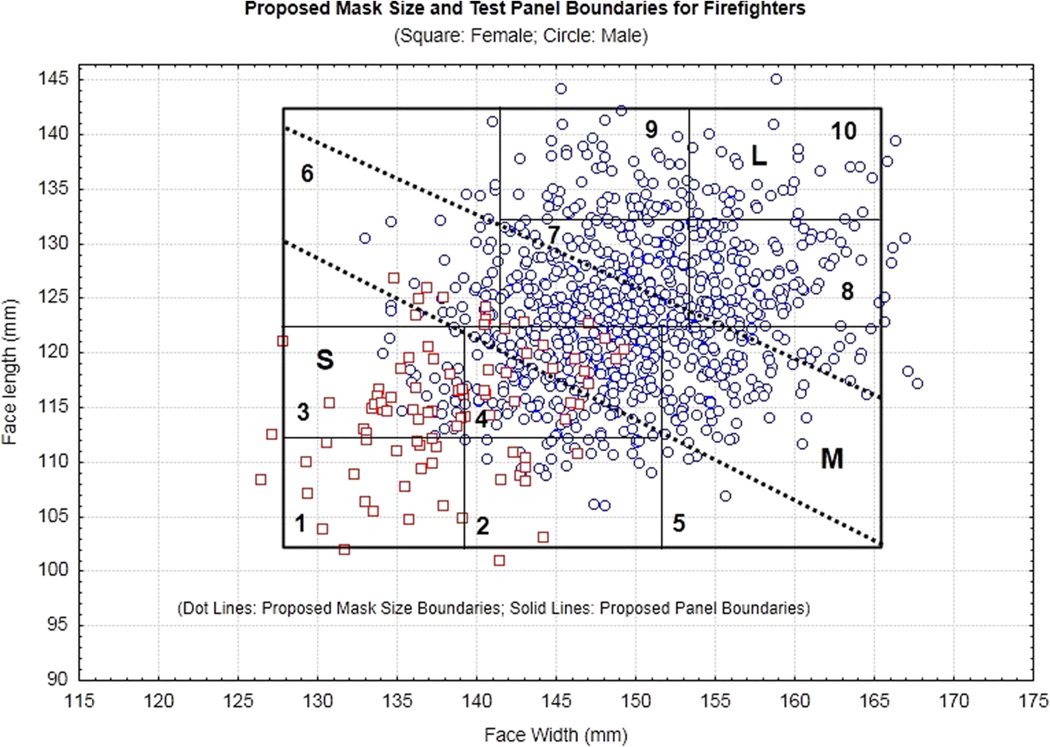
For better firefighter protection, it is suggested that the test panel be adjusted for firefighter respirator testing and that the respirator sizing ranges for firefighters be modified. A simple yet practical solution is to shift the entire 10-cell panel of the NIOSH 2007 panel to 7 mm greater in face width and 4 mm greater in face length. The firefighter masks/respirators can then be designed in three sizes to accommodate at least 95% of firefighters (Figure 4). The small size would be designed to accommodate subjects with face length of 102.5 mm to 122.5 mm and face width of 127.5 mm to 151.5 mm (Cells 1–4). The medium size would be designed to accommodate four cells (Cells 4–7) with face length by width combination of 122.5 mm to 132.5 mm × 139.5 mm to 151.5 mm, 102.5 mm to 122.5 mm × 151.5 mm to 165.5 mm, 122.5 mm to 142.5 mm × 127.5 mm to 141.5 mm, and 122.5 mm to 132.5 mm × 141.5 mm to 153.5 mm, respectively. The large size would be designed to accommodate individuals with face length of 122.5 mm to 142.5 mm and face width of 141.5 mm to 165.5 mm (Cells 7–10). Using face length and face width, the two size boundaries (dotted lines) for three mask/respirator sizes can be defined by two logistic regression models: (1) probability of wearing size S instead of size M = 1/(1 + exp (−324.6307 + 1.41566 × face length + 1.09007 × face width)) and (2) probability of wearing size L instead of size M =1/(1 + exp (217.913 – 1.001913 × face length − 0.6086544 × face width)), where the probabilities were set both at 0.5 (Figure 4).
Figure 4.
The proposed test panel for firefighter masks is a shift of the entire 10 cells of the National Institute for Occupational Safety and Health (NIOSH) 2007 panel to 7 mm greater in face width and 4 mm greater in face length. The numbers 1 to 10 represent the 10 panel cells. The dotted lines represent the size boundaries for three mask/respirator sizes (S, M, and L), which are defined by two logistic regression models.
DISCUSSION
A NIOSH study in 2002 found that on average firefighters were 6.8 kg heavier than other occupations for males and 10 kg heavier for females (Hsiao et al., 2002). This significant weight difference drastically affects other body component measurements. Univariate independent sample t tests of the data from this firefighter study (Hsiao, 2008) and the respirator users study (Zhuang et al., 2004) revealed that firefighters have larger face length (2.2 mm for men and 2.0 mm for women) and face width (6.4 mm for men and 3.3 mm for women) than the weighted average of other respirator user groups combined (p < .05). These differences are greater than measurement errors and thus have practical significance (Gordon et al., 1989). The scatterplot in Figure 5 further reveals that using industrial respirator user head-and-face anthropometric data would be inadequate for describing the facial anthropometric variability of the current firefighter workforce (p < .05). The NIOSH 2007 respirator test panel, which was developed to cover general industrial respirator users and was a significant update to the LANL panel, may have undercounted its impact on firefighters in that the firefighters with larger face length and width were excluded from the panel. Since firefighters represent a third of U.S. respirator users and are often at high risk for exposure to hazardous particles and gases, a modified respirator test panel for firefighter respirator is both relevant and necessary.
Figure 5.
The scatterplot revealed that on average firefighters (circles; N = 951) have larger face length and face width than those of other respirator user groups combined (triangles; N = 2,767) (t test; p < .05). Using industrial respirator user head-and-face anthropometric data would be inadequate for describing the facial anthropometric variability of the current firefighter workforce.
CONCLUSION (STUDY 2)
This study presented the bivariate anthropometric study method to evaluate the ability of LANL 1973 and NIOSH 2007 full-face-piece panels to accommodate the current firefighter population. It also introduced the probability distribution concept for determining product sizing boundaries. The LANL 1973 panel would have excluded 39% of the male firefighter population and 4.5% of the female firefighter population, and the NIOSH 2007 panel would have excluded 10% of the male firefighter population. For better firefighter protection, it is suggested that the boundaries of NIOSH 2007 test panel cells be systematically adjusted for 7 mm greater in face width and 4 mm greater in face length for firefighter mask/respirator testing applications. The sizing system then can be pinned to three sizes and defined based on the two logistic regression boundaries in Figure 4, of which they would be tested with subjects from Cells 1 through 4 for small, Cells 4 through 7 for medium, and Cells 7 through 10 for large, respectively.
STUDY 3: DESIGN WITH MULTIVARIATE CONSIDERATION—FIRE TRUCK CAB ACCOMMODATION
Background
In some design applications, equipment accommodation is a multifactor matter; an example is fire truck cab accommodation. The National Fire Protection Association (NFPA) estimates that there were approximately 1,103,300 firefighters in the United States in 2010 (Karter & Stein, 2011). There were an estimated 14,200 collisions involving fire department emergency vehicles in 2010 while departments were responding to or returning from incidents, which resulted in 775 firefighter injuries, not counting civilian injuries and separate firefighter injuries during the use of personal vehicles (Karter & Molis, 2011). There were also 11 firefighter fatalities in on-duty vehicle crashes in 2010 (Fahy, LeBlanc, & Mollis, 2011). While transportation incidents are a multifaceted issue, the general consensus is that the human-cab interface is a critical issue in many incidents. Also, fire truck drivers’ health and fatigue can be aggravated by a poorly designed driver-cab interface. The National Fallen Firefighters Foundation’s (NFFF) 2006 white paper identified firefighter anthropometry for fire apparatus and equipment design (i.e., cabs, seats, body restraints, egresses, bunker gear, etc.) as a pressing issue to prevent firefighter fatalities in crashes and rollover incidents, falls from vehicles, and excessive thermal and chemical exposure (Routley, 2006). There is a pressing need to revisit fire truck cab accommodation for safe and efficient operation.
Easy to reach controls, sufficient overhead clearance, proper seat belt restraint, and adequate visibility of both internal and external environments all are functions of the driver’s body size and position in the cab. Some people have long limbs and a short torso while others have short limbs and a long torso; the accommodation challenge is further compounded with each additional measurement used to specify the size of an individual and the driver-cab interface. A multivariate accommodation approach is a solution to address the multidegree anthropometry concerns for designing fire truck cabs. The driver/firefighter population percentage level can be accommodated by taking into account both their overall body size variance and body segment proportional variability. Principal component analysis is a multivariate statistical technique that is widely used by scientists to remove known noisy variables and reduce the data set to a more manageable size. It defines a new coordinate system using linear combinations of the original variables to describe trends in the data. The necessary number of principal components can be chosen using the Kaiser criterion (Kaiser, 1960) or scree test (Cattell, 1966). The scores from the principal component analysis can then be used to develop PCA models that match U.S. firefighters as closely as possible for cab mockup testing or for the development of digital human models for computerized cab design and evaluation.
Objective
The goal of this study is to develop a set of multivariate digital anthropometric models, which represent 95% of the current firefighter/fire truck driver population for next-generation computerized cab design. Based on the six-step paradigm for anthropometric product development, the essential dimensions for this study are stature, weight, sitting height, acromial height, elbow rest height, elbow-wrist length, knee height, buttock-knee length, acromion-grip length, hip breadth, and bideltoid breadth, as per cab design needs (Hsiao et al., 2005). The population to be considered is firefighters and the percentage of the population to be accommodated is 95% of firefighters. The study demonstrates the process of the next three steps of multivariate anthropometric procedures: data processing, computation, and adjustments.
METHODS
Participants
A total of 947 firefighters (861 men and 86 women) participated in the study. They were from four U.S. regions: Rockville, MD; Philadelphia, PA; Phoenix, AZ; and Fort Worth, TX. The sample took into account the geographic density of racial/ethnic distributions calculated from the U.S. Census 2000 (Hsiao, 2008). Their weighted average height was 176.9 cm (SD = 6.7 cm) and mass was 92.9 kg (SD = 14.8 kg) for men and 166.7 cm (SD = 6.0 cm) and 72.4 kg (SD = 12.9 kg) for women.
Independent Variables
The independent variables are participants’ stature, weight in kg, sitting height, acromial height (sitting), elbow rest height (sitting), elbow-wrist length (sitting), knee height (sitting), buttock-knee length (sitting), acromion-grip length (sitting), hip breadth (sitting), and bideltoid breadth (sitting).
Dependent Variables
The dependent variables are PCA scores and PCA models
Devices
A set of devices, including a GPM anthropometer (GPM, Switzerland), beam calipers (rearranged pieces of the anthropometer), a digital scale, a stool, and a computer, was used to complete anthropometric measurements.
Procedure
The whole body anthropometry measurement for fire truck cab design was part of a national firefighter anthropometry survey (Hsiao, 2008). Upon arrival, the participants viewed a PowerPoint presentation, which described the study. Each participant had the opportunity to ask questions before signing an informed consent form and filling out a short questionnaire related to the use of automotive fire apparatus. The participant was then taken to a dressing room, where men changed from street clothes into bicycle shorts and women changed into bicycle shorts with a halter top. The participants were measured in sitting posture; the participants sat on a stool and looked straight ahead with shoulders relaxed. They lined up their feet with the premarked footprints on a platform. The platform was adjustable through a hydraulic control such that the participant’s knee angle was kept at 90 degrees. The measurements were taken using the GPM anthropometer and beam calipers. Stature and body weight were then measured, using the same GPM anthropometer and a digital scale. After the measurements were completed, the participant was reimbursed and dismissed.
DATA ANALYSIS
The 11 measurements relevant to this fire truck cab accommodation application (see the Independent Variables section) were stratified into male and female categories and standardized with respect to their weighted mean and standard deviation first. Then PCA was applied separately to these standardized values using Statistical Analysis System software (SAS Institute, Cary, NC). This PCA procedure reduced the 11 dimensions to three principal components (PCs) to define body models on the basis of a scree plot (Cattell, 1966). These three PCs were orthogonal to one another and can be described as approximating an ellipsoid enclosing data points for 86% for females and 84% for males. The Bonferroni method was used with a single radius value (r = 2.44 for females and r = 2.40 for males) as the 95% enclosure criterion to achieve the 95% confidence level enclosure for each gender (Johnson & Wichern, 2007).
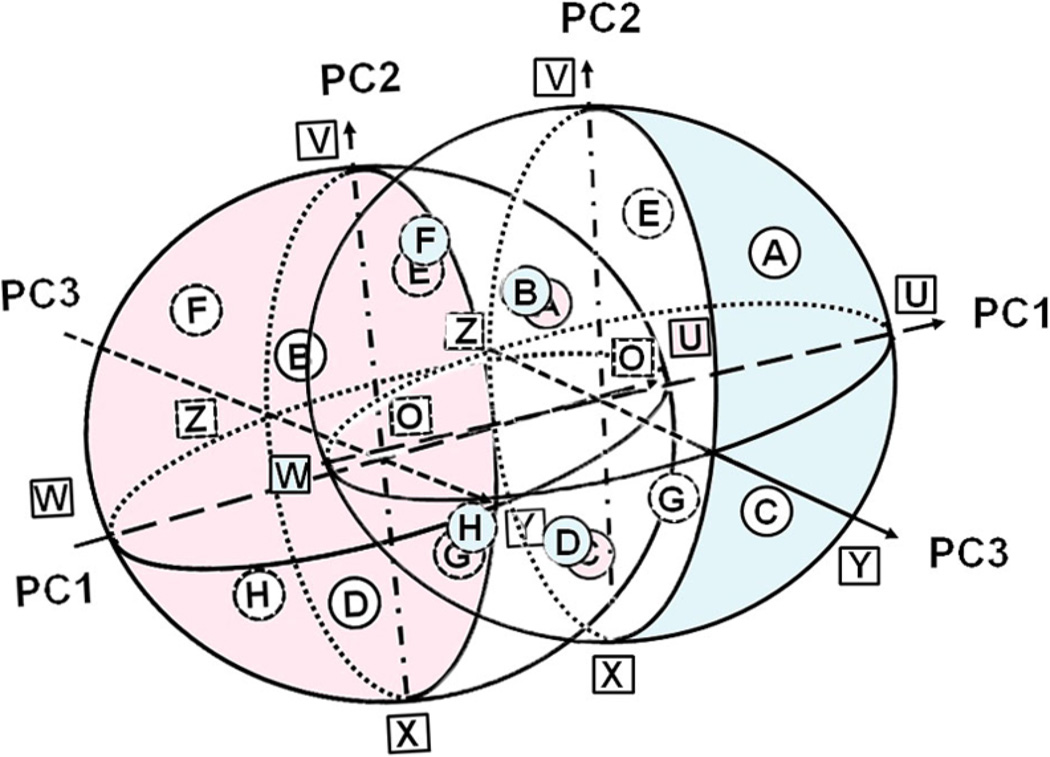
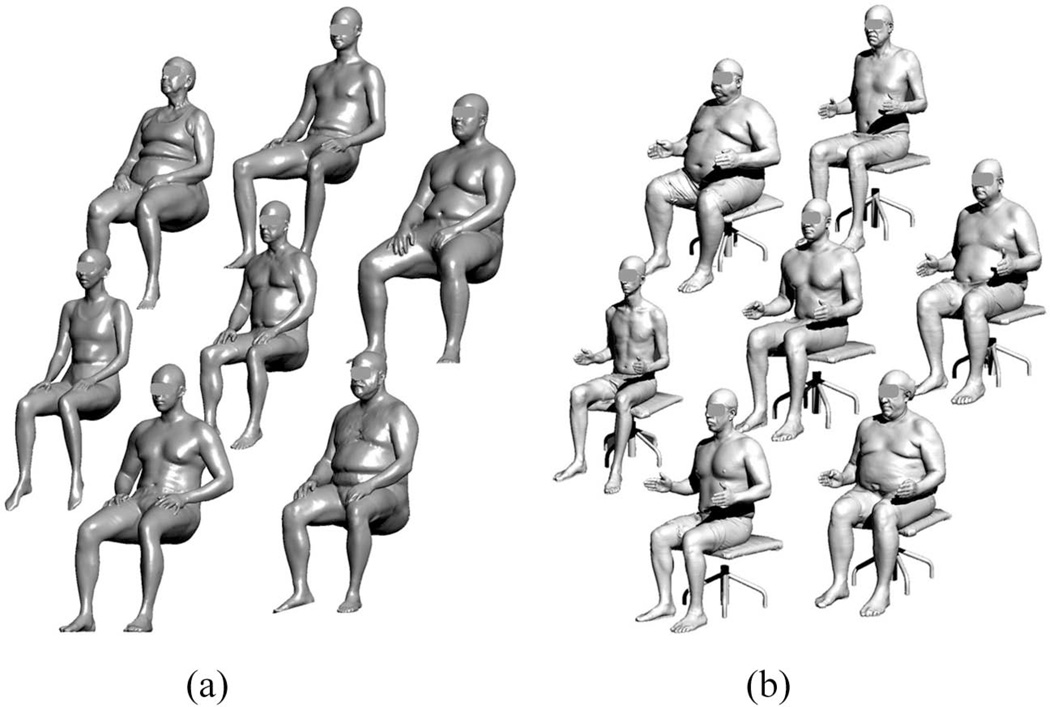
There are 14 points on the ellipsoid surface representing the diverse body size and shape combinations (Figure 6)—the six intercept points on the ellipsoid surface by the three axes (Points U, V, W, X, Y, and Z) and the eight octant midpoints located at the surface center of each of eight sections (octants) divided by the three axes of this ellipsoid (Points A, B, C, D, E, F, G, and H). These 14 points along with the centroid of ellipsoid (Point O) were the basis for the selection of the anthropometric models. The corresponding 11 anthropometric values of these 14 models were calculated through reverse processes of the eigenvalues and eigenvectors. The Euclidean distance from each participant to each model point was then evaluated; one closest-neighbor participant for each model was chosen.
Figure 6.
There were 14 points on each ellipsoid surface representing the diverse body size and shape combinations within each gender group (left: women; right: men). There were also two average models (one O for each gender). Four models for women (A, C, E, and G) were redundant to four models for men (B, D, F, and H). In addition, female model U was redundant to males model O; and male model W was redundant to female model O. The joint male and female enclosure space consists of 24 models which included 14 models for men (A, B, C, D, E, F, G, H, U, V, X, Y, Z, and O) and 10 models for women (B, D, F, H, V, W, X, Y, Z, and O).
Since fire truck cab workspaces are designed for both men and women, a combined set of male and female models is necessary for the design to be relevant (Hudson & Zehner, 2010). To achieve the goal of minimizing the number of models in the combined set, the models of each gender were put into the other gender’s 95% enclosure space, and those who were identified to be within the enclosure space of the opposite gender were considered redundant and discarded. For example, to identify whether a female model was a redundant model, the 11 derived body dimensions of that female model were first converted into z scores using the means and standard deviations of the corresponding variables in the male sample. Then, the three PCs were derived by multiplying the set of z scores with the matrix of component score coefficients. The Euclidean distance of this female model to the centroid of the 95% male enclosure was determined using the three PCs. If the distance was smaller than the r = 2.40 enclosure criterion, this female model was considered redundant and discarded. Otherwise, the model was retained for the joint male and female space. The male models were evaluated for possible redundancy in the same manner by placing each of them into the female 95% enclosure (r = 2.44) and following identical accept/reject procedures.
RESULTS
The three PCs for men accounted for 51%, 19%, and 14% of the total variation, respectively. PC1 predicted the overall body size. PC2 represented a contrast between dimensions correlated with body heights against those correlated with body width and depth. PC3 contrasted the measurements of five volume-and-length dimensions with the remaining six body dimensions. The three PCs for women followed the same patterns as in the male sample, accounting for 51%, 19%, and 16% of the total variation, respectively.
Five out of 15 female models (A, C, E, G, and U) were found to coincide with the male space because their respective Euclidian distance to the centroid of the 95% male enclosure was smaller than the r = 2.40 criterion. In addition, the Euclidian distance of five male models (B, D, F, H, and W) to the centroid of the 95% female enclosure was smaller than the r = 2.44 criterion. In all, the female models A, C, E, and G were redundant to male models B, D, F, and H; female model U was redundant to male model O; and male model W was redundant to female model O (Figure 6). The recombination procedure resulted in a joint male and female enclosure space of 24 models, which included 14 models for men (A, B, C, D, E, F, G, H, U, V, X, Y, Z, and O) and 10 models for women (B, D, F, H, V, W, X, Y, Z, and O). The dimensions of these models and their corresponding closest-neighbor human participants and dimensions are presented in Tables 1 and 2.
TABLE 1.
Hypothetical Anthropometry Models of the Participating Firefighters Corresponding to Multivariate Anthropometric Models (weighted)
| Male Model |
Stature | Wt in kg | Sit Ht | Acr Ht Sit |
Ebw Ht Sit |
Ebw Wrist Lgth |
Knee Ht Sit |
Butt- Knee Lg Sit |
Acr- Grip Lg |
Hip Bdth Sit |
Bidel Bdth Sit |
|---|---|---|---|---|---|---|---|---|---|---|---|
| O | 1,769 | 92.9 | 924 | 614 | 242 | 299 | 544 | 630 | 633 | 437 | 574 |
| A | 1,791 | 123.5 | 931 | 631 | 258 | 308 | 555 | 665 | 642 | 510 | 679 |
| B | 1,647 | 97.5 | 869 | 575 | 231 | 280 | 501 | 606 | 587 | 462 | 611 |
| C | 1,834 | 109.2 | 917 | 607 | 210 | 325 | 584 | 684 | 680 | 474 | 621 |
| D | 1,691 | 83.2 | 854 | 551 | 184 | 297 | 530 | 625 | 625 | 426 | 554 |
| E | 1,847 | 102.6 | 994 | 677 | 301 | 302 | 557 | 634 | 641 | 448 | 593 |
| F | 1,704 | 76.7 | 932 | 621 | 274 | 274 | 504 | 575 | 586 | 399 | 526 |
| G | 1,891 | 88.3 | 980 | 653 | 253 | 319 | 587 | 653 | 679 | 411 | 536 |
| H | 1,747 | 62.3 | 917 | 597 | 227 | 291 | 533 | 594 | 624 | 363 | 468 |
| U | 1,912 | 118.9 | 987 | 670 | 269 | 327 | 597 | 689 | 688 | 485 | 641 |
| V | 1,726 | 107.2 | 939 | 638 | 290 | 282 | 514 | 611 | 595 | 473 | 631 |
| W | 1,626 | 67.0 | 862 | 558 | 216 | 272 | 490 | 571 | 578 | 388 | 506 |
| X | 1,812 | 78.6 | 910 | 590 | 195 | 316 | 573 | 649 | 671 | 400 | 516 |
| Y | 1,729 | 107.7 | 880 | 582 | 212 | 304 | 542 | 652 | 633 | 481 | 634 |
| Z | 1,809 | 78.2 | 969 | 647 | 273 | 295 | 546 | 608 | 633 | 392 | 513 |
| Female model | |||||||||||
| O | 1,667 | 72.4 | 874 | 583 | 237 | 275 | 510 | 606 | 597 | 426 | 490 |
| A | 1,721 | 84.6 | 931 | 644 | 301 | 279 | 520 | 595 | 601 | 447 | 536 |
| B | 1,599 | 61.4 | 875 | 594 | 271 | 253 | 470 | 554 | 546 | 388 | 466 |
| C | 1,779 | 68.4 | 934 | 627 | 260 | 293 | 542 | 607 | 639 | 402 | 464 |
| D | 1,656 | 45.1 | 878 | 577 | 230 | 268 | 492 | 566 | 585 | 342 | 394 |
| E | 1,679 | 99.6 | 869 | 589 | 244 | 282 | 528 | 646 | 610 | 509 | 585 |
| F | 1,556 | 76.4 | 813 | 539 | 213 | 256 | 478 | 605 | 555 | 450 | 515 |
| G | 1,736 | 83.3 | 873 | 573 | 203 | 296 | 550 | 658 | 649 | 464 | 513 |
| H | 1,613 | 60.1 | 817 | 522 | 172 | 271 | 500 | 617 | 594 | 405 | 443 |
| U | 1,790 | 95.6 | 930 | 633 | 267 | 300 | 560 | 647 | 652 | 485 | 560 |
| V | 1,610 | 88.6 | 870 | 600 | 278 | 260 | 488 | 594 | 559 | 471 | 561 |
| W | 1,545 | 49.1 | 818 | 533 | 206 | 249 | 461 | 565 | 543 | 367 | 419 |
| X | 1,725 | 56.1 | 877 | 566 | 196 | 289 | 532 | 618 | 636 | 380 | 418 |
| Y | 1,698 | 61.8 | 917 | 622 | 277 | 273 | 504 | 570 | 591 | 382 | 455 |
| Z | 1,637 | 82.9 | 830 | 545 | 196 | 277 | 516 | 642 | 604 | 470 | 524 |
Note. N = 861 for men and N = 86 for women; models in italic font are redundant models when male and female models are combined; unit in kg for weight and others in mm. Wt in kg = weight in kg; Sit Ht = sit height; Acr Ht Sit = acromial height, sitting; Ebw Ht Sit = elbow rest height sitting; Ebw-Wrist Lgth = elbow-wrist length; Knee Ht Sit = knee height, sitting; Butt-Knee Lg Sit = buttock-knee length, sitting; Acr-Grip Lg = acromion grip length, sitting; Hip Bdth Sit = hip breadth, sitting; Bidel Bdth Sit = bideltoid breadth.
TABLE 2.
Anthropometry of the Closest-Neighbor Participating Firefighters Corresponding to 24 Combined Male and Female Multivariate Anthropometric Models
| Model | Stature | Wt in kg |
Sit Ht | Acr Ht Sit |
Ebw Ht Sit |
Ebw- Wrist Lg |
Knee Ht Sit |
Butt- Knee Lg Sit |
Acr- Grip Lg |
Hip Bdth Sit |
Bidel Bdth Sit |
|---|---|---|---|---|---|---|---|---|---|---|---|
| O (M) | 1,759 | 92.1 | 924 | 616 | 242 | 295 | 528 | 630 | 637 | 438 | 574 |
| A (M) | 1,815 | 114.5 | 937 | 650 | 248 | 315 | 561 | 658 | 658 | 479 | 679 |
| B (M) | 1,647 | 86.3 | 869 | 560 | 231 | 284 | 505 | 607 | 569 | 414 | 609 |
| C (M) | 1,825 | 94.5 | 923 | 619 | 231 | 300 | 560 | 685 | 678 | 460 | 622 |
| D (M) | 1,707 | 79.5 | 899 | 566 | 197 | 298 | 524 | 626 | 627 | 437 | 569 |
| E (M) | 1,844 | 104.4 | 990 | 671 | 302 | 307 | 556 | 631 | 636 | 446 | 583 |
| F (M) | 1,770 | 89.5 | 946 | 612 | 245 | 281 | 526 | 629 | 612 | 417 | 524 |
| G (M) | 1,810 | 94.5 | 945 | 627 | 257 | 307 | 558 | 644 | 669 | 425 | 529 |
| H (M) | 1,765 | 76.8 | 941 | 599 | 218 | 294 | 529 | 617 | 630 | 409 | 534 |
| U (M) | 1,918 | 103.6 | 982 | 671 | 265 | 315 | 603 | 699 | 677 | 460 | 627 |
| V (M) | 1,748 | 96.7 | 914 | 619 | 254 | 299 | 546 | 582 | 600 | 444 | 618 |
| X (M) | 1,763 | 89.5 | 895 | 605 | 234 | 300 | 538 | 654 | 656 | 399 | 542 |
| Y (M) | 1,742 | 93.5 | 903 | 603 | 232 | 288 | 549 | 630 | 636 | 438 | 619 |
| Z (M) | 1,763 | 93.5 | 937 | 629 | 269 | 310 | 550 | 613 | 651 | 425 | 549 |
| O (F) | 1,682 | 73.1 | 897 | 598 | 233 | 271 | 504 | 602 | 583 | 411 | 468 |
| B (F) | 1,590 | 58.0 | 846 | 577 | 255 | 259 | 482 | 576 | 572 | 396 | 456 |
| D (F) | 1,666 | 62.3 | 867 | 569 | 226 | 284 | 506 | 580 | 582 | 394 | 458 |
| F (F) | 1,624 | 66.6 | 854 | 558 | 239 | 279 | 489 | 616 | 595 | 406 | 512 |
| H (F) | 1,674 | 62.9 | 860 | 540 | 201 | 257 | 500 | 615 | 560 | 400 | 431 |
| V (F) | 1,599 | 67.2 | 851 | 567 | 244 | 268 | 491 | 579 | 593 | 443 | 499 |
| W (F) | 1,597 | 55.4 | 837 | 556 | 217 | 266 | 488 | 573 | 586 | 383 | 434 |
| X (F) | 1,686 | 64.0 | 880 | 561 | 205 | 279 | 519 | 612 | 608 | 415 | 448 |
| Y (F) | 1,685 | 69.5 | 879 | 614 | 260 | 279 | 518 | 583 | 600 | 395 | 486 |
| Z (F) | 1,666 | 75.3 | 857 | 572 | 220 | 272 | 524 | 635 | 619 | 473 | 488 |
Note. N = 861 for males and N = 86 for females; unit in kg for weight and others in mm; M = male; F = Female. Wt in kg = weight in kg; Sit Ht = sit height; Acr Ht Sit = acromial height, sitting; Ebw Ht Sit = elbow rest height sitting; Ebw-Wrist Lg = elbow-wrist length; Knee Ht Sit = knee height, sitting; Butt-Knee Lg Sit = buttock-knee length, sitting; Acr-Grip Lg = acromion grip length, sitting; Hip Bdth Sit = hip breadth, sitting; Bidel Bdth Sit = bideltoid breadth.
DISCUSSION
Accounting Both the Overall Body Size and Body Segment Proportional Variances
In cab or cockpit design, multiple measurements must be considered; among them are easily accessible controls, sufficient overhead clearance, internal and external visibility, clearance between control elements and driver body, and seat height. When each dimension is arranged sequentially to cover the 2.5th to 97.5th percentile population, the design would include 95% of the user population for each specific function but suffer from a compounded decrease in level of overall accommodation, which would result in design inefficiency.
Instead of focusing on each of 11 individual dimensions, this study relied on three PCs that are linear combinations of the 11 original variables. These PCs are orthogonal to each other and approximate an ellipsoid in distribution. A 95% accommodation level was then selected as this threshold was found to sufficiently balance cab efficiency and cost-effectiveness. This approach resolved the problem of the univariate approach for multiple measurements by taking into account both the overall body size variance and body segment proportional variability (Hsiao et al., 2005; Zehner, Meindl, & Hudson, 1993). The models generated in this study therefore include not only overall large and small persons but also individuals of different body configurations. For example, the closest-neighbor participant of male Model F has a medium stature (50th percentile; 1,770 mm) but a tall sitting height (73th percentile; 946 mm). In contrast, the closest-neighbor participant of male Model C has a tall stature (80th percentile; 1,825 mm) but medium sitting height (49th percentile; 923 mm). This variability in body sizes and configurations reflect the real-world human models much better than the traditional multiple-tier univariate method and will help improve the conformity of mannequins or digital human models in cab workspace design.
Selection of Closest-Neighbor Participant for Each PCA Model
The study determined 24 principal component analysis–based firefighter body models to facilitate fire truck cab design. Their corresponding closest-neighbor human participants were also identified. From a design point of view, the statistically created 24 “PCA case models” serve as good design targets. If a virtual “fitting” is to be used in which the 3D scans of actual subjects are needed, the best approach would be to use the closest-neighbor “real persons.” The closest-neighbor real persons also offer other dimensions not in the original PCA analysis. For instance, eye height (sitting) is an important dimension to consider when evaluating internal and external visibility. Due to its high correlation with sitting height, it was not included in the original 11 measurements for PCA process. The 24 “PCA case models” would not have the eye height (sitting) information. The closest-neighbor “real persons” fill in this gap.
CONCLUSION (STUDY 3)
This study introduced the principal component analysis method for PE designs utilizing multivariate anthropometry. It also presented a theory for the composition of PCA models of two groups. The PCA-based study identified 24 representative body models, each of which represents a unique combination of body size and physique for male and female firefighters. These models, together with the anthropometric values of their closest-neighbor participants, are useful for the design of next-generation fire truck cabs. Developers of ergonomics software may utilize these models when generating digital mannequins for evaluating fire truck cab configurations. Cab designers can utilize these models to prototype or verify their driver-cab interface designs. The PCA-derived representative body models provide a level of anthropometric variability that cannot be delivered by traditional percentile models.
STUDY 4: DESIGNING EFFECTIVE SIZING SCHEMES—FALL-ARREST HARNESS DESIGN AND SIZING
Background
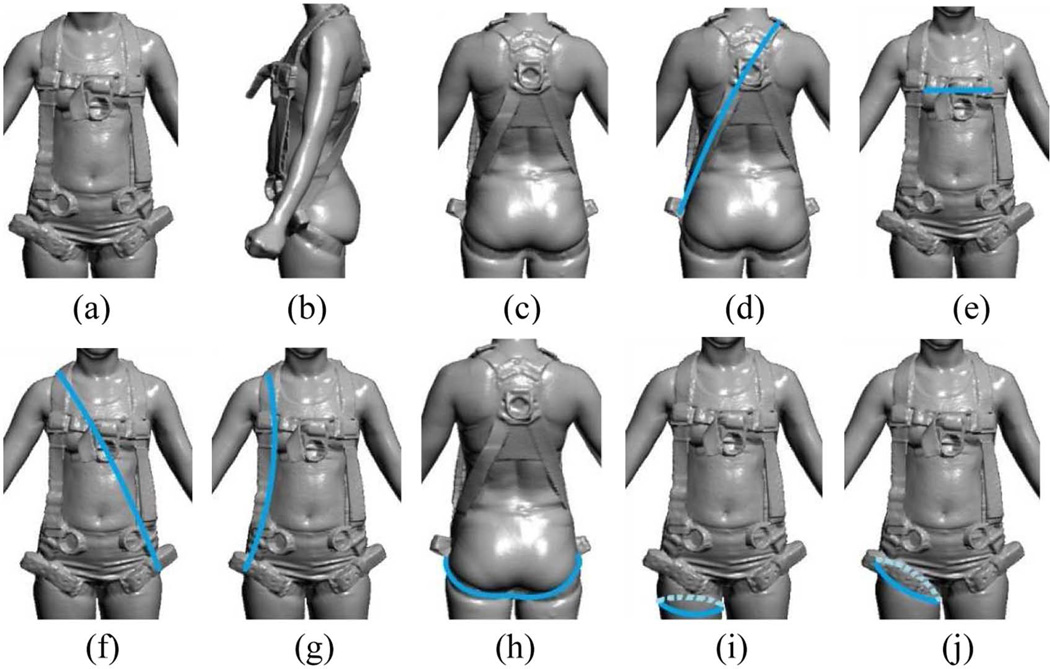
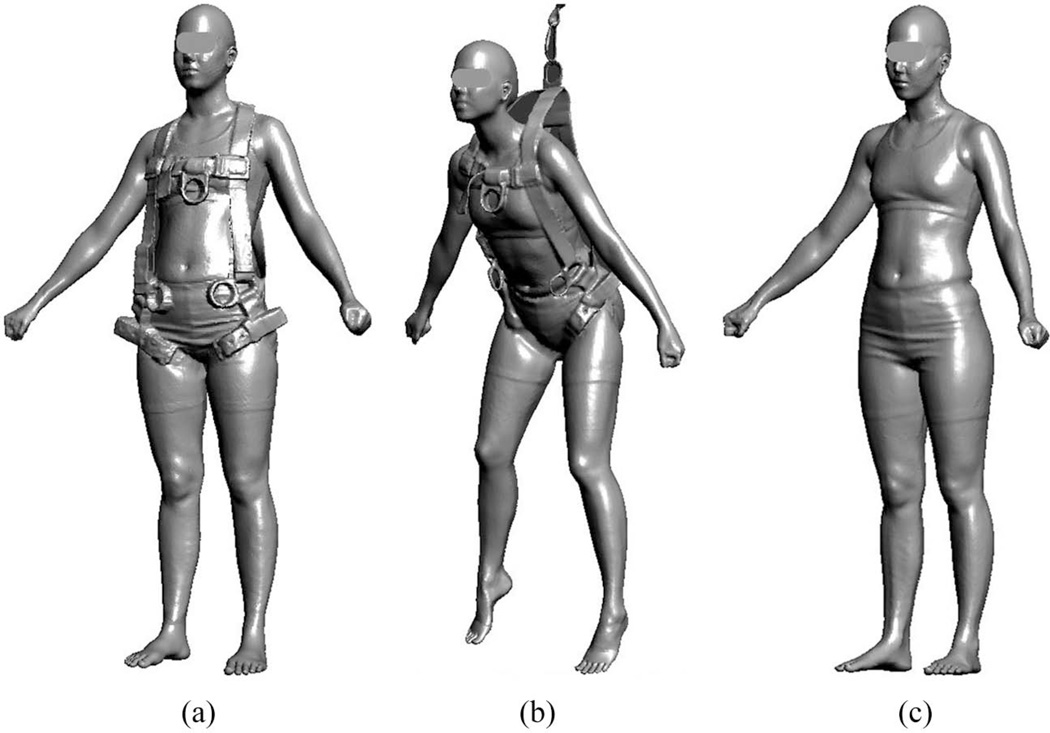
In some design applications, the proper accommodation of a product to the user population is not a matter of “one size fits all” or “one configuration accommodates all” as was the case with the truck cabs presented in Study 3. Fall-arrest harness design falls within this paradigm. Personal fall-arrest harnesses provide the last line of defense to 5.5 million U.S. construction workers in areas where fall hazards cannot be completely eliminated (Bureau of Labor Statistics, 2012). The simplest fall-arrest harness may consist of back strap, chest strap, front or cross-front strap, thigh or crotch strap, and hip strap, which are associated with back, chest, trunk or stomach, thigh, crotch, and hip sizes and shapes (Figure 7). Many workers have the experience that one of their body parts (e.g., torso) requires them to use one harness size while another body part (e.g., thigh) necessitates the use of a different size. A small size harness may fit a short individual well in torso areas but may be too tight at his or her belly. Similarly, a large size harness may fit a tall person in torso areas but be too loose in his or her thigh area. The difference in chest and pelvic configurations between men and women represents another challenge for harness designers in finalizing harness sizing and designs for diverse workforces. In addition to hindering worker performance, literature has shown that an improperly sized harness greatly increases the risk of suspension trauma, a potentially fatal reduction of return blood flow from legs to the heart and brain, after a successfully arrested fall (Hsiao et al., 2012).
Figure 7.
A fall-arrest harness (a: front view; b: side view; c: rear view) may consist of a back strap (d), chest strap (e), cross-front (f) and/or front strap (g), hip strap (h), and thigh (i) and/or crotch (j) strap, which are associated with back, chest, trunk/stomach, hip, and thigh/crotch sizes and shapes.
Since harness assemblies are 3D in nature and their strap components are linked to each other, traditional linear anthropometry-based strap incremental adjustments are not informative in harness design. If three adjustment ranges are used for three of six harness straps to address the worker–harness-fit issue, 27 sizes of harnesses will be required. The complexity of the sizing scheme very quickly becomes unworkable if additional adjustment dimensions are required. Fortunately, mathematical techniques can be used to reduce the complexity involved with all relevant measurements into a manageable number of harness sizes.
Objective
The objectives of this study were to (1) develop a harness sizing system to accommodate diverse workforces in U.S. industries and (2) define the adjustable range for each component of a given harness size for design and production purposes. Steps 1 through 3 of the six-step anthropometric analysis procedure are as follows: The essential dimensions for this study are human torso size and shape. The population to be considered is fall-arrest harness users (construction personnel and civilian workers), and the percentage of the population to be accommodated is 95%. This study reports the shape-analysis-based anthropometric theory and process, which addresses Steps 4 through 6 of the procedure: Elliptic Fourier Analysis (EFA) concept for data processing, computation, and adjustments.
METHOD
This study contains two parts. The first part identified the relationship between body shapes and harness fit using 216 participants and developed equations for predicting the best-fit harness size for any given 3D torso scan. The second part established an improved harness sizing system based on the equations developed in Part 1, using 600 3D torso scans (Hsiao, Friess, et al., 2009).
Participants
In Part 1 of the study, 108 male and 108 female construction workers participated. Their average height was 175.7 cm (SD = 6.5 cm) and mass was 85.5 kg (SD = 14.2 kg) for men and 162.6 cm (SD = 6.6 cm) and 66.2 kg (SD = 12.4 kg) for women. In Part 2, which was a retrospective study, 298 men and 302 women were included. They were representative samples drawn from the Civilian American and European Surface Anthropometry Resource (CAESAR) project of 2,382 participants (SAE International, 2008). Their average height was 177.4 cm (SD = 8.2 cm) and mass was 86.0 kg (SD = 18.0 kg) for men and 163.4 cm (SD = 7.6 cm) and 69.0 kg (SD = 18.7 kg) for women.
Independent Variables
Harness size assignment through live fit evaluation
A set of vest-type harnesses was used in the study. Four sizes of harnesses were tested—extra small (XSM; or size 1), standard (STD; or size 2), extra large (XLG; or size 3), and super extra large (SXL; or size 4). Each of the 216 participants was first fitted in the harness while standing for all sizes. The investigator adjusted the harness to achieve the best possible fit with inputs from participants about the comfort level of the harness. This feedback was used to select a harness size for the subsequent test.
Harness fit rating
The harness chosen was then tested while the participant was both standing and suspended. A pass or fail rating was assigned based on three criteria that are used in the harness manufacturing industry to minimize any potential biomechanical stress and suspension trauma: (1) The harness back D-ring was positioned between the inferior and superior borders of the scapula while the participant was standing, (2) the suspension angle (torso angle from vertical suspension line) was equal to or less than 35 degrees during the suspension condition, and (3) the chest strap did not make contact with or move above the neck while the participant was suspended. A harness fit rating of “pass” was assigned if all three criteria were met.
Dependent Variables
Elliptic Fourier coefficients of torso outlines
A three-dimensional extension to the Elliptic Fourier Analysis approach (Hsiao, Friess, et al., 2009) was used to quantify body configuration (size and shape) variation and to determine the correlation between body configuration and harness size and fit. The EFA approach is based on the mathematical decomposition of a curve into a series of ellipses that can be described by coefficients and constants (Kuhl & Giardina, 1980; Lestrel, 1997). These coefficients and constants, in turn, are treated as ordinary variables that describe the original curve of the size and shape of a human torso (Figure 8a–8d), for statistical analyses. The coordinates of a point along the curve and its constants are defined as:
| (1) |
| (2) |
and
| (3) |
where x(t), y(t), and z(t) are coordinates of a position along the curve; A0, C0, and E0 are the coordinates of the first harmonic (centroid); an, bn, cn, dn, en, and fn are the six coefficients of the nth elliptic harmonic; n is the harmonic number; N is the maximum number of harmonics; and the variable t is the position along the curve scaled to range from 0 to 2π.
Figure 8.
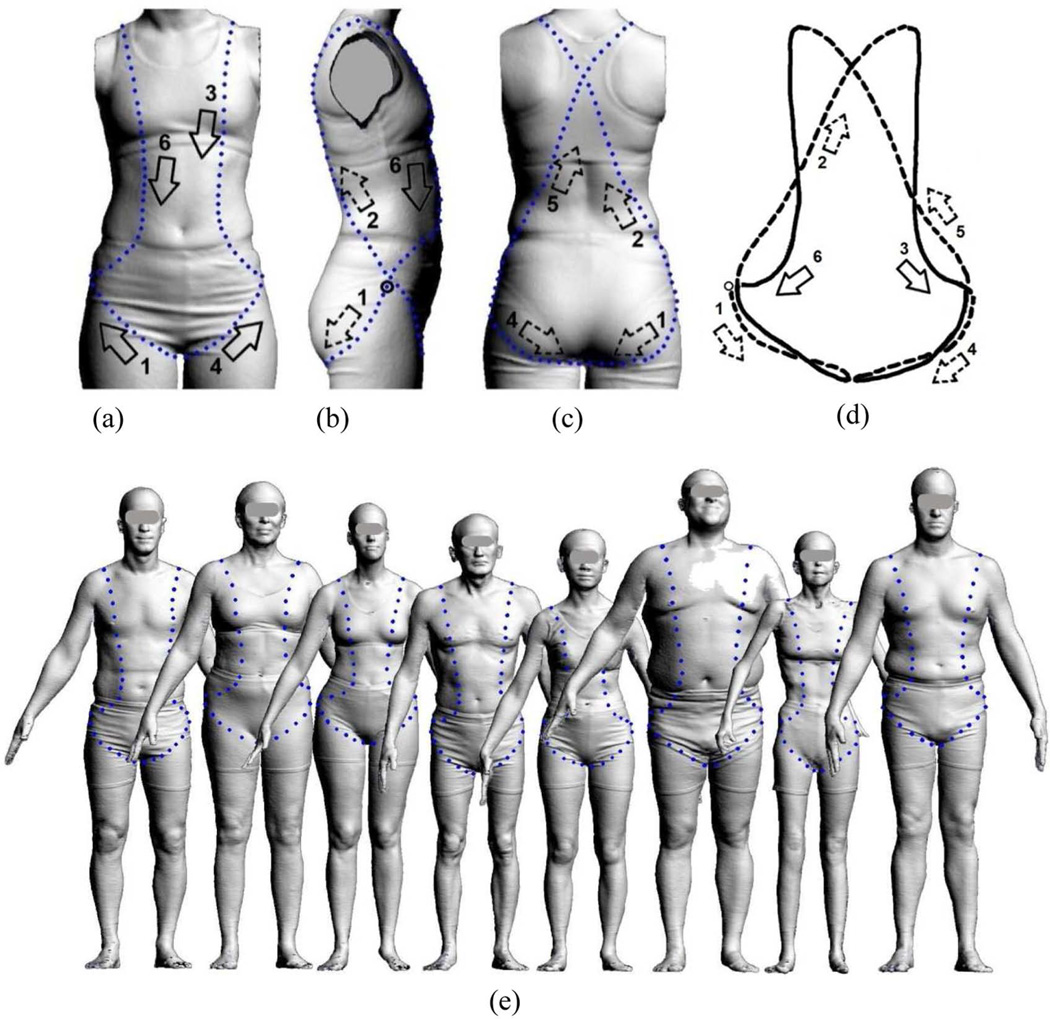
The outline that describes the curve of the shape of a human torso corresponds to the form of a vest-type harness; it is presented in (a) front, (b) right side, (c) back, and (d) perspective views. The outline started with (1) the right thigh strap at the right trochanter, then (2) the right side of the back strap, (3) the left side of the front strap, (4) the left thigh strap, (5) the left side of the back strap, and (6) finally the right side of the front strap. The dotted line in (d) represents the outline of the back side while the solid line describes the outline at the front side. The arrows indicate the direction of the Elliptic Fourier Analysis harmonic; dotted arrows represent the outlines at the back side while the solid arrows represent the outlines at the front side. The anterior iliac spines, shoulder blade point at mid-sagittal plane, trochanters, and two abdominal points were the landmarks that the outline was to pass through. Note that the cross-chest strap shown in Figure 7 was not part of the extracted outline in Figures 8a and 8d, nor the Elliptic Fourier Analysis computations, since it was easily done with a two-point digitization. Figure 8(e) demonstrates the torso outline curves of eight of the 600 three-dimensional torso scans from the CAESAR database in Part 2 of the study (Study 4).
The coefficients are defined as:
| (4) |
and
for the x projection,
| (5) |
and
for the y projection, and
| (6) |
And
for the z projection, where q is the number of points in the outline, Δtp is the distance between point p and p + 1 along the outline, and Δxp, Δyp, and Δzp are the x, y, and z components of the line segment from p – 1 to p.
EFA coefficients were calculated using the program EFA3D (Rohlf, 2003). The coefficients served as dependent variables in Part 1 in establishing harness-size prediction equations while acting as independent variables in Part 2 to predict the best-fit harness size for each participant (Figure 8e). The input to an EFA3D was a series of Cartesian coordinates that represent an individual’s torso outline in three dimensions. In this study, 49 data points on the torso outline (i.e., q = 49) were used. The output was a series of coefficients (weighted sums of the ellipses) that mathematically describe the outline and are used like any continuous variable for statistical purposes. The maximum number of harmonics (N) was set at 20, which yielded 123 EFA variables: 20 × 6 coefficients + 3 constants.
Predicted best-fit harness size
In Part 2, the predicted best-fit harness size, based on the Elliptic Fourier coefficients of torso outlines, was treated as a continuous rather than an ordinal variable. The predicted sizes then can be grouped by using certain cut-off points to establish an ordinal scale based on any proposed adjustment range of harness straps.
Devices
An anthropometer (GPM Instruments Inc., Zurich, Switzerland) and a Toledo scale (Mettler-Toledo Inc., Worthington, OH) were used to measure stature and body weight. A Cyberware WB4 3D full-body scanner (Cyberware Inc., Monterey, CA) was used to record the interface between the harness and participant during both normal standing (with and without a harness) and suspended conditions for Part 1. The same model of scanner was used in Part 2 to register torso images of 600 participants (without a harness) while standing.
Procedure
In Part 1, upon arrival, participants viewed a Web page that described the details of the study. Each participant signed an informed consent form. The participant was then taken to a dressing room, where men changed from street clothes into bicycle shorts and women changed into bicycle shorts with a halter top. After body weight and height were measured, the participant tried on four sizes of vest-type harnesses. Two investigators performed the fit test with feedback from the participant and recorded the fitting result. The “best-fitting” size was then selected for a subsequent fit assessment, in which the participant was scanned with the Cyberware full-body scanner in an erect standing posture with a harness. The participant lined up his or her feet with the premarked footprints on the scanner platform. The participant’s arms were held 45° laterally away from his or her torso, and the legs were about 41 cm apart at the heels with the toes angled about 30° away from the sagittal plane (referred to as the A scan; Figure 9a). The scan took 17 seconds. After the first scan, investigators attached the steel cable of a suspension system above the scanner in the laboratory to the back D ring of the harness and raised the participant until the participant’s toes were off the floor to simulate a post fall condition. While the participant was off the floor, he or she was scanned a second time (referred to as the B scan; Figure 9b), which allowed for assessment of the suspension angle. After the second scan, the participant was lowered to the floor and the fall-arrest harness was removed. The participant was then scanned a third time without the harness (referred to as the C scan; Figure 9c), which allowed for extraction of EFA coefficients. Finally, the participant changed back into street clothes, was compensated for his or her time, and was then dismissed.
Figure 9.
Participants were scanned three times with a Cyberware full-body scanner in the Part 1 study in: (a) an erect standing posture with a harness (A scan), (b) a suspended mode (B scan), and (c) a standing posture without the harness (C scan). In Part 2, participants were scanned for only the standing without a harness condition (i.e., C scan).
In Part 2, 600 selected scans from the CAESAR project database collected in 1998–2001 (SAE International, 2008) were used; the participants were scanned for only the standing condition without a harness (i.e., C scan), using the same procedure as Part 1.
DATA EXTRACTION AND ANALYSIS
Outline Data Extraction
For both Part 1 and Part 2, a continuous outline with 49 landmarks following the position of a harness on a human torso, as illustrated in Figure 8, was developed using C scans. The anterior iliac spines, shoulder blade point at mid-sagittal plane, trochanters, and two abdominal points were the landmarks that the outline was to pass through. The harness outline was extracted using Cyslice; and the B-spline feature of the software was used to place 49 landmarks (data points) spread approximately evenly onto the outline to complete a 3D curve (Figure 8). The xyz coordinates were exported as ASCII text and then used for further analyses.
Outline Data Process and Size
Prediction
Scans of participants in Part 1 with a passing test result were used to develop the prediction equations of the best-fit harness size using the EFA coefficients. The multiple homologous landmarks approach (Bookstein, 1991) was used to normalize outlines prior to Fourier analysis.
In Part 2, EFA coefficients of 298 men and 302 women were used to determine the harness sizes for them based on the prediction procedure developed in Part 1. It should be noted that while the participants with passing test results in Part 1 had their original best-fit harness sizes reported as integers, in the standard EFA process the best-fit harness size is treated as a continuous, rather than an ordinal variable. Once predicted, sizes can be rounded to the nearest integer or set at any cut-off point based on the adjustment ranges of harness components defined in order to reestablish an ordinal scale. The approach can, in theory, allow for prediction of any number of sizes, depending on the range of the predictor variables (body shape). In Part 2, the final sizes were set at cut-off points through an iterative process based on the goal that adjustment ranges of the front, back, chest, and cross-chest straps were within 17 cm of the target value and that the adjustment ranges of thigh/crotch and hip straps were within 23 cm of the target value (Hsiao, Whitestone, Taylor, Godby, & Guan, 2009).
RESULTS
Harness Sizing
Harness fit rate
While the difference in fail rates for harness-participant fit between women and men (35% vs. 28%) was not statistically significant, χ2(1) = 1.37, p = 0.24, the gender-by-harness-size fit rating analysis revealed that the failure rate of a given harness size is dependent upon gender, χ2(1) = 15.08, p < .001, discounting the XLG size, which has small cell numbers. This leads to the need for gender-specific harness designs and/or sizing plans.
Sizing prediction
Participants in Part 1 who received a passing fit rating (i.e., 78 men and 70 women) were used to establish harness sizing prediction equations for Part 2. Given the known contribution of gender to physical variation in torso shape, gender-specific regressions were computed. In order to maintain observation numbers (i.e., 78 men and 70 women) above variable numbers, the EFA coefficients (123 coefficients) were reduced by principal component analysis of the covariance matrix. Twenty components, accounting for over 96% (96.1% for men and 96.4% for women) of the total variance were retained. The sizing prediction equations were
and
where PC1, PC2, ‖, PC20 are the 20 principal component factors (Hsiao, Friess, et al., 2009).
The predicted best-fit sizes for the 600 participants in Study 2, based on 20 rank-ordered PCA estimators using EFA coefficients, were in the range of 0.92 to 3.49 for men and 0.32 to 2.96 for women, respectively.
Sizing Structure and Strap Lengths
Following standard manufacturing and design practices, a 17 cm range for back strap, chest strap, front cross-chest strap, and front strap and a 23 cm range for hip strap (gluteal furrow arc), thigh flat strap (thigh circumference), and thigh bikini strap (trochanter-crotch circumference) were determined to be cost-effective designs that had the additional value of not being cumbersome. An iterative process of grouping the predicted sizes was performed to identify the smallest number of sizes needed while meeting the aforementioned criteria on the adjustable ranges of the harness components. Three sizes for men and three sizes for women were developed. The sizes were defined by four cut-off points (i.e., sizes 0.9, 1.6, 2.515, and 3.5) for men and four (i.e., sizes 0.31, 0.916, 2.0613, and 3.0) for women. The adjustment ranges to cover 95% size-specific subpopulation for 7 harness-strap dimensions are presented in Table 3. The adjustment ranges of women size L were slightly greater than 17 cm for the torso straps and slightly greater than 23 cm for the thigh and hip straps. Producing an additional size (i.e., XL) for women is unnecessary due to a very small number of expected users in this category.
TABLE 3.
The Adjustable Ranges of the Harness Components With Three Sizes for Each Gender When Four Cut-Off Points (i.e., scores 0.9, 1.6, 2.515, and 3.5) for Men and Four (i.e., scores 0.31, 0.916, 2.0613, and 3.0) for Women Were Employed
| Male | Female | |||||
|---|---|---|---|---|---|---|
| Strap Size | Size S (mm) |
Size M (mm) |
Size L (mm) |
Size S (mm) |
Size M (mm) |
Size L (mm) |
| Back strap | 98 | 139 | 154 | 116 | 142 | 175 |
| Chest strap | 67 | 80 | 113 | 58 | 71 | 112 |
| Front cross-chest strap | 97 | 150 | 175 | 115 | 143 | 206 |
| Front strap | 101 | 142 | 146 | 94 | 122 | 172 |
| Gluteal furrow arc | 183 | 157 | 229 | 157 | 184 | 170 |
| Thigh circumference | 140 | 186 | 218 | 179 | 211 | 283 |
| Trochanter-crotch circumference | 132 | 203 | 228 | 201 | 232 | 269 |
Note. Bold is used to indicate the adjustment ranges of women size L were slightly greater than the target values of 17 cm for the torso straps and 23 cm for the thigh and hip straps.
Harness manufacturers can use the 97.5th percentile values of the back strap, chest strap, front cross-chest strap, front strap, gluteal furrow arc, thigh circumference, and trochanter-crotch circumference presented in Table 4 as the basis to determine strap cut lengths. They can also use the 2.5th percentile value of the strap length in Table 4 to define the tightest position for each harness component.
TABLE 4.
Proposed Sizing Plan for the Vest-Type Harness and the Adjustment Ranges (unit: mm) for Seven Harness-Strap Dimensions; Three Sizes Were Defined by Four Sizing Scores for Each Gender (men 0.9, 1.6, 2.515, 3.5; women: 0.3, 0.916, 2.016, 3.0)
| Male | Female | |||||||
|---|---|---|---|---|---|---|---|---|
| Size S | ||||||||
| Harness component | Lower | Mean | Upper | Range | Lower | Mean | Upper | Range |
| Back strap (Figure 7d) | 650 | 693 | 750 | 101 | 572 | 637 | 691 | 119 |
| Chest strap (Figure 7e) | 173 | 215 | 247 | 74 | 140 | 171 | 200 | 60 |
| Front cross-chest strap (Figure 7f) | 619 | 676 | 726 | 107 | 575 | 629 | 696 | 121 |
| Front strap (Figure 7g) | 520 | 586 | 633 | 114 | 517 | 562 | 612 | 95 |
| Gluteal furrow arc (Figure 7h) | 472 | 582 | 671 | 199 | 532 | 615 | 700 | 168 |
| Thigh circumference (Figure 7i) | 455 | 565 | 647 | 192 | 470 | 561 | 665 | 195 |
| Troch-crotch circumference (Figure 7j) | 563 | 691 | 762 | 199 | 577 | 669 | 781 | 204 |
| Size M | ||||||||
| Harness component | ||||||||
| Back strap (Figure 7d) | 679 | 737 | 818 | 139 | 603 | 674 | 745 | 142 |
| Chest strap (Figure 7e) | 200 | 239 | 280 | 80 | 157 | 190 | 228 | 71 |
| Front cross-chest strap (Figure 7f) | 661 | 734 | 811 | 150 | 610 | 676 | 754 | 143 |
| Front strap (Figure 7g) | 557 | 630 | 699 | 142 | 553 | 613 | 675 | 122 |
| Gluteal furrow arc (Figure 7h) | 558 | 624 | 715 | 157 | 568 | 644 | 753 | 184 |
| Thigh circumference (Figure 7i) | 546 | 617 | 732 | 186 | 525 | 614 | 736 | 211 |
| Troch-crotch circumference (Figure 7j) | 688 | 767 | 891 | 203 | 617 | 720 | 849 | 232 |
| Size L | ||||||||
| Harness component | ||||||||
| Back strap (Figure 7d) | 746 | 794 | 900 | 154 | 677 | 773 | 852 | 175 |
| Chest strap (Figure 7e) | 213 | 267 | 326 | 113 | 186 | 235 | 298 | 112 |
| Front cross-chest strap (Figure 7f) | 756 | 820 | 930 | 175 | 724 | 812 | 931 | 206 |
| Front strap (Figure 7g) | 641 | 692 | 787 | 146 | 631 | 723 | 802 | 172 |
| Gluteal furrow arc (Figure 7h) | 556 | 656 | 785 | 229 | 655 | 734 | 825 | 170 |
| Thigh circumference (Figure 7i) | 601 | 675 | 819 | 218 | 690 | 802 | 974 | 283 |
| Troch-crotch circumference (Figure 7j) | 764 | 854 | 992 | 228 | 806 | 929 | 1075 | 269 |
Note. See Figure 7d through 7j for a graphical description of harness components. The strap adjustment ranges were set to accommodate at least 95% of the estimated population within the specified size categories. The small size was set at 96.5% level (adjustable range = percentile 97.5 – percentile 1.0). The medium size was set at 95% level (adjustable range = percentile 97.5 – percentile 2.5), and the large size was set at 96.5% level (adjustable range = percentile 99 – percentile 2.5). The overall arrangement provides an opportunity to accommodate 98% of the estimated overall population.
DISCUSSION
The study showed that the predicted optimal sizes based on the EFA outputs ranged from 0.92 to 3.49 for men and 0.32 to 2.96 for women. Four sizes for men and three sizes for women can be generated by rounding the ranges to the nearest integers, or four sizes for men and four sizes for women can be generated by rounding the ranges to the nearest 0.5. However, given current design and production practices and constraints, neither of these proposals necessarily represents the optimal choice. The allowable or tolerable adjustable range of each harness component and the cost to stock uncommon sizes can affect user adoption and acceptance significantly. The study result determined that three sizes for men (defined by four scores: 0.9, 1.6, 2.515, and 3.5) and three sizes for women (defined by four scores: 0.3, 0.916, 2.016, and 3.0) were the smallest number of sizes that met the design constraint that the adjustment length of the front, back, chest, and cross-chest straps was no more than 17 cm, and the thigh and hip strap adjustment range was no more than 23 cm. The cross-chest strap, thigh strap (thigh circumference), and bikini thigh strap (trochanter-crotch circumference) for the female large size turned out to be slightly over the preset range criteria (see Table 3, Female L size). Since this size covers a wide combination of body dimensions and the extra 3 cm to 5 cm adjustment range is not extreme, this size category was not further subdivided.
It must be noted that an adjustment for clothing or other equipment is necessary as described in Step 6 of the six-step anthropometric procedure in the Introduction section (Hsiao & Halperin, 1998). In the harness design application, the additional clothing that workers wear in the winter time needs to be accounted for; harness users usually want one harness for all seasons. An additional 2.5 cm range for back strap, 2.5 cm for front cross-chest strap, and 7.5 cm for thigh-hip strap (i.e., gluteal furrow arc, thigh circumference, and trochanter-crotch in combination) would therefore be necessary (Hsiao, Friess, et al., 2009). Some specialized designs may require an additional 7 cm for the thigh-hip area for improved mobility. No additions would be needed for the chest strap and front strap.
CONCLUSION (STUDY 4)
This study introduced the 3D Elliptic Fourier Analysis procedure for human torso size and shape quantification, and thus the determination of harness sizing schemes. It established an improved sizing system that contains three sizes for women and three sizes for men to replace the current four- to seven-size unisex system. The adjustment ranges of the front, back, chest, and cross-chest straps were within the industry-standard adjustment range of 17 cm and the thigh and hip straps were within the 23 cm adjustment range, except for the female “large” size, which has a slightly wider range of adjustment. Harness manufacturers can utilize the parameters in Table 4 plus the adjustment for clothing (2.5–7.5 cm) to set harness cut lengths for improved harness assemblies, which would help the construction industry and civilians who work at height to reduce the risk of worker injury that results from poor harness fit or selection.
OVERALL DISCUSSION (STUDIES 1, 2, 3, AND 4)
Theories of Anthropometry and Implications for Design
The importance of anthropometric data for product efficacy and safety has been recognized by various industries. The use of anthropometric theories to inform PE product design, however, has not been systematically explored. In the past, designers typically used tabulated anthropometric data to justify design decisions. This univariate approach is sufficient in designing for extremes but has limited applications in 3D product design. A bivariate method has been useful for products that primarily involve two essential dimensions, such as in shoe-sizing and respirator panel design applications. The bivariate method is actually a type of size-classification process; a product that is designed based on multiple variables may also be displayed based on two essential dimensions for users’ convenience in selecting a size, especially when many sizes are available. For many other applications, a multivariate accommodation approach is necessary to account for both body size and body proportion variability. With the growth of multidimensional anthropometric databases and the availability of multivariate statistical analysis techniques, scientists are able to define space requirements for more design applications than ever before by removing known noisy variables and reducing the dataset to a more manageable size. The availability of 3D scanning technologies and 3D shape-quantification approaches have created new avenues for determining sizing schemes and size ranges of personal protective equipment, such as fall protection harnesses. This article offers four theories (descriptive statistics, probability modeling, principal component analysis, and Elliptic Fourier Analysis–based shape expression) for PE sizing and accommodation, which can be applied to many product design tenders. The six-step paradigm for anthropometric design introduced in this article serves as a guideline for designers in transferring anthropometric data into product design practices effectively.
Value and Limitations of Specific Methods
Study 1 presented a descriptive statistical approach, which represents the traditional procedure for anthropometric analysis. This method is typically used to define an extreme value of a single anthropometric measurement, such as the maximum gap between fan guards to prevent finger entrapment or the minimum seat width for a truck driver seat. Though literature provides a multitude of anthropometry tables, many publications do not offer important weighting factors (e.g., age and ethnicity distributions); engineers designing products without accurate target demographic data may produce deviated design outcomes.
Study 2 used a bivariate method to gauge the need for revised firefighter respirator test panels and introduced probability models for defining firefighter-specific respirator/mask sizing schemes. The probability models reflect the reality that some individuals may fit to two sizes of equipment, while others can’t. This method by itself does not determine the number of needed sizes for protective equipment; rather, it offers a means of improving sizing charts for product design and end-user size-selection purposes. Human protective equipment fit tolerance ranges often dictate the number of needed sizes.
Study 3 presents a multivariate accommodation concept using the principal component analysis method. This method quantifies overall size and shape information via multiple measurements in different coordinate orientations. It can be used for both linear and 3D description forms with multiple dimensions. Its typical application is to identify representative body models of a population. Designers can evaluate existing products or new prototypes digitally, improving workflow and end product efficacy. The most significant challenges for modelers/ergonomists in using this approach are obtaining raw data sets and adequate definition of the critical dimensions in PCA modeling; a suggested process for critical dimension selection can be found in an article on farm tractor cab design by Hsiao et al. (2005).
Study 4 introduces a 3D shape quantification method and a nondiscrete sizing determination approach. It offers an unparalleled solution to study human-equipment fit and identify the minimum number of sizes required to meet a defined fit tolerance range. This process requires a complete set of 3D images and a massive amount of data processing. Fortunately, cost-effective 3D scanners are becoming increasingly more available, and large-scale data processing can be handled by automation tools such as macros and software scripts. Because of its thoroughness and the realization of the tools to implement it cost-effectively, Study 4’s methodology is invaluable to advancing anthropometric science and ergonomic design practices.
Lessons Learned and Future Research
In many protective equipment design applications (i.e., protective clothing, gloves, boots, respirators, fall-arrest harness), the tolerance range of human–protective-equipment fit dictates the number of sizes and the increment range of dimensions among the sizes. A conservative adjustable range limit would potentially result in a larger number of needed sizes, which would increase production and stocking costs substantially. A wider adjustable range limit, on the other hand, may compromise the safety and health of end-users by failing to provide well-fit PE. Studies 2 and 4 used tolerance information from relevant industries. The literature does not offer much information on human–protective-equipment fit tolerance ranges for different lines of protective equipment; this is an area that deserves additional attention.
In Study 3, digital body models representing firefighters with unique combinations of body size and physique were developed. These models can be applied to fire truck cab design in a number of ways. Developers of ergonomics software may apply these models toward generating digital mannequins to improve the cab simulation environment. Rather than designing to specific dimensions, designers can use the models as representatives of a population that must be accommodated to evaluate different fit issues in cab designs. For instance, with the mannequins properly seated and their right heels placed on the accelerator heel point and hands on the steering wheel, the effects of cabs on drivers’ direct and indirect visibility can be accurately assessed. These mannequins provide a level of anthropometric variability that cannot be provided by the conventional percentile models. Several of these models, representing farm workers (Hsiao et al., 2005), general civilians (SAE International, 2008), military personnel (Hudson & Zehner, 2010), and truck drivers (Guan et al., 2012), are becoming available (Figure 10), which can be incorporated into commercial digital human software to assess the safety and effectiveness of products and workspaces.
Figure 10.
Digital models of (a) farm workers and (b) truck drivers are becoming available, which can be incorporated into commercial digital human software to assess the safety and effectiveness of products and workspaces.
With the increasing availability of 3D landmark information in anthropometric databases, 3D digital feature envelopes are becoming increasingly helpful for improving the placement of control components in workspaces. Feature envelopes define the location and orientation of areas of interest for equipment design, namely, the location of the landmark features that are important for optimal cab accommodation. For instance, designers need to know where the knees, elbows, and belly are with respect to the seat for positioning the steering wheel. Visually, a feature envelope can be thought of as an ellipsoid enclosing a cloud of three-dimensional data points representing the variability of a landmark location. Multiple landmarks can be considered at the same time and be aligned with a fixed reference plane (e.g., the seat reference point). For each feature landmark, a 3D ellipsoid, enclosing 95% of the population landmark points, can be constructed. Each ellipse is specified by a centroid, the length of its three axes and the orientation of the centroid and axes relative to the reference point. This serves as a useful companion approach to the multivariate procedure presented in Study 3 for cab design and evaluation, should designers have access to the 3D landmark raw data of the anthropometric database or the full set of representative digital models (i.e., 24 digital models in Study 3). This approach is particularly valuable for analyzing cab configurations during the virtual prototyping stage to avoid impeding body movements, allow effective operation of controls, and permit unobscured displays; it has been successfully used in farm tractor cab design (Hsiao et al., 2005).
OVERALL CONCLUSION (STUDIES 1, 2, 3, AND 4)
This article presented four theories (descriptive statistics, probability modeling, principal component analysis, and Elliptic Fourier Analysis–based shape expression) for PE sizing and accommodation. It also introduced a six-step anthropometric analysis procedure for informing product design. Examples of its application include the aforementioned farm tractor rollover protective structures, firefighter respirator test panels, fire truck cabs, and fall-arrest harnesses, which demonstrated the process of transferring the four theories into real-world practices for defining equipment fit and sizing schemes to advance protective equipment efficacy.
KEY POINTS.
Four anthropometry theories and a six-step anthropometric procedure for equipment design decisions were introduced, which can be used to improve operator protection and protective equipment efficacy.
A univariate method is useful in designing for extremes, such as in determining adequate vertical clearance levels of tractor rollover protective structures. A bivariate method is applicable to products that primarily involve two essential dimensions, such as respirator-sizing panels; and the probability model offers a means for better defining sizing charts for product design and end-user product size selection. A multivariate accommodation approach is necessary to account for body size variance and body proportion variability such as for fire truck cab interface design. A three-dimensional shape-based approach is desirable for determining sizing schemes and the size ranges of conformal personal protective equipment, such as fall arrest harnesses.
The vertical clearance for agriculture tractor roll-over protective structures (ROPS) in the current SAE International J2194 standard (90 cm) is too short. A modification of the standard to 98.3 cm to 101.3 cm with a foldable auto-deploying ROPS is desirable. The National Institute for Occupational Safety and Health 2007 respirator user test panel would have excluded 10% of the male firefighter population. For better firefighter protection, it is suggested that the boundaries of the test panel cells be systematically adjusted for 7 mm greater in face width and 4 mm greater in face length for the firefighter mask/respirator testing panel.
The principal component analysis–based study identified 24 representative body models that represent a unique combination of body size and physique of male and female firefighters. Cab designers can use these models to determine or verify their driver-cab interface designs. These models provide a level of anthropometric variability that cannot be delivered by the traditional percentile models. An improved harness sizing system was proposed that contains three sizes for women and three sizes for men to replace the current four- to seven-size unisex system. The adjustment ranges of straps were provided for harness manufacturers to set harness cut lengths for improved harness assemblies, which would help the construction industry reduce the risk of injury that results from poor harness fit.
ACKNOWLEDGMENTS
This article presents a series of efforts by the National Institute for Occupational Safety and Health (NIOSH) along with many partners and stakeholders in developing theories on anthropometric approaches for protective equipment design and in transferring research to practice for product efficacy and operator safety. Each of the four studies represents a unique anthropometric approach that when combined form a potent array of tools that can be used to inform protective equipment (PE) product design. Part of the information (Study 4) was previously published as a developmental theory for quantifying human torso size and shape (Hsiao, Friess, Bradtmiller, & Rohlf, 2009); however, the use of the six-step paradigm for anthropometric analysis procedures to inform fall-arrest harness design decisions is a new and integral part of this article. The success of the study clearly demonstrates the merits of size-and-shape–oriented anthropometric analysis.
The author gratefully acknowledges the support of his entire research team, including staff from several NIOSH Divisions, Total Contact Inc., Anthrotech Inc., several national professional associations, and apparatus manufacturers. The author is also in debt to many industrial partners and stakeholders, volunteer consultants, and many individuals who provided keen insight and helpful suggestions to the NIOSH studies.
The author extends his special appreciation to his research team members, colleagues, and collaborators: Tsui-Ying Kau and Matthew Reed (University of Michigan); Joyce Zweiner, Richard Whisler, Jinhua Guan, Paul Keane, Ziqing Zhuang, Ronald Shaffer, John Powers, Richard Current, Darlene Weaver, Bradley Newbraugh, Doug Cantis, Alfred Amendola, Tony McKenzie, and James Spahr (NIOSH); Christopher Lafferty, Robert Ferri, Stacie Taylor, and Jennifer Whitestone (Total Contact Inc.); Joseph Feldstein and Rich Reynolds (MSA Fall Protection); Tom Wolner (Capital Safety); Mary Godby and Bruce Bradtmiller (Anthrotech); Ronald Siarnicki and Gordon Routley (National Fallen Firefighter Foundation); Roger Lackore (Fire Apparatus Manufacturing Association); Mike Wilbur (Emergency Vehicle Response); Brian Corner (US Army); Martin Friess (Musée de l’Homme, Paris, France); James Rohlf (Stony Brook University); Jeffery Hudson (InfoSciTex); Gregory Zehner (US Air Force); and the many others who provided administrative support to these research projects.
Footnotes
DISCLAIMER
The findings and conclusions in this article are those of the author and do not necessarily represent the views of the National Institute for Occupational Safety and Health (NIOSH). Mention of company names or products does not imply an endorsement from NIOSH.
REFERENCES
- ASAE. ASAE Standards 2000. Joseph, MI: American Society of Agricultural Engineers; 2000. Roll-over protective structures (ROPS) for wheeled agricultural tractors (SAE J2194 SEP97) pp. 402–414. [Google Scholar]
- Bittner AC, Glenn FA, Harris RM, Iavecchia HP, Wherry RJ. CADRE: A family of mannequins for workstation design. In: Asfour SS, editor. Trends in ergonomics/human factors IV. North Holland: Elsevier; 1987. pp. 733–740. [Google Scholar]
- Bookstein FL. Morphometric tools for landmark data. Cambridge, UK: Cambridge University Press; 1991. [Google Scholar]
- Bureau of Labor Statistics. Respirator use and practices, USDL 02-141. 2002 Retrieved from www.bls.gov/iif/oshwc/osh/os/osnr0014.pdf.
- Bureau of Labor Statistics. Washington, DC: Author; 2012. The employment situation: April 2012 (USDL 12-0816) Retrieved from http://www.bls.gov/news.release/pdf/empsit.pdf. [Google Scholar]
- Cattell RB. The scree test for the number of factors. Multivariate Behavioral Research. 1966;1:245–276. doi: 10.1207/s15327906mbr0102_10. [DOI] [PubMed] [Google Scholar]
- Cole HP, Myers ML, Westneat SC. Frequency and severity of injuries to operators during overturns of farm tractors. Journal of Agriculture Safety and Health. 2006;12(2):127–138. doi: 10.13031/2013.20386. [DOI] [PubMed] [Google Scholar]
- Das B, Grady RM. Industrial workplace layout and engineering anthropometry. In: Kvalseth T, editor. Ergonomics of workstation design. London: Butterworths; 1983. [DOI] [PubMed] [Google Scholar]
- Fahy RF, LeBlanc PR, Mollis JL. Firefighter fatalities in the United States (NFPA No. FFD10-01) Quincy, MA: National Fire Protection Association, Fire Analysis and Research Division; 2011. Retrieved from http://www.nfpa.org/assets/files/pdf/osfff.pdf. [PubMed] [Google Scholar]
- Gordon CC, Bradtmiller B, Clauser CE, Churchill T, McConville JT, Tebbetts I, Walker RA. 1987–1988 anthropometric survey of U.S. Army personnel: Methods and summary statistics (Technical Report TR-89-044) Natick, MA: U.S. Army Natick Research, Development and Engineering Center; 1989. [Google Scholar]
- Guan J, Hsiao H, Bradtmiller B, Kau TY, Reed MR, Jahns SK, Piamonte DPT. U.S. truck driver anthropometric study and multivariate anthropometric models for cab designs. Human Factors. 2012;54:849–871. doi: 10.1177/0018720812442685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hack AL, Hyatt EC, Held BJ, Moore TO, Richards CP, McConville JT. Selection of respirator test panels representative of U.S. adult facial sizes. Los Alamos, NM: Los Alamos National Laboratory; 1973. Los Alamos National Laboratory Report, LA5488) [Google Scholar]
- Hack AL, McConville JT. Respirator protection factors: Part I—Development of an anthropometric test panel. American Industrial Hygiene Association Journal. 1978;39:970–975. doi: 10.1080/0002889778507897. [DOI] [PubMed] [Google Scholar]
- Hertzberg THE. Engineering anthropology. In: van Cott HP, Kincade RG, editors. Human engineering guide to equipment design. Rev ed. Washington, DC: U. S. Government Printing Office; 1972. pp. 468–584. [Google Scholar]
- Hsiao H. Sizing firefighters and fire apparatus: Safe by design. 2008 (NIOSH Project Proposal). Retrieved from http://www.cdc.gov/niosh/topics/anthropometry/
- Hsiao H, Friess M, Bradtmiller B, Rohlf J. Development of sizing structure for fall arrest harness design. Ergonomics. 2009;52(9):1128–1143. doi: 10.1080/00140130902919105. [DOI] [PubMed] [Google Scholar]
- Hsiao H, Halperin W. Occupational safety and human factors. In: Rom WN, editor. Environmental and occupational medicine. 3rd ed. Philadelphia, PA: Lippincott-Raven; 1998. pp. 919–932. [Google Scholar]
- Hsiao H, Long D, Snyder K. Anthropometric differences among occupational groups. Ergonomics. 2002;45(2):136–152. doi: 10.1080/00140130110115372. [DOI] [PubMed] [Google Scholar]
- Hsiao H, Turner N, Whisler R, Zwiener J. Impact of harness fit on suspension tolerance. Human Factors. 2012;54(3):346–357. doi: 10.1177/0018720811434962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsiao H, Whitestone J, Bradtmiller B, Whisler R, Zwiener J, Lafferty C, Gross M. Anthropometric criteria for the design of tractor cabs and protection frames. Ergonomics. 2005;48(4):323–353. doi: 10.1080/00140130512331332891. [DOI] [PubMed] [Google Scholar]
- Hsiao H, Whitestone J, Taylor S, Godby M, Guan J. Harness sizing and strap length configurations. Human Factors. 2009;51(4):497–518. doi: 10.1177/0018720809346320. [DOI] [PubMed] [Google Scholar]
- Hudson JA, Zehner GF. USAF multivariate accommodation method, example: BMC2 case generation (Internal USAF white paper) Washington, DC: U.S. Air Force; 2010. [Google Scholar]
- Hudson JA, Zehner GF, Meindl RS. The USAF multivariate accommodation method. Proceedings of the Human Factors and Ergonomics Society Annual Meeting. 1998;42:722–726. [Google Scholar]
- Johnson RA, Wichern DW. Applied multivariate statistical analysis. Upper Saddle River, NJ: Pearson Prentice Hall; 2007. [Google Scholar]
- Kaiser HF. The application of electronic computers to factor analysis. Educational and Psychological Measurement. 1960;20:141–151. [Google Scholar]
- Karter MJ, Molis JL. US firefighter injuries—2010 (NFPA No. FFI10) Quincy, MA: National Fire Protection Association, Fire Analysis and Research Division; 2011. Retrieved from http://www.nfpa.org/assets/files//PDF/OS.FFInjuries.pdf. [Google Scholar]
- Karter MJ, Stein GP. U.S. fire department profile through 2010 (NFPA No. USS07) Quincy, MA: National Fire Protection Association (NFPA), Fire Analysis and Research Division; 2011. Retrieved from http://www.nfpa.org/assets/files/pdf/os.fdprofile.pdf. [Google Scholar]
- Kuhl FP, Giardina CR. Elliptic Fourier features of a closed contour. Computer Graphics and Image Processing. 1980;18:236–258. [Google Scholar]
- Lestrel PE. Fourier descriptors and their applications. Cambridge, UK: Cambridge University Press; 1997. [Google Scholar]
- Meindl RS, Zehner GF, Hudson JA. A multivariate anthropometric method for crew station design (AL-TR-1993-0054) Dayton, OH: Crew Systems Directorate, Human Engineering Division; 1993. [Google Scholar]
- Myers JR, Snyder KA, Hard DL, Casini VJ, Cianfrocco R, Fields J, Morton L. Statistics and epidemiology of tractor fatalities: A historical perspective. Journal of Agriculture Safety and Health. 1998;4(2):95–108. [Google Scholar]
- National Fire Protection Association. NFPA survey of fire departments for U.S. fire experience, 2005—fire fighters and fire departments. 2006 Retrieved from http://www.nfpa.org/itemDetail.asp?categoryID=955&itemID=23688&URL=Research%20&%20Reports/Fire%20statistics/The%20U.S.%20fire%20service. [Google Scholar]
- Pheasant S, Haslegrave CM. Bodyspace: Anthropometry, ergonomics and the design of work. 3rd ed. Boca Raton, FL: CRC Press, Taylor & Francis Group; 2006. [Google Scholar]
- Robinson JC, Robinette KM, Zehner GF. User’s guide to anthropometric data base at the Computerized Anthropometric Research and Design (CARD) Laboratory. 2nd ed. Dayton, OH: Crew Systems Directorate, Human Engineering Division; 1992. ALTR-1992-0036. [Google Scholar]
- Roebuck JA, Kroemer KHE, Thomson WG. Engineering anthropometry methods. New York, NY: Wiley Series in Human Factors, John Wiley & Sons Inc; 1975. [Google Scholar]
- Rohlf FJ. EFA3D v. 1.0. Stony Brook, NY: State University of New York at Stony Brook, Department of Ecology and Evolution; 2003. [Google Scholar]
- Routley J. Safe seating and seatbelts in fire apparatus. Paper presented at the Firehouse Expo; Baltimore, MD. 2006. Jul, [Google Scholar]
- SAE International. Surface vehicle standard—operator space envelope dimensions for off-road machines, SAE J154. Warrendale, PA: Society of Automotive Engineers, Inc; 1992. [Google Scholar]
- SAE International. Civilian American and European Surface Anthropometry Resource Project—CAESAR™. Warrendale, PA: Society of Automotive Engineers, Inc; 2008. [Google Scholar]
- Zehner GF, Meindl RS, Hudson JA. A multivariate anthropometric method for crew station design: Abridged (AL-TR-1992-0164) Dayton, OH: Air Force Material Command, Wright-Patterson Air Force Base; 1993. [Google Scholar]
- Zhuang Z, Bradtmiller B, Shaffer RE. New respirator fit test panels representing the current U. S. civilian work force. Journal of Occupational and Environmental Hygiene. 2007;4(9):647–659. doi: 10.1080/15459620701497538. [DOI] [PubMed] [Google Scholar]
- Zhuang Z, Guan J, Hsiao H, Bradtmiller B. Evaluating the representativeness of the LANL respirator fit test panels for the current U.S. civilian workers. Journal of the International Society for Respiratory Protection. 2004;21:83–93. [Google Scholar]