Abstract
Background
Survival estimation guides surgical decision-making in metastatic bone disease. Traditionally, classic scoring systems, such as the Bauer score, provide survival estimates based on a summary score of prognostic factors. Identification of new factors might improve the accuracy of these models. Additionally, the use of different algorithms—nomograms or boosting algorithms—could further improve accuracy of prognostication relative to classic scoring systems. A nomogram is an extension of a classic scoring system and generates a more-individualized survival probability based on a patient’s set of characteristics using a figure. Boosting is a method that automatically trains to classify outcomes by applying classifiers (variables) in a sequential way and subsequently combines them. A boosting algorithm provides survival probabilities based on every possible combination of variables.
Questions/purposes
We wished to (1) assess factors independently associated with decreased survival in patients with metastatic long bone fractures and (2) compare the accuracy of a classic scoring system, nomogram, and boosting algorithms in predicting 30-, 90-, and 365-day survival.
Methods
We included all 927 patients in our retrospective study who underwent surgery for a metastatic long bone fracture at two institutions between January 1999 and December 2013. We included only the first procedure if patients underwent multiple surgical procedures or had more than one fracture. Median followup was 8 months (interquartile range, 3-25 months); 369 of 412 (90%) patients who where alive at 1 year were still in followup. Multivariable Cox regression analysis was used to identify clinical and laboratory factors independently associated with decreased survival. We created a classic scoring system, nomogram, and boosting algorithms based on identified variables. Accuracy of the algorithms was assessed using area under the curve analysis through fivefold cross validation.
Results
The following factors were associated with a decreased likelihood of survival after surgical treatment of a metastatic long bone fracture, after controlling for relevant confounding variables: older age (hazard ratio [HR], 1.0; 95% CI, 1.0–1.0; p < 0.001), additional comorbidity (HR, 1.2; 95% CI, 1.0–1.4; p = 0.034), BMI less than 18.5 kg/m2 (HR, 2.0; 95% CI, 1.2–3.5; p = 0.011), tumor type with poor prognosis (HR, 1.8; 95% CI, 1.6–2.2; p < 0.001), multiple bone metastases (HR, 1.3; 95% CI, 1.1–1.6; p = 0.008), visceral metastases (HR, 1.6; 95% CI, 1.4–1.9; p < 0.001), and lower hemoglobin level (HR, 0.91; 95% CI, 0.87–0.96; p < 0.001). The survival estimates by the nomogram were moderately accurate for predicting 30-day (area under the curve [AUC], 0.72), 90-day (AUC, 0.75), and 365-day (AUC, 0.73) survival and remained stable after correcting for optimism through fivefold cross validation. Boosting algorithms were better predictors of survival on the training datasets, but decreased to a performance level comparable to the nomogram when applied on testing datasets for 30-day (AUC, 0.69), 90-day (AUC, 0.75), and 365-day (AUC, 0.72) survival prediction. Performance of the classic scoring system was lowest for all prediction periods.
Conclusions
Comorbidity status and BMI are newly identified factors associated with decreased survival and should be taken into account when estimating survival. Performance of the boosting algorithms and nomogram were comparable on the testing datasets. However, the nomogram is easier to apply and therefore more useful to aid surgical decision making in clinical practice.
Level of Evidence
Level III, prognostic study.
Electronic supplementary material
The online version of this article (doi:10.1007/s11999-015-4446-z) contains supplementary material, which is available to authorized users.
Introduction
Estimated survival is an important factor in the decision to operate and operative strategy in patients with bony metastasis [2, 24]. Physicians often estimate survival based on their clinical assessments and previously described risk factors. Several tools in the form of scoring systems have been developed to assist clinicians with their estimation [2, 8, 9, 19, 24]. However, these tools lack accuracy and identification of additional and more-specific risk factors might improve survival estimation [14, 24].
Historically, tools like scoring systems that are used to provide survival probability are based on a summary score of weighted clinical or laboratory factors [2, 19, 24]. The Bauer [2] score is such a classic scoring system commonly used for estimation of survival in patients with bone metastases. It is a summary score of five prognostic factors: (1) no pathologic fracture, (2) no visceral or brain metastases, (3) a solitary bone metastasis, (4) no lung cancer, and (5) multiple myeloma, lymphoma, breast or kidney carcinoma. Fulfilling four to five criteria corresponded to a 1-year survival probability of 0.5, two to three criteria to a 1-year survival probability of 0.25, and all patients who fulfilled none or only one criterion were deceased within 6 months after surgery [2]. Another frequently used tool to estimate survival in patients with cancer is the nomogram, which is a simple figure that generates an individualized numerical probability of survival based on a patient’s unique set of characteristics; a number of points is assigned to each prognostic factor, which can be read from the nomogram and the sum of these points corresponds to a survival probability [17, 20, 25]. The nomogram can be seen as an extension of the classic scoring system. Advances in computer science have led to the development of more sophisticated boosting (machine learning) algorithms [13, 33]. Machine learning is a method of automatically developing and constantly adjusting computer algorithms to recognize patterns in data and improve predictions (eg, filtering spam email) [13]. Boosted regression emerged from this field and is a method that iteratively applies classifiers (variables) in a sequential way–each step building on the previous step aiming to fit the residuals–and subsequently combines them to obtain predictions [13, 33]. This can improve the accuracy of predicting an outcome based on weak learners (ie, classifiers that are only slightly better than random guessing). A boosting algorithm provides outcome probabilities based on every possible combination of variables [33].
We aimed to assess factors associated with survival in patients with long bone metastatic fractures. Based on those factors, we created a classic scoring algorithm, a nomogram, and boosting algorithms to estimate survival. Specifically, we sought to (1) assess factors independently associated with decreased survival in patients with metastatic long bone fractures, and (2) compare the accuracy of a classic scoring system, nomogram, and boosting algorithms in predicting 30-, 90-, and 365-day survival.
Patients and Methods
This retrospective study was approved by our institutional review board and a waiver of informed consent was granted. To identify patients with a metastatic long bone fracture, we retrieved all medical record data of patients who had an International Classification of Diseases, 9th Revision (ICD-9) code for a metastatic long bone fracture or a Current Procedural Terminology (CPT) code for prophylactic fixation of a long bone fracture (Appendix 1. Supplemental material is available with the online version of CORR®.), at two tertiary care referral centers.
After operative report and medical record screening, we included all 927 patients older than 18 years who had surgery for a pathologic or impending metastatic long bone fracture between January 1999 and December 2013. We included only the first surgery per patient if patients underwent multiple operations on different occasions so as to not violate the statistical assumption of independence [3]. We defined long bones as the femur, humerus, tibia, fibula, radius, and ulna; multiple long bones operated on during the same procedure were categorized separately. Metastatic disease included, in addition to metastases from solid organs, multiple myeloma and lymphoma. We included patients regardless of followup duration. Exclusion criteria were (1) revision procedures, (2) metastatic involvement of the acetabulum or pelvis requiring reconstruction, and (3) operative treatments other than endoprosthetic reconstruction, plate-screw fixation, intramedullary nailing, and dynamic hip screw.
The decision to operate and the selection of operative strategy were made by the surgeon together with the patient. These decisions were based on factors including type of fracture, primary tumor type, extent of the metastatic lesion, level of disability and pain, and the estimated survival.
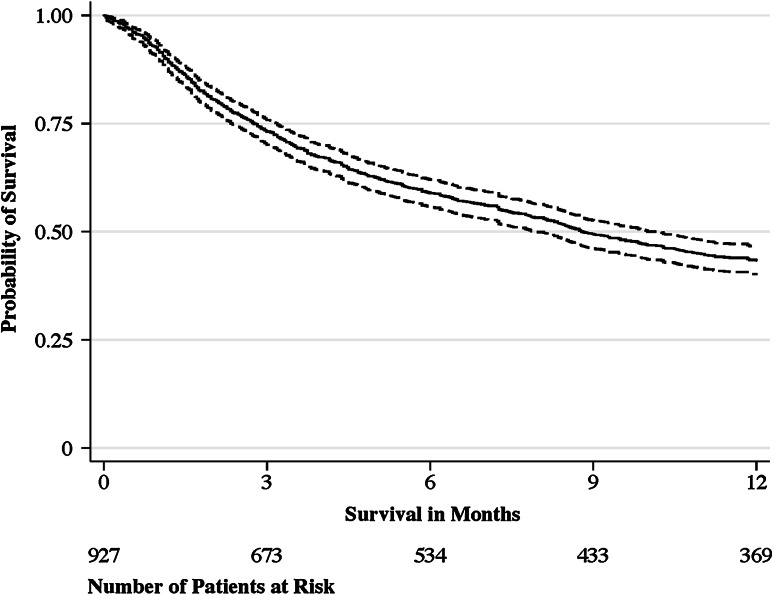
Our primary outcome was survival, defined as the time from operative treatment until death resulting from any cause. Date of death was extracted from the medical records and Social Security Death Index database (database of death records created from the US Social Security Administration), last updated February 24, 2014 [16]. This date also provided the moment of final followup for all patients alive in our study. Median followup was 8 months (interquartile range, 3–25 months). All patients who were alive at 30 days were still in followup (n = 853), 673 of 678 patients (99%) who were alive at 3 months were still in followup, and 369 of 412 (90%) patients who were alive at 1 year were still in followup (Fig. 1).
Fig. 1.
The Kaplan-Meier plot shows the probability of survival (solid line) with 95% CI (dashed line). The median survival is 268 days (95% CI, 241–309), with an interquartile range from 84 (95% CI, 72–97) to 1089 days (95% CI, 922–1262).
We selected the following explanatory variables based on the existing studies [19, 24, 31] or theoretical association with survival: age, sex, BMI, comorbidity status, primary tumor type, type of fracture, anatomic location of fracture, time from diagnosis of the primary tumor until operative treatment, other bone metastases, other previous metastatic fractures, visceral metastases, previous systemic therapy, previous local radiotherapy of the affected long bone, and preoperative hemoglobin level, platelet level, white blood cell count, creatinine, and serum calcium level.
We categorized BMI into: less than 18.5 kg/m2 (underweight), between 18.5 and 30 kg/m2 (normal weight), and 30 kg/m2 or greater (obese) based on previously published cutoff points as we expect a nonlinear association of BMI with survival [10, 37].
We used the modified Charlson Comorbidity Index [28, 29] to indicate comorbidity status. This index provides a score ranging from 0 to 24 with a higher score representing more severe comorbidity status based on 12 weighted comorbidities (congestive heart failure, dementia, chronic pulmonary disease, rheumatologic disease, mild liver disease, diabetes with chronic complications, hemiplegia or paraplegia, renal disease, any malignancy, moderate or severe liver disease, metastatic solid tumor, and HIV/AIDS). We determined the modified Charlson Comorbidity Index through a previously described algorithm based on ICD-9 codes given before the day of surgery [6, 30, 38] (Appendix 2. Supplemental material is available with the online version of CORR®.). The modified Charlson Comorbidity Index was dichotomized into any additional comorbidity (additional to the malignancy and metastatic disease) or none.
Based on a study by Katagiri et al. [19], we dichotomized primary tumor types into tumors with a relatively good prognosis (breast, kidney, prostate, thyroid, myeloma, and lymphoma) and tumors with a poor prognosis (lung and all other tumor types).
Fracture type was classified as pathologic or impending. The latter was defined as bone with no visible fracture line, loss of height, rotation, or angulation, but the degree of destruction did mandate, in the surgeon’s opinion, operative treatment. Previous pathologic fractures or prophylactically treated impending fractures were categorized into none, previous long bone fracture, and previous spine fracture (with or without previous long bone fracture).
We extracted the presence of bone metastases from bone scan, CT, and other imaging reports. Bone metastases were categorized into single bone metastasis, multiple bone metastases without spinal involvement, and multiple bone metastases with spinal involvement. The presence of visceral metastases was derived from CT and positron emission tomography scan reports. We regarded lung, liver, and brain metastases as visceral metastases and grouped lung and/or liver metastases together; brain metastases (with or without lung/liver metastases) were categorized separately.
We used laboratory values measured within 7 days before operative treatment.
Statistical Analysis
Variables are presented with frequencies and percentages for categorical variables and as mean with SD for continuous variables. In bivariate analyses, the association between the response variable survival and the explanatory variables was assessed using Cox regression analysis (Appendix 3. Supplemental Materials are available with the online version of CORR®.). The proportional hazards assumption was tested using Schoenfeld residuals and verified by assessing if Kaplan-Meier survival curves crossed. Our exploratory analysis identified the following variables: age (p < 0.001), BMI less than 18.5 kg/m2 (p < 0.001), additional comorbidity (p < 0.001), multiple long bones surgically treated during the same procedure (p = 0.077), poor prognosis tumor type (lung and all other tumor types) (p < 0.001), multiple bone metastases without spinal involvement (p = 0.096) and with spinal involvement (p = 0.014), lung and/or liver metastasis (p < 0.001) and brain metastasis (p < 0.001), previous systemic therapy (p = 0.057), hemoglobin level (p = 0.001), and platelet level (p = 0.004), which then were incorporated in our multivariable model (Appendix 3. Supplemental materials are available with the online version of CORR®.). We recategorized bone metastases as single and multiple metastases as exploratory analysis showed no difference in hazard ratios (HR) between patients with multiple bone metastases without spinal involvement (HR, 1.2; 95% CI, 1.0–1.5) and those with spinal involvement (HR, 1.3; 95% CI, 1.0–1.5; p = 0.67). Visceral metastases also was recategorized as none and any visceral metastases as there was no difference in hazard ratios between lung and liver metastases (HR, 1.9; 95% CI, 1.6–2.2) and brain metastases (HR, 1.8; 95% CI, 1.5–2.2; p = 0.82) (Appendix 3. Supplemental material is available with the online version of CORR®.).
We entered these explanatory variables with a p value less than 0.10 on bivariate analysis in a backward stepwise multivariable Cox regression analysis to assess the independent association with survival [1, 15]. We did not test interactions of variables. HRs and beta regression coefficients are presented to quantify the association of explanatory variables with survival. The HR indicates the relative likelihood of death in one group compared with another group. HRs are adjusted for all explanatory variables included in the multivariable Cox regression analysis. We assume missing values–BMI (21%, 197 of 927 patients) and hemoglobin (6%, 59 of 927 patients)–to be random and used multiple imputation to replace missing values 40 times based on the remaining explanatory variables [22].
A two-sided p value less than 0.05 was considered significant; all statistical analyses were performed using Stata® 13.0 (StataCorp LP, College Station, TX, USA).
Development of A Classic Scoring System, Nomogram, and Boosting Algorithms
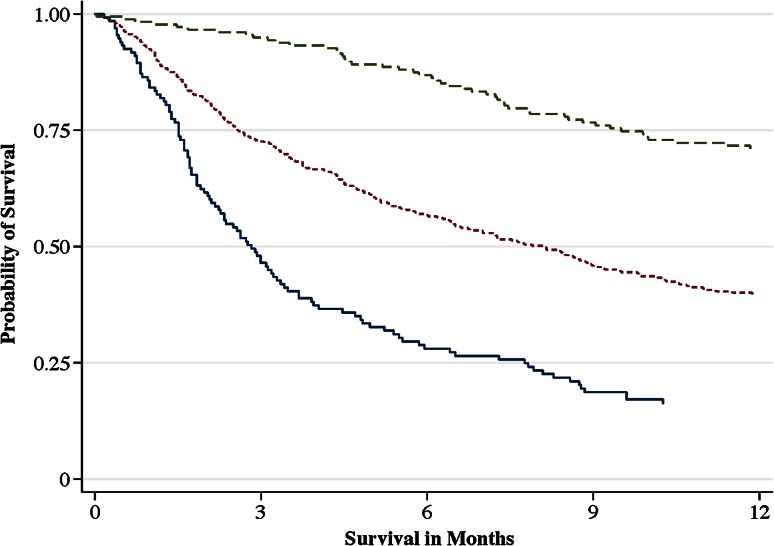
We developed a classic scoring system to estimate survival probability by assigning a weighted score to every factor independently associated with survival by rounding its HR to the nearest integer [2, 19, 31]. To allow for scoring of continuous variables, we dichotomized age (65 years and older) and hemoglobin level (10 g/dL and less) and rounded the HRs of the mean difference between the dichotomized groups to the nearest integer (mean difference in age, 20 years [HR, 1.34] and mean difference in hemoglobin level 2.6 g/dL [HR, 1.27]) [24]. The total score of the classic scoring system ranges from 0 to 10 (Table 1). We categorized scores as: good prognosis, (0–2 points), intermediate prognosis (3–5 points), and poor prognosis (6–10 points) based on the survival probability curves (Fig. 2). Survival probability was shown per prognostic group for each prediction period (30, 90, and 365 days)(Table 2) [2, 19].
Table 1.
Classic scoring system
| Variable | Points |
|---|---|
| Age 65 years or older | 1 |
| Additional comorbidity | 1 |
| BMI less than 18.5 kg/m2 | 2 |
| Tumor type other than breast, kidney, prostate, thyroid, myeloma, and lymphoma | 2 |
| Multiple bone metastases | 1 |
| Visceral metastases* | 2 |
| Hemoglobin level 10 g/dL or less | 1 |
* Visceral metastases include lung, liver, and/or brain metastases.
Fig. 2.
The Kaplan-Meier plot shows the probability of survival per prognostic group of the classic scoring algorithm: good prognosis (0–2 points; green dashed line), intermediate prognosis (3–5 points; dotted red line), and poor prognosis (6–10 points; solid blue line).
Table 2.
Survival probability per prognostic group and prediction period (n = 927 patients)*
| Prognostic groups | Probability of survival (95% CI) |
|---|---|
| Good prognosis (score 0–2 points) | |
| 30 days | 0.98 (0.96–0.99) |
| 90 days | 0.93 (0.89–0.96) |
| 365 days | 0.66 (0.60–0.73) |
| Intermediate prognosis (score 3–5 points) | |
| 30 days | 0.92 (0.90–0.94) |
| 90 days | 0.73 (0.69–0.76) |
| 365 days | 0.39 (0.34–0.43) |
| Poor prognosis (score 6–10 points) | |
| 30 days | 0.84 (0.79–0.89) |
| 90 days | 0.49 (0.41–0.56) |
| 365 days | 0.17 (0.11–0.23) |
* Missing values for BMI and hemoglobin level were imputed using multiple imputation.
We developed a nomogram by ranking the effect estimates (β regression coefficients) of all factors independently associated with survival to a scale ranging from 0 to 100 points [17, 20]. The predicted probability of 30-, 90-, and, 365-day survival were calculated for each patient using the multivariable Cox regression model underlying the nomogram [17, 21].
Boosting algorithms to predict 30-, 90-, and 365-day survival were developed using the “multiple additive regression trees” gradient boosting technique implemented in Stata® 13.0 [13, 33]. Boosting is a machine learning technique that produces a prediction algorithm based on additive decision trees to classify outcome (30-, 90-, and 365-day survival) in a stepwise fashion [13, 33]. We included the same set of factors independently associated with survival for development of the boosting algorithms. Each boosting algorithm allowed for two-way interactions. The algorithm provides an estimated survival probability for every possible combination (permutation) of the included variables for each prediction period, thereby taking into account the interaction of the included variables [33].
All three prediction models were compared using fivefold cross validation on the 40 multiple imputed datasets, meaning that the models were created five times on randomly selected training subsets (80%) of the data and tested on the remaining 20% [12, 36]. The average performance (the ability of a model to separate patients with different outcomes) was calculated over the five training and testing repetitions per multiple imputed dataset for all three models and prediction periods and subsequently pooled. Performance was assessed using receiver operating characteristic (ROC) curves [4, 11, 27]. ROC curves are made by plotting the rate of false positives (1 – specificity) on the x-axis and the rate of true positives (sensitivity) on the y-axis for all threshold values. The area under the ROC curve (AUC) represents its discriminatory power; an AUC of 1.0 indicates perfect discrimination (100% sensitivity and 100% specificity), whereas an AUC of 0.50 represents no discriminatory power (a coin toss).
The final classic scoring system, nomogram, and boosting algorithms were developed on the 40 multiple imputed datasets and results were pooled [12, 36].
Patient Characteristics
Among the 927 patients, 401 (43%) were men, and the mean age of the patients was 62 years (Table 3). There were 515 (56%) pathologic fractures and 412 (44%) impending fractures. The femur (70%; 646 of 927 patients) and humerus (23%; 210 of 927 patients) were most commonly affected. Most tumors originated from the breast (23%; 216 of 927 patients), lung (23%; 215 of 927 patients), myeloma (16%; 148 of 927 patients), kidney (9%; 87 of 927 patients), and prostate (5%; 48 of 927 patients) (Table 4). Median overall survival was 9 months (Fig. 1). Ninety-two percent of the patients survived 30 days (853 of 927 patients), 73% (676 of 922 patients) survived 90 days, and 42% (368 of 884 patients) survived 365 days. The median time from diagnosis of the primary tumor until operative treatment of the metastatic fracture was 21 months. Five-hundred sixty (60%) patients underwent intramedullary nailing, 209 (23%) had endoprosthetic reconstruction, 140 (15%) had plate-screw fixation, and 18 (2%) had placement of a dynamic hip screw.
Table 3.
Baseline characteristics
| Demographics | Mean (± SD) |
|---|---|
| Age (years) | 62 (± 13) |
| BMI (kg/m2)* | 27 (± 5.8) |
| Modified Charlson Comorbidity Index | 6.7 (± 2.0) |
| Number (%) | |
|---|---|
| Men | 401 (43) |
| Pathologic fracture | 515 (56) |
| Anatomic location | |
| Femur | 646 (70) |
| Humerus | 210 (23) |
| Tibia | 31 (3.3) |
| Radius | 3 (0.32) |
| Ulna | 2 (0.22) |
| Multiple locations§ | 35 (3.8) |
| Oncologic status | Number (%) |
|---|---|
| Bone metastases | |
| Single bone metastasis | 202 (22) |
| Multiple bone metastases without spinal involvement | 185 (20) |
| Multiple bone metastases with spinal involvement | 540 (58) |
| Previous pathologic fractures | |
| None | 662 (71) |
| Previous long bone (impending) pathologic fracture | 79 (8.5) |
| Previous spine (impending) pathologic fracture† | 186 (20) |
| Visceral metastases | |
| None | 504 (54) |
| Lung and/or liver metastases | 273 (29) |
| Brain metastases (with or without lung/liver metastases) | 150 (16) |
| Previous systemic therapy | 577 (62) |
| Previous local radiotherapy of the affected long bone | 170 (18) |
| Laboratory values‡ | Mean (± SD) |
|---|---|
| Hemoglobin (g/dL) | 11 (± 1.6) |
| Platelets (1000/mm3) | 254 (± 116) |
| White blood cell count (1000/mm3) | 9.7 (± 4.9) |
| Creatinine (mg/dL) | 0.94 (± 0.81) |
| Calcium (mg/dL) | 8.8 (± 0.93) |
Number of patients = 927; * BMI was available for 730 patients; §multiple metastatic fracture locations undergoing fixation during the same procedure were: bilateral femur (12 patients), femur and humerus (16 patients), bilateral humerus (2), tibia and femur (1), tibia and humerus (1), fibula and tibia (1), radius and humerus (1), ulna and radius (1); †with or without previous long bone pathologic fracture; ‡hemoglobin level was available in 868 patients, platelet level in 866 patients, white blood cell count in 867 patients, creatinine in 812 patients, and calcium in 654 patients.
Table 4.
Origin of primary tumors
| Tumor distribution | Number (%) |
|---|---|
| Breast | 216 (23) |
| Lung | 215 (23) |
| Myeloma | 148 (16) |
| Kidney | 87 (9) |
| Prostate | 48 (5) |
| Lymphoma | 43 (5) |
| Melanoma | 25 (3) |
| Esophagus | 18 (2) |
| Colorectal | 16 (2) |
| Thyroid | 15 (2) |
| Hepatocellular | 12 (1) |
| Bladder | 10 (1) |
| Other* | 35 (4) |
| Unknown | 39 (4) |
Number of patients = 927; * neuroendocrine (n = 6), salivary gland (n = 5), nasopharyngeal squamous cell carcinoma (n = 5), pancreas (n = 4), ovaries (n = 4), endometrium (n = 3), skin squamous cell carcinoma (n = 3), stomach (n = 2), vulva (n = 2), and mesothelioma (n = 1).
Results
Explanatory Variables Associated With Survival
The following factors were associated with a decreased likelihood of survival after surgical treatment of a metastatic long bone fracture, after controlling for relevant confounding variables: older age (HR, 1.0; 95% CI, 1.0–1.0; p < 0.001), additional comorbidity (HR, 1.2; 95% CI, 1.0–1.4; p = 0.034), BMI less than 18.5 kg/m2 (HR, 2.0; 95% CI, 1.2–3.5; p = 0.011), tumor type with poor prognosis (HR, 1.8; 95% CI, 1.6–2.2; p < 0.001), multiple bone metastases (HR, 1.3; 95% CI, 1.1–1.6; p = 0.008), visceral metastases (HR, 1.6; 95% CI, 1.4–1.9; p < 0.001), and lower hemoglobin level (HR, 0.91; 95% CI, 0.87–0.96; p < 0.001)(Table 5).
Table 5.
Hazard ratios for survival from stepwise backward multivariable Cox regression analysis§
| Explanatory variables | β regression coefficient | Standard error | Hazard ratio (95% CI) | p value |
|---|---|---|---|---|
| Age (in years) | 0.015 | 0.003 | 1.015 (1.008–1.021) | < 0.001 |
| Additional comorbidity | 0.164 | 0.077 | 1.179 (1.013–1.372) | 0.034 |
| BMI | ||||
| Less than18.5 kg/m2* | 0.707 | 0.276 | 2.027 (1.175–3.480) | 0.011 |
| Between 18.5 and 30 kg/m2* | Reference | Reference | Reference | Reference |
| Greater than 30 kg/m2* | 0.045 | 0.106 | 1.046 (0.549–1.288) | 0.672 |
| Tumor type other than: breast, kidney, prostate, thyroid, myeloma, and lymphoma | 0.609 | 0.080 | 1.839 (1.574–2.150) | < 0.001 |
| Multiple bone metastases | 0.254 | 0.095 | 1.290 (1.069–1.555) | 0.008 |
| Visceral metastases | 0.500 | 0.079 | 1.649 (1.412–1.926) | < 0.001 |
| Hemoglobin level (g/dL)* | −0.094 | 0.025 | 0.911 (0.867–0.956) | < 0.001 |
Number of patients = 927; * BMI was available for 730 patients; hemoglobin level available for 868 patients; missing values were imputed using multiple imputation; §variables were selected using stepwise backward multivariable Cox regression analysis retaining variables with a p value less than 0.10.
Comparing Performance of the Classic Scoring, Nomogram, and Boosting Algorithms
The survival estimates by the nomogram were moderately accurate for predicting 30-day (AUC, 0.72), 90-day (AUC, 0.75), and 365-day (AUC, 0.73) survival and remained stable after correcting for optimism through fivefold cross validation (Table 6). Boosting algorithms were better predictors of survival at all prediction periods on the training datasets; however, after applying these to the testing datasets we found that accuracy of the boosting algorithms decreased substantially for the 30-day (AUC, 0.83 to 0.69), 90-day (AUC, 0.81 to 0.75), and 365-day (AUC, 0.78 to 0.72) prediction periods resulting in a performance comparable to the that of the nomogram (Table 6). Performance of the classic scoring system was lowest for all prediction periods.
Table 6.
AUC for the classic scoring algorithm and boosting algorithm from receiver operating characteristic analysis
| Prediction period | Classic scoring system AUC (95% CI) | Nomogram AUC (95% CI) | Boosting algorithm AUC (95% CI) | p value |
|---|---|---|---|---|
| Training subsets | ||||
| 30 days | 0.66 (0.60–0.72) | 0.72 (0.66–0.78) | 0.83 (0.78–0.88) | < 0.001 |
| 90 days | 0.70 (0.66–0.73) | 0.76 (0.72–0.80) | 0.81 (0.78–0.85) | < 0.001 |
| 365 days | 0.68 (0.65–0.72) | 0.73 (0.70–0.77) | 0.78 (0.75–0.81) | < 0.001 |
| Testing subsets | ||||
| 30 days | 0.67 (0.55–0.78) | 0.72 (0.59–0.84) | 0.69 (0.55–0.83) | 0.328 |
| 90 days | 0.70 (0.62–0.77) | 0.75 (0.68–0.83) | 0.75 (0.67–0.83) | 0.075 |
| 365 days | 0.68 (0.61–0.75) | 0.73 (0.65–0.80) | 0.72 (0.65–0.80) | 0.125 |
AUC = area under the curve.
Discussion
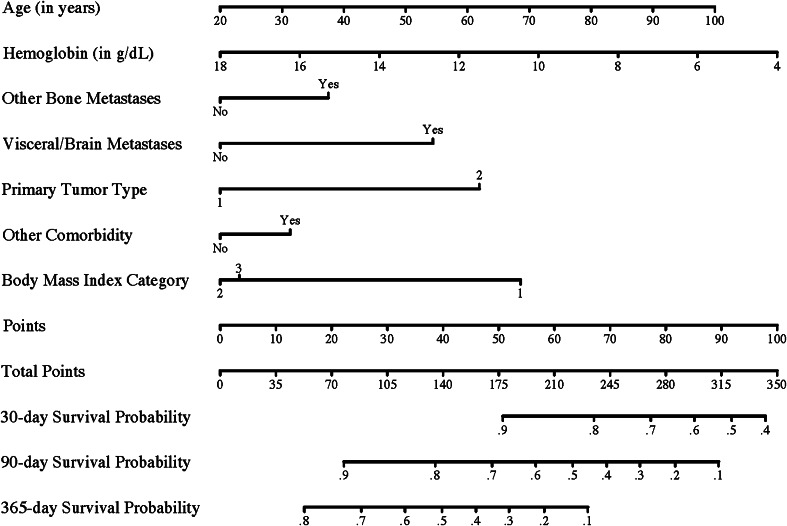
Expected survival is an important factor in the decision to operate and in the selection of a surgical strategy for patients with metastatic fractures [2, 24]. Previous studies developed scoring algorithms to estimate survival [2, 8, 9, 19, 24, 31], but survival estimates remain imprecise [24]. In an attempt to improve survival estimation, we assessed which clinical factors and laboratory values were independent predictors of survival. Additionally, we developed a classic scoring system, nomogram, and boosting algorithms to estimate 30-, 90-, and 365-day survival and compared the accuracy of these methods. We found that older age, additional comorbidity, BMI less than 18.5 kg/m2, primary tumor type with poor prognosis, multiple bone metastases, visceral metastases, and lower hemoglobin level, were independently associated with decreased likelihood of survival. The survival estimates by the boosting algorithm were most accurate on the training datasets, but comparable to those derived from the nomogram when applied to the testing datasets for 30-, 90-, and 365-day survival. We emphasize the use of the nomogram (Fig. 3) for estimating survival as it is simpler to use in clinical practice.
Fig. 3.
The nomogram for prediction of 30-, 90-, and 365-day survival is shown. Locate the patients age on the age axis and draw a straight line to the points axis. Repeat this process for all variables and sum the points obtained for each predictor. Locate the total points on the total points axis and draw a line straight down to find the 30-, 90-, and 365-day survival probabilities. BMI categories are: (1) less than 18.5 kg/m2, (2) between 18.5 and 30 kg/m2, and (3) 30 kg/m2 or greater (obese). The primary tumor Group 1 includes breast, kidney, prostate, thyroid, myeloma, and lymphoma; Group 2 includes lung and all other primary tumor types. This nomogram is not applicable to a patient who otherwise is not a candidate for operative treatment of a metastatic fracture. The outcome is a point estimate and the nomogram does not include the uncertainty of the estimate.
This study has some limitations. First, there were no uniform criteria for operative treatment because the study was retrospective. This might have resulted in selection bias and potentially influenced accuracy of the prediction models; for example, patients with a very poor overall health status might not have been considered for operative treatment. Although this might limit the usefulness of the algorithms in these patients, we believe that this did not compromise the comparison of performance of the algorithms in our study. Second, we used diagnostic and billing codes to identify potentially eligible patients. We might have missed patients using this methodology; however, we expect this number to be low and therefore not influence our conclusions. Third, although we internally validated the algorithms through fivefold cross validation, predictive performance can worsen substantially on external validation. External validation should be performed before widespread use of a prediction algorithm [5, 34]. Fourth, we did not assess how discriminant the predicted probabilities by the different models were. We see this as a minor limitation and emphasized performance of the models as better performance (higher AUC) implies less uncertainty–more precision–of the points estimate of the predicted probability. Fifth, because the study was retrospective, we could not include performance status of the patient. Including this might have improved the predictive accuracy of our algorithms as previous studies showed a strong association with survival [19, 24]. Sixth, we decided to select variables for inclusion in the boosting algorithms based on theory. Including all explanatory variables using a kitchen-sink approach (having the algorithm select variables) could improve its accuracy. However, this might have resulted in a large number of factors to consider when estimating survival, making it less useful in clinical practice, and potentially worsening its external validity. We aimed to compare the performance of prediction models based on the same set of variables supported by theory. Seventh, we did not define minimum followup. We see this as a minor limitation as we used Cox regression analysis to account for right censoring (loss to followup) and followup was 90% for patients alive at 1 year.
Previous studies of patients with metastatic fractures found that visceral metastases, primary tumor type, number of bone metastases, time from diagnosis of primary tumor to surgery for metastatic fracture, fracture type, performance status, previous chemotherapy, and hemoglobin level were independently associated with survival [2, 19, 24, 31, 32]. We identified additional factors associated with survival in patients with metastatic fractures, namely, comorbidity status and BMI. The association of comorbidity status with overall and cancer-specific survival has been shown in patients with primary malignancies [7, 26, 35] but not in patients with metastatic fractures. BMI can be considered a surrogate marker of cancer severity because low body weight often is associated with more advanced cancer. Previous studies showed an association of BMI with survival in patients with cancer [18, 23]. Furthermore, we divided multiple bone metastases into those with and those without spinal involvement and visceral metastases into lung and/or liver metastases and brain metastases to explore differences in their association with survival. However, we found no differences between these groups in terms of survival nor did we find an association of previous pathologic fractures with survival. The difference in survival between impending and pathologic fractures, found by Bauer and Wedin [2], was not found in our study. Based on our findings, future studies should explore how specific comorbidities influence survival in patients with metastatic fractures and if optimizing perioperative nutritional status improves survival in these patients.
Although the boosting algorithm was most accurate in estimating survival on the training samples, its performance decreased when applied to the testing subsets of the data. This might be a result of overfitting of the boosting algorithm on the training data. Performance of the boosting algorithm was comparable to that of the nomogram when applied to the testing subsets. We therefore prefer using the nomogram in estimating survival as it is simpler to use in daily practice. However, the nomogram does not make treatment recommendations, it simply provides estimated survival probabilities and can enable a more informed decision-making process. Thirty-, 90-, and 365-day survival probabilities are based on the sum score of the points assigned to the prognostic factors of an individual patient (Fig. 3). For example, a 77-year old patient with breast carcinoma, normal BMI, multiple bone metastases, but no visceral metastases, diabetes with chronic complications (additional comorbidity), and a preoperative hemoglobin of 9.4 g/dL gets assigned 157 points which corresponds to a 30-day survival probability of 0.93, 90-day survival probability of 0.74, and 365-day survival probability of 0.42. The mean total points in our cohort was 156 points (SD, 39). Forsberg et al. [8, 9] described the development and testing of machine learning algorithms in determining survival of patients with metastatic fractures. The algorithms they developed, based on a prospective cohort of 189 patients, had an AUC of 0.85 for 3-month survival and 0.83 for 1-year survival, indicating a higher accuracy compared with our algorithms [8]. The prospective collection of their data might have been more accurate and less prone to bias, resulting in higher accuracy. Future studies should externally validate survival prognostication models and assess which algorithm is most accurate in predicting survival for patients with extremity metastases.
Comorbidity status and BMI are two additional factors associated with survival and should be taken into account when estimating survival. These factors should be incorporated in survival prediction models. The nomogram remained most accurate in predicting survival after correcting for optimism and could be used on paper; however, its estimates will be more precise when implemented in an application. The nomogram could be made available on interfaces convenient in clinical practice (such as smartphone applications) to aid surgical decision making. We are working on external validation of the developed algorithms and aim to develop an online tool to estimate survival for use in clinical practice.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgments
We thank the Harvard Catalyst (Boston, MA, USA) for their statistical support.
Footnotes
One author (SJ) certifies that he has received, an amount less than USD 10,000, from the Anna Foundation (Oegstgeest, The Netherlands), an amount less than USD 10,000 from the De Drie Lichten Foundation (Hilversum, The Netherlands), an amount less than USD 10,000 from the KWF Kankerbestrijding (Amsterdam, The Netherlands), and an amount less than USD 10,000, from the Michael van Vloten Foundation (Rotterdam, The Netherlands). One author (JS) certifies that he or a member of his family has or may receive payments or benefits, an amount less than USD 10,000, from Stryker (Kalamazoo, MI, USA), and an amount less than USD 10,000, from Biom’up (Saint-Priest, Lyon, France).
All ICMJE Conflict of Interest Forms for authors and Clinical Orthopaedics and Related Research ® editors and board members are on file with the publication and can be viewed on request.
Each author certifies that his or her institution approved the human protocol for this investigation, that all investigations were conducted in conformity with ethical principles of research.
This work was performed at Massachusetts General Hospital, Boston, MA, USA.
References
- 1.Allison PD. Survival Analysis Using SAS®: A Practical Guide, Cary, NC: SAS® Institute; 2010.
- 2.Bauer HC, Wedin R. Survival after surgery for spinal and extremity metastases: prognostication in 241 patients. Acta orthopaedica Scandinavica. 1995;66:143–146. doi: 10.3109/17453679508995508. [DOI] [PubMed] [Google Scholar]
- 3.Bryant D, Havey TC, Roberts R, Guyatt G. How many patients? How many limbs? Analysis of patients or limbs in the orthopaedic literature: a systematic review. The J Bone Joint Surg Am. 2006;88:41–45. doi: 10.2106/JBJS.E.00272. [DOI] [PubMed] [Google Scholar]
- 4.Cleves MA. From the help desk: Comparing areas under receiver operating characteristic curves from two or more probit or logit models. Stata J. 2002;2:301–313. [Google Scholar]
- 5.Collins GS, Reitsma JB, Altman DG, Moons KG. Transparent reporting of a multivariable prediction model for individual prognosis or diagnosis (TRIPOD): the TRIPOD statement. BMJ. 2015;350:g7594. doi: 10.1136/bmj.g7594. [DOI] [PubMed] [Google Scholar]
- 6.Deyo RA, Cherkin DC, Ciol MA. Adapting a clinical comorbidity index for use with ICD-9-CM administrative databases. J Clin Epidemiol. 1992;45:613–619. doi: 10.1016/0895-4356(92)90133-8. [DOI] [PubMed] [Google Scholar]
- 7.Edwards BK, Noone AM, Mariotto AB, Simard EP, Boscoe FP, Henley SJ, Jemal A, Cho H, Anderson RN, Kohler BA, Eheman CR, Ward EM. Annual report to the nation on the status of cancer, 1975–2010, featuring prevalence of comorbidity and impact on survival among persons with lung, colorectal, breast, or prostate cancer. Cancer. 2014;120:1290–1314. doi: 10.1002/cncr.28509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Forsberg JA, Eberhardt J, Boland PJ, Wedin R, Healey JH. Estimating survival in patients with operable skeletal metastases: an application of a bayesian belief network. PloS One. 2011;6:e19956. doi: 10.1371/journal.pone.0019956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Forsberg JA, Wedin R, Bauer HC, Hansen BH, Laitinen M, Trovik CS, Keller JO, Boland PJ, Healey JH. External validation of the Bayesian Estimated Tools for Survival (BETS) models in patients with surgically treated skeletal metastases. BMC Cancer. 2012;12:493. doi: 10.1186/1471-2407-12-493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Goodwin PJ, Ennis M, Pritchard KI, Koo J, Trudeau ME, Hood N. Diet and breast cancer: evidence that extremes in diet are associated with poor survival. J Clin Oncol. 2003;21:2500–2507. doi: 10.1200/JCO.2003.06.121. [DOI] [PubMed] [Google Scholar]
- 11.Gupta S, Tran T, Luo W, Phung D, Kennedy RL, Broad A, Campbell D, Kipp D, Singh M, Khasraw M, Matheson L, Ashley DM, Venkatesh S. Machine-learning prediction of cancer survival: a retrospective study using electronic administrative records and a cancer registry. BMJ Open. 2014;4:e004007. doi: 10.1136/bmjopen-2013-004007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Harrell FE, Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med. 1996;15:361–387. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 13.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York, NY: Springer-Verlag; 2009. [Google Scholar]
- 14.Henderson R, Keiding N. Individual survival time prediction using statistical models. J Med Ethics. 2005;31:703–706. doi: 10.1136/jme.2005.012427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hosmer D, Lemeshow S. Applied Survival Analysis: Regression Modeling of Time to Event Data. New York, NY: John Wiley & Sons; 1999. [Google Scholar]
- 16.Huntington JT, Butterfield M, Fisher J, Torrent D, Bloomston M. The Social Security Death Index (SSDI) most accurately reflects true survival for older oncology patients. Am J Cancer Res. 2013;3:518–522. [PMC free article] [PubMed] [Google Scholar]
- 17.Iasonos A, Schrag D, Raj GV, Panageas KS. How to build and interpret a nomogram for cancer prognosis. J Clin Oncol. 2008;26:1364–1370. doi: 10.1200/JCO.2007.12.9791. [DOI] [PubMed] [Google Scholar]
- 18.Jung SH, Yang DH, Ahn JS, Lee SS, Ahn SY, Kim YK, Kim HJ, Lee JJ. Decreased body mass index is associated with poor prognosis in patients with multiple myeloma. Ann Hematol. 2014;93:835–840. doi: 10.1007/s00277-013-1977-9. [DOI] [PubMed] [Google Scholar]
- 19.Katagiri H, Takahashi M, Wakai K, Sugiura H, Kataoka T, Nakanishi K. Prognostic factors and a scoring system for patients with skeletal metastasis. J Bone Joint Surg Br. 2005;87:698–703. doi: 10.1302/0301-620X.87B5.15185. [DOI] [PubMed] [Google Scholar]
- 20.Kattan MW, Eastham JA, Stapleton AM, Wheeler TM, Scardino PT. A preoperative nomogram for disease recurrence following radical prostatectomy for prostate cancer. J Natl Cancer Inst. 1998;90:766–771. doi: 10.1093/jnci/90.10.766. [DOI] [PubMed] [Google Scholar]
- 21.Kim MS, Lee SY, Lee TR, Cho WH, Song WS, Koh JS, Lee JA, Yoo JY, Jeon DG. Prognostic nomogram for predicting the 5-year probability of developing metastasis after neo-adjuvant chemotherapy and definitive surgery for AJCC stage II extremity osteosarcoma. Ann Oncol. 2009;20:955–960. doi: 10.1093/annonc/mdn723. [DOI] [PubMed] [Google Scholar]
- 22.Mackinnon A. The use and reporting of multiple imputation in medical research: a review. J Intern Med. 2010;268:586–593. doi: 10.1111/j.1365-2796.2010.02274.x. [DOI] [PubMed] [Google Scholar]
- 23.McTiernan A, Irwin M, Vongruenigen V. Weight, physical activity, diet, and prognosis in breast and gynecologic cancers. J Clin Oncol. 2010;28:4074–4080. doi: 10.1200/JCO.2010.27.9752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nathan SS, Healey JH, Mellano D, Hoang B, Lewis I, Morris CD, Athanasian EA, Boland PJ. Survival in patients operated on for pathologic fracture: implications for end-of-life orthopedic care. J Clin Oncol. 2005;23:6072–6082. doi: 10.1200/JCO.2005.08.104. [DOI] [PubMed] [Google Scholar]
- 25.Oberije C, De Ruysscher D, Houben R, van de Heuvel M, Uyterlinde W, Deasy JO, Belderbos J, Dingemans AM, Rimner A, Din S, Lambin P. A validated prediction model for overall survival from stage III non-small cell lung cancer: toward survival prediction for individual patients. Int J Radiat Oncol Biol Phys. 2015;92:935–944. doi: 10.1016/j.ijrobp.2015.02.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Patnaik JL, Byers T, Diguiseppi C, Denberg TD, Dabelea D. The influence of comorbidities on overall survival among older women diagnosed with breast cancer. J Natl Cancer Inst. 2011;103:1101–1111. doi: 10.1093/jnci/djr188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pepe M, Longton G, Janes H. Estimation and comparison of receiver operating characteristic curves. Stata J. 2009;9:1. [PMC free article] [PubMed] [Google Scholar]
- 28.Poeran J, Rasul R, Suzuki S, Danninger T, Mazumdar M, Opperer M, Boettner F, Memtsoudis SG. Tranexamic acid use and postoperative outcomes in patients undergoing total hip or knee arthroplasty in the United States: retrospective analysis of effectiveness and safety. BMJ. 2014;349:g4829. doi: 10.1136/bmj.g4829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Quan H, Li B, Couris CM, Fushimi K, Graham P, Hider P, Januel JM, Sundararajan V. Updating and validating the Charlson comorbidity index and score for risk adjustment in hospital discharge abstracts using data from 6 countries. Am J Epidemiol. 2011;173:676–682. doi: 10.1093/aje/kwq433. [DOI] [PubMed] [Google Scholar]
- 30.Quan H, Parsons GA, Ghali WA. Validity of information on comorbidity derived rom ICD-9-CCM administrative data. Med Care. 2002;40:675–685. doi: 10.1097/00005650-200208000-00007. [DOI] [PubMed] [Google Scholar]
- 31.Ratasvuori M, Wedin R, Keller J, Nottrott M, Zaikova O, Bergh P, Kalen A, Nilsson J, Jonsson H, Laitinen M. Insight opinion to surgically treated metastatic bone disease: Scandinavian Sarcoma Group Skeletal Metastasis Registry report of 1195 operated skeletal metastasis. Surg Oncol. 2013;22:132–138. doi: 10.1016/j.suronc.2013.02.008. [DOI] [PubMed] [Google Scholar]
- 32.Schneiderbauer MM, von Knoch M, Schleck CD, Harmsen WS, Sim FH, Scully SP. Patient survival after hip arthroplasty for metastatic disease of the hip. J Bone Joint Surg Am. 2004;86:1684–1689. doi: 10.2106/00004623-200408000-00011. [DOI] [PubMed] [Google Scholar]
- 33.Schonlau M. Boosted regression (boosting): an introductory tutorial and a Stata plugin. Stata J. 2005;5:330–354. [Google Scholar]
- 34.Siontis GC, Tzoulaki I, Castaldi PJ, Ioannidis JP. External validation of new risk prediction models is infrequent and reveals worse prognostic discrimination. J Clin Epidemiol. 2015;68:25–34. doi: 10.1016/j.jclinepi.2014.09.007. [DOI] [PubMed] [Google Scholar]
- 35.Sogaard M, Thomsen RW, Bossen KS, Sorensen HT, Norgaard M. The impact of comorbidity on cancer survival: a review. Clin Epidemiol. 2013;5(suppl 1):3–29. doi: 10.2147/CLEP.S47150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Steyerberg EW, Harrell FE, Jr, Borsboom GJ, Eijkemans MJ, Vergouwe Y, Habbema JD. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol. 2001;54:774–781. doi: 10.1016/S0895-4356(01)00341-9. [DOI] [PubMed] [Google Scholar]
- 37.US National Heart Lung and Blood Institute. The Practical Guide: Identification, Evaluation, and Treatment of Overweight and Obesity in Adults. National Institutes of Health; 2000. Available at: http://www.nhlbi.nih.gov/files/docs/guidelines/prctgd_c.pdf. Accessed June 26, 2015.
- 38.Voskuijl T, Hageman M, Ring D. Higher Charlson Comorbidity Index Scores are associated with readmission after orthopaedic surgery. Clin Orthop Relat Res. 2014;472:1638–1644. doi: 10.1007/s11999-013-3394-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.