Abstract
PURPOSE: This study presented a three-dimensional magnetic resonance (MR)–based method to separate a breast into four quadrants for quantitative measurements of the quadrant breast volume (BV) and density. METHODS: Breast MR images from 58 healthy women were studied. The breast and the fibroglandular tissue were segmented by using a computer-based algorithm. A breast was divided into four quadrants using two perpendicular planes intersecting at the nipple or the nipple-centroid line. After the separation, the BV, the fibroglandular tissue volume, and the percent density (PD) were calculated. The symmetry of the quadrant BV in the left and right breasts separated by using the nipple alone, or the nipple-centroid line, was compared. RESULTS: The quadrant separation made on the basis of the nipple-centroid line showed closer BVs in four quadrants than using the nipple alone. The correlation and agreement for the BV in corresponding quadrants of the left and the right breasts were improved after the nipple-centroid reorientation. Among the four quadrants, PD was the highest in the lower outer and the lowest in the upper outer (significant than the other three) quadrants (P < .05). CONCLUSIONS: We presented a quantitative method to divide a breast into four quadrants. The reorientation based on the nipple-centroid line improved the left to right quadrant symmetry, and this may provide a better standardized method to measure quantitative quadrant density. The cancer occurrence rates are known to vary in different sites of a breast, and our method may provide a tool for investigating its association with the quantitative breast density.
Introduction
Mammographic density is well known as an independent risk factor for breast cancer [1–4], but the biologic basis for the mammographic densities to increase cancer risk is not fully understood. Dense tissues in mammography are associated with increased epithelial cellular concentration and stromal fibrosis [5]. A fundamental question that has yet to be answered is whether cancers tend to arise in mammographically dense tissue. Among few studies exploring the question, one study showed that ductal carcinoma in situ occurs overwhelmingly in the mammographically dense areas, suggesting that some aspect of glandular/stromal tissue comprising the dense tissue directly influences the carcinogenic process [6]. A recent study also noted that tumors arise predominantly within the radiodense breast tissue [7].
Many studies have shown that the incidence of breast cancer is much higher in the upper outer (UO) quadrant of the breast than in the other three quadrants [8–10]. A study [9] consisting of 746 consecutive breast core biopsies noted 62% of 349 malignant lesions (95% confidence interval 57-67%) occurred in the UO quadrant. An adequate explanation for this asymmetric rate of cancer within the breast has never been established. Because breast cancer is predominantly occurring within dense tissue, it was speculated that the differences in density among four quadrants might explain the differences in the cancer occurrence rate. Quadrant or local breast density based on mammography has been proposed before [2,6,7]. However, Vachon et al. found that accounting for overall percentage density, density in the region where the cancer subsequently developed was not a significant risk factor [2]. Because mammography acquires two-dimensional (2D) projection images, it cannot provide a reliable assessment of density in four quadrants, and also, it is not able to provide quantitative dense tissue volume.
Breast magnetic resonance imaging (MRI) acquires 3D volumetric images that show a good contrast between fibroglandular and fatty tissues, and many segmentation methods have been developed and shown capable of analyzing breast volume (BV) and fibroglandular tissue volume (FV) quantitatively [11–19]. However, to date, there has not been any report to divide one breast into four quadrants and measure density, presumably due to the lack of well-defined landmarks in the breast. In this work, we presented an objective method to separate a breast into four quadrants, based on the nipple alone in the original MRI space coordinates, or the reoriented breast based on the nipple to the centroid line. The centroid, or the center of mass (COM), was calculated from the segmented breast in the 3D space. After the separation, the BV, FV, and percent density (PD) in each of the four quadrants were measured.
Because there are no other established imaging modalities capable of providing quantitative BV and FV to serve as the ground truth, it also is not possible for a human observer to visually divide a breast into four quadrants and provide qualitative assessments for comparison, therefore it is difficult to validate the quadrant separation results obtained in this MRI study. As an alternative, we will compare the BV in the corresponding quadrant of the left and the right breasts of healthy women as a precision test [20]. Many factors may affect the shape of breast in the MRI examination; therefore, simply dividing a breast into four quadrants based on the nipple in the imaging space may lead to a high variation in the left to right comparison. We are expecting that dividing the quadrants based on the nipple-centroid line of the breast can achieve a better standardization and yield a higher correlation in the left to right comparison. After the four breast quadrants are separated, the FV and the PD in different quadrants are measured and compared.
Materials and Methods
Study Subjects
Fifty-eight healthy Asian women (range 20-61, mean 34 years old) were included in this study. These subjects came from two previous studies of breast density using healthy volunteers, 30 women from a menstrual cycle study [18], and 28 women from an MR scanner study [19]. Of them, 47 were pre-menopausal and 11 were post-menopausal women. The Body Mass Index (BMI) ranged from 17.1 to 33.1 (mean ± SD, 21.3 ± 3.1). At the time of participation in this study, they were all healthy without any breast-related symptoms. In addition, none of them had been diagnosed with any breast diseases. This study was approved by the Institutional Review Board and was Health Insurance Portability and Accountability Act (HIPAA)-compliant. All subjects provided written informed consent.
MRI Acquisition
All MRI studies were performed on a 1.5-T MR scanner (Siemens, Somatom, Erlangen, Germany) with a four-channel flat-bed breast coil. The subject was carefully positioned into the coil in a straight prone position (facing down), and the breast tissues were pulled down into the open coil space. Because the purpose of this study was to measure breast density and not to diagnose lesions, the MR studies were performed without the injection of contrast agent. In 30 women (menstrual cycle study), MR T1-weighted images were acquired using the 3D non–fat-suppressed gradient echo pulse sequences. The imaging parameters were field of view = 350 mm, slice thickness = 2 mm, repetition time/echo time = 11/4.7 milliseconds, flip angle = 20°, and matrix size = 256 × 256. In another 28 women (MR scanner study), MR T1-weighted images were acquired using a 2D fast spin echo pulse sequence. The imaging parameters were repetition time/echo time = 650/9.8 milliseconds, parallel imaging with Sensitivity-Encoding (SENSE) factor = 2, slice thickness = 2 mm, slice gap = 0, phase encoding Right-Left (R-L), bandwidth per pixel = 181 Hz, field of view = 330 mm, number of signal average = 1, and imaging matrix = 330 × 384 (660 × 768 with interpolation). Although different imaging sequences were used in these two studies, the contrast between dense and fatty tissues was comparable on acquired images, and both were excellent for dense tissue segmentation.
Whole Breast and Fibroglandular Tissue Segmentation
The whole breast and the fibroglandular tissue within each breast were segmented using a computer-based algorithm. Detailed step-by-step procedures and illustration examples, as well as segmentation reproducibility and error analysis results based on radiologists’ correction, were given in four methodology papers published before [11–14]. Because the breast was connected with the body without a clear boundary, one major task was to determine the superior, inferior, and the posterior-lateral boundaries so the breast could be separated from the body using a standardized criterion. The superior and inferior boundaries of the breast (that is, where the breast begins and ends) were determined by comparing the thickness of breast fat layer with the body fat layer. For the posterior-lateral boundary, in this study, we used a horizontal line through the sternum to perform the initial cut, and the fatty tissue above this line was considered as breast fat (procedures and examples shown in [13]). Because a flat-bed breast coil was used, and the subjects were small Asian women, the posterior breast laid flat on the coil and a horizontal line determined on the basis of the slice of the sternum could be applied to all imaging slices of this data set and defined as the z = 0 plane shown in Figure 1. After the three boundaries were determined, the key steps for breast segmentation were given as follows: 1) identify the chest wall muscle by applying the Fuzzy C-means clustering and b-spline curve fitting (examples are shown in [11–14]); 2) separate the left and the right breasts by using a vertical line perpendicular to the sternum in the middle of the bilateral breasts [13]; 3) exclude the skin along the breast boundary by applying dynamic searching [11]; 4) correct the bias field and intensity nonuniformity (since a surface breast coil was used) by applying the nonparametric nonuniformity normalization plus Fuzzy C-means algorithm for segmentation of fibroglandular tissue and fatty tissue (detailed procedures and examples are shown in [12]). After the breast was segmented and the intensity correction procedures were completed, the next job was to separate the fibroglandular and fatty tissues using the k-means clustering. When non–fat-suppressed images were analyzed, we have tested different settings and found that by using a total cluster number of 6, the lower three clusters for the fibroglandular tissue and the higher three clusters for the fatty tissue, this setting worked very well for most breast MRI data sets. A detailed description about the testing of the setting was given in [11], and many examples of the segmentation quality were shown in [12–14] and other breast density publications of our group.
Figure 1.

A diagram illustrating the volume-preserving affine transformation to reorient a 3D breast to align with the nipple-centroid line in the L/R direction. An axial projection view is shown, with the x-axis coordinates representing the L/R direction, and the z-axis coordinates representing the A/P direction. The posterior boundary along the sternum of the woman used in the initial cut for breast segmentation is defined as the z = 0 plane. The centroid of the breast is marked by an asterisk. After the transformation, the nipple-centroid line becomes perpendicular to the z = 0 axis. Similar transformation is performed in the y-axis shown in Figure 2.
Breast Separation into Four Quadrants
Classification of Breast Quadrants
A single breast can be divided into four quadrants: UO, upper inner (UI), lower outer (LO), and lower inner (LI) by two perpendicular planes intersected at the nipple. In MRI, the breasts are imaged using a 3D volumetric acquisition and shown as a stack of images; therefore, it can be reconstructed as a 3D object represented with coordinates. In this study, the coordinate in the left/right (L/R) direction is represented by x, in the superior/inferior direction it is represented by y, and in the anterior/posterior (A/P) direction it is represented by z. The nipple location was visually marked by a trained operator and recorded as {x_nipple, y_nipple, z_nipple} based on the center of the nipple. The nipple was clearly visible on MRI, and there was very little room for observer variation. After the nipple coordinate was defined, as a very simple approach based on the original imaging space coordinates, we used the y_nipple to separate the upper region (superior, y > y_nipple) and the lower region (inferior, y < y_nipple). The perpendicular plane based on x_nipple was used to separate the inner (x < x_nipple) and the outer (x > x_nipple) for the left breast and reversed for the right breast. After the separation, the BV in each quadrant was calculated. Then, on the basis of the segmented fibroglandular tissue in each separated quadrant, the FV was calculated. The PD in each quadrant can then be calculated as the ratio of FV/BV.
Breast Orientation Correction Based on Centroid
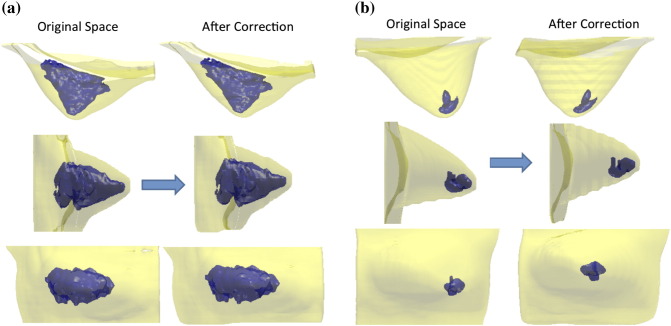
The simple method described above did not consider the orientation (or tilt) of the breast; therefore, the regional separation done using that way would be heavily dependent on how the breast was positioned into the MR coil (in a prone position). If it was freely hanging with the centroid and the nipple aligning at the same (x, y) location, then the separation could be done on the basis of the nipple alone. However, in most cases, they were not aligned, and a reorientation algorithm could be applied to perform the quadrant separation based on the corrected planes. The centroid, or COM, was calculated from the segmented breast in the 3D space. Depending on the angle of the centroid-nipple line, a simple volume-preserving Affine transformation was applied (see the example shown in Figure 1). The horizontal line through the sternum used to perform the initial cut was defined as the z = 0 plane, and voxels on each plane along the z-axis would be shifted by the amount of {dx, dy} on the L/R direction and superior/inferior direction and no movement along the A/P direction. After the reorientation based on the nipple-centroid line was done, the four quadrants could be separated, and the BV, FV, and PD in each quadrant after correction were calculated. Figure 2 illustrates two cases, one case without much shift and another case with a substantial shift after the correction.
Figure 2.
Two women showing different degrees of correction after the nipple-centroid reorientation by affine transformation. (A) The right breast of a woman, with the nipple-centroid line close to perpendicular to the z = 0 axis on the axial projection view (top figure) and the sagittal projection view (middle figure). The coronal projection view (shown in the bottom figure) does not change much. (B) The left breast of another woman with a substantial tissue shift after the positional correction. The nipple-centroid line is clearly tilted, far away from perpendicular to the z = 0 axis on the axial projection view (top figure) and the sagittal projection view (middle figure). The location of the breast density also shows a substantial change in the coronal projection view (bottom figure) after the correction.
Statistical Analyses
The quality of the quadrant separation without correction and after nipple-centroid line reorientation is evaluated on the basis of the bilateral symmetry between the left and the right breasts of these healthy women as a precision test. The BV in each quadrant in the left and right breasts of the same woman was measured. For each quadrant, the concordance correlation coefficient using all 116 breasts was calculated [21], and the Bland–Altman plot was done [22] to quantitatively evaluate the symmetry. Concordance correlation coefficient is a number between 0 and 1. A value closer to 1 indicates a higher symmetry. For Bland–Altman method, 95% limits of agreement between each quadrant of the bilateral breasts (average difference ± 2 SD of the difference) were computed. The smaller the range between these two limits the better the agreement is, indicating a higher level of symmetry. Wilcoxon signed-rank test [23] was used to compare the FV and the PD measured in different quadrants of the same breast of the same woman. P < .05 was considered as significant.
Results
Comparison of Breast Symmetry before and after Correction
Figure 3 shows the correlation of separated BV in each quadrant of the left and the right breasts before and after correction. The data points are falling closer to the unity line after correction, demonstrating that the symmetry is improved. Table 1 summarizes the left to right concordance correlation coefficients of BV in the four quadrants before and after the correction. Figure 4 shows the Bland–Altman plots comparing the symmetry of BV in each quadrant before and after correction. The range and the variance of the percentage difference became smaller after correction. The 95% limits of agreement of BV in each quadrant measured between the left and right breasts before and after correction are also shown in Table 1. The correlation and agreement for the measured BV in each of the four quadrants are all improved after the standardization by using the nipple-centroid line.
Figure 3.
The correlation of BV measured from the corresponding quadrant of the left and right breasts of 58 healthy women, before and after positional correction. Blue dots are before correction, and pink triangles are after correction based on the nipple-centroid line. The correction clearly improves the correlation, with data points falling closer to the unity line.
Table 1.
Concordance Correlation Coefficient and 95% Limits of Agreement of the Measured BV in Each Quadrant between the Left and the Right Breasts of the Same Women. Results before and after the Positional Correction Are Shown
| UO | UI | LO | LI | ||
|---|---|---|---|---|---|
| Concordance correlation coefficient | No Correction | 0.86 | 0.85 | 0.75 | 0.77 |
| Correction | 0.97 | 0.98 | 0.99 | 0.98 | |
| 95% Limits of agreement | No Correction | ||||
| Mean + 2SD (%) | 68.7 | 58.2 | 61.4 | 73.9 | |
| Mean − 2SD (%) | − 52.5 | − 77.1 | − 75.7 | − 52.5 | |
| Range (%) | 121.2 | 135.3 | 137.1 | 126.4 | |
| Correction | |||||
| Mean + 2SD (%) | 38.2 | 18.8 | 16.3 | 34.3 | |
| Mean − 2SD (%) | − 20.2 | − 32.9 | − 34.6 | − 12.5 | |
| Range (%) | 58.4 | 51.7 | 50.9 | 46.8 | |
Figure 4.
The Bland–Altman plots comparing the symmetry of BV measured from the corresponding quadrant of the left and right breasts of 58 healthy women, before and after positional correction. The blue dots are before correction, and the pink triangles are after correction based on the nipple-centroid line. The x-axis denotes the mean BV of the left and right breasts, calculated as (left BV + right BV)/2. The y-axis denotes the percentage difference calculated as (left BV − right BV)/mean BV × 100%. The correction improves the agreement showing a smaller SD.
Measurements of BV, FV, and PD in Each Quadrant
Table 2 lists the mean values of BV, FV, and PD in the four quadrants of the bilateral breasts before and after nipple-centroid standardization. The main effect of the positional correction is to recategorize breast tissues from the upper to the lower breast. The mean BV in the UO quadrant of the right breast was 82.3 ± 40.2 cm3 without correction and decreased to 67.0 ± 30.8 cm3 after correction, and the volume in the LO quadrant was increased from 56.0 ± 29.0 to 66.4 ± 29.1 cm3 after correction. The result in the left breast was similar. The BV in the UO quadrant was decreased from 75.8 ± 39.0 to 61.4 ± 27.3 cm3 after correction, and in the LO breast, it was increased from 60.7 ± 32.3 to 72.0 ± 29.5 cm3 after correction. The correction decreased the BV in 85 of 116 (73%) breasts in the UO quadrant and in 90 of 116 (78%) breasts in the UI quadrant and increased the BV in 92 of 116 (79%) breasts in the LO quadrant and in 81 of 116 (70%) breasts in the LI quadrant. As anticipated, the quadrants separated on the basis of the nipple-centroid line had closer BVs compared to volumes separated on the basis of the nipple alone.
Table 2.
The Mean BV, FV, and PD in Each Quadrant before and after Correction
| UO | UI | LO | LI | ||
|---|---|---|---|---|---|
| Right breast | |||||
| BV (cm3) | No Correction | 82.3 ± 40.2 | 71.2 ± 37.4 | 56.0 ± 29.0 | 60.7 ± 32.3 |
| Correction | 67.0 ± 30.8 | 59.5 ± 26.2 | 66.4 ± 29.1 | 66.1 ± 28.7 | |
| FV (cm3) | No Correction | 14.6 ± 15.6 | 14.4 ± 12.8 | 13.4 ± 8.5 | 11.6 ± 9.0 |
| Correction | 11.4 ± 12.5 | 11.3 ± 9.2 | 16.9 ± 10.8 | 14.2 ± 8.5 | |
| PD (%) | No Correction | 17.1 ± 13.1 | 20.1 ± 13.7 | 25.7 ± 12.7 | 21.2 ± 12.4 |
| Correction | 16.5 ± 13.2 | 19.8 ± 13.4 | 27.2 ± 13.8 | 23.7 ± 13.2 | |
| Left breast | |||||
| BV (cm3) | No Correction | 75.8 ± 39.0 | 74.3 ± 29.9 | 60.7 ± 32.3 | 54.4 ± 34.4 |
| Correction | 61.4 ± 27.3 | 63.1 ± 25.5 | 72.0 ± 29.5 | 59.1 ± 25.1 | |
| FV (cm3) | No Correction | 11.8 ± 12.0 | 14.6 ± 10.2 | 15.6 ± 11.3 | 10.8 ± 14.5 |
| Correction | 8.9 ± 8.5 | 12.0 ± 8.4 | 18.1 ± 11.5 | 10.9 ± 6.7 | |
| PD (%) | No Correction | 15.6 ± 11.1 | 20.1 ± 12.7 | 26.1 ± 12.9 | 18.6 ± 11.3 |
| Correction | 14.6 ± 10.9 | 20.0 ± 12.2 | 26.9 ± 13.9 | 20.3 ± 11.8 | |
Comparison of FV and PD between Different Quadrants
After the quadrant separation, the FV was measured in each quadrant of all 116 breasts, and the PD was calculated as a ratio of FV/BV using respective results measured in each quadrant. Because the correction recategorized breast tissues from the upper breast to the lower breast, the correction effect on FV was similar to that of BV, showing decreased FV in the upper breast and increased FV in the lower breast, as shown in Table 2. The PD was calculated as a ratio, and it did not change much after correction. The comparison of FV and PD in different quadrants of the same breast in the same woman was analyzed using the pair-wise Wilcoxon signed-rank test. The analysis was done on the basis of 58 left breasts, 58 right breasts, and combined 116 breasts, respectively. As shown in Table 2, among the four separated quadrants, the mean PD is the highest in the LO quadrant (significantly higher than in the other three quadrants) and the lowest in the UO quadrant (significantly lower than in the other three quadrants).
Discussion
The cancer occurrence rate is much higher in the UO quadrant than in the other three quadrants, but there is very little evidence to explain this regional differential rate [8–10]. Many studies have investigated the association of mammographic density with breast cancer risk and found it to be a strong independent risk factor [1–4]. However, the conclusion is mainly reached on the basis of large epidemiology studies from a statistical perspective, and the most noticeable difference in risks is between women with extremely dense breast compared to women with almost entirely fatty breast [24–27]. The current knowledge and direct evidence regarding whether breast tumors arise directly within the dense breast tissue is still lacking [2,6,7]. Because breast density is a strong risk factor, investigation of the distribution of regional breast density in four different quadrants may help our understanding about its involvement in the much higher cancer incidence rate found in the UO quadrant [7]. As the first step to address this question, a quantitative method that can reliably separate a breast into four quadrants on the basis of internal landmarks within the breast is required.
In this study, we proposed a quantitative method using the nipple and the centroid, or the COM, of the segmented 3D breast to measure volumetric breast density in four quadrants. A group of 58 healthy normal women was used in this study, so we could use the left to right symmetry as a precision test to investigate the quadrant separation effect using our proposed method. The results showed that the breast separation using the corrected planes based on the nipple and centroid has a higher left to right symmetry compared to results obtained using the nipple alone, as reflected in a higher concordance correlation coefficient and 95% limits of agreement in the Bland–Altman plot. On the basis of the separation using the nipple-centroid line, we found closer BVs in the four quadrants compared to the separation using the nipple alone and that the FV and the PD were the highest in the LO quadrant and the lowest in the UO quadrant among the four quadrants.
Only a few studies investigating quadrant breast density on mammography were reported [2,6], and so far there has not been any study to report quadrant breast density on breast MRI. On the craniocaudal view (CC) and mediolateral oblique (MLO) view mammography, each image could be divided into two regions. Because a projection image was acquired, the boundary of the chest wall on MLO could be easily recognized on the basis of the pectoralis muscle and the extension of this muscle, which may be used to perform regional division by drawing a perpendicular line through the nipple. For CC view, the edge of the image is assumed to be parallel to the chest wall plane, which is used for regional division by drawing a perpendicular line through the nipple [2]. With this approach, the mammographic quadrant density could be estimated as the average of density assessments from two mammographic areas. For example, the UO quadrant breast density can be calculated as the average of the CC-lateral and MLO-superior density. Obviously, a fundamental problem of this approach is that the density in a specific breast region cannot be measured on the basis of two projection views; particularly when the MLO is taken at 45° angle, which is not optimal to separate the upper and lower breasts. Recently, a study to investigate the relationship of the breast tumor with respect to the location of dense tissue proposed a square-specific density analysis method by generating a virtual 1-cm square grid on a mammogram, but this method is not capable of measuring quadrant density either [7]. MRI acquires 3D images to cover the whole breast, therefore providing a suitable method for regional volumetric measurements. In addition, because the nipple is clearly visible and the COM can be computed from the segmented breast, regional division based on these two landmarks and an assumed flat chest wall (z = 0 plane) provide an objective method for volumetric quantification.
Because there is no ground-truth or well-established method for validation of the separated quadrants, to evaluate the robustness of the proposed MR-based method in this study, the symmetry of BV in bilateral breasts of healthy women was used as a precision test [20]. Morphologically, bilateral breasts in a healthy woman can be assumed to be symmetrical to some extent, at least much smaller compared to the person-to-person variations [28–32]. A study [28] to investigate the spatial distribution of density within the breast using 493 mammographic images from a sample of 165 premenopausal women showed that the degree of the spatial clustering of density was similar between a woman's two breasts and did not change with aging. Most mammography studies analyzing breast symmetry were aimed to predict risk of developing cancer [33–35]. In mammography, different degrees of tissue compression and distortion between the left and the right breasts are likely to occur, and as such, symmetry measures can be confounded by the nature of the imaging procedure itself [31].
Breast MRI acquires 3D images without compression; in addition, the dedicated breast coil for most clinical scanners uses the flat-bed design, thus the MRI procedure is unlikely to distort the breast tissue and can provide optimal images for symmetrical analysis. It was found that the quadrant separation using the corrected planes based on the tilted angle between nipple and the centroid yields a closer separated quadrant BV and a higher left to right symmetry with improved concordance correlation coefficients. Likewise, in the Bland–Altman plots, the 95% limits of agreement (the range of percentage difference) between bilateral breasts became smaller after the correction. The results suggested that the correction method could take into account the natural orientation difference from person to person (e.g., two cases shown in Figure 1), thus providing a more reliable quadrant separation method compared to the method without correction by using the nipple alone. In most cases, the correction recategorized some tissues in the upper breast to the lower breast; therefore, BVs in the UO and UI quadrants decreased after correction, while the BVs in the LO and LI quadrants increased after correction. In contrast, the correction did not recategorize tissues between the inner and outer breast regions much. The results indicated that when the breasts were positioned into the breast coil, they were not freely hanging (i.e., only being pulled by gravity), rather there was a shift of upper body superiorly relative to the nipple. Therefore, the reorientation based on the tiled angle between the nipple and the centroid could achieve a better positional standardization. It should be noted that the subjects analyzed in this study were slim Asian women with relatively small breasts compared to Caucasian and Hispanic women, and the gravity may not be sufficient to pull the entire breast straightly down. The correction effect may be different in different subject groups.
The comparison of the distribution of FV and PD in the four separated quadrants found that the breast density was the lowest in the UO quadrant and the highest in the LO quadrant, which was statistically significant when comparing to the other three quadrants. The motivation for the quadrant separation in this work was to provide a tool for studying the association between the amounts of dense tissue with different cancer occurrence rates in different quadrants; however, they have to be compared using quadrants defined in exactly the same way. The widely reported finding of a higher cancer incidence in the UO quadrant was concluded on the basis of the clinical evaluation and the biopsy location guided by mammography and/or ultrasound imaging, when women were lying on the back in a supine position. Therefore, the body position and the shape of the breast were very different from the prone position used for MRI. As a result, the quadrants separated using the method proposed in this MRI study were not corresponding to the quadrants reported for cancer incidence, and they could not be compared to draw any conclusion yet. Although most of the studies on the quadrant disparity of cancer risk were from the observation of western women [8–10], the effect was very strong and this finding was also true in Asian women. We found two papers reporting the site incidence rates around the same time: Darbre [10] found 53.3% cancer in the UO quadrant of women in the Great Britain in 2000, and Chen et al. [36] found 52.3% cancer in the UO quadrant of women enrolled in 2001 to 2002 in a hospital in Taiwan. Although this published study in Taiwan is from a small series, the finding is consistent with our own clinical experience in several hospitals in Taiwan. Therefore, this site disproportionality is very likely not race, or ethnicity, specific. We believe the quadrant separation method reported in this work can provide a very useful tool for investigating the relationship between the quantitative volumetric breast density and the cancer incidence found in MRI, based on exactly the same definition for quadrant separation.
Our study had several limitations. This was a pilot study mainly reporting the development of a standardized quadrant separation method on 3D breast MRI. Only a small number of Asian subjects were included in the analysis. The obtained results in the distribution of quadrant density have to be further validated using more subjects, and it should be noted that results found in this study may not be applicable to a Western cohort that includes women with very diffident body figures and breast sizes. Because there is no commonly agreed well-established method to separate a breast into four quadrants, there is no ground truth for validation in this study. Therefore, we used the left to right symmetry comparison as a precision test. Although it is agreed that the bilateral breasts of healthy women have a high degree of symmetry, yet they are known to be not completely symmetric. Lastly, the method proposed in this work was based on many segmentation procedures that were developed by us using MR images acquired in similar experimental conditions. For example, the images were acquired using a flat-bed breast coil with the chest laying flat on the coil, and the breast tissues pulled down into the open space; therefore, we could use the z = 0 plane as the fixed reference for the affine transformation. When an angled breast coil was used, the orientation of the z = 0 plane would change and our method might not be applicable. In addition, for women with very large breasts, the breast might not completely fall into the open space and the shape might vary substantially depending on how it was positioned. In this situation, it would be very difficult to yield a consistent quadrant separation despite that a standardized method was used.
In summary, in this study, we presented a standardized analysis method to use the nipple and the centroid of the segmented breast to divide a breast into four quadrants. The results showed that the division done using this method has a better left to right quadrant volume symmetry compared to a method based on the nipple alone without the positional correction. We found that the PD in this group of slim Asian women was the lowest in the UO quadrant compared to the three other quadrants; however, because our quadrants were different from those reported in the literature, the density results could not be directly compared to the cancer incidence rates. Further investigation using exactly the same quadrant division method is needed to explore the direct association of quadrant breast density with cancer occurrence risk. With the increasing use of breast MRI for cancer detection and diagnosis, the method proposed in this study may provide a suitable tool for investigating the relationship between quadrant breast density and cancer location detected by MRI.
Footnotes
This work was supported in part by National Institutes of Health (NIH)/National Cancer Institute (NCI) grants R01 CA127927, R21 CA170955, and R03 CA136071.
References
- 1.Boyd NF, Guo H, Martin LJ, Sun L, Stone J, Fishell E, Jong RA, Hislop G, Chiarelli A, Minkin S. Mammographic density and the risk and detection of breast cancer. N Engl J Med. 2007;356:227–236. doi: 10.1056/NEJMoa062790. [DOI] [PubMed] [Google Scholar]
- 2.Vachon CM, Brandt KR, Ghosh K, Scott CG, Maloney SD, Carston MJ, Pankratz VS, Sellers TA. Mammographic breast density as a general marker of breast cancer risk. Cancer Epidemiol Biomarkers Prev. 2007;16:43–49. doi: 10.1158/1055-9965.EPI-06-0738. [DOI] [PubMed] [Google Scholar]
- 3.Titus-Ernstoff L, Tosteson AN, Kasales C, Weiss J, Goodrich M, Hatch EE, Carney PA. Breast cancer risk factors in relation to breast density (United States) Cancer Causes Control. 2006;17:1281–1290. doi: 10.1007/s10552-006-0071-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boyd NF, Dite GS, Stone J, Gunasekara A, English DR, McCredie MR, Giles GG, Tritchler D, Chiarelli A, Yaffe MJ. Heritability of mammographic density, a risk factor for breast cancer. N Engl J Med. 2002;347:886–894. doi: 10.1056/NEJMoa013390. [DOI] [PubMed] [Google Scholar]
- 5.Ghosh K, Brandt KR, Reynolds C, Scott CG, Pankratz VS, Riehle DL, Lingle WL, Odogwu T, Radisky DC, Visscher DW. Tissue composition of mammographically dense and non-dense breast tissue. Breast Cancer Res Treat. 2012;131:267–275. doi: 10.1007/s10549-011-1727-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ursin G, Hovanessian-Larsen L, Parisky YR, Pike MC, Wu AH. Greatly increased occurrence of breast cancers in areas of mammographically dense tissue. Breast Cancer Res. 2005;7:R605–R608. doi: 10.1186/bcr1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pinto Pereira SM, McCormack VA, Hipwell JH, Record C, Wilkinson LS, Moss SM, Hawkes DJ, dos-Santos-Silva I. Localized fibroglandular tissue as a predictor of future tumor location within the breast. Cancer Epidemiol Biomarkers Prev. 2011;20:1718–1725. doi: 10.1158/1055-9965.EPI-11-0423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Blumgart EI, Uren RF, Nielsen PM, Nash MP, Reynolds HM. Lymphatic drainage and tumour prevalence in the breast: a statistical analysis of symmetry, gender and node field independence. J Anat. 2011;218:652–659. doi: 10.1111/j.1469-7580.2011.01362.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee AH. Why is carcinoma of the breast more frequent in the upper outer quadrant? A case series based on needle core biopsy diagnoses. Breast. 2005;14:151–152. doi: 10.1016/j.breast.2004.07.002. [DOI] [PubMed] [Google Scholar]
- 10.Darbre PD. Recorded quadrant incidence of female breast cancer in Great Britain suggests a disproportionate increase in the upper outer quadrant of the breast. Anticancer Res. 2005;25:2543–2550. [PubMed] [Google Scholar]
- 11.Nie K, Chen JH, Chan S, Chau MK, Yu HJ, Bahri S, Tseng T, Nalcioglu O, Su MY. Development of a quantitative method for analysis of breast density based on three-dimensional breast MRI. Med Phys. 2008;35:5253–5262. doi: 10.1118/1.3002306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lin M, Chan S, Chen JH, Chang D, Nie K, Chen ST, Lin CJ, Shih TC, Nalcioglu O, Su MY. A new bias field correction method combining N3 and FCM for improved segmentation of breast density on MRI. Med Phys. 2011;38:5–14. doi: 10.1118/1.3519869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chang DH, Chen JH, Lin M, Bahri S, Yu HJ, Mehta RS, Nie K, Hsiang DJ, Nalcioglu O, Su MY. Comparison of breast density measured on MR images acquired using fat-suppressed versus nonfat-suppressed sequences. Med Phys. 2011;38:5961–5968. doi: 10.1118/1.3646756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin M, Chen JH, Wang X, Chan S, Chen S, Su MY. Template-based automatic breast segmentation on MRI by excluding the chest region. Med Phys. 2013;40:122301. doi: 10.1118/1.4828837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wei J, Chan HP, Helvie MA, Roubidoux MA, Sahiner B, Hadjiiski LM, Zhou C, Paquerault S, Chenevert T, Goodsitt MM. Correlation between mammographic density and volumetric fibroglandular tissue estimated on breast MR images. Med Phys. 2004;31:933–942. doi: 10.1118/1.1668512. [DOI] [PubMed] [Google Scholar]
- 16.Khazen M, Warren R, Boggis C, Bryant EC, Reed S, Warsi I, Pointon LJ, Kwan-Lim GE, Thompson D, Eeles R. A pilot study of compositional analysis of the breast and estimation of breast mammographic density using three-dimensional T1-weighted magnetic resonance imaging. Cancer Epidemiol Biomarkers Prev. 2008;17:2268–2274. doi: 10.1158/1055-9965.EPI-07-2547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Klifa C, Carballido-Gamio J, Wilmes L, Laprie A, Shepherd J, Gibbs J, Fan B, Noworolski S, Hylton N. Magnetic resonance imaging for secondary assessment of breast density in a high-risk cohort. Magn Reson Imaging. 2010;28:8–15. doi: 10.1016/j.mri.2009.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chan S, Su MY, Lei FJ, Wu JP, Lin M, Nalcioglu O, Feig SA, Chen JH. Menstrual cycle-related fluctuations in breast density measured by using three-dimensional MR imaging. Radiology. 2011;261:744–751. doi: 10.1148/radiol.11110506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen JH, Chan S, Liu YJ, Yeh DC, Chang CK, Chen LK, Pan WF, Kuo CC, Lin M, Chang DH. Consistency of breast density measured from the same women in four different MR scanners. Med Phys. 2012;39:4886–4895. doi: 10.1118/1.4736824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ding H, Klopfer MJ, Ducote JL, Masaki F, Molloi S. Breast tissue characterization with photon-counting spectral CT imaging: a postmortem breast study. Radiology. 2014;272:731–738. doi: 10.1148/radiol.14132732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.King TS, Chinchilli VM, Carrasco JL. A repeated measures concordance correlation coefficient. Stat Med. 2007;26:3095–3113. doi: 10.1002/sim.2778. [DOI] [PubMed] [Google Scholar]
- 22.Myles PS, Cui J. Using the Bland–Altman method to measure agreement with repeated measures. Br J Anaesth. 2007;99:309–311. doi: 10.1093/bja/aem214. [DOI] [PubMed] [Google Scholar]
- 23.Conover WJ. 2nd ed. John Wiley & Sons; New York: 1980. Practical Nonparametric Statistics. [Google Scholar]
- 24.Barlow WE, White E, Ballard-Barbash R, Vacek PM, Titus-Ernstoff L, Carney PA, Tice JA, Buist DS, Geller BM, Rosenberg R. Prospective breast cancer risk prediction model for women undergoing screening mammography. J Natl Cancer Inst. 2006;98:1204–1214. doi: 10.1093/jnci/djj331. [DOI] [PubMed] [Google Scholar]
- 25.Boyd NF, O’Sullivan B, Campbell JE, Fishell E, Simor I, Cooke G, Germanson T. Mammographic signs as risk factors for breast cancer. Br J Cancer. 1982;45:185–193. doi: 10.1038/bjc.1982.32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Saftlas AF, Hoover RN, Brinton LA, Szklo M, Olson DR, Salane M, Wolfe JN. Mammographic densities and risk of breast cancer. Cancer. 1991;67:2833–2838. doi: 10.1002/1097-0142(19910601)67:11<2833::aid-cncr2820671121>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 27.Boyd NF, Byng JW, Jong RA, Fishell EK, Little LE, Miller AB, Lockwood GA, Tritchler DL, Yaffe MJ. Quantitative classification of mammographic densities and breast cancer risk: results from the Canadian National Breast Screening Study. J Natl Cancer Inst. 1995;87:670–675. doi: 10.1093/jnci/87.9.670. [DOI] [PubMed] [Google Scholar]
- 28.Pinto Pereira SM, McCormack VA, Moss SM, dos Santos Silva I. The spatial distribution of radiodense breast tissue: a longitudinal study. Breast Cancer Res. 2009;11:R33. doi: 10.1186/bcr2318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Macea JR, Fregnani JHTG. Anatomy of the thoracic wall, axilla and breast. Int J Morphol. 2006;24:691–704. [Google Scholar]
- 30.Eder M, Waldenfels FV, Swobodnik A, Klöppel M, Pape AK, Schuster T, Raith S, Kitzler E, Papadopulos NA, Machens HG. Objective breast symmetry evaluation using 3-D surface imaging. Breast. 2012;21:152–158. doi: 10.1016/j.breast.2011.07.016. [DOI] [PubMed] [Google Scholar]
- 31.Alterson R, Plewes DB. Bilateral symmetry analysis of breast MRI. Phys Med Biol. 2003;48:3431–3443. doi: 10.1088/0031-9155/48/20/011. [DOI] [PubMed] [Google Scholar]
- 32.Stines J, Tristant H. The normal breast and its variations in mammography. Eur J Radiol. 2005;54:26–36. doi: 10.1016/j.ejrad.2004.11.017. [DOI] [PubMed] [Google Scholar]
- 33.Wang X, Lederman D, Tan J, Wang XH, Zheng B. Computerized detection of breast tissue asymmetry depicted on bilateral mammograms: a preliminary study of breast risk stratification. Acad Radiol. 2010;17:1234–1241. doi: 10.1016/j.acra.2010.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang X, Lederman D, Tan J, Wang XH, Zheng B. Computerized prediction of risk for developing breast cancer based on bilateral mammographic breast tissue asymmetry. Med Eng Phys. 2011;33:934–942. doi: 10.1016/j.medengphy.2011.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nielsen M, Karemore G, Loog M, Raundahl J, Karssemeijer N, Otten JD, Karsdal MA, Vachon CM, Christiansen C. A novel and automatic mammographic texture resemblance marker is an independent risk factor for breast cancer. Cancer Epidemiol. 2011;35:381–387. doi: 10.1016/j.canep.2010.10.011. [DOI] [PubMed] [Google Scholar]
- 36.Chen YW, Lai YC, Hsu CC, Chuang YW, Hou MF. Value of nodal drainage patterns and tumor location from lymphoscintigraphic mapping in detecting axillary sentinel lymph node status in breast cancer: experience at Kaohsiung Medical University Hospital. Kaohsiung J Med Sci. 2005;21:251–257. doi: 10.1016/S1607-551X(09)70197-4. [DOI] [PMC free article] [PubMed] [Google Scholar]