Generalization and transfer of contextual cues in motor learning

Abstract

We continuously adapt our movements in daily life, forming new internal models whenever necessary and updating existing ones. Recent work has suggested that this flexibility is enabled via sensorimotor cues, serving to access the correct internal model whenever necessary and keeping new models apart from previous ones. While research to date has mainly focused on identifying the nature of such cue representations, here we investigated whether and how these cue representations generalize, interfere, and transfer within and across effector systems. Subjects were trained to make two-stage reaching movements: a premovement that served as a cue, followed by a targeted movement that was perturbed by one of two opposite curl force fields. The direction of the premovement was uniquely coupled to the direction of the ensuing force field, enabling simultaneous learning of the two respective internal models. After training, generalization of the two premovement cues' representations was tested at untrained premovement directions, within both the trained and untrained hand. We show that the individual premovement representations generalize in a Gaussian-like pattern around the trained premovement direction. When the force fields are of unequal strengths, the cue-dependent generalization skews toward the strongest field. Furthermore, generalization patterns transfer to the nontrained hand, in an extrinsic reference frame. We conclude that contextual cues do not serve as discrete switches between multiple internal models. Instead, their generalization suggests a weighted contribution of the associated internal models based on the angular separation from the trained cues to the net motor output.

our brain is able to adapt our movements to changes in the dynamics of our body and environment by building and adjusting internal models, thought to be formed by changes to motor primitives (Donchin et al. 2003; Poggio and Bizzi 2004; Thoroughman and Shadmehr 2000). These changes cause an internal model for reaching, acquired at a specific movement direction, not only to guide movements in that direction but also to generalize to neighboring movements (Izawa et al. 2012; Mattar and Ostry 2010). The extent of this generalization reduces as a function of the angular separation from the trained movement direction.

If multiple internal models are learned for the same movement direction, the same set of motor primitives will be involved in the adaptation. This typically causes interference between representations, slowing down or even abolishing learning of the internal models (Caithness et al. 2004).

Contextual cues are known to reduce this interference. Multiple internal models can be learned and recalled in parallel if each of them is uniquely linked to a contextual cue, like wrist posture (Gandolfo et al. 1996), a visuomotor association (Hirashima and Nozaki 2012), a premovement (Howard et al. 2012), or vestibular input (Sarwary et al. 2013).

If multiple internal models can be learned based on contextual cues, how does the brain generalize across these cue representations (“cues” for short)? Analogous to the generalization of an internal model around the trained movement direction, cue-related internal models could also show generalization around the trained cue dimension. If so, one would predict that in a paradigm in which two distinct contextual cues are linked to two distinct internal models, the net generalization represents the combined effect of the two single cues' generalization profiles. In support of this, Ghahramani and Wolpert (1997) reported that when subjects learn two starting point-dependent visuomotor mappings, the generalization of this learning to untrained starting points can be described by a mixture of the two learned maps. The first objective of this study was to test cue-based generalization in human subjects adapting their reaches to two opposite curl force fields each associated with its own contextual premovement cue (Howard et al. 2012).

An internal model acquired for reaching with one hand not only generalizes within that hand but also generalizes to the untrained hand. This transfer is only ∼10% (Joiner et al. 2013), with ongoing debate on whether it takes place in extrinsic (Criscimagna-Hemminger et al. 2003; Dizio and Lackner 1995) or intrinsic (Galea et al. 2007; Wang and Sainburg 2004) coordinates. Following from this notion, our second objective was to test whether and, if so, in which reference frame, the cue-related generalization transfers to the untrained hand.

Our subjects made two-stage reaching movements (Fig. 1): The first movement served as a contextual cue for the perturbing forces in the second movement (Howard et al. 2012). Two premovement directions were uniquely coupled with opposite force fields. After adaptation, we quantified generalization around the trained premovement directions and transfer of this generalization pattern to the untrained hand. In a second experiment we focused on interference between the two cue-related internal models by changing the relative strength of the associated force fields. In a third experiment we determined the generalization pattern around a single association between a premovement cue and a force field.

Fig. 1.

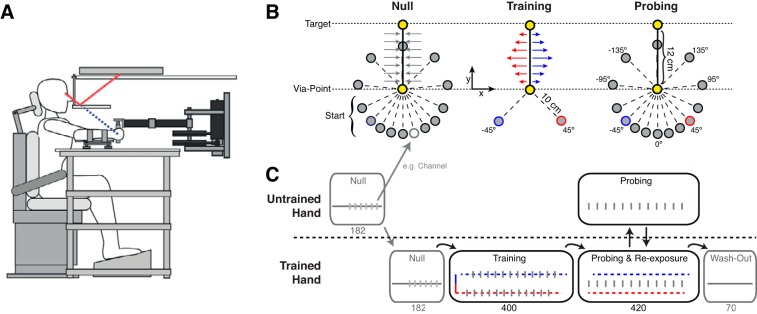
Experimental design. A: setup. Subjects were seated in front of a robotic rig performing reaches while holding the handle of a planar robotic manipulandum (vBot). Both arms were resting on air sleds floating on a glass-top table. Reproduced from Franklin and Wolpert (2008) with permission. B: task. Reaches were performed starting with a premovement from start position to via-point. This was followed by a movement from via-point to target. Premovement directions and perturbation couplings used within the null, training, and probing blocks are shown. C: paradigm: illustration of the force field schedule within each block. Vertical gray bars denote error-clamp trials.

We show that generalization of the contextual premovement cue follows a Gaussian-like decay around the trained direction. Individual cue generalizations interfere at intermediate directions, as revealed by a mixed expression of the two associated internal models. Furthermore, cue-related generalization transfers to the untrained hand in an extrinsic frame of reference, irrespective of whether learning was performed with the dominant or nondominant hand.

MATERIALS AND METHODS

Participants

Experiments were conducted under the general approval for behavioral experiments by the institutional ethics committee. In total 40 (30 women, 10 men) naive subjects between 18 and 28 yr of age (mean = 23.4, SD = 3.0) gave their written consent to participate in the experiments. Reimbursement was provided in terms of payment. All subjects had normal or corrected-to-normal vision and had no known motor deficits. All subjects were right hand dominant with a laterality index of 100 according to the Edinburgh test of handedness (Oldfield 1971).

Apparatus and Setup

Subjects were seated on a height-adjustable chair in front of a robotic rig (Fig. 1A). Both their right and left arms rested on air sleds floating on a glass-top table. Reaches were performed while holding the handle of a planar robotic manipulandum, vBot (Howard et al. 2009). The vBot in combination with the air sled only allows movement in the horizontal plane and measures position and generates forces at the handle that are updated at 1,000 Hz. Stimuli were presented within the plane of movement via a semisilvered mirror, reflecting the display of an LCD monitor suspended horizontally above (Fig. 1A). This configuration also allowed visual feedback of hand position to be overlaid into the plane of the movement. Subjects were prevented from viewing their arm directly. Start position, via-point, and target position were presented as circles of 1.5-cm radius. Current hand position was represented by a red circle of 0.5-cm radius.

Reach Task

Subjects had to perform reaching movements consisting of two stages. The first stage was an unperturbed contextual premovement (10-cm amplitude) from the start position to the via-point. The second stage was a target-directed movement from the via-point to the target position (12-cm amplitude). At the beginning of a trial, start position (in gray), via-point (in yellow), and target position (in yellow) were simultaneously displayed.

Contextual premovement.

Before the start of a trial the subject had to place the hand cursor within the start position and stay still (cursor speed < 5 cm/s for 100 ms). Then, a tone instructed the subject to start the contextual premovement reach. If the reach was initiated before the tone or started >1 s after the tone, an error message appeared on the screen (“wait for beep” or “move after beep”) and the trial was repeated. If the premovement ceased at the via-point with a speed < 5 cm/s, the via-point turned green and a second tone signaled the subject to continue the reach toward the target. If the subject did not stop her/his movement at the via-point, or the premovement had a duration > 500 ms, an error message was displayed on the screen (“stop at via-point” or “move faster”) and the trial was repeated. During the premovement stage of the reach the vBot's motors were always turned off.

Targeted movement.

The start of the targeted movement was defined as the first point at which the hand speed was >5 cm/s after the second tone. If the subject did not initiate the targeted movement within 400 ms after the second tone, an error message was given (“move after second beep”) and the trial was repeated. The end point of the targeted movement was defined as the first point at which the speed < 5 cm/s. If this end point was within the target position, the target turned from yellow to green. If the end point was not within the target position, a feedback message was given (“stop at target”). If the end point was within the target position but the movement duration was >500 ms, a “move faster” feedback message was given. These feedback messages were used to make the reaches more consistent but did not lead to rejection of the trial.

During the targeted movement the motors could be off (null), produce a curl force field [clockwise (CW) or counterclockwise (CCW)], or produce an error clamp (Scheidt et al. 2000; Smith et al. 2006).

A curl force field produces forces that are perpendicular to movement direction and proportional to the reach velocity:

$$\left[\begin{array}{l}{F}_x\\ F_y\end{array}\right]=b\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{l}\stackrel{·}{x}\\ \stackrel{·}{y}\end{array}\right]$$ (1)

in which the damping constant b was set to +13 and −13 Ns/m (equal-strength CW and CCW force fields) or to +16 and −8 Ns/m (unequal-strength CW and CCW force fields, respectively). The sign of b thus determined the direction of the force field (CW or CCW) and was uniquely coupled to a contextual premovement direction.

Error-clamp trials constrain the movement onto a straight line from the start to the target position. The hand was constrained to a straight path with a spring constant of 6,000 N/m and a damping constant of 7.5 Ns/m. Both the curl force fields and error clamps were initiated at the onset of the second tone, from which damping and spring constants were linearly ramped up over 50 ms to avoid instabilities due to discontinuities in the forces.

Experiment 1: Equal-Strength Force Fields

Two groups of eight subjects performed the reach task. One group learned to compensate for the cued force fields with their dominant (i.e., right) hand, and the other group learned this with their nondominant (i.e., left) hand. Start positions for the premovements were defined on a 10-cm-radius circle centered around the via-point. A total of 14 premovement directions (−135°, −95°, −65°, −45°, −30°, −15°, 0°, 15°, 30°, 45°, 65°, 95°, 135°, 180°) were defined on this circle (Fig. 1B). Only the −45° and 45° premovement directions were linked to a force field in the subsequent targeted movement. This 12-cm targeted movement was always in the midsagittal plane, for both the right and left hands.

Subjects started an experimental session using the untrained hand. With this hand they performed 182 null trials (13 batches of the 14 premovement cues) to get accustomed to the passive robot dynamics and the experimental constraints. In each batch the 14 premovement cues were presented in random order. Within these 13 batches, each premovement direction was randomly probed five times with an error clamp to assess baseline force expression during the targeted movement.

The same 182 null trials were repeated with the opposite hand, i.e., the hand that would subsequently learn the associations between the two premovement cues and force fields.

After the baseline performance for each hand was established, a block of 400 adaptation trials followed (group 1: right hand; group 2: left hand) in which subjects learned the premovement cue-to-force field associations. The premovements were made from the −45° and 45° start positions (Fig. 1B), which provided a unique cue to the force field of the subsequent targeted movement (−45° premovement cued the CW field; 45° premovement cued the CCW field). The two premovement cues were presented pseudorandomly, such that a batch of 10 trials contained 4 CW trials, 4 CCW trials, and 2 error-clamp trials, 1 for each premovement cue. The error-clamp trials measured the degree of adaptation to each cued force field.

Subsequently, the generalization of the force fields in relation to the two premovement cues was probed by testing the force expression in the trained and untrained hands for all 14 premovement directions with error clamps. Probe trials were mixed with reexposure trials to keep adaptation at an asymptotic level. Reexposure trials were applied to the originally trained hand for the two trained premovement cues and their respective force fields (Fig. 1B). In each batch of six trials, the third trial was an error-clamp trial with the untrained hand, the sixth was an error-clamp trial with the trained hand, and the remaining four trials were reexposure trials to the trained hand. A message in the workspace display indicated the hand switches. Each hand was supported by its own air sled, and the subject only needed to change the hand that grasped the handle of the vBOT. All 14 premovement directions were probed five times in each hand, resulting in a total of 420 trials (6 × 14 × 5).

Finally, the session ended with a washout block of 70 trials, entailing reaches with the trained hand in all possible premovement directions, each presented five times in random order.

Experiment 2: Unequal-Strength Force Fields

In a second experiment we examined in further detail the interference between the two cue-related internal models. To this end, eight new subjects performed our cued reaching task, but now the opposite force fields had unequal strengths. This experiment was similar to experiment 1; however, we only trained and probed generalization of the dominant right hand. Subjects were exposed to one null block (182 trials), an adaptation block (400 trials), a probing block (140 trials), and a washout block (70 null trials). During the probing block all 14 cue angles (same as in experiment 1) were probed five times. Reexposure trials were mixed in with error-clamp trials such that every second trial was a reexposure trial.

Experiment 3: Single Premovement Cue

In a third experiment, we investigated whether the simultaneously observed generalization patterns of two cue representations relate to the generalization of a single cue after having learned a single force field. We tested 16 right-hand subjects, divided into two groups, using right-hand reaching movements. One group (n = 8) had the −45° premovement cue coupled with a CW force field; the other group had the 45° cue coupled to a CCW force field (field strengths as in experiment 1). Subjects were exposed to one null block (182 trials), an adaptation block (200 trials), a probing block (140 trials), and a washout block (70 null trials). All 14 cue angles (same as in experiment 1) were probed five times during the probing block. Every second trial of the probing block was a reexposure trial.

Analysis

Data were stored for off-line analysis in MATLAB (The MathWorks). Kinematics and dynamics of the targeted movement were the main focus of the analyses. For completeness, we also analyzed the kinematics of premovements to ensure that kinematic differences between the cue movements cannot drive our effects.

Start (t₀) and end point (t_f) of the targeted movement were determined based on a speed threshold of 5 cm/s. In all but the error-clamp trials, deviation of the movement trajectory from a straight line was calculated using the signed hand-path error (E) defined as

$$E={\displaystyle \underset{t_0}{\overset{{}^{t}f}{\int }}x\left(t\right)\cdot \stackrel{\cdot }{y}\left(t\right)dt}$$ (2)

where x(t) is the perpendicular distance of the actual trajectory compared with a straight line joining start position at the via-point and target position and ẏ(t) is the hand velocity in the direction of the target (Franklin et al. 2003).

From the error-clamp trials, we computed an adaptation index (AI) representing the degree of force compensation to the curl force field. For each trial, the theoretical time-varying force generated by the curl field was calculated based on actual hand velocity. This theoretical force was regressed against the force measured in the error clamp, providing a regression coefficient in the range of −1 to 1 (Smith et al. 2006). The sign was introduced to separate the compensatory forces for the CW and CCW curl fields. Adaptation indexes were baseline corrected by subtracting for each premovement direction the mean AI derived in the null trials, recorded in the beginning of the paradigm. In the analyses of experiment 2 we regressed the force expression against the theoretical forces of the strongest force field. As a result, perfect compensation for the weaker force field would result in an AI of 0.5.

To assess learning during the adaptation block we looked at kinematic (E) and dynamic (AI) learning parameters. We used paired t-tests comparing the average of the initial 5 versus final 5 Es and the average of the first 2 versus last 2 AIs. To check whether adaptation levels remained at an asymptotic level during the generalization block, we performed ANOVAs with E or AI as dependent variable.

Learning rates.

To quantify learning rate in the adaptation blocks, we fitted a single-rate exponential function to the pattern of the hand-path error:

$$\text{E}\left(n\right)={\text{E}}_0\cdot e^{-\frac{n}{\tau }}+{\text{E}}_{\text{f}}$$ (3)

in which E₀ + E_f represent the error at the first trial, τ the time constant (in trials) of adaptation, E_f the asymptote error, and n the trial number. As two internal models (CW and CCW) were learned simultaneously, we flipped the sign of the 45° cue hand-path errors and collapsed the data of the opposite field before performing an exponential fit. We used confidence intervals assessed via bootstrapping (1,000) to compare exponential fit values of dominant hand and nondominant hand training.

Generalization curves.

During the adaptation block, the two opposite force fields were trained simultaneously with −45° and 45° premovement cue directions. To infer the generalization around the premovement cues, we assumed the force expressed during the targeted movement, as measured by AI, to fall off in a Gaussian fashion with angular deviation of the premovement from the trained direction. Because each cue is associated with its own internal model, the observed cue generalization curve was regarded as a net expression of two cue-based internal model representations. As a result, we modeled the generalization of the trained cues as two overlapping Gaussian-shaped functions, both centered at their trained premovement direction (−45° and 45°):

$$\text{AI}\left(c\right)=A_{-45}\cdot \exp \left(-\frac{{\left(c-c_{-45}\right)}^2}{2{\sigma }_{-45}^2}\right)+A_{45}\cdot \exp \left(-\frac{{\left(c-c_{45}\right)}^2}{2{\sigma }_{45}^2}\right)+B$$ (4)

in which c represents premovement direction, with c₋₄₅ and c₄₅ referring to the trained directions. The model contains five free parameters: two gain factors A₋₄₅ and A₄₅, which represent the force expression at the two trained cue angles, two width parameters σ₋₄₅ and σ₄₅, which represent the angular extent of generalization around the trained cue angles, and an overall offset term B. This model was fit independently to the AI data from the trained and untrained hands. Statistical differences between model parameters for the trained and untrained hands were assessed with t-tests.

The model was then used to make predictions for the interference levels between internal models of unequal strength in experiment 2. These predictions were based on σ set to the combined average of σ₋₄₅ and σ₄₅ across all subjects obtained from experiment 1. The offset parameter (B) was set to 0, and the gain parameters A₋₄₅ and A₄₅ stemmed from the behavioral data of experiment 2, by averaging the final six AIs of the −45° and 45° cue on an individual subject basis. We also fitted the model to the individual subjects' data with four free parameters (A₄₅, A₋₄₅, B, and σ₋₄₅ = σ₄₅) and then compared the fitted parameters to the parameters we used to make predictions with t-tests.

Finally, a similar but reduced model was used to fit the data of experiment 3, in which the generalization of a single cue in relation to a single force field was investigated. Therefore, the model contained only a single Gaussian-shaped function centered at the trained premovement direction in combination with an offset term.

RESULTS

We performed three experiments. In the first experiment, subjects learned to compensate for two opposite force fields of equal strengths, each cued by a unique premovement direction (−45° or 45°). After learning, we probed the spatial generalization of these premovement cues in the trained hand and their transfer to the untrained hand. In the second experiment, subjects also learned two cue-related (−45° and 45°) opposite force fields, but now of unequal strength. This should result in different interference levels of premovement cues. We used a cue-based generalization model to interpret generalization of both the equal- and unequal-strength force field representations. The validity of this model was further investigated in a third experiment in which we quantified generalization around a single cue in relation to a single force field.

We start with the description of the results of the first experiment in which one group trained with their dominant (right) hand and another group with their nondominant (left) hand (Fig. 1B). After both force fields had been learned, the force expression during the targeted movement was measured for untrained premovement directions, for both trained and untrained hands (Fig. 1C).

Simultaneous Learning of Two Internal Models

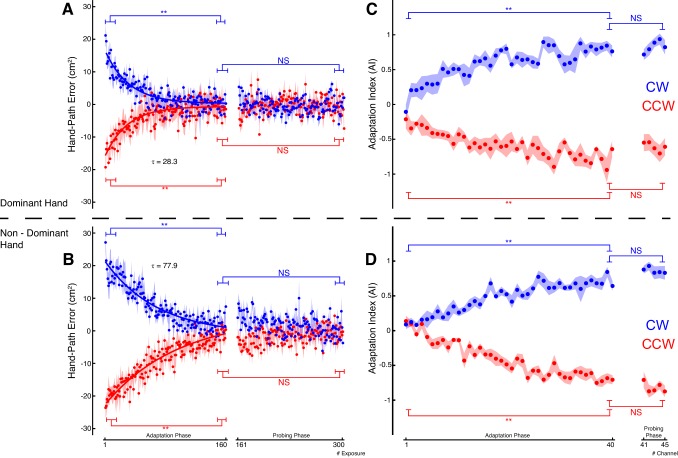
Both the dominant and nondominant hand training groups learned to compensate for the CW and CCW force field. Figure 2, A and B, show the evolution of the hand-path error over the adaptation and generalization phase of the experiment for training with the dominant and nondominant hands, respectively. Both groups show adaptation to the two force fields, which was verified by a significant decrease in hand-path error from the first five to the last five trials of the adaptation block (each P < 0.001). This observation was corroborated by a significant increase in AI, a measure of the compensatory force into the error clamps, over the course of the adaptation (first 2 vs. last 2 trials; each P < 0.001) for both force fields and subject groups (Fig. 2, C and D).

Fig. 2.

Hand-path error (A and B) and adaptation index (AI; C and D) during adaptation and probing phases of the paradigm, averaged across subjects. Shaded areas denote SE. A and C: dominant hand trained. B and D: nondominant hand trained. Blue, clockwise force field (CW); red, counterclockwise force field (CCW).

Figure 2 also suggests that the nondominant hand is slower in learning to compensate for the force fields. To quantify this, we fitted a single rate exponential function to the hand-path error (see materials and methods). For this analysis we collapsed the data of the two cues (−45° and 45°) after changing the sign of the force expression from the 45° cue. The exponential function represents the speed of learning by the parameter τ. Comparing the τ values across groups based on 1,000 bootstraps, the dominant hand (τ = 28.3 trials, 95% CI [13.5 43.1]) learns significantly faster than the nondominant hand (τ = 76.7 trials, 95% CI [55.5 97.9]).

The paradigm was designed such that the level of adaptation, as obtained at the end of the adaptation phase, should remain unchanged during the subsequent block that probes generalization. Figure 2 shows E and AI for the trained cue locations for the trained hand during the probing phase of the paradigm, which both remain virtually constant. To substantiate this observation, we performed a three-way ANOVA on E and AI with the factors block (adaptation, probing), premovement direction (−45°, 45°), and hand (dominant, nondominant). When comparing E averaged across the final 15 trials of the adaptation versus probing phase, there was no significant effect of block [F_(1,57) = 0.09; P = 0.77], premovement direction [F_(1,57) < 0.001; P = 0.99], or hand [F_(1,57) = 0.03; P = 0.87] or any of their interactions (each P > 0.26). Likewise, comparing AI (taking the mean of the final 2 trials of each phase) revealed no significant effects of block [F_(1,57) = 0.02; P = 0.88], premovement direction [F_(1,57) = 0.15; P = 0.7], or hand [F_(1,57) = 0.05; P = 0.83] or their interactions (each P > 0.66). Together, this indicates that adaptation levels indeed remained unchanged during the probing phase, a prerequisite to be able to probe reliably the generalization of premovement cue representations.

Generalization of Premovement Cue Representations

Our data so far show that two internal models of reach dynamics are formed simultaneously, each contextually associated with a distinct premovement cue (−45° or 45°). The next question is whether and how these premovement cue representations generalize to untrained premovement directions.

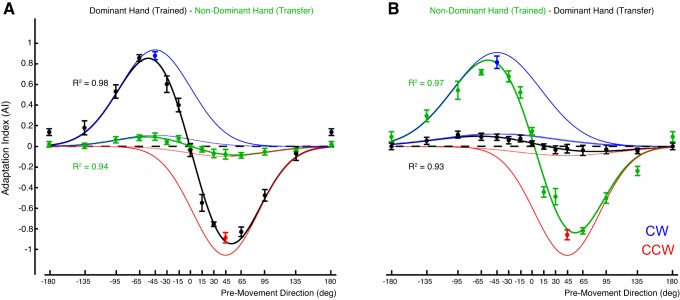
Figure 3 shows the AIs as determined during the error-clamp trials of the probing phase, plotted as a function of premovement direction. Data are organized separately for the two groups (Fig. 3A: training of dominant right hand; Fig. 3B: training of nondominant left hand). Both panels of Fig. 3 show clear generalization of context within the trained hand, i.e., the force expression during the targeted movement depends on the direction of the premovement. The falloff in force expression, as measured by AI, seems steeper between the two trained premovement directions (between −45° and 45° premovement directions) than for premovement directions outside this range (|direction| > 45°). Furthermore, Fig. 3 illustrates that the generalization effects of the premovement representations, as seen in the trained hand, transfer to the untrained hand, irrespective of whether the dominant (right) or nondominant (left) hand was trained. Next we analyze these data in more detail, first for generalization in the trained hand and then for transfer of this generalization to the untrained hand.

Fig. 3.

AI as a function of premovement direction. A: dominant hand training to nondominant hand transfer. B: nondominant hand training to dominant hand transfer. Error bars denote SE. Red and blue dots represent force field trained at premovement directions. The Gaussian fits are superimposed: black, dominant hand;, green, nondominant hand. The model-based generalization curves of the single cues are plotted in blue and red, respectively.

Generalization of Context in the Trained Hand

To quantify the generalization results within the trained hand, we fitted two superimposing Gaussians (see materials and methods), centered at −45° (CW) and 45° (CCW) premovement directions, in terms of gain (A) and width (σ). The fitted net generalization curves are overlaid onto the data points, yielding R² values of 0.98 (P < 0.001) for the dominant and 0.97 (P < 0.001) for the nondominant hand, respectively, in Fig. 3. From the underlying representations, it can now be clearly seen that their overlap explains the steep falloff at the intermediate premovement direction (≈ 0°).

The gain values (A₋₄₅ and A₄₅) indicate the fraction of compensatory force at the trained cue locations, which are comparable to the asymptotic AI values at the end of learning. They are significantly different from zero (P < 0.001) for both the dominant hand (A₋₄₅ = 1.12, SE = 0.05; A₄₅ = −0.92, SE = 0.05) and the nondominant hand (A₋₄₅ = 1.06, SE = 0.08; A₄₅ = −0.96, SE = 0.05).

The widths of the Gaussians, characterizing the generalization curve of the cue representation, range from 39° to 57°. The width of the Gaussians associated with the −45° and 45° cues are not significantly different (dominant: σ₋₄₅ = 40°, SE = 2°; σ₄₅ = 47°, SE = 4°; P = 0.13; nondominant: σ₋₄₅ = 57°, SE = 5°; σ₄₅ = 44°, SE = 4°; P = 0.12). Therefore, we collapsed σ₋₄₅ and σ₄₅ for each subject before comparing the extent of cue generalization in the dominant and nondominant hand training groups. The nondominant hand shows a significantly (P = 0.01) broader generalization for a single premovement cue (σ_nondominant = 51°, SE = 2°) than the dominant hand (σ_dominant = 43°, SE = 2°). This difference can also be observed in Fig. 3, comparing the underlying representations across the trained hands (Fig. 3, A vs. B). The offset term B was not significantly different from zero (P = 0.07).

Context Transfers to Untrained Hand

The next question to be addressed with experiment 1 was whether the observed generalization pattern in the trained hand also transfers to the untrained hand. Apart from the generalization within the trained hand, Fig. 3 also shows the transfer of generalization of premovement cue representations to the untrained hand. Using the same Gaussian mixture modeling approach as for the trained hand, we quantified the force expression in the nontrained hand. There is clear transfer from the trained dominant hand to the untrained nondominant hand as indicated by the force expression, quantified by A, being significantly different from zero for both cues (A₋₄₅ = 0.11, SE = 0.03; A₄₅ = −0.14, SE = 0.03; P₋₄₅ = 0.02, P₄₅ = 0.002). Both cue representations also show the same amount of transfer to the untrained hand (∼10%, P = 0.45). There is also significant transfer from the trained nondominant to the untrained dominant hand (A₋₄₅ = 0.13, SE = 0.02; A₄₅ = −0.12, SE = 0.02; P₋₄₅ = 0.001, P₄₅ < 0.001). Again, the two cue representations are similar in the amount of transfer (∼10%) (P = 0.65).

The width of the fitted Gaussians for the −45° and 45° premovement cues do not differ in the untrained hand, either in the dominant-to-nondominant hand transfer group (Fig. 3A; σ₋₄₅ = 46°, SE = 13°; σ₄₅ = 48°, SE = 9°; P = 0.9) or the nondominant-to-dominant hand transfer group (Fig. 3B; σ₋₄₅ = 66°, SE = 13°; σ₄₅ = 59°, SE = 11°; P = 0.63). The offset B is also not significantly different from zero (P = 0.2).

Finally, we asked in which reference frame this transfer took place. An intrinsic reference frame would suggest that the pattern of cue generalization of the trained hand is mirrored along the midsagittal plane, i.e., around the 0° direction, in the transfer to the untrained hand. Transfer in an extrinsic reference frame would entail that the same, nonmirrored, pattern of generalization would be observed in the untrained hand. Figure 3 clearly indicates the latter, suggesting that transfer of the premovement cue representations across hands occurs in an extrinsic reference frame.

Interference Between Contexts: Force Fields of Unequal Strength

Thus far, we have shown that the pattern of generalization observed in experiment 1 is consistent with a model in which motor output is the weighted sum of separate internal models of the CW and CCW fields. The contribution of each internal model is weighted by a separate Gaussian function, which is tuned to the direction of the contextual premovement. At intermediate premovement directions this results in interference between representations. To further test this model, we performed an additional experiment (experiment 2) testing generalization and interference of cued internal models associated with unequal field strengths (CW = 2 × CCW). The prediction is that the increased output from the internal model associated with the CW field should skew the context-dependent pattern of generalization toward the CW cue direction.

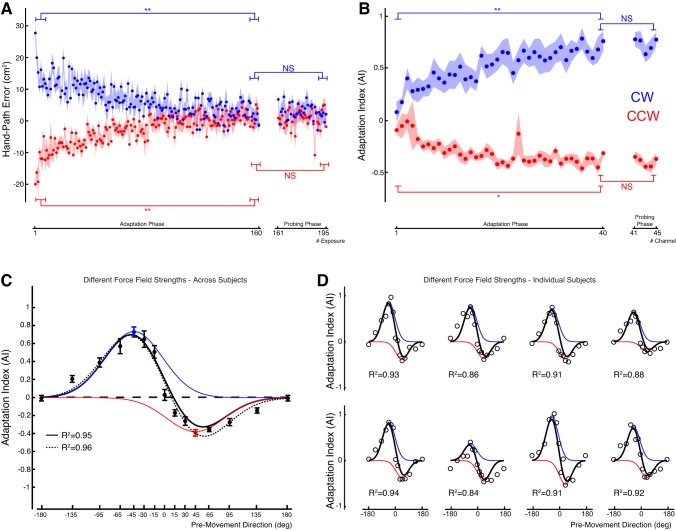
Figure 4A shows that subjects can learn two force fields of unequal strength based on premovement cues. The hand-path error (Fig. 4A) demonstrates a significant decrease over the course of trials (both P < 0.001), which was complemented by a significant increase of the AI (both P < 0.01). A two-way ANOVA on E (averaged across the final 15 trials of each phase) revealed no differences between adaptation and probing blocks [F_(1,28) = 4.25; P = 0.29] or between the two premovement directions [F_(1,28) = 54.98; P = 0.09]. The interaction between the two factors was also not significant [F_(1,28) = 0.03; P = 0.87]. The two-way ANOVA results of the AI (taking the mean of the final 2 trials of the adaptation and probing blocks) revealed no significant difference between the adaptation and probing blocks [F_(1,31) = 18.95; P = 0.14], either. However, there was a significant effect of premovement direction [F_(1,31) = 5936; P = 0.008] on the magnitude of the AI, caused by the different force field strengths. The interaction of block × premovement is not significant [F_(1,31) = 0.004; P = 0.95], confirming that adaptation levels remained constant throughout the probing phase for both force fields.

Fig. 4.

Adaptation with unequal-strength force fields. A: hand-path error of both force fields during adaptation and probing phases: blue, CW; red, CCW. B: AI of both force fields during adaptation and probing phases. C: group average data; error bars denote SE. The model predictions are superimposed: black, net expression; single cue representation in red and blue, respectively; dotted black line, model fit. D: single-subject data (circles) with superimposed model predictions.

The results from experiment 1 were interpreted in terms of a mixture of two Gaussian-shaped generalization curves. Based on the parameters of this model we made predictions for experiment 2 based on Eq. 4. The σ₋₄₅ and σ₄₅ values, obtained independently in experiment 1, did not show a significant difference and were therefore set to their combined average of σ_dominant (43°). The offset parameter B of Eq. 4 was set to 0 for each subject. Gain parameters were derived from the individual subject data, taken as the average of the final six AIs for each cue separately on an individual subject basis.

In addition, we fitted the model from Eq. 4 leaving all parameters free (σ₋₄₅ = σ₄₅, A₄₅, A₋₄₅, and B) on an individual subject basis. Figure 4C shows the model predictions and model fit based on the group average. The prediction (R² = 0.95) and the model fit (R² = 0.96) match closely. Figure 4D shows the model predictions with data points for the individual subjects. The data points closely match with the prediction of the model, with correlations that have R² values > 0.84 (each P < 0.001).

However, it is important to point out that our behavioral data represent the net generalization output. The values of A₋₄₅ and A₄₅ that we used to make predictions were based on the net generalization output and do not necessarily represent the true gain of the underlying cue generalization curves. This explains why the model underestimates the net AI for the 45° cue in Fig. 4C. We also cannot rule out changes of σ and B in experiment 2. Therefore we also fitted the four-parameter model and compared the fitted values to the values we used to make predictions.

The σ and B parameters are not significantly different between the prediction and the model fits (P_σ = 0.48, P_B = 0.26). The A₋₄₅ gain also shows no significant difference (P = 0.98). However, as expected from Fig. 4C, the A₄₅ values directly derived from the AIs are significantly different from those of the model fits (P = 0.03). This confirms that the underlying representation of the force field obtained at the 45° cue is stronger than suggested by the net generalization curve. This can be explained by the interference of the stronger representation for the −45° cue representation.

Further support for altered levels of interference between cues that represent unequal-strength force fields is provided by the angular shift of the zero crossing of the AI. Based on the model, the zero AI crossing point is not at 0° anymore (like in experiment 1) but is now shifted toward the 45° cue, which represents the weaker force field. This is also confirmed in the AI data, where the AI amplitude of the −15° cue is significantly larger than the AI amplitude of the 15° cue (P = 0.008, AI_−15° = 0.49, SE = 0.07 and AI_15° = −0.17, SE = 0.04).

Taken together, the results from the prediction, model fit, and raw data further validate the cue-based weighted contribution of the two internal models that we proposed in experiment 1.

Generalization of a Single Context in the Trained Hand

Experiments 1 and 2 involved two premovement cues associated with their own force field, CW or CCW. Our model could describe the generalization results assuming two independent, superimposing Gaussians. How valid is this assumption? In a third experiment, using two groups of eight subjects, we investigated the generalization of a single cue representation (−45° or 45°) after single force field adaptation.

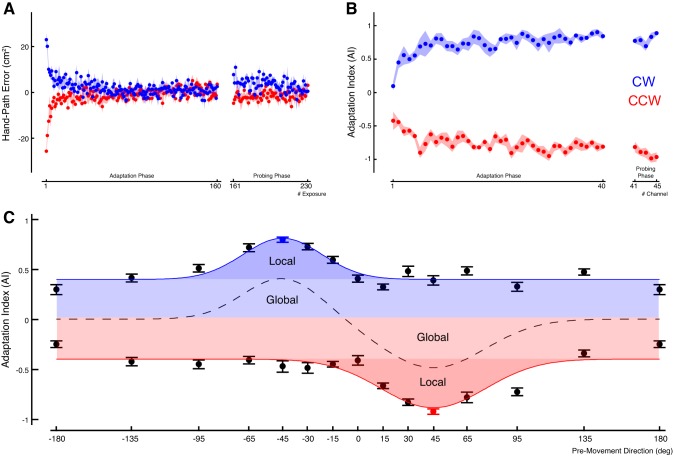
Figure 5, A and B, show that both groups adapted to the force field, indicated by a significant decrease in hand-path error (both P < 0.01) and a significant increase in AI (both P < 0.001). A two-way ANOVA using E (averaged across the final 15 trials of each phase) revealed no significant difference between adaptation and probing blocks [F_(1,28) = 0.02; P = 0.91] or between the trained premovement directions [F_(1,28) = 0.13; P = 0.78] or interaction [F_(1,28) = 1.92; P = 0.18]. This is also supported by the absence of change in AI (taking the mean of the final 2 trials of the adaptation and probing blocks) for the factors of block [F_(1,28) = 2.28; P = 0.37] and premovement direction [F_(1,28) = 0.31; P = 0.68] and the interaction [F_(1,28) = 0.79; P = 0.38].

Fig. 5.

Adaptation and generalization to single premovement cue representations. A: hand-path error of each group adapting to either a CW (blue) or CCW (red) force field. B: AI of both force fields (1 group each). C: generalization around the trained premovement direction. The model fits of single cue representations are superimposed in red and blue, respectively. Group average data, error bars denote SE. Dashed line shows the net sum of the 2 single cue representations.

Our main question concerns the generalization around the trained premovement cue. As Fig. 5C illustrates, the generalization curve is composed of a global (offset B) and a local Gaussian modulation. The overall offset, captured by B, is ∼0.4 (SE = 0.02). Furthermore, the local Gaussian modulation had a gain (A) of ∼0.46 (SE = 0.02) and a width of ∼27.4° (SE = 1.9°), which is significantly smaller than the width estimated in experiment 1 (P < 0.001).

Premovement Kinematics Cannot Explain Generalization

Howard et al. (2012) showed that dwell time, i.e., the time the hand stays in the via-point, influences the expression of an internal model in the subsequent targeted movement. Therefore we checked whether dwell time (the time that the velocity remained below 5 cm/s in the via-point) systematically varied with respect to premovement direction. We also checked whether peak speed and premovement duration (start and end point of the premovement were determined based on a 5 cm/s speed threshold) systematically varied with premovement direction. We performed three ANOVAs, one for each dependent variable (dwell time, peak speed of premovement, premovement duration) with the factors premovement angle, hand, and trained hand. None of the main factors was significant, and they therefore cannot explain our results (Table 1).

Table 1.

ANOVA results of premovement analysis

	Dwell Time	Peak Speed	Duration
Premovement angle	F13,517 = 1.23; P = 0.35	F13,517 = 11.74; P = 0.25	F13,517 = 4.83; P = 0.06
Hand	F1,517 = 0.09; P = 0.81	F1,517 = 0.001; P = 0.97	F1,517 = 0.38; P = 0.63
Trained hand	F1,517 < 0.001; P = 0.99	F1,517 < 0.001; P = 0.99	F1,517 = 0.04; P = 0.88
Premovement angle × hand	F13,517 = 1.83; P = 0.04	F13,517 = 0.96; P = 0.49	F13,517 = 1.7; P = 0.06
Premovement angle × trained hand	F13,517 = 10.52; P < 0.001	F13,517 = 0.31; P = 0.99	F13,517 = 0.28; P = 0.99
Hand × trained hand	F1,517 = 10.95; P = 0.001	F1,517 = 11.89; P < 0.001	F1,517 = 7.32; P = 0.007

Premovement was analyzed with respect to dwell time, peak speed, and duration. None of these main factors showed a significant effect, and they therefore cannot explain our results.

With respect to the interactions, the only consistent significant effect across these three dependent variables is the hand × trained hand interaction. In other words, the right hand performed faster reaches when it was the hand that had learned the force fields (trained hand). If the left hand was trained, it performed the faster reaches. This all stems from the far greater number of premovements made with the trained compared with the nontrained hand (80% vs. 20%).

DISCUSSION

We studied the generalization of contextual premovement cues that enable simultaneous learning of two opposite force environments. Our results show that the force expression based on individual contextual cues follows a Gaussian-like pattern around the trained cue. For equal-strength force fields this results in a steep falloff for cue angles between the two trained cues. For unequal force field strengths this also results in skewing the pattern of generalization toward the strongest field. We further find that these cue-related force expressions transfer both from dominant to nondominant hand and vice versa, in an extrinsic frame of reference. Finally, we show that the generalization of the two simultaneously learned cue representations cannot simply be described as the combined generalization of single cue representations after adaptation to a single force field.

Generalization of Contextual Cues

Our results confirm previous findings (Howard et al. 2012) that premovement cues enable the acquisition of multiple motor memories at the same time. The two cues that were used to provide context for two opposite force fields are single instances from a continuum of possible premovement directions, here across angular space. The novelty of our research is that we tested whether and how these single cue instances generalize along the premovement dimension.

We show that the amount of force expression reduces with angular separation from the originally coupled cue. We quantified the spatial extent of this generalization by fitting two Gaussian-shaped functions to the AIs. The estimated widths of the generalization functions show that the nondominant hand has a wider cue representation compared with the dominant hand.

Supporting evidence for a wider generalization pattern in the nondominant hand is also provided by a recent study that used bimanual movements: Reaches of one arm were perturbed and uniquely coupled to one movement direction of the other arm (Yokoi et al. 2014). After training, generalization was assessed by measuring force expression of the perturbed arm using error clamps, for different movement direction of the unperturbed arm. Their results also revealed a Gaussian-like pattern of generalization, which was wider when the dominant hand was perturbed compared with the nondominant hand. The authors attribute this finding to the perturbed hand, arguing that the dominant hand shows wider generalization than the nondominant hand. However, we favor an alternative interpretation. The untrained hand's movement direction served as a contextual cue, implying that the wider generalization is attributed to the nondominant rather than the dominant hand. What could account for this difference in representation between the two hands?

One explanation is related to the encoding of the contextual cue information. Contextual information derived from the premovement can be derived from visual or proprioceptive signals. Visual input is equivalent for both hands and therefore cannot explain the difference in width. However, proprioceptive signals are likely to differ: It has been shown that the proprioceptive sense of the nondominant hand is more variable than that the dominant hand in the central workspace (Wong et al. 2014). As a result, the nondominant hand's cue information is more variable, which in turn explains a wider generalization pattern.

In our first two experiments we estimated the generalization of individual premovement cues based on a Gaussian model fit to the net generalization pattern. In our third experiment we specifically tested the generalization of a single premovement cue after single force field adaptation. This revealed a global and a local generalization component, which were both different from generalization pattern in the first two experiments, which showed no global component and wider local tuning. We showed that the sum of the independently assessed curves (Fig. 5C) does not capture the net generalization curve obtained in experiment 1. What can explain this discrepancy?

A possible explanation may be found in the actual role of a contextual cue. A contextual cue contains information that can successfully aid in distinguishing one force environment from another. If there is only one such environment, then a cue may be superfluous to the information provided by the targeted movement through the force field. If the brain considers the cue irrelevant, subjects will always show full expression of their internal model in the targeted movement, irrespective of the premovement direction. However, if the cue is part of the internal model, one could expect a Gaussian falloff as the direction of the cue-movement changes.

Our data show a mixture of both the presence of a global component and the narrower tuning of the local component, indicating the qualitative difference between the information represented by a single premovement cue compared with the information represented if two premovement cues to two opposite force fields are trained.

An alternative explanation may be that the number of premovement cues changes their underlying representation. Support for this notion stems from findings by Thoroughman and Taylor (2005), testing adaptation of reaching movements to perturbing forces that changed directions at different rates relative to the direction of movement. They reported that subjects narrowed the spatial extent of generalization with increasing complexity of the environmental dynamics. In the present case, the increase in complexity is not related to the force field perturbations but originates in the number of cue-related force fields learned. This could explain why generalization is wider for the single cue compared with the more complex dual-cue experiment. Further support comes from a recent study in which the single cue was not an active but a passively induced premovement (Howard and Franklin 2015). The authors observed a global AI of 0.6, which is higher than the present AI of 0.4. This larger extent of generalization suggests that the complexity of the environment is lower with passive compared with active premovements.

Transfer of Cue-Related Internal Models

We also show that contextual premovement cues transfer to the untrained hand in an extrinsic reference frame, consistent with findings of Criscimagna-Hemminger et al. (2003) and Joiner et al. (2013). This suggests that the internal model and its associated contextual cues share similar underlying representations, although we do not want to claim that a single reference frame is involved. Indeed, recent work has demonstrated that generalization takes place in a mixture of many reference frames (Berniker et al. 2013). In this light, our paradigm only unveiled the net result of multiple underlying reference frames, which appeared to be the extrinsic reference frame.

The present results also speak to the debate about the direction of transfer. Some studies have suggested that internal models are transferred from the dominant to the nondominant hand but not vice versa (Criscimagna-Hemminger et al. 2003; Sainburg 2002). Our results clearly show transfer in both directions, using a similar adaptation task. What could give rise to this discrepancy?

Studies that showed an asymmetry of transfer across hands used the learning rate as an indicator of transfer (Criscimagna-Hemminger et al. 2003; Sainburg 2002). In these studies, one hand is first exposed to a force field block and subsequently the opposite hand (learning rate paradigm). If transfer of learning between hands occurs, the subsequent opposite hand should be faster in learning compared with naive, which is what they found for the nondominant but not the dominant hand. In our paradigm we assessed transfer by using error-clamp trials, thereby avoiding any exposure of the untrained hand to the force field. Using this way of testing, we found that ∼10% of the learned internal model transferred to the untrained hand, irrespective of hand dominance. We suggest that this difference in transfer can be explained by how it is tested.

If one tests transfer based on increased learning rate, there are two possible ways of how transfer could be revealed: First, learning of the opposite hand could start from a reduced initial kinematic error, caused by the 10% compensatory force transferred from the trained hand, but with the learning rate itself untouched. However, 10% compensatory force is small, and could easily go unnoticed if not specifically tested using error clamps as we did here.

Second, initial errors might start from the same level as naive, but the reduction of these errors, i.e., learning rate, is ramped up. It was recently shown that the history of errors influences the learning rate (Herzfeld et al. 2014). This means that if errors are experienced during testing of transfer, as in a learning rate-based transfer paradigm, the learning rate itself can be influenced by previously experienced errors. However, because we used error clamps, our subjects never experienced any errors while testing transfer. This line of reasoning would suggest that in a learning rate paradigm past errors from the trained hand are incorporated differently with respect to transfer—i.e., they are incorporated in dominant hand learning and ignored in nondominant hand learning. How could this be explained?

One possibility could be that the uncertainty of the observed errors is part of the internal representation of past errors. In force field learning one source of error is detected through proprioception. Proprioception of the dominant hand is known to be more precise than that of the nondominant hand (Wong et al. 2014). As a result, the internal representation of past errors from the dominant hand may be more precise than that of the nondominant hand. This difference in precision may explain why the internal model of errors of the nondominant hand has little effect on the learning rate of the dominant hand. Conversely, the nondominant hand benefits from the more precise internal representation of past errors of the dominant hand, increasing the learning rate of the nondominant hand.

Alternatively, the difference in learning rate paradigms can also be explained by the suggestion that dominant and nondominant hands respond differently to errors (Shabbott and Sainburg 2008). This could explain why learning rate studies only reported unidirectional transfer, while our study based on error clamps shows a clear bidirectional transfer between hands.

Learning Rate Differences Between Dominant and Nondominant Hands

We show that the dominant hand is faster in learning cue-based internal models compared with the nondominant hand—most prominently seen in error-clamp trials. One might argue that this difference in learning rate is caused by differences in the specialization of the dominant and nondominant hands. The nondominant hand may rely more on impedance control and therefore shows less force in the channels, whereas the dominant hand may rely more on feedforward force control (Sainburg 2002). Alternatively, the learning rate differences could be related to the wider generalization in the nondominant hand compared with the dominant hand. Internal models with broader generalization curves show more interference, which would slow down learning. This explanation is in line with the finding of Yokoi et al. (2014) of a slower learning rate when the nondominant hand codes for context while the dominant hand is exposed to multiple force fields.

Implications for Models of Sensorimotor Learning

Several computational models of motor adaptation have been proposed in the past. However, very few models contain a notion of context that would enable learning of multiple internal models.

The modular selection and identification for control (MOSAIC) model, proposed by Haruno et al. (2001), entails two parts within its architecture: one part enables internal model selection prior to movement onset, and the other permits dynamic selection during movement execution. Lee and Schweighofer (2009) proposed a two-state model containing a fast process (fast learning, fast forgetting) and a slow process (slow learning, slow forgetting) arranged in a parallel architecture to update the beliefs about the perturbations. Their model uses contextual cues to switch between the states associated with the slow process. Thus, in both models, contextual cues serve as discrete switches to select one of multiple internal models.

Only the modular decomposition model proposed by Ghahramani and Wolpert (1997) contains a notion of cue generalization but lacks a notion of the learning process. In their study, two unique start positions were coupled to opposite visuomotor mappings. After training, generalization was tested at untrained starting locations. The authors showed that a mixture of Gaussian representations around the trained starting locations could explain the observed pattern of generalization. The present results suggest that their conclusions also apply to force field learning, even with cues that are not part of the perturbed movement itself. In addition, the findings of our second experiment, with unequal force field strengths, show that the mixture proportion of the two internal models is preserved along the premovement dimension (i.e., the generalization width remains the same) but that the difference in peak force of the internal models results in a behavioral shift of the generalization curve.

In conclusion, we show that two cue-related internal models are weighted along the cue dimension, modulating a single internal model's contribution to the net motor output. In addition, we show that the untrained hand has access to this representation of internal models and cues in an extrinsic reference frame.

GRANTS

This work was supported by an internal grant from the Donders Centre for Neuroscience and by the European Research Council (EU-ERC-283567), an EU-FP7-FET grant (SpaceCog 600785), and the Netherlands Organization for Scientific Research (NWO-VICI: 453-11-001 and NWO-VENI: 451-10-017).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.M.E.S., L.P.J.S., and W.P.M. conception and design of research; A.M.E.S. performed experiments; A.M.E.S. and L.P.J.S. analyzed data; A.M.E.S., D.F.S., L.P.J.S., and W.P.M. interpreted results of experiments; A.M.E.S. prepared figures; A.M.E.S. drafted manuscript; A.M.E.S., D.F.S., L.P.J.S., and W.P.M. edited and revised manuscript; A.M.E.S., D.F.S., L.P.J.S., and W.P.M. approved final version of manuscript.