A Scalable Approach for Protein False Discovery Rate Estimation in Large Proteomic Data Sets

Abstract

Calculating the number of confidently identified proteins and estimating false discovery rate (FDR) is a challenge when analyzing very large proteomic data sets such as entire human proteomes. Biological and technical heterogeneity in proteomic experiments further add to the challenge and there are strong differences in opinion regarding the conceptual validity of a protein FDR and no consensus regarding the methodology for protein FDR determination. There are also limitations inherent to the widely used classic target–decoy strategy that particularly show when analyzing very large data sets and that lead to a strong over-representation of decoy identifications. In this study, we investigated the merits of the classic, as well as a novel target–decoy-based protein FDR estimation approach, taking advantage of a heterogeneous data collection comprised of ∼19,000 LC-MS/MS runs deposited in ProteomicsDB (https://www.proteomicsdb.org). The “picked” protein FDR approach treats target and decoy sequences of the same protein as a pair rather than as individual entities and chooses either the target or the decoy sequence depending on which receives the highest score. We investigated the performance of this approach in combination with q-value based peptide scoring to normalize sample-, instrument-, and search engine-specific differences. The “picked” target–decoy strategy performed best when protein scoring was based on the best peptide q-value for each protein yielding a stable number of true positive protein identifications over a wide range of q-value thresholds. We show that this simple and unbiased strategy eliminates a conceptual issue in the commonly used “classic” protein FDR approach that causes overprediction of false-positive protein identification in large data sets. The approach scales from small to very large data sets without losing performance, consistently increases the number of true-positive protein identifications and is readily implemented in proteomics analysis software.

Shotgun proteomics is the most popular approach for large-scale identification and quantification of proteins. The rapid evolution of high-end mass spectrometers in recent years (1–5) has made proteomic studies feasible that identify and quantify as many as 10,000 proteins in a sample (6–8) and enables many lines of new scientific research including, for example, the analysis of many human proteomes, and proteome-wide protein–drug interaction studies (9–11). One fundamental step in most proteomic experiments is the identification of proteins in the biological system under investigation. To achieve this, proteins are digested into peptides, analyzed by LC-MS/MS, and tandem mass spectra are used to interrogate protein sequence databases using search engines that match experimental data to data generated in silico (12, 13). Peptide spectrum matches (PSMs)¹ are commonly assigned by a search engine using either a heuristic or a probabilistic scoring scheme (14–18). Proteins are then inferred from identified peptides and a protein score or a probability derived as a measure for the confidence in the identification (13, 19).

Estimating the proportion of false matches (false discovery rate; FDR) in an experiment is important to assess and maintain the quality of protein identifications. Owing to its conceptual and practical simplicity, the most widely used strategy to estimate FDR in proteomics is the target–decoy database search strategy (target–decoy strategy; TDS) (20). The main assumption underlying this idea is that random matches (false positives) should occur with similar likelihood in the target database and the decoy (reversed, shuffled, or otherwise randomized) version of the same database (21, 22). The number of matches to the decoy database, therefore, provides an estimate of the number of random matches one should expect to obtain in the target database. The number of target and decoy hits can then be used to calculate either a local or a global FDR for a given data set (21–26). This general idea can be applied to control the FDR at the level of PSMs, peptides, and proteins, typically by counting the number of target and decoy observations above a specified score.

Despite the significant practical impact of the TDS, it has been observed that a peptide FDR that results in an acceptable protein FDR (of say 1%) for a small or medium sized data set, turns into an unacceptably high protein FDR when the data set grows larger (22, 27). This is because the basic assumption of the classical TDS is compromised when a large proportion of the true positive proteins have already been identified. In small data sets, containing say only a few hundred to a few thousand proteins, random peptide matches will be distributed roughly equally over all decoy and “leftover” target proteins, allowing for a reasonably accurate estimation of false positive target identifications by using the number of decoy identifications. However, in large experiments comprising hundreds to thousands of LC-MS/MS runs, 10,000 or more target proteins may be genuinely and repeatedly identified, leaving an ever smaller number of (target) proteins to be hit by new false positive peptide matches. In contrast, decoy proteins are only hit by the occasional random peptide match but fully count toward the number of false positive protein identifications estimated from the decoy hits. The higher the number of genuinely identified target proteins gets, the larger this imbalance becomes. If this is not corrected for in the decoy space, an overestimation of false positives will occur.

This problem has been recognized and e.g. Reiter and colleagues suggested a way for correcting for the overestimation of false positive protein hits termed MAYU (27). Following the main assumption that protein identifications containing false positive PSMs are uniformly distributed over the target database, MAYU models the number of false positive protein identifications using a hypergeometric distribution. Its parameters are estimated from the number of protein database entries and the total number of target and decoy protein identifications. The protein FDR is then estimated by dividing the number of expected false positive identifications (expectation value of the hypergeometric distribution) by the total number of target identifications. Although this approach was specifically designed for large data sets (tested on ∼1300 LC-MS/MS runs from digests of C. elegans proteins), it is not clear how far the approach actually scales. Another correction strategy for overestimation of false positive rates, the R factor, was suggested initially for peptides (28) and more recently for proteins (29). A ratio, R, of forward and decoy hits in the low probability range is calculated, where the number of true peptide or protein identifications is expected to be close to zero, and hence, R should approximate one. The number of decoy hits is then multiplied (corrected) by the R factor when performing FDR calculations. The approach is conceptually simpler than the MAYU strategy and easy to implement, but is also based on the assumption that the inflation of the decoy hits intrinsic in the classic target–decoy strategy occurs to the same extent in all probability ranges.

In the context of the above, it is interesting to note that there is currently no consensus in the community regarding if and how protein FDRs should be calculated for data of any size. One perhaps extreme view is that, owing to issues and assumptions related to the peptide to protein inference step and ways of constructing decoy protein sequences, protein level FDRs cannot be meaningfully estimated at all (30). This is somewhat unsatisfactory as an estimate of protein level error in proteomic experiments is highly desirable. Others have argued that target–decoy searches are not even needed when accurate p values of individual PSMs are available (31) whereas others choose to tighten the PSM or peptide FDRs obtained from TDS analysis to whatever threshold necessary to obtain a desired protein FDR (32). This is likely too conservative.

We have recently proposed an alternative protein FDR approach termed “picked” target–decoy strategy (picked TDS) that indicated improved performance over the classical TDS in a very large proteomic data set (9) but a systematic investigation of the idea had not been performed at the time. In this study, we further characterized the picked TDS for protein FDR estimation and investigated its scalability compared with that of the classic TDS FDR method in data sets of increasing size up to ∼19,000 LC-MS/MS runs. The results show that the picked TDS is effective in preventing decoy protein over-representation, identifies more true positive hits, and works equally well for small and large proteomic data sets.

MATERIALS AND METHODS

Data Sets and Data Processing

The data basis for this study was a large collection of LC-MS/MS runs along with the derived human protein identification data deposited in ProteomicsDB (https://www.proteomicsdb.org). At the time of writing, this comprised 19,013 LC-MS/MS runs, the majority of which represent two recently published drafts of the human proteome (9, 10). In ProteomicsDB, biological samples are grouped into experiments of varying number of LC-MS/MS runs. Raw MS files from each experiment were searched in parallel using Mascot (Matrixscience, London, UK) (16) and Maxquant/Andromeda (15, 33) against a concatenated protein sequence database containing the UniProtKB complete human proteome (download date: September 5, 2012; 86,725 sequences) and cRAP (common Repository of Adventitious Proteins; download date: September 5, 2012; 113 sequences) as described (9). Briefly, in the Mascot workflow, MS files were processed using Mascot Distiller using peak picking, deisotoping, and charge deconvolution. The resulting peaklist files were searched with the target–decoy option enabled (on-the-fly search against a decoy database with reversed protein sequences), a precursor tolerance of 10 ppm and a fragment tolerance of 0.5 Da for collision-induced dissociation (CID) spectra and 0.05 Da for higher energy collision-induced dissociation (HCD) spectra, an enzyme specificity of trypsin, LysC, GluC, or chymotrypsin (as appropriate), a maximum of two missed cleavages sites, the Mascot ¹³C option of 1 and oxidation of Met as well as acetylation of protein amino terminus as variable modifications. Additional variable and fixed modifications were set as appropriate for individual experiments (e.g. stable isotope labeling with amino acids in cell culture, tandem mass tag, or phosphorylation etc.). In the Maxquant workflow, MS files were searched against the same target–decoy protein sequence database as described above but using the Andromeda search engine. Proteases, variable and fixed modifications were specified as above. Mass accuracy of the precursor ions was determined by the time-dependent recalibration algorithm of Maxquant, and fragment ion mass tolerance was set to 0.6 Da and 20 ppm for CID and HCD, respectively. Further details regarding sample handling and data acquisition can be found in (9). All numerical data required to reproduce the figures in this manuscript as well as the associated protein lists are tabulated in supplemental Table S1. Mascot and Andromeda database search parameters for selected reference data sets detailed in Fig. 4B are listed in supplemental Table S2.

Fig. 4.

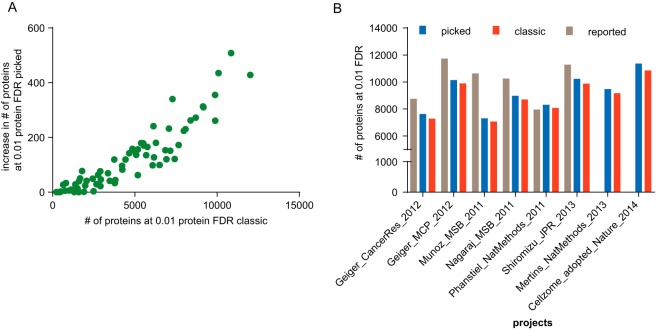
Effects of the picked approach on focused data sets. A, To investigate the effect of the picked approach on studies of varying size, we plotted the increase of confidently identified proteins using the picked approach versus the number of proteins reported by the classic approach for 76 data sets (green dots). The picked approach invariably identifies more proteins than the classic approach and the difference increases with the number of proteins identified in a given data set. B, Reassessment of the number of proteins reported in a number of publications showed that the picked approach (blue) identified more proteins than the classic approach (red). It is also evident that the picked TDS is more conservative than the number of proteins reported in many of these publications (gray).

Procedure for Peptide Length-dependent Score Normalization

Search engine-specific local peptide length-dependent score cutoffs as reported in Wilhelm et al. (9) were calculated as follows. All peptide spectrum matches (PSMs) of the same length were binned separately for Mascot and Andromeda in intervals of one score point and smoothed by a moving average with a window size of five to account for fluctuations likely introduced by the scoring algorithm. The local false discovery rates in each score bin were calculated by dividing the number of decoy PSMs by the number of target PSMs and the resulting distribution was smoothed using a moving average with a window size of five to account for small fluctuations. The minimum score over all bins with a local false discovery rate less than 0.05 was defined to be the local peptide length-dependent cutoff. Normalized scores of PSMs were calculated by dividing the Mascot ion score or Andromeda score by the corresponding search-engine specific local peptide length-dependent cutoff.

PCM Q-value Calculation

For the purpose of this study, a q-value is defined to be the minimum FDR at which a PSM, peptide, or protein will appear in the filtered output list. Such q-values are commonly used to filter a list of observations to obtain a particular FDR. Instead of using all PSMs for this purpose, we chose the PSM with the highest normalized search engine score that represents one peptide sequence detected at one charge state and carrying a particular peptide modification (termed PCM). PCMs for each LC-MS/MS run were then sorted in decreasing order by their normalized Mascot or Andromeda scores. Empirical q-values were calculated by traversing the list from top to bottom and dividing the cumulative number of decoys by the number of cumulative targets. To assure monotonicity a second traversal from bottom to top changes the empirical q-value from the top to bottom traversal to the minimum q-value observed so far. Next, the relationship between logarithmic q-values and normalized scores was modeled by a linear regression using the highest and lowest scoring PCMs with an empirical q-value below 0.01 as fulcrums. Then, all q-values were recalculated using the predicted slope (a) and intercept (b) of the model: −log₁₀ q-value = a * normalized score + b, by multiplying the normalized score with the predicted slope a and adding the predicted intercept b. Last, the resulting list of PCMs was filtered at 1% FDR.

Protein Inference

Peptides matching to either one particular protein isoform (protein unique) or to multiple protein isoforms originating from the same gene (gene unique) are classified as unique peptides. All other peptides are classified as shared (supplemental Fig. S1). Shared peptides were discarded from protein inference. For the purpose of this study, it is not differentiated between the identification of a specific protein isoform and the identification of at least one protein isoform of a gene.

Protein Score Calculation

For data presented in Fig. 1A, protein scores were calculated as the sum of Mascot ion scores of the best scoring peptide matches below 1% PSM FDR. For all other analyses, protein scores were calculated either as the sum of the Q-scores (−log₁₀ transformed q-values) of all matched PCMs that passed a defined q-value threshold or by the maximum Q-score of all PCMs. Again, all methods only considered unique peptides.

Fig. 1.

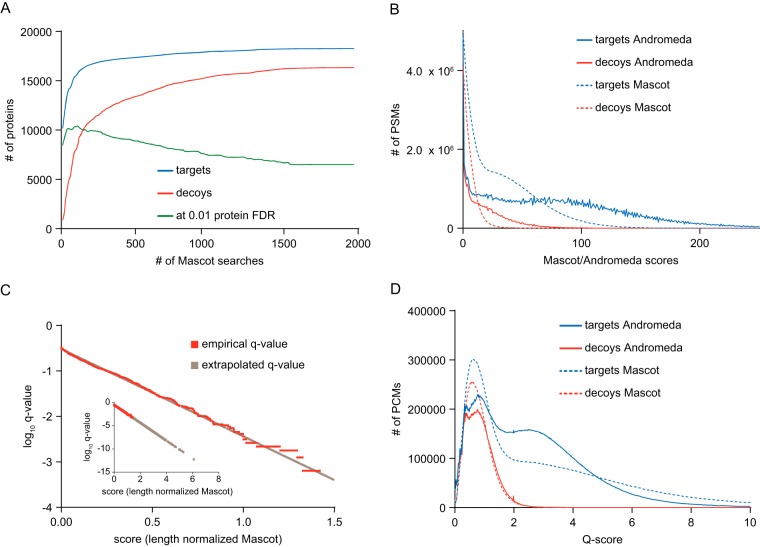
Breakdown of the classic TDS and q-value calculation for data harmonization. A, To illustrate the breakdown of the classic TDS we cumulatively aggregated 1970 Mascot search results (18754 raw files) filtered at 1% PSM FDR and calculated the number of proteins at 1% protein FDR at each step. Protein scores were derived by summing Mascot ion scores of the best peptide matches. The number of target (blue) and decoy (red) proteins saturated quickly, whereas the number of proteins at 1% protein FDR (green) reached its maximum at an early stage but then continuously decreased and stopped at fewer proteins than in the beginning. This indicates that the classic TDS is not working when dealing with large data. B, The Mascot (dashed) and Andromeda (solid) target (blue) and decoy (red) PSM score distributions show vast differences in the scoring scheme precluding their combination without prior normalization. C, To obtain continuous PCM q-values, we used a linear extrapolation model (black) trained on the empirically calculated PCM q-values (orange). The inset shows that after extrapolation, meaningful q-values can be assigned to PCMs that have a higher score than the best decoy. D, Following q-value extrapolation (Qscore is defined as −log₁₀(q-value)), Mascot (dashed) and Andromeda (solid) target (blue) and decoy (red) q-value distributions align well, particularly in the q-value range where most false positive identifications are expected, and thus, allow the combination of the search results.

Protein Q-value Calculation

To estimate protein q-values, proteins were sorted in decreasing order by their score. Empirical protein q-values were calculated by traversing the list from top to bottom and dividing the cumulative number of decoys by the number of cumulative targets. To assure monotonicity, a second traversal from bottom to top changes the empirical q-value to the minimum q-value observed so far. This step was repeated each time a new data set was introduced. For Fig. 1A, we started with the experiment containing the largest number of identifications (IDs) followed by the experiment with the second largest number of IDs and so forth. This was necessary to illustrate that the number of protein IDs at 1% FDR initially rises, reaches a maximum, and then decreases again. For data shown in Fig. 3, data were aggregated in random order.

Fig. 3.

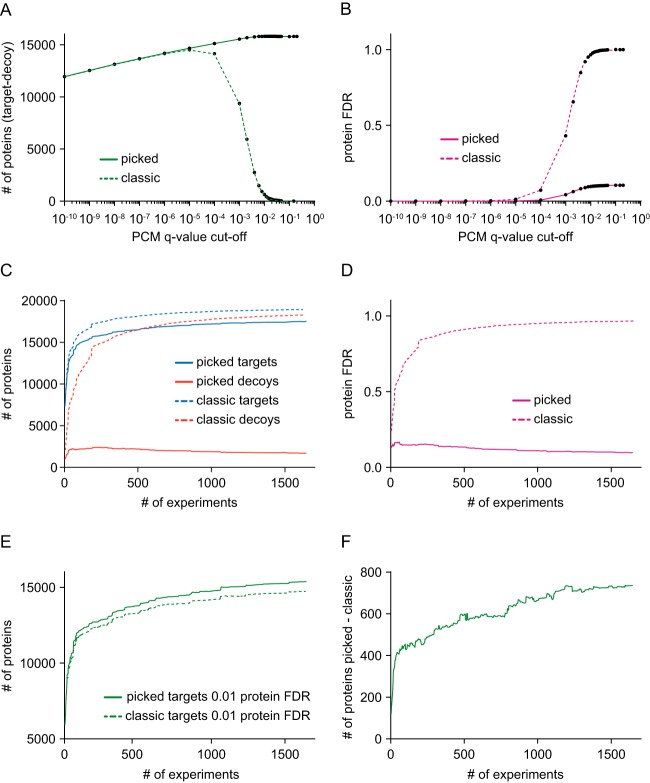
Comparison of the classic TDS to the picked TDS. First, we compared the performance of the picked (solid) and classic (dashed) approach when filtering the PCMs on various FDR cutoffs using the best PCM q-value as protein score. A, With increasing PCM q-value cutoffs, the number of true positive protein identifications (number of target proteins − number of decoy proteins) increases and is comparable between the picked and classic approach. At roughly 10⁻⁴ PCM q-value cutoff, the number of true positive proteins starts to decrease and quickly drops to almost zero for the classic approach, whereas true positive proteins IDs increase further and converges at stable plateau of 15,817 proteins in the picked approach. B, The estimated protein FDR of the classic and picked approach mirrors the trend seen in panel A. Although the estimated protein FDR increases constantly when increasing the PCM q-value cutoff and eventually reaches 100%, the picked approach starts to rise much later and plateaus at roughly 10%. C, Then we compared the classic and picked approach when accumulating experiments. The cumulative number of target (blue) protein identifications of the classic and picked approach increases with more data, whereas the classic approach saturates more rapidly and reports higher numbers of proteins. Conversely, although the number of decoy (red) protein identifications reported by the classic approach saturate and approach the number of target proteins, the number of decoy proteins reported by the picked approach quickly reaches a maximum and decreases when adding more experiments. D, This is again mirrored in the estimated overall protein FDR of the picked and classic approach. E, The number of proteins identified at 1% proteins FDR is increasing in both picked and classic approach, but the picked approach consistently reports higher numbers of proteins. F, The difference between the number of proteins reported at 1% proteins FDR between the picked and classic approach increases with increasing number of experiments reaching close to 800 proteins.

Picked Protein FDR Approach

In contrast to the classic TDS, the picked TDS treats target and decoy sequences of the same protein as a pair. If the protein score for the target (forward) amino acid sequence is higher than that of the respective decoy (reversed) sequence, the target sequence is counted as a hit and the decoy sequence is discarded. Conversely, if the decoy sequence scores higher than the target sequence, it counts as a decoy hit and the target sequence is discarded. This way, no bias is introduced with respect to how target and decoy proteins contribute to the protein FDR. The protein FDR was estimated using the target and decoy hits in the same way as in the classic approach.

RESULTS

Breakdown of the Classic Target–Decoy Protein FDR Model

In large proteomic studies identifying tens or hundreds of thousands of peptides, the classic target–decoy strategy (TDS) model overestimates protein FDR because the higher the number of genuinely identified target proteins gets, the more imbalanced the ratio of potential new target and decoy protein identifications becomes, thus, inevitably leading to an accumulation of decoy proteins and overestimated protein FDR. To illustrate this problem, we used protein identification results from 1974 aggregated Mascot searches (representing a total of >18,000 distinct LC-MS/MS runs) and analyzed how protein identification saturation impacts protein FDR predictions using the classic TDS (Fig. 1A). Search results of each LC-MS/MS run were filtered at 0.01 PSM FDR threshold and all search results were subsequently ranked in descending order according to the number of proteins identified. Individual protein scores were calculated by summing up Mascot ion scores of the best PSM for all unique peptides of that protein. Based on these criteria, the largest search result contained 8255 target proteins and 321 decoy proteins with 7250 identified proteins at <1% protein FDR. We then added the second largest, third largest search result and so on and repeated the protein FDR estimation procedure at each step. Fig. 1A shows that the number of identified target proteins quickly rose when adding further search results and that considerable saturation occurred by the time 100–150 search results had been combined. Decoy protein identifications rose at a slower rate but nevertheless approached the number of target hits as the number of aggregated search results reached completion. As an example, 14,137 target proteins were identified when aggregating the first 50 search results but the protein FDR had meanwhile reached 35%. Adding another 1924 search results increased the target protein IDs by 4137 proteins but also increased the classic TDS FDR to ∼89% implying that only 1936 of all proteins were true. It is obvious, that the latter figure cannot be correct if the first search results alone already contained 7250 proteins at 1% FDR.

The situation could only be partially remedied by introducing a protein FDR filter. When forcing a 1% protein FDR at each aggregation step, protein coverage peaked at the 110th search result (10,433 proteins) but then dropped to 6511 proteins when 1860 further search results were added. Given this clear breakdown of the classic TDS protein FDR approach, we sought to investigate an alternative idea we refer to as the “picked” target decoy strategy (picked TDS, see below). Before introducing this concept, the heterogeneous nature of the data in ProteomicsDB required data harmonization that is described in the following section.

Data Harmonization Using Extrapolated Q-values

The human proteome data deposited in ProteomicsDB comes from a wide variety of biological samples and biochemical experiments and was acquired on different generations of Thermo Orbitrap instruments and using different fragmentation methods as well as resolution settings. Therefore, the data needed to be aggregated and harmonized in a way that allows a consistent and unified treatment of the results. At the time of writing ProteomicsDB contained 18,754 Thermo Orbitrap raw files for which Mascot was used as a search engine and 17,471 raw files for which Andromeda was used. We found profound differences in the score distribution of the two search engines, which is rooted in the differences in the underlying scoring schemes (Fig. 1B). In addition, we and others have observed a bias in Mascot and Andromeda scores for PSMs according to peptide length. To correct for that, we normalized both scores using length dependent thresholds (see experimental section for details and supplemental Fig. S2A, S2B) (9, 21, 33, 34).

We also observed that the target decoy score distributions are strongly dependent on the type of sample analyzed and the type of fragmentation method used (high or low resolution CID, HCD). For instance, dimethyl labeled tryptic digests of human embryonic stem cells measured by low resolution CID yielded very different target–decoy distributions compared with unlabeled tryptic digests of the melanoma cell line A375 measured by HCD (supplemental Fig. S2C, S2D). Thus it is not sensible to use a single threshold value to achieve say 1% PSM FDR in heterogeneous and large data sets. Instead, these thresholds should be derived for each LC-MS/MS run separately (supplemental Fig. S2E, S2F). This is achieved by calculating q-values or posterior error probabilities, e.g. using routines implemented in Maxquant (33) for Andromeda results and Percolator (24) or PeptideProphet (35), for Mascot results. In order to be consistent for both Andromeda and Mascot data sets, we implemented a simple procedure for q-value calculation compatible with both search engines. Instead of using all PSMs for this purpose, we chose the highest scoring PSM that represents one peptide sequence that can carry modifications and is detected with a certain charge state (termed PCM, the best PSM so to speak) because we and others have observed that reducing the redundancy of the PSM information (i.e. many spectra hitting the same peptide) into the best PCMs (here) or the best peptide (21, 36) results in more robust significance-threshold estimates that are less affected by the oversampling of high abundance peptides compared with using PSMs (37). Further, we found it necessary to extrapolate the empirical q-values linearly and to then recompute these values in order to appropriately deal with the fact that the number of decoy hits is very small for high scoring PCMs (Fig. 1C). Without extrapolation, there would be no difference in q-value between say a PCM of Mascot score of 70 and 150 even though the PCM with the higher score should carry more weight than the lower scoring PCM (or peptide for that matter). This procedure allowed us to combine results from the two search engines because the distributions of −log₁₀ transformed q-values (referred to as Q-scores) aligned very well (Fig. 1D), particularly at low q-values where most of the false positives are expected. Target and decoy PCMs that passed the q-value requirement of 0.01 showed only a weak saturation trend as a function of the size of the data set and consequently lead to only a minimal increase in global PCM FDR (supplemental Fig. S3A, S3B).

A “Picked” TDS Approach to Estimate Protein FDR

With the data harmonization in hand, we next investigated overestimation of false positive protein identifications with the classic TDS approach. The PCM q-value cutoff was set to 0.01. For protein scoring, we used the Q-score mentioned above and note that we only used best scoring unique peptide for every protein (the peptide with the best PCM Q-score). Although other more sophisticated strategies exist for calculating protein scores (22, 28), using the best peptide hit or the sum of peptide scores are common practice in the proteomics community. The resulting Q-score distribution of target and decoy proteins according to the classical TDS is shown in Fig. 2A. As one might expect, the bimodal appearance suggests that the lower score range mainly contains false positive protein identifications (35). At the same time, the number of decoy proteins in that score range is massively higher than that of the target proteins clearly illustrating the aforementioned overestimation of false positive proteins.

Fig. 2.

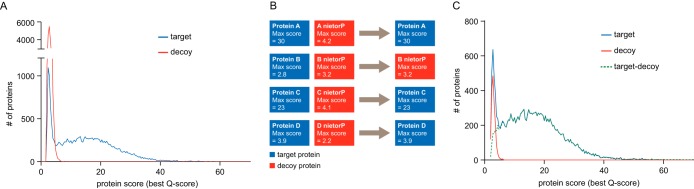
Protein FDR estimation using the classic and picked target–decoy strategy. A PCM q-value cutoff of below 0.01 was used. A, Using the number of decoy proteins from the classic TDS massively overestimates the number of false-positive protein identifications. This is apparent by the almost sixfold higher amplitude of the decoy (red) protein distribution in the low scoring region compared with that of the target proteins (blue). B, The picked TDS treats target and decoy sequences of the same protein as a pair. If the protein score of the target (blue) amino acid sequence is higher than that of the respective decoy (red) sequence, the target sequence is counted as a hit and the decoy sequence is discarded. Conversely, if the decoy sequence scores higher than the target sequence, it counts as a decoy hit and the target sequence is discarded. C, After applying the picked approach, the decoy (red) protein distribution superimposes with the target (blue) protein distribution that allows proper protein FDR estimation using the number decoy proteins, and yields a reasonable distribution of true protein hits (green dashed line), calculated as the difference between the distributions of target and decoy hits.

We therefore investigated an alternative approach that we termed “picked” TDS (Fig. 2B). In contrast to the classic TDS, the picked TDS treats target and decoy sequences of the same protein as a pair rather than as individual entities. If the protein score (Q-score) for the target sequence is higher than that of the respective decoy sequence, the target sequence is counted as a hit and the decoy sequence is discarded. Conversely, if the decoy sequence scores higher than the target sequence, it counts as a decoy hit and the target protein is discarded. This idea was in part inspired by the decoy fusion approach used for peptides (38), and in part by the established practice in the field of using a concatenated target and decoy database in order to select only for those PSMs that have the best score in either the target or the decoy space, rather than selecting hits that pass a score threshold in both target and decoy space (20, 36). This binary or picking approach is symmetrical as it has no built-in bias for the selection of either a decoy protein or a false positive target protein. For the picked TDS, the target distribution is again bimodal (Fig. 2C), but now, the decoy distribution is nearly identical to the low Q-score range of the target distribution as would be expected for well-functioning FDR approach (35). As a result, the distribution of true positive protein identifications (i.e. the difference between the target and decoy hits, dotted green line in Fig. 2C) approaches zero for very low protein scores indicating that the estimation of false positive IDs is accurate. Results also compared favorably to the recently described R-factor correction approach (29) that addresses overestimation of decoy hits by an empirically derived correction factor. The R-factor corrected decoy distribution alternates between positive and negative values for true positive protein identification at low protein scores, but still provides a much more sensible overall picture than the classic approach (supplemental Fig. S4).

Interestingly, when using the sum of Q-scores of all PCMs of a given protein as a score, we observed a much poorer separation between the distribution of false positive and true positive protein IDs (supplemental Fig. S5A, S5B), which might be attributed to the fact that large decoy proteins can accumulate high Q-scores by way of many low scoring peptides.

Performance Evaluation of the Picked Target–Decoy Strategy

We next compared the classic TDS and picked TDS methods for their ability to detect true positive proteins in the aggregated data. As one might expect, when comparing the differences between target and decoy protein identifications at different PCM q-value cut-offs Fig. 3A, very similar numbers of proteins were observed for low PCM q-values. However, at higher q-value cut-offs (starting at ∼10⁻⁴), the number of true positive identifications approaches zero for the classic TDS. Conversely, the number of true positive protein identifications for the picked TDS reaches a stable plateau at 15,817 proteins. The nondecreasing true positive trend as a function of more permissive q-value cutoffs is a hallmark of a well-functioning FDR estimation method (35). When examining protein FDR in the same way (Fig. 3B), the classic TDS protein FDR approaches 1.0 for q-values of 0.001 and higher. Instead, the picked TDS protein FDR plateaus at a maximum of 10%. Interestingly, the picked TDS protein FDR using summed Q-scores showed similar performance suggesting that the picked TDS is a more reliable and generally applicable protein FDR estimation method (supplemental Fig. S5C, S5D).

We next repeated the analysis shown in Fig. 1A and calculated the number of identified target and decoy proteins as a function of aggregating more and more experiments. This time, however, we applied a PCM q-value cutoff of 0.01, used the best PCM for protein scoring as described above, aggregated the experiments in a random order, and combined both Mascot and Andromeda search results. The data was analyzed both using the classic as well as the picked TDS methods. It is apparent, that the picked TDS identifies fewer target proteins than the classic TDS but, importantly, shows a massively lower number of decoy protein identifications too (Fig. 3C and supplemental Fig. S6A). We note that at some point, the decoys increase faster than the targets when using the classic TDS (supplemental Fig. S6B). For the picked TDS, the decoy protein hits show the opposite trend: After an initial very mild increase, the number of decoys actually decreases (supplemental Fig. S6C) implying that addition of new data holds the potential that a protein previously assigned as a false positive (or not identified at all) is supported by a high quality PCM in the new data. The above trends are mirrored in the respective protein FDR calculations (Fig. 3D and supplemental Fig. S6D): As the protein FDR increases for the classic TDS as the data set grows larger, it steadily decreases for the picked TDS. When we then filter the data at 0.01 protein FDR, the number of confidently identified proteins increases for both the classic and the picked TDS as the analyzed data set grows larger Fig. 3E. However, the picked TDS is consistently more sensitive and the absolute difference of identified proteins also steadily increases as the data set grows larger (Fig. 3F). In the complete data set, the classic approach detects 14,638 proteins at 1% protein FDR whereas 15,375 proteins are found with the picked TDS. It is worth noting that the before mentioned R-factor correction approach only partially compensates for this difference (supplemental Fig. S7). We next applied the described data analysis strategy to the subset of data stored in proteomicsDB corresponding to our earlier publication on a mass spectrometry based draft of the human proteome (9). Using the classic FDR strategy 14,035 proteins were observed at 1% protein FDR compared with 14,714 proteins using the picked strategy. Applying the picked strategy without any protein score threshold yielded 17,326 proteins of the target database at 11.3% protein FDR corresponding to 15,290 true positive protein identifications in the data set. When analyzing the complete current content of proteomicsDB (including the data of the Pandey proteome (10) and a number of further data sets), the number of protein identifications at 1% FDR increased to 14,638 (classic) and 15,375 proteins (picked) respectively. Applying the picked strategy to this combined data set without any protein score threshold yielded 17,518 proteins of the target database at 9.7% protein FDR corresponding to 15,817 true positive protein identifications in the data set (supplemental Table S3).

An interesting detail in the described analysis is the observation that using the best PCM for a protein is very robust with respect to which PCM q-value threshold is applied, whereas the results of protein identification using the sum of Q-scores of PCMs for a protein are much more sensitive to picking an optimal PCM q-value threshold and may completely collapse at high PCM q-values (supplemental Fig. S8). The picked TDS using the sum of Q-scores does however perform as well as the best Q-score approach at a PCM FDR of 0.0001 (supplemental Fig. S8). It is important to note though, that permissive FDR thresholds (e.g. FDR > 0.01) lead to accumulation of false peptide identifications in the data set and might impair other aspects of data analysis such as quantification, identification of post translational modifications, and protein isoforms and therefore should be avoided in practice. Applying too stringent PCM FDR criteria, however, can also impair subsequent analyses, e.g. quantification, because a lot of good peptide data are excluded. Filtering the PCMs for each LC-MS/MS run in the data set to q < 0.01 and applying 1% protein FDR yields 0.13% PCM FDR using the classic TDS and 0.086% PCM FDR with the picked TDS and provides a good balance between peptide coverage and FDR.

In the above sections, we have shown that the picked TDS outperforms the classical TDS for very large data sets. Its utility is, however, already evident for small or medium sized individual studies (Fig. 4A). In no case does the picked TDS result in less protein identifications and, interestingly, the gain in protein IDs becomes larger as the number of protein identifications in a particular study increases. Finally, we applied the picked TDS to the reanalysis of a number of published large-scale protein identification projects (9, 39–45) and found that the picked TDS consistently identified a larger number of proteins than the classic TDS (Fig. 4B). We note though that differences in data processing, the search engine, and database used and other parameters might also contribute to the observed differences to published protein identifications (supplemental Table S2).

DISCUSSION

In this study, we investigated the scalability and performance of the “picked” target decoy strategy for estimating protein false discovery rates in large proteomics data sets. The picked TDS addresses decoy protein overestimation typically observed for the classic TDS and takes into account that the probability of creating a false positive PSM is not equal for all proteins. For example, large target and decoy proteins are more prone to accumulating high scoring random matches and are likely to accrue higher protein scores than small proteins both of which artificially inflates the protein FDR. Other parameters that may give rise to similar or related effects are amino acid composition, the number of measurable proteolytic peptides, the type of protease used, the number of tolerated missed cleavages sites, type of mass spectrometer and fragmentation technique used and so on. All of these can be at least partially addressed by simple data harmonizing steps and conceptually extending the line of reasoning from the commonly employed approach of concatenating target and decoy sequences for database searching, to treating target and decoy versions of a given protein sequence as a pair. For proteins that have PSMs/PCMs in both their respective target and decoy sequences, our algorithm will only “pick” the one with the highest score and discard the other. As shown above, this approach does not create the excess of decoy hits observed for the classic TDS FDR but does not alter the target protein distribution. The almost perfect overlap of target and decoy distributions in the low-scoring region suggests little or no bias and, therefore, explains the superior performance of the picked TDS, in line with prior work on the theoretical treatment of the matter (35). The obtained results also compare favorably to the previously described R factor approach that corrects for over-representation of decoy hits by normalizing the distribution with an empirically derived factor (29). The superior performance of the picked TDS is likely because it avoids a bias intrinsic in traditional target decoy strategies, whereas the R factor approach aims at compensating for this bias using a simple but assumption-based model.

A major shortcoming of any decoy generation method is the uncertainty regarding whether or not a decoy peptide is in fact a decoy peptide. Although this is easily checked by comparing all peptide sequences to the limited target space that is typically used for protein identification (e.g. Uniprot), it is quite difficult to exclude the possibility that a decoy sequence may actually represent a genuine variant of a known peptide sequence or indeed a genuine but so far undetected or modified peptide. Even if this number of peptides may be fairly low, each might contribute one high scoring decoy protein identification and thus increase the protein FDR. If there are more such cases, it may even substantially limit the number of proteins that can be identified in a complete proteome because the control of protein FDR may create a glass ceiling, a barrier that cannot be breached no matter how good the mass spectrometric data may be.

The analysis further revealed that protein scoring using the best PCM score for a given protein performed better than summing up all PCM scores for a protein. This is partly because the latter is more susceptible to protein length bias, and that the inevitable accumulation of low-scoring peptide matches observed in large data sets has a stronger impact on sum-based protein scoring be it the number of PSMs, the search engine score, or posterior error probabilities. Similar observations have lead researchers to adopt the “best peptide” approach, which is conceptually similar to our PCM scoring (22). Applying extremely stringent peptide filters might improve scalability of sum-based protein scoring, however this will come at the loss of protein and peptide coverage.

For both protein scoring approaches (best Q-score or sum of Q-scores), and in contrast to the classic TDS FDR estimate that approaches 100% protein FDR as the data set grows larger, the number of decoy hits is actually reduced upon adding new experimental data when using the picked TDS. This is an entirely expected behavior because a false positive protein identification represented by a low scoring target or decoy hit might “switch” to become a true positive, high scoring target hit when new high quality experimental evidence (i.e. a good tandem MS spectrum) is added to the data set. It is often assumed that adding more data to an already large data set will only add more false positives. This is a misconception, at least as far as whole proteome identification is concerned because the quality of the extra data will determine if a novel protein can or cannot be identified (supplemental Fig. S5C).

In our previous publication on a draft human proteome, (9) we stated that, at the time of writing, the database contained protein evidence for 18,097 of the 19,629 protein coding genes in humans (using the filtering method we described in detail). We further pointed out that we were unable to provide a robust estimation of protein FDR for such a very large data set at that time. The values we report now as a result of applying the picked FDR approach described above provide a more reasonable estimate of the total number of reliably identified proteins in proteomicsDB. To raise awareness that not all protein identifications in proteomicsDB have the same quality and to offer guidance to users of the data, we have recently implemented a “traffic light” system that categorizes the identifications in green, yellow, and red depending on what confidence level the respective IDs attain.

An important conclusion from this analysis is that it should be possible, at least in principle, to identify confidently all proteins in a proteome by accumulating large quantities of high quality LC-MS/MS data provided that all the relevant biological protein sources of an organism have been sampled with sufficient depth. Given the fact that the picked TDS FDR approach performed consistently better than the classic TDS FDR for any size of data, we conclude that this approach is generally applicable and recommend its broad implementation in proteomic software.