Abstract
Neuroimage registration is crucial for brain morphometric analysis and treatment efficacy evaluation. However, existing advanced registration algorithms such as FLIRT and ANTs are not efficient enough for clinical use. In this paper, a GPU implementation of FLIRT with the correlation ratio (CR) as the similarity metric and a GPU accelerated correlation coefficient (CC) calculation for the symmetric diffeomorphic registration of ANTs have been developed. The comparison with their corresponding original tools shows that our accelerated algorithms can greatly outperform the original algorithm in terms of computational efficiency. This paper demonstrates the great potential of applying these registration tools in clinical applications.
Introduction
Neuroimage registration is useful for many neuroimage applications such as statistical quantification of human brain morphometry and computer-aided diagnosis. Neuroimage registration aims at aligning brain images in such a way that the same anatomical structure can correspond spatially by finding an optimal spatial mapping. Given two images, a reference image and a moving image to be registered, the registration problem is to find a transformation that minimizes the disparity by measuring the similarity between the transformed moving image and the reference image. Registration algorithms can be classified as linear and non-linear registration according to the type of transformations they permit.
Image registration often requires a long computational time due to the intensive computation of the transformation and similarity measure, which are considered as the bottleneck of image registration computational cost. Optimization algorithms in high-dimensional spaces are usually complex and time-consuming, which prolong data analysis and limit their use in clinical applications such as image-guided intervention. Using multi-core CPUs is one way to speed up the registration. On the other hand, GPUs have also been widely used for image processing applications including medical registration due to their inherent massive data parallelism [1][2][3][4]. Aiming at solving the computational bottleneck of image registration, some methods have been proposed to accelerate the similarity metric computation on GPU platform. Shams [5] accelerated 3D medical images registration by computing mutual information (MI) as the similarity metric on GPU. For registration algorithm based on MI, histogram computation is an essential component [6]. There have been several approaches to compute the histogram efficiently on the GPUs. Shams et al. [7] maintained a number of sub-histograms in global memory (due to shared memory volume restriction) and sum-up afterwards, or fit a few sub-histograms in shared memory but access the image volumes several times to cover the entire bins. Vetter et al. [8] presented a pre-processing sort to reduce the usage of shared memory and to guarantee coalesced write operations at the same time. For introduction of shared memory please refer [9]. They further facilitated the histogram collisions by allocating more counters for "fat bin" according to the intensity distribution obtained from a low cost one-dimensional histogram of the moving image during the pre-processing phase. For nonlinear registrations, Muyan-Ozcelik implemented a CUDA version of DEMONS registration algorithm [10]. James et al. introduced some GPU implementations of nonlinear registration such as the B-spline method [11]. And Mark et al. developed a open-source software tool NiftyReg for registration on GPU, which implemented a parallel version of the well-known free-form deformation algorithm using CUDA[12].
GPUs also bring opportunities for existing neuroimage registration tools such as FLIRT (FMRIB's Linear Image Registration Tool) [13][14][15]in FMRIB Software Library (FSL), which may be redeveloped and redesigned for a massive multi-processing architecture. FLIRT is demonstrated to be one of the highest robust and widely used linear image registration tools [15]. However, performing FLIRT on single CPU is time consuming. It took about one hour to register two brain volumetric images when it was first proposed in 2001 [14], and now, it still took a few minutes to perform affine registration based on our tests with workstations (2.53G Xeon processor 4GB RAM). To improve the efficiency, Chen [16] implemented the FLIRT algorithm with MI as the similarity metric on GPU. Since correlation ratio (CR) is a more widely used similarity metric in many applications [14], Li presented an accelerated FLIRT for volume image registration with CR as the similarity metric on GPUs [17].
Because linear registration algorithms are still inadequate to align brain structures perfectly, numerous nonlinear registration tools have been proposed, such as FNIRT (FMRIB’s nonlinear image registration tool) [15], SPM[18] and ANTs (Advanced Normalization Tools) [19][20][21]. Built on ITK framework, the ANTs open-source library provides a suite of tools on diffeomorphic normalization, image segmentation and template building, and it is commonly used in the medical image analysis field. According to a review paper [22], ANTs is one of the nonlinear registration methods with top performance. However, computational speed is still an issue for ANTs. It took about one and half hour to perform diffeomorphic registration for two 3D images (voxel resolutions: 256×256×128) on our tests with the workstation (2.53G Xeon processor, 4GB RAM). Because ANTs is rather complex, there is no hardware acceleration for it to the best of our knowledge.
The main contribution of this paper is to achieve fast implementation of the popularly used linear and non-linear image registration tools on the GPU platform. For FLIRT acceleration, the method was proposed in[17] is adopted, which just focused on the accelerating scheme on the linear registration tool FLIRT with CR as the similarity measure. This paper extends it with more experiments about neuroimage registration and further analysis about the accelerated algorithm. For accelerating CR calculation, an array for the reference image is first constructed, which is pre-sorted according to its intensity once on the GPU. Then CR is computed efficiently on the GPU kernel. In addition, we also implement a fast calculation of correlation coefficient (CC) on the GPU for the symmetric diffeomorphic registration of ANTs for non-linear neuroimage registration. For CC calculation on the GPU, 3D volume filtering with surface and texture memory is used. Finally the GPU implementations of both FLIRT and ANTs are extensively evaluated with datasets from public neuroimage databases. Our accelerated algorithms are compared with their original implementations in terms of both registration accuracy and computation efficiency.
Preliminaries
The FLIRT algorithm and Correlation ratio
FLIRT is a linear image registration tool freely available for precompiled binaries for non-commercial use [13]. Given a reference image I, and a moving image J, it uses a multistart, multiresolution global optimization method to find the affine transformation that minimizes the disparity between the reference image and the moving image [14]. It divides the process of searching for the best transformation at four different resolution levels: 8, 4, 2, 1mm. In practice, as in the original FLIRT, images are sub-sampled such that the voxel side-length becomes 1 mm according to their original physical dimensions of each voxel. The 2-, 4- and 8-mm sub-sampled volumes are obtained according to the isotropic 1-mm resolution volume.
For each search in each stage of the FLIRT algorithm, the transformed image J T (J T = J ∘ T) is obtained, and then the similarity metric between J T and I is calculated for all the candidate transformations in the search space, which means that the computation of J T and similarity metric is carried out iteratively.
The CR of two variables P and Q is defined as [23]:
| (1) |
where Var[E(Q | P)] is the part of Q predicted by P, and Var(Q) is the total "energy" of Q. CR measures the functional dependence between P and Q. It takes on values between 0 (no functional dependence) and 1 (purely deterministic dependence).
Given a reference image I, and a transformed image J T, they may be seen as two discrete random variables, and their CR is computed as [23]:
| (2) |
| (3) |
| (4) |
where σ 2 and m are the variance and mean of voxels within Ω in J T, respectively. Ω denotes the overlapping region between the two images, and N is the number of voxels in Ω. Ωi = {ω ∈ Ω, I(ω) = i} is the isointensity set of I and N i is the number of voxels in Ωi. For image registration, the isointensity set of I is computed by the histogram bins of I, Ωi = {ω ∈ Bin[i]}, in which i represents a gray-level of I. Compared with MI, the computation of CR does not require computing 2D-histograms of the images. The computational complexity of CR is O(X) O(nx) instead of O(nxny) for a conventional algorithm for computing MI, X and Y being the number of gray levels in I and J T. Image registration with CR as the similarity metric is able to generate comparably accurate results and shows better robustness at low resolutions, compared with MI as similarity metric [14]. These advantages make CR especially useful for multi-resolution methods such as the FLIRT algorithm.
Symmetric diffeomorphic image registration in ANTs with cross-correlation
The ANTs toolkit provides a hierarchy of transformations with adjustable levels of complexity, regularization, degrees of freedom and behavior as optimizers. Symmetric diffeomorphic image registration in ANTs is based on optimizing and integrating a time-varying velocity field. The map ϕ, over time, denotes a family of diffeomorphisms, ϕ(x,t): Ω×t → Ω, generated by integrating a time-dependent, smooth velocity field, , through the ordinary differential equation(o.d.e.): Ω is the image domain. To construct a symmetric implementation, the diffeomorphism, ϕ, in ANTs is decomposed into two components ϕ 1 and ϕ 2, according to composition property of diffeomorphisms, and the first integral is split into two time intervals reflecting the underlying optimized components of the velocity field. Avants et al define the variational optimization problem driven by CC based on the generalized standard Large Deformation Diffeomorphic Metric Matching (LDDMM) equation[21],
| (5) |
where v(x, t) = v 1(x, t) in t ∈ [0, 0.5],and v(x, t) = v 2(x, 1 − t) in t ∈ [0.5, 1], and
| (6) |
in which I T = I ∘ ϕ 1(x, 0.5), J T = J ∘ ϕ 2(x, 0.5) and is mean value computed over a local (2×r+1)D window centered at each position x in I T, where r, is the neighborhood radius and D is the image dimension.
Calculation of CC is time consuming when done natively, especially for 3D images. To generate CC(I T, J T, x) for each pixel, the following three intermediate values need to be calculated:
| (7) |
| (8) |
| (9) |
where n = (2×r+1)3, is the number of voxels in the local window.
To get the above values, ∑ I T(x i), ∑ J T(x i), ∑ I T(x i)2, ∑ J T(x i)2, ∑ I T(x i)J T(x i) are calculated. When iterating through an image volume voxel by voxel, only a few of the voxels that are used to calculate these five values change, i.e. the voxels in the boundaries of the local window. The sum of most voxel in the local window can be reused to speed up the calculation.
The Proposed Method
GPU accelerated FLIRT with CR as similarity metric
An implementation of the original FLIRT framework specialized for GPUs was designed as in [17]. The sequential search was performed on the CPU, while all the computation-intensive processes such as re-sampling, transformation, interpolation of J and the computation of CR were performed on the GPU. An overview of the GPU implementation is shown in Fig 1. The process started with reading I and J to the global memory in the GPU, as well as binding J to the texture memory. I and J were re-sampled (if of sufficient quality) to an isotropic grid with voxel size 1-mm cubed in the GPU. The re-sampled 1-mm images were down-sampled three times to get the 2-, 4- and 8-mm images successively on the GPU. For each stage, by constructing an array, the subsampled reference image I' was sorted according to its intensity, and then a fast local optimization [5] was done to find the candidate transformations.
Fig 1. Flowchart of the GPU implementation for a stage of FLIRT.
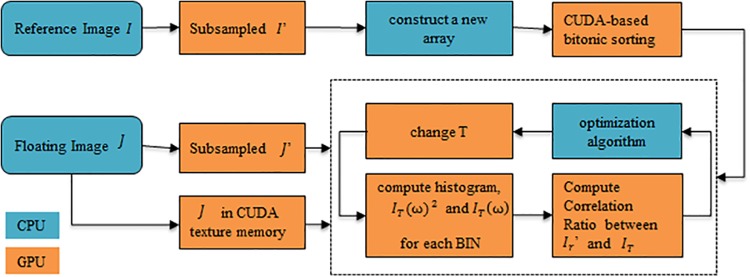
A pre-sorting of I' was required as a preprocessing step in each stage. An array L was constructed, each element of which contained a voxel’s coordinate and intensity. A CUDA-based sorting process [24][25] was applied to L with the intensity value as the key, guaranteeing that all the voxels belonging to the same histogram bin were distributed continuously.
| (10) |
The sorted array L was then passed to the CPU and a small routine was employed to mark the starting (and ending) index of each bin. The starting (and ending) index of each bin was kept in a marked array and transferred to the GPU’s global memory. The preprocessing step was executed once for each stage while the result might be used iteratively during the stage.
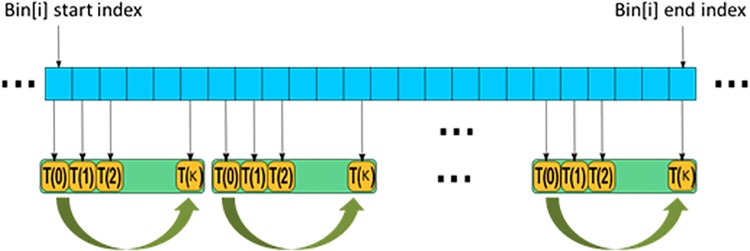
When the sorted array L was available and the array saving the starting (and ending) index of each bin was transferred to the GPU, the CR computation kernel was called. Taking the formulas (2) to (3), , (ω ∈ Bin[i]) and number of voxels within the mapped Ωi were calculated to obtain and m i of those mapped voxels for this bin. The same number of thread blocks as that of the histogram bins was allocated so that each block would traverse the voxels from the start index to the end index for the bin on the sorted data, as shown in Fig 2 as in [17]. The pseudocode of the CR computation kernel is listed in algorithm in S1 Appendix. K (K = WARP_SIZE×WARP_COUNT) threads were allocated in each block, so the blocks need to execute (The end index of Bin[i]–the start index of Bin[i])/K or ((The end index of Bin[i]–the start index of Bin[i])/K + 1) times to process all the voxels from the start index to the end index for the corresponding histogram Bin[i].
Fig 2. Sketch map of a block execution for computation of Bin[i].
After the number of voxels within Ωi, and for each bin were obtained, a CR sum kernel based on the reduction algorithm in CUDA was called for summing those results of each bin to get CR.
GPU-accelerated CC calculation in ANTs
Symmetric diffeomorphic image registration in ANTs was implemented based on ITK framework, which provides lots of iterators to traverse an image. The iterator operator sequentially traverses an image volume, leading to a long calculation time. To explore the possibility of its hardware acceleration, the time consuming calculation of CC was done in parallel according to Eq 6, i. e., each voxel is calculated separately and independently, therefore great time saving is expected.
Based on the source code of ANTs, I T and J T were obtained from ITK image classes for the reference image and the moving image, respectively, transferred to the GPU global memory, and bound to two 3D texture memories. Five 3D surface memories were defined and , , A, B and C were bound to them for calculating CC, respectively, as surface memories in CUDA program environment can both read and write. Once the five values were calculated in the GPU, they were copied to the corresponding CPU memory allocated to store them for the subsequent calculation of ANTs.
, and were obtained by mean filter of I T and J T, respectively. They were implemented by volume filtering. The offsets of voxels in the local window respect to the center voxel were obtained in the CPU and copied to constant memory of the GPU. , , A, B and C were computed according to Eqs 7–9 in a GPU kernel. Each voxel was assigned to one thread, as the calculation is independent. Full description of the kernel is given in algorithm in S2 Appendix.
Experimental Results and Discussion
Datasets
For repeatable comparison, all datasets were downloaded from public databases. 4 datasets (NewHaven_b: Dataset 1, Bangor: Dataset 2, Oxford: Dataset 3, PaloAlto: Dataset 4) were downloaded from [26], and 10 subjects were chosen randomly in each datasets. In addition, the dataset including 18 subjects from IBSR (Dataset 5) with labeled data was also used [27]. For each dataset, a randomly selected image was chosen as the reference image, and the other images were considered as moving images and registered to the reference image.
Implementation environment
A GPU version of FLIRT with CR as the cost function was implemented based on NVIDIA’s GPGPU programming environment, CUDA v6.5. The accelerated FLIRT runs on a workstation with Intel(R) Xeon(R) CPU W3505 @2.53GHz (RAM 4.00GB) and GTX 680 (Workstation 1). The detailed configuration of GTX 680 is listed in Table 1. The original FLIRT in FSL run with CentOS 7 installed on the same workstation.
Table 1. The hardware specification of theworkstastions with GTX680 and GTX 660, respectively.
| Device specification (GPU) | GTX680 | GTX660 |
|---|---|---|
| Number of multiprocessors | 8 | 2 |
| Number of cores per multi-processor | 192 | 192 |
| Total amount of global memory | 4096 MBytes | 512 MBytes |
| Total number of registers available per block | 65536 bytes | 65536 bytes |
| Total amount of shared memory per block | 49152 bytes | 49152 bytes |
| Total amount of constant memory | 65536 bytes | 65536 bytes |
| Maximum number of threads per block | 1024 | 1024 |
| Warp size | 32 | 32 |
| CPU specification | Intel(R) Xeon(R) CPU W3505 @2.53GHz (RAM 4.00GB) | Intel(R) Core(TM) i5-3470S CPU @2.90GHz (RAM 8.00GB) |
The original ANTs and the accelerated ANTs with CC calculation on GPU also run on (Workstation 1). To exam the impact of hardware configuration, the original ANTs and the accelerated ANTs with CC calculation on GPU run on another workstation with Intel(R) Core(TM) i5-3470S CPU @2.90GHz (Memory 8.00GB) and GTX 660 (Workstation 2) as well. The software can be downloaded through the website: http://figshare.com/articles/GPU_accelerated_FLIRT_and_ANTs_zip/1501449.
Registration with FLIRT and the accelerated one
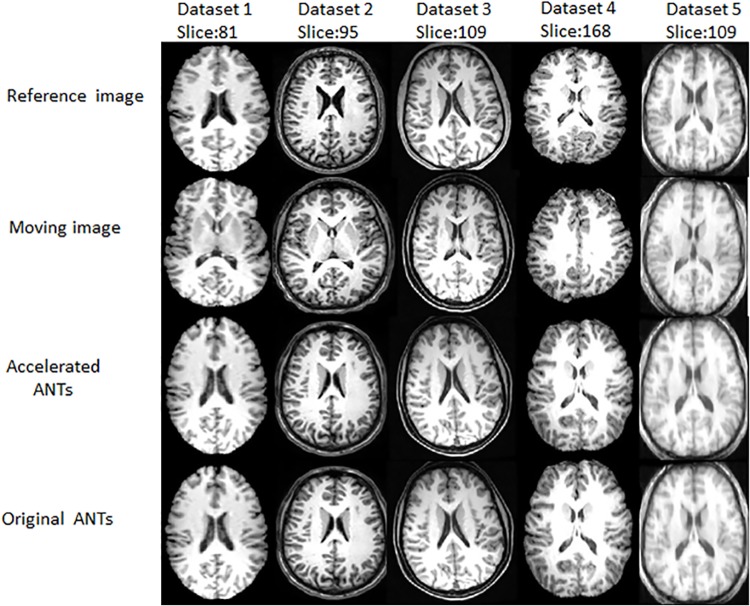
For visual comparison, the slices of the registered results of the 5 datasets by original FLIRT and the accelerated FLIRT with CR as similarity measure are given in Fig 3. The slices with distinct features are displayed for easy visual comparison. Images in the first row are the reference images, images in the middle row are the results obtained by the accelerated FLIRT with CR as similarity measure, while those in the third row are results obtained from the original FLIRT. Fig 3 shows registered results of the accelerated FLIRT appear the same as those of the original tool.
Fig 3. Registered results obtained by the accelerated FLIRT with CR as similarity metric and original FLIRT with CR as similarity metric.
The total runtimes of the accelerated FLIRT and original FLIRT for the 5 datasets are listed in Table 2. Each subject in each dataset was registered to the reference image 3 times. The mean runtime of the subjects in the same dataset is considered as the runtime of that dataset. On Workstation 1, the accelerated FLIRT took less than 30 seconds for all datasets, while the original FLIRT took about 1–2 minutes and scaled linearly with the number of voxels. Table 2 shows that the runtime of our accelerated FLIRT doesn’t increase clearly as the number of voxels of images increase. We get 4 times speedup with the accelerated FLIRT, while 18 times is achieved in [17]. This is because not only the hardware configurations of our workstation is different from that in [17], but also the operating system. They used Nvidia Tesla C2075, which is better than our GTX 680. On the other hand, as original FLIRT can only run in a virtual machine in windows system as in our case, it would take more time than in a linux system as in [17].
Table 2. Mean runtimes for registration of images from the 5 datasets of the original FLIRT and the accelerated FLIRT with Workstation 1.
(Time: seconds).
| Dataset time (s) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Dimensions (Width*Height*Depth) | 131×179×137 | 162×215×157 | 176×192×192 | 256×124×256 | 256×256×128 |
| Size of voxels | 3212513 | 5468310 | 6488064 | 8126464 | 8088608 |
| Original FLIRT | 46.9 | 63.74 | 75.66 | 95.51 | 118.29 |
| Accelerated FLIRT | 13.72 | 23.17 | 25.05 | 25.54 | 24.56 |
| Total speedup | 3.4 | 2.8 | 3 | 3.7 | 4.8 |
The overall performance of a registration algorithm depends on the efficiency of the optimization strategy decided by the iterations required by the algorithm to converge. If a single computation of the similarity metric is considered in one iteration, the total runtime depends on the number of iterations and effectiveness in computing the similarity metric. For FLIRT, it uses a multistart, multiresolution global optimization method to eliminate the occurrence of gross misalignments in affine image registration. Its search space is relatively stable, then the key factor of running time of FLIRT is the time each iteration takes. As CR is calculated in each iteration, the runtime scales with the image sizes when it is calculated in the original FLIRT on CPU. While for the accelerated FLIRT with CR as similarity metric, the total runtime mainly depends on runtime of the sorting process and the time of CR calculation. When calculating CR on GPU, the voxels are grouped according to histogram bin, voxels in the same bin are calculated in parallel, i.e. voxels within the mapped Ωi, , (ω ∈ Bin[i]) for each bin are calculated in a CR computation kernel at the same time to obtain and m i for that bin. Then another CR sum kernel is called to sum the above , (ω ∈ Bin[i]) of all bins to get CR. Due to the above parallel computation of CR, CR calculation consume just increases slightly as the sizes of images increase. Meanwhile, the sorting time is random according to the reference image. Because the time increase due to the reference image size is not very obvious, in addition to the affection of sorting, the total runtime doesn’t scale with the image size clearly.
For GPU kernels, when called, they are executed N times in parallel by N different CUDA threads. And the threads schedule is according to the kernel parameters: grid size, block size and shared memory size. The block size of the CR computation kernel was set to WARP_SIZE*WARP_COUNT according to the configuration of the GPU used, being 32*8 for GTX 680. The grid size was set to the number of bins, which was 256/n used at resolution n (n = 8, 4, 2, 1). Because the number of bins for each stage of the native FLIRT algorithm is fixed, the runtime of CR computation kernel depends on the time required for traversing voxels in each bin, which is decided by the size of the reference image. The shared memory size for each block, local registers for each thread took by the GPU kernels were fixed and far less than the resources GTX 680 may afford, so the limitation of the GPU implementation comes from the global memory size and texture memory size. The original and the 1-, 2-, 4- and 8-mm moving and reference images were all kept in the global memory, as well as the sorted array L.
Registration with ANTs and the accelerated one
The slices of the registered results of the original ANTs and the accelerated ANTs with CC calculation on GPU are displayed in Fig 4. The images in the second row look almost the same as those in the third row, showing the accuracy of the acceleration algorithm. Figs 3 and 4 also show ANTs, as nonlinear registration tools, performs better than the linear FLIRT, as images registered with ANTs are more similar to the reference images than those with FLIRT.
Fig 4. Registered results obtained by the GPU accelerated CC calculation for the symmetric diffeomorphic registration of ANTs and the original ANTs.
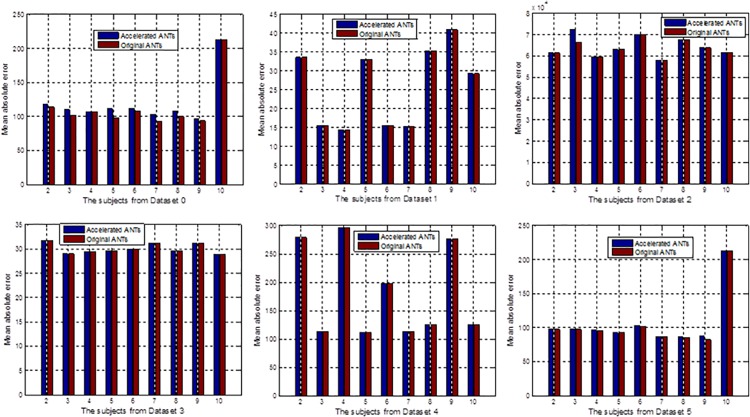
To qualitatively evaluate the nonlinear registration accuracy, for the first four datasets without ground truth label images, mean absolute difference (MAD) between the registered results obtained by the original tools and the reference images, and MAD between the results achieved by the accelerated implementations and the same reference images were calculated and compared in Fig 5. The red bars show the MADs between the registered results using original tools and the reference image, while the blue bars are the MADs between the registered results using the accelerated implementations and the reference image. For the dataset IBSR, for each pair of registration, the resulting transformation was also applied to transform the brain structure label images provided by IBSR. The transformed label images were compared with the ground truth labels of the reference image in terms of structure volume overlap [28]. The structure volume overlap is measured with the Jaccard index:
| (11) |
Fig 5. Registered results of region labeled images provided by the IBSR by the GPU accelerated CC calculation for the symmetric diffeomorphic registration of ANTs and the original ANTs.
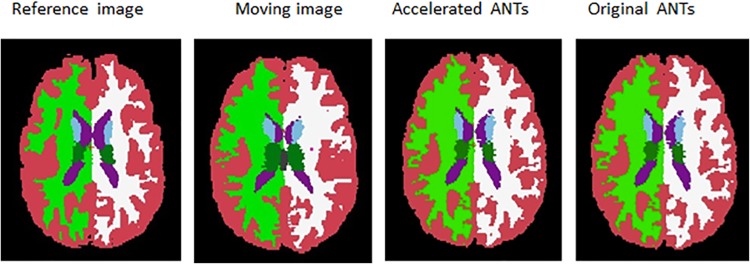
The Jaccard indice are almost the same between accelerated ANTs and original ANTs. Figs 5 and 6 also shows that the accelerated ANTs with CC calculation on GPU is nearly as accurate as the original ANTs. The results are slightly different because NVIDIA GPUs differ from the x86 architecture in that rounding modes are encoded within each floating point instruction instead of dynamically using a floating point control word. And sometimes the results by the accelerated ANTs are even slightly more accurate thanks to the fused multiply-add operator on GPU.
Fig 6. Mean absolute differences between the registered results obtained by original ANTs and the reference image, and those between the reference and the results obtained by the accelerated ANTs with CC calculation on GPU.
For the symmetric diffeomorphic image registration in ANTs, the total runtimes of original ANTs and that with GPU accelerated CC calculation are compared and given in Tables 3 and 4. From Table 3, it can be seen that the accelerated implementation achieved about 113.7 times speed up for CC calculation, and about 2 times speed up in total for all the datasets on Workstation 1. On Workstation 2, the accelerated implementation achieved about 16.7 times speed up for CC calculation, and about 2.2 times speed up in total, as listed in Table 4. Tables 3 and 4 shows the better the graphic card the faster CC calculation is, as the mean speed up times for CC calculation on GTX 680 is about 6.8 of that on GTX 660. GTX 680 has 8 multiprocessors, while GTX 660 only has 2 multiprocessors. However, Workstation 2 is equipment with a more powerful CPU than Workstation 1, so there is not much difference in the overall speed ups.
Table 3. Mean runtimes and speedups for registration of images from the 5 datasets of the original ANTs and the accelerated ANTs with Workstation 1 (Time: seconds).
| Dataset time (s) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Dimensions (Width*Height*Depth) | 131×179×137 | 162×215×157 | 176×192×192 | 256×124×256 | 256×256×128 |
| Size | 3212513 | 5468310 | 6488064 | 8126464 | 8088608 |
| Time for CC in Original ANTs | 1050.79 | 1699.62 | 2002.19 | 3170.54 | 3461.48 |
| Total time for Original ANTs | 1972.19 | 3062.61 | 3526.72 | 5023.48 | 6197.47 |
| Percent of time for CC | 53% | 55% | 57% | 63% | 56% |
| Time for CC in Accelerated ANTs | 11.46 | 17.45 | 19.79 | 28.87 | 29.27 |
| Total time for Accelerated ANTs | 934.81 | 1398.15 | 1566.96 | 3713.58 | 3452 |
| Speedup of CC | 91.69 | 97.4 | 101.17 | 109.82 | 118.26 |
| Total Speedup | 2.11 | 2.19 | 2.25 | 1.35 | 1.81 |
Table 4. Mean runtimes and speedups for registration of images from the 5 datasets of the original ANTs and the accelerated ANTs with Workstation 2. (Time: seconds).
| Dataset time (s) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Dimensions (Width*Height*Depth) | 131×179×137 | 162×215×157 | 176×192×192 | 256×124×256 | 256×256×128 |
| Size (voxels) | 3212513 | 5468310 | 6488064 | 8126464 | 8088608 |
| Time for CC in Original ANTs | 591.31 | 966.86 | 1126.05 | 1742.72 | 1982.59 |
| Total time for Original ANTs | 996.81 | 1616.6 | 1838.79 | 2627.15 | 3039.34 |
| Percent of time for CC | 59% | 60% | 61% | 66% | 62% |
| Time for CC in Accelerated ANTs | 39.37 | 60.83 | 72.76 | 109.88 | 107.26 |
| Total time for Accelerated ANTs | 443.37 | 676.57 | 781.64 | 1011.11 | 1108.66 |
| Speedup of CC | 15.02 | 15.9 | 15.48 | 15.86 | 18.48 |
| Total Speedup | 2.25 | 2.38 | 2.35 | 2.6 | 2.74 |
For the two graphic cards, the detailed configurations of the CC computation kernel are the same. The block size was set to (8, 8, 1), with each thread calculating a voxel, while the grid size is set according to the image volume size and the block size, as that in the example of volume filtering in the CUDA SDK. As listed in algorithm in S2 Appendix, I T and J T are bound to texture memory, and , , A, B and C are bound to surface memory, so the limitation of implementation is the texture memory size GTX 680 and GTX 660 may afford. The offsets of voxels in the local window respect to the center voxel are kept in the GPU constant memory. The size of the offsets depends on the neighborhood radius r set for CC calculation, now r can be set to a maximum 8 as the constant memory sizes of GTX 680 and 660 are both 65536 bytes, while r is usually set 5 according to [20]. In the above experiments, all r are set to 5.
Conclusions
A GPU implementation of FLIRT with CR as the similarity metric is developed. On the GPU device a pre-sorting on the reference image is computed once. Then CR, the default cost function of FLIRT, is calculated efficiently on the GPU without read-write conflict. A GPU accelerated CC calculation for the symmetric diffeomorphic registration of ANTs is also implemented. Comparisons with the corresponding original tools have shown the advantages of the proposed methods in terms of computational efficiency and accuracy. The proposed method improved the usefulness of the original tools for clinical applications. Our future work includes further accelerating deformable registration algorithms, such as the whole algorithms in the ANTs based on the proposed method.
Supporting Information
(DOCX)
(DOCX)
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
The work described in this paper was supported by grants from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No.: CUHK 475711, CUHK 416712, CUHK 473012, CUHK 14113214), a grant from Ministry of Science and Technology of the People's Republic of China (Project No.: 2013DFG12900), and grants from the National Natural Science Foundation of China (Project No. 61233012, and 81201157), and grants from The Science, Technology and Innovation Commission of Shenzhen Municipality (No. CXZZ20140606164105361, JCYJZ20130401112102666), a grant of Shenzhen Basic Research Project (No. CYJ20130402113127511), a grant from Natural Science Foundation of Guangdong (No. S2013010014973) and by project BME-p2-13/BME-CUHK of the Shun Hing Institute of Advanced Engineering, The Chinese University of Hong Kong.
References
- 1. Shams R, Sadeghi P, Kennedy RA, Hartley RI (2010) A Survey of Medical Image Registration on Multicore and the GPU, IEEE Signal Processing Mag., March 2010. pp. 50–60. [Google Scholar]
- 2. Shi L, Liu W, Zhang H, Xie Y, Wang D (2012) A survey of GPU-based medical image computing techniques. Quant Imaging Med Surg. 2(3): 188–206. 10.3978/j.issn.2223-4292.2012.08.02 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Chou C-Y, Dong Y, Hung Y, Kao Y-J, Wang W, Kao C-M, et al. (2012) Accelerating Image Reconstruction in Dual-Head PET System by GPU and Symmetry Properties. PLoS ONE 7(12): e50540 10.1371/journal.pone.0050540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Eklund A, Dufort P, Forsberg D, LaConte SM (2013) Medical image processing on the GPU-Past, present and future, Medical image analysis 17(8):1073–1094. 10.1016/j.media.2013.05.008 [DOI] [PubMed] [Google Scholar]
- 5. Shams R, Sadeghi P, Kennedy R, Hartley R (2010) Parallel computation of mutual information on the GPU with application to real-time registration of 3D medical images, Computer methods and programs in biomedicine 99:133–146. 10.1016/j.cmpb.2009.11.004 [DOI] [PubMed] [Google Scholar]
- 6. Podlozhnyuk V., 64-bin histogram, Technical Report, NVIDIA, 2007. [Google Scholar]
- 7.Shams R, Kennedy RA Efficient histogram algorithms for NVIDIA CUDA compatible devices. In: Proc. Int. Conf. on Signal Processing and Communications Systems (ICSPCS), Gold Coast, Australia, 2007. pp. 418–422.
- 8.Vetter C, Westermann R (2011) Optimized GPU histograms for multi-modal registration, In IEEE International Symposium on Biomedical Imaging, pp. 1227–1230.
- 9.Available: www.bu.edu/pasi/files/2011/07/Lecture31.pdf
- 10.Muyan-Ozcelik P, Owens J D, Xia J, Samant SS. Fast deformable registration on the GPU: A CUDA implementation of demons. Computational Sciences and Its Applications, 2008. ICCSA'08. International Conference on. IEEE, 2008: 223–233.
- 11. Shackleford J, Kandasamy N, Sharp G. High Performance Deformable Image Registration Algorithms for Manycore Processors, 1ST EDITION-ELSEVIER, 2013. [Google Scholar]
- 12.Available: https://www.nitrc.org/projects/niftyreg/
- 13.Available: http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FLIRT
- 14. Jenkinson M, Smith S (2001) A global optimization method for robust affine registration of brain images. Med Image Anal. 5(2): 143–56. [DOI] [PubMed] [Google Scholar]
- 15. Jenkinson M, Bannister PR, Brady JM, Smith S (2002) Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 17 (2): 825–841. [DOI] [PubMed] [Google Scholar]
- 16.Chen S, Qin J, Xie Y, Pang WM, Heng P-A CUDA-based Acceleration and Algorithm Refinement for Volume Image Registration, International Conference on Future BioMedical Information Engineering. 2009. pp. 544–547.
- 17.Ang L, Akash K. Accelerating Volume Image Registration through Correlation Ratio based Methods on GPUs. Digital System Design (DSD), 2014 17th Euromicro Conference on. pp. 82–89.
- 18.Available: http://www.fil.ion.ucl.ac.uk/spm/
- 19. Avants B, Tustison NJ, Song G, Advanced normalization tools (ANTS), Insight J, 2009. [Google Scholar]
- 20. Avants B, Epstein CL,Grossman M, Gee JC (2008) Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal., 12(1): 26–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Avants B, Tustison NJ, Song G, Cook PA, Klein A, Gee JC (2011) A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage 54: 2033–2044. 10.1016/j.neuroimage.2010.09.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, et al. (2008) Evaluation of 14 nonlinear deformation algorithms applied to human brain mri registration, NeuroImage 46 (3): 786–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Roche A, Malandain G, Pennec X, Ayache N (1998) The Correlation Ratio as a New Similarity Measure for Multimodal Image Registration, Medical Image Computing and Computer-Assisted Interventation-MICCAI’98 LNCS, 1496: 1115–1124. [Google Scholar]
- 24.Satish N, Harris M, Garland M (2009) Designing efficient sorting algorithms for many core GPUs, In Parallel Distributed Processing, IEEE International Symposium on, pp. 1–10.
- 25. Chen S, Qin J, Xie Y, Zhao J, Heng P-A (2009) A Fast and Flexible Sorting Algorithm with CUDA, Lecture Notes on Computer Science (ICA3PP09), 5574: 281–290. [Google Scholar]
- 26.Available: http://fcon_1000.projects.nitrc.org/fcpClassic/FcpTable.html
- 27.Internet Brain Segmentation Repository (IBSR) [Online]. Available: http://www.cma.mgh.harvard.edu/ibsr/
- 28. Rohlfing T. Image Similarity and Tissue Overlaps as Surrogates for Image Registration Accuracy: Widely Used but Unreliable. IEEE TRANSACTIONS ON MEDICAL IMAGING, VOL. 31, NO. 2, February 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.