Abstract
In pharmaceutical research, making multiple statistical inferences is standard practice. Unless adjustments are made for multiple testing, the probability of making erroneous determinations of significance increases with the number of inferences. Closed testing is a flexible and easily explained approach to controlling the overall error rate that has seen wide use in pharmaceutical research, particularly in clinical trials settings. In this article, we first give a general review of the uses of multiple testing in pharmaceutical research, with particular emphasis on the benefits and pitfalls of closed testing procedures. We then provide a more technical examination of a class of closed tests that use additive-combination-based and minimum-based p-value statistics, both of which are commonly used in pharmaceutical research. We show that, while the additive combination tests are generally far superior to minimum p-value tests for composite hypotheses, the reverse is true for multiple comparisons using closure-based testing. The loss of power of additive combination tests is explained in terms worst-case "hurdles" that must be cleared before significance can be determined via closed testing. We prove mathematically that this problem can result in the power of a closure-based minimum p-value test approaching 1, while the power of an closure-based additive combination test approaches 0. Finally, implications of these results to pharmaceutical researchers are given.
Keywords: Clinical Trials, Closure-based multiple testing, P-Value Combination Tests, Power, Simulation
1 Introduction
Interesting questions in clinical trials often involve a collection, or family, of inferences, wherein the goal is to make conclusions that are defensible over the entire set. Such inferences may involve comparing several treatment or dose groups, multiple endpoints and/or time points, interim analysis, multiple tests of the same hypothesis, variable and model selection, and subgroup analyses (e.g. Dmitrienko and Offen, 2005). The issue of whether, when, and how to adjust the conclusions of the study to account for multiple simultaneous inferences is referred to herein concisely as the multiplicity issue.
The multiplicity issue arises when pragmatism, technology, and elementary probability theory intersect. The relatively inexpensive ability to obtain additional measurements on an experimental unit (as opposed to obtaining additional experimental units) and the ease by which analyses on these measurements may be conducted in software leads to the inescapable fact that multiple statistical tests, each of which has a nonzero probability of rejecting a null hypothesis, will have a higher "overall error rate" than when any one test is considered individually unless the researcher adapts the usual testing procedure to acknowledge the other tests in the family.
The phrase "overall error rate" is, of course, imprecise. Many approaches to quantifying the notion of overall error have been devised (see Hochberg and Tamhane, 1987; Westfall and Young, 1993; Shaffer, 1995; Hsu, 1996; Westfall et al., 2011; Bretz et al., 2010, for overviews). A common approach is to control the "familywise error rate" (FWER). To define FWER, let V denote the (random) number out of m > 1 hypotheses H1, …, Hm that are falsely rejected (i.e., the number of Type I errors). Then a multiple comparison procedure that controls the FWER at α (in the "strong sense," which is usually what is desired) is one for which . That is, a multiple testing method controls the FWER in the strong sense if the probability of any false rejection is bounded by a regardless of which subset of nulls happens to be true. In the simple case of three hypotheses Hl, H2, and H3, there are eight of states of nature that are possible. All three hypotheses could be true, any of the three pairs could be true, any of the three individual hypotheses may be true, or none could be true. When discussing the FWER of a particular procedure, one is implicitly referring to the maximal FWER among all possible configurations of true and false null hypotheses (Westfall et al., 2011). Because of this, many researchers regard the Bonferroni method (wherein Hi is rejected when pi < α/m) as suboptimal for a large number of hypothesis tests unless one assumes that there are really few real effects (i.e., few false null hypotheses) among the many tests (O’Brien, 1984; Pocock et al., 1987).
Instead of the simple Bonferroni method, pharmaceutical researchers often prefer the versatile and powerful methods of FWER control known based on the closure principle (Marcus et al., 1976). Closure-based testing begins by forming the set of all intersections null hypotheses of the individual (or elementary) hypotheses Hi. Rejection of an elementary hypothesis requires rejection of all intersection hypotheses HI that "include" Hi in the intersection. Any α-level test may be used to test the intersections HI.
In the pharmaceutical industry, methods based on closure are popular because of their incredible flexibility and generality. Under the banner of "closed testing" lie O’Brien-type tests (Lehmacher et al., 1991), fixed-sequence methods (e.g. Wiens, 2003; Huque and Alosh, 2008), gatekeeping methods (e.g. Westfall and Krishen, 2001; Dmitrienko et al., 2007), weighted methods, dose-response methods, and methods that consider multiple endpoints and multiple doses simultaneously (Westfall and Bretz, 2010). The recently popular graphical methods of Brannath and Bretz (2010) are also derived from the closure principle.
We structure the remainder of this article as follows. Section 2 motivates closed testing by reviewing some issues related to multiplicity in clinical trials, aimed at a general audience. Sections 3 through 7 are aimed at more technical audience. In Section 3 we discuss the closure method in more detail. Section 4 presents some recent results on preserving the directional, or Type III, error rate in closed testing. In Sections 6 - 7 we provide some optimality results for p-value combination tests (PVCTs) that may be used to test the subset intersection null hypotheses. We show, using analytic proof and simulation, that the optimality of an intersection test is not inherited when the test is used in the closure setting. Finally in Section 8 we provide general recommendations for the use of these tests in biopharmaceutical research, based on the results in previous sections.
2 Multiplicity in Clinical Trials
Multiplicity is an effect, as real as the effects of covariates and confounding variables, non-response, missing data, and measurement errors that researchers regularly discuss without much controversy. Yet among many practicing scientists, the attitude toward multiplicity adjustments seems to range from "inconsequential nuisance" to "necessary evil." The extra burden of proof on researchers that multiplicity adjustments require remains the primary objection to their use within the larger scientific community. A multiplicity adjustment represents a tempering of the natural desire of researchers to herald any nominally significant result as evidence that supports whatever claim they are trying to make. The "publish or perish" imperative in universities and medical research centers, and the profit motive of pharmaceutical companies and other private enterprises, can force researchers into an ethical bind in some cases, such as with post-marketing investigations for alternative outcome measures or for additional subgroups to support labeling extensions. These additional analyses might be performed as a single trial for efficiency and ethical reasons, and the question of whether to adjust for multiplicity comes down to a choice between the scientific mandate of skepticism and capitulating to the pressure to publish significant results (Bretz et al., 2009).
However, in the pharmaceutical arena, the multiplicity issue is generally better understood if not thoroughly enjoyed. For example, (Scott et al., 2008) state
…we believe the most likely explanation for the lack of riluzole efficacy in our report is that the effect published in the original riluzole studies must be attributed to type I error…Riluzole is an example of how bias toward type I error is propagated when negative results are not routinely reported in the literature (p.12).
Concerns over the efficacy of drugs, especially psychiatric medication, fuel costly lawsuits and public concern over the nature of the clinical trials process (Graham, 2006; Mallinckrodt, 2006; Dyer, 2007; Wisniewski et al., 2009; Wilson, 2010). Although estimates vary by firm and drug class, costs to bring a new drug to market beginning with Phase I trials can range from $868 million to $2 billion (Adams and Brantner, 2006). The consequences of pursuing every apparent significance would logically result in a kind of inverse of Rosenthal’s (1979) "file drawer problem;" rather than potentially informative but non-statistically significant results never being published, spurious relationships would the enter the literature and ineffective therapies would become part of treatment protocols.
Confirmatory Phase III clinical trials represent a critical period for pharmaceutical companies. As the final phase before a drug receives regulatory approval, Phase III trials must provide compelling evidence of efficacy and safety (Westfall and Bretz, 2010). Failing to account for multiplicity can lead to approval of a drug over existing drugs as an improvement, when there is in fact no beneficial effect. Conversely, a drug may appear worse for some side effect when it is indeed not worse at all, preventing the release of a potentially useful drug. Thus, the multiplicity issue has received a good deal of attention from regulatory agencies, who are aware that profit motives can hinder scientific objectivity. The U. S. Food and Drug Administration (FDA) has adopted the efficacy guidelines proposed by the International Conference on Harmonisation (1998, ICH[) which state, in part,
When multiplicity is present, the usual frequentist approach to the analysis of clinical trial data may necessitate an adjustment to the Type I error. Multiplicity may arise, for example, from multiple primary variables…multiple comparisons of treatments, repeated evaluation over time, and/or interim analyses…[A]djustment should always be considered and the details of any adjustment procedure or an explanation of why adjustment is not thought to be necessary should be set out in the analysis plan. (p. 26)
The European Union’s analog of the FDA, the European Medicines Agency, has also released guidelines on the appropriate application of multiplicity in clinical trials (see Committee for Proprietary Medicinal Products, 2002).
Of special concern in pharmaceutical research is the failure of a significant result to replicate in subsequent trials. The concept of replication comprises two types, which Lindsay and Ehrenberg (1993) call "close" and "differentiated." Close replication attempts to reproduce the original conditions in the study as much as possible, using the same techniques, methods of analysis, background conditions, and patient populations populations. Differentiated replication establishes the generalizability of findings and assesses the robustness of the findings obtained in close replications. Differentiated replication in a pharmaceutical context, for example, might suggest additional indications for a drug or additional patient groups. Keeping the concept of replication firmly in mind makes the need for multiplicity adjustment clear. The level of significance invoked in any hypothesis test conducted from a frequentist perspective is an implicit reference to repeated applications of the test on different random samples from the same process wherein the null hypothesis is true. The familywise error rate, in turn, expands the scope of error protection to multiple tests. Inasmuch as replication is central to pharmaceutical science, so should be multiplicity be a central concern.
Several examples of replication failure exist. Fleming (1992) reports that a conclusion of an effect of preoperative radiation therapy on survivability of colon cancer was actually based on a subgroup analysis and did not replicate. King (1995) highlights an example of the financial consequences–a 68% drop in shareholder value–of seemingly promising results from Phase II clinical studies failing to replicate in a Phase III trial. More recently, the issue of replication in genetic association studies has been addressed, with an increasing focus on the issue of chance results (Colhoun et al., 2003). In genetic studies, the multiplicity problem is rampant (Efron, 2004), with myriad genes to be tested, and even multiple tests within genes, e.g., for dominant, recessive, and additive allelic effects (see Westfall et al., 2002).
A main criticism of multiplicity adjustment centers on how the family of hypotheses ought to be formed (O’Neill and Wetherill, 1971; Cook and Farewell, 1996; O’Keefe, 2003). Natural questions arise regarding the spatial and temporal boundaries that govern family creation, and how increasing researchers’ burden of proof affects the progress of scientific inquiry. Indeed, constructing a family of hypotheses is a highly discipline-dependent and ultimately subjective endeavor (Hochberg and Tamhane, 1987; Westfall and Young, 1993; Westfall et al., 2011).Fortunately, guidelines exist for pharmaceutical research: Westfall and Bretz (2010) provide some useful guidelines for selecting families involving primary, secondary, safety and exploratory endpoints in clinical trials.
Related to the issue of determination of family size is the determination of the appropriate error rate to control. Westfall and Bretz (2010) suggest that FWER control, e.g., by closed testing, is essential for multiple endpoints and doses in confirmatory Phase III clinical trials, but that less stringent type I error rate control may be appropriate for pre-clinical, safety, and exploratory research. For example, in high-throughput and genomics research there are typically thousands of hypotheses to be tested, and strict FWER control over the entire family is often considered too conservative. Instead, methods to control the false discovery rate (Benjamini and Hochberg, 1995) or generalized familywise error rate (Korn et al., 2004) are often recommended in these cases. However, our focus is on standard closed testing procedures, and we do not consider these methods in this paper.
Another complicating issue regarding multiplicity adjustment is the Bayesian/frequentist paradigm split. The skepticism inherent in multiple comparisons procedures falls naturally within the Bayesian realm in the form of prior selection. For instance, the statement that motivates the multiplicity argument–"What if all (or many) null hypotheses are true?"–is actually a statement about prior plausibility of the collection of null hypotheses. Bayesians have long held that the appropriate response to the multiplicity problem lies in proper specification of a prior distribution that effectively "shrinks" the most extreme observed effects toward the mean,thereby making them, in a sense, "less significant"(Lindley, 1990). While frequentist methods are similar in the sense that the significances of the most extreme effects also are downplayed, or "shrunk," the degree of shrinkage for the frequentist methods is orders of magnitude more extreme than that of the Bayesian methods using the "usual" priors. But for experiments where multiplicity adjustments are considered appropriate, the "usual" Bayesian priors are inappropriate. Instead, researchers should employ "skeptical" mixture priors that incorporate point probability near zero (Berger and Sellke, 1987; Gonen et al., 2003; Westfall and Bretz, 2010).
The focus of this article is frequentist, not Bayesian. In the next sections, we discuss the theory of the closure method in much more detail and then provide some recent results that we hope will guide its use in clinical trials applications and spur new theoretical developments. Some of the material in the next few sections is more theoretical, but a generally accessible practical summary and conclusions are given in Section 8.
We give particular emphasis to two types of base tests that are prevalent in clinical trials: additive combination (AC) and minimum p-value based (MINP) tests. One example of the former is the O’Brien test (O’Brien, 1984), which has been proposed for analyzing multiple endpoints within a closure setting (Lehmacher et al., 1991). Other examples of the former include the inverse normal sum test and the Fisher combination test, which are popular for the analysis of group sequential trials (Brannath et al., 2002). Closed testing using MINP based methods and their variants is also very popular, particularly for use with graphical-based protocols for testing endpoints and doses sequentially (Brannath and Bretz, 2010). We compare the AC and MINP classes of closed tests in Sections 6 - 7, and make recommendations concerning their use in clinical trials in Section 8.
3 Overview of Closed Testing
To employ closed testing, one first identifies the family of tests (e.g., the set of dose/endpoints or subgroup tests of interest) and then constructs all subset intersection hypotheses HI, I ⊆ M = {1, 2, …, m} involving these tests. The closure family is then , and one rejects Hi at level α if and only if all hypotheses with i ∈ I, are rejected at level α. In multiple testing, an adjusted p-value is the smallest level of significance at which an elementary null hypothesis can be rejected while accounting for multiplicity (Wright, 1992; Westfall and Young, 1993). The closure adjusted p-value for an individual hypothesis Hi is simply . Proof that the closure method controls the FWER in the strong sense is simple and elegant (p. 137 Hsu, 1996).
Closed testing requires in general test evaluations, since there are 2m − 1 subset intersection hypotheses. In many cases, however, shortcuts exist for certain classes of tests (one of which, p-value combination tests, we discuss in this article) that allow either evaluations (Hochberg and Tamhane, 1987; Grechanovsky and Hochberg, 1999; Romano and Wolf, 2005). The two most important conditions are that the test statistic behaves monotonically in the data, and that the critical region is determined by subset size.
The monotonicity requirement allows one to select particular subsets for each cardinality |I| or "level" within the closure tree; the idea in that one need test all of the intersection hypotheses if some intersections will always produce a value of the test statistic that is more extreme than the others of the same cardinality |I|. The additive combination (AC) p-value combination tests we consider later in this article have the property. That is, for an additive combination test statistic CAC (·), CAC (p1, …, pj , …, pm) < CAC (p1, …, pj′, …, pm) whenever pj > pj′. A combination test of the minimum-p (MINP) class rejects for small values of the test statistic CMINP (·), so the monotonicity requirement is instead CMINP (p1, …, pj , …, pm) ≥ CMINP (p1, …, pj′, …, pm) whenever pj > pj′. The equality is required because, by construction, MINPs do not use the magnitude of all the p-values directly but only their relative ordering. For example, using the Bonferroni global test, we reject if mp(1) ≤ α, with p(1) the minimum of the set of p-values p1, …, pm, does not change if p(2), …, p(m) change in magnitude.
The second condition for the closure shortcut is that the critical value depends on subset size |I| alone; this is the "cardinality" condition. This condition, along with monotonicity, prunes the closure tree by requiring a test of only one of the subsets for a given cardinality |I|. If the critical value of a combination test for cardinality |I| is constant for fixed |I|, and the combining functions are monotonic in the pi, then for each level in the tree, only the subset that produces the smallest (for ACs) or largest (for MINPs) test statistic must be examined for each subset of size k = 1, 2, …, m. Such subsets are "hurdles" in the sense that a test of these subsets must be significant if an elementary hypothesis is to be rejected.
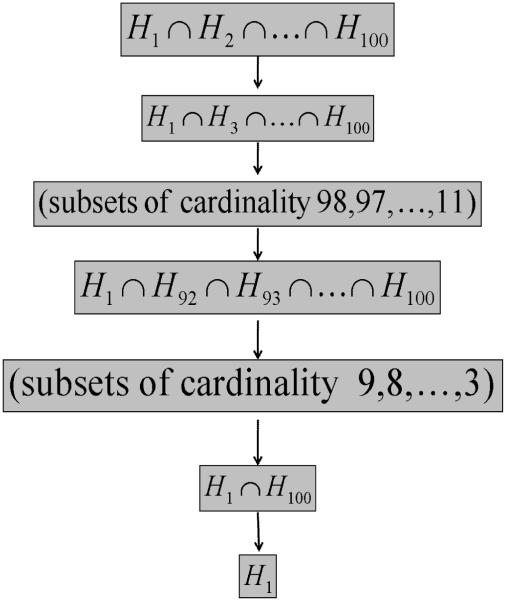
Operationally, the shortcut proceeds as follows. Without loss of generality, relabel the individual hypotheses and p-values according to the order of the p-values, so that H1 has p-value p1 ≡ p(1), H2 has p-value p2 ≡ p(2), etc. Now consider testing an individual Hi, with p-value pi, using closure and a PVCT as the test of the intersection hypotheses. The closure shortcut requires that we identify the "hurdle" subset for each cardinality k = 1, 2, …, m. This subset produces the largest combined p-value and is the "hurdle" that must be rejected if Hi is to be rejected. To describe the closure shortcut in its full generality requires that we consider two cases for each k : the case where pi is among the k largest p-values ("Case 1") and the case where pi is not among the k largest p-values ("Case 2").
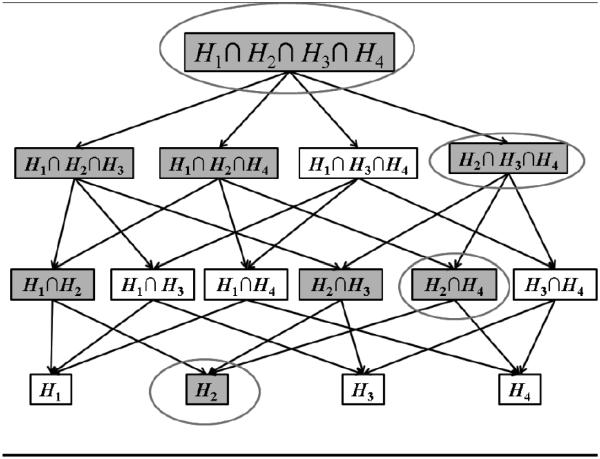
An example of the shortcut is shown in Figure 1 for testing H2. We assume again for ease of exposition that the hypotheses are labeled according to the order of their p-values. To reject H2, all intersection hypotheses that involve H2 must be rejected. At each cardinality level in the tree, however, only the intersection hypothesis that will produce the largest combined p-value needs to be tested; if that intersection hypothesis is rejected, all other intersections at that level can automatically be rejected because each one has the same critical value. Thus the test of H2 can be performed in four steps, signified by the ovals, rather than eight. Shortcut procedures are discussed further in Brannath and Bretz (2010).
Figure 1.
The closure hierarchy for m = 4 hypotheses illustrating the shortcut. All circled hypotheses must be rejected if H2 is to be rejected.
4 Closed Testing and the Directional Errors Problem
That closed testing methods control the FWER is simple to prove. Less well known is whether such methods control directional errors. Such an error occurs when a hypothesis is correctly rejected, but one misclassifies the sign of the effect. Controlling the directional error rate is a natural concern in pharmaceutical research, where one wants to know if a drug makes you better and/or has side effects.
To formally define the problem in a general setting, let Hi : θi = 0 be point null hypotheses tested against (or the one-sided alternative ), i = 1, 2, …, m. Given an estimate and a rejection of the null hypothesis, the researcher would like to conclude the sign of θi using the sign of . A directional error occurs when Hi is rejected but when the researcher concludes when in reality . Letting V1 be the (random) number of true null hypotheses rejected and V2 be the (random) number of sign errors, an error rate of interest to researchers is the combined error rate CER = Pr(V1 > 0 ∪ V2 > 0), the probability of making at least one Type I error or making at least one Type III error.
Control of the CER by controlling the FWER is not automatic. Shaffer (1980) investigates Holm’s (1979a) stepdown procedure, a particular implementation of closed testing, showing that under the assumption of independent test statistics from a wide variety of distributional families, CER is indeed controlled. She illustrates the failure of Holm’s method to control the CER in the case of a shifted Cauchy distribution, which is not typically seen in applications. Holm (1979b; 1981) demonstrates that the stepdown approach controls the CER in a certain normal error regression setting with unknown variance. Finner (1999) examines the issue further and derives some results for step-up tests, closed F tests, and the modified Scheffé S method. He further notes that directional error control for stepwise procedures for the many-to-one and all-pairwise comparison situations remains to be solved. More recently, in a specific clinical trials setting, Goeman et al. (2010) have tackled the directional issue by using the partitioning principle (e.g. Bretz et al., 2010) to test for inferiority, non-superiority, and equivalence simultaneously.
Westfall et al. (2013) systematically examine the CER of closed testing procedures using a combination of analytical, numerical, and simulation techniques. For a class of tests involving multivariate noncentral T distributions, they demonstrate using a highly efficient Monte Carlo technique that no excess directional errors occur with closed testing. Their simulation study uses a one-way ANOVA model with up to 13 groups of varying sizes and several types of comparisons (all pairwise, many-to-one, sequential, and individual means with the average of other means). They demonstrate that an exception to CER control using Bonferroni tests (both one- and two-sided) in closure can occur for nearly collinear combinations of regression parameters in the simple linear model. However, they note that this situation would arise rarely if at all in pharmaceutical practice.
5 Closed Testing Using P-Value Combination Tests
In this section we investigate the power of a specific type of intersection test known as a p-value combination test (PVCT) or "p pooler" (e.g. Darlington, 1996; Darlington and Hayes, 2000) . As the name suggests, tests of this type combine the p-values obtained from tests of several individual hypotheses to test the intersection of those hypotheses. The original motivation for tests that only require p-values arose from meta-analysis, in which several tests (usually assumed to be independent) are combined (Hedges and Olkin, 1985; Hedges, 1992; Hedges et al., 1992; Becker, 1994; Rhodes et al., 2002). Independence is a valid assumption for AC tests done on separate patient pools, for example, in group-sequential clinical trials and in the analysis of disjoint patient subgroups. Therefore, the results of these next sections apply directly to those cases. For correlated multiple endpoints and/or multiple dose contrasts, our results do not apply directly, but we expect that some aspects of our general conclusions will remain intact.
The well-known Holm (1979a) and Hommel (1988) methods use the Bonferroni and Simes global tests, respectively, within the closure framework (Dmitrienko and Offen, 2005; Hommel et al., 2011; Westfall et al., 2011). PVCTs have also been used frequently in adaptive clinical trials (Bauer and Kieser, 1999; Kieser et al., 1999; Lehmacher and Wassmer, 1999; Hommel, 2001; Bretz et al., 2006).
Three basic classes of PVCTs exist. Additive combination (AC) methods first transform each p-value by qi = hi(pi), where the hi(·) may be different for each i, if, for example, weights λi are applied to each pi (Mosteller and Bush, 1954; Good, 1955; Benjamini and Hochberg, 1997; Westfall and Krishen, 2001; Zaykin et al., 2002; Westfall et al., 2004; Whitlock, 2005; Chen, 2011). In the present paper, we assume λi ≡ 1, which allows us to use the closure shortcut described in the previous section. After transforming each p-value, one then compares the test statistic to the appropriate quantile of the distribution of , where Qi = hi(Pi) and Pi is a random p-value. The function hi(·) is usually chosen such that Qi with distribution dQi is in a class F of probability distributions that is closed under addition; that is, . The normal and gamma distribution families are examples.
Minimum–p (MINP) methods use only the smallest p-value of all of the hypotheses in the intersection. MINP methods are functions of the ordered p-values p(1), …, p(m). The simplest example is the global version of the Bonferroni test, which takes the form C(p(1), …, p(m)) = mp(1). In general, MINP tests use the rank-order information about the p-values, while AC methods incorporate the actual magnitudes of the p-values. As it turns out, the inherent differences in the way each type of test uses the information contained in p-values drastically affect their behavior in closed testing.
Hybrid PVCTs such as the truncated product method (TPM) proposed by Zaykin et al. (2002) also exist; their power properties are intermediate to AC and MINP methods. We include a plot of the performance of the TPM to give an idea of its performance relative to the pure AC and MINP methods. Details of the TPM are provided in Henning (2011).
Optimality properties of PVCTs have been studied extensively (e.g. Birnbaum, 1954; Bhattacharya, 1961; Berk and Cohen, 1979; Marden, 1982, 1985; Westberg, 1985; Loughin, 2004), but optimality results for these tests when employed in closed testing are less well known (Romano et al., 2011). We fill this gap by evaluating the power of several PVCTs in the closure setting and comparing the results to the power of the tests when they are used to test "global" (intersection) null hypotheses, which has been their traditional application. As documented in the literature, tests in the AC class generally perform well as global tests (Loughin, 2004). We show that they perform terribly in closed testing unless the proportion of alternative hypotheses among the original set of m > 1 hypotheses is extremely high. Conversely, tests in the MINP class make for lackluster global tests, as expected (Westberg, 1985; Zaykin et al., 2002; Loughin, 2004), unless the proportion of alternatives among the original set of m hypotheses is small. However, these tests are far superior to AC tests, and approach optimal, under closure.
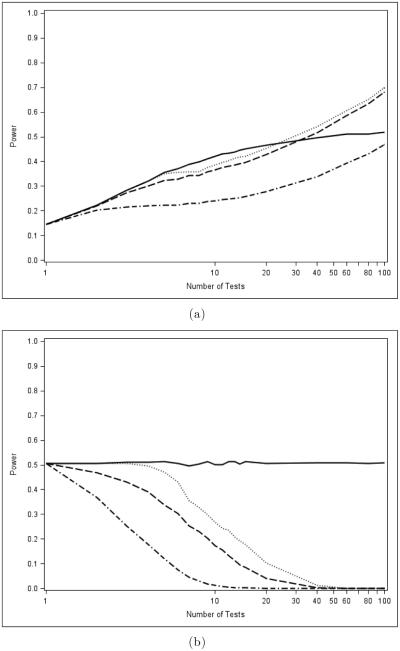
Figure 2 illustrates the main point. Panel (a) shows how the power of the Bonferroni test (a MINP test) for an intersection hypothesis compares to the power of the Fisher combination test (an AC test) as the number m of hypotheses increases under a common sampling frame described in Section 6. The Bonferroni method fares poorly compared to the Fisher combination test as m increases. But in panel (b), the average power of the Bonferroni test under closure (which is equivalent to the Holm test) is seen to be much higher than the power of the Fisher combination test under closure, under the same sampling scheme.
Figure 2.
A comparison of global (a) and closure (b) powers of the Bonferroni (Holm) (solid line) and Fisher combination (dashed line) tests, exemplars of the MINP and AC test classes, respectively.
5.1 Some Additive Combination Methods
The basis of many AC tests is the fact that under common assumptions, when a null hypothesis Hi is true, the (random) p-value Pi has the U(0, 1) distribution. The well-known Fisher combination test uses the fact that, for a set of independent p-values {P1, P2, …, Pm} arising from hypotheses {H1, H2, …, Hm}, the statistic is distributed as under ∩Hi, where Qi = −2ln(Pi). The combined p-value for the Fisher test is then
| (1) |
Optimality properties of the test have been examined extensively in the literature (Birnbaum, 1954; Littell and Folks, 1971; Koziol and Perlman, 1978; Marden, 1982; Koziol and Tuckwell, 1999) and it is quite popular in the biological sciences (Peng et al., 2009; Kechris et al., 2010; Ouellette et al., 2011)
A similar test is the chi-square method suggested by Yates (1955) and Lancaster (1961), and studied by Loughin (2004). Specifically, let
| (2) |
with Ψv (·) the cumulative distribution function of a central chi-squared random variable with v degrees of freedom. By a standard result, . The combined p-value is then
| (3) |
Another test that has seen wide application in a number of diverse fields (e.g. Kechris et al., 2010; Ryan et al., 2010; Lange, 2011) is known variously as the inverse normal method (Hedges, 1992; Becker, 1994; Piegorsch and Bailer, 2009), Stouffer’s method (Stouffer et al., 1949; Darlington and Hayes, 2000), or the Liptak method, after (Liptak, 1958). The combined test statistic is
| (4) |
where Φ(·) is the standard normal cumulative distribution function. The test is attractive because the linearity property of the normal distribution implies that under ∩Hi, and the combined p-value can be readily calculated as
| (5) |
with Z ~ N(0, 1). The flexibility of the normal distribution makes the Liptak test especially attractive. For example, while determining the null distribution of a weighted Fisher-type statistic is cumbersome (Good, 1955), a weighted Lipták test is relatively simple (e.g. Koziol and Tuckwell, 1994; Whitlock, 2005).
5.2 Some Minimum-P Methods
The simplest MINP method is based on the Bonferroni test, which rejects ∩Hi if
| (6) |
with combined p-value
| (7) |
Unlike typical AC tests, the Bonferroni test requires no assumption about the dependence relationships among the tests. As discussed in Section 3, Holm’s (1979a) method is obtained by applying the simple Bonferroni global test the intersection hypotheses in the closure method.
Under independence, a test proposed by Tippett (1931) and S̆idák (1967) is more powerful. The global null hypothesis is rejected if
| (8) |
For Tippett’s test the combined p-value is
| (9) |
One may use other order statistics as well. However, these tests tend to perform poorly (Birnbaum, 1954; Loughin, 2004), so we do not consider them here.
A more useful method is one proposed by Simes (1986), wherein ∩Hi is rejected when p(i) ≤ iα/m for at least one i, or equivalently when
| (10) |
The Simes test is uniformly more powerful than the Bonferroni test, at the expense of dependence assumptions: Under certain types of positive dependence, Simes is well known to be conservative (Samuel-Cahn, 1996; Sarkar and Chang, 1997), and the situations in which it is highly liberal (the Type I error rate exceeding α) are unusual, occurring in special cases of pathological dependence structure (Rødland, 2006). The Simes test is also popular because its critical values, iα/m, are those used in Benjamini and Hochberg’s classical false discovery rate controlling method (Benjamini and Hochberg, 1995).
As originally derived, Simes’ test is only valid for an intersection null hypothesis, not as a method for evaluating individual hypotheses. Hochberg (1988) and Hommel (1988) derive closure-based methods using Simes’ test to control the FWER; this method is popularly known as the "Hommel method," and is the one we employ in this paper. Like the AC methods, the Hommel method has a shortcut of O(m2), requiring only the evaluation of the same "worst-case scenarios" described in Section 3.
Table 1 summarizes the various p-value based global tests. In the next section, we discuss the methodology for evaluating these tests in the closure setting.
Table 1.
Summary of the combination tests and their associated critical values. Pure AC methods reject for values larger than the critical value. Pure MINP methods and the TPM reject for values smaller than the critical value.
| Test | Statistic | Critical Value | Type |
|---|---|---|---|
| Fisher | AC | ||
| Chi-Squared | AC | ||
| Liptak | AC | ||
| Bonferroni | mp (1) | α | MINP |
| Simes | mini mp(i)/i | α | MINP |
| Tippett | 1 – (1 – p(1))m | α | MINP |
6 Comparing the Methods
We now compare the power properties of PVCTs when they are used in their traditional setting as intersection tests for the composite hypotheses. The results in this section and in the subsequent section allow the number of tests, m, to grow large, and the tests are assumed independent. One application of such a case in pharmaceutical research is in the analysis of a large collection of non-overlapping patient subgroups. Other cases where m may be large include preclinical research where large numbers of hypotheses (e.g., genomic) are tested, the analysis of safety data in Phase III clinical trials, and the analysis of a large collection of secondary endpoints in Phase III clinical trials. While the results of this section do not apply directly to those cases because they all involve dependent tests, we expect that similar results can be shown with dependent test statistics due to diminishing tail dependence with smaller a thresholds (Clarke and Hall, 2009).
To generate the p-values, we use the two-level hierarchical model
| (11) |
| (12) |
where
is a two-point mass function for the alternative mean µ. The parameter 7r allows us to control the proportion of alternative hypotheses in a long-run average sense. For one particular simulation, the proportion of false null hypotheses may differ from π, but the average proportion of alternatives over all simulations will be very close to π, by the Law of Large Numbers. This approach to generating null and alternative hypotheses has been employed by, e.g., Davidov (2011) and Newton et al. (2007), and is briefly discussed in Taylor and Tibshirani (2006). An advantage of the hierarchical model over a fixed alternatives model is that the proportion 7r can be set to anything, whereas in the fixed alternative model π can only take values k/m for k = 0, 1, …, m.
Specifying a δ ≠ 0 for each of the tests lets us control the "strength of evidence", a term used by Loughin (2004), against a particular null hypothesis, with larger δ representing larger evidence. We set δ such that a particular test (a "power anchor") has a fixed power of approximately β. For both the global and closure simulation studies, we use the Bonferroni test for the anchor because it is simple, widely known, analytically tractable, and is intuitively appealing as a benchmark against which to compare supposedly more sophisticated procedures. However, because what constitutes the alternative of interest is substantively different between global tests and individual tests, we need two separate power criteria, one for the global case and another for the closure case.
6.1 The Global Case
Consider the global null hypothesis , with alternative . The power of the global test is . There are 2m − 1 possible configurations that result in a false HM, so we must specify what points in are of interest. We choose the alternative means δ in the hierarchical model by anchoring the Bonferroni global test to have power βBon when k = m × π hypotheses are false. This power setting will be approximate because we assume k is an integer in the calculations. All tests will be assumed two-sided; similar results are obtained for one-sided tests as shown in Henning (2011).
We now demonstrate the calculation of δ > 0. We desire that
Substituting in the Bonferroni procedure and the form of , we have
where Pi is again a (random) p-value. Now, we can solve (13) for δ as follows:
| (14) |
where B = (1 − (βBon)/(1 − α/m)m−k and Φ(·) is the standard normal cumulative distribution function.
Power is estimated in the global case as the ratio of the number of rejections of the global null hypothesis to the total number of simulations. For a combination test Cj = C(Pj), Pj a vector of p-values, and number of simulations N,
| (15) |
with estimated standard error
| (16) |
For all of our simulations of global power, we use N = 50, 000, which is more than adequate (Zaykin et al., 2002; Whitlock, 2005; Loughin, 2004).
6.2 The Closure Case
The closure method admits inferences about the individual null hypotheses, and thus we need another power criterion. We use proportional (or average) power, defined as the expected value of the ratio of correctly rejected null hypotheses to all false null hypotheses (Westfall et al., 2011, chap. 18 and Bretz et al., 2010, chap. 2).
Let M1 = |I1|, where I1 ⊆ {1, 2, …, m} denotes the index set of the alternative hypotheses; M1 is the number of alternative hypotheses among the m hypotheses. Note that, according to our two-level model discussed at the beginning of this section, I1 is a random set and M1 ~ binomial(m, π). The average power βavg is related to the individual power of a test βi as follows:
| (17) |
As in the global case discussed above in Section 6.1, we choose the Bonferroni test as our anchoring procedure. Letting z1-α/2m denote the critical value for a two-sided α-level test of H0 : µ = 0 using the Bonferroni procedure, we can specify δ > 0 as
| (18) |
because Pr (Z ≤ −z1−α/2m − δ) ≈ 0 for even moderate m, so we set δ = z1−α/2m − Φ−1 (1 − βBon).
We also specify a variety of values m. Because even the shortcut to the closure procedure involves certain "hurdles" as discussed in Section 3, the maximum number of tests we consider should be large enough to bring the effects of closure into sharp relief, but not so large as to be computationally infeasible. The shortcut requires in general O(m2) steps. When multiplied by a number of simulations N, the total number of evaluations can quickly become quite large. To account for this in a systematic way, we set N = 90, 000/m which keeps the "effective sample size" constant at 90, 000 as m grows.
Next we consider how to choose the patterns of evidence. Each pattern consists of a choice of anchoring power βBon and proportion of alternatives π. We consider three levels of anchoring power, assigning the following descriptive names: βBon = 0.50 : "Moderate"; βBon = 0.75 : "Strong"; and βBon = 0.90 :"Very Strong." We consider three levels of π, namely, π = 0.10 : "Sparse"; π = 0.50 : "Even"; and π = 0.90 : "Concentrated". Table 2 summarizes these patterns. In the global case, for example, the configuration βBon = 0.50 and π = 0.10 ("Moderate & Sparse") refers to the situation in which there is moderate power against the global null hypothesis, but this evidence is thinly apportioned among the m tests. Conversely the pattern of βBon = 0.90 and π = 0.90 implies an abundance of very strong evidence against the global null. In the closure case, the "Moderate & Sparse" case indicates that there are relatively few hypotheses among the m that are true alternatives, but that the individual power for the tests associated with the true alternatives is moderately high.
Table 2.
Descriptors for the patterns of evidence we consider for both the global and closure cases.
| Proportion of Alternatives(π) | ||||
|---|---|---|---|---|
|
Power (βBon) |
0.50 0.75 0.90 |
0.10 | 0.50 | 0.90 |
| Moderate & Sparse | Moderate & Even | Moderate & Concentrated | ||
| Strong & Sparse | Strong and Even | Strong and Concentrated | ||
| Very Strong & Sparse | Very Strong & Even | Very Strong & Concentrated | ||
To estimate the proportional power given in equation 17, we define
| (19) |
| (20) |
to be the observed proportion of false null hypotheses rejected among the m1j false null hypotheses in the original set of mj hypotheses for a particular simulation j. When there are no false null hypotheses, we define Aj to be 0. We then estimate the average power as
| (21) |
That is, we take the average of the Aj over all simulations with at least one alternative hypothesis in the set of m hypotheses. We estimate the standard error as
| (22) |
7 P-Value Combination Tests: Global Vs. Closure
We present the results of each row of Table 2 separately. For purposes of clarity, we do not depict the power curves for the Tippett or Bonferroni (Holm) tests, as these tests are consistently outperformed by the Simes (Hommel) test; further, we found that the chi-square test performs similarly to the Fisher test, so it is also not depicted. Results using all tests are shown in Henning (2011).
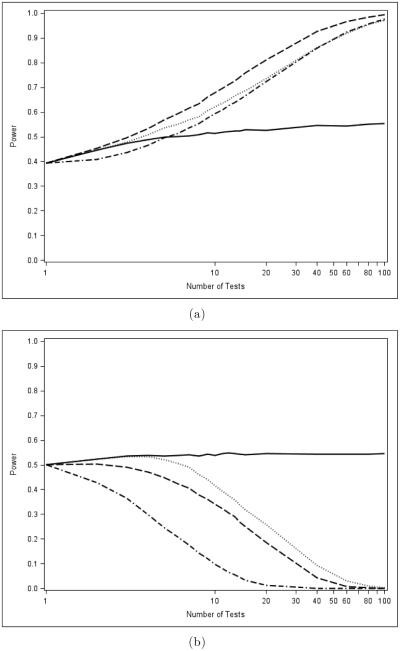
First, we consider the performance of PVCTs when there is moderate power sparsely distributed among the tests. We see in Figure 3a that, as global tests, MINP methods outperform all of the AC tests except the Liptak if the number of tests is fairly small. The Liptak test is the clear laggard, only showing signs of outperforming the MINP methods if the number of tests is large. This result is not unexpected (see O’Brien, 1984; Pocock et al., 1987; Sankoh et al., 1997; Aickin, 1999; Bender and Lange, 1999; Bittman et al., 2009), and our simulation results are consistent with those presented in Westberg (1985) and Loughin (2004). MINP tests make good use of sparse information because one only has to have the smallest p-value be "small enough." Conversely, the AC methods use the magnitude of every p-value, and large p-values shrink the test statistic, leading to fewer rejections.
Figure 3.
Comparison of global (a) and closure (b) powers of p-value combination tests for the "moderate and sparse" evidence pattern. Fisher is dashed, Liptak is dash-dot, Hommel is solid, and TPM is dotted.
The story is radically different when considering the closure case, however, which is shown in Figure 3b. Here we see that MINP methods consistently outperform the AC tests, with the power of the AC tests dropping to essentially 0 as the number of tests increases. This illustrates our main point: using a powerful global test in the closure setting can lead to dramatic power losses.
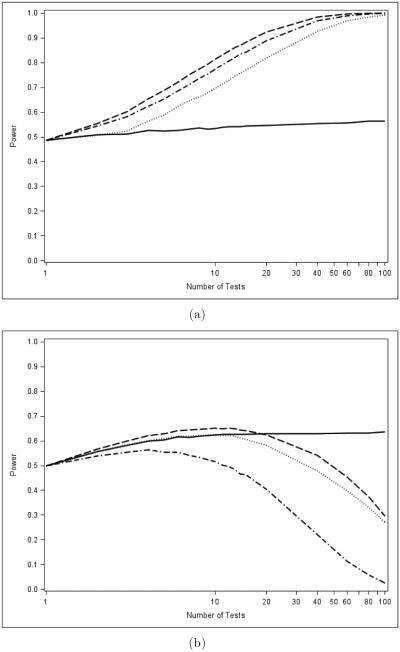
When considering the "Moderate and Even" configuration, as shown in Figure 4, the results are even more striking. Here, the global power of the AC methods increases in m, eventually far outpacing that of the MINP tests. In the closure setting, however, the AC tests again falter. Only when the proportion of alternatives is quite high (π = 0.90) do AC tests begin to perform well in closure, as shown in Figure 5. However, even in this configuration, the power of these methods drops as m increases.
Figure 4.
Comparison of global (a) and closure (b) powers of p-value combination tests for the "moderate and even" evidence pattern. Fisher is dashed, Liptak is dash-dot, Hommel is solid, and TPM is dotted.
Figure 5.
Comparison of global (a) and closure (b) powers of p-value combination tests for the "moderate and concentrated" evidence pattern. Fisher is dashed, Liptak is dash-dot, Hommel is solid, and TPM is dotted.
Similar results are obtained for other patterns in Table 2, as shown in Henning (2011). The generally poor performance of AC tests persists when the proportion of alternatives is increased to 50%. Only when the proportion of alternatives is at least 90% do AC tests begin to gain power relative to the MINPs (figures not shown but available from authors). However,this power advantage is slight.
A natural question is whether any configuration allows AC methods to outperform MINP methods. Figure 6, which depicts the closure power of PVCTs in the case of moderate (50%) power and 100% alternatives, provides an answer; the performance of the methods for higher powers is similar. Here we see the first real reversal of the pattern: AC tests (including Liptak) now outperform the MINP methods.
Figure 6.
AC methods are more powerful than MINP methods over the full range of the number of tests we consider when π = 1. Fisher is dashed, Liptak is dash-dot, Hommel is solid, and TPM is dotted.
Tables 3 and 4 below summarize the results. When the proportion of alternatives is small, MINP methods perform better as global tests than their AC counterparts. This is so because MINP methods succeed or fail on the strength of the "signal" contained in the smallest p-values, while the AC methods incorporate the specific magnitudes of all p-values, mixing signal with "noise." The upshot of combining the actual magnitudes of the p-values is that when signal strength increases (in the form of a greater proportion of alternative hypotheses), the associated small p-values can compound to give a powerful global test. MINP tests disregard the additional evidence against the global null contained in other small p-values in favor of examining just the smallest.
Table 3.
Recommended classes of PVCT for testing global hypotheses, considering the number of tests and the dispersion of evidence among the tests, based on simulated power behaviors in this section. An asterisk indicates that the Liptak test, although it is an AC test, is not recommended.
| Recommended Tests | Proportion of Alternatives | ||
|---|---|---|---|
| m | 0.10 (Sparse) | 0.50 (Even) | 0.90 (Concentrated) |
| ≤ 20 | MINP | AC* | AC |
| 21 – 50 | MINP;AC*; TPM | AC* | AC |
| > 50 | AC*;TPM | AC;TPM | AC;TPM |
Table 4.
Recommended classes of PVCT for use in closure, considering the number of tests and the dispersion of evidence among the tests, based on simulated power behaviors in this section. An asterisk indicates that the Liptak test, although it is an AC test, is not recommended.
| Recommended Tests | Proportion of Alternatives | |||
|---|---|---|---|---|
| m | 0.10 (Sparse) | 0.50 (Even) | 0.90 (Concentrated) | 1.0 |
| ≤ 20 | MINP | MINP | MINP; AC*;TPM | AC |
| 21 – 50 | MINP | MINP | MINP | AC |
| > 50 | MINP | MINP | MINP | AC |
7.1 Related Research
In the context of testing multiple related clinical endpoints for common effect direction, and assuming multivariate normal test statistics with a unit-variance compound symmetric covariance matrix, Bittman et al. (2009) demonstrate that a maximin test for the intersection null HI : θi = 0 ∀i ∈ I = {1, 2, … m} can be uniformly improved upon if one is interested in making inferences on the individual Hi using closure. A global test is maximin according to Bittman et al. (2009) if it maximizes
where . They propose a procedure for closure that is both consonant (i.e., rejection of an intersection implies rejection of at least one of the intersection components) and that maximizes the probability of at least one rejection. They discuss their consonant test for the special case of testing two two-sided normal means. Their global test statistic has rejection region
| (23) |
where c(1-α) is a constant such that the test has level α under (θ1, θ2)′ = 02×1. A notable feature of the region in (23) is that it combines features of both AC and MINP methods. We see that . They investigate the power of their test with a simulation study, and find that this test outperforms the Holm method and a test based on just the sum (equivalent to the Liptak test in their setup) when both hypotheses are false. When only one hypothesis is false, Bittman et al. (2009) note that the a test based on max(|X1| , |X2|) (which is equivalent to a MINP test) performs better. Their simulation results, therefore, agree with ours.
Romano et al. (2011) show that power inheritance is possible but not automatic. More precisely, if an optimal global test of an intersection hypothesis H1 exists and results in a consonant multiple testing procedure, then that multiple testing procedure will have maximum power to reject at least one false null hypothesis among all procedures controlling the FWER at α. Thus, when working with consonant tests, the authors prove that an "inheritance property" exists for closed testing, as long as one begins with an optimal consonant global procedure. Finding such an optimal global test is generally a nontrivial task when working with PVCTs (Birnbaum, 1954).
Romano et al. (2011) go on to define a test that has this desirable power inheritance property for the problem of testing several normal means, that is,
They examine the power properties of their test for points of the form {(θ1, …, θm) : |θi| ≥ ε for at least one i}, with ε > 0. Their global maximin consonant test is , where cosh(·) is the hyperbolic cosine function. Interestingly, Romano et al. (2011) note that for large ε, their test nearly reduces to the ordinary Bonferroni global test, which supports our general conclusion that MINP tests are far better suited to closure than AC methods.
In our simulation study, the MINP tests we consider are consonant (this is proven rigorously by Sonnemann, 2008). To see this, consider the test of H12, where we have the observed p-values p1 = 0.023 and p2 = 0.06, with α = 0.05. The closed testing procedure using Bonferroni global tests rejects H12 with a combined p-value = 2(0.023) = 0.046. This implies that H1 can automatically be rejected, since = 0.023. Hence, consonance is satisfied. The other MINP tests are consonant for similar reasons. To see why AC tests are not consonant in general, consider Fisher’s test with p1 = 0.06 and p2 = 0.07. The test statistic for H12 is then c = −2 ln(0.06) − 2 ln(0.07) = 10.95, giving a combined p-value of 0.027. However, none of the component hypotheses can be rejected because both have p-values larger than 0.05.
Our simulation study enhances the theory in Romano et al. (2011) by showing empirically how dramatic and pervasive the loss of power can be when using dissonant (i.e., non-consonant) tests in the closure framework. The only situation that allows the dissonant AC tests to perform reasonably well is the 100% alternative case, which is quite restrictive. Although dissonant procedures are not optimal for rejecting individual null hypotheses, recent work by Goeman and Solari (2011) demonstrates that such procedures can be highly useful in an exploratory context. They show how to construct such confidence sets using the closure method (and, in one example, Fisher’s test), noting that dissonant procedures result in smaller (i.e., more precise) confidence sets than consonant procedures.
7.2 The Problem of Hurdles
7.2.1 Conceptual Issues
As discussed in detail in Section 3, to test Hi using the closure shortcut with PVCTs, we need only explicitly test those intersection hypotheses associated with the largest p-values and pi. If these "worst-case" (or "highest hurdle") intersection hypotheses, one for each level in the closure hierarchy, can be rejected, all of the other intersection hypotheses involving Hi can also be rejected. Some of the points we will mention here have been discussed before (e.g. Goutis et al., 1996), but not in the closure context, which adds an additional layer of complexity.
Let us consider how AC and MINP combination methods work. To ease notation, we will assume again that the hypotheses have been relabeled according to the order of their associated p-values, so that H1 has p-value p1 ≡ p(1), etc. Let us begin with the Bonferroni procedure applied to each intersection test, i.e., Holm’s procedure. This procedure compares the smallest p-value in each intersection hypothesis H1 with α/K, where K = |I|, I ⊆ {1, 2, …, m}, is the number of p-values in the intersection test. If m = 10, K = 5, α = 0.05, and we are interested in testing H1, then we only need p1 to be smaller than 0.05/5 = 0.01. The null-hypothesis p-values in this intersection, p7, p8, p9, and p10, can each be as large as 1 and the intersection test will still reject.
Conversely, the magnitude of the p-values strongly influences the AC methods. Consider first the Fisher method for this same situation, where K = 5 and α = 0.05. Assume that p1 = 0.009 and p7 = p8 = p9 = p10 = 1. Then the Fisher test statistic is cFisher = −2 ln(0.009) + 0 + 0 + 0 + 0 = 9.42, resulting in a combined p-value of 0.493. Thus, by closure, we can already conclude that H1 cannot be rejected at FWER = 0.05. In fact, in this extreme case, we must have to achieve significance for the intersection test. The Lipták test performs even worse in this example, because limpi → 1 Φ−1(1 − pi) = −∞, which implies that if the other p-values in the intersection are sufficiently large, no amount of evidence contrary to the intersection null will ever lead to rejection.
Even when the proportion of alternatives is high, the hurdles problem remains. Suppose we have a collection of 100 elementary hypotheses H1, H2, …, H100, and again these hypotheses have been labeled as usual according to the order of their p-values. Further suppose that in this particular collection, 90% of the hypotheses are alternative (false nulls), and that the collection of alternative hypotheses is {H1, H2 …, H10}. This latter assumption eases the exposition and is not unreasonable, as p-values tend to be small under the alternative hypothesis.
Figure 7 depicts the testing pattern for H1. Each of these hypotheses must be rejected if H1 is to be rejected. As we move through the closure tree, eventually H1 with p-value p1 is tested in an intersection in which all of the hypotheses except H1 are true nulls, and will thus tend to have large p-values. If a PVCT incorporates the actual magnitude of every p-value, as does an AC test, whatever "signal" is found in the small p-value for H1 will be drowned out in the "noise" of the large p-values. However, if we are using an MINP method, the magnitude of the large p-values matters little as long as p1 is "small enough."
Figure 7.
The intersection hypotheses ("hurdles") that must be explicitly tested using the closure shortcut. If any one of these hypotheses cannot be rejected, H1 cannot be rejected. The small p-value for H1 is combined with the largest (K − 1) p-values in the closure shortcut.
To highlight just how much of an effect the hurdles problem has on AC tests, we will examine the algorithm for the case depicted in Figure 7, but at the other extreme: the case in which there is exactly one alternative among the m = 100 tests (that is, 1% alternatives). We will assume, as before, that H1 is the hypothesis we wish to reject. The intersection hypotheses, one for each cardinality K, will then involve p1 and the (K − 1) largest p-values. The set of hypotheses that must be explicitly tested in order to reject H1 is {H1, H1,100, H1,99, …, H1,2,…,100}.
To provide a clear picture of how differently the MINP methods perform compared to the AC tests, we wish to set the anchor of the Bonferroni global test to βBon = 0.90 for every intersection. To make the narrative a bit cleaner, we make the mild assumption that p1, the p-value for H1, will always be the p-value used for the Bonferroni global test, the other p-values being greater than α/K with probability 1. This reduces the problem to finding an alternative mean δK such that Pr(P1 ≤ α/K) = βBon. Making this assumption, and using notation from Section 6, we have
| (24) |
Solving (24) for δK gives δK = Φ−1(1 − α/2K) − Φ−1(1 − βBon).
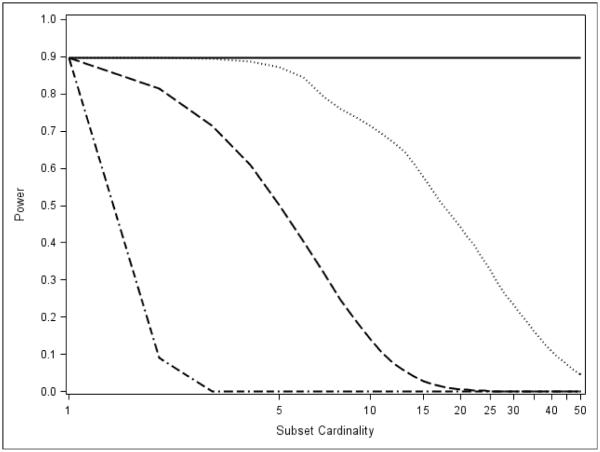
Figure 8 depicts the estimated power curves for the MINP and AC methods when taking subsets of size K = 1, 2, …, 50 out of a total of m = 100 hypotheses. This models the situation in which there is very strong evidence against the intersection null, but this evidence is extremely sparse (present in exactly one test). Because we assume H1, with p-value p1, is the elementary hypothesis of interest, each intersection hypotheses involves p1 and the (K − 1) largest p-values. Each intersection hypothesis is a hurdle that must be cleared if H1 can be rejected using closure.
Figure 8.
Estimated power curves for the MINP and AC methods when taking subsets of size K = 1, 2, …, 50 out of a total of m = 100 hypotheses. Each intersection hypothesis of cardinality K contains p1 and the (K − 1) largest p-values. The rejection probability using Bonferroni for each intersection hypothesis is set at β = 0.90. Fisher is dashed, Liptak is dash-dot, Hommel is solid, and TPM is dotted.
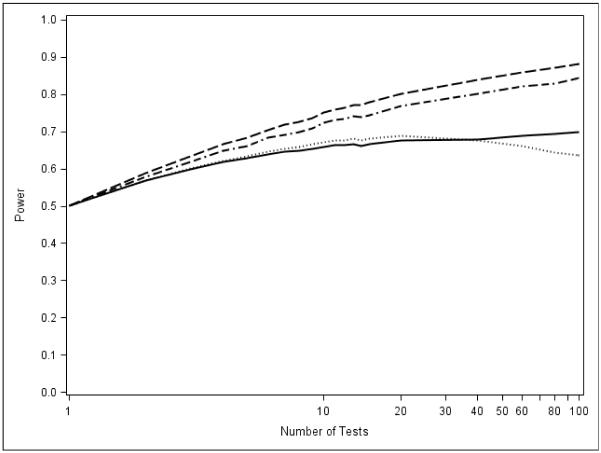
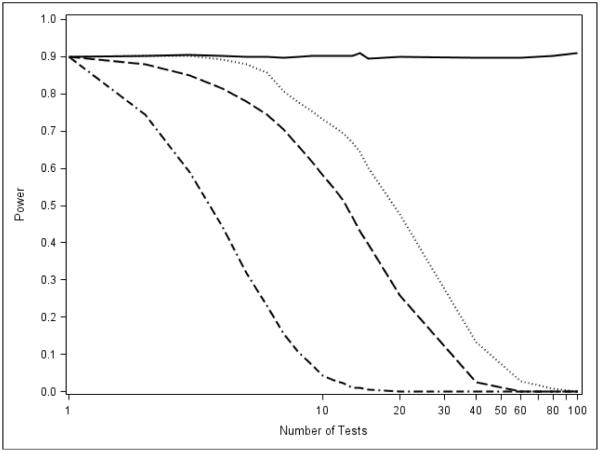
The results shown in Figure 8 suggest that, in the extreme case of exactly one alternative, the AC methods will perform poorly in a closure setting because these tests will quickly lose the power to reject the intersection hypotheses involving the elementary hypothesis of interest, and thus, lose power to reject the elementary hypothesis. We now show that this is indeed the case. The power curves in Figure 9 depict the power of the closure method to reject H1 when H1 is the only alternative among the collection of m hypotheses. Even when given "a fighting chance" to perform by setting the power to 0.90, the AC methods drop precipitously.
Figure 9.
Power of the closure method using AC and MINP tests to reject H1, the only alternative among the m hypotheses. The power of the Bonferroni test is set at βBon = 0.90. Fisher is dashed, Liptak is dash-dot, Hommel is solid, and TPM is dotted.
7.3 Proof of the Hurdles Problem
In this section, we give a formal argument to supplement the intuitive one presented in the previous section. Specifically, we give conditions under which the power of MINP tests approaches 1, while the power of the Fisher combination AC test approaches 0.
Assume there are M tests, with M tending to infinity. Null hypotheses are denoted , with M0 = [(1 − π)M], for some fixed proportion π ∈ (0, 1) of alternative hypotheses. Alternative hypotheses are denoted , with M1 = M − M0. Assume independent p-values U (0, 1), i = 1, …, M0, for testing each of the MO hypotheses . Also assume p-values, , for testing each of the M1 hypotheses , where for U ~ U(0,1), for some fixed d ∈ (0, 0.5). The can be arbitrarily dependent on each other and on the . Under these conditions, we have the following results.
Theorem 1 The power of the Bonferroni-Holm (B-H) test of converges to 1.0 for any nominal FWER α ∈ (0, 1).
Proof. Since the Bonferroni-Holm procedure is at least as great as the power of the ordinary Bonferroni (BON) procedure,
Pr(Reject using B-H) ≥ Pr(Reject using BON) = Pr( ≥ α/M ) = Pr(UMd < α/M) = Pr{Mdln(U) ≤ ln(α) − ln(M)} = Pr{−ln(U) ≥ − ln(α)/Md + ln(M)/Md} → 1.0, since −ln(U) ≈ Exp(1) and − ln(α)/Md + ln(M)/Md → 0 for all α ∈ (0, 1) and d ∈ (0, 0.5).
Corollary 2 The average power of the Bonferroni-Holm (B-H) test of converges to 1.0 for any nominal FWER α ∈ (0, 1).
Proof. The argument of Theorem 1 holds by simple substitution for all , i = 1, …, M1. Since the average power of B-H is using B-H), and since each summand converges to 1.0, the average also converges to 1.0.
Theorem 3 The power of the closed Fisher combination (CFC) test of converges to 0 for any nominal FWER α ∈ (0, 1).
Proof. First, since closure requires all intersection tests to be significant, the power of CFC for is no more than the power of any intersection test that includes . It is sufficient to consider a aworst-case scenario" described in the previous subsection, where the one alternative p-value is combined with the largest null p-values. Let m = [(M0)1/2] and consider the ordered null p-values . Then
by Markov’s Inequality.
Now, for all α (0, 1), . Noting that − ln(x) ≤ x−1 − 1 for all x ∈ (0, 1), we have , when X is a random variable between 0 and 1. By properties of uniform order statistics, , implying . Hence, using the Markov bound, Pr(Reject using CFC) ≤ {2Md + 2m2/(M0 − m)}/2m(1 + o(1)) → 0 for d ∈ (0, 0.5).
Corollary 4 The average power of the CFC test of converges to 0 for any nominal FWER α ∈ (0, 1).
Proof. The proof is by symmetry of arguments as shown in the proof of Corollary 1.
8 Conclusion
Closed multiple testing is a highly flexible and relatively simple approach to multiple testing, which explains its popularity in biopharmaceutical research settings. With these benefits come a few issues that researchers should keep in mind. One is that the set of hypotheses that must be formed and tested can be quite large, containing up to 2m nulls. If a shortcut such as the one described in Section 3 cannot be applied, the number of calculations to perform closure can quickly become infeasible. Fortunately, the conditions for a shortcut to exist are met with AC and MINP tests, which are common in clinical trials.
Also, while closed testing controls the probability of at least one incorrect rejection by design, other error rates, such as the probability of at least one incorrect rejection or incorrectly declaring the direction of an effect (defined as the combined error rate CER), are not necessarily controlled. However, as Westfall et al. (2013) note, the cases in which the CER is not controlled are rather pathological. Nevertheless, as these authors also note, the existence of excess Type I directional errors suggests that it is safest to supplement the results of multiple testing procedures in pharmaceutical research with compatible confidence intervals, in which case the directional error problem disappears.
Another conclusion from this article that is of interest to biopharmaceutical research, particularly clinical trials, is the relatively poor performance of the AC types of tests relative to MINP tests when used in a closure setting. In this article, we illustrate that the power properties of the intersection tests are not inherited automatically when these tests are used in the closure setting. The lack of power is most pronounced with large numbers of tests with a degree of sparseness of a signal. However, for researchers considering using AC tests in group sequential trials, this is not a problem: the number of tests is usually small, the signal is consistent across groups assuming a relatively homogeneous patient pool, and the main emphasis is usually on the overall test rather than group-specific tests. On the other hand, if non-homogenous subgroup analyses are entertained, then the results of this paper suggest using closed MINP tests rather than closed AC tests. A further benefit of MINP tests is that dependence structures are allowed, whereas to perform AC tests with correlated data, the correlations must be incorporated into the critical values, for example, by bootstrapping. With positively correlated endpoints as found in clinical trials, the "borrowing strength" effect that one gets via additive combination will likely make the results shown in this article more favorable towards the AC types of tests, but of course comparative power analysis is always prudent before selecting a method for the data analysis plan. A final take-home message is that the recently popular graphical methods (Brannath and Bretz, 2010), being Bonferroni-based, are well supported by the analyses shown in this paper, particularly for larger numbers of heterogeneous hypotheses.
Acknowledgement
The authors thank the reviewers for comments that improved the manuscript. Peter Westfall’s contribution was partially supported by the National Institutes of Health (NIH RO1 DK089167).
References
- Adams CP, Brantner VV. Estimating the cost of new drug development: Is it really $802 million? Health Affairs. 2006;25(2):420–428. doi: 10.1377/hlthaff.25.2.420. [DOI] [PubMed] [Google Scholar]
- Aickin M. Other method for adjustment of multiple testing exists [Letter] British Medical Journal. 1999;318(7176):127. doi: 10.1136/bmj.318.7176.127a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer P, Kieser M. Combining different phases in the development of medical treatments within a single trial. Statistics in Medicine. 1999;18(14):1833–1848. doi: 10.1002/(sici)1097-0258(19990730)18:14<1833::aid-sim221>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Becker BJ. Combining significance levels. In: Cooper HM, Hedges LV, editors. The Handbook of Research Synthesis. Russell Sage Foundation; New York: 1994. pp. 215–230. [Google Scholar]
- Bender R, Lange S. Multiple test procedures other than Bonferroni’s deserve wider use [Letter] British Medical Journal. 1999;318(7183):600. doi: 10.1136/bmj.318.7183.600a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society. 1995;57(1):289–300. [Google Scholar]
- Benjamini Y, Hochberg Y. Multiple hypotheses testing with weights. Scandinavian Journal of Statistics. 1997;24(3):407–418. [Google Scholar]
- Berger JO, Sellke T. Testing a point null hypothesis: The irreconcilability of p values and evidence. Journal of the American Statistical Association. 1987;82(397):112–122. [Google Scholar]
- Berk RH, Cohen A. Asymptotically optimal methods of combining tests. Journal of the American Statistical Association. 1979;74(368):812–814. [Google Scholar]
- Bhattacharya N. Sampling experiments on the combination of independent χ2 tests. Sankhya: The Indian Journal of Statistics, Series A. 1961;23(2):191–196. [Google Scholar]
- Birnbaum A. Combining independent tests of significance. Journal of the American Statistical Association. 1954;49(267):559–574. [Google Scholar]
- Bittman RM, Romano JP, Vallarino C, Wolf M. Optimal testing of multiple hypotheses with common effect direction. Biometrika. 2009;96(2):399–410. [Google Scholar]
- Brannath W, Bretz F. Shortcuts for locally consonant closed test procedures. Journal of the American Statistical Association. 2010;105(490):660–669. [Google Scholar]
- Brannath W, Posch M, Bauer P. Recursive combination tests. Journal of the American Statistical Association. 2002;97(457):236–244. [Google Scholar]
- Bretz F, Hothorn T, Westfall PH. Multiple Comparisons Using. R. Chapman & Hall/CRC; Boca Raton, FL: 2010. [Google Scholar]
- Bretz F, Maurer W, Gallo P. Discussion of "some controversial multiple testing problems in regulatory applications" by H. M. J. Hung and S. J. Wang. Journal of Biopharmaceutical Statistics. 2009;19(1):25–34. doi: 10.1080/10543400802541693. [DOI] [PubMed] [Google Scholar]
- Bretz F, Schmidli H, Konig F, Racine A, Maurer W. Confirmatory seamless phase II/III clinical trials with hypotheses selection at interim: General concepts. Biometrical Journal. 2006;48(4):623–634. doi: 10.1002/bimj.200510232. [DOI] [PubMed] [Google Scholar]
- Chen Z. Is the weighted z-test the best method for combining probabilities from independent tests? Journal of Evolutionary Biology. 2011;24:926–930. doi: 10.1111/j.1420-9101.2010.02226.x. [DOI] [PubMed] [Google Scholar]
- Clarke S, Hall P. Robustness of multiple testing procedures against dependence. The Annals of Statistics. 2009;37(1):332–358. [Google Scholar]
- Colhoun HM, McKeigue PM, Smith GD. Problems of reporting genetic associations with complex outcomes. The Lancet. 2003;361(9360):865–872. doi: 10.1016/s0140-6736(03)12715-8. [DOI] [PubMed] [Google Scholar]
- Committee for Proprietary Medicinal Products Points to consider on multiplicity issues in clinical trials. 2002 Retrieved from http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2009/09/WC500003640.pdf.
- Cook RJ, Farewell VT. Multiplicity considerations in the design and analysis of clinical trials. Journal of the Royal Statistical Society. Series A (Statistics in Society) 1996;159(1):93–110. [Google Scholar]
- Darlington RB. A meta-analytic "p-pooler" with three advantages. 1996 Retrieved March 18, 2011, from http://www.psych.cornell.edu/darlington/meta/pprod1.htm.
- Darlington RB, Hayes AF. Combining independent p values: Extensions of the Stouffer and binomial methods. Psychological methods. 2000;5(4):496–515. doi: 10.1037/1082-989x.5.4.496. [DOI] [PubMed] [Google Scholar]
- Davidov O. Combining p-values using order based methods. Computational Statistics 8 Data Analysis. 2011;55(7):2433–2444. [Google Scholar]
- Dmitrienko A, Offen W. Analysis of Clinical Trials Using SAS: A Practical Guide. SAS Publishing; Cary, NC: 2005. [Google Scholar]
- Dmitrienko A, Wiens BL, Tamhane AC, Wang X. Tree-structured gatekeeping tests in clinical trials with hierarchically ordered multiple objectives. Statistics in Medicine. 2007;26(12):2465–2478. doi: 10.1002/sim.2716. [DOI] [PubMed] [Google Scholar]
- Dyer O. Lilly investigated in US over the marketing of olanzapine. British Medical Journal. 2007;334(7586):171. doi: 10.1136/bmj.39105.427731.DB. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Efron B. Large-scale simultaneous hypothesis testing: The choice of a null hypothesis. Journal of the American Statistical Association. 2004;99(465):96–104. [Google Scholar]
- Finner H. Stepwise multiple test procedures and control of directional errors. The Annals of Statistics. 1999;27(1):274–289. [Google Scholar]
- Fleming TR. Current issues in clinical trials. Statistical Science. 1992;7:428–456. [Google Scholar]
- Goeman J, Solari A. Multiple testing for exploratory research. Statistical Science. 2011;26(4):584–597. [Google Scholar]
- Goeman JJ, Solari A, Stijnen T. Three-sided hypothesis testing: Simultaneous testing of superiority, equivalence and inferiority. Statistics in Medicine. 2010;29(20):2117–2125. doi: 10.1002/sim.4002. [DOI] [PubMed] [Google Scholar]
- Gonen M, Westfall PH, Johnson WO. Bayesian multiple testing for two-sample multivariate endpoints. Biometrics. 2003;59(1):76–82. doi: 10.1111/1541-0420.00009. [DOI] [PubMed] [Google Scholar]
- Good IJ. On the weighted combination of significance tests. Journal of the Royal Statistical Society. 1955;17(2):264–265. [Google Scholar]
- Goutis C, Casella G, Wells MT. Assessing evidence in multiple hypotheses. Journal of the American Statistical Association. 1996;91(435):1268–1277. [Google Scholar]
- Graham DJ. Cox-2 inhibitors, other nsaids, and cardiovascular risk: The seduction of common sense. JAMA. 2006;296(13):1653–1656. doi: 10.1001/jama.296.13.jed60058. [DOI] [PubMed] [Google Scholar]
- Grechanovsky E, Hochberg Y. Closed procedures are better and often admit a shortcut. Journal of Statistical Planning and Inference. 1999;76(1-2):79–91. [Google Scholar]
- Hedges LV. Meta-analysis. Journal of Educational and Behavioral Statistics. 1992;17(4):279–296. [Google Scholar]
- Hedges LV, Cooper H, Bushman BJ. Testing the null hypothesis in meta-analysis: A comparison of combined probability and confidence interval procedures. Psychological Bulletin. 1992;111(1):188–194. [Google Scholar]
- Hedges LV, Olkin I. Statistical Methods for Meta-Analysis. Academic Press; San Diego, CA: 1985. [Google Scholar]
- Henning KSS. The Effects of Closure-Based Multiple Testing on the Power of P-Value Combination Tests. Lubbock, TX: 2011. Doctoral Dissertation. [Google Scholar]
- Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika. 1988;75(4):800–802. [Google Scholar]
- Hochberg Y, Tamhane AC. Multiple Comparison Procedures. Vol. 1. John Wiley & Sons; 1987. New York. [Google Scholar]
- Holm S. A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics. 1979a;6(2):65–70. [Google Scholar]
- Holm S. A stagewise directional test based on t statistics. Chalmers University of Technology; 1979b. Research report. [Google Scholar]
- Holm S. In: Bereanu B, Grigorescu S, Josifescu M, Postelnicu T, editors. A stagewise directional test for the normal regression situation; Proceedings of the Sixth Conference on Probability Theory; National Institute of Metrology; 1981. pp. 103–106. [Google Scholar]
- Hommel G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika. 1988;75(2):383–386. [Google Scholar]
- Hommel G. Adaptive modifications of hypotheses after an interim analysis. Biometrical Journal. 2001;43(5):581–589. [Google Scholar]
- Hommel G, Bretz F, Maurer W. Multiple hypotheses testing based on ordered p values-a historical survey with applications to medical research. Journal of Biopharmaceutical Statistics. 2011;21(4):595–609. doi: 10.1080/10543406.2011.552879. [DOI] [PubMed] [Google Scholar]
- Hsu JC. Multiple Comparisons: Theory and Methods. Chapman & Hall/CRC; Boca Raton, FL: 1996. [Google Scholar]
- Huque MF, Alosh M. A flexible fixed-sequence testing method for hierarchically ordered correlated multiple endpoints in clinical trials. Journal of Statistical Planning and Inference. 2008;138(2):321–335. [Google Scholar]
- International Conference on Harmonisation: Efficacy . Statistical principles for clinical trials: E9. ICH; 1998. Technical report. [Google Scholar]
- Kechris KJ, Biehs B, Kornberg TB. Generalizing moving averages for tiling arrays using combined p-value statistics. Statistical Applications in Genetics and Molecular Biology. 2010;9(1) doi: 10.2202/1544-6115.1434. Article 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kieser M, Bauer P, Lehmacher W. Inference on multiple endpoints in clinical trials with adaptive interim analyses. Biometrical Journal. 1999;41(3):261–277. [Google Scholar]
- King RT. The tale of a dream, a drug, and data dredging. 1995 Retrieved from http://www.apnewsarchive.com.
- Korn EL, Troendle JF, McShane LM, Simon R. Controlling the number of false discoveries: application to high-dimensional genomic data. Journal of Statistical Planning and Inference. 2004;124(2):379–398. [Google Scholar]
- Koziol JA, Perlman MD. Combining independent chi-squared tests. Journal of the American Statistical Association. 1978;73(364):753–763. [Google Scholar]
- Koziol JA, Tuckwell HC. A weighted nonparametric procedure for the combination of independent events. Biometrical Journal. 1994;36(8):1005–1012. [Google Scholar]
- Koziol JA, Tuckwell HC. A Bayesian method for combining statistical tests. Journal of Statistical Planning and Inference. 1999;78(1-2):317–323. [Google Scholar]
- Lancaster HO. The combination of probabilities: An application of orthonormal functions. Australian 8 New Zealand Journal of Statistics. 1961;3(1):20–33. [Google Scholar]
- Lange NMLC. The Fundamentals of Modern Statistical Genetics. Springer; New York: 2011. Genome wide association studies; pp. 175–189. Statistics for Biology and Health. [Google Scholar]
- Lehmacher W, Wassmer G. Adaptive sample size calculations in group sequential trials. Biometrics. 1999;55(4):1286–1290. doi: 10.1111/j.0006-341x.1999.01286.x. [DOI] [PubMed] [Google Scholar]
- Lehmacher W, Wassmer G, Reitmeir P. Procedures for two-sample comparisons with multiple endpoints controlling the experimentwise error rate. Biometrics. 1991;47(2):511–521. [PubMed] [Google Scholar]
- Lindley DV. The 1988 Wald memorial lectures: The present position in bayesian statistics. Statistical Science. 1990;8(1):44–65. [Google Scholar]
- Lindsay RM, Ehrenberg ASC. The design of replicated studies. The American Statistician. 1993;47(3):217–228. [Google Scholar]
- Liptak T. On the combination of independent events. Magyar Tud. Akad. Mat. Kutato Int. Kozl. 1958;3:171–197. [Google Scholar]
- Littell RC, Folks JL. Asymptotic optimality of Fisher’s method of combining independent tests. Journal of the American Statistical Association. 1971;66(336):802–806. [Google Scholar]
- Loughin TM. A systematic comparison of methods for combining p-values from independent tests. Computational Statistics 8 Data Analysis. 2004;47(3):467–485. [Google Scholar]
- Mallinckrodt CH. The test of public scrutiny. Pharmaceutical Statistics. 2006;5(4):249–252. doi: 10.1002/pst.243. [DOI] [PubMed] [Google Scholar]
- Marcus R, Peritz E, Gabriel KR. On closed testing procedures with special reference to ordered analysis of variance. Biometrika. 1976;63(3):655–660. [Google Scholar]
- Marden JI. Combining independent noncentral chi squared or F tests. The Annals of Statistics. 1982;10(1):266–277. [Google Scholar]
- Marden JI. Combining independent one-sided noncentral t or normal mean tests. The Annals of Statistics. 1985;13(4):1535–1553. [Google Scholar]
- Mosteller F, Bush RR. Selected quantitative techniques. In: Lindzey G, editor. Handbook of Social Psychology. Vol. 1. Addison-Wesley; Reading, MA: 1954. pp. 289–334. [Google Scholar]
- Newton MA, Quintana FA, den Boon JA, Sengupta S, Ahlquist P. Random-set methods identify distinct aspects of the enrichment signal in gene-set analysis. The Annals of Applied Statistics. 2007;1(1):85–106. [Google Scholar]
- O’Brien PC. Procedures for comparing samples with multiple endpoints. Biometrics. 1984;40(4):1079–1087. [PubMed] [Google Scholar]
- O’Keefe DJ. Colloquy: Should familywise alpha be adjusted? Human Communication Research. 2003;29(3):431–447. [Google Scholar]
- O’Neill R, Wetherill GB. The present state of multiple comparison methods. Journal of the Royal Statistical Society. 1971;33(2):218–250. [Google Scholar]
- Ouellette SP, Dorsey FC, Moshiach S, Cleveland JL, Carabeo RA. Chlamydia species-dependent differences in the growth requirement for lysosomes. PLoS ONE. 2011;6(3):e16783. doi: 10.1371/journal.pone.0016783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng G, Luo L, Siu H, Zhu Y, Hu P, et al. Gene and pathway-based second-wave analysis of genome-wide association studies. European Journal of Human Genetics. 2009;18(1):111–117. doi: 10.1038/ejhg.2009.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piegorsch WW, Bailer AJ. Combining information. Wiley Interdisciplinary Reviews: Computational Statistics. 2009;1(3):354–360. doi: 10.1002/wics.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pocock SJ, Geller NL, Tsiatis AA. The analysis of multiple endpoints in clinical trials. Biometrics. 1987;43(3):487–498. [PubMed] [Google Scholar]
- Rhodes DR, Barrette TR, Rubin MA, Ghosh D, Chinnaiyan AM. Meta-analysis of microarrays. Cancer Research. 2002;62(15):4427–4433. [PubMed] [Google Scholar]
- Rødland EA. Simes’ procedure is ’valid on average’. Biometrika. 2006;93(3):742–746. [Google Scholar]
- Romano J, Shaikh A, Wolf M. Consonance and the closure method in multiple testing. The International Journal of Biostatistics. 2011;7(1):1–38. [Google Scholar]
- Romano JP, Wolf M. Exact and approximate stepdown methods for multiple hypothesis testing. Journal of the American Statistical Association. 2005;100(469):94–108. [Google Scholar]
- Rosenthal R. The "file drawer problem" and tolerance for null results. Psychological bulletin. 1979;86(3):638–41. [Google Scholar]
- Ryan SM, Jorm AF, Lubman DI. Parenting factors associated with reduced adolescent alcohol use: A systematic review of longitudinal studies. Australian and New Zealand Journal of Psychiatry. 2010;44(9):774–783. doi: 10.1080/00048674.2010.501759. [DOI] [PubMed] [Google Scholar]
- Samuel-Cahn E. Is the Simes improved Bonferroni procedure conservative? Biometrika. 1996;83(4):928–933. [Google Scholar]
- Sankoh AJ, Huque MF, Dubey SD. Some comments on frequently used multiple endpoint adjustment methods in clinical trials. Statistics in Medicine. 1997;16(22):2529–2542. doi: 10.1002/(sici)1097-0258(19971130)16:22<2529::aid-sim692>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- Sarkar SK, Chang C. The Simes method for multiple hypothesis testing with positively dependent test statistics. Journal of the American Statistical Association. 1997;92(440):1601–1608. [Google Scholar]
- Scott S, Kranz JE, Cole J, Lincecum JM, Thompson K, et al. Design, power, and interpretation of studies in the standard murine model of ALS. Amyotrophic Lateral Sclerosis. 2008;9(1):4–15. doi: 10.1080/17482960701856300. [DOI] [PubMed] [Google Scholar]
- Shaffer JP. Control of directional errors with stagewise multiple test procedures. The Annals of Statistics. 1980;8(6):1342–1347. [Google Scholar]
- Shaffer JP. Multiple hypothesis testing. Annual Review of Psychology. 1995;46(1):561–584. [Google Scholar]
- S̆idák Z. Rectangular confidence regions for the means of multivariate normal distributions. Journal of the American Statistical Association. 1967;62(318):626–633. [Google Scholar]
- Simes RJ. An improved Bonferroni procedure for multiple tests of significance. Biometrika. 1986;73(3):751–754. [Google Scholar]
- Sonnemann E. General solutions to multiple testing problems. Biometrical Journal. 2008;50(5):641–656. doi: 10.1002/bimj.200810462. [DOI] [PubMed] [Google Scholar]
- Stouffer SA, Suchman EA, DeVinney LC, Star SA. The American Soldier: Adjustment During Army Life. Vol. 1. Princeton University Press; Princeton, NJ: 1949. Jr., R. M. W. Studies in Social Psychology in World War II. [Google Scholar]
- Taylor J, Tibshirani R. A tail strength measure for assessing the overall univariate significance in a dataset. Biostatistics. 2006;7(2):167–181. doi: 10.1093/biostatistics/kxj009. [DOI] [PubMed] [Google Scholar]
- Tippett LHC. The Methods of Statistics. 1st Williams and Northgate; London: 1931. [Google Scholar]
- Westberg M. Combining independent statistical tests. The Statistician. 1985;34(3):287–296. [Google Scholar]
- Westfall PH, Bretz F. Multiplicity in clinical trials. In: Chow SC, editor. Encyclopedia of Biopharmaceutical Statistics. 3rd Vol. 2. Informa Healthcare; New York: 2010. pp. 889–896. [Google Scholar]
- Westfall PH, Bretz F, Tobias RD. Directional error rates of closed testing procedures. Statistics in Biopharmaceutical Research. 2013;5(4):345–355. [Google Scholar]
- Westfall PH, Krishen A. Optimally weighted, fixed sequence and gatekeeper multiple testing procedures. Journal of Statistical Planning and Inference. 2001;99(1):25–40. [Google Scholar]
- Westfall PH, Kropf S, Finos L. Recent Developments in Multiple Comparison Procedures. Institute of Mathematical Statistics; 2004. Weighted FWE-controlling methods in high-dimensional situations; pp. 143–154. [Google Scholar]
- Westfall PH, Tobias RD, Wolfinger RD. Multiple Comparisons and Multiple Tests Using the SAS System. 2nd SAS Institute Inc.; Cary, NC: 2011. [Google Scholar]
- Westfall PH, Young SS. Resampling-Based Multiple Testing: Examples and Methods for P-Value Adjustment. John Wiley & Sons; New York: 1993. [Google Scholar]
- Westfall PH, Zaykin DV, Young SS. Multiple tests for genetic effects in association studies. In: Looney SW, editor. Biostatistial Methods. Vol. 184. Humana Press; Totowa, NJ: 2002. pp. 143–168. Methods in Molecular Biology. [DOI] [PubMed] [Google Scholar]
- Whitlock MC. Combining probability from independent tests: The weighted z method is superior to Fisher’s approach. Journal of Evolutionary Biology. 2005;18(5):1368–1373. doi: 10.1111/j.1420-9101.2005.00917.x. [DOI] [PubMed] [Google Scholar]
- Wiens BL. A fixed sequence Bonferroni procedure for testing multiple endpoints. Pharmaceutical Statistics. 2003;2(3):211–215. [Google Scholar]
- Wilson D. Side effects may include lawsuits. The New York Times. 2010 page http://www.nytimes.com/2010/10/03/business/03psych.html.
- Wisniewski S, Rush A, Nierenberg A, Gaynes B, Warden D, et al. Can phase III trial results of antidepressant medications be generalized to clinical practice? a STAR* d report. American Journal of Psychiatry. 2009;166(5):599–607. doi: 10.1176/appi.ajp.2008.08071027. [DOI] [PubMed] [Google Scholar]
- Wright SP. Adjusted p-values for simultaneous inference. Biometrics. 1992;48(4):1005–1013. [Google Scholar]
- Yates F. A note on the application of the combination of probabilities test to a set of 2×2 tables. Biometrika. 1955;42(3/4):404–411. [Google Scholar]
- Zaykin DV, Zhivotovsky LA, Westfall PH, Weir BS. Truncated product method for combining p-values. Genetic Epidemiology. 2002;22(2):170–185. doi: 10.1002/gepi.0042. [DOI] [PubMed] [Google Scholar]