Exploring the Dynamics and Mutational Landscape of Riboregulation with a Minimal Synthetic Circuit in Living Cells

Abstract

The regulation of gene expression, triggered by conformational changes in RNA molecules, is widely observed in cellular systems. Here, we examine this mode of control by means of a model-based design and construction of a fully synthetic riboregulatory device. We present a theoretical framework that rests on a simple energy model to predict the dynamic response of such a system. Following an equilibrium description, our framework integrates thermodynamic properties—anticipated with an RNA physicochemical model—with a detailed description of the intermolecular interaction. The theoretical calculations are confirmed with an experimental characterization of the action of the riboregulatory device within living cells. This illustrates, more broadly, the predictability of genetic robustness on synthetic systems, and the faculty to engineer gene expression programs from a minimal set of first principles.

Introduction

It is now widely recognized that phenotypic evolution often occurs through genetic changes in regulatory (noncoding) regions of the genome that affect fundamental parameters of gene expression (1). Most of the attention on how these changes alter expression has been focused on sequences associated with transcriptional regulation (2), but sequences related to other types of control should also matter. In particular, noncoding regions linked to regulatory RNA molecules are being progressively identified as instrumental modulating agents at work in many taxonomically diverse genomes (3,4). In the specific case of riboregulation, the capacity to change expression typically relies on the assembly of flexible structures constituted by combinations of interacting RNAs (4), i.e., between a small noncoding RNA (sRNA) and a messenger RNA (mRNA). In this situation, it is important to first understand how the species involved determine different expression features to then inspect how sequence mutations could reshape these parameters.

Notably, some of these matters have begun to be examined in recent studies on natural riboregulation in bacteria—studies that have identified a number of principles. For example, the following has been confirmed: there is an activation threshold from which the system responds (5); the sRNA action on target genes is fast and linear, and this imposes a moderate dynamic range (5–7); and levels of gene expression appear to be correlated with the predicted free energies of the system (8,9). However, more work is needed to fully recognize the design principles of RNA-based control, such as the impact of species stoichiometry or interaction strength on its function, and how the corresponding sequences encode this information. To what extent these principles are influenced (or not) by more complex processes linked to the intricate regulatory circuitry of the cell is also not entirely known.

To investigate how several basic aspects of riboregulation predictably determine function, in this article we followed a bottom-up approach complementary to the analysis of natural systems. We engineered a simple synthetic riboregulatory device, in which the sequences of its RNA species were designed computationally (using energetic and conformational criteria) (10). Synthetic approaches have successfully contributed to appreciation of the many fundamental aspects of gene regulation (11) by constructing tunable systems that limit any unexpected interplay with the hosting cell, and they are expected to be equally productive in the case of RNA, with many practical implications (12). We aimed to characterize quantitatively how the conformations, energetics, and concentrations determine expression in the synthetic system, and how this information is encoded in the nucleotide sequences. This requires solving the equilibrium and simulating the intra- and intermolecular structures of the species involved with the use of energy models (13,14). The validity of this class of models is expected from its effective prediction of macromolecular structures even at atomic accuracy (15).

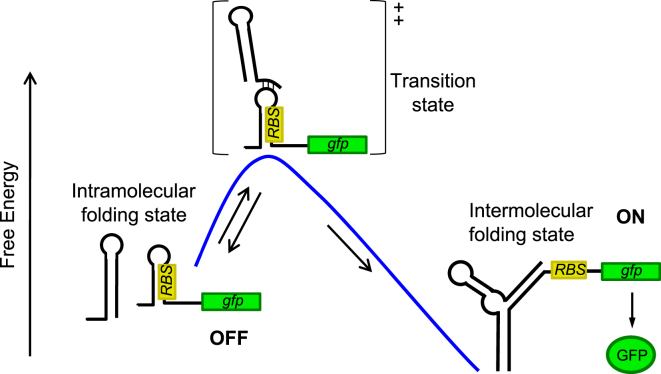
In the following, we initially discuss the theoretical framework required to characterize the response of the (synthetic) riboregulatory system. We focused on an essential mechanism that achieves control of protein concentration through a conformational change affecting the interaction of an mRNA with the ribosome (16). An sRNA interacts with the 5′ untranslated region (UTR), which codes for the gene acting as the output of the system (Fig. 1). This allowed us to anticipate how RNA abundances primarily determine the dynamic response, and how response becomes modified by mutations that reshape the core sRNA-mRNA interacting capacities. We then present experimental results testing the framework in Escherichia coli, with an RNA switch that follows the theoretical proposal (we termed this switch “RAJ11”). The system incorporates a green fluorescent protein (GFP) as riboregulated element as well as the capacity to modulate the expression of the RNA molecules involved with the presence of external inducers in the appropriate bacterial genetic background (Fig. S1 in the Supporting Material) (17).

Figure 1.

Scheme of a simple (synthetic) riboregulation system. A cis-repressed gene, where the ribosome-binding site is trapped, is trans-activated by a small RNA (sRNA) that induces a conformational change to release the ribosome-binding site. The output of the regulation resides in the expression of a gfp gene. To see this figure in color, go online.

Materials and Methods

Calculation of RNA free energies and secondary structures

The synthetic riboregulatory system RAJ11 was studied in this work (Fig. S1), which was obtained by computational design (10), together with manually designed sequence mutants, to derive an energy-based model for predicting riboregulatory activity. The natural riboregulatory systems IS10 (9) and RyhB (8) and the synthetic system RR12 (16) (together with the corresponding mutants) were also considered. To compute the free energies and secondary structures of the different RNA species of the system (intra- and intermolecular) the VIENNARNA package (http://www.tbi.univie.ac.at/RNA/) was used (18).

Plasmids, strains, and media

All plasmids characterized in this work were constructed from plasmids pRAJ11 and pRAJ11m, coding for the riboregulatory device RAJ11 (10). Mutations were introduced in both the sRNA and 5′ UTR, and all new mutants were sequenced. As negative control, a plasmid pBlueScript was used. As positive control, a plasmid with GFP under the control of promoter P_LtetO1 was used. To perform the stationary characterization, E. coli DH5α was transformed. This allowed expressing constitutively the sRNA and mRNA. However, to perform the dynamic characterization, E. coli MG1655Z1 (17) was transformed. This allowed controlling the expression of the sRNA with aTc (anhydrotetracycline), and the expression of the mRNA with IPTG (isopropyl-β-D-1-thiogalactopyranoside). Luria-Bertani medium was used for overnight cultures, and minimal medium M9 (1 × M9 salts, 2 mM MgSO₄, 0.1 mM CaCl₂, 0.4% glucose) for characterization cultures. IPTG was used at the concentration of 1 mM, and aTc was varied from 0 to 100 ng/mL. Ampicillin was used at the concentration of 50 μg/mL. See the Supporting Material for details on transcript quantification and genome integration.

Characterization by fluorometry

Cultures inoculated from single colonies (three biological replicates) were grown overnight in Luria-Bertani medium at 37°C and 220 rpm. Cultures were then diluted 1:100 in minimal medium M9, and were grown in the same conditions to reach higher OD₆₀₀. Subsequently, a multiwell plate was loaded with 200 μL for each sample, which was assayed in a Victor X5 Multilabel Plate Reader (Perkin Elmer, Waltham, MA) to measure absorbance (600 nm absorbance filter) and fluorescence (485/14 nm excitation filter, 535/25 nm emission filter, for GFP). Background values of absorbance and fluorescence, which corresponded to medium M9, were subtracted to correct the signals, and the normalized fluorescence was calculated as the ratio of fluorescence and absorbance (see the Supporting Material for more details). Growth rates were obtained as the slope of a linear regression between the log values of the corrected absorbance and time.

Results and Discussion

Theoretical prediction of dynamic behavior

We examined the fold change in expression of the riboregulated protein (f), i.e., the ratio in protein concentration at steady state when the sRNA is present (p₁) or absent (p₀), as an effective score to quantify the performance of the system (f = p₁/p₀) (19). This required us to put forward a simple differential equation to describe protein dynamics, $dp/dt=R-\delta p$. Here, p denotes the concentration of the protein, R is the translation rate (determined by the interaction between the sRNA and mRNA; see below), and δ is the effective protein degradation rate (a function of the rates of protein degradation and maturation and cell growth; defined in the Supporting Material) (20).

One can then generally write the translation rate as R = ρ₀(x_m – y) + ρ₁y, a combination of translation rates when sRNA is absent (ρ₀) or present (ρ₁), with y being the concentration of the sRNA-mRNA complex, x_m denoting the total concentration of mRNA (so that x_m − y denotes concentration of free mRNA species). While ρ₁ is of course an average over the ensemble of conformational states for the complex (i.e., ${\rho }_1={\sum }_i{\rho }_{1i}{\Pi }_i$, where ρ_1i is the translation rate of the ith conformational state and Π_i is the corresponding Boltzmann probability), we considered here the ensemble dominated by the optimal state (10) as the sequences in RAJ11 were computationally optimized.

To model the concentrations of the corresponding molecular species, we considered a hybridization reaction between sRNA and mRNA with an intermediary state, and followed a law of mass action characterizing the resulting equilibrium state. The concentration of the complex is given by

$$y=\frac{x_s+x_m+K}{2}\left(1-\sqrt{1-\frac{4x_s{x}_m}{{\left(x_s+x_m+K\right)}^2}}\right)$$

(see the Supporting Material), where K is the effective dissociation constant of the hybridization reaction, and x_s denotes the total concentration of the sRNA species (recall that x_m indicates the equivalent for mRNA). To derive this expression, we discarded the formation of homodimers, as the sequences of the RNA species were designed to minimize this type of interactions (10).

Note also that K represents a threshold value with respect to the amount of sRNA. This threshold-lineal behavior (at low sRNA concentrations there is no interaction; beyond the threshold the expression of the riboregulated gene increases linearly) was initially observed in studies of natural systems (5,7). To overcome this threshold, the concentrations of the RNA molecules at play must be high (in contrast to the dozens or even hundreds of molecules required to regulate transcription with proteins). Thus, certain sRNA molecules have evolved sequence domains able to recruit RNA chaperones to help in the intermolecular interaction (e.g., Hfq) (21). This is achieved in our model by lowering the value of K.

For the synthetic riboregulatory system RAJ11, in which the sequences were designed by only accounting for structural and energetic considerations, Hfq and eventually other host helpers are expected to play a minor role, i.e., K presents an even higher value. We thus approximated at first-order the expression for y, with K >> x_m + x_s, to obtain y ≃ x_sx_m/K. This imposes a condition of high gene expression to secure hybridization between the RNA species, which could be achieved by using a high-copy number plasmid and strong promoters (10,22).

Finally, and given that in our experimental system ρ₀ → 0 (i.e., p₀ → 0; very efficient cis-repression), we can write $p_1\simeq {\rho }_{1}y/\delta ={\rho }_1{x}_s{x}_m/\delta K$. The very low value of p₀ limits the confident experimental determination of f. We thus introduced a modified expression of f that we termed “apparent dynamic range” (f_app). This new measure, to our knowledge, controls for the strong cis-repression of the riboregulated gene (GFP) by including explicitly a parameter that denotes the autofluorescence (θ, such that p₀ +θ ≃ θ, i.e., the level of fluorescence of cells expressing the mRNA alone is very similar to the one detected in control cells; see the Supporting Material). This is defined as

$$f_{\text{app}}=\frac{p_1+\theta }{p_0+\theta }\simeq 1+\frac{p_1}{\theta }.$$ (1)

We can substitute the previous expression of p₁ to obtain a full theoretical prediction for f_app that we can also quantify experimentally.

Theoretical prediction of effects of mutations

In addition, we analyzed the impact of the thermodynamic properties of the system, which affect the value of K. In this way, we can anticipate the changes in riboregulatory activity with mutations. We assumed a thermodynamic equilibrium of the system, which has two states according to the reaction coordinate: sRNA and mRNA separate, or sRNA and mRNA hybridized. Then, the free energy of each state determines the probability of finding the system in that state. For this calculation, we predicted the associated free energies (14), and then followed the many particle partition function (23) to get $1/K=\left(1/K_0\right)W_{sm}\left(Z_{sm}/Z_s{Z}_m-1\right)$, where K₀ is a constant that ultimately represents an asymptotic effective dissociation constant (see the Supporting Material). W_sm is an entropic factor that accounts for the initiation of the reaction. Z_s is the partition function of the sRNA, Z_m is the partition function of the mRNA, and Z_sm is the partition function of the complex formed between the sRNA and mRNA.

Even though a living cell integrates multiple dynamic processes of differing nature, the high number of molecules in the system of interest (the amount of sRNA and mRNA is estimated in hundreds of molecules per gene copy), the difference in timescales between processes (intramolecular folding faster than sRNA-mRNA interaction, which in turn is faster than translation), and the dominance of certain processes over others (which serve to simplify the great complexity of biological systems), ultimately make useful thermodynamic descriptions to model and predict experimental results. Indeed, thermodynamic models have been proven quite helpful to study transcription regulation (24), and here we applied the same framework in a riboregulatory context.

In a living cell, the intermolecular interaction starts with highly accessible, unstructured regions in both species (25), forming an intermediary state. We considered that the free energy of activation depends on the length and composition of the seed sequence. This consideration makes that K, in the case of riboregulation, is approached not only by the free energy of hybridization, but also by the free energy of activation. (Note that previous models considered a sequence-independent activation barrier, but recent data has shown that the dynamic range is well explained by a composition of these two free energies (9).)

Therefore, if we calculate the free energy of the seed (or toehold) interaction (ΔG^#), the term W_sm can be approached by $e^{-\beta \Delta G^{\#}}$. In addition, because we considered the ensembles dominated by the optimal states (and given ΔG as the free energy of the whole hybridization), we can approach the ratio of partition functions by $e^{-\beta \Delta G}$. This gave the following energy model:

$$\frac{K_0}{K}=e^{-\beta \Delta G^{\#}}\left(e^{-\beta \Delta G}-1\right).$$

Experimental validation of dynamic behavior

We next assessed experimentally the preceding theoretical framework. We initially examined the influence of RNA concentration (of both species and of sRNA). To this end, we expressed f_app as

$$f_{\text{app}}=1+\varphi S{D}^2,$$ (2)

with S denoting the ratio between the sRNA and mRNA concentrations (S = x_s/x_m), D indicating the normalized gene dosage (D = x_m/M, with M representing the highest mRNA concentration attainable from plasmid expression), and ϕ an empirical constant given by $\varphi ={\rho }_1{M}^2/\theta \delta K$ (see details in the Supporting Material). At maximal expression of the RNA species for system RAJ11 (i.e., mounted in a plasmid; D = 1), we obtained the experimental value of f_app = 7.9. Under these conditions, we also quantified S by measuring transcript abundance, obtaining S ≃ 1 (Fig. S2, and see experimental details in the Supporting Material; note that other riboregulatory systems may, however, present different relative concentrations, even when the species share gene copy number). With the previous estimates, the value of ϕ was simply calculated (not fitted) as f_app − 1 = 6.9 (see also Fig. S5). Note that ϕ includes all complexity of the dynamic model (i.e., it integrates all dynamic parameters used to construct it), and then only one empirically calculated parameter was used to make predictions.

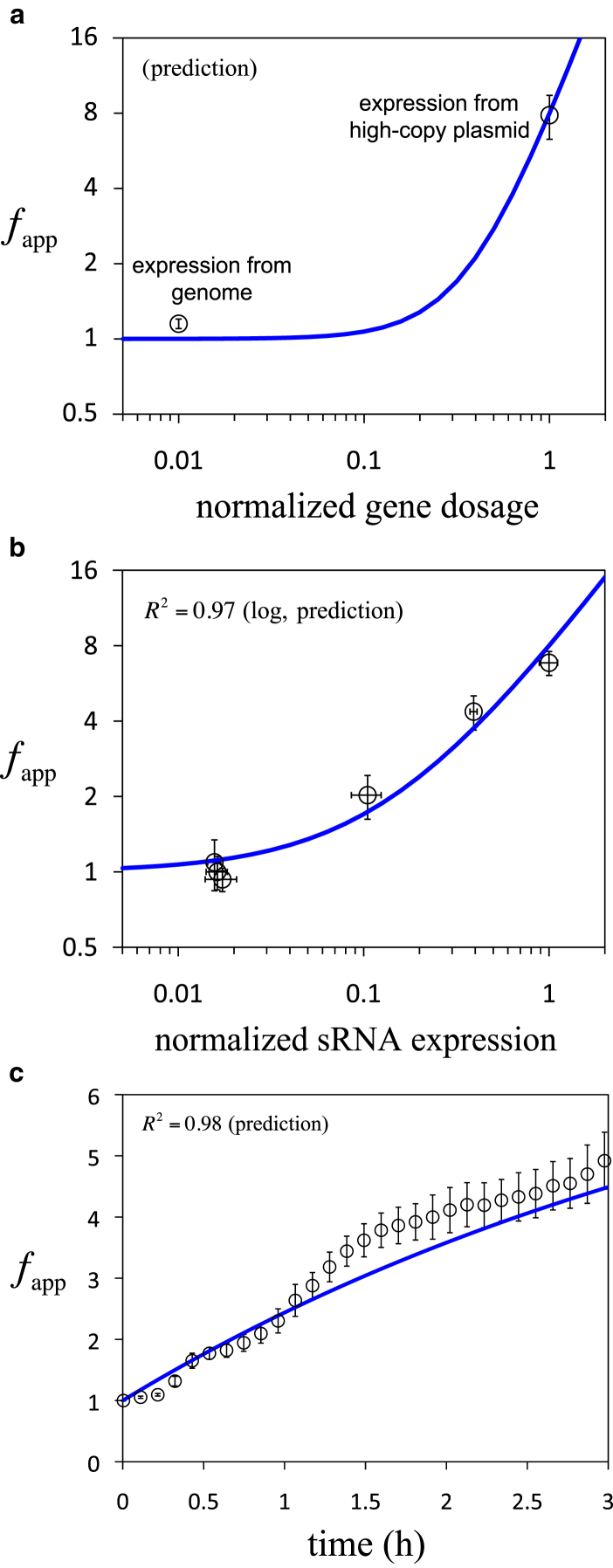
In this way, we can predict the behavior of f_app using Eq. 2 as a function of gene dosage and sRNA expression, D and S (solid lines in Fig. 2, a and b). We tested the model by mounting alternatively the system RAJ11 into the bacterium chromosome (with expected 100-fold decrease in gene dosage with respect to the plasmid; experimental details in the Supporting Material). As predicted, we observed no significant activation by the sRNA in this case (Figs. 2a and S3). Moreover, by varying the concentration of one of the inducers (anhydrotetracycline), we could modulate sRNA expression (Fig. S1). We employed an alternative synthetic construction to obtain, with the use of a gfp gene, the values of S for different concentrations of anhydrotetracycline (Fig. S4; and see experimental details in the Supporting Material). Experimental results were in tune with the prediction (Fig. 2b), highlighting that the system was not at saturation.

Figure 2.

Dynamics of the riboregulated gene. Dynamic range (f_app) as a function of normalized gene dosage (a), normalized sRNA expression (b), and time (c). (Circles) Average of biological replicates and (error bars) standard deviation correspond to experimental data; (solid lines) predictions from the models in Eqs. 2 and 3. R² quantifies the agreement between theoretical and experimental calculations (no fitting). To see this figure in color, go online.

In addition to the predictions at steady state, we studied the transient response. The goal here was to examine to what extent the dynamics of the sRNA-mRNA interaction influences the protein dynamics (i.e., if it changes its shape and scale, incorporates delays, etc.) (26). This is important because it quantifies the rate at which the phenotype changes—either as a result of an environmental perturbation (change in the concentration of one species) or as a mutational effect. By assuming a fast scale of RNA interactions, we have a dynamic equilibrium where the system maintains the linear dependence of y with x_s upon changes in transcription with time. Then, the differential equation is analytically solvable, resulting in $p\left(t\right)=({\rho }_{1}M/K)e^{-\delta t}{\int }_0^t{e}^{\delta \tau }{x}_s\left(\tau \right)d\tau$, with the initial condition of p(0) = 0. The timescale of the sRNA dynamics is much faster than that of the protein (i.e., the sRNA is quickly degraded). To model an experiment of induction at t = 0 with maximal concentration of anhydrotetracycline, we assumed constant sRNA expression (i.e., quasi-steady state) to solve the integral, obtaining

$$f_{\text{app}}\left(t\right)=1+\varphi S{D}^2\left(1-e^{-\delta t}\right).$$ (3)

To predict the dynamic response, we needed an estimation of δ. For that, we first measured the cell growth rate in our experimental conditions, obtaining 0.18 h⁻¹, and then we took advantage of the measurement of the GFP maturation time from earlier work (27), known to be ∼10 min. In this case, GFP lacks any additional degradation tag, so it is as stable as ∼1 day. Taking these values together, we calculated δ = 0.23 h⁻¹ (see the Supporting Material). We performed a time-dependent experiment to monitor GFP upon induction with anhydrotetracycline, showing similar characteristic times (∼1/δ) in the theoretical and experimental dynamics (Fig. 2c); note that in this case, S = 1 and D = 1. We also analyzed the effect of different maturation rates and protein stabilities in Fig. S6. This showed that the sRNA-mRNA interaction is fast and then can be treated in quasi-steady state.

Experimental validation of effects of mutations

We next examined the effect of mutations in the RNAs involved in the riboregulation. To address this experimentally, we considered maximal expression of both species (hence, in the following, S = 1 and D = 1). Mutations modify the effective dissociation constant of the system (K) and consequently ϕ in Eq. 2. Thus, by introducing ${\varphi }_0={\rho }_1{M}^2/\theta \delta K_0$, we have

$$f_{\text{app}}=1+{\varphi }_{0}S{D}^2{e}^{-\beta \Delta G^{\#}}\left(e^{-\beta \Delta G}-1\right).$$ (4)

Note then that ϕ₀ is a parameter whose value is not affected by the mutations introduced. The value of the parameter β is then critical to make predictions. We here assumed that β is a global constant that can be employed to characterize bacterial riboregulation. To estimate it in an independent way, we considered previous experimental data on natural and synthetic riboregulation (8,9,16). Equation 4 can be reorganized to make explicit the linear dependence of log(f_app – 1) with ΔG^# + ΔG (assuming βΔG << 0), given −β as the slope. We obtained β = 0.38 mol/Kcal with a linear regression between the logarithm of relative f and ΔG^# + ΔG (Fig. S7; note that, without loss of generality, f was used instead of f_app). We also performed a K-fold cross validation to analyze the estimation of β (Fig. S8). With this value and having calculated ΔG^# = −10.3 Kcal/mol and ΔG = −14.5 Kcal/mol for system RAJ11 (recall f_app = 7.9), we calculated (not fitted) the value of the empirical constant ϕ₀ = 5.7 × 10⁻⁴ (see details in the Supporting Material).

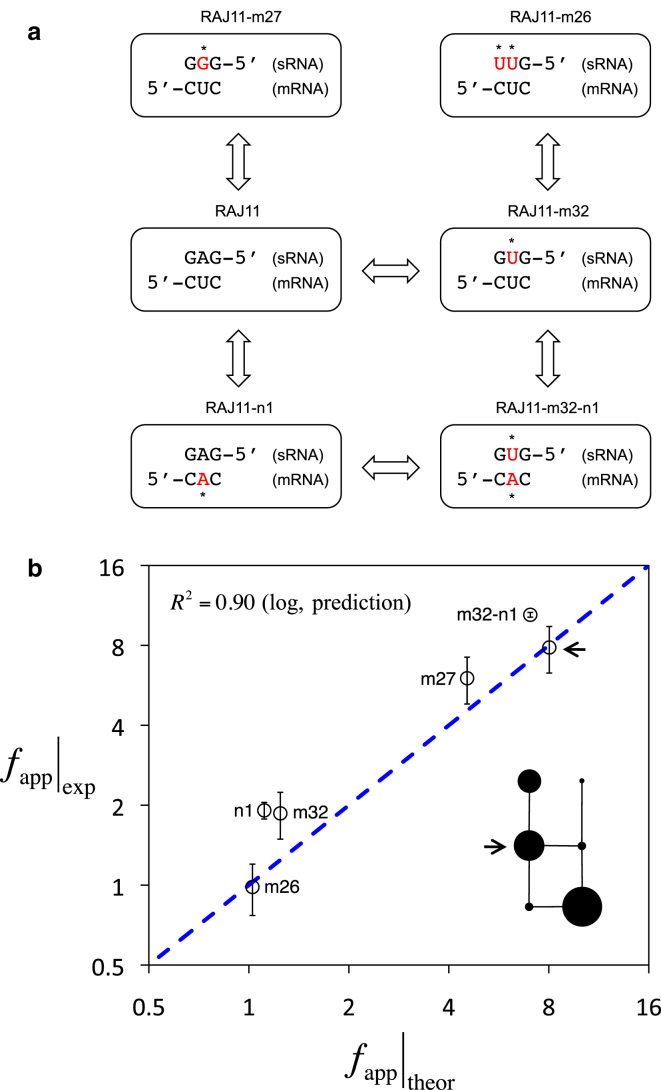
To assess the predictability of our energy model, Eq. 4, we constructed different genotypes from the riboregulatory system RAJ11 and characterized experimentally the resulting apparent dynamic ranges (f_app). We mutated the seed region in both sRNA and 5′ UTR to get six different genotypes (Fig. S9; and see experimental details in the Supporting Material). Experimental results nicely followed the predictions (Fig. 3, and see the Supporting Material for details on the free energy calculations). We also observed that our model could roughly be used to predict activity with free-energy calculations using different empirical parameterizations of the RNA physicochemical model (Fig. S10). Additional predictions showed that point mutations in the seed region contribute in higher extent to reduce activity (Fig. S11). Note in this case that only two empirically calculated parameters (β and ϕ₀) are used in the energy model.

Figure 3.

Sequence-to-function map. (a) Mutated systems from the native RAJ11. We show three nucleotides of the seed region (for both sRNA and 5′ UTR of the mRNA) chosen to contain mutations (marked by an asterisk). (b) Experimental versus theoretical dynamic range (f_app) for different mutant systems with different values of ΔG and ΔG^#. Note that Eq. 4 is used here to calculate f_app. (Dashed line) Equal experimental and theoretical values. (Inset) Network of mutants (edges connect genotypes differing in a single mutation, and node size corresponds to the value of dynamic range). Arrows point to the native system RAJ11. R² quantifies the agreement between theoretical and experimental calculations (no fitting). To see this figure in color, go online.

We also analyzed the degree of cis-repression of this synthetic system. We engineered different mutants of the 5′ UTR to alter the predicted free energy of it (G_m) (see the Supporting Material). Experimentally, we calculated the ratio between fluorescence and autofluorescence for each mutant system, which is a measure of 1 + p₀/θ. Indeed, autofluorescence is given by θ, and mutations in the 5′ UTR lead to different levels of cis-repression, which changes the value of apparent fluorescence in the absence of sRNA (p₀ + θ). According to previous work that examined multiple 5′ UTR sequences (28), and having the value of β, we proposed an empirical exponential trend $\left(p_0\propto e^{\beta G_m}\right)$ to model changes in p₀ with G_m (Fig. S12).

Conclusions

To sum up, our results showed that interacting RNAs need to face thermodynamic equilibria with large effective dissociation constants in a cellular context (e.g., in comparison with transcription factors). This imposes several constraints on their gene expression attributes. For instance, in a fully synthetic riboregulatory system (e.g., RAJ11), it was essential to have high gene dosage (i.e., reach high concentrations) to obtain a significant dynamic range. Those equilibria also entail a linear effect with the sRNA expression on the response genes. The use of a synthetic system was otherwise instrumental to take out the contribution of the protein machinery (21) to the equilibrium, serving to confirm that mere physicochemical criteria are sufficient to explain the observed behavior. Note nevertheless that the binding sites for those chaperones can be exploited in synthetic systems to achieve a higher dynamic range (29). To circumvent the lack of helping-protein-binding sites, interacting RNAs could evolve toward higher free-energy gaps, both in hybridization and activation, to properly work in a living cell. This strategy has been used to design riboregulatory devices with very high dynamic ranges (22).

Of relevance, our energy-based dynamic model accurately predicted the effect of those features on riboregulatory activity in E. coli. In particular, the model correctly explained changes in the observed dynamic range due to changes in RNA expression and mutations introduced in the sequences of the two species. Mutations in the seed region were shown to impact much more on activity due to RNA’s double contribution in ΔG and ΔG^#. This clearly highlights distinct regions on the RNA molecules with different selection pressures. These results pointed out, together with previous observations in natural systems (5,9), general design principles that can be exploited to engineer more sophisticated riboregulatory systems (30).

Although we focused on positive riboregulation, this model could also be applied to account for repressors of translation, and even combined with other bottom-up approaches to account, for instance, for RNA-small-molecule interactions (31,32) or transcription control (19,33), making it relevant in studying layered and integrative regulatory mechanisms. Yet, the combination of systems biology principles together with synthetic biology platforms is expected to illustrate the mechanistic basis and limitations of function, robustness, and evolvability of different riboregulatory circuits.

Author Contributions

G.R. designed the research; G.R., E.M., S.P., J.-A.D., and A.J. performed the research and contributed with materials/tools; and G.R. and J.F.P. analyzed the data and wrote the article.

Editor: Daniel Beard.