The Phylogenetic Signature Underlying ATP Synthase c-Ring Compliance

Abstract

The proton-driven ATP synthase (F_OF₁) is comprised of two rotary, stepping motors (F_O and F₁) coupled by an elastic power transmission. The elastic compliance resides in the rotor module that includes the membrane-embedded F_O c-ring. Proton transport by F_O is firmly coupled to the rotation of the c-ring relative to other F_O subunits (ab₂). It drives ATP synthesis. We used a computational method to investigate the contribution of the c-ring to the total elastic compliance. We performed principal component analysis of conformational ensembles built using distance constraints from the bovine mitochondrial c-ring x-ray structure. Angular rotary twist, the dominant ring motion, was estimated to show that the c-ring accounted in part for the measured compliance. Ring rotation was entrained to rotation of the external helix within each hairpin-shaped c-subunit in the ring. Ensembles of monomer and dimers extracted from complete c-rings showed that the coupling between collective ring and the individual subunit motions was independent of the size of the c-ring, which varies between organisms. Molecular determinants were identified by covariance analysis of residue coevolution and structural-alphabet-based local dynamics correlations. The residue coevolution gave a readout of subunit architecture. The dynamic couplings revealed that the hinge for both ring and subunit helix rotations was constructed from the proton-binding site and the adjacent glycine motif (IB-GGGG) in the midmembrane plane. IB-GGGG motifs were linked by long-range couplings across the ring, while intrasubunit couplings connected the motif to the conserved cytoplasmic loop and adjacent segments. The correlation with principal collective motions shows that the couplings underlie both ring rotary and bending motions. Noncontact couplings between IB-GGGG motifs matched the coevolution signal as well as contact couplings. The residue coevolution reflects the physiological importance of the dynamics that may link proton transfer to ring compliance.

Introduction

Macromolecular ring assemblies have central roles in key physiological processes. Well-studied examples include rotary catalysis (ATP synthase or F_OF₁) (1), chemotactic response (bacterial flagella) (2), and coincidence activation (calcium-calmodulin dependent kinase) (3). Here we combine stochastic simulations of conformational dynamics (4,5) and coevolution analysis (6,7) to decipher the conformational flexibility of ATP synthase c-rings, and diagnose its molecular basis. The c-ring of F_O couples transmembrane proton (or sodium ion) transport to ATP synthesis/hydrolysis by the F₁ motor. Flexibility is important for energy transduction as single-molecule measurements have established that the two stepping rotary motors are coupled by an elastic power transmission (8). The elastic transmission is a necessary requirement for a high turnover rate under load (9).

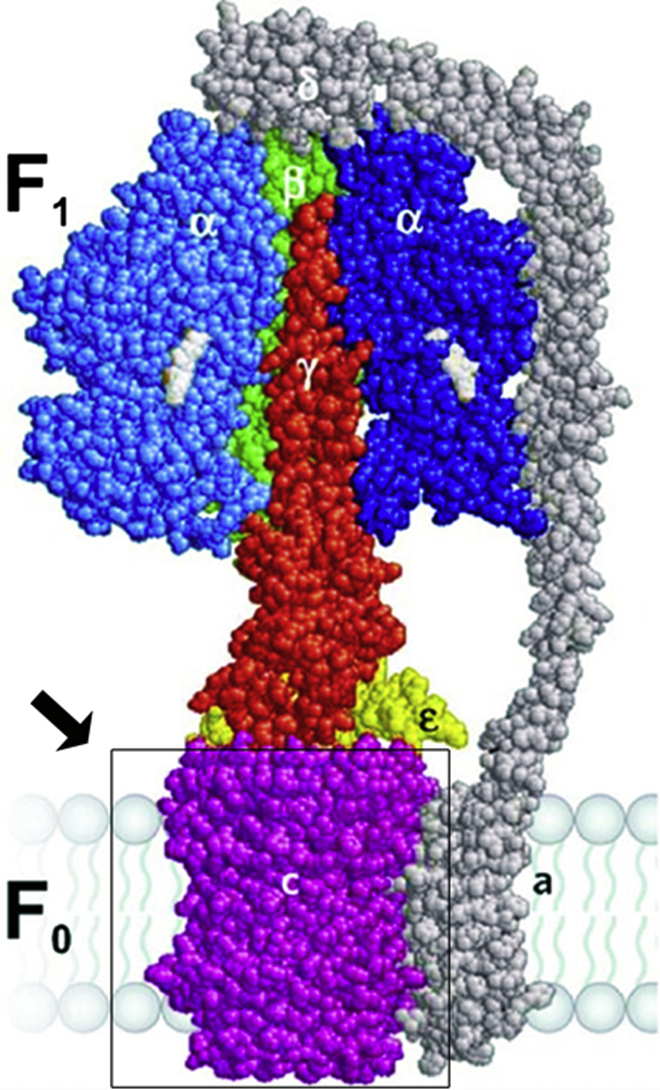
The atomic structure of the ATP synthase is shown (Fig. 1). The c-subunit (AtpE or atpE gene product) forms a helical hairpin (10). The proton/sodium coordination site (ion-binding site (IB)) is built around an essential acid residue at the interface between adjacent subunits in the membrane midplane. A long-standing hypothesis (11–14) is that protons transported from the external medium through a half-channel in the F_O a-subunit bind the c-ring acid residue before ring rotation aligns the residue with a second half-channel. Cryo-electron microscopy has given insight into the structural interactions between the a-subunit and c-ring (15). X-ray crystallography and molecular dynamics (MD) have detailed how local IB motions gated by pH and the adjacent F_O a-subunit mediate acid residue pK changes in nanoseconds (16–19). A similar scenario has been proposed for an F/V hybrid rotor ring in the sodium-coupled ATP synthase (20). If F_O is uncoupled from F₁ the rate of proton transfer at 200-mV driving force is ∼10⁴ s⁻¹ (21), which is equivalent to ∼10³ revolutions/s for a c₁₀-ring. The subsequent subunit motions are debated. Mixed solvent nuclear magnetic resonance (NMR) reported pH-dependent reorientation of the acid residue coupled to twist of the external helix in the c-subunit hairpin (22,23). MD simulations have shown how residue protonation-deprotonation can bias the rotation of the c-subunit by such a mechanism (24). On the other hand, coarse-grained simulations of the c-subunit embedded in a lipid bilayer report have documented relative rotation of the subunit helices (i.e., swirling) (25), distinct from the helix swiveling proposed on the basis of in situ crosslinking to support the NMR (26).

Figure 1.

Homology model of the E. coli F_OF₁, based on the bovine mitochondrial F_OF₁ structure (taken with permission from Wächter et al. (8)). The F_O a-subunit is not part of the structure. (Arrow) Indicating c-ring (boxed). To see this figure in color, go online.

A conserved glycine GXGXGXG (GGGG) motif, with X a variable residue, in the inner helix next to the essential acid residue resembles the dimerization domains in transmembrane α-helices (10). The motif regulates subunit stoichiometry (27) that varies from 8 to 15 between species (17,27,28), ruling out an obligatory match with the invariant F₁ hexamer pseudo-symmetry. Although rotation steps equal to the subunit stoichiometry have been recorded in the Escherichia coli c₁₀-ring (29,30), elastic power transmission best accommodates the F_O and F₁ subunit stoichiometry mismatch. Fluctuation analysis of the motion of the E. coli F₁F_O showed that the major elastic compliance resided in the rotor module (comprising the c-ring together with the F₁ε-and γ-subunits (8,31)). The module had an overall 68 pN.nm torsional stiffness, whereas the stiffness of the stator a/b2 subunits was greater by an order of magnitude. Subsequent simulation of the collective motions of six isolated c-rings (32) using a Gaussian network model (GNM) (33) suggested that part of the rotor compliance might reside in the c-ring.

In this work, we simulated, with atomistic detail, the dynamics of the bovine mitochondrial F_O c₈-ring as well as the dynamics of monomer and dimer subunits isolated from c-rings with different stoichiometry to learn more about the molecular basis for its elastic compliance. Elastic force/torque transmission is a fundamental property of nature’s nanomotors. In molecular motors, chemical or ionic gradients drive steps when running free of load. When coupled to a heavy load (viscous load) that is not specifically tuned to the same steps, rapid turnover necessitates an elastic transmission between the drive and the load. This necessity is a consequence of the interplay of conservative and stochastic forces (Langevin dynamics) that rules nanomechanics. The dependence of the turnover rate on the elastic stiffness has been worked out for the ATP synthase (34), while for another rotary motor, the bacterial flagellar motor, temperature and isotope effects indicate that similar considerations apply (35). A detailed localization of stiffness and compliance of the F₁ enzyme, based on its structure, has been the subject of theoretical investigations (36,37). This work was inspired by the experimental determination of the internal elastic parameters of domains in the complete F_OF₁ noted above (8,9,31).

A wider conformational sampling than achievable with continuous-time equilibrium methods can be obtained by stochastic methods, whose sampling widths are determined by the move set instead of local energy barriers. tCONCOORD (http://wwwuser.gwdg.de/∼dseelig/tconcoord.html) (38), a stochastic method (5,39), was used to access the slow collective motions responsible for the compliance. tCONCOORD compared well with MD based on a large set (7739) of structures that included both soluble and membrane proteins, as reported in 2013 (40). The collective motions were identified by principal component analysis (PCA) (41). The rotary twist of the ring was mediated by interactions within the IB-GGGG central hinge at subunit interfaces that propagated radially across subunits. Shear between the subunit helices generated rotation of one relative to the other. Conserved residues show functionally important positions (27,42), but cannot resolve the interaction networks that determine collective properties. We therefore exploited the >10,000 sequences of the c-subunit for covariance analysis of coevolved residue mutations (6) for this purpose. The coevolution revealed general features of subunit architecture that were deconvolved by match against local structural changes based on a structural alphabet (SA) (43). The phylogenetic record reflected both ring and subunit rotations.

Materials and Methods

Conformational analysis

X-ray c-ring structures PDB: 2XND (bovine c₈-ring), PDB: 2WGM (Ilyobacter tartaricus c₁₁-ring), and PDB: 2WIE (Spirulina platensis c₁₅-ring) and NMR structures of the E. coli c-subunit (PDB: 1C0V and PDB: 1C99) were downloaded from the Protein Data Bank (PDB; http://www.rcsb.org/pdb/home/home.do). They were visualized with visual molecular dynamics (VMD; http://www.ks.uiuc.edu/) and PYMOL (http://www.pymol.org/). PDB structure files of ring and smaller assemblies were prepared for simulation at neutral pH in the Molecular Operating Environment (MOE, Version 2013.08; Chemical Computing Group, Montreal, Quebec, Canada), using the AMBER12EHT force field (http://www.ambermd.org) (44). The system was then energy-minimized using the OPLS-AA force field (40) before simulation with tCONCOORD.

tCONCOORD (4,5,45) utilizes a set of distance constraints, based on the statistics of residue interactions in an x-ray structure library (39), to generate conformational ensembles from an initial structure without inclusion of solvent. The stability of hydrogen bonds is estimated based on MD simulations of the solvation by neighbor residues (38). We used a solvation score of 2.2. Sets of 16⁴ = 65,536 equilibrium conformations with full atom detail were generated for each structure. Comparison with experimental B-factors and geometrical analyses were performed with the GROMACS, Ver. 4.5.5, g_rmsd and g_sgangle functions (http://www.gromacs.org), respectively (46). Crystal contacts were extracted from the PDB files with the CCP4 suite NCONT utility (http://www.ccp4.ac.uk/html/INDEX.html) (47). The overlap between ensemble subsets indicated >99% overlap when subset size was <1/2 of the total ensemble.

We used a structural alphabet (SA) to encode the conformational dynamics of four residue fragments (43,48). Statistically significant correlations between columns were identified with GSATools (http://mathbio.nimr.mrc.ac.uk/wiki/GSATools) (50) and recorded as a correlation matrix. The correlation of conformational changes in a pair of protein segments (i,j) was calculated as normalized mutual information (nMI) between the associated columns in the structural string alignment:

$$nMI\left(Ci;Cj\right)=\left(I\left(Ci;Cj\right)-\epsilon \left(Ci;Cj\right)\right)/H\left(Ci,Cj\right).$$ (1)

Here Ci and Cj are the relevant columns in the structural string alignment, I(Ci;Cj) is the mutual information between them, H(Ci,Cj) is the joint entropy, and ε(Ci;Cj) is the expected finite size error. The correlation matrix was used to generate a network model, with the fragments as nodes and the correlations as edges. The contribution of a node to the network scaled with its connectivity. It was estimated by the eigenvector centrality, E, calculated directly from the correlation matrix,

$$E{\left[M\right]}_{\text{corr}}=E\lambda ,$$ (2)

where [M_corr] is the correlation matrix and λ is the corresponding eigenvalue. Fig. S1 in the Supporting Material illustrates the processing of the 2XND dimer ensemble as described above.

Collective motions, henceforth referred to as global motions, were identified by PCA of the conformational ensembles (49). Principle components (PCs) were generated by diagonalization of the covariance matrix of C^α positions. The variance of the states at both local and global levels was taken as a measure of motion. The motions have no timescale, but it is reasonable that the collective motions represented by the first few PCs are slow relative to smaller-amplitude motions recorded by the later PCs. The correlation between local and global motions was also calculated as the nMI value, but now between the array of fragment states and the array of global motion states,

$$nMI=I\left(Ci;sPCj\right)/H\left(Ci,sPCj\right),$$ (3)

where Ci is the vector of states sampled by fragment i, sPCj (48) is the vector of global states associated with the jth principle component (SI (48,50)), I(Ci;sPCj) is their MI, and H(Ci,sPCj) is their joint entropy.

Phylogenetic analysis

The Pfam (51) HMMER-based (http://www.hmmer.janelia.org) multiple sequence alignment (MSA) for the c-ring subunit family (PF00137) was downloaded, together with all sequences. Incomplete sequences were removed, resulting in a final MSA of 10,111 sequences. The PDB: 2XND c-subunit sequence was added to the edited MSA with MAFFT (http://mafft.cbrc.jp/alignment/server/) and the MSA trimmed to eliminate residue positions not actually in the subunit. Trimmed MSAs were also generated for the PDB: 2WGM and PDB: 2WIE c-ring subunit sequences. JALVIEW (http://www.jalview.org) and SCORECONS (http://www.ebi.ac.uk/thornton-srv/databases/cgi-bin/valdar) were used for the conservation score (52,53). The SCORECONS entropy has elevated scores at positions where gaps predominate because gaps are encoded as an additional amino acid (53).

The MSA underwent format conversion for precise structural contact prediction using sparse inverse covariance (PSICOV; http://bioinfadmin.cs.ucl.ac.uk/downloads/PSICOV/) (54). PSICOV utilizes the BLOSUM matrix and average product correction (55) to measure positive correlations within the dataset. Sparse inverse covariance estimation corrects for phylogenetic bias and indirect couplings. The direct information between two residue positions is given as

$$Dij=Wij/\sqrt{\left(Wii.Wjj\right)},$$ (4)

where W_ii, W_jj, and W_jj are the inverse of the respective, nMI matrices. Custom scripts mapped the correlations onto structure. Additional scripts read out the C^α−C^α distance, physical distance, and orientation of the correlations. A network model of the PSICOV residue coevolution matrix was analyzed as described for the dynamic correlation matrices. The structure maps of residue/fragment correlations and global motions were examined with VMD and PYMOL.

Statistics

Array (list/matrix) operations and statistical tests were conducted within the software R (http://www.r-project.org/). Linear Pearson correlation coefficients (P_corr) were computed for matches between the PSICOV and dynamic network centrality profiles, as well as between the PSICOV centrality and nMI profiles of the contribution of local fragments to PC motions.

Residual correlations in the coevolution matrix due to finite MSA depth and diversity were characterized by generation of the library of randomized MSAs in which the amino-acid residues were shuffled column by column to preserve the entropy at residue positions. The randomized MSA correlation matrix will generate a random network with nodes connected with equal strength to each other. The difference profile between the original matrix centrality and the mean of the randomized library centrality is given as

$$\Delta \left(i\right)=E\left(i\right)-\left(\frac{M_E}{M_R}\right)E_R\left(i\right),$$ (5)

where Δ(i), E(i), and E_R(i) are the difference, real, and mean random centralities at residue position I; and M_E and M_R are the means of the real and random profiles, respectively. The expected deviation due to entropy differences between residue positions was (2(σ_rand)²)^1/2, normalized by $\left(M_E/M_R\right)$. The value σ_rand is the standard deviation of E_R.

The software packages ROCR (https://rocr.bioinf.mpi-sb.mpg.de/) (56) and BIO3D (http://thegrantlab.org/bio3d/index.php) (57) were used for statistical comparison of individual elements of two matrices, one being the PSICOV matrix. The receiver operator characteristic (ROC) plots employ a false-true binary logic to match matrices. The plot axes are fp (= number of false positives/number of negative samples) and tp (number of true positives/number of positive samples). The absolute match is recorded by the area under the curve (AUC) that equals the value for the Wilcoxon-Mann-Whitney test statistic.

Results

Our study may be broken down into three parts: We conducted PCA of the complete ring ensemble, characterized the PCs, and determined the contribution of the conformational dynamics of individual SA-encoded fragments to these components. Then we conducted similar PCA of monomer and dimer structures to identify motions due to intrinsic flexibility of the subunit or subunit contacts, and document their modulation within the ring assembly. Finally, we used network analysis to relate coevolved mutations to local dynamic correlations of the fragments within and between subunits in the larger assemblies.

Rotary compliance of the c-ring measured by tCONCOORD conformational ensembles

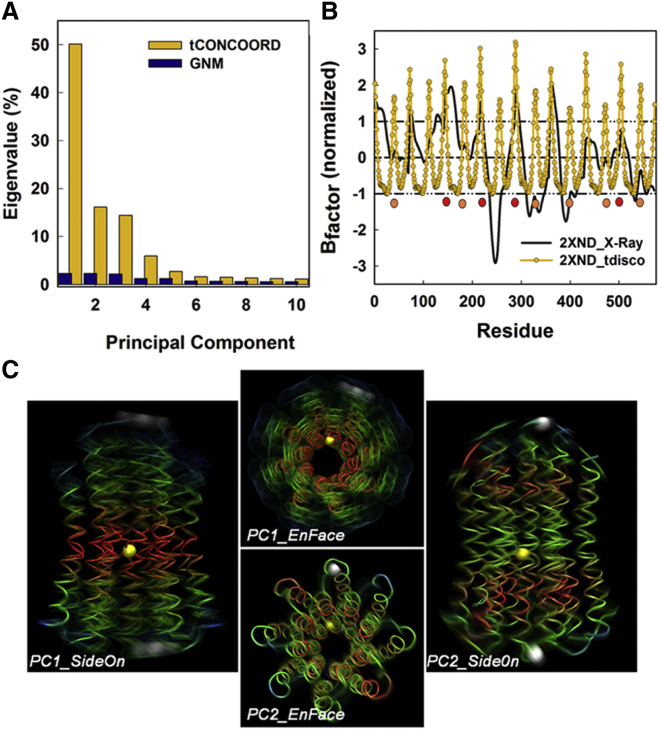
We first investigated the conformational flexibility of the c-ring. The root-mean-square fluctuations (RMSF) of the tCONCOORD c-ring conformational ensembles for PDB: 2XND were decomposed with PCA. The normalized amplitudes for the first 10 PCs were compared with the corresponding values obtained by GNM analysis of the green pea c-ring (32) (Fig. 2A). In contrast to the flat distribution among the GNM PCs, most of the variance (∼81%) within the PDB: 2XND conformational ensembles was accounted for by the first three PCs that represented the largest collective motions. These components had overlapping, but distinct profiles (Fig. S2).

Figure 2.

Principal component motions of the PDB: 2XND c-ring. (A) The normalized eigenvalue spectrum generated by analysis of the tCONCOORD ensemble, compared with the spectrum reported for the GNM analysis (32). The PC values were normalized by their sum. (B) Comparison of B-factors generated from the tCONCOORD ensemble, with the experimental B-factors. (C) En face and side-on kymo-images constructed from a 256-conformer ensemble for the first two PCs (Movies S1, S2, and S3). The C^α backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow spheres) residue G21 within the GGGG motif at the membrane midplane. To see this figure in color, go online.

Residue B-factors obtained from simulated RMSF values were compared against values recorded for the x-ray crystal structure. The simulated B-factor profile had twice the subunit periodicity corresponding to the subunit ends. The experimental B-factor profile had lower peak amplitudes and disrupted periodicity. These differences were due to crystal contacts. In the PDB: 2XND crystal, the F₁ module of the adjacent synthase abuts on the external face of the PDB: 2XND c-ring. The cytoplasmic faces of the c-subunits contact their F₁ε- and γ-subunits. The contacts dampen the large collective motions that account for the peaks in the simulated profile, as well as disrupt the periodicity (Fig. 2B). The crystal contact dependence of the differences between the simulated and experimental B-factors endorses the predictive value of the motions recorded by the conformational ensembles.

We next characterized the first three PCs. The PC ensemble distributions were recorded as movies (Movies S1, S2, S3, and S4), with markers used for estimation of the rotational and translational motions. Superimposed movie snapshots of tCONCOORD trajectories (kymo-images), for side-on and en face views for the first two principal components, are shown (Fig. 2C). The dominant first PC motion (50%) of the c-ring is a twist of its two halves relative to the central IB-GGGG segments. The angular displacement of the marker residues at the membrane interfaces is a monotonic function with a spread of ∼14°. The second PC motion (16%) is more complex, with three segments composed of two terminal domains that execute bending movements relative to the c-ring central axis, balanced by radial displacements of the central segment. The third PC (14.5%) has bending movements orthogonal to those of the second PC and gave similar displacements.

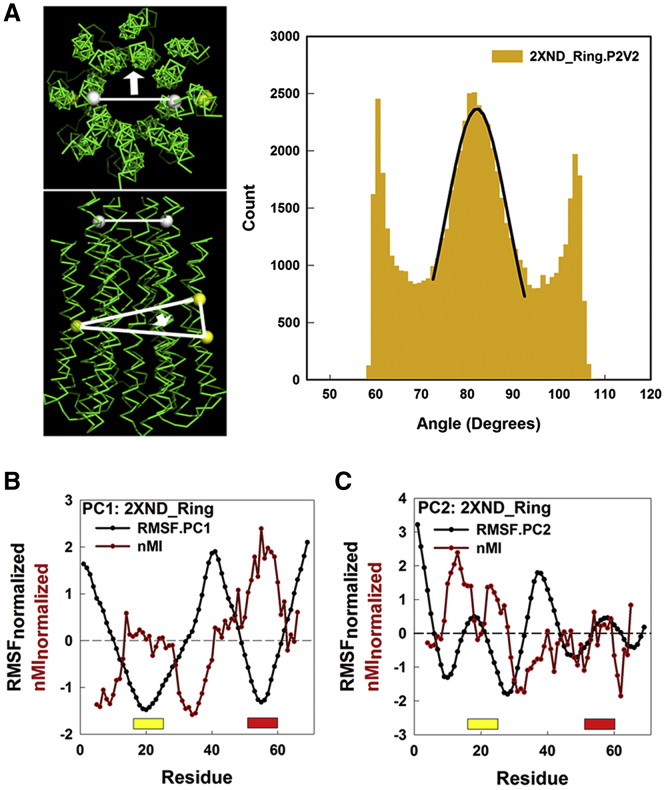
The PC1 motions were examined in detail (Fig. 3A). The distribution was fit with a Gaussian to extract the torsional stiffness, K⁻¹, following Sielaff et al. (31). The variance of the Gaussian, σ², is related to the torsional stiffness by the equation

$${\sigma }^2=k_{\text{B}}T{\mathit{K}}^{-1}.$$

The vectors used for measurement of the angular displacements are shown in the schematic, with the relative motion of one angular displacement with respect to the other being measured. The vectors were chosen based on evaluation of the RMSF profiles and kymo-images (Fig. 2C). The first PC comprises a 13° rotation of the distal end of the c-ring relative to the central midplane. The complete set of measurements on the 2XND ring is given in Fig. S3.

Figure 3.

The IB-GGGG hinge for the principal component rotation. (A) (Left) Vectors for measurement of the PC1 motion superimposed on the ribbon diagram of the PDB: 2XND c-ring. (Top, en face view; bottom, side-on view) The vectors are formed between residues (white spheres) A5 and K294 (medium bar), and the perpendicular (thick bar with arrow) to the plane (thin lines) formed by residues F53, G80, and E345 (yellow spheres). The vectors were chosen based on the kymo-images (Fig. 2C) and movies (Movies S1 and S2) of the motion. (Right) The angular dispersion of the rotary twist of the top of the c-ring relative to its center measured by relative motion of the two vectors shown (left). (Black line) Gaussian fit to the central peak of the distribution (count, c = a × exp(−0.5 × ((x–xo)/b)²), where a = 2369, b = 6.8°, and xo = 82°). (B and C) The contribution of local fragment motions measured as the nMI to the RMSF for PC1 (B) and PC2 (C). (Yellow and red bars) GGGG motif and IB site positions, respectively. To see this figure in color, go online.

The central two-thirds of the distribution followed a Gaussian profile consistent with motion in a harmonic potential well, as expected for a Hookean spring. The variance of the central peak yielded an estimated K_c-ring of 100 pN.nm. The measured torsional stiffness for rotor compliance, K_R, was 68 pN.nm (31). The rotor stiffness was K_T = ((1/K_c-ring) + (1/K_other))⁻¹, where the c-ring is in series with other components. Therefore, K_other is 212 pN.nm. This result implies that the c-ring makes a substantial contribution to the rotor compliance. The sharp peaks at the ends of the angular distribution were the other standout feature.

The proton-binding site and adjacent GGGG motif form the hinge for the rotary compliance

We adopted a twofold strategy to identify the determinants for the c-ring motions. To begin, we correlated local motions of SA-encoded fragments with the global motions recorded by the PCs. Correlative analysis of local motions was used to diagnose central features of the PC motions. The ion-binding pocket (IB) contributed most strongly to the PC1 motion, followed by the adjacent GGGG motif (Fig. 3B). The strong couplings linked the two segments, while weaker couplings residue positions extended from the GGGG motif to the membrane-solvent interface. (We will henceforth use the IB-GGGG motif to refer together to the spatially contiguous GGGG motif and ion-binding pocket.) IB-GGGG and adjacent segments were the primary instigator of the first three PC motions; but their role varied. The segment was a hinge for the PC1 rotary twist motion as diagnosed by the observed anticorrelation between the IB-GGGG local correlation (expressed as nMI) and the global flexibility (RMSF along PC1). The PC2 and PC3 motions, on the other hand, described bending motions. In both these cases, as illustrated for PC2, fragments adjacent to the GGGG motif served as hinge elements to drive the bending motions, as judged by the nMI-RMSF anticorrelation.

Dimer architecture determines the coupling between local hinge and collective global motions

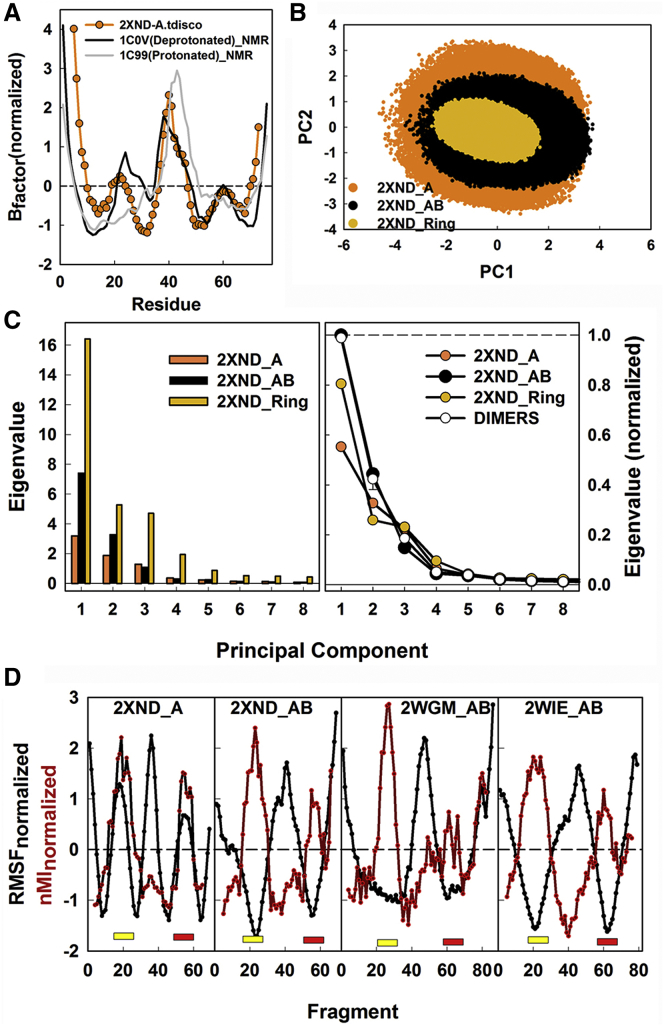
The second stage of our strategy aimed to separate constraints due to the intrinsic subunit architecture from constraints due to subunit packing and the ring geometry. We extracted a single subunit from the c-ring and generated its conformational ensemble. B-factors obtained from this ensemble were compared with those determined from NMR structures of the E. coli c-subunit in mixed solvent (Fig. 4A). The E. coli subunit has a five-residue-greater length than the bovine PDB:2XND subunit. This difference was minimized by superposition of the central peaks in the B-factor profiles. The agreement, given the structures may have been perturbed by solvent, gave encouragement. It was better for the B-factor profile of the deprotonated conformation, consistent with the preparation of the structure files for simulation. The agreement supports the tCONCOORD approach for components isolated from x-ray structures.

Figure 4.

Hinge formation depends on the monomer to dimer transition. (A) B-factors generated from the conformational ensemble for the isolated PDB: 2XND c-subunit, compared with those generated from the NMR structures of the E. coli c-subunit. The correlations, P_corr values, of the simulated B-factors with those from the structures were 0.48 (PDB: 1C0V) and 0.43 (PDB: 1C99). (B) PC1PC2 plots show the decrease in amplitude and increase in anisotropy with assembly size. The dimer and ring PC1 amplitudes were 0.88 and 0.55 relative to the monomer PC1. The amplitudes of the dimer and ring PC2 were 0.69 and 0.36 relative to the PC2 monomer amplitude. The anisotropy (PC1/PC2) increased from 1.2 to 1.5 (dimer), then 1.8 (ring). (C) (Left) Distribution of the first eight PCs in the monomer (PDB: 2XND_A), dimer (PDB: 2XND_AB) and complete PDB: 2XND c₈-ring. PC1 contributed 41.5, 55.8, and 50.1% of the total variance, respectively. (Right) The normalized eigenvalue distribution shows a sharp increase in the contribution of the first two principal motions upon the monomer to dimer transition. (D) The contribution of local fragment motions (nMI, red lines) to the PC1 global motion RMSF (black lines) for the 2XND_A monomer and the three dimer (PDB: 2XND_AB, PDB: 2WGM_AB, and PDB: 2WIE_AB) structures. The three PCs of the dimer structures contributed 87.7 ± 0.1% of the total motion. The contribution of the first PC was 55–56%. (Yellow and red bars) GGGG motif and IB site positions as in Fig. 3. To see this figure in color, go online.

PCA of the extracted monomer and dimer subunit ensembles was performed and compared with the c-ring PCA. The PC1PC2 plots show that the relation between the first two PCs becomes progressively more coupled and anisotropic upon dimer and ring formation (Fig. 4B). As subunit number increases, the PC2 bending motions are reduced to a greater extent than the PC1 rotary twist. The eigenvalue spectra of the ensembles are compared in Fig. 4C. The effects of size are reflected in the amplitudes of the dominant eight PCs. There is an almost twofold increase in the fractional contribution of PC1 to the total eigenvalue spectrum upon the monomer to dimer transition. This fractional PC1 contribution is somewhat reduced, but that of the subsequent four PCs increased, for the c-ring. The first three PCs contribute a similar fraction for both ring and dimer ensembles. The fractional PC contributions were remarkably similar for dimer structures extracted from c-rings with subunit symmetries of 8 or 15.

In addition to the different contribution to the eigenvalue distribution, there was a qualitative difference in the nature of the PC1 between the monomer and dimer. The monomer PC1 (46%) is dominated by bending motions of the helical hairpin as expected for an elastic rod (58) (Movie S5). The IB-GGGG both contributed to and instigated the PC1 (Fig. 4D). Dimer structures from all three c-rings (PDB: 2XND, PDB: 2WGM, and PDB: 2WIE) gave similar PC1 RMSF and nMI profiles, with the IB-GGGG being the major instigator as hinge (Fig. 4D). The dimer PC1s (56%) are dominated by rotary twist of the two subunits (Movies S6 and S7). The dimer PC1 is related to the ring PC1 as considered below. Thus, the emergence of the IB-GGGG as principal hinge depends on dimer assembly.

We next compared the PDB: 2XND ring PC1, PC2 motions with those of the monomer and dimer structures to assess the constraints due to ring geometry. The angular displacements of selected vectors relative to one another were measured (Fig. S3). The monomer PC1 was dominated by 10° bending of the hairpin perpendicular to the plane defined by the long axes and the vector linking the central G19 and E57 residues, and PC3 was dominated by bending parallel to this plane. In contrast, the rotation of the external helix around the internal helix (∼15°), as reported in Sengupta et al. (25), was the dominant motion for the monomer PC2, with the IB-GGGG as hinge (Movie S8).

The bending motions are retained in the dimer to generate a dispersion of the termini relative to the dimer long axis of ∼20°, but these do not contribute to the principal component, PC1. The dimer PC1 is marked by rotation of the cytoplasmic half of one subunit relative to the other. This movement results in 25° rotation of the two subunits relative to each other. The monomer PC2 could be a precursor of the dimer PC1, being strengthened as the bending modes are suppressed upon dimer assembly. The angular distribution showed peaks at the boundaries of an otherwise flat distribution (Fig. 5). Superposition of 24 conformers, two groups of 12 from each end of the distribution, revealed distinct populations with opposing twist. Salient features of the dimer PC1 are illustrated by the kymo-images and schematics of two conformers from the boundaries of the distribution (Fig. 5A). The cytoplasmic loops of both subunits are in a different orientation in the conformer groups relative to the central IB-GGGG hinge. The loops, although flexible, are not entirely unstructured as the sampled conformations are limited (Fig. S1). Radial and axial displacement of the essential glutamate is the last difference between the two groups. Further twist is blocked by steric constraints. These are localized in the IB-GGGG hinge as deduced from increased residue contact. The peaks obtained at the boundaries may then represent energy minima due to weak attraction before contact and subsequent repulsion.

Figure 5.

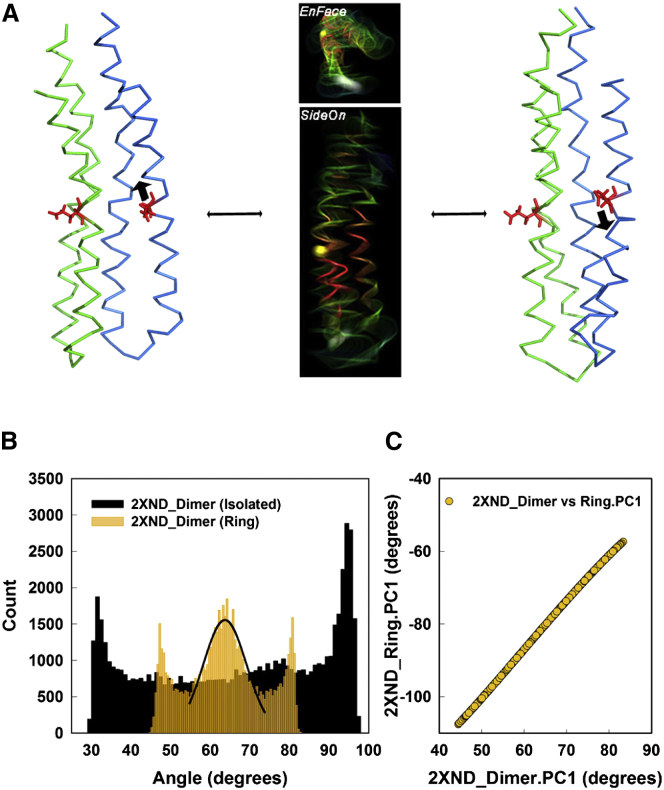
The relation between the principal subunit and ring motions. (A) (Movies S5 and S6). Kymo-images of PC1 motions constructed from a 256-conformer ensemble generated for the isolated PDB: 2XND dimer. Backbone motions and residue positions are color-coded as in Fig. 2C. Ribbon traces of conformations at the extremes of the motion range flank the kymo-images. The two subunits are color-coded. (Thick black arrows) Axial motions of one glutamate residue (red) relative to the other. Note different orientations of the cytoplasmic loops in the two conformers. (B) The angular distributions of the rotary twist of subunit helices relative to one another measured relative to the vector between the N-terminal helices of the dimer subunits. The distribution for dimers within the c-ring (gold) is superimposed against the distribution obtained for the isolated dimer (black). (Black line) Gaussian fit to the central peak of the ring dimer distribution (count, c = a × exp(−0.5 × ((x−xo)/b)²), where a = 1555, b = 5.5°, and xo = 64°). (C) Linear relation for PC1 between the angular distribution of the c-ring (Fig. 3A) and the helix rotation of the dimer component (B). To see this figure in color, go online.

The same vector pair used to measure the intrasubunit helix rotations in the isolated dimer was used to measure this movement in dimers within the c-ring (Fig. 5B). The variance of its angular distribution was reduced twofold with emergence of a new feature: a central peak. The torsional stiffness, K, of this configuration, estimated from the variance, was 609 pN.nm (Fig. 5B, legend). The angular distribution for the dimer PC1 within the ring was remarkably similar to the angular distribution of the PDB: 2XND ring PC1 (Fig. 3A). The pairing of the two angle values over the complete 65,536 conformer ensemble revealed a linear relation between the two PC1 motions, the ring rotary dispersion versus the intrasubunit helix rotations (Fig. 5C). We conclude that packing constraints on both sides of the individual subunits created by the ring geometry act to hold the subunits in a potential energy well between the two extreme, bent conformations. Motions in the well are entrained to the rotary twist of the c-ring. The two extreme conformations are presumably stabilized in the ring by the same weak forces as those that operate in the isolated dimer.

C-subunit residue coevolution gives a readout of the principal collective motions

Thus far, we have shown that the IB-GGGG motif forms a central hinge for both the PDB: 2XND c-ring and dimer PC1 motions. We have found that these motions are coupled due to the common hinge. We now characterize the IB-GGGG interactions to understand the coupling between hinge movements and ring collective motions in single-residue detail. Residue coevolution was used to parse out structural and functional features of the dynamics.

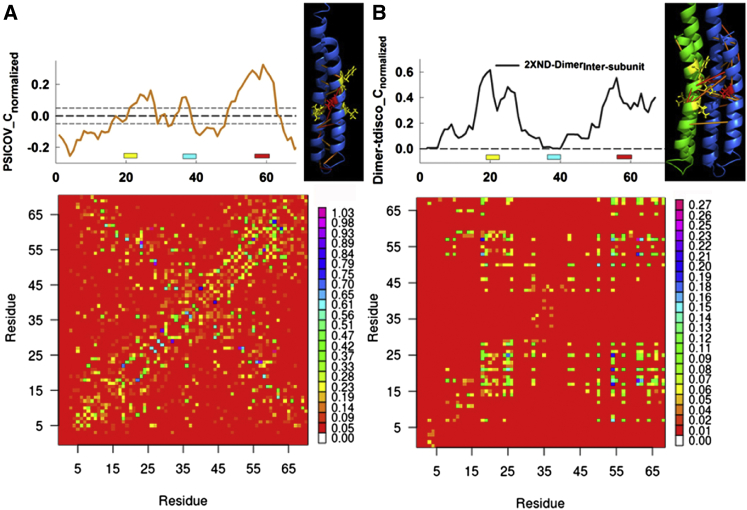
The PSICOV residue coevolution matrix (Fig. 6A) is characterized by a cross-pattern diagnostic for a helical hairpin. The pattern arises because the axial α-helical repeat generates short-range correlations that are spaced four residue positions apart parallel to the positive slope diagonal, while radial correlations among adjacent residues between the two helices are recorded in the negative slope diagonal. Weaker correlations connect the IB-GGGG to the conserved cytoplasmic loop segment and the N- and C-termini. The α-helical repeat is reflected in the centrality profile (Fig. S4). The filtered difference profile corrected for residual correlations (Fig. S4) is plotted on top of the coevolution matrix. The IB is the central node marked by the dominant peak in the profile. The GGGG motif and the cytoplasmic loop form secondary peaks. The top-scoring (0.1%) correlations were mapped onto the structure of the subunit (Fig. 6A). The correlations clustered between the essential glutamate and the four residue positions that form the IB site. The PDB: 2XND positions were related by MSA to positions important for pK modulation (PDB: 2WIE c₁₅-ring (16)) or sodium ion coordination (PDB: 2WGM c₁₁-ring (59)).

Figure 6.

Relation between subunit architecture and residue coevolution. (A) The PSICOV coevolution matrix for the trimmed MSA, based on the PDB: 2XND subunit sequence. Matrix elements are color-coded based on correlation strength normalized between 0 and 1. The matrix centrality profile, corrected for residual correlations, is on top. (Short dashed lines) Either side of the zero mean (dashed line) difference shows deviation (±1σ) scaled to the variation in the mean randomized library profile (Fig. S4). The PDB: 2XND subunit map adjacent to the centrality profile shows the top-scoring correlations (blue, weak to red, strong) cluster between the essential E57 glutamate (red) and IB-site residue I24, L55, M59, and F62 (yellow) side chains. (B) The intersubunit, dynamic correlation matrix for the isolated PDB: 2XND dimer (see Fig. S4 for full matrix). Matrix elements are color-coded according to their nMI value. The PDB: 2XND dimer, with color-coded subunits, adjacent to the centrality profile shows the strongest correlations (nMI > 0.20), color-coded as in (A). The E57 and IB-site residues are now in proximity. (Yellow and red bars) GGGG-motif and IB-site positions as in Fig. 3. (Cyan bar) Position of the conserved cytoplasmic loop. To see this figure in color, go online.

The IB residue side chains do not interact in the monomer, suggesting their coevolution reflects interfacial dynamics consistent with localization at the subunit interface. The intersubunit dynamic correlation submatrix, extracted from the complete correlation matrix (Fig. S4 B), also had α-helical periodicity due to helix-helix close-packing. It was composed predominantly of correlations between IB-GGGG residue positions in the two dimer subunits, as recorded in the centrality (Fig. 6B), but with the IB-site side chains now in contact. The dynamic correlations argue that the imprint of the IB-GGGG motif in the coevolution network is partly determined by interfacial contacts.

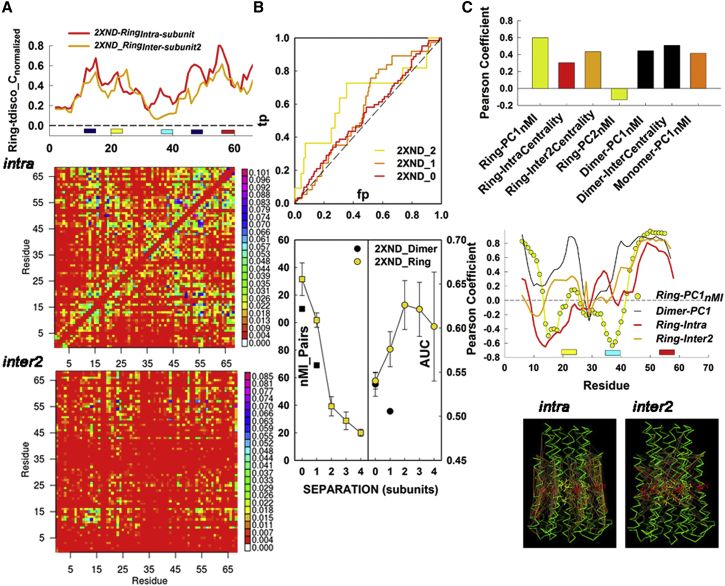
We decomposed ring-network architecture to distinguish long- versus short-range couplings. The couplings were matched to the coevolution network. There are four distinct intersubunit couplings with subunit separation, n = 1 (contacting subunits), 2, 3, and 4, respectively, in addition to intrasubunit couplings (n = 0). For each of the five cases (n = 0,1,2,3,4), eight submatrices with dimensions corresponding to one subunit were extracted from the complete ring correlation matrix as described for the dimer correlation matrix (Fig. S4). The eight submatrices were then averaged. We found unexpectedly strong correlations between distant subunits. The averaged intrasubunit (n = 0) and intersubunit (n = 2) correlation matrices are shown (Fig. 7A). The intrasubunit correlation matrix generated five primary nodes (IB, GGGG motif, two adjacent segments, and the cytoplasmic loop) with diagonal bands due to the axial α-helical repeat. The n = 2 (inter2) matrix resembled the intersubunit correlation matrix for the dimer (Fig. 6B).

Figure 7.

Residue coevolution reflects composite c-ring architectural dynamics. (A) Centrality profiles (top) for the correlation matrices for intrasubunit (intra) and intersubunit coupling between physically separate subunits (inter2) (bottom). Matrix elements are color-coded based on their nMI values as in Fig. 6. The corresponding centrality profiles are on top. (Yellow, red, and cyan bars) GGGG-motif, IB-site, and cytoplasmic-loop positions as in Fig. 6. (Blue bars) Segments (A11-G17 and F45-L50) that form hinges for motion PC2 (Movie S3). (B) ROC analysis of the match between residue coevolution and local dynamic networks. (Top) ROC plots of the match as the local dynamic correlation nMI threshold is increased for n = 0, 1, and 2. Computed probability values for the AUC of the plots were 0.2 (n = 0), 0.1 (n = 1), and 0.05 (n = 2). (Bottom, left) The number of couplings with nMI > 0.075 as a function of n. (Right) AUC values as a function of n. Each value was averaged over the eight PDB: 2XND ring subunits. AUC = 0.5 for a random match. (C) (Top) Pearson correlation coefficients (P_corr) for the match between the centrality profile of the PSICOV matrix and the nMI profiles of correlations between local versus global (PC1, PC2) motions or local dynamic network centrality. (Middle) P_corr variations along the subunit sequence (12-residue or SA window). (Bottom) Intrasubunit and intersubunit (subunit separation, n = 2) dynamic couplings (nMI > 0.075) mapped onto the PDB: 2XND ring. nMI strength (gray, weak to red, strong). The glutamate (red) and GGGG motif glycine (yellow) side chains are shown. To see this figure in color, go online.

We used ROC analysis (56) to compare the complete coevolution and dynamics correlation matrices (Fig. 7B). The ROC plots record correct versus incorrect matches at different cutoffs for the test distribution. Representative plots for the ring intrasubunit and intersubunit (n = 2) couplings are shown. The predominance of correct matches was measured as the AUC (60). While the number of high-scoring correlations decreased with subunit separation, the match with the PSICOV matrix increased. The match peaked at subunit separation, n = 2, and for n > 2 it remained higher than that for interfacial couplings (n = 1). The ring interfacial couplings gave a better match with the PSICOV matrix than internal subunit couplings (n = 0), in contrast to the isolated dimer.

The correlation (P_corr) values for the match of the PSICOV coevolution network centrality with the intrasubunit and intersubunit centrality were 0.3 and 0.43, respectively, consistent with the ROC analysis (Fig. 7C). The match between the PSICOV centrality and local determinants of PC motions, given by the nMI profiles in Fig. 3, B and C, was determined similarly. Strikingly, there was correlation (0.6) with the ring PC1, but not PC2. The correlation was worse for the dimer PC1 (0.44) and worst for the monomer PC1 (0.41). P_corr sequence profiles showed how the matches partitioned to distinct segments. The dominant fraction of intrasubunit correlations are oriented parallel to the helix axes, while intersubunit correlations between the IB-GGGG hinge elements band across the c-ring, as realized from the structural maps of the top-scoring (0.1%) correlations. These patterns are compatible with the PDB: 2XND c-ring PC1 and PC2 motions. The longitudinal intrasubunit correlations generate the PC2 bending motions. The transverse IB-GGGG motif correlations form the hinge for the rotary twist PC1 motion.

The comparison between coevolution and dynamics

In summary, the salient features are: 1) residue coevolution provides a readout of the helical hairpin subunit architecture. 2) The IB site forms the central node in the coevolution network, coupled to the lesser GGGG motif node. The dynamic couplings between these nodes show the interfacial nature of the IB-GGGG contacts. 3) IB-GGGG motifs in physically distant subunits are also dynamically coupled. The rotary twist of the c-ring, hence elastic compliance, is presumably mediated by these long-range couplings that add to the known functional importance of IB-GGGG contacts for protonation-deprotonation and subunit stoichiometry (16,17,27,61). 4) The coevolution matrix records correlations between the cytoplasmic loop and membrane residue positions in the c-subunit. Cytoplasmic loop residue conservation must reflect contacts with the F_O a-subunit and F₁, but it may also influence c-subunit dynamics that regulate shear and angular dispersion during helix rotation. 5) The coevolution reflects both short- and long-range couplings.

Discussion

This study provides, to our knowledge, new information on 1) the conformational flexibility of the c-ring in the ion-motor of ATP synthase and its relation to subunit motions and 2) the relation between c-subunit residue coevolution and ring/subunit architectural dynamics.

Conformational flexibility of the c-ring and its building blocks

PCA characterized the collective motions of the ring assembly. The dominant PC1 is a rotary twist of the two ring halves around a central IB-GGGG hinge. The second and third PCs together consisted of bending motions that produced axial and tangential displacements of the essential, proton-binding glutamate residues. The displacements may mediate alternating access and/or pK modulation as suggested in Saroussi et al. (32). Much of the elasticity resides in the rotor module rather than the relatively stiff stator (8,31). While the GNM PC distribution does not permit close comparison, the PC1 matches motion type III, and PC2, PC3 motion type III described by the GNM (32). Previous studies demonstrated a better agreement between tCONCOORD and MD than GNM and MD for the main-chain C^α atoms (40), consistent with the importance of side-chain steric constraints to backbone motions. We measured an angular dispersion of ∼14° for the ring halves and the motions of each half are uncorrelated. Synchronized movement is not needed because c-ring interactions with the stator are restricted to the solitary F_O a-subunit. The measured angular dispersion, based on a Gaussian fit to its central peak, may be used to estimate a torsional stiffness of 100 pN.nm. This estimate implies that the c-ring contributes to the measured rotor compliance.

We analyzed the dynamics of monomers and dimers isolated from the c-ring to understand the emergence of collective motions upon ring assembly. The monomer dynamics approximated that for an elastic rod with bending motions dominant in the first three PCs. However, helix rotation similar to that reported from simulations of the E. coli F_O c-ring (25) characterized the monomer PC2. In contrast to the E. coli study, no secondary structure constraints were applied in our work. Intrasubunit couplings constituted the major fraction of the dynamic network in both the c-ring and dimer structures. They increase linearly with subunit number. PCA documented that relative rotation of the subunit helices emerged as the dominant (PC1) motion in the isolated dimer. The motion was correlated with displacements of the glutamate. The internal mobility of the F_O c-ring has been previously addressed by Dmitriev et al. (62). They compared their structural model (by solution NMR) of the monomeric c-subunit (in a mixed solvent) with their proximity data obtained by intersubunit cross link in situ. To make these data sets compatible with each other, they postulated helix swiveling (63). This interpretation was no longer met after the first x-ray structure of the c-ring (28). This study shows helix movements intrinsic to the c-subunit protonated state unrelated to the cited previous opinion. Fillingame et al. (64) in 2002 and then Moore and Fillingame in 2013 (65) revived the idea of helix swiveling, but now addressing transmembrane helices 2 and 5 of subunit a. The motions of the isolated c-subunit we describe are retained, but differentially reduced, within the c-ring. The cytoplasmic loops have limited flexibility and may be harnessed by a-subunit interactions as suggested in Steed et al. (66), as well as by deprotonation. Constraints due to the ring architecture produce a flexible intermediate state between the two extreme twist conformations. There is a strict relation between the collective rotary twist of the c-ring and the individual twist of the component subunits. The relation arises because in both cases, the same hinge element, the IB_GGGG motif, is responsible for the respective motions.

IB-GGGG is the major element in the intrinsic motions of isolated subunits. It instigates PC1 motions in the dimers and PC2 motion in the monomer as a central hinge. The second and third PC motions of the dimer structures are analogous to the monomer PC1. In the c-ring, the IB-GGGG motifs of physically distant subunits are dynamically coupled. The couplings have a finite spatial range with two subunits as optimal separation. These facts suggest that c-ring collective motions originate from the intrinsic twist of the helical-hairpin subunit that is refined and strengthened by intersubunit contact. IB-GGGG hinge motions driven by protonation deprotonation reactions can then, in principle, modulate the dependent collective motions. The blockage of proton transport would be predicted to reduce hinge mobility with an associated increase in torsional stiffness of the F_O motor.

Architectural dynamics and residue coevolution

The IB site was the central feature of the coevolution matrix consistent with its functional importance. The coevolution may tune the local dielectric to adjust the different pK values of the acid residue (aspartate, 3.65 / glutamate, 4.25) occupying this position, to the physiological range. The IB site has coevolved with the GGGG motif. Related GXXXG (and AXXXA) motifs mediate α-helix-helix and helix-ligand interactions in proteins (67,68). This study adds a central role in c-ring architectural dynamics, as an IB-GGGG composite, to the known functions (17,27) of the GGGG motif.

Important advances have refined evolutionary covariance analysis for protein structure prediction (54,69–71). Identification of intersubunit contacts in multisubunit assemblies has been used, for example, to dock structural models onto electron cryo-microscopy maps of the assembly (72). Coevolution analysis can detect allosteric networks (73) and conformational states (74), supplemented by thermodynamic measures and experimental assays (75,76), but the mechanical or allosteric basis of coevolved networks (77,78) can be difficult to establish (79). We compared dynamic couplings within subunits, between adjacent subunits and distant subunits with residue coevolution. The most direct relation between coevolution and dynamics results from the short-range contacts due to the axial α-helical repeat. We also find a match of the coevolution network with the determinants for the principal collective c-ring motion as well as the dynamic interaction network coupling physically distant subunits. In both cases the match is better than with intrasubunit dynamics. If the relation between coevolution and dynamics were based entirely on residue contacts, the match should decrease dramatically with distance in contrast to what is observed. Thus, our results argue for a long-range contribution to the relation between residue coevolution and c-ring dynamics.

Conclusions

We have analyzed conformational ensembles to describe collective c-ring motions of importance for the measured F_O rotor compliance. In the process, we identified hinge elements that determine these motions and resolved their intrasubunit and intersubunit couplings. We identified a phylogenetic signature for c-subunit architecture and deconvolved this signature in terms of interactions that drive the coupled subunit and ring architectural dynamics. The dynamic correlations provide a mechanical framework for c-ring compliance that may be extended to other modules of the ATP synthase for elucidation of the energy coupling mechanism.

Author Contributions

A.P., J.K., and S.K. wrote scripts and designed simulations; W.R.T. and J.K. designed ROC analysis; and W.J. and S.K. wrote the article.

Editor: Bert de Groot.

Supporting Material

Movie S1. 2XND ring, PC1, en face view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow sphere) residue G21 within the GGGG motif at the membrane midplane.

Movie S2. 2XND ring, PC1, side-on view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow sphere) residue G21 within the GGGG motif at the membrane midplane.

Movie S3. 2XND ring, PC2, side-on view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow sphere) residue G21 within the GGGG motif at the membrane midplane.

Movie S4. 2XND ring, PC3, side-on view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow sphere) residue G21 within the GGGG motif at the membrane midplane.

Movie S5. 2XND monomer, PC1, side-on view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (Yellow spheres) Residues G19, V17, and G21 on the internal helix; (white spheres) residues E57, G9, I31, Q44, and L69.

Movie S6. 2XND dimer, PC1, side-on view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow sphere) residue G21 within the GGGG motif at the membrane midplane.

Movie S7. 2XND dimer, PC1, en face view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (White spheres) Residues A5 and P39 at the membrane boundary; (yellow sphere) residue G21 within the GGGG motif at the membrane midplane.

Movie S8. 2XND monomer, PC2, side-on view

The Cα backbones are color-coded (red, low; green, medium; blue, high) to indicate the RMSF. (Yellow spheres) Residues G19, V17, and G21 on the internal helix; (white spheres) residues E57, G9, I31, Q44, and L69.