Quantitative Analysis of Intracellular Fluorescent Foci in Live Bacteria

Abstract

Fluorescence microscopy has revolutionized in vivo cellular biology. Through the specific labeling of a protein of interest with a fluorescent protein, one is able to study movement and colocalization, and even count individual proteins in a live cell. Different algorithms exist to quantify the total intensity and position of a fluorescent focus. Although these algorithms have been rigorously studied for in vitro conditions, which are greatly different than the in-homogenous and variable cellular environments, their exact limits and applicability in the context of a live cell have not been thoroughly and systematically evaluated. In this study, we quantitatively characterize the influence of different background subtraction algorithms on several focus analysis algorithms. We use, to our knowledge, a novel approach to assess the sensitivity of the focus analysis algorithms to background removal, in which simulated and experimental data are combined to maintain full control over the sensitivity of a focus within a realistic background of cellular fluorescence. We demonstrate that the choice of algorithm and the corresponding error are dependent on both the brightness of the focus, and the cellular context. Expectedly, focus intensity estimation and localization accuracy suffer in all algorithms at low focus to background ratios, with the bacteroidal background subtraction in combination with the median excess algorithm, and the region of interest background subtraction in combination with a two-dimensional Gaussian fit algorithm, performing the best. We furthermore show that the choice of background subtraction algorithm is dependent on the expression level of the protein under investigation, and that the localization error is dependent on the distance of a focus from the bacterial edge and pole. Our results establish a set of guidelines for what signals can be analyzed to give a targeted spatial and intensity accuracy within a bacterial cell.

Introduction

Fluorescence microscopy is an indispensable tool for studying the behavior of proteins and protein complexes. The exact labeling of the protein of interest by means of an in vivo fluorescent protein (FP) fusion, enables scientists to address a plethora of questions in the natural environment of the cell (1–5). Because of technical advances over recent years, it has become possible to localize, track, and even count molecules in live cells (1,6–8). This is accomplished by studying the position and intensity behavior of the intracellular focus detected when the FP-fusion is excited (Fig. 1). An intracellular focus is indicative of either immobile FP-fusions within a diffraction-limited focus, being, for example, DNA-bound (1), or a FP-fusion moving throughout the cell (9–11). The latter detection is only possible if the excitation and image acquisitions are sufficiently fast (requiring typically ∼ ms frame rate, but somewhat dependent on the biological process being studied).

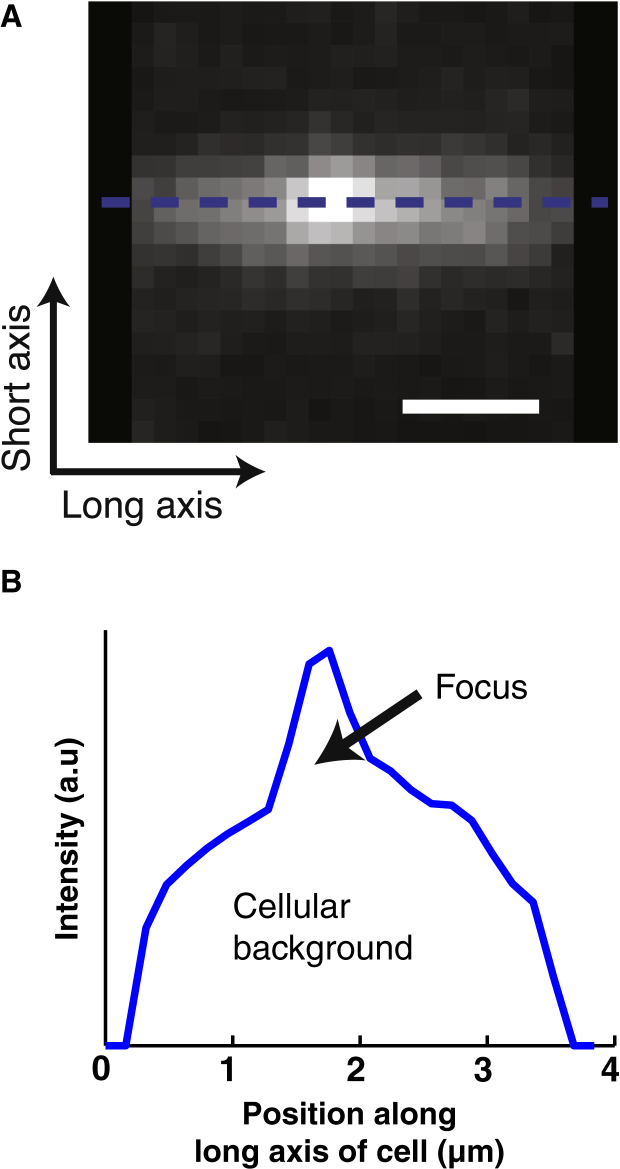
Figure 1.

Studying a fluorescent focus in the inhomogeneous background of a bacterial cell. (A) Sample fluorescence signal of a focus and cellular background as measured in a single E. coli cell. Here the dashed blue line indicates where the line profile in (A) was taken. (B) The corresponding line profile of the sample image in (A). Here we indicate the focus and the cellular background to illustrate the nonnegligibility of the background signal when analyzing foci in this context. Scale bar: 1 μm. To see this figure in color, go online.

It has become common practice to fit a model function to an intracellular focus to determine its position and intensity value (12–15). One common algorithm for the analysis of a diffraction-limited focus is direct fitting to a Gaussian function. In doing so, one can in principle determine both the position (localization) of the focus with subpixel resolution and also the amount of fluorescence that originates from it by direct integration. Although this type of analysis has been described and evaluated in detail for ideal in vitro and theoretical conditions (14–19), its applicability and reliability in the context of the living cell have not been sufficiently and quantitatively characterized.

The crowded environment of the cell differs significantly to that of a cleaned flow-cell, in which molecules are immobilized in an environment optimized for very limited autofluorescence and background from the sample. The cellular environment on the other hand has an in-homogenous and variable background. For example, within a cell cycle the protein of interest may be regularly expressed, become mature or degraded, and aspecifically bind to DNA or other proteins. All of this leads to a background fluorescence level that is uneven and constantly fluctuating. Also, the compact and crowded environment of the cell (20) can add to the inhomogeneity of the background fluorescence because of unspecific interactions. Substantial errors can arise when one does not accurately address the influence of the background signal before the fitting of the FP-fusion focus under investigation.

In this study, we systematically characterize the influence of background fluorescence on the analysis of a diffraction-limited focus in a bacterial cell. We strive to make as few assumptions as possible concerning the background signal, and we utilize, to our knowledge, a novel approach that combines simulations and experiments. Modeling this background and assuming it is an exact representation of the true cellular context may result in erroneous conclusions. For that reason, we choose to simulate a diffraction-limited focus, containing varying known signal content at a defined position, within an experimentally measured background. This allows us to have an exact representation of the cellular background signal. We use these generated images to assess the different background subtraction algorithms in combination with the different focus analysis algorithms (Fig. 2). The different background subtraction algorithms (see Material and Methods) are applied to the same generated image, after which the results are subsequently analyzed by different focus analysis algorithms (Materials and Methods). For background subtraction we employ bacteroidal background subtraction, region of interest (ROI) background subtraction (21–24), iterative median background subtraction (25), and ridge-filtering by SpotfinderZ (26) (part of the commonly employed MicrobeTracker package (26–28) (Materials and Methods)). We determine the position and signal content of a focus using our custom written algorithms (one-dimensional (1D) and two-dimensional (2D) Gaussian fitting), and SpotFinderZ. The resulting localization and fluorescence intensity content from these algorithms are then compared with the known input values. Unsurprisingly all evaluated algorithms are sensitive to low focus intensity levels, both in terms of the focus intensity estimation error and as the localization error. We furthermore show that the choice of background subtraction is dependent on the expression of the protein under investigation, and that the localization error is dependent on the distance a focus is from the bacterial edge and pole. Our results allow us to establish a set of guidelines for what signals can be analyzed to a specific degree of spatial and intensity accuracy within a bacterial cell.

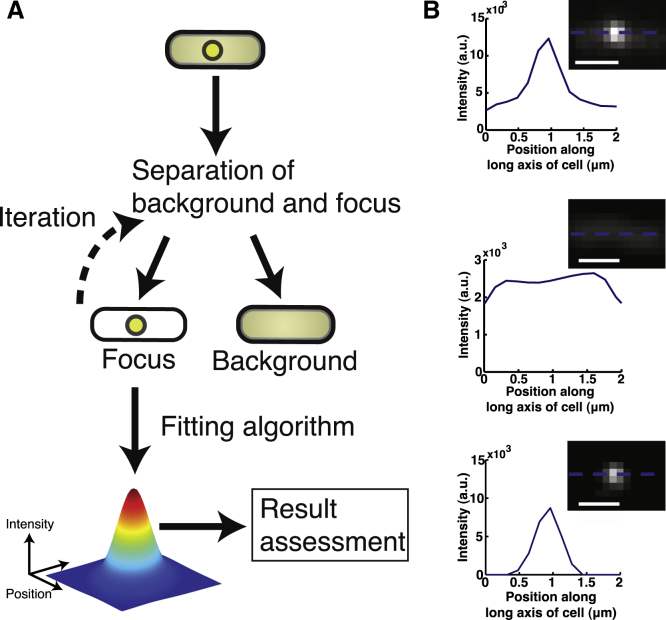
Figure 2.

Separation of focus and background signals. (A) General workflow used to assess background removal methods and their effect on focus analyses. First, the focus and background signals are split using one of the methods described in Materials and Methods. The resulting focus signal is processed by the different focus analysis methods as described in Materials and Methods. The result is assessed in terms of estimating the focus signal content and focus position. (B) A sample result of subtracting the background using our bacteroidal background subtraction algorithm. (Top) The line profile of the original image (inset). (Middle) The line profile of the bacteroidal background generated (inset) using the steps described in Materials and Methods. (Bottom) The result of subtracting the date in the middle panel from the date in the top panel. One can appreciate that the background has been substantially reduced. In all the images the dashed blue line indicates where the line profile was taken. Scale bars: 1 μm. To see this figure in color, go online.

Materials and Methods

Microscope setup, data acquisition, and strains for imaging

The microscope setup used for data acquisition was a commercial Nikon Ti (Amstelveen, The Netherlands) equipped with an Andor U897 Electron Multiplying Charge Coupled Device (EMCCD), a Nikon CFI Apo TIRF 100× oil (NA 1.49) objective, and a personal computer running Nikon NIS elements. A Cobolt Fandango 515 nm continuous wave (CW) diode-pumped solid-state (DPSS) laser was used to excite YPet. Images were acquired with an exposure time of 80 ms and the EMCCD camera gain set to 100.

The bacterial strains used for imaging are derived from Escherichia coli (E. coli) K12 AB1157. Two independent strains are employed for this study, namely a chromosomal fusion of YPet to the β₂ sliding clamp (YPet-dnaN), and a chromosomal fusion of YPet to the $\mathit{ϵ}$-subunit of DNA polymerase III (dnaQ-YPet). These strains and their construction are fully described in previous studies (22,29).

Cellular background estimation

Cellular background estimation was performed using four different algorithms.

Bacteroidal background subtraction

For the bacteroidal background subtraction (this work), we proceed as follows. First, the sample autofluorescence (dark level) is determined from a region outside the bacterium. All fluorescence signal counts in the bacterium that exceeds the dark level by one standard deviation (SD) are analyzed further. These counts are summed along the short axis of the bacterium (summed line-profile). The median of this summed-profile is taken to be representative of the cytoplasmic content in the bacterium (cellular background) in 1D. The advantage in using this algorithm for determining the cellular background is that it is not sensitive to the influence of fluctuations.

The median of the summed profile is further utilized to build up a 2D representative background image (bacteroidal image), which is constructed as follows. First, the backbone of the original bacterial image (Fig. 2B) is determined. The backbone of the bacterium is defined as the maximum of the fluorescence signal along the short axis of cell for each of the x-positions along the long axis of the cell. Subsequently, we convoluted a spike with a width of one pixel with an amplitude of the summed median value at that position, with a normalized Gaussian focus having a full width half maximum (FWHM) comparable with the width of a typical bacterium (∼1 μm) at each backbone position along the long axis of cell.

This results in a noise-free, nonfluctuating 2D bacteroidal shape that contains exactly the same number of counts as the median cellular value, and follows the slightly curved shape of the original bacterium (Fig. 2B). This image is defined as the bacteroidal image and is seen to be representative of the cellular background signal of the cell. This bacteroidal background is subtracted from the original bacterial image (Fig. 2B, top), which is further processed by the respective algorithms for focus analysis. See Fig. S1 in the Supporting Material for an example implementation of this algorithm.

Region of interest background subtraction

This approach of background subtraction has been used by others, and we only briefly describe it here; for a more in-depth description, the reader is referred to earlier studies (21–24). In summary, a fixed, limited circular or square area (the region of interest (ROI) is first defined in which a putative focus is expected. Such an area is commonly found by time-averaging multiple consecutive images. Within this area, an iterative masked centroid tracking procedure yields a smaller, circular focus area. The signal level associated with the square, excluding the focus area, is then taken as a measure for the background. This method assumes that the region in which the focus is to be found is situated inside the initially chosen ROI. In our work where we overlay a simulated spot on the cytoplasmic image, we therefore choose a random preestimate within a distance of five pixels of the true location, with a square ROI size of 16 pixels. We note that this presetting of a nearby, approximate position may give this method some advantage in comparison with the other algorithm tests, especially when the focus is small compared with the cytoplasmic fluctuations. See Fig. S1, for an example implementation of this algorithm.

Iterative median background subtraction

In this approach as described by Bisicchia et al. (25) a background image is created by median filtering the original image on a length scale that surpasses the radius of the point spread function of a focus. After removal of this background from the original, focus detection is performed via 2D Gaussian fitting (13). Focus fits are then removed from the original and the whole process is iterated until convergence (Fig. 2A). Although in this original work a median-filter square size of five pixels was used, we found the method most effective for our images when we chose a square size of only three pixels. See Fig. S1, for an example implementation of this algorithm.

Ridge-filtering by SpotFinderZ

This method of background subtraction is described in Sliudarenko et al. (26). The algorithm essentially suppresses the strong signal gradients that are associated with the edges of the cell before focus detection by a 2D Gaussian fit is carried out.

Focus analysis algorithms

The following different algorithms are utilized to determine how well a focus is localized and its total intensity is deduced using the aforementioned background subtraction algorithms.

• 1)A conventional 1D Gaussian fit with a predetermined fixed width (1D fixed-width Gaussian) on the summed line-profile of the image from which the bacteroidal background has been subtracted (see above). The width was chosen to equal the FWHM of the point spread function of the imaging system. The result provides one with focus signal content and the position along the long axis of the cell. This algorithm yields subpixel position information with a minimum of free parameters.
• 2)A conventional 2D Gaussian fit with a fixed-width is fitted to the focus of the image where the bacteroidal background has been subtracted (2D fixed-width Gaussian). Similar to the SpotfinderZ tool (see below), a constant-background is included as a free fit parameter. As a preestimate (initial guess), the results of the 1D fixed-width Gaussian are used. When determining the focus signal content in this case we use the median excess signal above the bacteroidal background. The median of the image is determined from which the bacteroidal background has been subtracted. We define all counts above this median level as focus content, which we define as median excess. Although being a good estimator of focus signal content, this algorithm yields no information on focus position, hence the use of it in combination with a 2D Gaussian fit.
• 3)SpotFinderZ. This freely available foci analysis tool was utilized in analyzing the focus position and total intensity in combination with the artificial PH images. The tool utilizes a multifocus, 2D Gaussian fit with the width being a free parameter, in combination with the ridge filter background subtraction (26). Before analysis, we systematically varied the available parameters to find the best settings to use under these conditions. These settings were determined for 45% of the total signal being situated in the focus. This resulted in utilizing the default settings with the upper limit of the high cutoff parameter set to 2. For the single-focus analysis in this study, we set the focus threshold levels low such as to always obtain multiple foci. The brightest focus is subsequently selected for comparison with the simulation input.

Artificial phase contrast image database generation

We created artificial phase contrast (PH) images from the experimentally measured diffuse cellular background fluorescence images to use as input for the MicrobeTracker. Because it is customary to use the mesh-based analysis of the MicrobeTracker/SpotfinderZ package with phase contrast images, and no phase images were acquired (see Materials and Methods), we constructed an artificial PH image by inverting the bacteroidal and adding it to its own, positive blurred variant. This resulted in a smooth, dark, white rimmed cell picture on a gray background that is easily compatible with the MicrobeTracker phase signal detection software. We note that, as far as focus detection and analysis is concerned, this step is not of further influence.

Addition of a focus to the diffuse cytoplasmic background in a cell

We employ two different approaches to add a simulated diffraction-limited focus of varying intensity to the cytoplasmic background of a bacterial cells.

Constant cellular level approach

For this method we keep the total signal from the whole cell at a constant level while increasing the focus intensity. In other words, when the intensity of a focus is increased, the background intensity is decreased. This is done by first determining the total cellular intensity above the noise level of the experimental image. This value is then taken as a measure of the total counts in the cell. This approach mimics a typical experimental situation, where the formation of foci depletes the cytoplasmic pool of free proteins (assuming that protein expression and maturation are much slower processes than the formation of foci). Note that this approach keeps the relative contribution of the background noise to the total fluorescence counts constant, but it does lower cytoplasmic fluctuations relative to the focus strength.

Incremental focus approach

In this approach we utilize the cytoplasmic image as is, and we add a focus of slowly increasing intensity. Because we do not change the background noise and cytoplasmic fluctuation contributions here, it is appropriate to include a noise contribution in the focus, which we simply do by considering the focus signal as from a poissonian emitter. To do so, we translate the fluorescence signal F to a poissonian count N by using C = N × F, with C = (background noise)²/(background intensity) as taken from the edges of the experimental image. Although this approach involves a minimum of changes to the experimental image, it deviates somewhat of an experimental situation in that the focus grows without affecting the pool of proteins in the cytoplasm.

Random position of a focus

A random walk of a focus is constructed as follows. First, a contour edge was defined by applying a threshold to the fluorescent signal. The threshold level was taken as four SDs of the dark-signal noise above the dark background level. This contour was used as a bounding box for a simple trace of 25 points, starting at a random position within the cell contour. Each subsequent point of the trace was taken as a random point within three pixels distance of the last point and within the bounding contour, thus mimicking a diffusion process. The three pixel radius was large enough to ensure that the whole cell was sampled within 25 points. For each cytoplasmic image taken from the database, a new trace was constructed. Localization errors were binned for all images (42 cells, each with a trace of 25 points) in bins of shortest distance to the nearest cell contour (the edge distance) or the distance to the nearest cell pole (pole distance). Longer traces (up to 100 points) did not yield any different results. These generated random traces were subsequently tested with a constant focus intensity and repeated for a number of different focus intensities. In doing so, we also kept track of the average localization error per focus intensity.

Results and Discussion

Approach of using simulated and experimentally obtained data to evaluate the algorithms used to study intracellular foci

We quantify the effect that cellular background fluorescence and its estimation have on the accuracy with which the total intensity and position localization of a diffraction-limited focus can be estimated inside a bacterial cell. An E. coli cell is small, having a length, width, and height of approximately 3 μm × 1 μm × 1 μm (depending on growth conditions and its stage in the cell cycle). A typical point spread function having a FWHM of 0.25 μm comprises thus 1/10 of the total length of the cell. The contribution of the fluorescence originating from diffusing molecules nearby the focus, together with the background because of the height of the cell, and the nearby presence of cell edges, is thus nonnegligible when determining the total intensity of a focus situated in a cell.

To study the influence of background fluorescence estimation on focus analysis, we simulate a diffraction-limited focus of known total intensity inside the experimentally measured fluorescence background in the cell. We do this by fixing the total fluorescence in the cell constant while increasing the focus content (constant cellular level approach; Materials and Methods; Fig. 3A). Using a constant cellular background fluorescence signal and incrementally increasing the intensity of the focus (incremental focus approach; Materials and Methods; Fig. S2) yields very similar results (Figs. 4 and S2). The position of the simulated focus was chosen to be at ∼1/3 position from the center of the cell, except when we specifically evaluated the edge sensitivity of the different algorithms. In the latter case, we randomly move the focus throughout the cell. The experimental images used to construct the cellular background results from diffusion of two different bacterial strains of E. coli, each having a different protein chromosomally fused to a FP: YPet-DnaN (the β₂ sliding clamp) protein fusion, and the DnaQ-YPet fusion ($\mathit{ϵ}$-subunit of DNA Polymerase III) (see Material and Methods). It has been shown previously that the fluorescence detected from the YPet-DnaN corresponds to 60 to 120 YPet-DnaN dimer molecules, depending on the stage of the cell cycle (29). DnaQ-YPet has approximately half the amount of proteins compared with DnaN (22). A substantial number of proteins in E. coli have this range of copy numbers (30), which makes these two expression levels representative for a wide range of different proteins. For the constant cellular level approach of simulating the increasing focus intensity, we vary the focus versus total cell intensity ratio (FCR) incrementally, from 0 % fluorescence in the focus to 99 % fluorescence in the focus (Fig. 3B). The three sample images together with the respective line profile plots (Fig. 3C) illustrate the setup of our approach. We perform this operation for different individual cells (n = 42) to include cell-to-cell variability. This database of cells with varying FCRs is subsequently used as input for the different algorithms tested (see Materials and Methods).

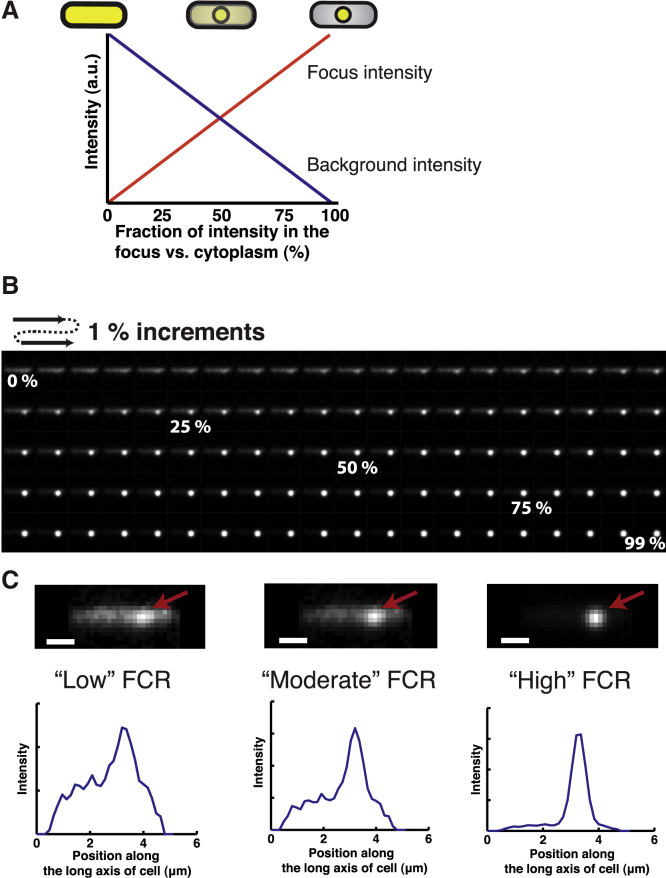
Figure 3.

The approach taken to systematically evaluate the different algorithms of analyzing a focus. (A) Illustration of our approach of increasing the amount of signal in a focus, while simultaneously maintaining a constant total fluorescence value in the cell. For each increment we simulate a diffraction limited focus with more fluorescence content (red line), while also subtracting that amount of fluorescence from the cellular signal (blue line). We schematically illustrate the effect on the focus and cytoplasmic signal. (B) A sample temporal montage of a complete simulation from no signal in a focus (far left side of A) until the signal consists only of a focus (far right side of A). (C) Three sample simulations of different focus fluorescence content together with their corresponding line profile plots. Scale bars: 1 μm. Note that the cellular background is measured and not simulated. To see this figure in color, go online.

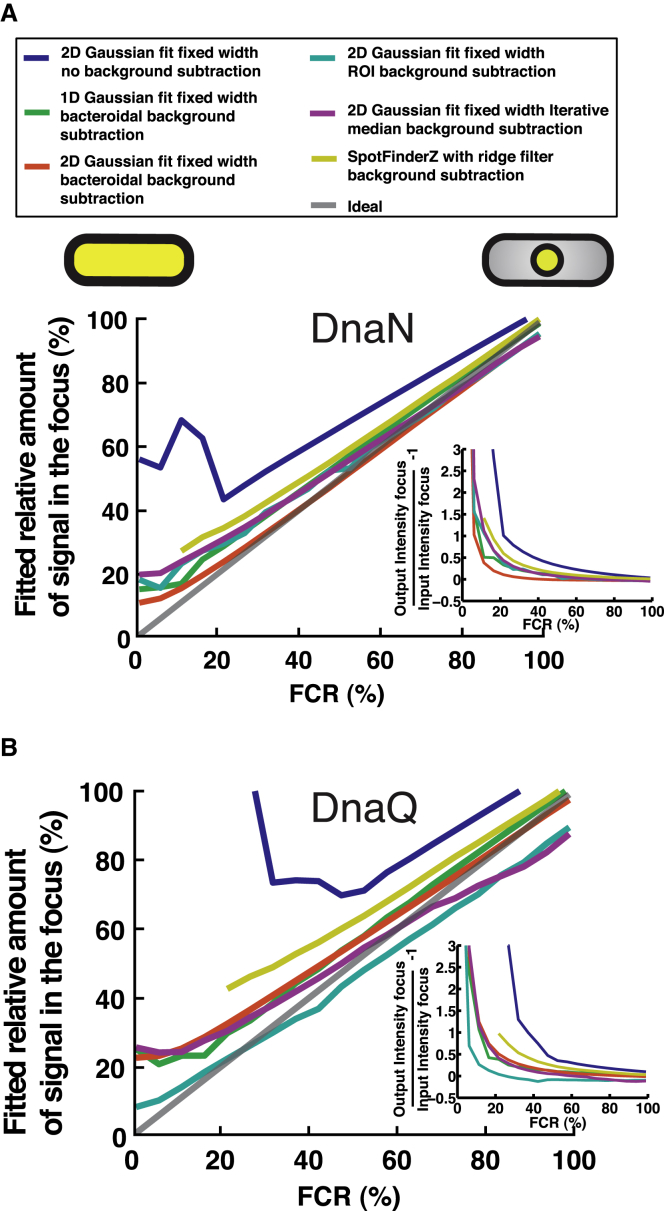
Figure 4.

Comparison of the different algorithms for determining the total intensity of a focus. (A and B) The ratio of the signal in the focus (as estimated utilizing the different algorithms) versus the known total cellular signal plotted for the two different strains DnaN (A) and DnaQ (B), respectively. Here we plot the percentage of the estimated focus content divided by the known total signal. (Inset) The resulting error in terms of the difference between the focus content from the fit and the known focus content divided by the known focus content, plotted as function of FCR. We only show the fitted results up and until 100%. n = 42 cells for both (A) and (B). To see this figure in color, go online.

Estimating the amount of fluorescence intensity contained in an intracellular focus

We investigate the accuracy of the different algorithms in estimating the amount of fluorescence contained in a focus at different FCRs in combination with the different background subtraction methods for the two E. coli strains (Fig. 4). We simulate a focus of varying FCR in the cell, input the resulting images to the background subtraction algorithms, and subsequently apply the different focus analysis algorithms to those results. The amount of signal in the focus versus the known input value is compared for DnaN (Fig. 4A) and DnaQ (Fig. 4B). For reference we have included the ideal case (gray line) and the case in which no background subtraction was performed (blue line). As expected, the no background corrected scenario is the worst algorithm across the whole range of FCRs for both the strains. One can clearly observe that all the algorithms display overestimates at low focus intensity levels (FCR < 15%) independent of the protein copy number in the cell as can be seen by comparing the DnaN (Fig. 4A) and DnaQ (Fig. 4B). The main difference (although not very large) between the DnaN and DnaQ results for low FCR values is that for the case of DnaN the bacteroidal background subtraction algorithm in combination with the median excess algorithm (red curve) is best, whereas in the case of DnaQ the ROI background subtraction in combination with the 2D Gaussian fit is best. All algorithms essentially converge to the correct value as the FCR is increased (Fig. 4, A and B). Here the main difference between the DnaN and DnaQ results is that for the DnaN case there are effectively no underestimates, whereas for the DnaQ results, both the ROI background subtraction and the iterative median background subtraction both in combination with a 2D Gaussian fit display some underestimation of the focus content. The overestimation (low FCR) and underestimation (high FCR) are mostly because of incorrect evaluation of what a focus is under these intensity conditions, and thus incorrectly including too much of the signal from the cytoplasm when determining the intensity of the focus, or too little of the actual focus.

From these results one observes that the accuracy with which the focus signal content can be determined depends on the background subtraction and focus analysis algorithm utilized and on the copy number of the protein in the cell. The algorithms of choice for medium protein expression (DnaN) and low protein expression (DnaQ) at low FCR (<15%) are the bacteroidal background subtraction algorithm in combination with the median excess focus algorithm (Fig. 4A, red curve), and the ROI background subtraction algorithm in combination with a 2D Gaussian fit (Fig. 4B, cyan curve). The error in estimating the total intensity in a focus using these strategies is <10% at a FCR of a few percent, which converges very rapidly (at ∼15 % FCR) to the correct value (Fig. 4A, red curve, Fig. 4B, cyan curve). In contrast with this, all the other algorithms overestimate the focus signal content for FCRs <15% (Fig. 4, A and B). Care should thus be taken when quantifying these low FCR fluorescence signals. At higher FCRs (>30%), all the algorithms converge to the correct value, with the iterative median background subtraction and ROI background subtraction in combination with the 2D Gaussian fitting underestimating the signal focus content for high FCR values (>70%) in the DnaQ case. The favorable characteristic of the bacteroidal background subtraction in combination with the median excess algorithm, for not overestimating the focus intensity at low FCRs, was recently exploited to reliably quantify the number of DNA-bound sliding clamps in live E. coli cells (29), where the FCR valued between 30% and 60% depending on the point in the cell cycle.

Localization of an intracellular focus

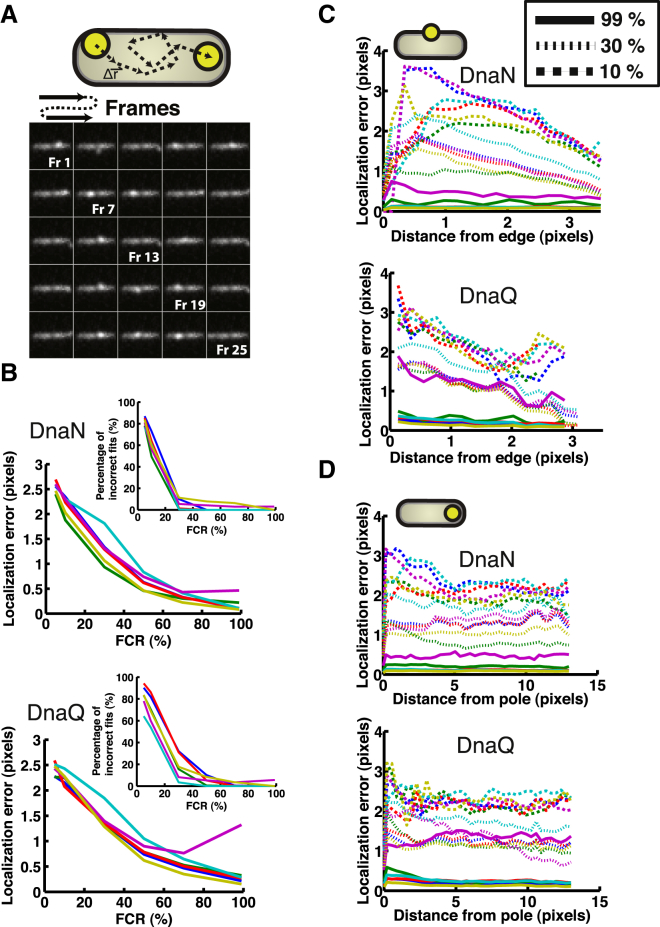
Having established the reliability in determining the total focus intensity for varying FCR, we investigate the accuracy of the different algorithms in combination with the respective background subtraction algorithms in estimating the position of a focus for a range of FCRs (Fig. 5). To sample all possible positions within the cellular surroundings, we model a simple random walk by displacing the position of a focus randomly throughout the cell (see Materials and Methods). In doing so, we keep track of the distance of the focus, as determined from the simulated position, to the nearest cell edge. Here we make a distinction between and edge and a pole. The edge distance is the nearest cell edge in any direction, and the pole distance is the distance to one of the poles of the cell. Subsequently, each of the algorithms is used to determine the position of the focus, and compared with the known value. This is performed for 25 positions at three different FCRs: 10%, 30%, and 99% for each of the strains (Fig. 5).

Figure 5.

Comparison of the performance of different background subtraction and focus analysis algorithms in localizing a focus. (A) An example montage of a simulated focus positioned at random positions in the cell. The cartoon illustrations the approach. Note that the focus appears less bright in Fr 2 compared with, for example, Fr 1. This is because of the background signal of the cell, and emphasizes the relevance of this work. (B) The error in localization of a focus utilizing the different background subtraction and analysis algorithms for the (top) DnaN and (bottom) DnaQ scenarios, respectively. Here the error is taken as 2× SD (95% confidence internal) of the distribution of the values resulting by subtracting the fit from the input value for each of the cells at a specific ratio value. (Inset) The percentage of incorrect fit positions for the different algorithms. An incorrect fit is defined here as a fit position that differs by >2 pixels from the input value. Only FCRs at 5%, 10%, 30%, 50%, 70%, and 99% were simulated because of the time-consuming nature of these simulations (n = 42 cells). The color code used is the same as used in Fig. 4. (C) Assessing the dependency of the localization error on the position of a focus from the cell edge for (top) DnaN and (bottom) DnaQ. Here we depict the error in localization for three different FCRs, namely 10% (dashed), 30% (striped), and 99% (solid). (D) Assessing the dependency of the localization error on the position of a focus from the cell pole: (top) DnaN and (bottom) DnaQ. Here we depict the error in localization for three different FCRs, namely 10% (dashed), 30% (striped), and 99% (solid). To see this figure in color, go online.

Using this analysis series, we first investigate the accuracy of the algorithms in determining the focus position as a function of FCR, averaging per cell over all randomized positions. The error in localizing a focus at different FCRs is only slightly different for all the algorithms evaluated (Fig. 5, B and C). For the DnaN case (Fig. 5B, top), the ROI background subtraction algorithm in combination with a 2D Gaussian fit performs slightly less well than the other algorithms. This could be because of the sensitivity of the center-of-mass based method that is sensitive to the steep signal gradients at the edges of the bacterium image. For the DnaQ case (Fig. 5B, bottom), the ROI algorithm displays similar behavior, whereas the iterative median background subtraction in combination with a 2D Gaussian fit performs less well (∼1.5 pixel error) at higher FCR values. Likewise, this could be because of the fact that the bacterium edges exhibit a similar width as the foci, and therefore are hard to separate out by an aspecific median smoothing approach. As can be expected, the localization error is dependent on the signal to noise: one observes a decrease in error with increased FCR for all the algorithms independent of the strain (Fig. 5). Interestingly, the error in estimating the position of a focus is not dramatically affected by the type of algorithm employed. Only the ROI algorithm and the iterative median methods perform slightly less well than the other algorithms (0.5 to 1.5 pixels). Even though this may not appear as a huge difference, this localization error becomes critical when one wishes to measure positions in the range of tens of nanometers. We do note that, irrespective of the algorithm used, in this more realistic system the errors are more in the pixel than subpixel range despite the fact that the latter should theoretically be possible (19).

All algorithms display a significant number (50% to 90%) of incorrect fits at FCRs <20%, with the ROI algorithm performing the best and the no background subtraction method performing the worst (Fig. 5B, insets). Here an incorrect fit is defined as a fit position that results in being >2 pixels different than the known (input) value. At FCRs of ∼25%, the number of incorrect fits drops to essentially zero.

Secondly, we investigate whether the localization error is affected by where the focus is positioned in the cell. This is relevant, because numerous different proteins localize at disparate positions in the cell (31). To do so, we now bin the positions errors at one FCR as a function of distance to the cell edge or a pole (Fig. 5, C and D). It is evident that at low FCRs, the localization error is a function of the distance of the focus to the edge or to the pole for all the algorithms. The localization error seems to be more sensitive to the distance of the focus to the edge of the cell (Fig. 5, C and D, top panels), than the distance to the cell pole (bottom panels). The observation that the distance of the focus to the cell edge has an effect on the localization accuracy is an interesting and important result, because many biological processes occur in the vicinity of the cell wall. Examples are proteins involved in cell wall synthesis (32), and proteins that make up the flagella motor (33). The increased error when the focus is positioned at the edge of the cell is most likely because of the large background intensity gradient. It is thus crucial when calculating the localization error to take this uncertainty into account when nanometer-range movement or distances are reported.

Analysis guidelines when studying intracellular foci

Our evaluation of the different algorithms for analyzing a focus within the natural in-homogenous cellular environment enables us to provide quantitative guidelines when investigating foci in the cell. We have shown that, independent of the choice of analysis algorithms, one should be extremely careful when investigating a focus that has a low FCR (< 10%). For these cases, we recommend two options to increase the FCR. First, if conventional wide-field microscopy is used for imaging, one could first bleach a fraction of the cellular fluorescence using a diffraction-limited focus. This would lower the cellular background without seriously affecting the focus intensity. Second, if possible one could use photoactivatable FPs (33). Using a low-activation laser would allow one to activate only a small subset of these FPs in the cell. If optimized, one could in principle image less than one molecule on average per cell (11), thus obtaining a higher FCR because of the low cellular background while still having a clear focus and having a high copy number of the protein under investigation in the cell. Two other sources of background are autofluorescence of the cell and autofluorescence of the microscope slide. These sources can be minimized by growing cells in a low fluorescence growth medium, and using slides that have autofluorescence.

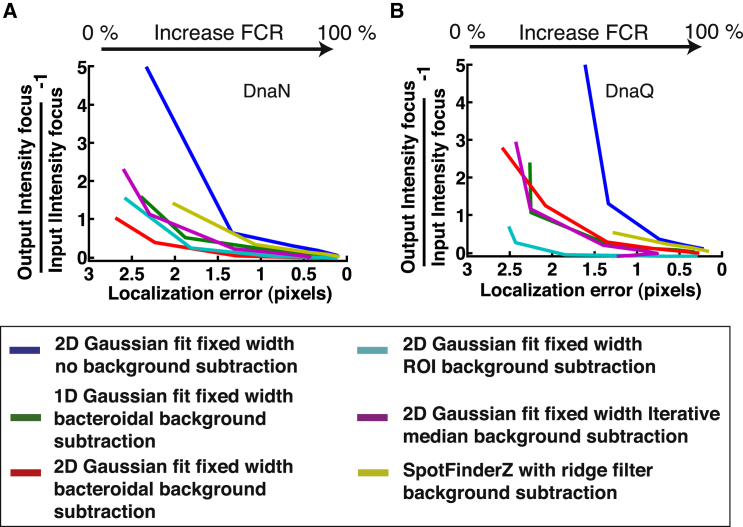
To obtain more insight into the trade-off between the error in determining the total focus intensity and the error in localization, we plot both these quantities simultaneously for different FCRs (Fig. 6). Under our evaluation conditions, it appears that the choice of algorithm is dependent on the concentration of the protein of interest in the cell. In the case of DnaN, the superior algorithm is the bacteroidal background subtraction with a 2D Gaussian fit, whereas for DnaQ the ROI algorithm with a 2D Gaussian fit is best when both total intensity of the focus as well as localization accuracy is required. The error in both intensity and localization drops the fastest for these algorithms in the respective strains.

Figure 6.

Summary of localization versus total intensity error. A comparison of the position and intensity errors for different FCR, namely 5%, 10%, 30%, 50%, 70%, and 99%. For (A), we combine Figs. 4A and 5B, top. For (B), we combine Figs. 4B and 5B, bottom. The results are shown for all the different algorithms. To see this figure in color, go online.

In summary, we showed that care must be taken when judging the accuracy of a measurement on theoretical exceptions from the focus brightness alone; experimental accuracy may well be much lower than expected from ideal in vitro conditions because of the cellular context. In general, a proper choice of analysis may include more aspects than just the theoretical accuracy of an algorithm; for example, the relative positions of multiple foci to each other or to the edge of the cell could play a role in the decision. Specific multifoci, mesh-based approaches such as the versatile MicrobeTracker/SpotfinderZ package may then be preferable. Likewise, a prior knowledge of where a focus is situated might favor time-averaging prefitting, such as with the local ROI method, whereas accurate single-focus content analysis may favor taking into account the general bacteroid shape, such as with the median excess approach. Because we showed that the measurement error for a focus in a cell may depend more on its position in the cell than on the algorithm used, this factor should be taking into account during analysis when quantifying the focus position and signal content.

Author Contributions

M.C.M., J.W.J.K., and N.H.D. designed the research. J.W.J.K. and M.C.M. wrote software to analyze the data and performed the analysis. M.C.M., J.W.J.K., and N.H.D. wrote the article.

Editor: Antoine van Oijen