Migration in Confined 3D Environments Is Determined by a Combination of Adhesiveness, Nuclear Volume, Contractility, and Cell Stiffness

Abstract

In cancer metastasis and other physiological processes, cells migrate through the three-dimensional (3D) extracellular matrix of connective tissue and must overcome the steric hindrance posed by pores that are smaller than the cells. It is currently assumed that low cell stiffness promotes cell migration through confined spaces, but other factors such as adhesion and traction forces may be equally important. To study 3D migration under confinement in a stiff (1.77 MPa) environment, we use soft lithography to fabricate polydimethylsiloxane (PDMS) devices consisting of linear channel segments with 20 μm length, 3.7 μm height, and a decreasing width from 11.2 to 1.7 μm. To study 3D migration in a soft (550 Pa) environment, we use self-assembled collagen networks with an average pore size of 3 μm. We then measure the ability of four different cancer cell lines to migrate through these 3D matrices, and correlate the results with cell physical properties including contractility, adhesiveness, cell stiffness, and nuclear volume. Furthermore, we alter cell adhesion by coating the channel walls with different amounts of adhesion proteins, and we increase cell stiffness by overexpression of the nuclear envelope protein lamin A. Although all cell lines are able to migrate through the smallest 1.7 μm channels, we find significant differences in the migration velocity. Cell migration is impeded in cell lines with larger nuclei, lower adhesiveness, and to a lesser degree also in cells with lower contractility and higher stiffness. Our data show that the ability to overcome the steric hindrance of the matrix cannot be attributed to a single cell property but instead arises from a combination of adhesiveness, nuclear volume, contractility, and cell stiffness.

Introduction

Cell migration through a three-dimensional (3D) extracellular matrix is important for numerous physiological processes such as morphogenesis, wound healing, immune cell trafficking, and organ formation, but also for pathological processes such as cancer metastasis (1,2). The process of cell migration is governed by a balance between protrusive forces that drive cell motion, and frictional forces that resist cell motion (3,4). Protrusive forces can arise from actin polymerization (5) or actomyosin contractions (6), whereas frictional forces result from cell adhesions to the matrix and from friction with the environment (7). For cells migrating in a two-dimensional (2D) environment, viscous friction with the cell culture medium can be neglected, and thus friction arises mostly from cell adhesion to the substrate. For cells migrating in a 3D environment, additional friction forces arise from the steric hindrance imposed by the matrix. Steric hindrance occurs when the cross section of the open spaces or pores of the matrix are smaller than the cross section of the cell. In this case, the cell can either deform itself, or it can deform the matrix to squeeze through. Matrix deformations require the cell to generate forces to widen the matrix pores, whereas cell deformations require the cell to generate forces to overcome the elastic and frictional forces of its nucleus and cytoskeleton. Thus, steric hindrance is set not only by matrix properties such as stiffness and pore size, but also by cell viscoelastic properties and cell size. In addition, cells can secrete matrix-degrading enzymes to widen pores and soften the matrix.

It is widely believed that low cell stiffness promotes cell mobility through the narrow pores of the matrix (8,9). Although it is clear that contraction and adhesion are also important for cells to overcome steric barriers (3,10), the question remains whether larger contractile forces or larger adhesive forces increase or decrease cell migration and invasion. Even though firm adhesion to the matrix is required to convert contractile forces into traction forces for a forward movement (3,11,12), strong adhesions at the trailing end of the cell can also resist a forward movement (13). Indeed, conflicting data in the literature point to increased adhesion as either promoting (14) or hindering (15) tumor cell migration through tissue. Another prerequisite for cell invasion are sufficiently high contractile forces (10). However, strong contractile forces also stiffen the cell (16) and may thus increase the steric hindrance; according to several studies, cell stiffness is inversely correlated with invasiveness (8,17,18).

Similar conflicting data exist for the mechanical properties of the matrix. A minimum tissue stiffness of around 100 Pa appears to be required for cell invasion (19), but invasion is also severely impeded when cells encounter a combination of high tissue stiffness and small pore size (3,19). However, other studies report that matrix stiffness has no influence on the cells’ ability to migrate through small pores (4). Given these disparate results, it is likely that cells may employ multiple strategies to optimize invasion.

Our aim in this study is to clarify the influence of contractility, adhesiveness, cell size, and cell stiffness on the cells’ ability to migrate through narrow pores. To address this question, we measure the migration of four different cancer cell lines of varying cell size, stiffness, contractility, and adhesiveness. As a 3D matrix, we use two different systems. The first system is a nondegradable and stiff (E = 1.77 MPa) polydimethylsiloxane (PDMS) microfluidic device consisting of a linear array of 10 parallel channel rows, each consisting of 15 channels with a length of 20 μm and a width ranging from 11.2 μm for the first channel to a width of 1.7 μm for the last channel. Neighboring channels in a row are separated by a 20 × 20 μm chamber. The channels and chambers have a height of 3.7 μm. The microfluidic device allows us to precisely control steric hindrance of the matrix without altering matrix stiffness. As a second system, we use collagen gels at a concentration of 2.4 mg/ml that have an average pore size of 3 μm (corresponding to a cross section of ∼7 μm²) and a stiffness of 550 Pa (19). Therefore, the average cross section of the collagen pores matches the cross section of the smallest PDMS channels (width = 1.7 μm, height = 3.7 μm, cross section ∼6.5 μm²). We also change the adhesiveness of the PDMS device by coating the channel walls with different ligands at different densities, and we alter the stiffness of two of the cell lines by increasing lamin A expression levels.

We show that cells move faster and with higher persistence along the narrow channels than in the wider chambers. In channels with cross sections below 30 μm², the cell nucleus stalls at the channel entrance as it deforms to the width of the channel; once fully deformed, the cell exits the channel with a higher velocity. The stalling of the nucleus at the entrance of the narrow channels suggests that cell migration is impeded by steric hindrance. To test the role of cell and nuclear stiffness, we investigate cells overexpressing the nuclear envelope protein lamin A; these cells show impeded cell migration, which can be attributed to their substantially higher cell stiffness and slightly lower adhesiveness. Overall, we find that migration is severely impeded in cells with a larger nuclear volume and lower adhesiveness, and to a lesser degree in cells with lower contractility and higher stiffness. These data point to the nucleus as a major source of migration-resisting forces in environments with high steric hindrance, but multiple other parameters must also be considered when evaluating the invasive potential of cells.

Material and Methods

Detailed descriptions of materials and experimental methods are given in the Supporting Material. In brief, A125 lung carcinoma cells, MDA-MB-231 breast carcinoma cells, HT-1080 fibrosarcoma cells, and primary breast cancer cells (IFDUC1) of mesenchymal origin with high E-cadherin levels isolated from a patient with inflammatory ductal breast cancer are maintained at 37°C and 5% CO₂ in cell culture medium. Human sample collection was approved by the Ethics Committee of the University of Erlangen-Nürnberg (ethics application #264_13B) in accordance with the World Medical Association Declaration of Helsinki. Informed consent was obtained from the patient.

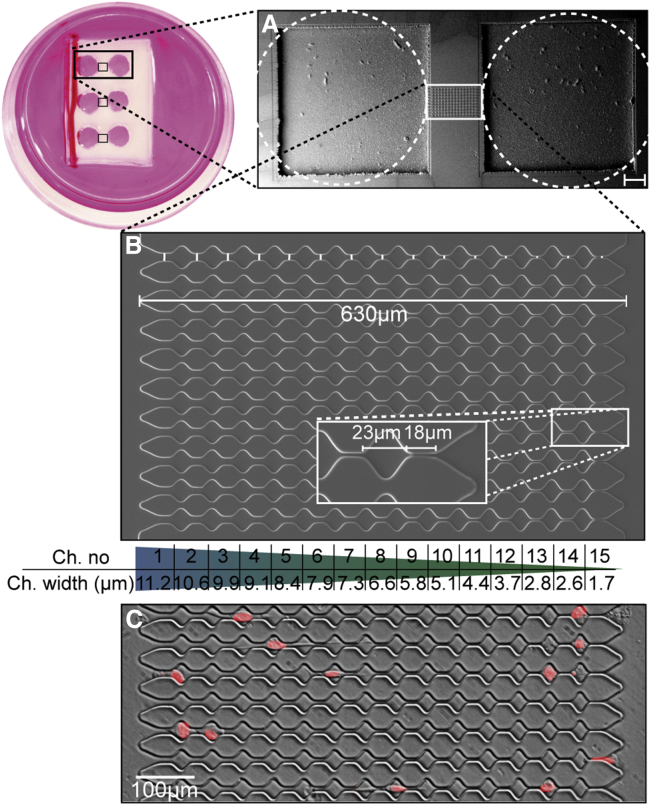
Before plating, cells are rinsed with phosphate buffered saline and trypsinized with 0.05% trypsin/EDTA. We use lentiviral transduction to generate MDA-MB-231 and HT1080 cells that express enhanced green fluorescence protein (eGFP)-lamin A. Channel devices are molded in PDMS from photolithographically developed masters (see Fig. S3). Each device contains 2 cell reservoirs connected by 10 linear arrays of 15 channels with decreasing width (11.2–1.7 μm diameter) separated by 20 × 20 μm chambers (Fig. 1, A and B). PDMS devices are coated with different concentrations of fibronectin or with collagen. Cells are seeded in the reservoir near the larger channels and incubated for 1 week. Before imaging, cell nuclei are stained with 1.5 μg/ml Hoechst 33342 (Fig. 1C). During time-lapse imaging (frame rate 0.2/min) over the following 12 h, cells are kept at 37°C and 5% CO₂ in a stage incubator. With a custom-written MATLAB image analysis software (The MathWorks, Natick, MA), cell nuclei are detected and their projected x-y areas are computed after image binarization with a threshold determined using Otsu’s method (20). Nucleus positions (center of mass) are computed using the brightness information of the fluorescently labeled nuclei. In some cases, we also identify the leading and trailing edge of the nucleus from binarized images. The trajectories of the nuclei are transformed to the coordinate system of the microchannel array. From the trajectories, the instantaneous or momentary velocity vector in the x-direction is calculated from the nucleus movements between two consecutive images (taken 5 min apart). The time course of migratory persistence and activity are extracted with a Bayesian method of sequential inference as described in (21,22). From the measured positions x_t of the cell along the channel array, we compute a time series of steps u_t = x_t – x_t–1. Locally, this time series is modeled as an autoregressive process of first-order (AR-1), defined by u_t = q_tu_t–1 + a_tn_t. The parameter q_t ∈ [−1,+1] describes the local persistence of the random walk, with q_t = −1 corresponding to antipersistent motion, q_t = 0 to nonpersistent diffusive motion, and q_t = +1 to persistent motion. The parameter a_t ∈ [0, ∞] describes the local activity (noise amplitude) and sets the spatial scale of the random walk. Together, the two parameters determine the variance of the displacements according to var(u) = a_t² /(1−q_t²). The quantity n_t is normally distributed, uncorrelated random noise with unit variance.

Figure 1.

Architecture of PDMS device. (A) Scanning electron microscope image of the channel array and reservoirs (scale bar 100 μm), and photo of a petri dish with three attached channel arrays. (B) Scanning electron microscope image of the channel array. (C) Channel structure with invading breast cancer cells. Nuclei are stained with Hoechst and shown in red. To see this figure in color, go online.

To measure 2D cell migration, cells are plated 24 h before measurements on fibronectin-coated petri dishes. During time-lapse imaging (frame rate 0.2/min) over 24 h, cells are kept at 37°C and 5% CO₂ in a stage incubator. Cell movements are tracked with custom-written MATLAB image analysis software, and the mean square displacement (MSD) is calculated as previously described (23). Cell traction forces, strain energies, and contractility are computed from the displacements of beads embedded in an elastic polyacrylamide gel with a Young’s modulus of 11.3 kPa (24). Immunoblot analysis is performed using standard protocols (25,26) with anti-lamin A/C, anti-lamin A, anti-β-actin and anti-β-tubulin antibodies. To test cell adhesion strength, a fluid shear stress of 32 dyn/cm² is applied for 5 min to the cells using a spinning disk device. The fraction of detached cells is measured from images taken before and after the application of shear stress. Cell stiffness is measured as described in (27) from the applied pressure and the transit time of cells passing through a microfluidic device consisting of a parallel array of micron-sized constrictions with a diameter of 5 μm, which is smaller than the diameter of the nucleus so that the measured cell stiffness includes the stiffness of the nucleus. Invasion assays are performed in 2.4 mg/ml collagen gels as described in (12). In brief, cells are seeded on top of collagen gels (thickness 1 mm), and the invasion profiles are measured after a 3-day incubation period and plotted as cumulative probability of finding a cell at or below a given depth of the gel. The invasion profile is fitted with an exponential function as expected from the experimentally observed exponential (and not Gaussian) step width distribution of randomly migrating cells (21), yielding the fraction of invaded cells and the characteristic invasion depth.

Results

Cell movements through confinements

To investigate how cells overcome the steric hindrance of the extracellular matrix, we designed microchannel structures that have a series of channels with decreasing cross sections that are separated by larger chambers. Cells are seeded in a reservoir at the side of the channel array and spontaneously enter the channel structures even in the absence of a chemoattractant gradient (Movie S2).

Steric hindrance

Cells migrate at a nearly constant velocity through channels wider than 8 μm, whereby the nucleus remains in the center or the front of the cell body (Fig. 2A) and is not visibly stretched (Fig. 2B). In channels narrower than 8 μm (30 μm² cross section), however, the movement of the nucleus is impeded, and fluctuations in the migration velocity emerge. The leading edge of the cell body passes into the channel first, whereas the nucleus stalls at the channel entrance and first needs to be deformed to fit through (Fig. 2, C–E). Once fully deformed, the nucleus rapidly slides through the channel (Movie S1) and once again assumes its center position within the cell.

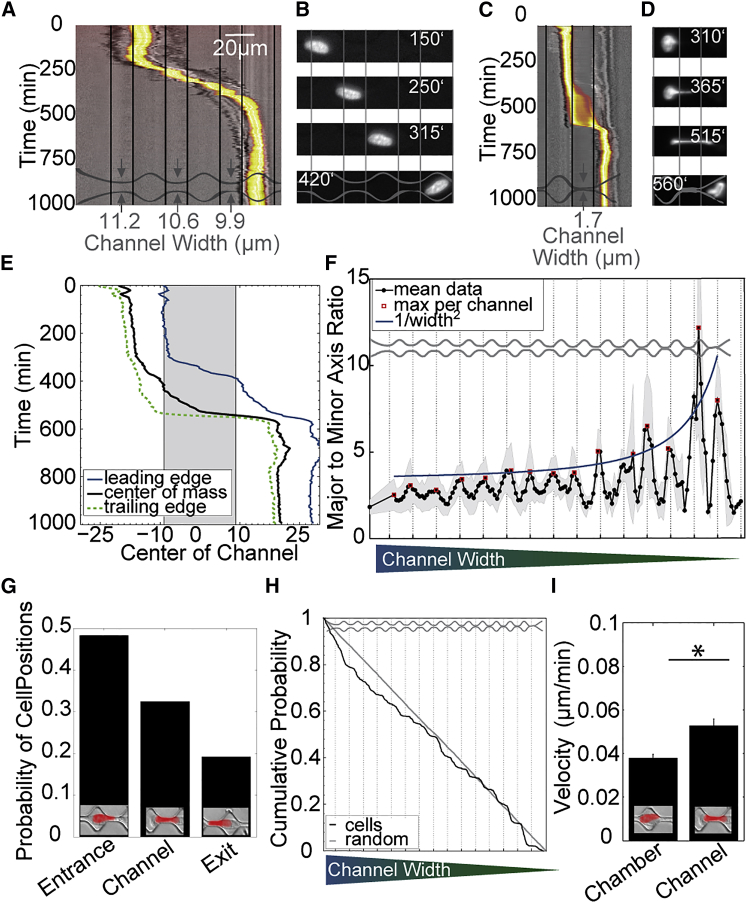
Figure 2.

Cell movement through the channel array. (A) Kymograph of an MDA cell (gray) and nucleus (yellow-red) migrating through large channels (11.2–9.9 μm). (B) Corresponding nuclear shapes in channels (top 3 images) and in the following chamber (bottom). (C) Kymograph of an MDA cell migrating through a 1.7 μm wide channel. (D) Corresponding nuclear shapes. (E) Trajectories of the nucleus’ leading edge, center, and trailing edge (from C). (F) Nuclear deformation (major to minor axis ratio) averaged for all nontransfected cells, showing increasing maximum deformation (red dots) in channels proportional to 1/channel width² (blue line) and full shape recovery in the chambers. (G) Probability of finding cells (center of nucleus) at the channel entrance, within the channel, or at the channel exit (measurements from all nontransfected cells are combined). (H) Cumulative probability of cell positions. (I) Cell velocities averaged for all channels and chambers (^∗indicates significant (p < 0.05) differences) (measurements from all nontransfected cells are combined). To see this figure in color, go online.

During migration through the smallest channels, the nucleus shows extreme shape changes (Fig. 2D). Similar shape changes have been reported during in vivo cancer cell dissemination (28–32) and transendothelial migration (33,34). To quantify nuclear deformation, we fit an ellipse to the shape of the nucleus and compute the ratio of the major to minor axes. We find that this ratio increases with 1/(channel width)² as the nucleus completely fills the cross section of the channel (Fig. S5). Interestingly, after each channel passage, this ratio recovers to a value of typically 1.5, regardless of the channel cross section. Thus, these nuclear deformations are completely reversible (Fig. 2F).

The stalling of the nucleus before it enters the channel can be clearly seen in the statistics of cell positions. When averaged over all channel sizes, we find the center of the nucleus to be twice as frequently at the channel entrance than within a channel or at the channel exit (Fig. 2G). Here, the channel entrance is defined as the 10 μm long region between the center line of the chamber and the beginning of the next channel; the channel exit is defined as the 10 μm long region from the end of the channel to the center line of the next chamber. This nuclear stalling is also seen in the cumulative probability of cell positions along the channel array (Fig. 2 H), which describes the probability of finding a cell at or beyond (right of) a given distance from the entrance to the microchannel array. After an incubation time of 7 days, the probability density to find a cell at a given position is nearly constant, implying steady state, and thus the cumulative probability decays approximately linearly with position. However, the cumulative probability shows clear steps, with a fast drop within the chambers and a nearly constant cumulative probability across the channels, indicating that the cells stall before they enter the channels. Stalling is also confirmed by the cell migration velocity in the channel (averaged over all channel sizes), which is 30% higher than the average migration velocity in the chambers (Fig. 2I). Together, these data suggest that the deformation of the nucleus is a major source for impaired migration under confinement.

Velocity of cell migration

To further explore how the nucleus impedes cell migration under confinement, we measured the instantaneous velocity of the nucleus along the channel array. We found that the nucleus accelerates when entering the channel and reaches a maximum velocity at the end of the channel (Fig. 3A, Movie S1). After the nucleus has exited the narrow channel and enters the wider chamber, it decelerates and reaches a minimum velocity before reaching the next channel (Fig. 3A). The maximum velocity at the end of each channel increases as the channel diameters decrease, down to channel diameters around 5 μm, below which the maximum velocity falls off sharply (Fig. 3, A and B). By contrast, the minimum velocity in front of the channel entrance steadily decreases with decreasing channel diameter (Fig. 3, A and B).

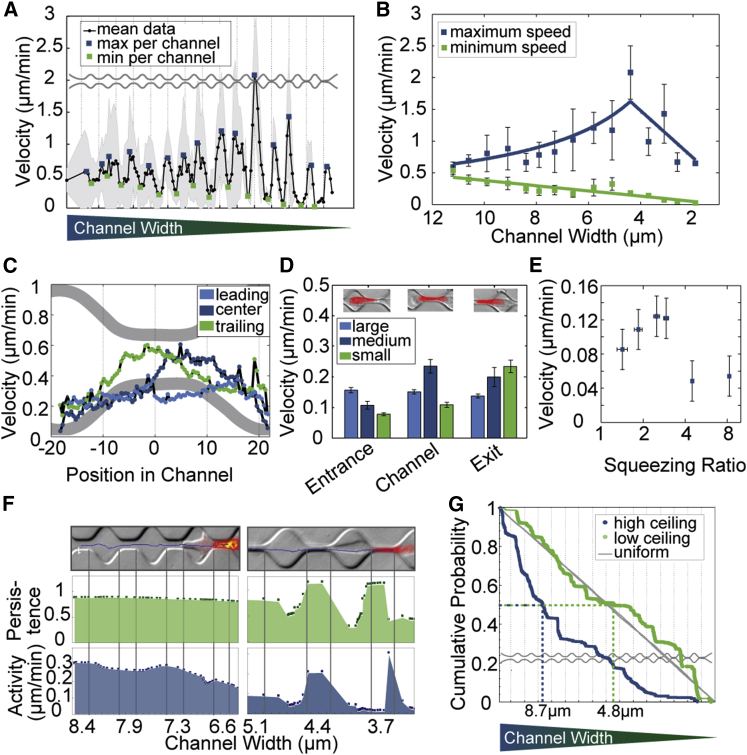
Figure 3.

Analysis of cell migration through channel structures of decreasing width. (A) Velocity of the nucleus (mean ± SE, n = 1004 cells; measurements from all nontransfected cells are combined). (B) Maximum velocities in channels show a biphasic response to channel width. Minimum velocities decrease linearly with channel width. (C) Average velocity distributions across all channel sizes for the nucleus’ center of mass, leading edge, and trailing edge. (D) Binned velocities for channel entrance, channel center, and channel exit, separately evaluated for large (width of 11.2–8.4 μm), medium (width of 7.9–5.1 μm), and small (width of 4.4–1.7 μm) channels. (E) Velocity in channels versus squeezing ratio of the nucleus (cross section of the round unconstrained nucleus to cross section of the channel, mean ± SE for 145 cells in each bin) (F) Persistence and activity level for a cell in channels of 8.4–6.6 μm width (left) and in channels of 5.1–3.7 μm width (right). (G) Cumulative probabilities of cell position throughout channel structures of 3.7 μm height (high ceiling) and 7.4 μm height (low ceiling). To see this figure in color, go online.

The initial increase of the maximum velocity at the end of each channel for decreasing channel diameters (down to 5 μm) suggests that the nucleus moves inside the channels with a constant volume flow (Φ) (Fig. 3B). For channels of constant height, as is the case in our study, a constant volume flow implies that the maximal velocity (v) scales inversely with channel width (w) (consistent with a constant volume flow Φ = v∙w), in agreement with our data (Fig. 3 B). For channel widths below 5 μm, however, the friction imposed by the channel or by the internal resistance of the deforming cell limits a further increase of the maximum velocity, as the cell cannot pull any longer with sufficient pressure ΔP (or force) to maintain a constant volume flow. Neglecting any elastic stresses and assuming Newtonian viscous behavior, Hagen-Poiseuille’s law suggests that friction in a channel with constant height scales with 1/w². Because channel resistance R = ΔP/Φ, it follows for a constant cell-generated ΔP that Φ ∼ w² and hence v ∼ w. Therefore, the velocity decreases linearly with channel width. Although this is a highly idealized situation with many simplifying assumptions, it fits our experimental data (Fig. 3B).

In agreement with an approximately constant volume flow in the larger channels, we found that the leading edge of the nucleus moves through the channels with nearly constant velocity (Fig. 3C). By contrast, the trailing edge first stalls in front of the channel, but once the nucleus is fully deformed, it slides through the channel with a higher velocity (Fig. 3C), reminiscent of a released spring. These velocity fluctuations of the trailing edge are also evident in the movement of the center of mass of the nucleus, except that the position of highest velocity is shifted further to the right due to the finite dimensions of the nucleus (Fig. 3C). This mode of migration can be compared to the push-and-pull movement that has been previously described for cells migrating along adhesive one-dimensional line patterns (35).

To obtain a robust measure for the velocity profile of the nucleus and how it depends on the channel diameter, we average nuclear velocities for large (11.2–8.4 μm), medium (7.9–5.1 μm), and small (4.4–1.7 μm) channels. We then bin the velocity data into three regions—entrance, channel, and exit—as defined previously. We found that the entrance velocity decreases with decreasing channel width, whereas the exit velocity increases (Fig. 3 D). The velocity in the channel shows a biphasic response, with the highest value for intermediate channel sizes (Fig. 3D).

A decreasing entrance velocity for decreasing channel sizes confirms the stalling of the nucleus, as seen in the kymographs (Fig. 2C). The biphasic behavior for the velocity within the channel, with the highest values for intermediate channel sizes, mirrors the biphasic behavior seen in the maximum velocities (Fig. 3B). The two phases refer to the region of the channel array where the migration velocity scales differently with channel width (Fig. 3B). Such biphasic behavior has been previously predicted in a theoretical study (36).

We reasoned that the migration velocity in the channels depends not only on the channel width but also on the diameter of the nucleus. Indeed, smaller than average nuclei show a considerably higher migration velocity in large and medium-sized channels, although in the smallest channels no difference is observed between the velocities of nuclei of different sizes. The parameter that governs this behavior is the squeezing ratio. The squeezing ratio is defined as the cross section of the undeformed nucleus divided by the cross section of the constriction. Note that the nucleus of most cells is already elongated with aspect ratios around 1.5 prior to entering a channel; thus, squeezing ratios below 1.5 do not require the nucleus to be squeezed.

We found that the average velocity in the channels increases up to a squeezing ratio of 3 but then declines sharply for a squeezing ratio of 4 (Fig. 3E). When the nucleus is squeezed beyond a ratio of 4, the migration velocity does not decrease further and is dominated by other cell properties and phenomena.

Perhaps the most surprising finding is the monotonic increase in the exit velocities for decreasing channel sizes (Fig. 3D). A possible explanation for this behavior is an increase of pulling forces that the cells generate to compensate for the increased friction in the smaller channels. Alternatively or additionally, this behavior could also arise from a larger pressure difference across the cell if the same force acts on a smaller cross-sectional area. These pulling forces lead to a deformation of the nucleus, whereby the deformation energy may be at least in part stored elastically. A sudden release of elastically stored energy would also explain the speedup of the trailing edge once the nucleus has been narrowed to the width of the channel (Figs. 2, C and E and 3D). The influence of nuclear deformability and pulling (and hence traction) forces for cell migration through narrow openings is explored in more detail further below.

Migration persistence

Although we have examined the horizontal velocity in the direction of the channels, the movement of cells as they migrate in chambers is not confined to a single dimension. To understand how confinement influences migration behavior, we next consider the momentary velocity magnitude and the migration persistence. We describe cell migration as a persistent random walk with the time-varying parameters persistence (q_t) and activity (a_t). The momentary velocity magnitude of cell migration (v_t) is v_t = a_t²/(1-q_t²). The time-dependent parameters (q_t and a_t) are determined from the (x,y)-trajectories using Bayesian sequential inference (22).

We found that the nucleus moves with a constant persistence both in chambers and in channels wider than 8 μm (Fig. 3F, Movie S3). In smaller channels, however, the persistence decreases during the stalling phase before the nucleus enters the channel, and then sharply increases once the nucleus is deformed to fit through the channel (Fig. 3F and Movie S4). These results show that persistence and activity of cell migration correlate with the degree of confinement, and that stronger confinement, which reduces the dimensional degrees of freedom, increases the migration persistence.

Influence of channel height

To investigate the influence of channel geometry on steric hindrance in more detail, we fabricated our channel devices with two different heights, 3.7 μm as used in all other experiments, and 7.4 μm. Channel structures are functionalized with collagen. MDA cells are able to migrate through channels as narrow as 1.7 μm for a channel height of 7.4 μm, and show an approximately uniform distribution throughout the channel structures (zero gradient of cell density), as seen by the linear decrease of the cumulative probability of cell positions (Fig. 3G). By contrast, these cells show a rapid decline of the cumulative probability distribution for migration through 3.7 μm high structures (Fig. 3G), suggesting they are impeded by steric hindrance. The smallest channel width that 50% of the cells are able to traverse (p50 value) is 8.7 μm for the low (3.7 μm) channel structures, compared to a p50 of 4.8 μm for cells in the high (7.4 μm) channel structures (Fig. 3G). As expected, the respective p50 values correspond to similar channel cross sections of 32–35 μm² for the respective low and the high channel structures.

Comparison of different cell lines

To explore how different cell lines are influenced by the steric hindrance of the stiff (1.77 MPa for PDMS) channel structures, we compared the migration behavior of the fibrosarcoma cell line HT-1080, the breast cancer cell line MDA-MB-231, the lung carcinoma cell line A125, and primary mesenchymal cells from a patient with inflammatory duct (IFDUC1) breast carcinoma.

To compare the 3D migration behavior in a stiff environment with the migration in a softer environment with similar pore sizes, we also probed the invasiveness of these cells in a 2.4 mg/ml collagen gel (Young’s modulus 550 Pa, average pore size 3 μm (19)). To understand which cell properties facilitate or impede the transmigration through narrow spaces in a 3D environment, we characterize the migration velocity and persistence of all cell lines on 2D planar substrates (fibronectin-coated plastic), as well as cell spreading area, adhesiveness, traction force generation, and cell stiffness.

Migration in stiff PDMS channel structures

We first analyzed the distribution of cell positions within the channels, by comparing the probability of finding a cell at the entrance of a large, medium, or small channel, relative to the probability of finding a cell at the exit of the respective channel. The channel entrance and exit regions are defined as above (Fig. 2G). The ratio of the probabilities of finding a cell at the entrance versus the exit of a channel is a measure of cell stalling, with higher values indicating a larger steric hindrance. We found that the stalling ratio is between 1 and 2 for large and medium-sized channels, and increases dramatically for narrow channels. Consistent with our results from a cumulative probability analysis (Fig. S4A), we found the largest stalling ratio for A125 cells, and the smallest stalling ratio for IFDUC1 and MDA cells (Fig. 4 A). These data show that different cell lines respond differently to confinement. Surprisingly, the migration of the primary IFDUC1 cells through narrow channels is not significantly (p > 0.05) impaired in comparison to their migration through wider channels, indicating that these cells can easily squeeze through pores that are much smaller than their own diameter.

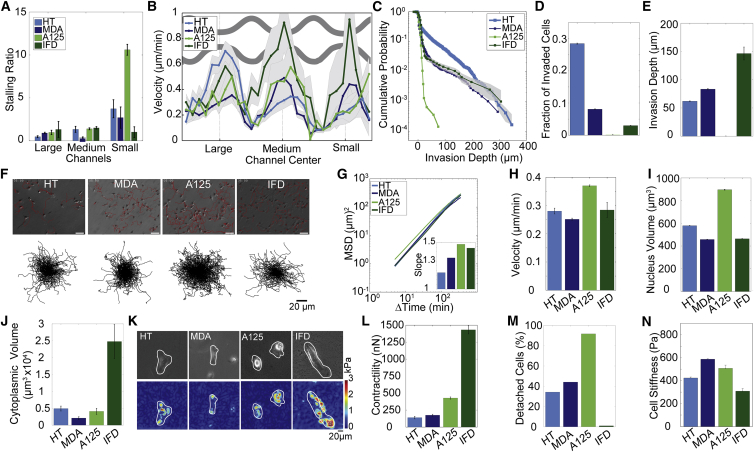
Figure 4.

Migration ability of different cell lines. (A) Stalling ratio of cells entering and exiting the channels, binned for large, medium, and small channels. (B) Velocities (mean ± SE) in channel array for HT (n = 53), MDA (n = 78), A125 (n = 64), and IFDUC1 (n = 26) cells. (C) Invasion profile in collagen gels. (D) Fraction of invaded cells and (E) characteristic invasion depth. (F) Top: images of cells on 2D substrates with their migration trajectories (red). Bottom: collapsed trajectories of 250 cells. (G) MSD of the different cell types (mean ± SE for n > 1000 cells). Inset: slope of the MSD. (H) Momentary migration velocity in 2D (mean ± SE for n > 1000 cells). (I) Nuclear volume (mean ± SE for n > 80 cells). (J) Cytoplasmic volume (mean ± SE for n > 100 cells). (K) Top: bright field image of representative cells grown on polyacrylamide gels. Bottom: corresponding traction maps. (L) Cell contractility (mean ± SE for n > 60 cells). (M) Percentage of detached cells under a shear flow of 32 dyn/cm² after 5 min (N) Cell stiffness (mean ± SE for n > 4000 cells). To see this figure in color, go online.

We next analyzed the absolute migration velocity across the channels. Channels are again binned into large, medium, and small channels. We found a significantly (p < 0.05) higher migration velocity of IFDUC1 cells in small channels compared to the other cell lines (Fig. 4B), supporting the previous finding that the mobility of primary IFDUC1 breast carcinoma cells is not hindered by small pores. By contrast, the velocity of A125 cells is highest in medium channels, but decreases strongly for small channels. HT cells also show a noticeable reduction of migration velocities in medium size and especially in small channels, whereas the migration velocities of MDA cells are approximately similar for all channel regions. Together, these results are in agreement with our data for the stalling ratio (Fig. 4A) and highlight important differences in the ability of these distinct cell lines to overcome the steric hindrance of the matrix.

Invasion into soft collagen gels

Steric hindrance is not solely determined by confinement or the cross section of the channel, but also by the stiffness of the surrounding extracellular matrix (ECM). The stiffness of the PDMS devices is in the range of MPa, and thus practically undeformable for cells. However, during in vivo invasion through the ECM, cells can deform the surrounding protein networks. To compare the ability of these four cell lines to migrate through a soft ECM, we set up an invasion assay where cells migrate through dense collagen matrices with average pore diameter 3 μm and a Young’s modulus of 550 Pa (19). The pores of these gels have an average cross section of ∼7 μm², which is comparable to the smallest channels in our PDMS device. We describe the invasion profile of these cells as the cumulative probability of finding a cell at or below a given depth (Fig. 4C).

The majority of the cells does not invade the gels and remain at the gel surface, as described previously (37). To compare the gel invasion data with the migration behavior in the channel arrays, we thus analyze only those cells that have invaded the gels. After the initial drop in the invasion profile at the gel surface that corresponds to the fraction of noninvaded cells, the invasion curves typically show an exponential decrease, as seen by the approximately linear shape of the invasion profile in a semilogarithmic plot (Fig. 4C). An exponential fit of the invasion profile (between the gel surface and the invasion front where the cell density falls off faster than exponentially) yields a characteristic invasion depth (Fig. 4D). Interestingly, the characteristic invasion depths of the four cell lines parallel their migration behavior through the smallest channels, with IFDUC1 cells showing the highest level of invasion, and A125 cells showing essentially no invasion into the gels. Therefore, despite the differences in the physical properties of the channel arrays and collagen gels, as well as the possible degradation of collagen by secreted proteases, it appears that the migration behavior of different cell lines is similarly impeded. Taken together, these results indicate that the cross-sectional area of the pores is the main parameter that limits cell invasion in confined environments.

2D migration

To understand how the migration in 2D relates to the migration behavior in a confined 3D environment, we track the movement of cells on planar fibronectin-coated culture dishes for 24 h. From the cell trajectories, we compute the MSD. We found only small differences among the cell lines (Fig. 4, F–H), suggesting that the migration behavior of cells on a planar substrate is not indicative of their migration behavior in a confined 3D environment.

Nuclear volume

It is expected that cells with larger nuclei experience a larger steric hindrance when migrating through confined spaces (38) (Fig. 3E). We therefore measure the nuclear volume of cells in the channel structure from the projected area of the nucleus multiplied by the structure height (3.7 μm). We found that MDA and IFDUC1 cells have relatively small nuclei compared to A125 and HT cells (Fig. 4I). Thus, in agreement with expectations, the volume of the nucleus scales inversely with the ability of cells to migrate through narrow channels or to invade dense collagen gels.

Cytoplasmic volume

Taken together, our data suggest that the nucleus causes a larger steric hindrance than the rest of the cell. To test the alternative hypothesis that cells with a larger cytoplasmic volume experience a greater steric hindrance, we measure the total cell volume from the diameter of cells in suspension and subtract the volume of the nucleus. IFDUC1 cells have the largest cytoplasmic volume, followed by HT, A125, and MDA cells (Fig. 4J). Thus, cytoplasmic volume scales with the ability of the cells to migrate through narrow channels or to invade dense collagen gels, suggesting that the cytoplasm is not a source of steric hindrance but rather facilitates migration through narrow pores, as it contains the contractile machinery that generates the forces needed to pull the cell forward.

Cell contractility

It has been previously shown that high contractile forces are necessary but not sufficient for cell invasion in dense collagen gels (10). We therefore measure the total contractility of the different cell lines. We find IFDUC1 cells with a total force of 1000 nN to be extremely contractile, A125 cells to be highly contractile, whereas the other two cell lines exhibit considerably weaker contractile forces (Fig. 4, K and L). However, in comparison to other highly contractile cells such as myoblasts and cardiac myocytes (contractile forces between 300 and 500 nN) (19,39,40), the HT and MDA cells (contractile forces of 100–200 nN) can still be considered as relatively strong. Thus, contractility scales only moderately well with the ability of the cells to migrate through narrow channels or to invade dense collagen gels, confirming that high contractile forces are necessary but not sufficient for invasion (10).

Cell adhesiveness

To convert actomyosin contractility into traction forces, the cell must adhere sufficiently to the matrix (8). We measured the adhesion strength by applying a constant fluid shear stress of 32 dyn/cm² to cells plated on fibronectin-coated plastic dishes, and counted the number of detached cells after 5 min. We found that only 1% of the IFDUC1 cells detach from the substrate, followed by HT cells (30%), MDA cells (40%), and A125 cells (90%) (Fig. 4M). Therefore, the adhesiveness of these cell types under 2D culture conditions scales with their ability to migrate through narrow channels or to invade dense collagen gels.

Cell stiffness

Cell stiffness is another important biophysical property that impacts cell migration through confined spaces: a lower cell stiffness is believed to help the cell to deform more easily and thus to migrate more quickly through narrow gaps (8). We measured the mechanical properties of suspended cells by analyzing of their entry times into a 5 μm wide constriction under a defined driving pressure. In contrast to our previous invasion experiments where cells are actively migrating and generating their own contractile forces, this assay uses external pressure to drive cells to transit through narrow pores on timescales much faster than the cells can actively migrate. The entry time results thus probe the passive deformability of the cells.

We found MDA and A125 cells to have the highest stiffness, followed by HT and IFDUC1 cells (Fig. 4N). However, the stiffness differences between the cell lines are relatively small, and having a low stiffness scales only weakly with the ability of the cells to migrate through narrow channels or to invade dense collagen gels. This result is surprising as recent studies correlate cell deformability with invasiveness (8,9,41,42). We comment on possible explanations for this discrepancy in the Discussion section.

Influence of cell/nuclear stiffness

Influence of lamin A overexpression on cell stiffness, adhesion, contractility, and 2D migration

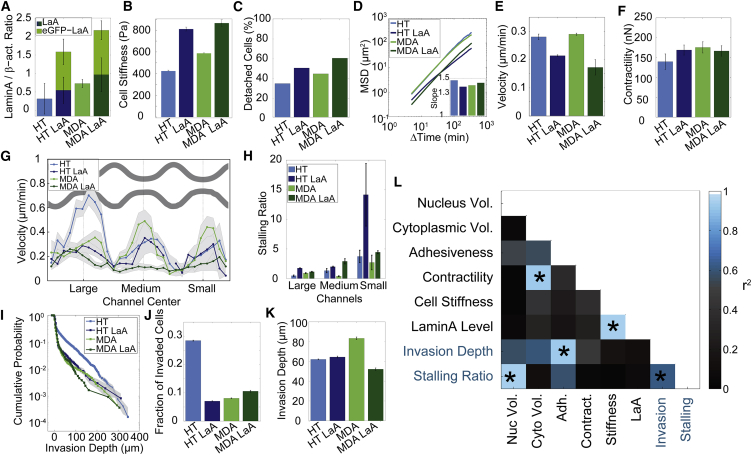
To separate the influence of cell stiffness from other invasion-modulating cell properties, we increased the expression levels of lamin A, which has been shown to correlate with nuclear stiffness (43,44). Lamin A/C is a protein of the nuclear lamina that is required for nuclear membrane organization and mechanical stability (45,46). By quantitative immunoblotting, we found that MDA cells have the highest levels of lamin A/C, followed by HT, A125, and IFDUC1 cells (Fig. S3, A and B). This ranking is the same that we found for cell stiffness (Fig. 4N). Therefore, lamin A/C levels correlate closely with cell stiffness across these different cell lines. We then increased lamin A expression levels in MDA and HT cells. We hypothesize that cells with higher lamin A levels experience a higher resistance when migrating through confined spaces due to the increased cell stiffness. Following transduction, expression of eGFP-lamin A is detectable in ∼95% of cells, and total average lamin A levels are approximately triple the endogenous lamin A levels (Fig. 5A, Fig. S3 C). We confirm a corresponding increase in cell stiffness by 92% in HT cells and 47% in MDA cells (Fig. 5B). Cell adhesion strength to a fibronectin-coated substrate (Fig. 5C) and migration velocity in 2D (Fig. 5E) are decreased by <25% upon lamin A transduction. Persistence of 2D cell migration (Fig. 5D) and contractility (Fig. 5F) are not affected.

Figure 5.

Influence of cell/nuclear stiffness on invasiveness. (A) Lamin A and eGFP-lamin A levels normalized to β-actin (mean ± SE) from three independent experiments. (B) Cell stiffness of WT and lamin A overexpressing cells (mean ± SE, n > 2000 cells). (C) Percentage of cells detached from a fibronectin-coated substrate after 5 min under a shear flow of 32 dyn/cm². (D) MSD (mean ± SE for n > 1000 cells). Inset: MSD slope. (E) Momentary velocity (mean ± SE for n > 1000 cells). (F) Cell contractility (mean ± SE for n > 100 cells). (G) Binned velocity in large, medium, and small channels (mean ± SE). (H) Ratio of cells entering and exiting the channels (binned for large, medium, and small channels) (mean ± SE). (I) Invasion profile (cumulative probability) in collagen gels. (J) Fraction of invaded cells. (K) Characteristic invasion depth in collagen. (L) Squared correlation coefficients (r²) for all six cell lines and cell properties measured. ^∗Indicates statistically significant correlations (p < 0.05). To see this figure in color, go online.

Invasion in channel structures and in collagen

We next analyzed and compared the velocity and stalling ratio of eGFP-lamin A overexpressing cells and wild-type (WT) cells during their migration through the channel array. In MDA cells, eGFP-lamin A overexpression leads to a marked decrease in the maximum migration velocity especially in the medium and small channels (Fig. 5G). In eGFP-lamin A overexpressing HT cells, the decrease in maximum migration velocity is already evident in the large channels (Fig. 5G). These data confirm previous reports (47) that cells with higher lamin A levels show an impaired ability to pass through micron-scale constrictions, and suggest an increased nuclear stiffness after lamin A overexpression to be the main reason for this response. This is also in good agreement with the increase of the stalling ratio that we observe for eGFP-lamin A overexpressing cells, particularly in the smallest channels (Fig. 5H).

We obtained similar findings for the invasion of these cells in soft (550 Pa) collagen gels, but subtle differences between MDA and HT cells became apparent. The fraction of cells that is able to invade soft but dense 3D collagen gels is greatly reduced in eGFP-lamin A overexpressing HT cells. However, the transduced cells that are able to migrate into the gel show a comparable invasion depth as the WT cells (Fig. 5, I–K). For eGFP-lamin A overexpressing MDA cells, the fraction of invaded cells remains unaltered but the invasion depth is decreased by 30% compared to WT. These differences between HT and MDA cells may reflect cell line-specific responses to matrix stiffness, but may also arise from different stiffness distributions among transduced and WT cells, as well as differences in contractility and the amount of lamin A-induced cell stiffening. Nonetheless, these data are in line with the hypothesis that cells with higher lamin A levels and hence higher stiffness experience a greater resistance to migration through confined spaces.

Correlation analysis

To identify the cell properties that most prominently influence cell invasiveness, we correlated the measured cell parameters from four cell lines plus the two lines that express eGFP-lamin A (HT, MDA, A125, IFDUC1, HT LaA, MDA LaA) with our findings of cell migration in small channels and collagen gels. Cell parameters for this analysis are nuclear and cytoplasmic volume, adhesiveness, cell contractility, stiffness, and total lamin A and C expression levels. As an index of invasiveness, we either use the stalling ratio in the smallest channels, or the characteristic invasion depth of the cells in 2.4 mg/ml collagen gels.

Cell invasiveness is significantly (p = 0.05) increased in cells with high adhesiveness (Pearson’s correlation coefficient of r = 0.78) and significantly (p = 0.001) decreased in cells with a large nuclear volume (r = −0.96) (Fig. 5 L). In soft collagen gels, invasiveness also correlates with contractility (r = 0.67, p = 0.14) and cytoplasmic volume (r = 0.77 p = 0.07), but both correlations do not reach statistical significance. As expected, our two measures for invasiveness (stalling ratio in microchannels, and characteristic invasion depth in collagen gels) are not perfectly correlated (r = 0.79, p = 0.06), indicating differences in the migration behavior of the cells in a soft, deformable versus a stiff, nondeformable 3D environment.

We also found two noteworthy correlations between the different cell properties that we examined: cytoplasmic volume and cell contractility are highly correlated (r = 0.97, p = 0.001) (Fig. 5L). This may explain why cells with a larger cytoplasmic volume show a higher invasiveness. Furthermore, as noted previously, we also found a strong correlation between cell stiffness and lamin A levels (r = 0.94, p = 0.001).

Influence of adhesive ligands

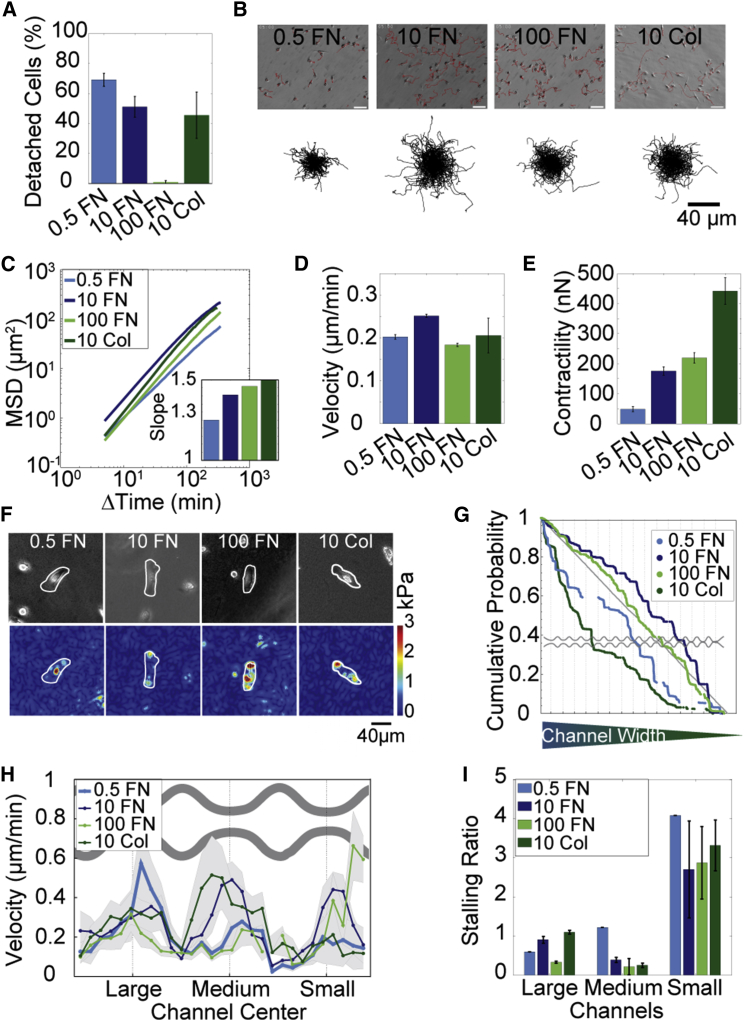
Because our results suggest that cell adhesion is important for invasion, we further studied the migration behavior of MDA cells in fibronectin- or collagen-coated channels, using a coating concentration of fibronectin between 0.5 and 100 μg/ml and collagen concentrations of 10 μg/ml. To confirm that cell adhesiveness depends on substrate coating, we applied a fluid shear stress of 32 dyn/cm² to the cells for 5 min with a spinning disk device and measured the fraction of detached cells. As expected, we found that cells exhibit the strongest adhesion to substrates coated with 100 μg/ml fibronectin, intermediate adhesion strength on 10 μg/ml fibronectin or collagen, and poor adhesion on 0.5 μg/ml fibronectin (Fig. 6A).

Figure 6.

Influence of ligand density on MDA cells. (A) Percentage of cells that have detached after 5 min when exposed to a shear stress of 32 dyn/cm² (mean ± SE from three independent experiments each with n > 1000 cells) (B) Top: images of cells on 2D substrates with trajectories measured over 12 h (red). Bottom: collapsed trajectories for n = 250 cells. (C) MSD. Inset: slope of the MSD (mean ± SE for n > 1000 cells). (D) Momentary velocity (mean ± SE for n > 1000 cells). (E) Contractility (mean ± SE for n > 100 cells). (F) Top: bright field image of representative cells on differently coated PAA gels. Bottom: cell tractions. (G) Cumulative probability of cell distribution throughout channel array. (H) Binned velocity in big, medium, and small channels (mean ± SE). (I) Stalling ratio of cells entering and cells exiting the channels binned for large, medium, and small channels (mean ± SE). To see this figure in color, go online.

2D migration and contractility

In agreement with previous reports (3,13), the persistence of cell migration on planar substrates increases with fibronectin density, whereas the momentary cell velocity exhibits a biphasic response, with a maximum velocity for intermediate coating concentrations of 10 μg/ml fibronectin (Fig. 6, B–D). For cells on 10 μg/ml collagen, we found an even higher persistence and an intermediate momentary velocity. Cell contractility, as measured with 2D traction microscopy, increases with fibronectin density (Fig. 6, E and F), and is highest for cells on collagen.

Invasion in channel structures and in collagen gels

We next studied migration in channel devices coated with different amounts of fibronectin (0.5, 10, 100 μg/ml) or with collagen (10 μg/ml). We analyzed the distribution of cell positions within the channel structure and take the slope of the cumulative probability as an indicator of relative migration velocity and hence relative accumulation in differently sized structures. We found the strongest decay of the cumulative probability for cells migrating in structures coated with 10 μg/ml collagen followed by 0.5 μg/ml fibronectin, with probabilities that are well below that of randomly distributed cells (Fig. 6G). The decay of the cumulative probability for cells in structures coated with 100 μg/ml fibronectin is almost identical to a uniformly random distribution and has a constant slope for all channel sizes. The decay of the cumulative probability for cells in channels coated with 10 μg/ml fibronectin is first slightly flatter but then shows a stronger decay for channels smaller than 4 μm.

We found comparable velocities for all coatings in large channels, but in medium and small channels, differences due to different coating densities became evident (Fig. 6 H). In agreement with the findings from the cumulative probability analysis, we find the highest velocities in the small channels when they are coated with 100 μg/ml fibronectin, followed by structures coated with 10 μg/ml fibronectin. By contrast, velocities are much lower for cells in structures coated with 0.5 μg/ml fibronectin or 10 μg/ml collagen.

Comparing the stalling ratio (ratio of cells at the channel entrance/channel exit) as a robust measure of steric hindrance, we find ratios below or around unity in large and medium channels regardless of adhesive ligand coating density (Fig. 6I). In the small channels, however, increased stalling becomes evident, especially for cells in 0.5 μg/ml fibronectin-coated channels and 10 μg/ml collagen-coated channels. Taken together, these data confirm that migration in confinement is facilitated by proper adhesion.

Discussion

Our results show that cells move faster and with higher persistence in narrow channels compared to wider chambers. This is partly the result of an increased directional persistence in the channels that results from a stronger confinement in one dimension. In large channels, the nucleus’ leading and trailing edge moves synchronously and smoothly in a sliding manner as described previously (35), whereas in small channels, the leading and trailing edge move asynchronously, reminiscent of a push-and-pull behavior (35,48). Upon closer inspection, however, the trajectories of nuclear motion are more in line with a pull-and-snap behavior: although the leading edge moves with approximately constant velocity, the trailing edge first stalls at the channel entrance and accelerates once the nucleus has deformed sufficiently to pass through the channel. Such behavior has been postulated for migration in 3D channels with cross sections smaller than the nuclear diameter (36).

We find that the maximum velocity of the nucleus occurs at the channel exit, in line with a previously suggested model where the cell is propelled by elastic restoring forces of the extracellular matrix once the bulk has slipped through a pore (31). However, the pores in our system are practically undeformable (<1% change in diameter for a pressure change of 100 kPa), and thus the speedup of the nucleus at the channel exit is more likely the combined result of elastic restoring forces from the nucleus (36), together with the pulling forces of the cytoskeleton.

The exit velocities of the nucleus increase with decreasing channel width but eventually decrease for very narrow channels. This observation confirms the previously postulated biphasic velocity response of cells to decreasing channel sizes (36). This biphasic response can be chiefly described by a constant volume flow that the cell maintains until, at a specific channel width, frictional forces dominate and slow down the cell. This specific channel width would be a sensitive measure for the cells’ migratory ability in confined spaces, as it indicates the onset of migration impairment for the different cell lines. However, due to the low cell throughput in the channel devices, we need to resort to more robust statistical descriptions for quantifying impaired migration. We therefore analyze the cumulative probability distribution of cell positions within the channel structures, and the stalling ratio defined here as the ratio of the probabilities of finding cells at the entrance versus the exit of a channel.

When we compare various cell properties among four different cell lines and correlate them with the stalling ratio, we find the nuclear volume to be the main source of migration impairment. This finding is consistent with the notion of the cell nucleus being the main source of steric hindrance in cell invasion (4). To further explore this, we overexpress lamin A in two cell lines and observe an increased stalling ratio in both cases, consistent with previous findings that lamin A overexpression increases nuclear stiffness (43) and impairs the passage of cells through micron-scale constrictions (47). In our setup, we find a positive correlation between the stalling ratio and cell stiffness across four different cell lines plus two cell lines where we overexpress lamin A, however, this correlation does not reach statistical significance. Hence, our results suggest that other factors in addition to cell stiffness have a stronger effect on impairing cell migration; these findings contrast previous studies that solely correlate cell stiffness with cancer aggression (8,9). However, cell stiffness is commonly measured over timescales of seconds using methods such as atomic force microscopy, micropipette aspiration, or microbead rheology, often imposing only small deformations that do not deform the nucleus. By contrast, it may take several hours for a cell to deform sufficiently to squeeze through a matrix constriction. Because cells are not purely elastic but viscoelastic, the effective cell stiffness, when measured over timescales of many hours, may be much smaller compared to values measured over timescales of seconds and therefore may be less important.

In our experiments comparing the migratory ability of different cell types, we find adhesiveness to be highly correlated both with the stalling ratio in small channels and with the invasion depth in collagen gels. For example, the much smaller adhesion forces seen in A125 cells allow for a high cell velocity in 2D but limit the migration velocity in 3D environments. Moreover, the smaller adhesion forces shift the onset of major migration impairment toward larger channel sizes (Fig. 4, A and B), and increase the stalling ratio in small channels. By altering the concentration of the adhesive ligand fibronectin, we show that good adhesion is critical for migration through small confinements; this is in contrast to 2D environments where strong adhesion impedes migration (13). Note, however, that we have investigated only mesenchymal cells or transformed cells that have undergone an epithelial to mesenchymal transition, and that these cell types thus use adhesion-dependent mechanisms of migration, which is different from the adhesion-independent migration mode found in dendritic cells or immune cells (49,50).

Cell migration in channels coated with medium (10 μg/ml) concentrations of collagen is also impaired, which we attribute to the poor binding of collagen to unfunctionalized PDMS as reported in the literature (51).

Apart from adhesion, we also find that cell contractility is correlated with the stalling ratio in small channels and the invasion depth in collagen gels, but the correlation between 3D migration and contractility in cell types does not reach statistical significance.

All four cell types investigated in our study have the ability to overcome small pores with cross sections of only 6.5 μm². However, there are marked differences in the velocity with which cells migrate under confinement, revealing large differences in the invasiveness among different cell types. Even though we find a clear tendency for smaller nuclear volume and higher adhesion strength as indicators of good migration ability in confinement, our results do not point to a single cell property that predicts cell migratory impairment. If we consider the correlation coefficient for each cell parameter relative to the sum of all four correlation coefficients, we find that a combination of low nuclear volume (30%), high adhesion strength (29%), high contractility (16%), and low cell stiffness (13%) contributes to a higher invasiveness in collagen or a lower stalling ratio for small channels.

In this study, we compare the 3D migration of cells in two distinct environments that have similar constriction dimensions but different mechanical and biochemical properties, as well as different geometries. The cross sections of the smallest channels of around 6.5 μm² in the PDMS device correspond to the cross sections of the pores in dense collagen gels of around 6.61 ± 1.77 μm² (19). When we compare the stalling of the nucleus at the entrance of small, stiff channels with the characteristic invasion depth in a dense but soft collagen gel across different cell types, we find consistent behavior. Our correlation analysis reveals similar cell properties that promote or impede cell invasion in both systems. One exception is that a large cytoplasmic volume is correlated with good invasion only in collagen gels. This finding is consistent with the notion that a larger cytoplasm can contain a higher number of contractile elements, which in turn enhance invasion through a deformable matrix by exerting contractile forces on the surrounding protein network.

Conclusions

Our data confirm the prevailing view that the nucleus is the main source of steric hindrance for 3D invasion in a confined environment. Furthermore, we show the biphasic response of cell velocity to the degree of confinement that has been predicted from theoretical models. In our study, we compare four cancer cell lines that are all able to squeeze through very small constrictions but differ in their migration velocity under 3D confinement, which we take here as a measure of their invasiveness. We find that for the cell lines investigated, cell adhesion and nuclear volume have a major influence on cell migration in confined spaces. In contrast to previous studies, cell stiffness is only weakly correlated with cell invasiveness. Clearly, invasion is a complex process, and it is therefore not surprising that it cannot be predicted by a single cell parameter. Our results highlight that a multiparameter analysis is essential to understand and predict the ability of cells to invade or migrate in a confined environment.

Author Contributions

L.L. and B.F. designed the experiments; L.L. performed the experiments and analyzed the data; C.K., J.L., T.K., A.S., and C.M., helped with measurements; P.S. and R.S. isolated the IFDUC1 cells; C.G. and A.R. designed the channel structure; L.L., A.R., and B.F. wrote the article.

Editor: Gijsje Koenderink.

Supporting Citations

Reference (52) appears in the Supporting Material.