Molecular Basis of the Membrane Interaction of the β2e Subunit of Voltage-Gated Ca²⁺ Channels

Abstract

The auxiliary β subunit plays an important role in the regulation of voltage-gated calcium (Ca_V) channels. Recently, it was revealed that β2e associates with the plasma membrane through an electrostatic interaction between N-terminal basic residues and anionic phospholipids. However, a molecular-level understanding of β-subunit membrane recruitment in structural detail has remained elusive. In this study, using a combination of site-directed mutagenesis, liposome-binding assays, and multiscale molecular-dynamics (MD) simulation, we developed a physical model of how the β2e subunit is recruited electrostatically to the plasma membrane. In a fluorescence resonance energy transfer assay with liposomes, binding of the N-terminal peptide (23 residues) to liposome was significantly increased in the presence of phosphatidylserine (PS) and phosphatidylinositol 4,5-bisphosphate (PIP₂). A mutagenesis analysis suggested that two basic residues proximal to Met-1, Lys-2 (K2) and Trp-5 (W5), are more important for membrane binding of the β2e subunit than distal residues from the N-terminus. Our MD simulations revealed that a stretched binding mode of the N-terminus to PS is required for stable membrane attachment through polar and nonpolar interactions. This mode obtained from MD simulations is consistent with experimental results showing that K2A, W5A, and K2A/W5A mutants failed to be targeted to the plasma membrane. We also investigated the effects of a mutated β2e subunit on inactivation kinetics and regulation of Ca_V channels by PIP₂. In experiments with voltage-sensing phosphatase (VSP), a double mutation in the N-terminus of β2e (K2A/W5A) increased the PIP₂ sensitivity of Ca_V2.2 and Ca_V1.3 channels by ∼3-fold compared with wild-type β2e subunit. Together, our results suggest that membrane targeting of the β2e subunit is initiated from the nonspecific electrostatic insertion of N-terminal K2 and W5 residues into the membrane. The PS-β2e interaction observed here provides a molecular insight into general principles for protein binding to the plasma membrane, as well as the regulatory roles of phospholipids in transporters and ion channels.

Introduction

The membrane association of peripheral proteins is critical for diverse cellular processes because such proteins are mainly responsible for the transduction of extracellular stimuli into cells. This association is often accomplished by a specific or nonspecific electrostatic interaction between membrane phospholipids and a polybasic group of these proteins (1–3). It is well known that these proteins, including Src, K-Ras, and myristoylated alanine-rich C kinase substrate (MARCKS), utilize electrostatic interactions as a means of membrane recruitment (4–6). For example, MARCKS plays an important role in regulating cell shape and motility through a reversible sequestration of membrane phosphatidylinositol 4,5-bisphosphophate (PIP₂) (7). It is also well established that membrane recruitment of MARCKS is mediated by an electrostatic interaction between a charged effector domain (composed of 13 basic and five phenylalanine residues) and anionic phospholipids in the inner leaflets of the plasma membrane (8,9).

Ca²⁺ is a ubiquitous second messenger that controls a number of cellular functions (10). Voltage-gated calcium (Ca_V) channels serve as major machinery for Ca²⁺ influx and involve muscle contraction, hormone secretion, neuronal excitability, and gene expression. Ca_V channels are composed of α1, β, and α2δ subunits (11,12). The α1 subunit, a major component of channel complexes, is a pore-forming subunit that contains both voltage-sensing domains and a selective filter. The auxiliary subunits β and α2δ play an important role in regulating the gating properties of the α1 subunit. Among the auxiliary subunits, molecular cloning has identified four isoforms of the β subunit (β1–β4) that are expressed in various neurons and other excitable cells. The β subunit, in particular, plays a pivotal role in membrane trafficking of the α1 subunit through direct interaction with the α-interaction domain in the I-II linker region of the α1 subunit and promotes membrane expression, thereby leading to an increase of current density (13–15). With regard to channel regulation, β subunit is a major determinant of the gating properties of the Ca_V channel and modulation of the Ca_V channel by lipids (16–19). In particular, the subcellular distribution of the β subunit is critical for the regulation of channel gating. In the absence of the α1 subunit, β subunits are expressed in the cytosol, and Ca_V channels with cytosolic β subunits exhibit fast inactivation and a high sensitivity to membrane lipids. In contrast, the β2a and β2e subunits, which are encoded by splicing variants of a Cacnb2 gene, are localized in the plasma membrane even in the absence of the α1 subunit (20). It is well known that membrane targeting of the β2a subunit is mediated by palmitoylation of its N-terminus, which is responsible for the slow inactivation and low sensitivity of Ca_V channels to lipids (20–22). Like the β2a subunit, the β2e subunit is localized in the plasma membrane and shows slow inactivation of Ca_V channels (20). However, the mechanism of its membrane targeting has remained unclear. Recently, it was reported that the β2e subunit is expressed in the plasma membrane via nonspecific electrostatic and hydrophobic interactions (23). That study suggested that the polybasic group of the N-terminal region is important for membrane association. However, the precise molecular mechanism of membrane targeting and regulation of Ca_V channel current by lipids remained to be further explained.

Here, we investigated the membrane-targeting mechanism of mouse Ca_Vβ2e subunits at the molecular level and elucidated their regulatory effects on Ca_V channel properties. For this purpose, we applied a combination of site-directed mutagenesis, in vitro assays of binding between peptides and liposomes, and multiscale molecular-dynamics (MD) simulation. Our results reveal a molecular mechanism whereby the β2e subunit is anchored on the plasma membrane through a nonspecific electrostatic interaction between a cluster of basic residues of the N-terminus and anionic membrane phospholipids. Based on our MD simulation, we suggest two modes of membrane binding of the β2e subunit: a stretched mode for strong binding, and an agglomerate mode for weak and transient binding. In addition, we found that the membrane-binding disruption of the β2e subunit increases the inactivation of Ca_V2.2 channels and inhibition of Ca_V currents by PIP₂ depletion. These findings could enhance our understanding of the structure-based molecular mechanism underlying the direct interaction between phospholipids and peripheral proteins.

Materials and Methods

DNAs

The following calcium channel subunits were used: rat α1B [37b] (AF055477), rat α1D (AF370009), and rat α2δ-1 (AF286488) (from Diane Lipscombe, Brown University, RI); danio rerio voltage-sensing phosphatase (Dr-VSP; Jill B. Jensen, University of Washington, Seattle, WA); and GFP-Lact-C2 (from Deok-Jin Jang, Kyungbook National University, Korea).

Molecular cloning

The cDNA encoding the mouse brain β2e subunit was TA cloned into T-Easy Vector (Promega, Madison, WI) and was cloned in pCDNA3.1 and in pEGFP-N1 or mCherry-N1 (Clonetech, Mountain View, CA) using Nhe1 and BamH1. For the mouse β2e subunit, the forward primer was 5′-CGCTAGCAATGAAGGCCACCTGGATCAGGCTT-3′, and the reverse primer was 5′-CGGATCCCCTTGGCGGATG-3′. The N-terminal deleted construct of β2e was amplified by PCR using the forward primer 5′-CGCTAGCATGAAGGCCACCTGGA-TCAGGCTT-3′ and the reverse primer 5′-CGGATCCCCTTGGCGGATGTATACATCCC-3′. Point mutants were obtained by PCR using the QuikChange Site-Directed Mutagenesis Kit (Agilent Technologies, Santa Clara, CA). The primers used for mutagenesis are listed in Table 1. Mutant constructs were verified by sequencing.

Table 1.

Primers Used for Mutagenesis

Primer (5′→3′)
	Sense	Antisense
K2A	CAGATCCGCTAGCATGGCGGCCACCTGGATCAGG	CCTGATCCAGGTGGCCGCCATGCTAGCGGATCTG
K2R	GTCAGATCCGCTAGCATGAGGGCCACCTGG	CCAGGTGGCCCTCATGCTAGCGGATCTGAC
W5A	GCTAGCATGAAGGCCACCGCGATCAGGCTTCTGAAAAG	CTTTTCAGAAGCCTGATCGCGGTGGCCTTCATGCAGC
W5F	GCTAGCATGAAGGCCACCTTCATCAGGCTTCTGAAAAGA	CTCTTTTCAGAAGCCTGATGAAGGTGGCCTTCATGCTAG
W5Y	GCTAGCATGAAGGCCACCTATATCAGGCTTCTGAAAAGA	CTCTTTTCAGAAGCCTGATATAGGTGGCCTTCATGCTAG
R7A	GAAGGCCACCTGGATCGCGCTTCTGAAAAGAGCC	GGCTCTTTTCAGAAGCGCGATCCAGGTGGCCTTC
K10A	CCTGGATCAGGCTTCTGGCAAGAGCCAAGGGAGGAA	TTCCTCCCTTGGCTCTTGCCAGAAGCCTGATCCAGG
R11A	CCACCTGGATCAGGCTTCTGAAAGCAGCCAAGGGAGG	CCTCCCTTGGCTGCTTTCAGAAGCCTGATCCAGGTGG
K13A	GGCTTCTGAAAAGAGCCGCGGGAGGAAGGCTGAAGA	TCTTCAGCCTTCCTCCCGCGGCTCTTTTCAGAAGCC
R16A	AAAAGAGCCAAGGGAGGAGCGCTGAAGAGTTCGGAC	GTCCGAACTCTTCAGCGCTCCTCCCTTGGCTCTTTT
K18A	CCAAGGGAGGAAGGCTGGCGAGTTCGGACATCTGTG	CACAGATGTCCGAACTCGCCAGCCTTCCTCCCTTGG
K2A/W5A	GCATGGCGGCCACCGCGATCAGGCTTCTGA	TCAGAAGCCTGATCGCGGTGGCCGCCATGCC
R7A/K10A	TCCTCCCTTGGCTCTTGCCAGAAGCGCGATCCAG	CTGGATCGCGCTTCTGGCAAGAGCCAAGGGAGGA
K13A/R16A	CTTCAGCGCTCCTCCCGCGGCTCTTTTCAGAAGC	GCTTCTGAAAAGAGCCGCGGGAGGAGCGCTGAAG
R17A/R18A	CGAACTCGCCAGCGCTCCTCCCTTGGCTCT	AGAGCCAAGGGAGGAGCGCTGGCGAGTTCG

Cell culture and transfection

TsA201 cells were maintained in Dulbecco’s modified Eagle’s medium (Hyclone; Thermo Scientific, Pittsburgh, PA) containing 10% fetal bovine serum and 0.2% penicillin/streptomycin at 37°C with 5% CO_2. For transfection, cells were plated in 3.5 cm culture dishes at 50–80% confluency. For Ca_V channel expression, cells were transiently transfected using Lipofectamine 2000 (Invitrogen, Carlsbad, CA). The transfected DNA mixture consisted of plasmids encoding α1, β, and α2δ-1 at a 1:1:1 molar ratio. When needed, enhanced GFP (eGFP) was also included in the DNA mixtures. Cells were plated on poly-L-lysine-coated chips the day after transfection. Currents were recorded within 2 days after transfection.

Preparation of liposomes

All lipids were purchased from Avanti Polar Lipids except for N-[5-(dimethylamino) naphthalene-1-sulfonyl]-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (dansyl-PE), which was purchased from Invitrogen. The liposomes consisted of PC (L-α-phosphatidylcholine), PE (L-α-phosphatidylethanolamine), PS (L-α-phosphatidylserine), cholesterol, PIP₂, and dansyl-PE (44:10:15:25:1:5 mol %). In the case of no PS or PIP₂, the PC content was adjusted according to the absence or presence of PS. Briefly, the lipid mixture was dissolved in a chloroform/methanol mixture (2:1 ratio) and dried under a gentle stream of nitrogen in the hood, thereby generating a lipid film. The film was then dissolved with 100 μL of buffer containing 150 mM KCl, 20 mM HEPES/KOH pH 7.4, and 5% sodium cholate (24). A size-exclusion column was applied to remove detergent (Sephadex G50 in 150 mM KCl and 20 mM HEPES, pH 7.4). Liposomes were collected as eluted (∼400 μL). Note that the liposomes were easily detected by UV because of the dansyl-PE.

Assay for peptide-liposome binding

Binding of peptide to liposomes was monitored by means of fluorescence resonance energy transfer (FRET) measurements (dansyl-PE incorporated into liposomes quenches the fluorescence of tryptophan in the peptide) (25). All measurements were carried out in a FluoroMax spectrofluorometer (Horiba Jobin Yvon, Germany) and performed at 37°C in 1 mL of buffer containing 150 mM KCl and 20 mM HEPES-KOH (pH 7.4). The peptide (750 nM) contained one tryptophan residue. Tryptophan was excited at 280 nm (slit width of 5 nm) and emission spectra were recorded from 320 nm to 420 nm (slit width of 5 nm), with the peak at 355 nm. FRET was normalized as F₀/F, where F₀ and F represent the fluorescence intensity at 355 nm before and after liposome addition, respectively. A peptide-liposome interaction increases FRET (F₀/F) as a result of tryptophan quenching.

Patch-clamp recording

Whole-cell Ba²⁺ currents or Ca²⁺ currents were recorded at room temperature (20–24°C) using a HEKA EPC-10 amplifier with pulse software (HEKA Elektronik; Lambrecht, Germany). Electrodes were pulled from a glass micropipette capillary (Sutter Instrument, Novato, CA) to yield pipettes with a resistance of 2–2.5 MΩ. Series-resistance errors were compensated to >60%, and fast and slow capacitances were compensated before the applied test-pulse sequences. Voltage-clamp records were acquired at 10 kHz and filtered at 3 kHz. For all recordings, cells were held at −80 mV. All data presented here were leak and capacitance subtracted before analysis. The external Ringer’s solution contained 150 mM NaCl, 10 mM BaCl₂, or CaCl₂, 1 mM MgCl₂, 10 mM HEPES, and 8 mM glucose, and the pH was adjusted to 7.4 with NaOH. The internal solution of the pipette consisted of 175 mM CsCl, 5 mM MgCl₂, 5 mM HEPES, 0.1 mM 1,2-bis(2-aminophenoxy)ethane N,N,N′,N′-tetraacetic acid (BAPTA), 3 mM Na₂ATP, and 0.1 mM Na₃GTP, and the pH was adjusted to 7.5 with CsOH. CsOH, BAPTA, Na₂ATP, and Na₃GTP reagents were obtained from Sigma (St. Louis, MO), and other chemicals were obtained from MERCK (Darmstadt, Germany).

Confocal imaging

TsA201 cells were imaged 24–48 h after transfection on poly-L-lysine-coated coverslips using a Carl Zeiss LSM 700 confocal microscope (Carl Zeiss MicroImaging, Jena, Germany). Cell images were scanned by using a 40×(water) apochromatic objective lens at 1024 × 1024 pixels with a digital zoom, and were processed in ZEN 2012 lite imaging software.

All-atom MD simulation

The three-dimensional structure for residues 41–136 of β2a (PDB ID: 1T0J for rat) is the only known x-ray structure (26); the structure for residues 1–40 is missing because they are intrinsically disordered (27). We noted from the multiple sequence alignment that rat β2a, rat β2e, and mouse β2e share the same sequence for residues of 41–136, and are therefore expected to have similar three-dimensional structures. This allowed us to reconstruct a structure of mouse β2e for residues 1–143 after using Modeller 9.11 (28) to generate a random-loop structure only for residues 1–40 and subsequently conducting an equilibrium MD simulation based on the AMBER12/ff99SB force field (29,30). We chose five representative structures of mouse β2e in which the structure for residues 1–47 is a random loop. We equilibrated the initial membrane lipid by using the CHARM-GUI membrane builder (31) with 100 Å x and y dimensions and a 15.0 dyne/cm surface tension. The assumed mole fractions of the lipids (cholesterol/POPC/POPE/POPS) were 25%:45%:15%:15%. The numbers of cholesterol, POPC, POPE, and POPS molecules on the upper leaflet were 45, 81, 27, and 27, respectively. In a rectangular box (100 Å × 100 Å × 200 Å) filled with TIP3 water molecules (32), we placed a β2e protein initially at 10 Å above the upper leaflet (the distance between the upper leaflet and the closest residue in a β2e protein to that is 10 Å along the normal direction of the upper leaflet). The water layer above and below the lipid-protein system was 20 Å thick and the periodic boundary condition was applied. To neutralize the protein-lipid-water system, the positions of 25 Na⁺ ions were assigned via the Monte Carlo replacement method. The numbers of atoms in the whole system were 41,892 for the lipid, 2302 for a β2e protein, 25 for Na⁺ ions, and 162,000 for waters.

To conduct an atomistic MD (ATMD) simulation for the protein-lipid-water system, we used PMEMD.CUDA (33) of the Amber12 simulation package with ff99SB (for protein and solution) and lipid11 (for lipid) force fields (34). The particle-mesh Ewald (PME) method was applied to treat long-range electrostatic interactions, and a 10 Å force-shifted cutoff was used for short-range, nonbonded interactions. The hydrogen atoms were constrained to the equilibrium bond length using the SHAKE algorithm (35). We performed 1,500 steps of steepest-descent minimization followed by 1500 steps of conjugate gradient minimization. The systems were subsequently subjected to a 100 ps heating process in which the temperature was gradually raised from 0 K to 300 K under the SHAKE algorithm. After the heating step, the production runs were carried out for 100 ns with a 2 fs time step and the NPT ensemble, i.e., a constant number of particles (N, 206,219 atoms), pressure (P, 1 atm), and temperature (T, 300 K). Temperature and pressure were controlled by a Langevin dynamics thermostat with a collision frequency of 1 ps⁻¹ and a weak-coupling barostat with a coupling constant of 1.0 ps (36,37). All trajectories were recorded every 10 ps. The main ATMD simulations for 50 independent trajectories for up to a 100 ns timescale each were performed for a β2e wild-type protein. The ptraj toolset that is provided with the AMBER program package and an in-house-written analysis program were used to analyze the resulting MD trajectories and calculate the distance, polar energy, and nonpolar energy. VMD software (38) was used to prepare structural figures.

Coarse-grained MD simulation

We performed a coarse-grained MD (CGMD) simulation using GROMACS 4.6.7 (39) and the Martini V2.2P polarized force field (40,41). The CGMD simulation started from the last snapshot of β2e (1–143) bound to the lipid bilayer from the ATMD simulation trajectory. The structure of β2e in atomic detail was converted to that of CG beads using martinize.py (40) and insane.py (42) scripts in Martini tools. The composition (cholesterol/POPC/POPE/POPS, 25:45:15:15) of the lipid bilayer and the size of the rectangular box of water molecules with the periodic boundary condition (100 Å × 100 Å × 200 Å) remained the same as in the ATMD simulation. The system was solvated by Martini polarized water and Na⁺ ions were added to keep the net electrostatic charge neutral. The following preparation procedures were used: energy minimization for 5000 steps, equilibration for 5 ns, and production CGMD simulation for 1.5 μs with a 20 fs time step. Temperature was coupled with a Berendsen thermostat (43) to a reference temperature of 300 K, with a coupling constant ${\tau }_{\text{T}}$ of 1.0 ps. Semi-isotropic pressure was coupled with a Berendsen barostat (43) in x and y at 1 bar with a coupling constant ${\tau }_{\text{P}}$ of 2.0 ps. We used the Verlet scheme (44) and calculated Coulombic interactions using the PME method with an 11 Å cutoff, van der Waals interactions with an 11 Å cutoff, and a dielectric constant of 2.5.

Calculation of binding free energy based on the thermodynamic integration method

We calculated the free energy for bringing a β2e protein in solution to the surface proximity of a membrane lipid using thermodynamic integration (TI) (45) with the Amber12 simulation package, with the ff99SB (for protein and solution) and lipid11 (for lipid) force field (34). We employed a thermodynamic cycle (see Fig. S1 in the Supporting Material) in which $\Delta G_{\mathrm{2,1}}\left(\Delta G_{\mathrm{3,4}}\right)$ is the difference between the free energy of a wild-type (mutant) protein that is bound to the membrane lipid and that of a wild-type (mutant) protein in solution. $\Delta G_{\mathrm{2,3}}\left(\Delta G_{\mathrm{1,4}}\right)$ is the difference between the free energy of a mutant protein in solution (a mutant bound to the membrane lipid) and that of a wild-type protein in solution (a wild-type protein bound to the membrane lipid). The thermodynamic equality $\Delta G_{\mathrm{1,2}}$ + $\Delta G_{\mathrm{2,3}}$ + $\Delta G_{\mathrm{3,4}}$ - $\Delta G_{\mathrm{1,4}}$ = 0 holds for the thermodynamic cycle in Fig. S1, where $\Delta G_{\mathrm{1,2}}=-\Delta G_{\mathrm{2,1}}$. This gives the binding free energy of a mutant with respect to that of a wild-type protein, namely, $\Delta \Delta \text{G}$ = $\Delta G_{\mathrm{3,4}}$ - $\Delta G_{\mathrm{2,1}}$ = $\Delta G_{\mathrm{1,4}}$ - $\Delta G_{\mathrm{2,3}}$. To calculate $\Delta G_{\mathrm{1,4}}$ and $\Delta G_{\mathrm{2,3}}$, we applied the TI method. Consider two systems, A and B, with potential energies $V_A$ and $V_B$, respectively. A new potential energy function is defined as $\text{V}(\lambda )=V_A+\lambda \left(V_B-V_A\right)$, where $\lambda$ is a coupling parameter with a value between 0 and 1. The case for $\text{ λ}$ = 0 (1) corresponds to system A (B). The canonical partition function of the system is written as $\text{Q}(\lambda )=\sum _c\text{exp}\left[-V_c(\lambda )/k_{B}T\right]$, where $V_c(\lambda )$ is the potential energy of a conformation c in the conformational ensemble as defined above, and the free energy is $\text{F}(\lambda )=-k_{B}T\text{lnQ}(\lambda )$. A straightforward calculation, after taking the derivative of F with respect to $\lambda$, allows us to evaluate the difference between the free energy of system A and that of system B by TI as follows:

$$\Delta \text{F}\left(\text{A}\to \text{B}\right)={\int }_0^{1}d\lambda \frac{\partial F(\lambda )}{\partial \lambda }={\int }_0^{1}d\lambda {\langle \frac{\partial V(\lambda )}{\partial \lambda }\rangle }_{\lambda }.$$

We carried out the integration after taking the ensemble average on the right-hand side of the above equation on nine discrete $\lambda$ points with an interval of 0.1, by performing separate ATMD simulations. Now, we regard $\Delta G_{\mathrm{1,4}}=\Delta \text{F}\left(1\to 4\right)\text{and}\Delta G_{\mathrm{2,3}}=\Delta \text{F}\left(2\to 3\right)$, from which $\Delta G_{\mathrm{1,4}}$ - $\Delta G_{\mathrm{2,3}}$ would result in the binding free energy of a mutant with respect to that of a wild-type β2e protein.

Starting from the last configurations of a wild-type β2e protein from ATMD for 100 ns, we subsequently equilibrated configurations of β2e protein by performing CGMD for a longer timescale of 1.5 μs. We employed CGMD for two reasons: 1) to allow lipid mixing (46–48), and 2) because our current computing capacity, based on ATMD using AMBER or GROMACS, is not good enough to simulate a wild-type β2e protein on a microsecond timescale within a reasonable time period. We ran 10 independent trajectories by CGMD and obtained further equilibrated configurations of a wild-type β2e protein bound to the lipid. The last configurations from CGMD trajectories were then transformed back to the all-atom structure using backward.py (49) in Martini tools. We then performed TI ATMD simulations (45) to calculate the binding free energy using the AMBER12 package with ff99SB, the lipid11 force field, and a modified van der Waals equation (softcore potentials) (50,51) as discussed above. We conducted ensemble averaging at nine discrete $\lambda$ points by performing ATMD simulations for 4 ns at each $\lambda$ increment of 0.1, and then performed TI.

Results

Basic and hydrophobic residues of the N-terminus affect the subcellular distribution of the β2e subunit

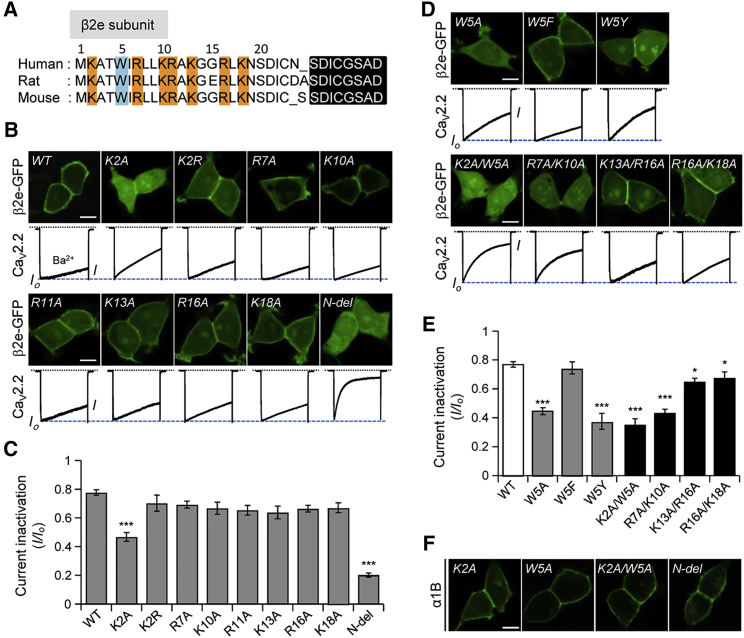
Multialignment of the N-terminus of several mammalian β2e subunits shows near identity (Fig. 1A), suggesting that membrane targeting would be conserved. A group of basic amino acids in the N-terminus is more prominent than other β2 variants that might contribute to recruitment of β2e subunits to the plasma membrane (1). It has also been reported that aromatic residues (Trp, Tyr, and Phe) play key roles in membrane incorporation of peripheral proteins (52). It was recently reported that electrostatic and hydrophobic interactions are key determinants for membrane targeting of the β2e subunit (23). We also tested whether the presence of charged residues and the Trp residue at position 5 of the β2e subunit might be a key factor in membrane association. We cloned a series of point-mutated constructs in which basic or aromatic residues were substituted by Ala, and visualized the distributions of these constructs by confocal imaging. The single-point mutagenesis analysis showed that when expressed alone, Lys at position 2 of the N-terminus was particularly important for membrane association, but the other basic residues were not significantly involved (Fig. 1B). We also examined whether these mutants had any effects on current inactivation of Ca_V2.2 channels. As expected, the K2A mutant displayed faster inactivation compared with other mutants (Fig. 1B, bottom, and C).

Figure 1.

Point mutation of Lys-2 (K2) or/and Trp-5 (W5) to Ala results in a cytosolic distribution of the β2e subunit. (A) Amino acid multialignment of the N-terminal region of β2e subunits among human, rat, and mouse. Positively charged Lys and Arg residues and a hydrophobic Trp residue are highlighted in yellow and blue, respectively, and conserved domains among β2e subunits are highlighted in black. (B) Top: confocal images of cells expressing point-mutated β2e subunits in which each basic residue of N-terminus was replaced with Ala. Scale bar, 10 μm. Bottom: current inactivation of Ca_V2.2 channels with mutant β2e subunits. Currents were measured during a 500 ms test pulse to +10 mV. (C) Summary of current inactivation in cells expressing single basic mutant β2e subunits (n = 5–6). Current inactivation (I/I_o) was calculated as current amplitude (I) divided by initial peak amplitude (I_o). ^∗∗∗p < 0.001, compared with wild-type; error bar, ± SEM. (D) Top: confocal images of cells expressing single- or double-mutated β2e subunits in which hydrophobic (Trp) and double-mutated residues of the N-terminus were replaced with Ala residues. Scale bar, 10 μm. Bottom: current inactivation of Ca_V2.2 channels in cells expressing mutant β2e subunits. Currents were measured during a 500 ms test pulse to +10 mV. (E) Summary of current inactivation in cells expressing single hydrophobic (n = 5–6) and double-mutated β2e subunits (n = 5–6). ^∗p < 0.05; ^∗∗∗p < 0.001, compared with wild-type; error bar, ± SEM. (F) Confocal images of cells expressing cytosolic mutants in the presence of an α1B subunit. Scale bar, 10 μm. To see this figure in color, go online.

Like the N-terminal deletion construct (N-del), the K2A mutant is expressed in the cytosol; however, the rate of current inactivation with K2A was only half that observed for N-del, raising the possibility that other residues are still required for membrane association of the β2e subunit. However, mutation of R7A, K10A, R11A, K13A, R16A, or K18A in the β2e subunit had no appreciable effect on current inactivation (Fig. 1, B and C). In addition to basic residues, we tested the involvement of the hydrophobic residue of the N-terminus in membrane targeting. A construct with Trp replaced by Ala (W5A) displayed a cytosolic distribution and resulted in increased inactivation of Ca_V2.2 channels, as anticipated (Fig. 1D, top, and E). When Trp was replaced with Phe (W5F), but not Tyr (W5Y), membrane targeting was preserved, possibly through the side-chain hydroxyl group. We also tested a few doubly mutated β2e subunits. First, the double mutant K2A/W5A accelerated current inactivation even more than the K2A or W5A mutants (Fig. 1D). R7A/K10A also showed a cytosolic distribution, whereas K13A/R16A and R16A/K18A were localized on the plasma membrane even though they showed slightly faster inactivation than the wild-type (Fig. 1D, bottom, and E). These results suggest that basic residues following Met-1 play more critical roles in membrane targeting of the β2e subunit, and that the basic amino acids cooperate in achieving a stable interaction with the plasma membrane. We also tested the distribution of cytosolic mutants in the presence of the α1 subunit (Fig. 1F). With the α1 subunit, cytosolic mutants were expressed on the plasma membrane, consistent with previous reports that β subunits are tightly associated with the α-interacting domain within the I-II linker of the α1 subunit (14,53). Overall, our findings suggest that basic and aromatic residues of the proximal N-terminus of the β2e subunit target this subunit to the plasma membrane; however, the molecular identity of this residue-specific interaction is not clearly understood.

Phospholipids determine the binding affinity of peptides to liposomes

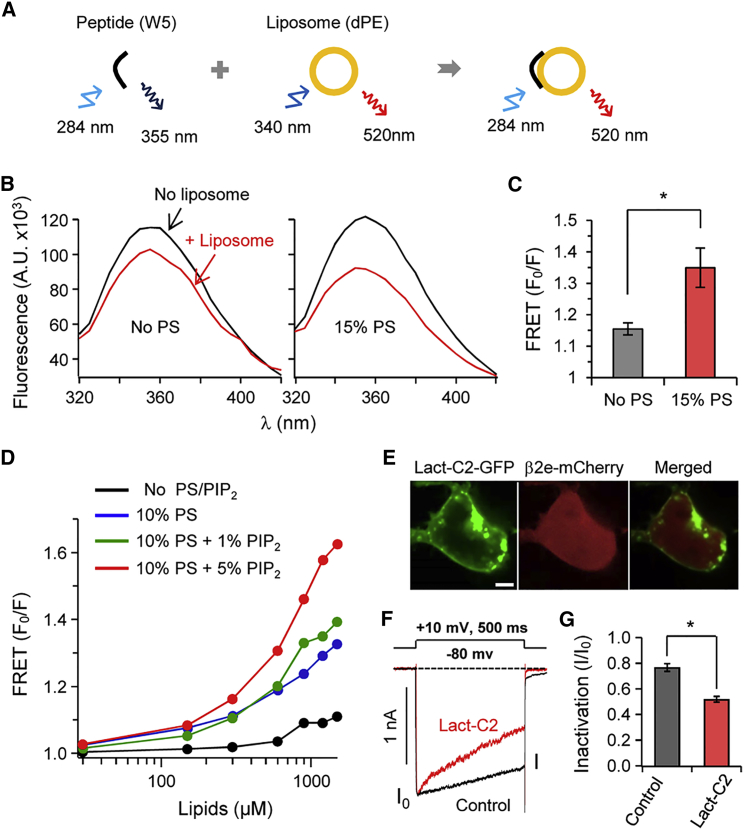
As shown in Fig. 1, positively charged residues of the N-terminus are important for membrane binding of the β2e subunit. Therefore, we reconstituted the N-terminal region in liposomes and analyzed the interaction between the N-terminus of the β2e subunit and liposomes composed of anionic phospholipids. For this purpose, we employed a peptide-to-liposome FRET assay and synthesized a 23-residue peptide of the N-terminus of the β2e subunit (MKATWIRLLKRAKGGRLKSSDIC) (Fig. 2A) (25). We first measured FRET with liposomes lacking anionic phospholipids (no PS). When liposomes were added to the peptide, the intensity of Trp fluorescence showed only a minor attenuation, possibly indicating a weak hydrophobic peptide-liposome interaction (Fig. 2B, left). However, when 15% PS was present in the liposome membranes, there was a marked decrease of Trp fluorescence (Fig. 2B, right), indicating strong binding of N-terminal peptides to these liposomes (Fig. 2C) (54). We also examined the effect of PIP₂ on the interaction between liposomes and peptides. Application of PIP₂ to PS further enhanced FRET (F₀/F) signals in a dose-dependent manner, even though a physiological concentration of PIP₂ (1%) had a minor effect on peptide binding to liposomes (Fig. 2D). These results suggest that anionic phospholipids, including PS and PIP₂, are involved in the membrane interaction of β2e in the cell membrane.

Figure 2.

The N-terminal affinity of liposomes is augmented in the presence of PS. (A) Cartoon of the FRET analysis. Binding was tested using FRET between a peptide containing Trp (W) (donor) and liposomes labeled with dansyl-PE (acceptor). The initial spectrum of Trp was determined in the absence of liposomes (F₀) and the subsequent spectrum was recorded after liposome addition (F). (B) Fluorescence of Trp in the absence (black trace) or presence (red traces) of liposomes with 15% PS. A.U., absorbance units. FRET is presented as F₀/F at 355 nm. (C) Summary of FRET changes with different lipid compositions of the liposomes. FRET is presented as F₀/F at 355 nm. n = 3; ^∗∗p < 0.05, compared with PS-free liposome; error bar, ± SEM. (D) FRET (F₀/F) signals in the presence of PS and/or PIP₂. FRET (F₀/F) is represented as a function of the concentration of lipids. (E) Confocal images of cells expressing the PS probe Lact-C2-GFP and the β2e subunit tagged with mCherry. Scale bar, 5 μm. (F) Effects of a transfected PS probe on the inactivation of Ca_V2.2 currents with the β2e subunit. PS masking by Lact-C2 accelerates the inactivation of Ca_V2.2 currents. Currents were measured during a 500 ms test pulse to +10 mV. The current trace obtained with the β2e subunit and Lact-C2 is scaled to the peak amplitude of currents obtained with the β2e subunit only (control). (G) Summary of current inactivation by Lact-C2 expression (n = 4–5). ^∗p < 0.05, compared with control; error bar, ± SEM. To see this figure in color, go online.

Next, using a specific probe for PS, we examined the lipid requirement for binding of the β2e subunit to membranes. In cells overexpressing the PS-scavenging probe Lact-C2-GFP, the β2e subunit was mostly redirected in the cytosol (Fig. 2E). Additionally, Ca_V2.2 current inactivation in the presence of the PS scavenger was significantly increased (Fig. 2, F and G). Thus, negatively charged PS, which comprises 20–30% of the plasma membrane, plays an important role in recruiting the β2e subunit to cell membranes (55,56). Together, these results suggest that electrostatic and hydrophobic interactions between basic amino acids and anionic phospholipids are of key importance for membrane targeting of the β2e subunit, consistent with a previous report (23).

MD simulations reveal two kinds of membrane-targeting mechanisms

Key factors that could determine the recruitment of the β2e subunit to the plasma membrane were clarified in the in vitro experiments discussed above. However, it is possible that only some of the configurations of the β2e subunit in the proximity of the plasma membrane are able to bind.

Therefore, by performing intensive multiscale simulations combining ATMD simulations (nanosecond timescale) with CGMD simulations (microsecond timescale) (47,57), we sought to obtain atom- and residue-level insights into membrane targeting of the mouse β2e subunit in the proximity of the plasma membrane. We simulated the binding of a fragment from the N-terminal 1–23 residues of the β2e subunit approaching a lipid membrane consisting of 25% cholesterol, 45% POPC, 15% POPE, and 15% POPS. The N-terminus was randomly disordered and fluctuating near the lipid. The distance between the upper leaflet and the closest residue of a β2e protein to the membrane was initially 10 Å along the normal direction of the upper leaflet. We performed 3000 steps of energy minimization and heated the system from 0 K to 300 K for a 100 ps equilibrium ATMD simulation. The main ATMD simulations for 20 independent trajectories, with up to a 100 ns timescale for each, were performed at 300 K under NPT (1 bar) and SHAKE conditions.

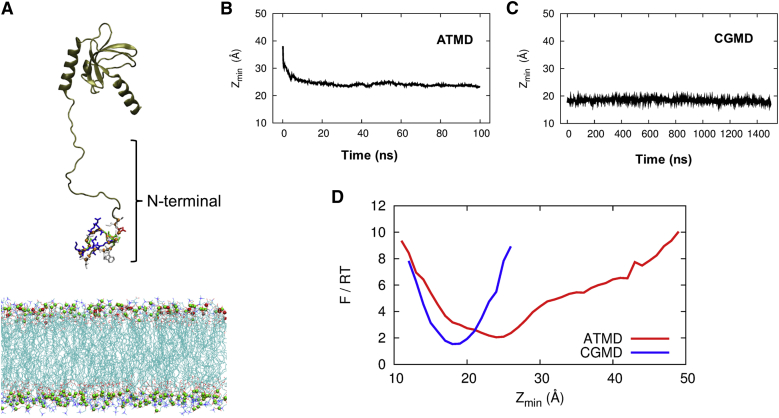
First, we asked whether changes in the composition of the membrane lipids would affect the propensity of the β2e subunit to bind to the membrane. To assess the binding propensity of a β2e protein, we set up a height coordinate Z(i), which is the position (height), along the perpendicular direction to the upper leaflet of lipid bilayer, of the residue i in a β2e protein with respect to the mid-point (Z = 0) of the lipid bilayer. The distance between the upper leaflet and the mid-point of the lipid bilayer is 20 Å. We define the reaction coordinate (i.e., average height) Z = ${\sum }_{i=1,23}Z\left(i\right)/23$ for a 23-residue peptide of the N-terminus of the β2e subunit (MKATWIRLLKRAKGGRLKSSDIC), which could be one measure for assessing the propensity of a β2e protein to bind to the membrane. How the binding free energy manifests the thermodynamic propensity for or against the binding propensity will be discussed later. We can also define Z_min, the minimum of the height coordinate Z(i) over i = 1, 2, .. 23. Z_min probes more sensitively than Z whether any one of the 23 residues touches the upper leaflet, where Z_min becomes 20 Å. Fig. 3 A shows the values of Z_min from a typical trajectory in our ATMD simulation as a function of time. When PS was not included in the lipid mix, a 23-residue peptide of the N-terminus of the β2e subunit comes down to touch and moves away from the upper leaflet of the membrane (see the blue line in Fig. 3, A and B). On the other hand, the inclusion of 15% PS (as an example of a negatively charged phospholipid in the lipid mix) leads to a decrease of Z_min toward 20 Å and increases the binding propensity of the β2e subunit interaction with the membrane, which then manifests as a strong association of the β2e subunit with the membrane as time goes by (see the red line in Fig. 3, A and C). Behaviors similar to that shown in Fig. 3 A could be observed from other trajectories as well (see Fig. S1).

Figure 3.

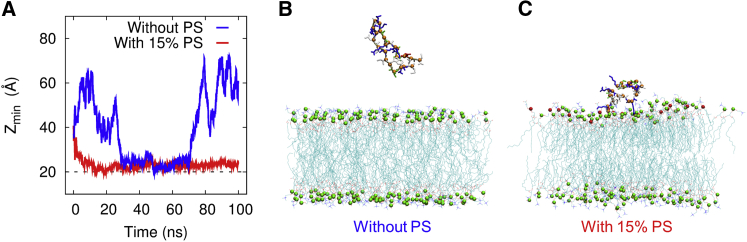
PS-dependent membrane anchoring of the β2e subunit is determined via ATMD simulation. (A) The minimum of the height coordinate Z(i) over i = 1, 2, .. 23 of an N-terminal fragment from a single trajectory in our ATMD is shown as a function of time, with (without) PS in the membrane denoted by a red (blue) line. The N-terminal fragment (1–23 amino acids) of the β2e subunit comes down to touch the membrane and moves away from (approaches and binds to) it with 0% (15%) PS in the membrane (see the blue (red) line). Similar behavior was observed from other trajectories as well (see Fig. S1). (B) Typical snapshot of an N-terminal fragment (1–23 amino acids) of a β2e subunit, which unbinds to the neutral membrane without PS in the membrane. (C) Typical snapshot of an N-terminal fragment (1–23 amino acids) of a β2e subunit, which binds to the membrane with 15% PS in the membrane. The headgroup of PS is represented by red spheres. To see this figure in color, go online.

We performed multiscale MD simulations for a β2e subunit with residues 1–143 after placing it initially at 10 Å above the upper leaflet, as shown in Fig. 4A. First, we performed ATMD simulations to generate 50 trajectories, each of which ran for 100 ns. Second, we further equilibrated the last configurations from these ATMD simulations by running CGMD simulations for 1.5 μs on each of 10 trajectories. Since our computing capacity was not sufficient to run ATMD on a microsecond timescale for a protein system with 143 residues, 41,892 atoms in the lipid, and 162,000 atoms in waters, we employed CGMD to reach a time window of 1.5 μs. We probed the equilibrium character of the binding propensity of a β2e subunit with residues 1–143 by measuring the value of Z for 23 residues in the N-terminus of a β2e subunit. Since Z_min is more sensitive than Z for probing whether any residues (1–143 amino acids) of the β2e subunit come down to touch the upper leaflet of the membrane, we plot the time evolution of Z_min in Fig. 4, B and C, which show a better convergence of Z_min toward 20 Å compared with Z as time goes by. ATMD on a 100 ns timescale was not sufficient to reflect the equilibrium binding behavior (Fig. 4B), whereas the 1.5-μs-timescale CGMD (Fig. 4C) showed the onset of the equilibrium binding behavior. We also noticed that whereas ATMD provided atom-level kinetic insight into the binding process en route to equilibrium, CGMD provided residue-level insight into the character of the equilibrium binding. Therefore, performing multiscale MD simulations by combining ATMD with CGMD is a useful approach for observing the short and long binding processes of a β2e protein. The value of Z at the surface of the upper leaflet is 20 Å because the thickness of the lipid bilayer is 40 Å. We note that Z_min in Fig. 4, B and C, is the averaged value of reaction coordinates over many different configurations within the window of time binning, and approaches to ∼20 Å as the time advances to 1.5 μs. Since the averaged Z_min value may or may not be the same as the most probable value depending on the underlying probability distribution, we turned our attention to calculate the probability p(Z_min) for β2e configurations to have a Z_min value within the time range of 100 ns in ATMD and 1.5 μs in CGMD. We constructed a free-energy landscape from the entire data from our ATMD and CGMD simulations by taking Z_min as a reaction coordinate and performing block averaging in the binning of Z_min. Therefore, we computed the free energy in the thermal energy unit F/RT = –ln p[Z_min], where p[Z_min] is the probability of finding a configuration with Z_min. Fig. 4D shows the free-energy landscape from ATMD for the short time window and from CGMD from the long time window. It shows that the value of Z_min at which the free energy becomes the minimum approaches 20 Å in the long time window. Taken together, Fig. 4, B–D, show the convergence of the equilibrium profile for Z_min. Therefore, the CGMD simulation provides residue-level insight into the equilibrium binding behavior, in that the most probable value reaction coordinate Z_min converges to the value near 20 Å as the time advances to 1.5 μs. This implies a strong association of the β2e subunit with the upper leaflet of lipid bilayer.

Figure 4.

Time dependence of the reaction coordinate Z_min of a β2e subunit (1–143) binding to membrane phospholipids, from a multiscale MD simulation of β2e. (A) Reconstructed structure of a β2e N-terminal domain (yellow cartoon) near the plasma membrane (cyan sticks and red and green balls). (B and C) Reaction coordinates Z_min for a β2e subunit (1–143) as a function of time for (B) the 100 ns ATMD simulation, which shows the initial decrease of Z_min during the 100 ns period, and (C) the 1.5 μs CGMD simulation, which shows the overall convergence of Z_min to ∼20 Å in the long time limit. (D) The free-energy landscape in a thermal energy unit –ln p[Z_min] is plotted as a function of Z_min for the 100 ns ATMD (red line) and 1.5 μs CGMD (blue line) simulations. The position of the minimum of –ln p[Z_min], i.e., the most probable value of the reaction coordinate, shows the overall convergence to ∼20 Å. The scale of free energy –ln p[Z_min] is in the thermal energy unit. To see this figure in color, go online.

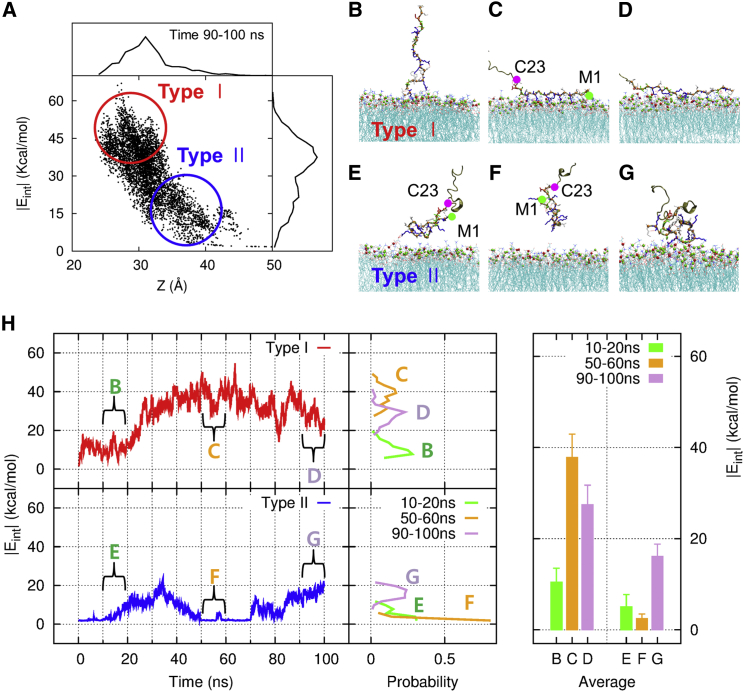
To obtain kinetic insight into the process of a β2e subunit binding to the membrane, we traced the structures of 5000 conformations near the upper leaflet of a lipid bilayer for a 10 ns time window over 50 trajectories from ATMD simulations. In addition to the reaction coordinate Z, another measure that can be used to probe the degree of binding is the interaction energy E_int between atoms of a β2e subunit and the lipid bilayer. The correlation between the reaction coordinate Z and the magnitude of interaction energy |E_int| for each 10 ns time window from 10 ns to 100 ns is plotted at Fig. S3, and Fig. 5 A presents the same plot for the time interval from 90 ns to 100 ns. The top (right) panel shows the distribution of the value of Z (|E_int|). As the time advances, the region where these two distribution functions attain their maximum value moves from the region of high Z and low |E_int| to the region of low Z and high |E_int|. On the short timescale, the binding mode has a type II character, and changes to type I as the time advances. On the long timescale, the binding through type I becomes dominant, giving rise to strong and stable binding. The binding modes differ depending on which residues first participate in making contact with the lipid, and whether residues starting from the end of the N-terminus bind to the lipid in a sequential manner. We call these modes the stretched binding mode (type I) and the agglomerate binding mode (type II), respectively. We monitored the structural character of these two groups of β2e configurations. The first group (type I, denoted by a red circle) includes residues that underwent a strong and stable binding to the lipid, and the second group (type II, denoted by a blue circle) includes those that underwent a weak and transient binding.

Figure 5.

Two kinds of binding modes are involved in the process of a β2e subunit (1–143) binding to membrane phospholipids, as shown by an ATMD simulation of β2e. (A) Correlation between the reaction coordinate Z and the magnitude of interaction energy E_int based on 5000 conformations of a β2e subunit (1–143) in the time window between 90 ns and 100 ns. The top (right) panel shows the distribution of the value of reaction coordinate Z (the interaction energy). As the time advances, the character of the binding mode changes from type II to type I (see also Fig. S3). In the long time limit, binding through type I becomes dominant, giving rise to strong and stable binding. Two dominant modes of binding are explained. (B–D) Type I, the stretched binding mode. The N-terminal residues M1 and K2 first anchor to the membrane and the other residues are then bound sequentially while maintaining their structure, which stretches progressively. (E–G) Type II, the agglomerate binding mode. The initial residues in the β2e N-terminus region do not bind first to the membrane; instead, other residues away from the N-terminus featuring the agglomerate structure make the initial contact with the membrane. (H) Time evolution of |E_int| from a given typical single trajectory. The middle panel of (H) represents the probability distribution of |E_int| constructed from 100 configurations in a given 10 ns time window corresponding to each of B, C, D, E, F, and G in the left panel of (H). The energetic character of |E_int| for configurations in each of these time windows were then clustered into. The right panel shows both the mean value and the error bar of |E_int| for a given time window of B, C, D, E, F, and G. To see this figure in color, go online.

In Fig. 5H, we provide the distribution functions of the interaction energies for time windows of 10–20, 50–60, and 90–100 ns. In the left panel of Fig. 5H, we show the time evolution of |E_int| from a given typical single trajectory, which is not the one simply averaged over all data from all trajectories. The middle panel of Fig. 5H represents the probability distribution of |E_int| constructed from |E_int| values of 100 configurations from each of a given 10 ns time window B, C, D, E, F, and G in the left panel of Fig. 5 H so that the energetic character of |E_int| for configurations in each of these time windows are clustered into. Although the error bar is embedded in the distribution curve and can be seen as the half-maximum full width of the distribution curve for B, C, D, E, F, and G, we provide in the right panel of Fig. 5H both the mean value and the error bar of |E_int| for a given time window of B, C, D, E, F, and G. Therefore, the clustered configuration of β2e at each of the time window B, C, D, E, F, and G is represented by the predominant configuration that sits on top of the distribution curve shown in the middle panel of Fig. 5H. These predominant configurations are depicted in B, C, D, E, F, and G in Fig. 5H. Fig. 5, B–D, depicts the type I stretched binding event in which residues M1 and K2 make the first strong electrostatic contact with the lipid, and the remaining residues bind to the lipid sequentially while keeping the structure of the N-terminus stretched on the surface of lipid bilayer, resulting in strong binding. However, the randomly disordered N-terminus of the β2e subunit sometimes forms an agglomerate structure, and thus residues away from the end of the N-terminus make the first contact with the lipid. In this case, the interaction energy with the lipid is weaker and transient, and thus there is less chance of M1 and K2 making contact with the lipid. Fig. 5, E–G, show such a type II agglomerate binding event. It shows clearly that the distribution functions of the interaction energy for the stretched binding mode merge around the window of the stronger interaction energy as time passes from ∼40 ns up to 100 ns. On the other hand, the distribution functions for the agglomerate binding stay in the window of interaction energies lower than ∼20 Kcal/mol even though the time approaches 100 ns. The converging behavior of the distribution functions of the interaction energies presented in Fig. 5H demonstrates these two different binding modes. It reflects that the stretched binding mode is more prone to involve strong binding to the lipid, in which M1 and K2 play a critical role. However, the binding of the β2e N-terminus still needs negative phospholipids in the membrane surface.

Binding free energy of mutants K2A, W5A, and K2A/W5A with respect to a wild-type β2e

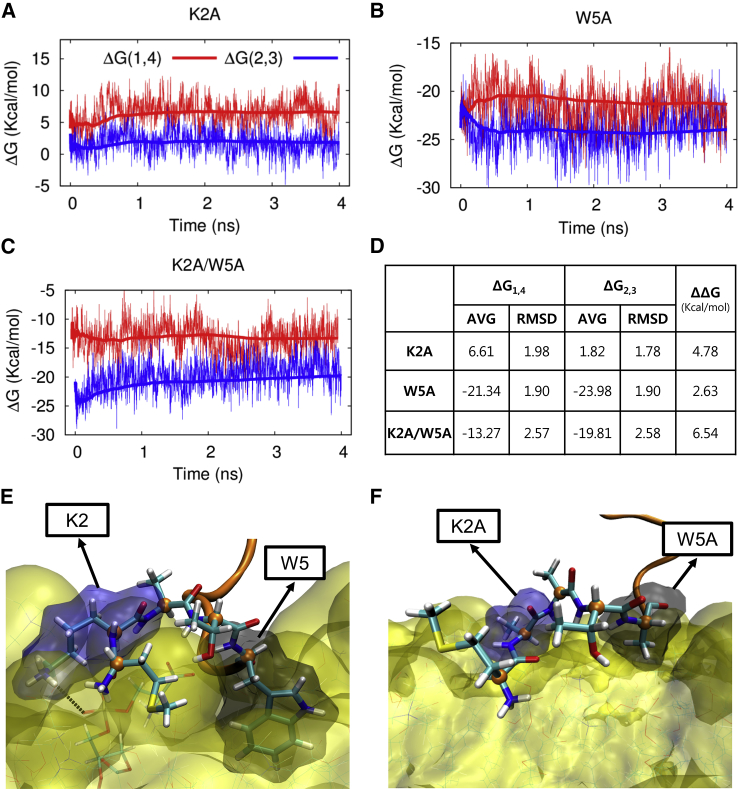
The reaction coordinate Z provided geometrical insight into the degree of binding of β2e to a lipid, but not into the binding free energy. Therefore, we tried to estimate the binding free energy (46,47,58–60) for mutants K2A, W5A, and K2A/W5A with respect to that of a wild-type β2e based on TI (see Materials and Methods). Based on the thermodynamic equality $\Delta G_{\mathrm{1,2}}$ + $\Delta G_{\mathrm{2,3}}$ + $\Delta G_{\mathrm{3,4}}$ - $\Delta G_{\mathrm{1,4}}$ = 0 around a thermodynamic cycle in Fig. S1, we evaluated the binding free energy $\Delta \Delta \text{G}$ = $\Delta G_{\mathrm{3,4}}$ - $\Delta G_{\mathrm{2,1}}$ = $\Delta G_{\mathrm{1,4}}$ - $\Delta G_{\mathrm{2,3}}$ of a mutant with respect to that of a wild-type protein. The last configurations of a β2e (1–143) from CGMD simulations for 1.5 μs on each of 10 trajectories were transformed back to all-atom structures using backward.py (49) in Martini tools. TI ATMD simulations (45) were performed for 4 ns to calculate $\Delta G_{\mathrm{1,4}}$ and $\Delta G_{\mathrm{2,3}}$ for mutants K2A, W5A, and K2A/W5A. Fig. 6, A–C, show the values of $\Delta G_{\mathrm{1,4}}$ (red line) and $\Delta G_{\mathrm{2,3}}$ (blue line) in the course of the TI ATMD simulation for the mutants K2A, W5A, and K2A/W5A, respectively. The table in Fig. 6D summarizes the binding free energies. The binding of mutants K2A, W5A, and K2A/W5A to the lipid is thermodynamically unfavorable by 4.78, 2.63, and 6.54 Kcal/mol, respectively, compared with that of the wild-type β2e.

Figure 6.

Binding free energy and atomistic view of the interaction of residues M1–W5 with the membrane. (A–C) TI for the binding free energy for (A) K2A, (B) W5A, and (C) K2A/W5A. $\Delta G_{\mathrm{2,3}}\left(\Delta G_{\mathrm{1,4}}\right)$ is the difference between the free energy of a mutant protein in solution (a mutant bound to the membrane lipid) and that of a wild-type protein in solution (a wild-type protein bound to the membrane lipid). (D) Summary of the binding free energies $\Delta \Delta \text{G}$ for K2A, W5A, and K2A/W5A. (E and F) Typical snapshots of the binding of β2e N-terminal residues M1–W5 to the membrane with (E) the wild-type and (F) the K2A/W5A mutant, showing their side chains (licorice) interacting with the membrane surface (yellow). To see this figure in color, go online.

Membrane targeting of the β2e subunit through both polar and nonpolar interactions

To examine the functional role of residues K2 and W5 in atomic detail, we repeated ATMD simulations for the K2A/W5A double mutant. Fig. 6, E and F, show a typical snapshot of the β2e N-terminal residues M1–W5 binding to the lipid. We first looked at the atomic interactions between K2, W5, and the lipid. Fig. 6E shows that the side chain of K2 is undergoing electrostatic interactions (hydrogen bonds, represented by black dotted lines) with the lipid molecules, whereas W5 is buried in the lipid and making hydrophobic interactions (represented by the black shadow) with the lipid. For the K2A/W5A mutant (Fig. 6F), the Ala residues make neither hydrogen-bond nor hydrophobic interactions with the lipid. Thus, any remaining lipid binding is weak.

The wild-type and mutants of the β2e subunit show differential effects on inhibition of Ca_V currents by PIP₂ depletion

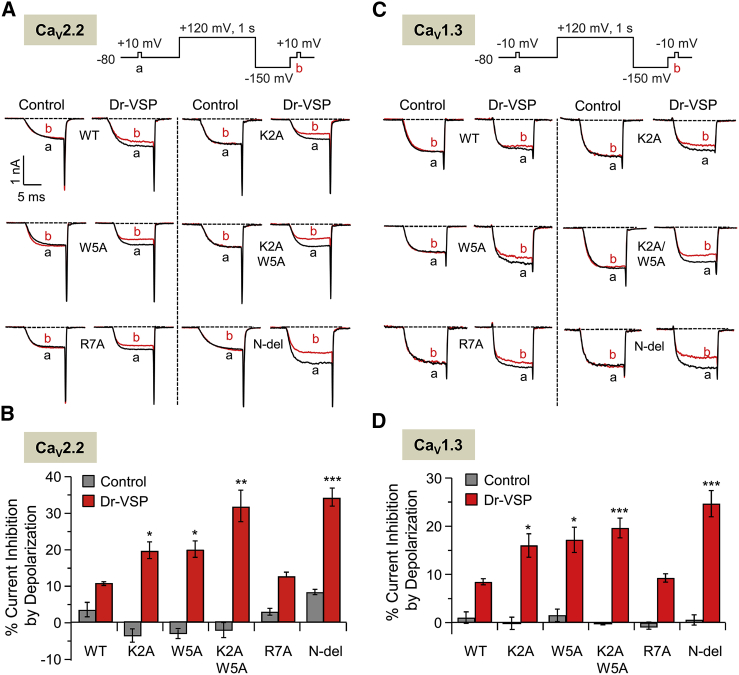
In addition to the molecular mechanism underlying the subcellular distribution of the β2e subunit, we examined the effects of PIP₂ depletion on the regulation of Ca_V channels with wild-type and mutated β2e subunits. Several studies have shown that β subunits regulate the PIP₂ sensitivity of Ca_V channels (18,61). To investigate modulation by lipids, we depleted PIP₂ using the voltage-sensing lipid phosphatase Dr-VSP, which can convert PIP₂ to PI(4)P during depolarizing voltage pulses (19,62). First, we tested the effects of K2A, W5A, and K2A/W5A on channel modulation by PIP₂ depletion. We used both the wild-type and the membrane-anchored R7A mutant as controls because they showed similar inactivation patterns. We also examined the effects of the cytosolic N-del mutant. When Ca_V2.2 channels were cotransfected with the wild-type β2e subunit or point-mutated R7A, inhibition by PIP₂ depletion was modest (Fig. 7A). It was stronger with the other point mutants. Thus, with either K2A or W5A, the inhibition increased to 19% ± 0.6% and 19% ± 0.9%, respectively. With K2A/W5A, it was 30% ± 3% (Fig. 7B), and with the N-del mutant it was similar, 34% ± 2%. In addition to Ca_V2.2 channels, we tested the effect of PIP₂ depletion on current inhibition in Ca_V1.3 channels (Fig. 7C). The patterns of inhibition by PIP₂ depletion in Ca_V1.3 channels were similar to those observed for Ca_V2.2 channels (Fig. 7D). These results confirm that the localization of the β subunits is a major determinant in the gating of Ca_V channels (17,18). Collectively, these data indicate that the increased PIP₂ sensitivity of the channels is the result of a decreased affinity for the membrane due to changes in β2e’s electrostatic and hydrophobic interactions with phospholipids after N-terminal mutagenesis.

Figure 7.

The wild-type and mutants of the β2e subunit show differential effects on Ca_V2.2 and Ca_V1.3 current inhibition by PIP₂ depletion. (A) Current inhibition of Ca_V2.2 channels with mutant β2e subunits by Dr-VSP activation. The currents in test pulses to +10 mV for 10 ms before (a) and after (b) the depolarizing pulse (+120 mV) are superimposed on nontransfected cells (control) and Dr-VSP-transfected cells. (B) Summary of Ca_V2.2 current inhibition (%) by Dr-VSP. For control, n = 4–5; for Dr-VSP, n = 4–5. ^∗p < 0.05; ^∗∗p < 0.01; ^∗∗∗p < 0.001, compared with wild-type; error bar, ± SEM. (C) Inhibition of Ca_V1.3 currents with different mutant β2e subunits by Dr-VSP. The currents in test pulses to −10 mV for 10 ms before (a) and after (b) the depolarizing pulse (+120 mV) are superimposed on nontransfected cells (control) and Dr-VSP-transfected cells. (D) Summary of current inhibition of Ca_V1.3 channels by Dr-VSP-induced PIP₂ depletion. For control, n = 3–5; for Dr-VSP, n = 4–5. ^∗p < 0.05; ^∗∗∗p < 0.001, compared with the wild-type; error bar, ± SEM. To see this figure in color, go online.

Discussion

Ca_V channels serve as key machinery for Ca²⁺ influx and initiate diverse physiological events. As one of several auxiliary subunits, β subunits have a significant effect on the gating properties and membrane trafficking of Ca_V channels. In particular, the subcellular localization of β subunits contributes unique properties to Ca_V channels, such as inactivation kinetics and modulation by lipids (63–66). A recent study reported that in addition to the β2a subunit, which is localized in the plasma membrane via palmitoylation, the β2e subunit is expressed in the plasma membrane via electrostatic and hydrophobic interactions (23). Although that study suggested electrostatic and hydrophobic interactions with the membrane, it did not provide an atomistic explanation for the membrane interaction. We anticipated that the electrostatic and hydrophobic interactions between the β2e subunit and the membrane might not always ensure that all configurations of the β2e subunit would dock successfully to the membrane, and we were able to determine the molecular trajectories that are responsible for the stable recruitment of the β2e subunit to the plasma membrane.

Building on previous revealing work (18,67) and a recent parallel study (23), we have described the molecular mechanism underlying binding of the β2e subunit to the plasma membrane in significant functional and theoretical detail. Our analysis of confocal images and current measurements via site-directed mutagenesis of the N-terminus indicates that two residues of the N-terminus, Lys (K2) and Trp (W5), are of key importance for stable binding to the membrane. In particular, we showed that the initial interaction of proximal N-terminal K2 and W5 residues with the membrane phospholipids is required for stable, nonspecific electrostatic interactions between the other basic amino acids of the N-terminus and acidic phospholipids on the membrane. The mutated forms, K2A and W5A, displayed a cytosolic distribution, induced fast inactivation, and enhanced the PIP₂ sensitivity of Ca_V1.3 and Ca_V2.2 currents, whereas mutations in other basic residues of the N-terminus had little effect. On a theoretical level, our multiscale MD simulations demonstrate that the basic K2 and hydrophobic W5 residues confer strong and sustained membrane interactions on the β2e subunit. The double mutant K2A/W5A binds to the membrane with relatively weaker polar and nonpolar interaction energies compared with K2A or W5A alone, suggesting that membrane binding results from a synergy of charge-charge and hydrophobic interactions. We also found that the K2R and W5F mutants still localize to the plasma membrane, indicating that the interaction depends on polarity and hydrophobicity rather than on detailed structure. This notion was further supported by an experiment with the W5Y mutant, in which the hydroxyl group could act as a steric hindrance, resulting in failure to incorporate the β2e subunit into the plasma membrane. Thus, our results are consistent with previous studies (68,69) showing that both basic and aromatic residues play a key role in the electrostatic interactions of cytosolic proteins with the plasma membrane. Because these interactions may apply quite generally to protein-membrane interactions, we were motivated to extend our microscopic analysis of the binding dynamics.

Our MD simulations provided atomistic descriptions of dynamic trajectories for binding of the β2e subunit that depended on its conformation close to the plasma membrane. The simulations demonstrated two microscopic mechanisms for membrane targeting, which we call the stretched binding mode and the agglomerate binding mode. Stable recruitment of β2e is facilitated by the stretched binding mode. Here, Met M1 of the N-terminus reaches out to make the first contact with the lipid and facilitates the subsequent binding of K2 with the lipid. For a posttranslational modification, N-terminal methionine can be cleaved by methionine aminopeptidase in a second-residue-dependent manner. If residues with small side chains are located in the second position of the N-terminus, the aminopeptidase can excise the methionine. However, residues with a bulky side chain (such as the lysine of the β2e subunit) prevent cleavage by the enzyme (70). Preservation of the methionine is consistent with our model in which Met initiates membrane binding of the β2e subunit. Taken together, these results suggest that the stretched binding mode could be a common general mechanism for stable recruitment of peripheral proteins. The mutated form K2A/W5A shows difficulty in stretching out the N-terminus, resulting in weaker and transient binding to the membrane.

In 2002, Wu and colleagues (71) reported that PIP₂ is an important factor in the regulation of Ca_V2.1 channels, and since then several studies have attempted to elucidate the precise regulatory mechanism underlying the effect of PIP₂ on Ca_V channels (65). It seems that the action of PIP₂ on Ca_V channels occurs by diverse modes depending on the nature of the microdomain. With cytosolic β subunits, PIP₂ facilitates Ca_V channel function and arachidonic acid inhibits it. Previous studies (22) proposed that the lipids interact with Ca_V channels in two ways, which by now are familiar. One is a hydrophobic interaction between the fatty acyl chains of the lipid and transmembrane regions of the α1 calcium channel subunit. The other is a hydrophilic interaction between the headgroup of PIP₂ and cytosolic gating domains of the α1 subunit. It has been suggested that when β2a is expressed with Ca_V channels, the palmitoyl fatty acid chains can compete with and replace thefatty acid chains of PIP₂ for binding to the channel hydrophobic binding sites, thereby replacing PIP₂ in channel function (16,61,72). As a result, the competitive suppressive effects of arachidonic acid are diminished, since the lipid-binding sites are already occupied by palmitoyl groups of the β2a subunit. We show that a simple electrostatic binding of the β2e subunit to several acidic lipid headgroups of the membrane suffices to reduce the sensitivity of Ca_V channels to PIP₂. Again, the cytosolic versus membrane distribution of β subunits is a key determinant in the regulation of Ca_V channels by lipids and G_q-protein-coupled receptors (17).

Conclusion

In conclusion, our results show that membrane localization of the β2e subunit relies on nonspecific electrostatic interactions between anionic lipids in the inner leaflet of the plasma membrane and positively charged N-terminus amino acids of the β2e subunit. Through mutagenesis of basic and hydrophobic residues, we show that cytosolic β2e mutants have a cytosolic distribution that leads to fast inactivation of Ca_V channels and higher sensitivity to PIP₂. At the microscopic level, our MD simulations suggest two different dynamic mechanisms for binding of the β2e subunit to the plasma membrane: the stretched binding mode and the agglomerate binding mode. The stretched binding mode facilitates stable recruitment of the β2e subunit to the plasma membrane. In particular, MD simulations in which K2A, W5A, and K2A/W5A mutants were applied explain the failure of an electrostatic interaction between mutant β2 subunits and the plasma membrane in cells. Thus, our findings should help elucidate the molecular characteristics of the electrostatic interaction between the plasma membrane and charged proteins.

Author Contributions

B.-C.S. and I.C. designed research. D.-I.K. and Y.P. performed biochemical and electrophysiological research. M.K., S.K., and J.L. performed MD simulations. D.-I.K., M.K., B.-C.S., and I.C. wrote the manuscript.

Editor: Michael Pusch.