Abstract
Highly symmetric nanoshells are found in many biological systems, such as clathrin cages and viral shells. Many studies have shown that symmetric shells appear in nature as a result of the free-energy minimization of a generic interaction between their constituent subunits. We examine the physical basis for the formation of symmetric shells, and by using a minimal model, demonstrate that these structures can readily grow from the irreversible addition of identical subunits. Our model of nanoshell assembly shows that the spontaneous curvature regulates the size of the shell while the mechanical properties of the subunit determine the symmetry of the assembled structure. Understanding the minimum requirements for the formation of closed nanoshells is a necessary step toward engineering of nanocontainers, which will have far-reaching impact in both material science and medicine.
Introduction
The spontaneous assembly of building blocks into complex ordered structures is ubiquitous in nature. Examples include the formation of symmetric shells with extraordinary accuracy such as clathrin vesicles for membrane trafficking in cells and viral shells for the protection and transportation of the viral genome. Based on very simple physical principles, it has been argued that small spherical viruses display structures with icosahedral symmetry (1), and while some larger clathrin vesicles are irregular in shape, the smallest clathrin shells observed in the in vitro studies tend to take on a discrete set of symmetric structures (2). Fig. 1 shows the three-dimensional image reconstructions of enterovirus 71, an icosahedral virus (3) and a D6 symmetric clathrin coat (4) obtained through the use of spatial averaging over the set of associated symmetries.
Figure 1.
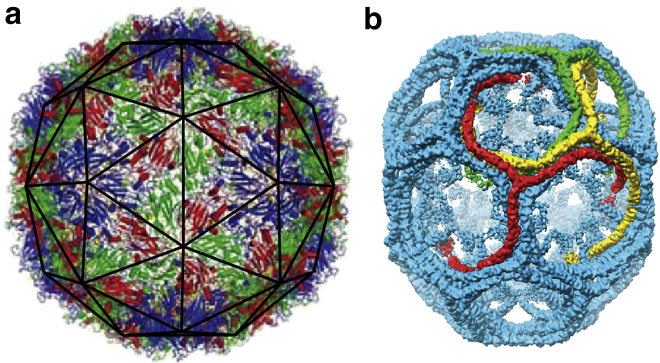
Images of (a) a viral shell (enterovirus 71) and (b) a small clathrin coat. The viral shell is a T = 3 icosahedral virus, constructed of 180 identical protein subunits. The proteins sit in three color-coded quasi-equivalent positions (grouped into triangles as seen with the dark outline in subfigure a). The clathrin coat (b) has a D6 dihedral symmetry, and is often referred to as a D6 barrel. The clathrin molecules have a triskelion (three-legged) shape that binds antiparallel leg-to-leg. The symmetries displayed by these shells allow for very detailed imaging through the technique of spatial averaging. To see this figure in color, go online.
The simplicity and highly symmetric shape of viral shells, with diameters ranging from 20 to 120 nm, have in particular attracted the attention of scientists for many decades (5–11). The simplest viruses are made of a genome encapsulated in a protein shell called the capsid. Quite remarkably, under many circumstances, the viral coat proteins assemble spontaneously around its genome or other negatively charged cargoes to form capsids identical to those observed in vivo (12–16). Despite the importance of engineered biological nanoshells in gene and drug delivery and other biomedical technologies, the mechanisms and factors that control the structure and stability of shells made of identical building blocks are just beginning to be understood. Constructing the building blocks with interactions similar to those in the natural nanocontainers may lead to the fabrication and design of precise synthetic nanostructures (11,17,18).
There have been many studies investigating the equilibrium shapes of shells formed from one or two identical subunits under external constraints (7–9,11,16,19–22). The simple case of spherical colloids or circular disks constrained to reside on the surface of a sphere shows that the stability of formed shells depends strongly on the number of assembly subunits and interactions between them. For example, the solutions of the optimal packing problem of N identical hard disks on the surface of a sphere, known as the Tammes problem, reveal the presence of a number of local maxima in the plot of the sphere coverage versus number of disks, N. The structures characterized by the “magic numbers”, N = 12, 24, 32, 44,… corresponding to the local maximum coverage, often have higher symmetry than their neighboring structures (8). A different set of magic numbers appear when minimizing the free energy of the N identical disks interacting through a Lennard-Jones potential. Some of these magic numbers and their associated shells coincide with the number of capsomers (protein multimers) in structures displaying icosahedral symmetry. Magic numbers corresponding to nonicosahedral shells with octahedral and cubic symmetries also appear in Monte Carlo simulations of disks sitting on the surface of a sphere (7,8) or prolate ellipsoids with an anisotropic Lennard-Jones potential (23), consistent with the structures observed in vitro virus assembly experiments.
The same magic numbers and structures were observed in the Monte Carlo simulations of the self-assembly of cone-shaped particles with attractive interactions (11). The authors in Chen et al. (11) showed that over a range of cone angles, a unique precise sequence of robust clusters form under equilibrium conditions. Note that the self-assembly of attractive spheres under a spherical convexity constraint reproduces exactly the same sequence of shells (24). The structure and symmetry of the small cluster sizes in these simulations (11,24) were identical to those observed in the experimental studies of evaporation-driven assembly of colloidal spheres (17).
Quite interestingly, some of these magic numbers also appeared in completely different experiments, which showed that, under appropriate conditions, clathrin molecules spontaneously assemble in vitro to form highly symmetric vesicles whose radii depend on the size of cargoes (2). The fact that in distinct systems we observe shells with identical symmetry reveals the existence of a common underlying design principle governing the assembly of these structures.
One can readily observe that the building blocks of all the aforementioned systems can be packed with hexagonal symmetry in a flat space. This is clearly illustrated in Fig. 2, which shows a viral capsid, a clathrin vesicle, and a shell constructed of spheres, all with their associated building blocks. All shells in Fig. 2 have icosahedral symmetry. While defect-free stacks of hexagonal layers in three-dimensional space can easily grow from irreversible accretion of Lennard-Jones particles, a closed shell requires the formation of 12 defects with a local fivefold rotational symmetry (pentamers). In symmetric shells, the position of pentamers with respect to each other is precise, i.e., the symmetry can be readily broken if one pentamer is slightly misplaced.
Figure 2.
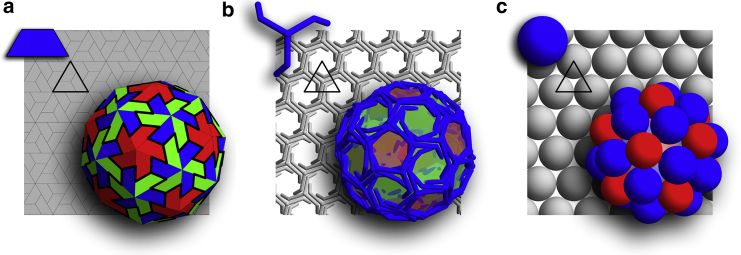
Three different systems that display a shell with the exact same symmetry. (Solid triangle) Background of each subfigure highlights the triangular subunits. Shell (a) is constructed of trimers similar to the viral shells, shell (b) is a soccer ball clathrin coat constructed from triskelion molecules, and shell (c) is built of small spheres connected through Lennard-Jones potential with a convexity constraint. As seen in the background, all the subunits display a local hexagonal symmetry if packed onto a flat surface. To see this figure in color, go online.
One would then expect that the assembly of highly symmetric shells proceeds reversibly. In fact, most previous studies and simulations were done assuming that the process of assembly is to some extent reversible, and that the subunits can dissociate from the shell, at least at the early stages of growth (10,15,20,23,25–29). This process of dissociation also allows the shell to correct mistakes in the growth process to some extent.
In this article, we investigate the growth of a shell by subunits that can connect to each other with a local hexagonal symmetry. Despite the sensitivity of the symmetry of shells to the exact location of pentamers, under many experimental conditions the self-assembly of perfect icosahedral virus capsids is robust and efficient. The robustness of the process raises the question of whether a reversible assembly pathway that allows for the dissociation of subunits at every step is necessary for the formation of symmetric nanocontainers. To this end, we develop a simple model to investigate the assembly of shells constructed from identical subunits, with the minimum set of designing principles for irreversible growth under which each subunit is permanently fixed in position upon addition to the growing shell. Unexpectedly, we find that the shells irreversibly grow to form the highly symmetric structures observed in biological systems and in equilibrium studies ((7,11,23,24); see Figs. 5, 6, and 7 in which the shells are shown with subunits from the systems of interest, as well as Fig. A1 in the Appendix representing all shells with the uniform triangular subunits).
Figure 5.
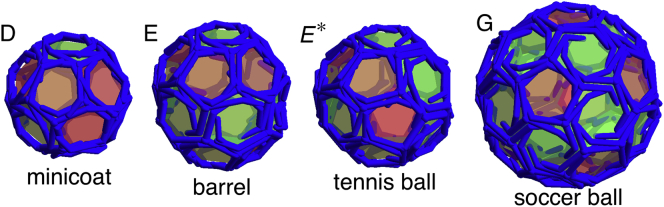
Structures presented with the three-legged triskelion subunits. These shells are very similar to clathrin coats. Of particular interest are the symmetric shells seen in the in vitro studies of empty clathrin coats, such as the minicoat with 28 subunits and tetrahedral symmetry (D), the hexagonal barrel with 36 subunits and D6 dihedral symmetry (E), the tennis ball with 36 subunits and D2 symmetry (E∗), and the soccer ball with 60 subunits and icosahedral symmetry (G). The (D), (E), (E∗), and (G) structures correspond to the labeled regions in Figs. 4 and 11. Note that (E∗) only appears in stochastic simulations (see the text). To see this figure in color, go online.
Figure 6.
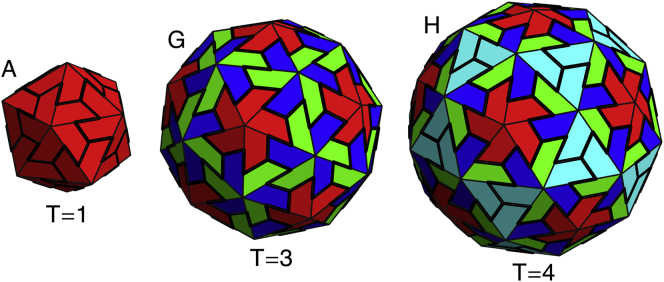
Three shells grown with icosahedral symmetry, reminiscent of viral shells. These shells contain (A) 20, (G) 60, and (H) 80 subunits corresponding to T = 1, T = 3, and T = 4 viral shells based on the Caspar-Klug classification of icosahedral shells. Larger icosahedral shells are not seen in the simulated nonreversible growth model, perhaps explaining why scaffolding is needed for all larger icosahedral viruses. To see this figure in color, go online.
Figure 7.
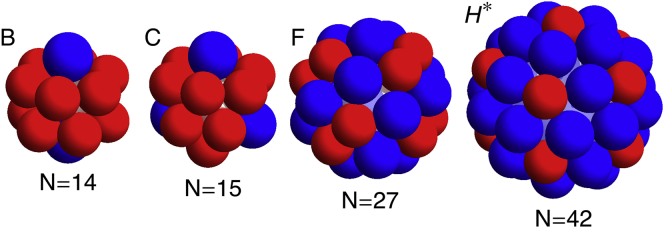
Additional shells matching the simulation results presented in Chen et al. (11,24). These include (B) N = 14 with D5h symmetry, (C) N = 15 with D3h symmetry, (F) N = 27 with S6 symmetry, and (H∗) N = 42 with D5h symmetry. To see this figure in color, go online.
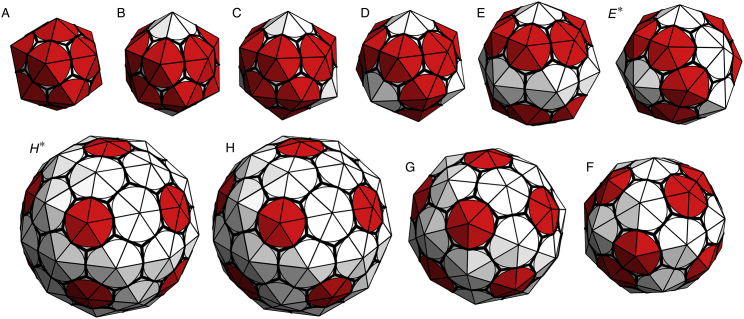
Figure A1.
Set of small symmetric shells formed in the similarly labeled shaded regions in the parameter space plots in Figs. 4 and 11. (Triangles) Subunits. The pentamers (points with five triangles attached) appear darker (red online) in the figure. The shells (A–H) have ns = 20, 24, 26, 28, 36, 50, 60, and 80 subunits or N = 12, 14, 15, 16, 20, 27, 32, and 42 vertices (pentamers and hexamers), respectively. It should be noted that the sets of shells (E) and (E∗), and (H) and (H∗), have the same number of subunits but different symmetries. The symmetries of the shells (left to right and top to bottom) are icosahedral, D6, D3; tetrahedral, D6, D2, D5; and icosahedral, S6. To see this figure in color, go online.
We emphasize that many previous simulations of shell assembly should not be considered completely reversible from the first step of assembly to the completion of the shell. If the binding energy between subunits is sufficiently large, subunits with multiple bonds, such as those in a complete shell, will not dissociate in the timescales simulated (10,25–27). In comparison with these simulations, this study sits at the limit of large binding energies between subunits. Note that the completely irreversible growth of shells has been previously studied and has successfully explained the irregular structures observed in retroviruses (6,30,31). Our focus in this article, however, is on the impact of irreversible assembly on the formation of symmetric shells.
It is worth mentioning that the previous kinetic studies of self-assembly of Lennard-Jones particles confined to the surface of a sphere show that it is impossible to assemble icosahedral or other symmetric shells when following reversible growth pathways that allow for the rearrangement of particles at any position in the growing shell (20). This effect could be explained by the work of Fejer et al. (23), in which the authors find that during the assembly process the incomplete shells relax to nonspherical configurations, and thus a spherical template with isotropic Lennard-Jones interaction between particles might not be able to completely explain the kinetic assembly of viral shells.
We note that while there is a striking similarity among the disparate systems of viral capsids, clathrin vesicles, and shells constructed from spheres or cones, there are also significant differences. Viral capsids in vivo tend to only form structures with icosahedral symmetry, while the clathrin molecules as well as conical particles form shells with additional symmetries. The goal of the article is to explain the basis of similarities and differences displayed in nature’s nanocontainers. According to our studies, the differences in these systems are the results of the distinct mechanical properties of their constituent building blocks. Our findings elucidate the kinetic pathways of assembly and fundamental packing principles in curved space observed in the distinct biological structures.
Materials and Methods
To study the kinetic pathways of the shell growth, we employed triangular subunits, which can represent a trimer of viral capsid proteins, a triskelion molecule, or a locus of three disks (see the highlighted triangles in Fig. 2). In the model, the growth proceeds through the irreversible addition of the triangular subunits to the exterior edges of the incomplete shell. After the addition of each subunit, the elastic sheet is allowed to relax and to find its minimum energy configuration. The minimization of the elastic energy of the growing shell is done numerically using a nonlinear conjugate gradient method (32).
The two-dimensional growing shell is a bond network built from triangles representing the smallest subunit of the shell (see Fig. 3a). While the subunit in Fig. 3a corresponds to the locus of three disks, any other trimers illustrated in Fig. 2 could be used. The energy of the triangular shell can then be separated into the bond stretching and bending energies (6,9). The stretching energy comes from deforming the subunits from the preferred shape of an equilateral triangle, and is modeled by considering each bond as a linear spring with spring constant ks. The stretching energy is then simply a sum of the deformation energy over all triangles,
| (1) |
where i indexes the triangular subunits, b0 is the equilibrium length of the bonds, and bia is the length of the ath bond in the ith subunit. The bending energy results from the deviation of the local radius of curvature from the preferred one and is calculated by summing over all neighboring pairs of triangular subunits
| (2) |
where 〈ij〉 indexes pairs of joined subunits, kb is the torsional spring constant, and θ0 is the preferred angle between two subunits determined by the spontaneous radius of curvature R0. The angle between neighboring subunits, θij, is defined by the relation , where is the normal vector for the ith subunit. The preferred angle θ0 is defined as the angle between the normal vectors of two equilateral triangles sharing a side of length b0 and whose vertices sit on a sphere of radius R0. The explicit relation between the preferred angle and radius of curvature is .
Figure 3.
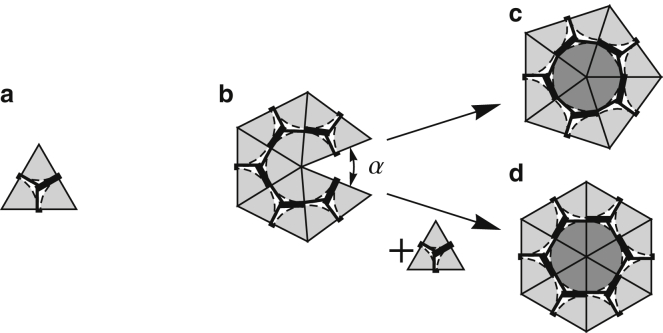
Subunit illustrated as an equilateral triangle (a). The subunits bond together edge to edge, and the growth of the shell proceeds by adding the subunit to the location with the smallest opening angle, α (b). As the shell grows, the two unbound edges can either bind to form a pentamer (c), or a new subunit can be added and bound along both edges to form a hexamer (d). The choice between forming a pentamer and a hexamer is based on what leads to a lower energy per subunit in the growing shell.
The total energy of the two-dimensional bond network depends upon two dimensionless parameters, and R0/b0. The parameter , the Foppl von Karman (FvK) number, presents the relative difficulty of deforming a subunit from its equilateral triangular shape versus the difficulty of bending away from the preferred radius of curvature. The second dimensionless parameter R0/b0 is simply the spontaneous radius of curvature. Note that the FvK number in this work is normalized with respect to size of the subunits b0. The FvK number and the spontaneous curvature R0/b0 both depend on intrinsic properties of proteins such as the equilibrium shape and resistance to deformation, and on solution conditions such as pH and ionic strength that can modify the protein surface charge resulting in a change in protein-protein interaction (23).
To assemble a shell, we assume the structure grows along the minimum free-energy path, so at each assembly step a new subunit is added to the growing edge such that it maximizes the number of neighbors at the vertices of the newly accreted subunit. This is accomplished in practice by adding the new subunit to the location with the smallest opening angle α (see Fig. 3b).
The assembly algorithm described above mimics the physical situation in which the line tension of partially assembled structure is high or protein-protein interaction is weak enough such that the subunits can easily move around to explore all configurations and then attach themselves to the location where they maximize the number of bonds. The idea that the subunit has time to explore the edge and find the optimal position is expected for the growth of symmetric shells (33). Furthermore, we allow the shell to relax between the addition of every subunit assuming that the relaxation time of the elastic stresses in the shell is shorter than the time it takes for the addition of next subunit to the growing shell, consistent with our assumption of high line-tension or weak protein-protein interaction. What distinguishes this work further from the previous kinetic and equilibrium studies of formation of icosahedral viruses is that while our assembly process mimics the situation in which each subunit is allowed to diffuse along the edge to find its optimum position, the attachment of each individual subunit is irreversible from the very first step of the growth process.
The formation of a pentamer or hexamer is shown in Fig. 3. If a vertex on the edge of a growing shell already has five triangles attached, then the assembly could proceed in two different ways: 1) joining the two neighboring edges without adding a new subunit and thus forming a pentamer as in Fig. 3c, or 2) inserting a new subunit and constructing a hexamer as in Fig. 3d. The choice between forming a pentamer or a hexamer is made based on the opening angle. In the previous versions of this model (30), if α was larger than a critical opening angle αcrit, a hexamer would be formed; otherwise, a pentamer would be assembled. In Levandovsky and Zandi (30) and Yu et al. (31), the value αcrit was ∼30, but the final structures were insensitive to the exact value of αcrit. For the purpose of this article, we used an additional method in which a pentamer or hexamer were chosen based on which configuration induces a lower energy per subunit in the elastic sheet. That is, when choosing between a pentamer and a hexamer during the growth process, two trial shells are formed—a pentamer and a hexamer. The shell with the lower energy per subunit is chosen, and the other shell is discarded. Quite interestingly, using the two aforementioned methods, we found qualitatively identical results. The phase diagram presented in Fig. 4 is obtained based on the latter method.
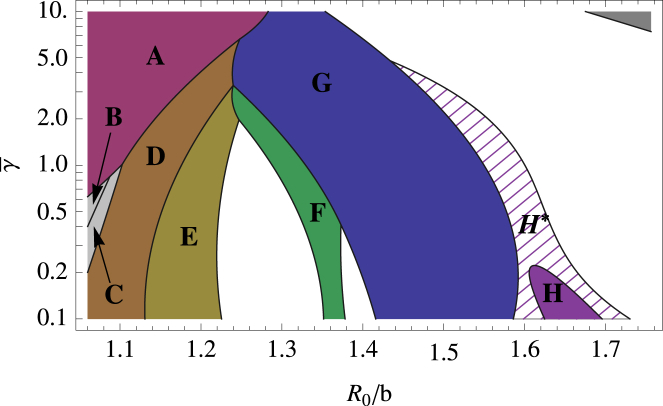
Figure 4.
Parameter space plot for the deterministic model showing the different kind of shells grown for values of the dimensionless parameters and R0/b0. (Dark-shaded contiguous regions, A–H) Regions where only a single type of symmetric shell is grown. These structures are shown in Figs. 5, 6, and 7. (Hashed region, H∗) Region where symmetric shell is found along with several similarly sized nonsymmetric shells. (Open areas) Regions in which different types of shells without any specific symmetry are grown. (Unlabeled dark-shaded region, upper-right corner of the plot with large FvK number and large spontaneous radius of curvature) Region in which no pentamers can be formed and the elastic sheet curves around to form a cylinder. To provide a consistent comparison between all symmetric shells, we illustrate them all using the same subunit; see Fig. A1. To see this figure in color, go online.
In addition to the deterministic simulations described above, we introduced stochasticity into the simulated growth. For the deterministic growth, each subunit is added to the location with the smallest opening angle, α. However, for the stochastic model, each position for addition of the next protein is weighted based on the following criteria: 1) the smallest opening angle is considered the most probable one; 2) opening angles within some range (α + σ) of the minimum are assumed to be about equally probable; and 3) opening angles much larger than the minimum should be very unlikely. A Gaussian-weighting function wi centered on the minimum angle, α with width σ, has all these properties, given as
| (3) |
with αi as the opening angle at the ith vertex along the exterior edge. The location of the new subunit is then randomly chosen from the list of possible vertices labeled index i, where the probability of choosing the ith vertex is proportional to the weight given in Eq. 3. In the stochastic model we still allow the shell to relax and reach its minimum elastic energy configuration after the addition of each subunit, and to choose between pentamers and hexamers in the same manner as in the deterministic model. It can be noted at this point that the deterministic model is simply the stochastic model in the limit as σ approaches zero. For nonzero σ, the stochastic nature of this second model allows for the possibility of multiple different shells to be grown from the same set of parameters.
Results and Discussion
We investigated the growth of shells as described in the previous section for several values of dimensionless parameters and 1.1 < R0/b0 < 1.8. As illustrated in Fig. 4, we found that over a large range of parameter space, only a few different structures formed. Most of these structures had high symmetry and were robust, insensitive to small changes in the subunit’s spontaneous radius of curvature or mechanical properties. The shaded regions labeled A–H in Fig. 4 correspond to the symmetric shells presented in Figs. 5, 6, and 7, respectively plotted with the subunits shown in Fig. 2, a–c. The reason we plotted the shells with different types of subunits will become clear below. All symmetric shells are shown together with the same type of subunit in Fig. A1 in the Appendix. The number of subunits ns and vertices N for each structure are given in the caption of Fig. A1.
To investigate the effect on the shell size of FvK number and the spontaneous radius of curvature, we studied in detail the growth of small shells for a fixed value of the FvK number and a range of spontaneous radius of curvatures. Note that the FvK number is the ratio of the stretching to bending modulus, and as such a large FvK number corresponds to a system in which the subunits significantly resist deformation from the shape of an equilateral triangle, while a small one corresponds to a system in which the subunits can be easily deformed.
The results of our simulations for an intermediate value of FvK number γ = 2 are plotted in Fig. 8, which shows the average radius of completed shells versus the spontaneous radius of curvature. The stair-step-like feature in Fig. 8 shows that there is a discrete set of shells, formed according to the spontaneous radius of curvature. In general for FvK numbers γ > 1.5, as the spontaneous radius of curvature increases, we observe discrete jumps from one symmetric shell type to another.
Figure 8.
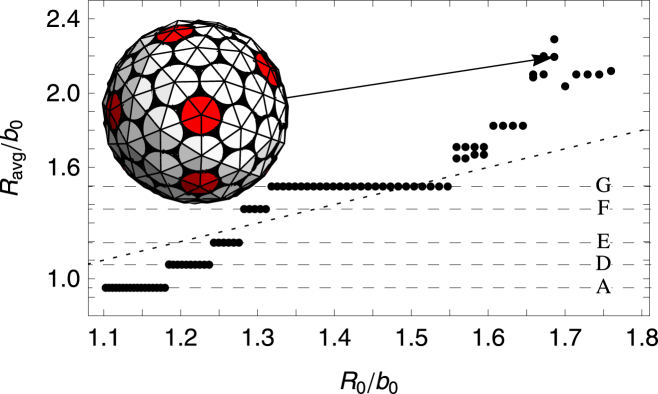
Plot of the average radius Ravg/b0, defined as the radius of gyration of the vertices of the shell, versus the spontaneous radius of curvature R0/b0. The FvK number is fixed at a smaller value of , which corresponds to a mildly flexible subunit. (Horizontal dashed lines) Average radius of the symmetric shells (A) and (D)–(G). It is possible to see a stair-step-like feature with each flat step corresponding to a single type of symmetric shell. With the exception of the shells (A) and (F), the corresponding shell types are all seen in the in vitro studies of empty clathrin coats. Representative shells are shown in Fig. 5. Note that the small radius of curvature of the shell (A) and the unreliable formation of shell (F) in the stochastic simulations could explain the absence of these shells in the experiments. To see this figure in color, go online.
Fig. 5 illustrates some of the structures associated with the labeled flat steps in Fig. 8 for γ = 2. These shells are similar to those observed in clathrin vesicles: the minicoat, the hexagonal barrel, the tennis ball, and the soccer-ball shells as illustrated in Fig. 5. The subunit of clathrin shells is a triskelion molecule, shown in the upper-left corner of Fig. 2b, whose legs bond antiparallel. While the molecules are relatively stiff, the long legs as well as the variability of the bond angle between the legs can lead to an intermediate FvK number γ = 2, and as a consequence, as seen in Fig. 5, a range of shells is grown.
The in vitro self-assembly studies of clathrin coats show that the size of cargo can modify the size of clathrin shells (4), explaining further the variability of the bond angle and the small FvK number. The smallest empty clathrin shell observed in the experiment is the so-called minicoat vesicle with 28 subunits, and not a dodecahedron with 20 subunits, which could be explained through the preferred spontaneous curvature between clathrin subunits.
Fig. 8 also shows that for FvK number γ = 2, as the spontaneous radius of curvature is increased, irregular shells without any underlying symmetry are assembled. An example of such a shell is shown in the inset of Fig. 8. The irregular shells in this regime are more spherical in comparison to those with a larger FvK number as discussed below, and the average radius of the completed shells closely matches the spontaneous radius of curvature of the subunits.
In contrast to clathrin vesicles and the shells obtained in theoretical simulations constructed from cones, spheres, or disks (7,11,24), which assemble into shells with different symmetries, viruses seem to only form structures with icosahedral symmetry in vivo. To explain this feature, we varied the FvK number and examined in detail its role on the shell symmetry. Our findings show that the FvK number can indeed restrict the set of symmetric shells allowed, and likely has some influence on the difference between shells appearing in viral capsids versus clathrin coats.
For a fixed large FvK number γ = 10, the size of shells grown as a function of the spontaneous radius of curvature is illustrated in Fig. 9. We find two large flat regions, where rather considerable changes in spontaneous radius of curvature have no effect at all on the size of shell. These two flat steps correspond to the shells A and G with icosahedral symmetry shown in Fig. 6. If the subunits are considered as capsid protein trimers, these correspond to T = 1 and T = 3 icosahedral shells based on the Caspar-Klug classification (see Fig. 6). As the spontaneous radius of curvature is increased R0/b > 1.38, we find that large irregular oblong and ellipsoidal shells form as illustrated in the inset to Fig. 9. If the spontaneous radius of curvature is increased even further, the formation of pentamers (which are required to form closed shells) is suppressed completely, and only rolled flat sheets are grown.
Figure 9.
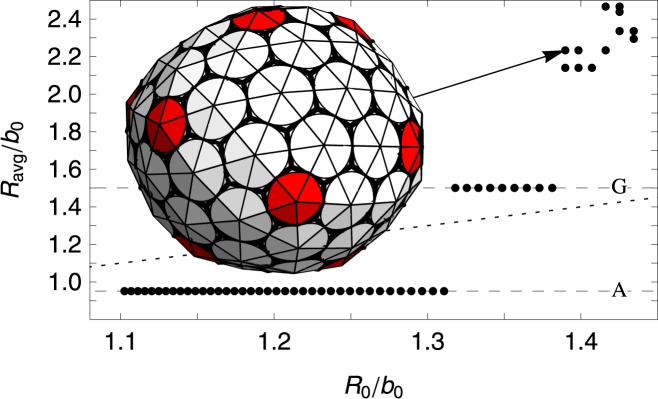
Plot of the average radius Ravg/b0 versus the spontaneous radius of curvature R0/b0. The FvK number is fixed at a large value of =10, corresponding to a very stiff subunit (difficult to deform). The two large flat regions seen in the plot correspond to small icosahedral-structure shell types (A) and (G) in Fig. 6. For spontaneous radius of curvatures larger than R0/b0 > 1.38, large nonsymmetric and nonspherical shells are grown; (inset) an example is given. To see this figure in color, go online.
Comparison of Figs. 8 and 9 shows that the more flexible subunits (lower FvK number) allow for a larger variety of shells to grow. In fact, Fig. 4 shows that for γ = 0.5 there exists a few more structures in addition to those associated with clathrin vesicles (γ = 2) or viral shells (γ = 10). These additional structures are plotted in Fig. 7. Interestingly, these shells were also observed in the molecular-dynamics simulation of conical particles (11) or spherical particles with convexity constraints (24) as explained in the Introduction. As the FvK number is decreased γ < 1.5, a new behavior emerges: the sharp transition between shell types (E) and (F) disappears, and if the FvK number is further decreased below γ < 0.4, the sharp transition between shell types (F) and (G) also disappears (see Fig. 10). In between these regions, small relatively spherical nonsymmetric shells, whose radii closely match the spontaneous radius of curvature, are grown.
Figure 10.
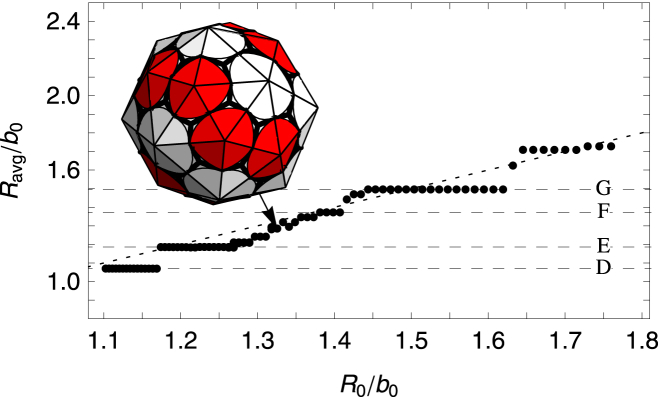
Plot of the average radius Ravg/b0 versus the spontaneous radius of curvature R0/b0. The FvK number is fixed at a small value of = 0.25 corresponding to a flexible subunit. (Horizontal dashed lines) Average radius of the symmetric shells (D–G) (see Fig. A1). (Dotted line) Where Ravg = R0. Note that between plateaus corresponding to shell types (E–G), there are several nonsymmetric shells whose average radius is closer to the spontaneous radius. (Inset) Example of a nonsymmetric shell. To see this figure in color, go online.
Our results illustrated in Figs. 4, 8, 9, and 10 clearly show that the small T = 1 and T = 3 icosahedral structures are robust and appear for all values of FvK numbers. The fact that most small spherical viruses only adopt T = 1 and T = 3 icosahedral structures, and not the other symmetric shells illustrated in Figs. 5 and 7, suggests that viral coat proteins for small viruses forming T = 1 and T = 3 structures should take on a rigid tertiary structure and be difficult to deform, as in the case of the γ < 10 structures illustrated in Fig. 9.
It is interesting to note that only at the smaller FvK numbers, , did we observe the ns = 80 icosahedral shell, corresponding to a T = 4 capsid in the Caspar-Klug classification (see Fig. 6). While icosahedral structures corresponding to ns = 20 and ns = 60 covered large areas of the parameter space in Fig. 4 and are still robust in the stochastic growth model (see below), the ns = 80 icosahedral shell only appeared in a small region of the phase space, and were not as robust. This might indicate that forming a T = 4 capsid with trimer subunits similar to those employed in our simulations is not feasible as it is for T = 4 structures or higher T numbers; here, the number of in-equivalent positions on the shell increases and it becomes almost impossible to form T > 3 made out of the rigid trimers associated with large FvK numbers.
In addition to the T = 4 structures, we found two other structures with ns = 80 subunits at intermediate FvK numbers, . However, these shells either displayed a fivefold D5 symmetry or no symmetry at all. The two nonicosahedral ns = 80 shells were not as spherical as the icosahedral one. The D5 structure (Fig. 7H∗), corresponding to the ns = 42 magic number shells also seen in Chen et al. (11,24), was slightly prolate spheroidal, while the completely nonsymmetric structure was ellipsoidal. Note that N = 42 icosahedral structures did not even appear in the simulations of Chen et al. (11,24); instead, they found the D5 shell mentioned above, and appeared in Zandi et al. (7) only if the overall system was under pressure.
In addition to the deterministic simulations, we studied the growth of shells for the stochastic model with the width of the distribution σ = 20° (see Eq. 3)—the smallest value of σ for which there is an appreciable difference between the stochastic and deterministic models. We found that the symmetric shells still reliably grow in the stochastic model in exactly the same regions in which they had appeared in the deterministic model, as shown in Fig. 11. This indicates that the stochastic choice of where to add the next subunit does not have a strong effect on the final structure of the symmetric shells. This is not, however, the case for the irregular shells corresponding to the open areas of Fig. 4. In these regions of parameter space for σ = 20°, multiple and new irregular shells were formed compared to the structures assembled in the deterministic model.
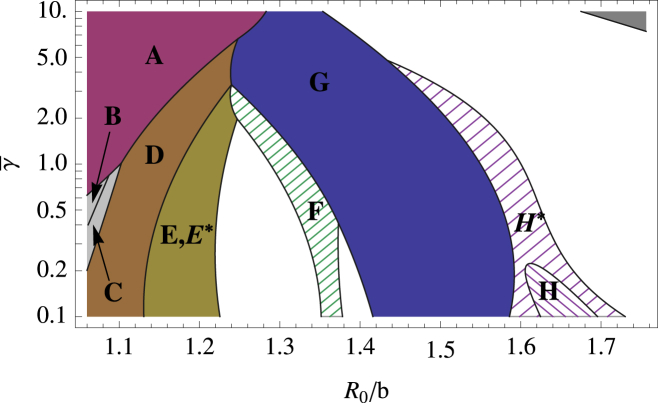
Figure 11.
Phase diagram for the stochastic model with σ = 20° showing the different kind of shells assembled for values of the dimensionless parameters and R0/b0. (Solid region) Despite the stochastic growth, only a single shell type is grown here. (Hashed region) Several similarly sized nonsymmetric shells are formed in addition to the symmetric shell. (Open areas) Regions where different types of shells without any regular symmetry are assembled. (Unlabeled dark-shaded area, upper-left corner of the plot with a large FvK number and large spontaneous radius of curvature) Region in which no pentamers can be formed and the elastic sheet curves around to form a cylinder. To see this figure in color, go online.
There were a few exceptions to the robustness of the assembly of symmetric shells in the stochastic model. Both the N = 27 (Fig. 7F) and T = 4 (Fig. 6H) shells were not reliably formed in the stochastic growth model in that, in addition to the symmetric structures, similar sized nonsymmetric shells were formed in the same region of parameter space. Further, one additional symmetric shell was observed in the stochastic model that did not appear in the deterministic one; the tennis-ball shell (Fig. 5E∗). The barrel (Fig. 5E) and tennis ball both have the same number of clathrin subunits, ns = 36, which consist of 12 pentagonal and 8 hexagonal faces. Shell (E), which is the only shell seen with ns = 36 in the deterministic simulation, contains two rings of six pentagons separated by a ring of six hexagons. Shell (E∗) has the 12 pentagons connected in a line that winds around the shell in the same manner as the seam on a tennis ball, and the eight hexagons lay in two patches of four. Note that both structures are observed in the experimental studies of assembly of clathrin coats (2).
If we keep increasing the width of the distribution in Eq. 3, σ, we will reach a regime in which more aberrant particles appear and the free-energy landscape becomes so large that it becomes almost impossible to extract any useful information with a limited number of simulations. That is why the focus of the article is on deterministic simulations that are supposed to follow the most probable assembly pathways, and thus create a meaningful representation of the final clathrin or capsid structures.
Remarkably, despite the nonequilibrium and stochastic assembly pathways, there are vast regions in the parameter space displaying shells with a high degree of symmetry (see Figs. 4 and 11). This is due to the interplay between spontaneous radius of curvature and response of the elastic triangular network to local stresses. The radius of curvature of a regular icosahedron made up of 20 triangular subunits is R0/b0 ≈ 0.915 while sheets made of only hexamers are perfectly flat with R0/b0 = ∞. For the range of R0 studied (1.1 < R0/b0 < 1.8) in this article, the introduction of a pentamer creates too much local curvature while the addition of a hexamer will induce too little curvature. Depending upon which type of capsomer creates more stress, we found that the local distortion tended to discourage the formation of similar capsomers in the immediate vicinity of each other. It is this effective repulsion that gives rise to the symmetric structures observed in different systems. Small spontaneous radius of curvature (R0/b0 < 1.3) promotes formation of pentamers and repulsion between hexamers, leading to the small shells with tetrahedral and dihedral symmetries. Larger R0/b0, on the other hand, favors formation of hexamers and repulsion between pentamers resulting in, for example, the ns = 60 and ns = 80 subunit shells with icosahedral symmetry.
For large values of spontaneous radius of curvature, we were indeed able to obtain similar results to the work of Hicks and Henley (6), Nguyen et al. (34), Levandovsky and Zandi (30), and Yu et al. (31), all of which used slightly different variants of the model studied in this work. For larger spontaneous radius of curvatures, we obtain mostly irregular capsids with many of the larger capsids displaying defects identical to those observed in Hicks and Henley (6). For large shells pertinent to retroviral shells and a fixed FvK number, we found a similar behavior to that seen in Levandovsky and Zandi (30), i.e., as spontaneous radius of curvature increases, the type of capsids formed changes from the irregular spheroidal capsids to larger irregular capsids, including cone-shaped structures and, finally, tube-shaped capsids.
Conclusions
In summary, we used a minimal nonequilibrium model to study the growth of nanostructures constructed with identical subunits. We found that large spontaneous curvatures between subunits lead to the growth of many small highly symmetric shells, consistent with those observed in nature. The formation of most of the symmetric shells is robust; they are formed over large areas of the parameter space despite the nonreversible and stochastic growth pathways used.
While the mechanical properties of the subunits, described by the single dimensionless FvK number, determines which set of shells is allowed to form as shown in Figs. 5, 6, and 7, the spontaneous radius of curvature determines the size of the shells. For fixed FvK number, the impact of spontaneous curvature on the size and structure of shells is demonstrated in Figs. 8, 9, and 10. These plots clearly indicate that the FvK number can explain why shells that formed from conical particles (11) or clathrin shells (2) display many more magic numbers than the shells formed from viral capsid proteins.
While a large implies that the subunits are difficult to deform from the preferred shape of an equilateral triangle, small implies more flexible subunits. The conical particles used in Chen et al. (11) do not have any explicit triangular symmetry; the underlying hexagonal symmetry only appears due to the close packing of circles in a plane (see Fig. 2). The lack of explicit triangular symmetry leads to a smaller FvK number , which allows for more diverse shells to be formed. The long legs and variability of the bonding angle of the triskelion molecules that make up clathrin shells results in a more flexible molecule, and thus a small FvK number compared to that of viral shells. In contrast to the conical particles employed in simulations and the triskelion molecules in clathrin shells, we expect the viral capsid proteins assume a large FvK number as they only form structures with icosahedral symmetry.
While the T = 1 and T = 3 icosahedra are the only symmetric shells seen at large γ-values, they are found over the full range of γ-values studied. For small values of FvK, in addition to structures with icosahedral symmetry, shells with other symmetries also form as the subunits can be stretched quite easily. The fact that we obtain T = 4 structures for small FvK is not surprising because the subunits must be somewhat flexible to deform to all four inequivalent positions. This could explain as noted above why our trimer system is not appropriate to obtain T > 3 for large FvK numbers.
Interestingly enough and consistent with our studies, many in vitro assembly experiments on icosahedral viruses show that a change either in capsid proteins through mutation or in the length of encapsidated genome modifies the size of the capsid but its symmetry is nevertheless preserved, i.e., a different T number with icosahedral symmetry forms. For example, the recent experiments performed on P22, a T = 7 virus, shows that while the mutant capsid proteins (E18C) of P22 form smaller procapsids, they still adopt structures with icosahedral symmetry, as T = 4 structures (35). The experimental and theoretical studies of Sun et al. (36) also show that as the size of the encapsulated gold nanoparticles increases, capsids with larger T numbers form. The same behavior has been observed in the self-assembly studies of CCMV capsid proteins with a linear anionic polymer (polystyrene sulfonate) (37) and with RNA (12) of different lengths. In these experiments, as the size of encapsulated PSS or RNA increases, the size of CCMV capsid increases from a pseudo T = 2 to T = 3 structure. Note that while in this article we do not explicitly take into account the impact of salt concentration, pH, or genome on the viral assembly, the interaction of genome or other anionic cargos with capsid proteins, pH, or salt concentration can modify protein’s spontaneous curvature and/or mechanical properties (FvK), leading to different structures with different symmetries (35–39). Obviously, if the change in the mutated capsid proteins, size of genome, or even concentration of protein subunits in solution is significant enough to completely drive the system out of equilibrium, other structures start to appear (40).
It is worth mentioning that while it is widely accepted that the shells with icosahedral symmetry constitute the lowest free-energy structures (7,11), our work shows that small highly symmetric shells can be reliably formed even under the very restrictive conditions of irreversible growth. We find that over a wide range of parameter space, growth following the local minimum free-energy path leads to shells identical to the symmetric minimum free-energy structures seen in equilibrium studies (7). A careful analysis of all the structures formed shows that in the range of curvatures studied in this article, the mismatch between the desired spontaneous radius of curvature and the local radius of curvature induced by a pentamer or hexamer tends to suppress the formation of similar types of capsomers in the vicinity of each other. This suppression tends to lead to the small shells being highly symmetric in nature. This effect seems to be short-ranged, which can explain both why larger clathrin vesicles display no symmetry and why larger viruses need scaffolding proteins or other mechanisms to form shells with icosahedral symmetry. While FvK equations can be solved in the absence of spontaneous curvature and give an estimate for the repulsion between pentamers (9), in the presence of spontaneous curvature, the highly nonlinear nature of equations makes solving these equations completely nontrivial.
Understanding the mechanisms and assembly pathways of formation of highly symmetric robust shells could have significant impact in the development of antiviral therapies and in design of novel biomimetic materials.
Author Contributions
J.W. wrote the simulation, performed research, performed analysis, and wrote the article; and R.Z. designed research, performed analysis, and wrote the article.
Acknowledgments
The authors thank Gonca Erdemci-Tandogan for many helpful discussions.
This work was supported by the National Science Foundation through grant No. DMR-1310687.
Editor: Markus Deserno.
Footnotes
Ten movies are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(15)00776-6.
Appendix A
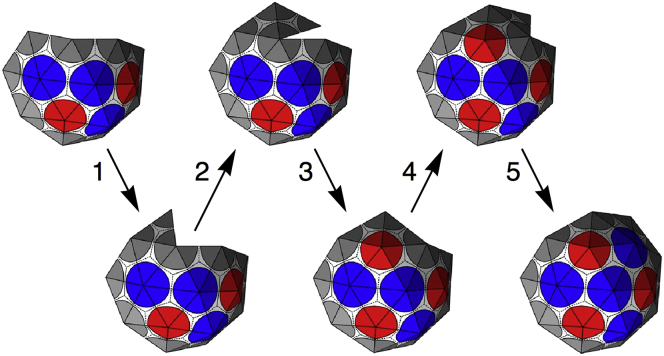
The symmetric shells assembled through the nonreversible addition of triangular subunits in our work found to match the symmetric structures in three disparate systems: viral capsids, clathrin coats, and theoretical simulations involving identical cone-shaped particles (1,2,11). The shells displayed in Figs. 5, 6, and 7 in the full article are plotted with the relevant subunits to each case to best show the match between our work and these systems. However, to provide a consistent comparison between all symmetric shells, we illustrate them all using the same subunit (see Fig. A1). As clearly revealed in the figure, as the size of shell increases, the strong repulsion between hexamers diminishes and repulsion between pentamers becomes stronger, leading to the shell with different symmetry type. Movies of the step-by-step growth of each shell are presented in the Supporting Material.
Fig. A2 demonstrates the steps taken in the assembly process by illustrating the snapshots of the growing shell. Most steps proceed through the addition of a new subunit to the edge with the smallest opening angle. This is the case for steps 1, 2, and 4. For steps 3 and 5, we see that there is a vertex on the edge with five subunits already attached, and a choice must be made to close into a pentamer (as done in step 3), or insert another subunit to form a hexamer (as done in step 5). This choice is made based on which capsomer, pentamer, or hexamer leads to a lower total energy per subunit for the shell.
Figure A2.
Step-by-step growth of the nanoshell shown by a series of snapshots. In steps 1, 2, and 4, a single new subunit is added at the location with the smallest opening angle. In step 3, the small opening wedge is closed without inserting another subunit, forming a pentamer. In step 5, a new subunit is inserted and bound along both edges, forming a hexamer. To see this figure in color, go online.
Supporting Material
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
References
- 1.Crick F.H.C., Watson J.D. Structure of small viruses. Nature. 1956;177:473–475. doi: 10.1038/177473a0. [DOI] [PubMed] [Google Scholar]
- 2.Crowther R.A., Finch J.T., Pearse B.M.F. On the structure of coated vesicles. J. Mol. Biol. 1976;103:785–798. doi: 10.1016/0022-2836(76)90209-6. [DOI] [PubMed] [Google Scholar]
- 3.Hogle J.M. A 3D framework for understanding enterovirus 71. Nat. Struct. Mol. Biol. 2012;19:367–368. doi: 10.1038/nsmb.2276. [DOI] [PubMed] [Google Scholar]
- 4.Fotin A., Cheng Y., Walz T. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 2004;432:573–579. doi: 10.1038/nature03079. [DOI] [PubMed] [Google Scholar]
- 5.Caspar D.L.D., Klug A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 1962;27:1–24. doi: 10.1101/sqb.1962.027.001.005. [DOI] [PubMed] [Google Scholar]
- 6.Hicks S.D., Henley C.L. Irreversible growth model for virus capsid assembly. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2006;74:031912. doi: 10.1103/PhysRevE.74.031912. [DOI] [PubMed] [Google Scholar]
- 7.Zandi R., Reguera D., Rudnick J. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA. 2004;101:15556–15560. doi: 10.1073/pnas.0405844101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bruinsma R.F., Gelbart W.M., Zandi R. Viral self-assembly as a thermodynamic process. Phys. Rev. Lett. 2003;90:248101. doi: 10.1103/PhysRevLett.90.248101. [DOI] [PubMed] [Google Scholar]
- 9.Lidmar J., Mirny L., Nelson D.R. Virus shapes and buckling transitions in spherical shells. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;68:051910. doi: 10.1103/PhysRevE.68.051910. [DOI] [PubMed] [Google Scholar]
- 10.Hagan M.F., Chandler D. Dynamic pathways for viral capsid assembly. Biophys. J. 2006;91:42–54. doi: 10.1529/biophysj.105.076851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chen T., Zhang Z., Glotzer S.C. Simulation studies of the self-assembly of cone-shaped particles. Langmuir. 2007;23:6598–6605. doi: 10.1021/la063755d. [DOI] [PubMed] [Google Scholar]
- 12.Cadena-Nava R.D., Comas-Garcia M., Gelbart W.M. Self-assembly of viral capsid protein and RNA molecules of different sizes: requirement for a specific high protein/RNA mass ratio. J. Virol. 2012;86:3318–3326. doi: 10.1128/JVI.06566-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ni P., Wang Z., Kao C.C. An examination of the electrostatic interactions between the N-terminal tail of the Brome Mosaic Virus coat protein and encapsidated RNAs. J. Mol. Biol. 2012;419:284–300. doi: 10.1016/j.jmb.2012.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lin H.K., van der Schoot P., Zandi R. Impact of charge variation on the encapsulation of nanoparticles by virus coat proteins. Phys. Biol. 2012;9:066004. doi: 10.1088/1478-3975/9/6/066004. [DOI] [PubMed] [Google Scholar]
- 15.Zlotnick A. To build a virus capsid. An equilibrium model of the self assembly of polyhedral protein complexes. J. Mol. Biol. 1994;241:59–67. doi: 10.1006/jmbi.1994.1473. [DOI] [PubMed] [Google Scholar]
- 16.Siber A., Zandi R., Podgornik R. Thermodynamics of nanospheres encapsulated in virus capsids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:051919. doi: 10.1103/PhysRevE.81.051919. [DOI] [PubMed] [Google Scholar]
- 17.Manoharan V.N., Elsesser M.T., Pine D.J. Dense packing and symmetry in small clusters of microspheres. Science. 2003;301:483–487. doi: 10.1126/science.1086189. [DOI] [PubMed] [Google Scholar]
- 18.Li C., Zhang X., Cao Z. Triangular and Fibonacci number patterns driven by stress on core/shell microstructures. Science. 2005;309:909–911. doi: 10.1126/science.1113412. [DOI] [PubMed] [Google Scholar]
- 19.ElSawy K.M., Taormina A., Vaughan L. Dynamical implications of viral tiling theory. J. Theor. Biol. 2008;252:357–369. doi: 10.1016/j.jtbi.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 20.Luque A., Reguera D., Bruinsma R. Physics of shell assembly: line tension, hole implosion, and closure catastrophe. J. Chem. Phys. 2012;136:184507. doi: 10.1063/1.4712304. [DOI] [PubMed] [Google Scholar]
- 21.Vernizzi G., Olvera de la Cruz M. Faceting ionic shells into icosahedra via electrostatics. Proc. Natl. Acad. Sci. USA. 2007;104:18382–18386. doi: 10.1073/pnas.0703431104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Vernizzi G., Sknepnek R., Olvera de la Cruz M. Platonic and Archimedean geometries in multicomponent elastic membranes. Proc. Natl. Acad. Sci. USA. 2011;108:4292–4296. doi: 10.1073/pnas.1012872108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fejer S.N., Chakrabarti D., Wales D.J. Emergent complexity from simple anisotropic building blocks: shells, tubes, and spirals. ACS Nano. 2010;4:219–228. doi: 10.1021/nn9013565. [DOI] [PubMed] [Google Scholar]
- 24.Chen T., Zhang Z., Glotzer S.C. A precise packing sequence for self-assembled convex structures. Proc. Natl. Acad. Sci. USA. 2007;104:717–722. doi: 10.1073/pnas.0604239104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Schwartz R., Shor P.W., Berger B. Local rules simulation of the kinetics of virus capsid self-assembly. Biophys. J. 1998;75:2626–2636. doi: 10.1016/S0006-3495(98)77708-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schwartz R., Garcea R.L., Berger B. “Local rules” theory applied to polyomavirus polymorphic capsid assemblies. Virology. 2000;268:461–470. doi: 10.1006/viro.1999.0180. [DOI] [PubMed] [Google Scholar]
- 27.Rapaport D.C. Self-assembly of polyhedral shells: a molecular dynamics study. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;70:051905. doi: 10.1103/PhysRevE.70.051905. [DOI] [PubMed] [Google Scholar]
- 28.Nguyen H.D., Reddy V.S., Brooks C.L., 3rd Deciphering the kinetic mechanism of spontaneous self-assembly of icosahedral capsids. Nano Lett. 2007;7:338–344. doi: 10.1021/nl062449h. [DOI] [PubMed] [Google Scholar]
- 29.Elrad O.M., Hagan M.F. Mechanisms of size control and polymorphism in viral capsid assembly. Nano Lett. 2008;8:3850–3857. doi: 10.1021/nl802269a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Levandovsky A., Zandi R. Nonequilibrium assembly, retroviruses, and conical structures. Phys. Rev. Lett. 2009;102:198102. doi: 10.1103/PhysRevLett.102.198102. [DOI] [PubMed] [Google Scholar]
- 31.Yu Z., Dobro M.J., Jensen G.J. Unclosed HIV-1 capsids suggest a curled sheet model of assembly. J. Mol. Biol. 2013;425:112–123. doi: 10.1016/j.jmb.2012.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Press, W. H., and S. A. Teukolsky, editors. 1992. Numerical Recipes in C—The Art of Scientific Computing, 2nd Ed., Chapt. 10, Section 6. Cambridge University Press, Cambridge, UK.
- 33.Whitelam S., Jack R.L. The statistical mechanics of dynamic pathways to self-assembly. Annu. Rev. Phys. Chem. 2015;66:143–163. doi: 10.1146/annurev-physchem-040214-121215. [DOI] [PubMed] [Google Scholar]
- 34.Nguyen T.T., Bruinsma R.F., Gelbart W.M. Continuum theory of retroviral capsids. Phys. Rev. Lett. 2006;96:078102. doi: 10.1103/PhysRevLett.96.078102. [DOI] [PubMed] [Google Scholar]
- 35.Cortines J.R., Motwani T., Teschke C.M. Highly specific salt bridges govern bacteriophage P22 icosahedral capsid assembly: identification of the site in coat protein responsible for interaction with scaffolding protein. J. Virol. 2014;88:5287–5297. doi: 10.1128/JVI.00036-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sun J., DuFort C., Dragnea B. Core-controlled polymorphism in virus-like particles. Proc. Natl. Acad. Sci. USA. 2007;104:1354–1359. doi: 10.1073/pnas.0610542104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hu Y., Zandi R., Gelbart W.M. Packaging of a polymer by a viral capsid: the interplay between polymer length and capsid size. Biophys. J. 2008;94:1428–1436. doi: 10.1529/biophysj.107.117473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sikkema F.D., Comellas-Aragonès M., Nolte R.J.M. Monodisperse polymer-virus hybrid nanoparticles. Org. Biomol. Chem. 2007;5:54–57. doi: 10.1039/b613890j. [DOI] [PubMed] [Google Scholar]
- 39.Salunke D.M., Caspar D.L., Garcea R.L. Polymorphism in the assembly of polyomavirus capsid protein VP1. Biophys. J. 1989;56:887–900. doi: 10.1016/S0006-3495(89)82735-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Katen S., Zlotnick A. The thermodynamics of virus capsid assembly. Methods Enzymol. 2009;455:395–417. doi: 10.1016/S0076-6879(08)04214-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)
The shell is presented with triangular subunits decorated with wedges in each corner, such that if the subunits are placed in a flat sheet, each vertex would be surrounded by a disk. (The wedges are colored gray, red, or blue, respectively, depending on whether the vertex is on the edge; or is in the interior as the locus of five subunits, i.e., part of a pentamer; or is in the interior as the locus of six subunits, i.e., part of a hexamer.)