Accurate Non-parametric Estimation of Recent Effective Population Size from Segments of Identity by Descent

Abstract

Existing methods for estimating historical effective population size from genetic data have been unable to accurately estimate effective population size during the most recent past. We present a non-parametric method for accurately estimating recent effective population size by using inferred long segments of identity by descent (IBD). We found that inferred segments of IBD contain information about effective population size from around 4 generations to around 50 generations ago for SNP array data and to over 200 generations ago for sequence data. In human populations that we examined, the estimates of effective size were approximately one-third of the census size. We estimate the effective population size of European-ancestry individuals in the UK four generations ago to be eight million and the effective population size of Finland four generations ago to be 0.7 million. Our method is implemented in the open-source IBDNe software package.

Introduction

The effective size of a population is defined with reference to an idealized random mating population that has similar random changes in allele frequencies over time to those occurring in the actual population. The effective size of the actual population is defined as the number of individuals in that idealized population.¹ Because of its effect on genetic drift, the effective population size affects the speed and effectiveness of selective forces.² In small populations, variants subject to weak negative selection have a non-negligible probability of drifting to high frequencies. This is why populations with a small historical effective population size, such as Finland,³ play an important role in the discovery of genetic variants that influence disease risk. In addition, estimates of historical effective population size reveal important demographic features, such as bottleneck events and rates of growth.^4,5

Demographic arguments suggest that in modern human populations, the effective size should be around one-third of the census size.⁶ However, existing genetics-based estimates are much lower. For example, a recent analysis of the site frequency spectrum (SFS) from sequence data on over 10,000 European-American individuals gave a current estimated effective population size of 1.1 million,^5,7 which is 0.5% of the census figure of 224 million white Americans (2010 US census; see Web Resources).

The SFS is an important tool for estimating effective population size, but several problematic issues surround its use. One issue is that it is difficult to make highly accurate genotype calls for alleles of very low frequency, especially in low-coverage sequence data, and this results in both false-negative and false-positive rare-variant calls. One way to get around this problem is to account for uncertainty when constructing the SFS,^8,9 although doing so relies on accurate assessment of uncertainty, which might be difficult to quantify. A second issue is that very large samples of sequenced individuals are required for accurately estimating recent population size from the SFS.⁵

Information in genetic data about effective population size comes from historical mutation events and also from historical recombination events. Approaches based on the ancestral recombination graph (ARG), such as the pairwise sequentially Markovian coalescent method,¹⁰ make use of both sources of information. However, because of computational constraints, they are limited to analysis of a small number of individuals,¹⁰ which restricts their ability to make inferences about the very recent past.¹⁰ A recently proposed method increases the number of haplotypes that can be analyzed to eight, allowing estimation of effective population size to extend up to 2,000 years, or approximately 70 generations, ago.¹¹

Many methods for inferring the history of effective population size, including those that use the SFS, take a parametric approach.¹² In a parametric approach, a class of models, parameterized, for example, by a recent growth rate and a time of commencement of growth, is considered across a grid of values for the parameters. Each such model is considered in turn, and the best-fit model is found. Uncertainty in the model fit can be addressed only with respect to the models that are considered. It is difficult to model complex or unanticipated features of population-size history with parametric methods because the user must pre-specify the class of models that are considered, and computational and statistical constraints limit the number of parameters that can be considered. For example, it is difficult to fully capture super-exponential growth with parametric methods.

Some parametric methods for inferring effective population size primarily use the information generated by historical recombination. These methods typically make use of the length of genomic segments that two individuals have inherited without recombination (identical by descent) from a common ancestor. Harris and Nielsen used sharing of identical-by-state haplotypes of length greater than 100 bp to estimate demographic history.¹³ Palamara et al. used inferred identity-by-descent (IBD) segments of length greater than 1 cM to estimate recent effective population size.⁴ Harris and Nielsen fit a piecewise constant effective population size, such that the fitted model for Europeans had size 13,000 for the past 6,000 years. Palamara et al. fit two periods of exponential growth or contraction separated by a founder event to their Ashkenazi Jewish data by using historical reports as well as model goodness of fit to guide their choice of model form.

In this study, we took a non-parametric approach and used inferred IBD segments with a length larger than a threshold. The threshold had to be large enough so that IBD segments were inferred with high power and a low false-positive rate. Consequently, the utilized IBD segments were relatively long and reflected recent demographic history. Thus, our method is designed to estimate recent effective population size. It cannot estimate ancient population size.

Our method is related to that of Palamara et al. in that it uses inferred IBD segments and relies on calculations based on the Wright-Fisher discrete-generation model.¹ However, the methods differ in the distributions that are estimated. Palamara et al. calculate the expected distribution of IBD-segment lengths given a parametrized demographic model. Our method calculates the expected distribution of the time to the most recent common ancestor (TMRCA) in generations, given an IBD-segment length. It uses the quantity of IBD assigned to each TMRCA to estimate the effective population size for that TMRCA. This fast and flexible approach frees our method from parametric constraints.

Our method is also related to Ralph and Coop’s method for estimating the age of IBD segments.¹⁴ Like Ralph and Coop, we fit a non-parametric model. However, our generalized expectation-maximization (EM) procedure for fitting the trajectory of the historical population size is very different from Ralph and Coop’s use of numerical optimization and penalized likelihoods to fit the coalescence-time distribution. Ralph and Coop do not directly estimate effective population size, but effective sizes can be obtained from their estimated coalescent rates.

Material and Methods

Overview of Estimation Procedure

We consider only detected IBD segments with an inferred genetic length (measured in cM) larger than a threshold.

We use an iterative, generalized EM algorithm.¹⁵ Our iterative approach is in the spirit of a standard EM approach, such that it has alternating steps that predict missing data and estimate parameters given the predicted complete data. However, our approach uses method-of-moments estimation rather than maximum-likelihood estimation. At each iteration, we start with a current estimate of the historical diploid effective population size, N = {N[g]; g = 0, 1, 2, …}, where g indexes the number of generations before the present. Initial values for N are generated with an auto-regressive model. We use the current estimate of N to estimate the observed and expected amounts of IBD due to the most recent common ancestors g generations before the present. We then fit a piecewise exponential growth function to the observed and expected amounts of IBD due to each generation to obtain an updated estimate of historical effective population size N.

We iterate this process of updating the estimate of N until convergence. We have found that 50 iterations are sufficient (data not shown). We repeat this iterative procedure by using multiple random initial values for the historical effective population size and then average the resulting estimated population sizes at each generation. We estimate confidence intervals for the effective population size at each generation from bootstrap samples.

The details of our estimation procedures are described below and in Appendix A.

Detecting IBD Segments

We used IBDseq¹⁶ version r1206 with default settings to infer IBD segments from real and simulated sequence and SNP array data. We used IBDseq rather than haplotype-based methods such as GERMLINE¹⁷ or RefinedIBD¹⁸ because switch errors in estimated haplotypes can cause haplotype-based methods to erroneously break long IBD segments into shorter sub-segments.

Filtering IBD Segments

We first applied a length filter that excluded IBD segments that were shorter than a threshold (typically 2 cM for sequence data and 4 cM for SNP array data). We used the HapMap recombination map¹⁹ to determine genetic distances in the non-simulated data. We then excluded genomic regions that had highly elevated levels of detected IBD. The excluded regions differed somewhat from one dataset to another, but they generally included some centromeres and telomeres, the major histocompatibility complex on chromosome 6, and the large chromosome 8 inversion. The excess IBD might be due to extended linkage disequilibrium in these regions. To identify regions with highly elevated levels of detected IBD, we first calculated the 3%-trimmed mean and 3%-trimmed SD for the number of IBD segments at 0.25 cM intervals in the genome. We then excluded genomic regions for which the number of IBD segments at a locus was more than 10 trimmed SDs from the trimmed mean. After excluding genomic regions with extreme amounts of IBD, we analyzed each remaining continuous chromosome interval as if it were a separate chromosome. We excluded any chromosome intervals that had a length less than 50 cM because inclusion of very short chromosome intervals in the bootstrap sampling could lead to higher bootstrap variability. For simplicity, we refer to each retained continuous chromosome interval as a chromosome in the following discussion.

Trimming Chromosome Ends

In the methodology described in Appendix A, we must account for whether an IBD segment reaches either end of the chromosome. For inferred IBD, it is not always clear whether the true underlying segment reaches the end of the chromosome. For example, the inferred IBD segment might end 1 kb from the end of the chromosome, whereas the true IBD might extend to the end of the chromosome. In comparing true and inferred IBD segments for simulated data, we found that when the true segment reached the end of the chromosome, the inferred segment almost always reached within 0.2 cM of the end of the chromosome. We thus trimmed 0.2 cM from each end of the chromosome after inferring IBD and removing regions with excess IBD. This reduced the total chromosome length and the lengths of some of the IBD segments. For example, an inferred segment starting at 0.1 cM started at 0.2 cM after trimming. We discarded any segments that were shorter than the threshold for IBD-segment length after trimming.

Removing Close Relatives

Full siblings create a problem for the analyses presented here because the IBDseq method that we used for detecting IBD assumes that individuals share zero or one identical-by-descent haplotype, and it does not consider the possibility that individuals share two pairs of haplotypes that are identical by descent, as occurs in full siblings. Hence, we chose to remove full siblings from the analysis. Full siblings have TMRCA = 1 for segments shared identically by descent through one of their parents, as do half siblings, so we removed all half siblings and closer relatives, and we did not directly estimate N[1]. Therefore, we estimated N[g] for g ≥ g^∗, where g^∗ = 2, and we extrapolated the exponential growth rate between N[3] and N[2] to estimate N[1] and N[0].

We can detect pairs of related individuals by using whole-genome rates of IBD-segment sharing.²⁰ In half siblings, the expected proportion of the genome covered by an IBD segment is 0.5, and there is variation around that value. We set the threshold of the IBD proportion at 0.4 and excluded all IBD segments for a pair of individuals if the sum of their IBD segment lengths exceeded this proportion of the genome. This filtering removed half siblings and closer relatives (full siblings and parent-offspring pairs). It also removed avuncular pairs (TMRCA = 1.5) but retained more-distant relative pairs.

Initial Values for N

We refer to the sequence of historical effective population sizes, N = {N[g]; g = 0, 1, 2, …}, as a trajectory. We simulated the log of the initial trajectory as an autoregressive model of order 1. This is the discrete time analog of an Ornstein-Uhlenbeck process and has the properties of being stationary and Markovian. We worked on the log scale because the effective population size is constrained below by 0. Because the effective population size in humans at the time of migration out of Africa is estimated to be approximately 10,000, our autoregressive process has a mean of log(N[g]) equal to μ = log(10,000) and a SD of log(N[g]) equal to σ = log(10,000)/10, which allows some variation around this mean, but not excessive levels. The parameter δ controls the degree of correlation between successive values, and we used δ = 0.02. Given the value of log(N[g − 1]), the value of log(N[g]) is (1 − δ)log(N [g − 1]) + Y, where Y is normally distributed with mean δμ and SD $\sqrt{1-{\left(1-\delta \right)}^2}\sigma$. This ensures that log(N[g]) also has a normal distribution with mean μ and SD σ.

Updating Estimates of N

We used the current estimate of N to estimate the observed and expected amounts of IBD due to the most recent common ancestors that are g generations before the present. We then fit a piecewise exponential growth function to these values to obtain an updated estimate of N. Complete mathematical details are presented in Appendix A.

Averaging Results from Multiple Random Starts

Averaging results from multiple random initial trajectories yields smoother and more accurate final estimates. We randomly generated 50 initial trajectories, and we used a harmonic mean to average the results. That is, if initial trajectory i has estimates ${\hat{N}}_i\left[g\right]$, the final estimate is

$$\hat{N}\left[g\right]=50/\sum _{i=1}^{50}1/{\hat{N}}_i\left[g\right].$$

We used a harmonic mean because ${\hat{N}}_i\left[g\right]$ is inversely proportional to the amount of observed IBD that is assigned to generation g.

Bootstrapping to Assess Uncertainty

We bootstrapped over chromosomes in order to assess precision of the estimated effective population sizes. For each bootstrap iteration, we resampled chromosomes with replacement. For each bootstrap iteration, we repeated the iterative process of estimating effective population sizes, including using 50 random initial trajectories. We performed 80 bootstrap replicates and used the 2.5^th and 97.5^th percentiles of the bootstrap values at each generation to obtain 95% confidence intervals.

Software

We implemented the above methods in a documented, open-source Java program called IBDNe (see Web Resources). The IBDNe program reads in IBD segments detected with the IBDseq program, filters IBD segments and genomic regions as described above, and reports an estimate and 95% confidence interval for the effective population size at generations g = 0, 1, 2, 3, …, G before the present generation, where G is a user-specified maximum number of generations. The software is parallelized to optimize computing times. Computing times for IBDNe are presented in the Results and were obtained on a 12-core 2.6 GHz computer with Intel Xeon E5-2630v2 processors running Red Hat Enterprise Linux release 6.6. For most datasets, computing times were approximately 30 min. These computing times did not include the time to run IBDseq to find the IBD segments.

Results

Simulated Data

We used simulated data to assess the number of past generations that can be accurately estimated from data with different marker densities and population histories.

We simulated three scenarios. In the first (“constant size”), the population had a constant size of 10,000. In the second (“exponential growth”), the population size was 10,000 until 150 generations ago and then grew at a rate of 3.07% per generation to a current size of 1,000,000. In the third (“super-exponential”), the population size was 10,000 until 100 generations ago and then grew at an increasing rate: 0.1% from generations 100 to 99, 0.2% from generations 99 to 98, 0.3% from generations 98 to 97, and so on. With this super-exponential growth rate, the population size g generations before the present is N = 10,000 × exp((101 − g)(100 − g)/2,000).

In all three scenarios, the mutation and recombination rates were 10⁻⁸ per bp, the genome size was 30 chromosomes of 100 Mb each (to approximate the total length of the human genome), and 1,000 diploid individuals were simulated. We used a coalescent-based simulator, MaCS²¹ version 0.5d, to generate the data; the MaCS command-line arguments are given in Table S1. We analyzed the output coalescent trees by using the DendroPy library²² to determine actual IBD status, interrogating the trees every 10 kb, and looking for segments over which the TMRCA remained constant for at least some minimum distance (2–4 cM for most of the experiments reported here).

We performed two sets of analyses, one with actual IBD segments and one with inferred IBD segments. Because the data are simulated under a coalescent model, the TMRCAs of the IBD segments can take fractional values. We verified that the expected rates of IBD are very similar between the Wright-Fisher model with TMRCA = g and the coalescent model with TMRCA between g − 0.5 and g + 0.5 (data not shown). When analyzing true IBD segments, we removed IBD segments with TMRCA less than 1.5 generations ago to match the removal of half siblings and closer relatives in the real data. When analyzing inferred IBD segments, we removed segments that overlapped a true IBD segment with TMRCA less than 1.5 generations ago.

We analyzed simulated SNP array and sequence data. The sequence data included all polymorphic variants. We obtained the SNP data by removing variants with a frequency less than 5%, and then we randomly selected and removed 90% of the remaining variants. This gave a final density of around 350,000 SNPs genome-wide in each scenario.

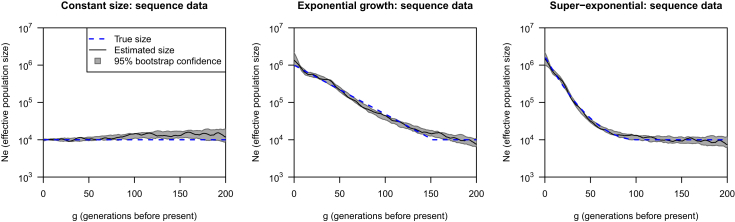
Figure 1 shows results for IBD inferred from simulated sequence data. We used a threshold of 2 cM because IBDseq has high power and precision for segments of length ≥ 2 cM in sequence data.¹⁶ (Other length thresholds are shown in Figure S1.) The lengths of the inferred IBD segments were almost unbiased (the mean difference between true and inferred IBD lengths was 0.06 cM), and the mean absolute difference between true and inferred IBD lengths for actual segments of length > 2 cM was 0.15 cM. Only 0.5% of the actual segments of length 2–2.1 cM were not found by IBDseq. The estimates of the effective population size from inferred IBD segments were similar to those obtained from the true IBD segments (Figure S2). Results for single random starts are shown in Figure S3 and demonstrate the need to average over multiple random starts to obtain more precise estimates.

Figure 1.

Estimating Effective Population Size by Using IBD Segments Inferred from Simulated Sequence Data by IBDseq

The threshold on inferred IBD length is 2 cM. Each plot shows a different simulation scenario (constant size, exponential growth, or super-exponential growth). The blue dashed line in each plot shows the true effective population size, the black line is the estimated effective population size, and the gray regions are bootstrap 95% confidence intervals. The y axes (effective population size) are plotted on a log scale.

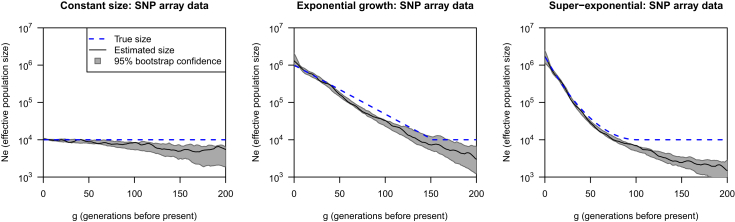
Figure 2 shows results for inferred IBD from moderate-density SNP data (350,000 SNPs genome-wide). Although IBDseq was designed for sequence data, we have found that it works quite well for SNP data in this context, provided that a sufficiently high IBD-length threshold is used. We used a threshold of 4 cM here. (Results for other thresholds are shown in Figure S4.) The lengths of the inferred IBD segments were almost unbiased (the mean difference between true and inferred IBD lengths was 0.02 cM), but the mean absolute difference between true and inferred IBD lengths for true IBD segments of length at least 4 cM was 0.28 cM, which is twice as high as for the sequence data. Only 0.8% of actual IBD segments of length 4–4.1 cM were not found by IBDseq. With the SNP data, there was some underestimation of effective population size, particularly for the more distant past (>50 generations ago). There were more true short segments than long ones, so added variability in length estimation resulted in more inferred segments passing the length threshold. In the growing population, the number of inferred segments of length at least 4 cM was 14% higher than the number of actual segments passing this threshold. This excess in inferred number of IBD segments resulted in underestimates of population size.

Figure 2.

Estimating Effective Population Size by Using IBD Segments Inferred from Simulated SNP Array Data by IBDseq

The threshold on inferred IBD length is 4 cM. The blue dashed line in each plot shows the true effective population size, the black line is the estimated effective population size, and the gray regions are bootstrap 95% confidence intervals. The y axes (effective population size) are plotted on a log scale.

Overall, the estimates track the true historical population sizes quite well, with two exceptions. First, if the population-size trajectory takes a sharp turn, the estimated trajectory over-smooths and misses the corner. The IBD segments cannot localize large changes in population size to a single generation. Second, in some cases, the estimated effective size oscillates somewhat around the true value. This is particularly evident in some scenarios with smaller sample sizes, such as 100 individuals (Figure S5). In most cases, the true effective size is contained within the bootstrap confidence interval; however, inferring changes in growth rates could be dangerous because such changes could reflect artifactual oscillation. The oscillation can occur when the information contained in the IBD segments cannot distinguish between an oscillating and smooth pattern of population change within a small window of generations. The issue of oscillation in the related context of estimating the distribution of coalescent times has been noted previously.¹⁴ Our strategy of fitting exponential growth curves to small windows of generations reduces the oscillation problem considerably, but its effects are still seen at low levels under some scenarios.

We also applied DoRIS (version 0.1.20130318), the software implementing the parametric method of Palamara et al.,⁴ with the actual IBD segments from the simulated data (Figure S6). We considered the two relevant inbuilt one-population models, which are constant size followed by a single expansion (exponential growth) and constant size followed by two periods of expansion with different growth rates. For each scenario, we chose parameter-value ranges that would allow the closest fit to the true values. Not surprisingly, DoRIS estimates effective sizes for the constant size and exponential growth scenarios very well.

For the super-exponential scenario, the single expansion model fit as well as possible given the single growth rate. The fit was slightly worse than that of our approach on the same data: DoRIS estimated the current size to be 1 million and the ancestral size to be 16,500 (the true current size is 1.56 million, and the true ancestral size is 10,000), and our method estimated the current size to be 1.47 million (95% confidence interval = 1.01–2.20 million) and the average ancestral size over generations 100–200 to be 8,900 (average 95% confidence interval = 7,200–10,800). DoRIS’s fitted double-expansion model had a significantly worse fit than its single-expansion model given that with five parameters rather than three, it was necessary to use a coarser grid of parameter values (see the Figure S6 legend for details).

DoRIS calculates a likelihood for each possible combination of the considered parameter values. For complex models, this leads to high computation times. We considered a grid of 30–40 values for each of the three parameters for DoRIS’s expansion model, resulting in 48,000 combinations, and computing times of 3–8 hr depending on the simulation scenario. All computation times are from a 2.6 GHz computer. For the five-parameter double-expansion model, we had to restrict attention to 10–11 values for each parameter, resulting in 110,000 combinations and computing times of 14–35 hr. Clearly, much more complex models are not computationally feasible with the current implementation of DoRIS. For example, in order to fit a different growth rate every eight generations (as we do with our method) for the past 200 generations, we would need 26 parameters, and even if we only considered five values for each (which is unlikely to be sufficient), we would need to consider over 10¹⁸ combinations. In contrast, fitting this model with an essentially unlimited number of possible values for each parameter took 13 min on a single computing core with our IBDNe software (without bootstrap replicates). When we included 80 bootstrap replicates to obtain confidence intervals, the computing time was 30 min on a 12-core computer.

Finland

We analyzed two Finnish datasets. The population of Finland has relatively low genetic diversity, attributable to a population bottleneck and isolation.³ Between 1750 and 1960, the population grew at an average annual rate of 1.13%, increasing its population 10-fold from 420,000 to 4.4 million over this period. After 1960, growth slowed somewhat, such that the population reached 5.5 million in 2013, representing an average growth rate of 0.39% per year since 1960 (census figures are from Statistics Finland; see Web Resources).

Northern Finland was sparsely populated until 300–500 years (10–17 generations) ago,²³ when migrants from elsewhere in Finland moved into the region, and population growth rates throughout Finland increased dramatically.³

The first Finnish dataset represents Finland as a whole and comprises 401 individuals diagnosed with amyotrophic lateral sclerosis (ALS [MIM: 105400; dbGaP: acphs000344.v1.p1]). The DNA for this study was collected between 1994 and 2008 from individuals who attended an ALS specialty clinic that receives referrals from neurologists throughout Finland.²⁴ The average age of these individuals was 57 years.²⁴ The genotypes were generated with Illumina SNP arrays. After we removed SNPs with more than 2% missing data, less than 1% minor allele frequency, or a Hardy-Weinberg equilibrium p value less than 10⁻⁴, 314,000 autosomal SNPs remained for analysis.

The second Finnish dataset is the 1966 Northern Finland Birth Cohort (NFBC) (dbGaP: phs000276.v1.p1). These genotype data are from 5,402 individuals whose mothers were living in the two northernmost provinces of Finland (Oulu and Lapland) and had expected delivery dates in 1966. The individuals were genotyped with an Ilumina HumanCNV370 array. We removed variants with a minor allele frequency < 2%, missing proportion > 2%, or Hardy-Weinberg p value < 10⁻⁵.

We used an IBD-length threshold of 6 cM. Estimated effective population sizes were similar with a 5 or 7 cM threshold, whereas results for a threshold of 4 cM had higher estimated population sizes for >30 generations in the past, indicating incomplete power to detect 4 cM segments (data not shown). Computing times were 11 min for ALS and 34 min for NFBC.

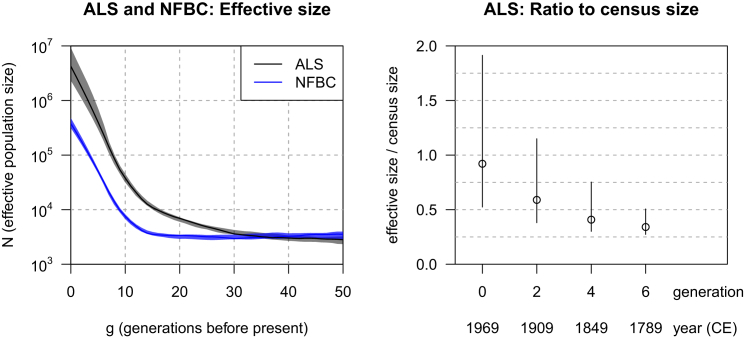
The left panel of Figure 3 shows the estimated history of the effective population sizes for the two samples. The estimated effective sizes (3,000) for both samples are similar for generations 30–50. The estimated effective size for the NFBC hovered around 3,000 until approximately 15 generations ago, at which point it began to grow at increasing rates. In contrast, growth of the estimated effective size began much earlier for the ALS sample. This difference is consistent with the late settlement of Northern Finland, whereby settlers came primarily from certain regions of Finland and thus had a smaller effective size than Finland as a whole at the time of settlement.

Figure 3.

Effective Population Size of Finland and Northern Finland

The left panel shows estimated effective sizes for the Finnish ALS cohort (black line) and the Northern Finnish NFBC (blue line). The threshold on inferred IBD length is 6 cM in both cases. Bootstrap 95% confidence intervals are shown as shaded regions (gray for ALS and blue for NFBC). The y axis is plotted on a log scale. Because the data are SNP data, only generations 0–50 are shown. The right panel shows the ratio of estimated effective size to census size (open circle) and bootstrap 95% confidence intervals (vertical lines). The effective sizes are from the ALS analysis, and the census sizes are for Finland for the years shown under the x axis.

The ALS sample might represent a somewhat random sample (except with respect to disease status) from Finland, if we assume that different regions of Finland have similar rates of the disease. The right panel of Figure 3 shows the ratio of the estimated effective size from the ALS cohort to the census size of Finland at selected time points. We chose to let the g = 0 generation correspond to the year in which the average age of the sample was 25, that is, in 1969. We assumed a 30 year generation time, so that, for example, the g = 2 generation corresponded to 1909.

We expect that the effective size will be several times smaller than census population sizes because of the inclusion of children and elderly individuals in the census, variance in reproduction rates, and other factors.²⁵ Demographic arguments based on one modern human population have suggested a ratio of effective size to census size of around one-third.⁶ The ratio was 0.34 (95% confidence interval = 0.27–0.51) for the g = 6 generation, 0.41 (95% confidence interval = 0.30–0.75) for the g = 4 generation, 0.59 (95% confidence interval = 0.38–1.15) for the g = 2 generation, and 0.92 (95% confidence interval = 0.52–1.91) for the g = 0 generation. Thus, the ratio matches expectation for the higher generations (4 and 6) but is too high for generation 0. It is likely that the effective size was overestimated at generations 0 and 2 because of the extrapolation of earlier growth rates to generations 0 and 1 and of the fitting of constant growth rates to groups of eight generations, both of which ignore a reduction in growth rates that occurred in the most recent generations. Finland’s per-year population growth rate averaged 1.4% between 1750 and 1850 (generations 4–7) but dropped to 0.9% between 1850 and 1950 (generations 1–4). Other factors, such as migration and changes in the variability of reproduction rates between individuals, might also affect the ratio.

The NFBC sample, being a birth cohort, should give a good representation of Northern Finland as it was in 1966. We compared the estimated effective size for the g = 0 generation to the census size of Northern Finland (Lapland, Kainuu, and North Ostrobothnia; the latter two regions compose the province of Oulu) in 1991, when the cohort individuals were 25 years old. The estimated effective population size for this generation was 380,000 (95% confidence interval = 327,000–459,000), whereas the census size was 648,000. This gives a ratio of 0.59 (95% confidence interval = 0.50–0.71). As well as the factors mentioned above for Finland as a whole, there might be significant migration in and out of Northern Finland, which would cause the effective size of this sample to represent more than just the individuals residing in the region at a given point in time. When looking at the effective population size in the more distance past, one must keep in mind that these estimated sizes apply to the ancestors of the current individuals, who include immigrants from other regions, rather than to only the population historically living in Northern Finland, which might have had a lower effective population size.

United Kingdom

We analyzed two datasets from the United Kingdom (UK): the UK10K sequence data and the Wellcome Trust Case Control Consortium 2 (WTCCC2) control group. Both datasets include only European-ancestry individuals living in the UK.

The UK10K sequence data that we analyzed consist of low-coverage sequence data on 1,927 individuals from the Avon Longitudinal Study of Parents and Children (ALSPAC) and 1,854 individuals from the TwinsUK cohort. The ALSPAC individuals are from the Bristol area, whereas the TwinsUK individuals are from throughout the UK. We downloaded the genotype data from the European Genome-phenome Archive (EGA) in April 2014 (release 20131101). We used only diallelic single-nucleotide variants from the autosomes, excluded variants that were monomorphic in either of the two cohorts, excluded variants with a Hardy-Weinberg p value < 10⁻⁶ in either of the two cohorts, and excluded variants with an average read depth of less than 2 per individual.

The WTCCC2 data that we analyzed consist of 5,200 individuals’ genotypes from a custom Illumina array with approximately 1.2 million variants.²⁶ The sample includes 2,699 individuals from the 1958 British Birth Cohort (58C) and 2,501 individuals from the National Blood Service (NBS) collection. All the individuals reside in Great Britain (England, Wales, and Scotland). We downloaded the data from the EGA in March 2011. We applied the WTCCC2 data-quality filters, which included removal of variants with a minor allele frequency < 1%, missing proportion > 2%, or Hardy-Weinberg p value < 10⁻²⁰.

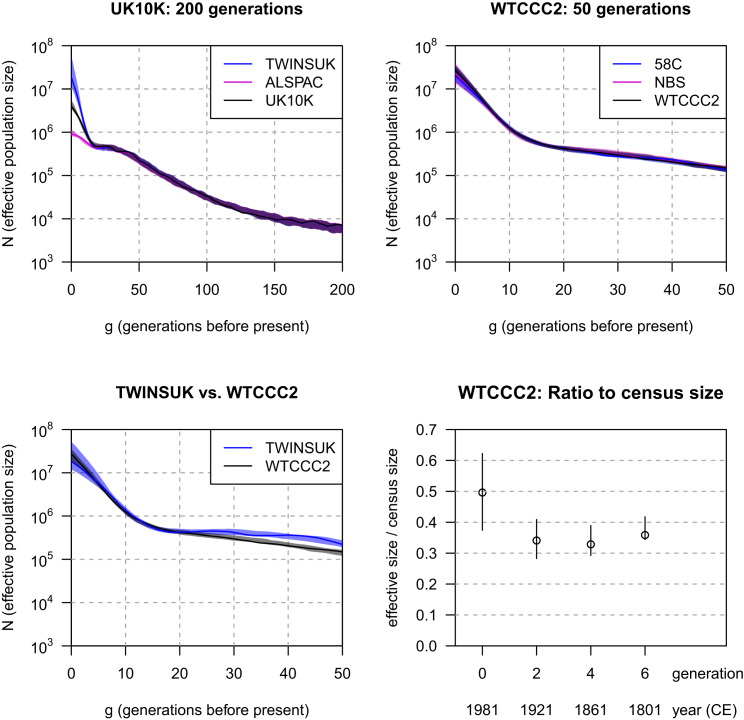
Shown in Figure 4, estimated effective population sizes for the UK10K and WTCCC2 data are based on IBD segments of length greater than 2 cM in the UK10K sequence data and greater than 4 cM in the WTCCC2 SNP data. Results with a 3 cM threshold in the UK10K data and with a 3 or 5 cM threshold in the WTCCC2 data are similar (data not shown). Computing times were 9 hr for the UK10K data and 27 min for the WTCCC2 data.

Figure 4.

Effective Size of the of UK Population

The threshold on IBD length is 2 cM for the UK10K sequence data and 4 cM for the WTCCC2 SNP array data. Estimated effective sizes are shown for 200 generations for the UK10K sequence data (upper left panel), whereas only 50 generations are shown for the WTCCC2 data (upper right panel) because they are derived from SNP array data. Bootstrap 95% confidence intervals are shown as shaded regions. The lower left panel overlays the results for the TWINSUK cohort with the results of the full WTCCC2 data. The lower right panel shows the ratio of estimated effective size to census size (open circle) and bootstrap 95% confidence intervals (vertical lines). The effective sizes are from the WTCCC2 analysis, and the census sizes are for Great Britain (England, Wales, and Scotland) for the years shown under the x axis.

The top left panel of Figure 4 shows estimated population sizes for the past 200 generations from the two UK10K samples, along with an estimate from the combined UK10K set. The ALSPAC cohort had a lower effective population size for the first 15 generations before the present. This is due to the localized sampling of the ALSPAC study in comparison to the nationwide sampling of the TwinsUK study. The effective population size around Bristol is less than that for the country as a whole because of limited migration in and out of this region over short time periods. The estimates for the combined UK10K data are intermediate between the estimates for the TwinsUK and ALSPAC cohorts.

The top right panel of Figure 4 shows the two WTCCC2 samples, along with an estimate from the combined WTCCC2 set. Only 50 generations are shown, given that the IBD was obtained from SNP array data. The concordance between the three sets of estimates is excellent.

One of the remarkable aspects of this analysis is the high degree of concordance between the estimates from the TwinsUK and WTCCC2 datasets. The lower left panel of Figure 4 shows estimates from TwinsUK against estimates from WTCCC2 for the past 50 generations. The estimates from these two samples are almost indistinguishable over this range of generations, particularly for generations 1–20. In generations 20–50, the estimates diverge slightly, such that the WTCCC2 estimates are lower because of the greater uncertainty in estimated lengths of IBD segments in the analysis of SNP data, as discussed above.

The confidence intervals for the combined WTCCC2 data are narrower than those for the TwinsUK cohort, because the sample size is much larger, so we used the estimates from the combined WTCCC2 in what follows. The estimated effective size for the g = 0 generation (for individuals born in or around 1958) is 27 million (95% confidence interval = 21–34 million). Because of extrapolation in a population with slowing growth rates, this estimate might be too high. As noted above with the Northern Finland results, the census size is expected to be several times larger than the effective population size. The lower right panel of Figure 4 shows the ratio of effective size to census size. A generation length of 30 years is assumed, whereby generation 0 corresponds to 1981, when the 58C individuals were 23 years old (census figures for the UK are provided at intervals of 10 years, so we could not use the year when this cohort was 25). The census figures include England, Wales, and Scotland (sources are A Vision of Britain through Time and the Office for National Statistics UK; see Web Resources). The estimated ratio was 0.36 (95% confidence interval = 0.34–0.42) for generation 6, 0.33 (95% confidence interval = 0.29–0.39) for generation 4, 0.34 (95% confidence interval = 0.28–0.41) for generation 2, and 0.49 (95% confidence interval = 0.37–0.62) for generation 0.

For comparison, we considered the UK results from Ralph and Coop.¹⁴ Ralph and Coop’s estimates were based on a smaller sample size (358 individuals from the UK). We obtained their estimates from the beige “smooth” curve of the top panel on page 81 of Figure S17 of their paper. Because the values are read from a figure rather than a table, they are approximate. Their results are presented in terms of the coalescence rate μ(g) = P(TMRCA = g). As we discuss in Appendix A,

$$P\left(\text{TMRCA}=g|\mathit{N}\right)=\frac{1}{2N\left[g\right]}\prod _{g^{\prime }=1}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right).$$

We can invert this to obtain

$$N\left[g\right]=\frac{1}{2\mu \left(g\right)}\prod _{g^{\prime }=1}^{g-1}\left(1-\mu \left(g^{\prime }\right)\right).$$

Because the estimated values of μ(g) are small for the UK (less than 10⁻⁵), we ignore the product term and use the simpler inversion N[g] = 1/(2μ(g)). We obtain the following trajectory: the effective size was greater than 4 million more than 3,900 years (130 generations) ago, dropped to 75,000 by 2,250 years (75 generations) ago, increased to over 4 million 1,380 years (46 generations) ago and stayed at over 4 million until 1,080 years (36 generations) ago, dropped to 250,000 around 660 years (22 generations) ago, and increased to stay at over 4 million for the most recent 420 years (14 generations). This trajectory is significantly more oscillatory than our estimates shown in Figure 4.

Discussion

We have presented a non-parametric method for estimating recent effective population size. In our analyses of data from Northern Finland and from the UK, results were consistent with the known history of these populations. In our analyses of simulated data, we found that even complex population histories with super-exponential growth rates can be estimated well. In contrast, the parametric approach implemented in the software DoRIS⁴ is constrained by computational feasibility to consider only simple parametric models with a handful of parameters, limiting its ability to flexibly estimate effective population size under complex population histories.

In our analyses, we used IBDseq¹⁶ to detect IBD segments. We verified through simulation that the IBD segments estimated with IBDseq result in accurate estimates of effective population size, as long as a sufficiently large length threshold is used on the IBD segments. The length threshold needs to be sufficiently large so that almost all actual IBD segments with a size exceeding the threshold are detected. For sequence data, we found that a threshold of 2 cM works well, whereas for SNP array data, a threshold of 3–6 cM is appropriate, depending on the SNP density. When SNP array data are used, uncertainty about IBD-segment endpoints results in an excess of segments exceeding the length threshold and hence an underestimation of effective population size more than 50 generations in the past. Thus, using SNP data allows one to estimate effective population sizes over the past 50 generations, or 1,500 years if the generation time is 30 years, with reasonable precision. With sequence data and a 2 cM threshold, one can estimate effective population sizes for the past 200 generations (6,000 years).

Unless the population is very small and the sample very large, IBD data contain little information about the most recent generation or two. For example, in a random mating population of effective size ten million, the chance that a randomly selected pair of individuals share a common grandparent (i.e., a most recent common ancestor two generations ago) is approximately 4²/10⁷. Thus, in a sample of 1,000 individuals, which has approximately 0.5 million pairs, one would expect 0.8 pairs of cousins, which is clearly not enough to be informative about the g = 2 generation. The chance that a randomly selected pair of individuals share a common great-grandparent is approximately 8²/10⁷, so 3.2 pairs of second cousins would be expected. Thus, it is difficult to estimate even the g = 3 generation in a population of this size, except by extrapolation of growth rates from earlier generations. Our method fits constant population growth over groups of eight generations, which enables estimation for the most recent generations if we assume that growth rates have stayed relatively constant over time. However, many human populations have undergone reductions in growth rates in the last few generations, as population densities have increased and birth-control methods have become more effective, so estimates for the most recent couple of generations should be interpreted with care.

IBD-segment data do not provide single-generation resolution in the estimation of historical effective population size because the probability distribution of the age of a segment given its length and the historical effective population size is quite wide. One consequence of this is that the iterative estimation procedure has a tendency to converge toward an oscillatory solution, in which the estimated effective population size oscillates between overly high and overly low. We were able to ameliorate this behavior by modeling the population-size history with piecewise exponential functions and by averaging results from multiple random starts. However, we found that some oscillatory behavior can still occur, particularly when the sample size is low. Although the bootstrap confidence intervals usually contain the true effective population size, the shape of the estimated trajectory might suggest growth-rate changes that are purely due to this artifactual oscillatory behavior. Thus, we caution against over-interpretation of apparent changes in growth rates over short timescales. An alternative approach to addressing the oscillation issue would be to use a penalized likelihood as in Ralph and Coop.¹⁴ However, examination of the estimates of coalescence rates from Figures S16 and S17 of Ralph and Coop’s paper indicates that their method gives significantly higher levels of oscillation than ours, albeit over longer timescales. Looking at the within-population results, we see that in almost all instances, the estimated coalescence rate increases significantly and then drops back (equivalently, the effective population size decreases substantially and then rises again) at least once across the 135 generations shown. Thus, the penalization approach employed by Ralph and Coop does not seem to be an adequate solution to the oscillation issue in the context of estimating effective population size.

Our approach works directly with inferred IBD segments. In contrast, the method of Harris and Nielsen¹³ skips detection of IBD segments and instead works directly with identical-by-state haplotypes as a proxy. A potential advantage of that approach is that one can examine shorter segments and hence look further back into the past. A disadvantage is that high-quality phased sequence, such as trio-phased high-coverage sequence data, is required. In Harris and Nielsen’s analyses, they used only one European trio (four parental haplotypes) and one African trio. As with the ARG-based methods¹¹ and SFS-based methods,⁷ the ability of IBD-based methods to estimate very recent effective population sizes is highly dependent on the sample size. In our results, we saw this phenomenon in the simulated data (200 versus 1,000 individuals) and UK datasets (2,000 versus 5,000 individuals). Harris and Nielsen did not infer changes in population size within the past several thousand years, and their final effective population size for Europeans was less than 20,000, whereas our estimate was over ten million for the UK.

The ability of our method to infer very recent effective population sizes is a major advantage over other methods. In previous human-population studies using demographic rather than genetic approaches, the ratio of effective population size to census size varied between 0.21 and 0.65.²⁷ However, many existing methods for estimating effective population size from genetic data yield estimates that are orders of magnitude smaller than the census size of the population from which the sample was drawn. In contrast, the ratio of our estimated effective population size four generations ago to the corresponding census size was 0.41 for Finland and 0.33 for the UK.

The sampled individuals are assumed to be a random sample from the population of interest. Our method appears to be robust to small deviations from this assumption. The UK NBS data might be somewhat non-random because certain sub-populations might be more or less likely to donate blood. Nonetheless, the NBS data gave essentially the same results as the 58C data. Similarly, the ALS sample from Finland is non-random with respect to disease status but is sufficiently representative of Finland’s population to give reasonable estimates. Although we focused on human populations, our method is also applicable to random samples from non-human diploid populations.

IBDseq assumes population homogeneity¹⁶ so that population-average allele frequencies are applicable to all pairs of individuals. Thus, we do not recommend the use of IBDseq in samples with multiple continental ancestries, including admixed populations. Other methods could also be used for detecting the IBD segments that are used in estimating the effective population size. We have found that haplotype-based methods such as Refined IBD¹⁸ are robust to admixture and other population heterogeneity (data not shown). However, for application to this problem, it is important that such methods allow for genotype error and haplotype phase error (if applicable) in order to avoid splitting large IBD segments into smaller pieces.

For application of this method, one must have moderately dense genome-wide genotype data for a random sample of at least several hundred individuals. In our analyses of human populations, we successfully analyzed three types of population samples: trait-based cohorts (TWINSUK and ALS) for which the ascertainment strategy uniformly covers the population of interest, birth cohorts (NFBC and 58C), and a blood-bank cohort (NBS).

Published: August 20, 2015

Appendix A: Details of the Estimation Procedure

Estimated Amount of Inferred IBD from Generation g

Let N = {N[g]; g = 0, 1, 2 …} be the current estimate of diploid effective population size (one-half of the effective number of haplotypes) at each generation g before the current generation. Let C be the minimum IBD-segment length in cM, and let G be the maximum number of generations over which we will compute the effective population size. G should be sufficiently large so that observing an IBD segment of size > C cM is very small if the common ancestor lived more than G generations ago. We will assume N[g] = N[G] for g > G. We also assume that all the IBD segments are from generation g^∗ or higher because of removal of IBD segments from close relatives. In the results, we use g^∗ = 2.

We define an IBD segment as a shared haplotype inherited identically by descent and unbroken by recombination. Consider a segment S, which is defined by its endpoints s₁ and s₂ and has an associated length l = s₂ − s₁, measured in cM.

If the TMRCA of S is g, there are g meioses from the most recent common ancestor to each of the two IBD haplotypes, and each meiosis has the potential for a crossover that would end the IBD segment. The probability distribution for l depends on whether we have selected S at random from a list of IBD segments discovered in the analyzed region or whether we have selected S at random from the set of IBD segments covering some specific position in the analyzed region. In the former instance, if we assume Haldane’s model for crossovers at each meiosis and assume that crossovers occur independently at each meiosis with rate 1/100 per cM, the distribution of l on a chromosome of infinite length is exponential with rate 2g/100 = g/50 per cM. In the latter instance, where S is selected from IBD segments covering some specific position on the chromosome, the distribution is different. Random longer segments are more likely than random shorter segments to cover the specified position; thus, the expected value of l is higher. If we assume Haldane’s model again, on a chromosome of infinite length, the distribution of the l of S on each side of the specified position is exponential with rate g/50 per cM, and thus the total l is Erlang with rate g/50 per cM and shape 2.⁴

We can also calculate the probability of IBD at a specified position for a randomly chosen pair of haplotypes. Under the Wright-Fisher model, the probability that two haplotypes sampled from the current population have a TMRCA of one generation is 1/(2N[1]). To see this, condition on the parental haplotype inherited by the first sampled haplotype. The parental haplotype inherited by the second sampled haplotype is chosen at random from the 2N[1] haplotypes in the population at generation 1. Similarly, the probability that two haplotypes sampled from the current population have a TMRCA of two generations is the product of the probability that they don’t have a TMRCA of one generation and the probability that the two inherited parental haplotypes at generation 1 are inherited from a common grandparental haplotype at generation 2. Taking this further, the probability of a TMRCA of g generations is⁴

$$P\left(\text{TMRCA}=g|\mathit{N}\right)=\frac{1}{2N\left[g\right]}\prod _{g^{\prime }=1}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right).$$

Because we don’t estimate N[g] for g < g^∗, we assume that N[g] is large enough so that 1 − 1/(2N[g]) is approximately equal to 1 for g < g^∗. Then,

$$P\left(\text{TMRCA}=g|\mathit{N}\right)=\frac{1}{2N\left[g\right]}\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right).$$ Equation A1

Thus, given a segment S with endpoints s₁ and s₂, we can calculate the distribution of its TMRCA by using Bayes rule:

$$P\left(\text{TMRCA}=g|s_1,s_2,\mathit{N}\right)=\frac{P\left(s_1,s_2\text{|TMRCA}=g,\mathit{N}\right)P\left(\text{TMRCA}=g|\mathit{N}\right)}{P\left(s_1,s_2|\mathit{N}\right)}.$$ Equation A2

The distribution P(s₁, s₂ | TMRCA = g, N) depends on whether the IBD segment reaches the ends of the chromosome. We show how to calculate this probability below.

The amount of IBD from S that can be attributed to a TMCRA of g generations is then

$$(s_2-s_1)\mathit{P}(\text{TMRCA}=\mathit{g}\text{|}{\mathit{s}}_1\text{,}{\mathit{s}}_2\text{,}\mathit{N})\text{.}$$

If we index IBD segments by j and sum over all IBD segments with length l = (s₂ − s₁) greater than the threshold C, the total amount of IBD attributable to a TMRCA of g is

$$\sum _{j}l\left(j\right)P\left(\text{TMRCA}=g|s_1\left(j\right),s_2\left(j\right),\mathit{N}\right).$$ Equation A3

Below, we provide equations for the amount of an IBD segment attributable to each TMRCA while conditioning on the observed length of the segment and the number of segment ends that reach the end of the chromosome.

When probabilistically allocating an IBD segment to each TMRCA, it is helpful to consider a specific point h on the chromosome. We first consider an observed IBD segment S that covers position h and that is interior to the chromosome (0 < s₁ < h < s₂ < L).

We want to estimate the probability that the most recent common ancestor corresponding to our IBD segment is at generation g (i.e., TMRCA = g), given that the segment with observed endpoints s₁ and s₂ is randomly chosen from segments covering h. Conditioning on the TMRCA and the fact that the segment covers h, we can consider s₁ and s₂ to be random variables. Similarly, conditioning on the observed segment endpoints, we can consider the TMRCA to be a random variable. With Equation A2,

$$P\left(\text{TMRCA}=g\text{|}{s}_1,s_2,h,\mathit{N}\right)\propto P\left(s_1,s_2\text{|TMRCA}=g,h,\mathit{N}\right)P\left(\text{TMRCA}=g\text{|}h,\mathit{N}\right)=P\left(s_1\text{|TMRCA}=g,h,s_1<h\right)P\left(s_2\text{|TMRCA}=g,h,s_2>h\right)P\left(\text{TMRCA}=g\text{|}\mathit{N}\right).$$

In the above equation, probability densities and discrete probabilities are both represented by P, and the symbol ∝ means “is proportional to.”

Conditional on TMRCA = g, h − s₁ is distributed exponentially with rate 2g/100 = g/50 per cM, and thus

$$P\left(s_1|\text{TMRCA}=g,h,s_1<h\right)=\text{exp}\left(-\left(h-s_1\right)g/50\right)\left(g/50\right).$$

Similarly,

$$P\left(s_2|\text{TMRCA}=g,h,s_2>h\right)=\text{exp}\left(-\left(s_2-h\right)g/50\right)\left(g/50\right).$$

Thus,

$$P\left(s_1\text{|TMRCA}=g,h,s_1<h\right)P\left(s_2\text{|TMRCA}=g,h,s_2>h\right)=\left(\frac{g}{50}\right)\exp \left(-\frac{(h-s_1)g}{50}\right)\left(\frac{g}{50}\right)\exp \left(\frac{-(s_2-h)g}{50}\right)={\left(\frac{g}{50}\right)}^2\exp \left(-\frac{\left(s_2-s_1\right)g}{50}\right)={\left(\frac{g}{50}\right)}^2\exp \left(-\frac{lg}{50}\right).$$

Note that this probability does not depend on the particular value of h.

Using the distribution of the TMRCA from Equation A1, we have

$$P\left(\text{TMRCA}=g\text{|}l,h,\mathit{N},0<s_1<h<s_2<L\right)=\frac{1}{{\gamma }_0\left(l,N\right)}{\left(\frac{g}{50}\right)}^2\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]},$$

where the constant of proportionality ${\gamma }_0\left(l,N\right)$ is

$${\gamma }_0\left(l,N\right)=\sum _{g=g^{\ast }}^{\infty }{\left(\frac{g}{50}\right)}^2\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}=\sum _{g=g^{\ast }}^G{\left(\frac{g}{50}\right)}^2\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}+\sum _{g=G+1}^{\infty }{\left(\frac{g}{50}\right)}^2\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}.$$

The left summand can be calculated directly. If G is sufficiently large, the right summand is approximately 0. However, because N[g] = N[G] for g ≥ G, the right summand has a closed-form solution. If we let α = l/50 and β = 1− 1/(2N[G]), the right summand is

$$\begin{array}{l}\sum _{g=G+1}^{\infty }{\left(\frac{g}{50}\right)}^2\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^{g-1}\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{1}{2N\left[g\right]}\\ =\sum _{g=G+1}^{\infty }\frac{g^2\left(1-\beta \right)e^{-\alpha g}}{2500}\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^{g-1}\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\\ =\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^G\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{2500}\sum _{g=G+1}^{\infty }{g}^2{e}^{-\alpha \left(g-G-1\right)}{\beta }^{g-G-1}\\ =\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^G\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{2500}\sum _{j=0}^{\infty }{\left(j+G+1\right)}^2{\left(\beta e^{-\alpha }\right)}^j\\ =\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^G\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{2500}\sum _{j=0}^{\infty }\left(G^2+\left(2G-1\right)(j+1)+(j+1)(j+2)\right){\left(\beta e^{-\alpha }\right)}^j\\ =\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^G\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{2500}\left(\frac{G^2}{1-\beta e^{-\alpha }}+\frac{2G-1}{{\left(1-\beta e^{-\alpha }\right)}^2}+\frac{2}{{\left(1-\beta e^{-\alpha }\right)}^3}\right).\end{array}$$

The last step uses the equalities ${\sum }_{j=0}^{\infty }{r}^j=1/\left(1-\text{r}\right)$, ${\sum }_{j=0}^{\infty }\left(j+1\right)r^j=1/{\left(1-\text{r}\right)}^2$, and ${\sum }_{j=0}^{\infty }\left(j+1\right)\left(j+2\right)r^j=2/{\left(1-\text{r}\right)}^3$, which hold for 0 < r < 1.

Thus,

$${\gamma }_0\left(l,N\right)=\sum _{g=g^{\text{∗}}}^G{\left(\frac{g}{50}\right)}^2\text{exp}\left(-\frac{lg}{50}\right)\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^{g-1}\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{1}{2N\left[g\right]}+\left(\prod _{g^{\text{′}}=g^{\text{∗}}}^G\left(1-\frac{1}{2N\left[g^{\text{′}}\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{2500}\left(\frac{G^2}{1-\beta e^{-\alpha }}+\frac{2G-1}{{\left(1-\beta e^{-\alpha }\right)}^2}+\frac{2}{{\left(1-\beta e^{-\alpha }\right)}^3}\right).$$

Similarly, we can consider a segment that is truncated by one end of the chromosome. Again, write s₁ and s₂ for the positions of the endpoints of the segments, but now either s₁ = 0 or s₂ = L. For concreteness, assume s₁ = 0. Our probability distributions for the length of the IBD segment assume a chromosome of infinite length. Conceptually, we can imagine that we do have a chromosome of infinite length and that on this chromosome, the true IBD segment has left end point $s_1^{\prime }\le 0$. Because the analyzed region doesn’t include the positions to the left of 0, we do not observe $s_1^{\prime }$, but the fact that s₁ = 0 implies that $s_1^{\prime }\le 0$. Thus, we can calculate

$$P\left(\text{TMRCA}=g\text{|}{s}_1,s_2,h,\mathit{N},0=s_1<h<s_2<L\right)=P\left(\text{TMRCA}=g\text{|}{s}_1^{\text{′}}\le 0,s_2,h,\mathit{N}\right)\propto P\left(s_1^{\text{′}}\le 0\text{|TMRCA}=g,h\right)P\left(s_2\text{|TMRCA}=g,h\right)P\left(\text{TMRCA}=g\text{|}\mathit{N}\right)=P\left(\left(h-s_1^{\text{′}}\right)\ge h\text{|TMRCA}=g,h\right)P\left(s_2\text{|TMRCA}=g,h\right)P\left(\text{TMRCA}=g\text{|}\mathit{N}\right)=\exp \left(-\frac{hg}{50}\right)\left[\left(\frac{g}{50}\right)\exp \left(-\frac{\left(s_2-h\right)g}{50}\right)\right]P\left(\text{TMRCA}=g\text{|}\mathit{N}\right)=\left(\frac{g}{50}\right)\text{exp}\left(-\frac{(s_2-s_1)g}{50}\right)P\left(\text{TMRCA}=g\text{|}\mathit{N}\right)=\left(\frac{g}{50}\right)\text{exp}\left(-\frac{lg}{50}\right)P\left(\text{TMRCA}=g\text{|}\mathit{N}\right).$$

Thus,

$$P\left(\text{TMRCA}=g\text{|}l,h,\mathit{N},0=s_1<h<s_2<L\right)=\frac{1}{{\text{γ}}_1\left(l,\mathbf{N}\right)}\left(\frac{g}{50}\right)\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]},$$

where

$${\gamma }_1\left(l,N\right)=\sum _{g=g^{\ast }}^G\left(\frac{g}{50}\right)\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}+\sum _{g=G+1}^{\infty }\left(\frac{g}{50}\right)\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}.$$

As for γ₀, the left summand can be calculated directly, and because N[g] = N[G] for g ≥ G, there is a closed form for the right summand. Letting α = l/50 and β = 1 − 1/(2N[G]), one can show (similarly as for γ₀) that

$${\gamma }_1\left(l,N\right)=\sum _{g=g^{\ast }}^G\left(\frac{g}{50}\right)\text{exp}\left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}+\left(\prod _{g^{\prime }=g^{\ast }}^G\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{50}\left(\frac{G}{1-\beta e^{-\alpha }}+\frac{1}{{\left(1-\beta e^{-\alpha }\right)}^2}\right).$$

The same formula holds for P(TMRCA = g | l, h, N, 0 < s₁ < h < s₂ = L) when the right end point of the IBD segment is censored by the end of the chromosome.

Similarly, if the IBD segment covers the whole region and is thus censored at both ends (s₁ = 0 and s₂ = L), we consider the conceptual uncensored end points $s_1^{\prime }<0$ and $s_2^{\prime }>L$ to calculate the following:

$$P\left(\text{TMRCA}=g\text{|}{s}_1,s_2,h,\mathit{N}\right)=P\left(s_1^{\prime }<0,s_2^{\prime }>L\text{|TMRCA}=g,h\right)=\text{exp}\left(-hg/50\right)\text{exp}\left(-(L-h)g/50\right)=\text{exp}\left(-\frac{Lg}{50}\right)=\text{exp}\left(-\frac{lg}{50}\right).$$

Thus,

$$P\left(\text{TMRCA}=g\text{|}l=L,h,\mathit{N}\right)=\frac{1}{{\text{γ}}_2\left(l,\mathbf{N}\right)}\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=1}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]},$$

where

$${\text{γ}}_2\left(l,\text{N}\right)=\sum _{g=g^{\ast }}^G\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}+\sum _{g=G+1}^{\infty }\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}.$$

As for γ₀ and γ₁, the left summand can be calculated directly, and because N[g] = N[G] for g ≥ G, there is a closed form for the right summand. Letting α = l/50 and β = 1 − 1/(2N[G]), one can show (similarly as for γ₀) that

$${\text{γ}}_2\left(l,\text{N}\right)=\sum _{g=g^{\ast }}^G\exp \left(-\frac{lg}{50}\right)\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}+\left(\prod _{g^{\prime }=g^{\ast }}^G\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{\left(1-\beta \right)e^{-\alpha \left(G+1\right)}}{1-\beta e^{-\alpha }}.$$

Binning by IBD Length to Reduce Computation Time

The probabilistic assignment of segments to TMRCAs depends only on the length l = s₂ − s₁ of the segment and the number of segment ends that reach the end of the chromosome. In our analyses, we binned the observed IBD segments by their length and number of ends reaching the end of the chromosome and calculated P(TMRCA = g | l, N) only once for each bin. We used bins with a length range of 0.05 cM, and we used the midpoint of the range as the length in our calculation.

Expected Amount of IBD from Generation g

We also need to calculate the expected amount of IBD due to most recent common ancestry g generations ago as a function of N. The probabilities in this section do not condition on data, but they do assume that historical effective population sizes are known for each generation before the present.

Let n_P be the number of pairs of haplotypes considered. If the sample of interest contains n_I diploid individuals, then the number of pairs of haplotypes where each haplotype is from a different individual is n_P = (2n_I)(2n_I − 2)/2. We consider pairs of distinct individuals because we are not considering homozygosity by descent (IBD between the two haplotypes within an individual).

If we consider an IBD segment covering a certain position on a chromosome of infinite length, as noted above, the length, l, of the segment is Erlang with rate g/50 and shape 2. Thus,

$$P\left(l>C\text{|TMRCA}=g\right)=\left(\frac{Cg}{50}+1\right)e^{-Cg/50}$$

and

$$P\left(l>C,\text{TMRCA}=g\right)=P\left(\text{TMRCA}=g\right)P\left(l>C|\text{TMRCA}=g\right)=\frac{1}{2N\left[g\right]}\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\left(\frac{Cg}{50}+1\right)e^{-Cg/50}.$$

If we integrate over all positions on an analyzed chromosome with length L cM and consider IBD from n_P pairs of haplotypes, the expected amount of IBD of length > C cM with TMRCA = g is

$$n_{P}LP\left(l>C,\text{TMRCA}=g\right)=n_{P}L\frac{1}{2N\left[g\right]}\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\left(\frac{Cg}{50}+1\right)e^{-Cg/50}.$$ Equation A4

Segments that occur at the ends of the analyzed chromosomes might be censored by the chromosome end, and thus the observed length might not meet the length threshold. For censoring at the left end of the chromosome, consider focal position h < C, and consider an IBD segment containing h with right end point s₂ < C (and thus with observed length < C cM). The probability that the segment has conceptual end point $s_1^{\prime }<s_2-C$ (and thus with conceptual length > C cM) is

$$P\left(s_1^{\prime }<s_2-C\text{|}{s}_1^{\prime }<h<s_2\right)=P\left(h-s_1^{\prime }>h-s_2+C\right)=e^{-\left(h-s_2+C\right)g/50}.$$

Thus, the probability that an IBD segment containing h has right end point s₂ < C (observed length < C) and conceptual left end point $s_1^{\prime }<s_2-C$ (conceptual length > C cM) is

$$\underset{h}{\overset{C}{\int }}P\left(s_2\right)P\left(s_1^{\prime }<s_2-C\right)d{s}_2=\underset{h}{\overset{C}{\int }}\frac{g}{50}{e}^{-\left(s_2-h\right)g/50}{e}^{-\left(h-s_2+C\right)g/50}d{s}_2=\underset{h}{\overset{C}{\int }}\frac{g}{50}{e}^{-Cg/50}d{s}_2=\left(C-h\right)\frac{g}{50}{e}^{-Cg/50}.$$

Integrating this over values of h < C and multiplying by the probability of IBD with TMRCA = g and by the number of pairs of haplotypes allow us to determine how much IBD in the region needs to subtracted from the total given in Equation A4. The amount to be subtracted as a result of censoring at this end of the chromosome is thus

$$n_P\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}\underset{0}{\overset{C}{\int }}\left(C-h\right)\frac{g}{50}{e}^{-Cg/50}dh=n_P\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}\frac{C^{2}g}{100}{e}^{-Cg/50}.$$

Doubling this to account for both ends of the region and subtracting from the expected amount of IBD when endpoint censoring is ignored in Equation A4, we obtain the following expectation for the amount of IBD with TMRCA = g and observed length > C cM on a single chromosome of length L:

$$n_P\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}\left\{\left(\frac{Cg}{50}+1\right)L-\frac{C^{2}g}{50}\right\}{e}^{-Cg/50}.$$

We obtain the expected amount of IBD with TMRCA of g generations from K chromosomes of lengths L_k (k = 1, 2, …, K) by summing the expected amounts from each chromosome:

$$n_P\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}{e}^{-Cg/50}\sum _{k=1}^K\left\{\left(\frac{Cg}{50}+1\right)L_k-\frac{C^{2}g}{50}\right\}.$$ Equation A5

Updating the Estimate of Historical Effective Population Size N[g]

We first show how to update the estimate of N[g] without the constraint of a piecewise exponential trajectory. By considering $\left\{N\left[g^{\prime }\right]:g^{\prime }=g^{\ast },\dots ,g-1\right\}$ to be fixed at their previous estimated values, we can equate the expected and observed values obtained from Equations A3 and A5 and solve for N[g]. That is, we solve

$$\sum _{j}l\left(j\right)P\left(\text{TMRCA}=g|s_1\left(j\right),s_2\left(j\right),\mathit{N}\right)=n_P\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2N\left[g\right]}{e}^{-Cg/50}\sum _{k=1}^K\left\{\left(\frac{Cg}{50}+1\right)L_k-\frac{C^{2}g}{50}\right\}$$

to estimate N[g] in terms of $N\left[g^{\ast }\right],N\left[g^{\ast }+1\right],\dots ,N\left[g-1\right]$ by

$$\hat{N}\left[g\right]=\frac{n_p\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2}{e}^{-Cg/50}\sum _{k=1}^K\left\{\left(\frac{Cg}{50}+1\right)L_k-\frac{C^{2}g}{50}\right\}}{\sum _{j}l\left(j\right)P\left(\text{TMRCA}=g|s_1\left(j\right),s_2\left(j\right),\mathit{N}\right)},$$ Equation A6

where the sum over j is over the observed IBD segments S(j) with length l(j) = s₂(j) − s₁(j) > C cM.

We now describe how to do the estimation when imposing the piecewise exponential constraint. First, we divide the range of considered generations, g^∗ ≤ g ≤ G, into intervals. We take the first interval to have length 4 + x, where x is uniformly distributed on 1, 2, …, 8. Thus, the first interval is g^∗ ≤ g ≤ (g^∗ + 3 + x). Except for the first and last intervals, the intervals have length 8, so the second interval is (g^∗ + 4 + x) ≤ g ≤ (g^∗ + 11 + x), and so on. The final interval has a length between 1 and 8. The uniformly distributed value x is generated independently for each iteration and each random start.

Write

$$X_g=\sum _{j}l\left(j\right)P\left(\text{TMRCA}=g|s_1\left(j\right),s_2\left(j\right),\mathit{N}\right),$$

which is the amount of observed IBD assigned to generation g (see Equation A3), and write

$$Y_g=n_p\left(\prod _{g^{\prime }=g^{\ast }}^{g-1}\left(1-\frac{1}{2N\left[g^{\prime }\right]}\right)\right)\frac{1}{2}{e}^{-Cg/50}\sum _{k=1}^K\left\{\left(\frac{Cg}{50}+1\right)L_k-\frac{C^{2}g}{50}\right\},$$

which is the product of N[g] and the expected amount of IBD from generation g (see Equation A5).

First, we calculate a constant N for the final interval of generations, g_z ≤ g ≤ G. This is obtained as

$$\sum _{g=g_z}^G{Y}_g/\sum _{g=g_z}^G{X}_g.$$

Next, we work our way from the high values of g toward the low values. If the interval is g₁ ≤ g ≤ g₂, we fit an exponential growth curve of the following form:

$$N\left[g\right]=N\left[g_2+1\right]e^{r\left(g_2+1-g\right)}.$$ Equation A7

To fit this, consider the following function:

$$f\left(r\right)=\sum _{g=g_1}^{g_2}{X}_g-\sum _{g=g_1}^{g_2}\frac{Y_g}{N\left[g\right]}=\sum _{g=g_1}^{g_2}{X}_g-\sum _{g=g_1}^{g_2}\frac{Y_g{e}^{r\left(g-g_2-1\right)}}{N\left[g_2+1\right]}.$$

That is, f is a function of the growth rate that takes value 0 when the observed and expected IBD (summed over the range of generations g₁ ≤ g ≤ g₂) are equal.

We solve for r by using Newton’s method: we start from an initial value of r = 0 and iterate until the difference in successive values of r is less than 0.001. Once the value of r is determined, the values of N[g₂], N[g₂ − 1], …, N[g₁] are obtained with Equation A7.

In some cases, Newton’s method fails to converge or takes too long to converge. If the number of iterations exceeds 100 or |r| > 2, we calculate N[g] individually for each g in the interval by using Equation A6.

Web Resources

The URLs for data presented herein are as follows:

• A Vision of Britain through Time: UK census for 1801, 1861, and 1921, http://www.visionofbritain.org

• dbGaP, https://dbgap.ncbi.nlm.nih.gov

• IBDseq, http://faculty.washington.edu/browning/ibdseq.html

• IBDNe, http://faculty.washington.edu/browning/ibdne.html

• Office for National Statistics UK: mid-1981 population estimates, http://www.ons.gov.uk/ons/publications/re-reference-tables.html?edition=tcm%3A77-162562

• OMIM, http://www.omim.org

• Statistics Finland: population structure tables, http://www.stat.fi/til/vaerak/tau_en.html

• UK10K, http://www.UK10K.org

• United States Census Bureau: 2010 demographic profile data, http://factfinder.census.gov/faces/tableservices/jsf/pages/productview.xhtml?pid=DEC_10_DP_DPDP1&src=pt

• WTCCC, http://www.wtccc.org.uk