Structural contributions to fibrillatory rotors in a patient-derived computational model of the atria

Abstract

Aims

The aim of this study was to investigate structural contributions to the maintenance of rotors in human atrial fibrillation (AF) and possible mechanisms of termination.

Methods and results

A three-dimensional human biatrial finite element model based on patient-derived computed tomography and arrhythmia observed at electrophysiology study was used to study AF. With normal physiological electrical conductivity and effective refractory periods (ERPs), wave break failed to sustain reentrant activity or electrical rotors. With depressed excitability, decreased conduction anisotropy, and shorter ERP characteristic of AF, reentrant rotors were readily maintained. Rotors were transiently or permanently trapped by fibre discontinuities on the lateral wall of the right atrium near the tricuspid valve orifice and adjacent to the crista terminalis, both known sites of right atrial arrhythmias. Modelling inexcitable regions near the rotor tip to simulate fibrosis anchored the rotors, converting the arrhythmia to macro-reentry. Accordingly, increasing the spatial core of inexcitable tissue decreased the frequency of rotation, widened the excitable gap, and enabled an external wave to impinge on the rotor core and displace the source.

Conclusion

These model findings highlight the importance of structural features in rotor dynamics and suggest that regions of fibrosis may anchor fibrillatory rotors. Increasing extent of fibrosis and scar may eventually convert fibrillation to excitable gap reentry. Such macro-reentry can then be eliminated by extending the obstacle or by external stimuli that penetrate the excitable gap.

What's new?

• Clinical data from a Focal Impulse and Rotor Mapping (FIRM) electrophysiology study was used to guide finite element simulations of cardiac electrophysiology simulations on a patient-specific atrial geometry.

• Computational results demonstrate that abrupt fibre discontinuities and inexcitable regions can transiently or permanently trap meandering rotors.

• Increasing the size of an inexcitable scar decreases the rotational frequency of a macro-reentrant circuit. This increases the spatially excitable gap and suggests one potential mechanism for rotor termination.

Introduction

The mechanisms by which atrial fibrillation (AF) initiates, sustains, and can be eliminated have been the subject of extensive investigation.^1–3 The local source hypothesis attributes persistent and permanent AF to a small number of sources including reentrant rotors or focal beats.^4,5 Recent computational mapping studies have revealed rotors or focal drivers in nearly all patients with wide presentations of AF,^6,7 in multicentre studies of Focal Impulse and Rotor Mapping (FIRM).^8,9 Although such AF rotors precess in limited spatial areas for prolonged periods of time,^10,11 the conditions that permit such precession (minimal meander) are unclear. Clinical observations suggest that rotors may preferentially locate to discontinuities in the fibre architecture, particularly in the right atrium,^12,13 and recent clinical studies show that human atria exhibit considerable fibrosis and scar outside the pulmonary veins that may contribute to the mechanisms for AF in many patients.¹⁴

Here we use a computational model to examine rotor behaviour in a realistic human atrial geometry. We demonstrate that meandering rotors can become transiently or permanently trapped by abrupt discontinuities in the fibre architecture. Furthermore, modelling of progressively larger regions of inexcitable tissue near the rotor core at the fibre discontinuity to simulate fibrosis or scar can anchor a meandering rotor, converting fibrillation to excitable gap reentry (macro-reentry). Macro-reentry may then terminate via established approaches including invasion of the excitable gap by external waves.

Methods

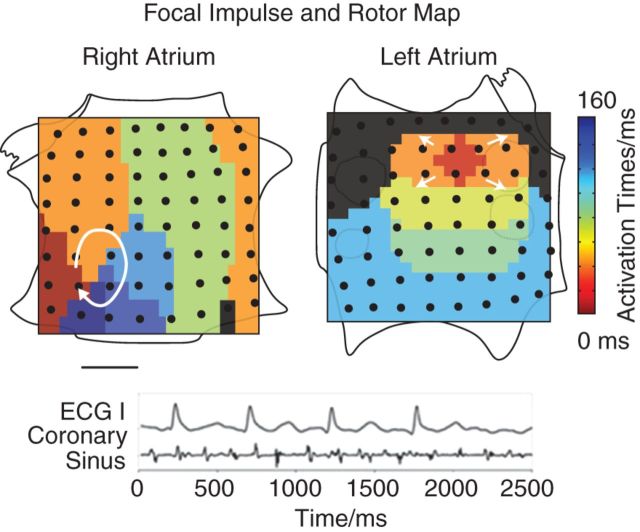
A male patient with a history of persistent AF was referred to the VA San Diego Healthcare System. He gave informed consent to participate in an Institutional Review Board-approved research study. He underwent a computed tomography (CT) study to evaluate atrial structure. At electrophysiology study, he underwent FIRM mapping, which uses phase-based algorithms to identify sources during AF (Topera, Inc.).⁶ Focal Impulse and Rotor Mapping maps indicated a rotor in the lateral right atrial wall and a concurrent left atrial focal source (Figure 1), as previously reported.¹⁵

Figure 1.

Focal impulse and rotor mapping reveals two independent sources: an AF rotor in an unconventional lateral RA location and a concurrent left atrial focal source. Orientation right atrium: top, superior vena cava; left, lateral tricuspid. Left atrium: top, superior mitral annulus. The right atrial AF rotor was the basis for subsequent modelling. Modified from Narayan et al.⁷

The CT images, combined with consensus literature fibre orientations and regional wall thicknesses, were used to construct a one element thick tricubic Hermite finite element model as described previously.¹⁶ This three-dimensional biatrial model was used for Galerkin finite element simulations of the monodomain equation using high-order cubic Hermite basis functions for the geometric and dependent variables. The electrophysiology model had 19 359 nodes, 154 872 degrees of freedom, and a mean element edge length of 1.9 mm. Operator splitting was used to simplify calculations, and a time step of 0.1 ms was used to solve the partial differential equation while the ordinary differential equations corresponding to the cellular ionic model were solved with a time step of 0.01 ms. Conductivities spanning two orders of magnitudes have been used to simulate electrical propagation in the atria; in the present work, the specific conductivity tensor was transversely isotropic with components: D_fibre = 0.9 mm²/ms, and D_cross-fibre = 0.1 mm²/ms for normal atrial propagation and D_fibre = 0.4 mm²/ms, and D_cross-fibre = 0.1 mm²/ms to account for decreased anisotropy of conduction seen with pathological remodelling during AF.¹⁷ Point stimulus in the region of the sinoatrial node with these diffusivities gave rise to a total biatrial activation time of ∼130 ms with the Fenton–Karma ionic model (typical p-wave durations are 80 ms, and customarily are longer in patients with atrial enlargement, as is the case here). The total activation time differed by <5% from the total activation time computed using a more refined model (114 670 nodes, 919 760 degrees of freedom). In a simple cuboid mesh with the same ionic model and conductivity parameters as the atrial electrophysiology simulations, the conduction velocity measured when the mesh was discretized to the same mean element edge length as the atrial model were within 0.5% of the converged conduction velocity measured using a 0.1-mm element edge length. The base parameter set used for the Fenton–Karma model was parameter set 1 in Fenton et al.¹⁸ The excitability value of the model could be adjusted by the parameter $\overline{g_{fi}}$—increasing (decreasing) excitability also caused the action potential duration to increase (decrease) by increasing (decreasing) magnitude of the fast inward current. The value used for $\overline{g_{fi}}$ was 2.95, except as noted because this gave rise to reentrant rotors with frequency approximately equal to that observed of the reentrant rotors in the patient (5 Hz). Action potential morphology (Figure 5C) was dependent both on the ionic model parameters (e.g. $\overline{g_{fi}}$) and the source-sink relationship along the rotor. In the simulations below, rotors were initialized with broken waves by depolarizing a line of tissue and altering the initial conditions on one side of the stimulus to make that region refractory.¹⁹ Structural remodelling (fibrosis and scarring) was simulated by decreasing the excitability in the scar region to zero and setting the diffusivities to one-tenth of their original value. Finally, it should also be noted that the atrial model is static—i.e. its mechanics are not being considered.

Figure 5.

Structural remodelling (fibrosis, scar) simulated by placing an inexcitable region near the rotor core trapped the meandering rotor from Figure 3 and converted it to stable macro-reentry. In (A) the rotor initially meanders around the inexcitable region and eventually becomes trapped indefinitely. This small scar area increased the rotational frequency of the rotor to ∼8.5 Hz. Increasing scar area (B) decreased its rotational frequency to ∼5.5 Hz. Decreasing the frequency also increased the spatially excitable gap. Panel (C) demonstrates the action potential morphology for a location between the inexcitable region and the tricuspid valve annulus in (B). Orientation: lateral right atrial view; top, superior vena cava; right, lateral tricuspid.

Results

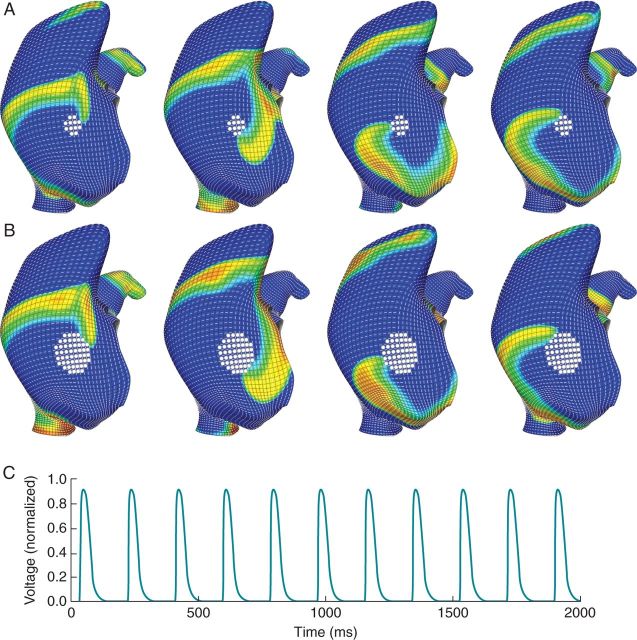
The computational model of action potential propagation on a realistic human atrial geometry was first used to investigate how normal physiology in the atria (vs. pathologic remodelling) might prevent a broken wave from stabilizing as a rotor. With normal cellular excitability, action potential duration (APD), conduction velocity and conduction anisotropy, a broken wave on the lateral wall of the right atrium was unable to sustain a rotor. Images from a representative simulation are presented in Figure 2A. Owing to the extended wave ‘tail’ of the physiological action potential, the wavefront collided with the refractory wavetail causing it to extinguish. Even with an inexcitable region about which to rotate (data not shown), normal myocyte properties prevented a localized source from forming. An anisotropy ratio of nine still prevented the broken wave from sustaining a rotor (Figure 2B) despite shortening the APD and effective refractory period (ERP) to broadly simulate the cellular remodelling seen in AF. Subsequent simulations all used an anisotropy ratio of four and reduced $\overline{g_{fi}}$ to emulate AF remodelling as these parameters consistently maintained rotors (Figure 2C). Importantly, the conduction velocity in the primary fibre direction was reduced by 47% with these modified parameters.

Figure 2.

Action potential duration, ERP, and conduction anisotropy all protect normal atrial tissue from sustaining a rotor from a broken wave on the lateral wall of the right atrium. (A) With healthy atrial parameters the broken wave runs into its wave tail. The normal atrial action potential has an extended repolarization phase (Phase 3), which prohibits formation of reentry, especially at resting activation rates. (B) Despite decreased APD, an anisotropy ratio of nine still prevents the broken wave sustaining a rotor. (C) Decreasing cellular APD together with a decreased anisotropy ratio of four readily permits rotor maintenance. Red and yellow regions are depolarized cardiac tissue while blue regions are quiescent. Orientation: lateral right atrial view; top, superior vena cava; right, lateral tricuspid.

In Figure 2C, a rotor initiated with a broken wave drifted towards the tricuspid valve orifice. The circumferential fibres about the orifice did not allow the spiral to continue rightward and annihilate at the valve orifice but instead ‘pulled’ the spiral away from the boundary and allowed it to pivot back towards the fibre discontinuity and become transiently attached at the interface between the adjacent fibre regions (continued in Figure 3A). The rotor continued to meander in the superior–inferior direction for the remainder of the 5 s simulation (Figure 3B), similar to the behaviour observed clinically in this patient (Figure 1). In simulations lacking this fibre discontinuity (not shown), the rotor did not become transiently fixed to this region, and instead meandered to the posterior right atrium.

Figure 3.

Fibre discontinuities help to stabilize a meandering rotor. (A) A broken wave on the lateral wall of the right atrium sustains a rotor. After briefly meandering towards the posterior RA, the rotor was ‘pulled’ to the fibre discontinuity surrounding the tricuspid valve annulus. (B) The rotor precessed inferiorly along the fibre discontinuity and anchoring transiently to it repeatedly for the remainder of the 5 s simulation. Orientation: lateral right atrial view; top, superior vena cava; right, lateral tricuspid.

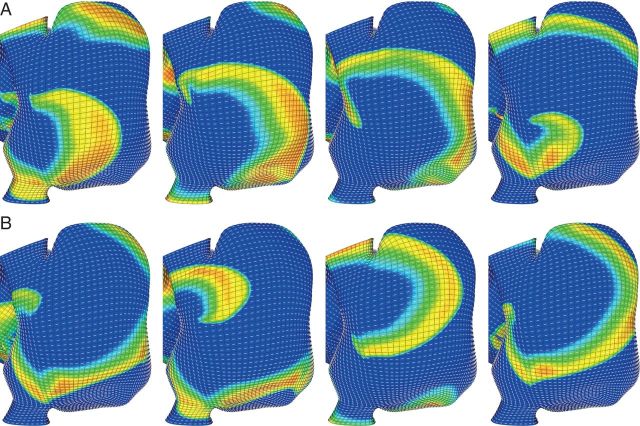
Rotors that meandered to the posterior right atrium were often trapped near the crista terminalis. Figure 4 depicts two rotors that meandered across the posterior right atrium and became trapped by the abrupt change in the fibre architecture and wall thickness at the crista terminalis. The counter-clockwise rotor in Figure 4A was confined to the discontinuity near the superior vena cava for 2000 ms before precessing inferiorly along the crista terminalis (Figure 4C). A rotor with the opposite chirality (Figure 4B) became permanently affixed to this region. Interestingly, the counter-clockwise rotor had a smaller precession area than the trapped clockwise rotor.

Figure 4.

Fibre discontinuities can trap a meandering rotor. Rotors drifting across the posterior right atrium were ‘pulled’ to the fibre discontinuity at the crista terminalis. (A) A couter-clockwise rotor became trapped by the fibre discontinuity for ∼2000 ms before precessing inferiorly along the crista terminalis. (B) A clockwise rotor became trapped by the fibre discontinuity and remained there for the remainder of the five-second simulation. Orientation: posterior right atrial view; top, superior vena cava; right, lateral right atrium.

The impact of structural remodelling was now simulated by placing inexcitable scar near the rotor core at the fibre discontinuity. After adding a scar near the tricuspid valve annulus, the rotor meandered about the scar initially before converting to stable macro-reentry about the inexcitable region (Figure 5). Broadly, the AF remodelling parameters allowed a fibrillatory rotor to readily attach to inexcitable regions, causing conversion to stable excitable gap reentry or macro-reentry. Increasing the size of the scar increased the path length for reentry and decreased its rotational frequency (Figure 5B). Similarly, the AF rotor near the crista terminalis became fixed to simulated dense scar (Figure 6), again converting it to excitable gap reentry. Again, increasing the size of the scar decreased the rotational frequency of the rotor. Decreasing the frequency of the rotor increased its spatially excitable gap. In Figure 6, an external wave invaded the excitable gap and displaced reentry away from its fixed location.

Figure 6.

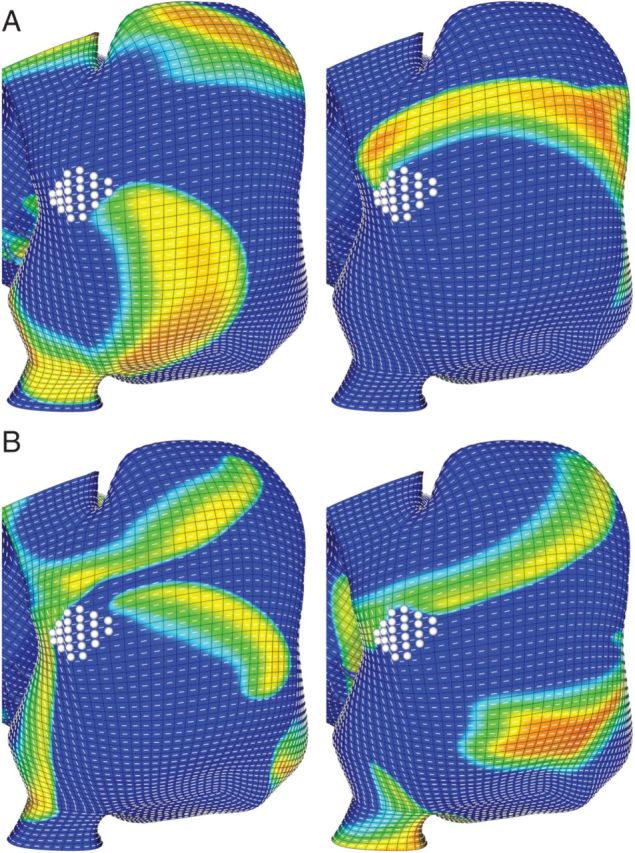
Structural remodelling (fibrosis) near the crista terminalis altered reentry dynamics and resulted in the rotor being displaced. (A) The rotor displaced from the fibre discontinuity and attached to the scar, with decreasing rotational frequency as in Figure 5. (B) The increased spatially excitable gap permits a wave (driven by more rapid activity originating in the left atrium) to impinge on the rotor core. Eventually the rotor is displaced by the invading wavefront suggesting that regions of fibrosis may enable the localized source to convert to macro-reentry with an excitable gap. Orientation: posterior right atrial view; top, superior vena cava; right, lateral right atrium.

Discussion

This study provides insights into the relatively stable, precessing rotors recently described during human AF in multicentre clinical studies. Our observations emphasize the potential importance of structural features of the myocardium in rotor dynamics, by showing that discontinuities in the fibre architecture and inexcitable regions can constrain rotors transiently or persistently. Moreover, structural remodelling in the form of scar or fibrosis near the centre of the rotor core can convert fibrillation to excitable-gap reentry, which can be terminated.

The normal atria may be protected from AF by all of the following: the absence of triggers, although recently challenged by data suggesting that triggers may exist for decades in patients without clinical AF,²⁰ the unlikelihood of wavebreak due to ‘protective’ conduction or repolarization dynamics,^21–23 and the absence of substrates for rotor maintenance or attachment. Our modelling results support two protective mechanisms in the normal atria. First, the prolonged spatial wavetail of an action potential in a normal atrial myocyte may prevent reentrant rotor formation by causing conduction block and propagation failure when a broken wave is pivoting (Figure 2A) or in the process of anchoring about an inexcitable region.

It is well known that ionic current remodelling promotes AF. Ionic currents such as I_K1²⁴ and I_CaL²⁵ change in magnitude in AF, shortening the ERP and APD. Specific ionic effects were not considered in the present study, but others have demonstrated the importance of these changes in atrial myoyte ionic current magnitudes on rotor dynamics in AF. Atienza et al.²⁶ demonstrated that upregulated I_K1 promotes AF stability by increasing rotor frequency in human studies and simulations. Sarmast et al.²⁷ showed that rotor frequencies increase and AF stabilizes by increased I_K,Ach in a cholinergic model of AF owing to the shorter ERP and APD. It is well known that short ERP and APD, dynamic oscillations in APD^22,28 and potentially steep rate response in APD²¹ can facilitate AF. It remains unclear under what conditions such AF can terminate in healthy control subjects.

The above results also support a protective role for normal conduction anisotropy and conduction velocity in preventing sustained rotor activity. The idea that normal uniform anisotropy of conductivity could be anti-arrhythmic was first proposed by Spach and Starmer.²⁹ In Figure 2B, an anisotropy ratio of nine again causes the wavefront to extinguish at the tricuspid valve orifice after running into its tail. The large electrotonic loads near the rotor core present with increased anisotropy may also prevent sustained rotors and the attachment of scroll waves to inexcitable regions. Whether anisotropy ratio increases or decreases in AF is somewhat controversial, but here we modelled the anisotropy ratio as decreased in AF. The rationale for this is the report of lateralization of connexin 43 in AF and a concomitant decrease in the anisotropy of apparent conduction velocity in intact tissue preparations in AF.³⁰ Others have argued that anisotropy might increase, since it is known that there is increased fibrotic septation between juxtaposed sheets of cells.³¹ These findings could be reconciled by the dependence of conduction anisotropy not only on gap junction connections but also on the magnitude of the fast inward sodium current, which may be depressed in AF,³² disproportionately decreasing the conduction velocity along the fibre axis. Recent clinical studies demonstrate conduction slowing (restitution) with markedly anisotropic dynamics (i.e. an abrupt shift in the vector of conduction slowing) immediately prior to AF onset.^23,33,34 Further studies are required to elucidate the tissue properties that underlie these mechanisms.

Clinical studies of FIRM demonstrate that rotors typically precess in areas of 2 to 3 cm².¹¹ The numerical simulations presented in Figures 3 and 4 suggest that discontinuities in the fibre architecture could play a role in such precession. Indeed, ongoing studies are exploring the relationship between rotor precession mapped by FIRM and areas of well-known fibre discontinuities. The ease with which rotors became trapped and converted into macro-reentry at sites of abrupt discontinuity in fibre orientation, particularly at the crista terminalis, is also consistent with previous clinical data. In 23 patients with suspected right atrial tachycardia, Kalman et al.¹² identified 18 focal arrhythmias originating from the crista terminalis with eight of these located in the high lateral region as in Figure 4. Interestingly, three focal right atrial tachycardias were localized to the lateral side of the triscuspid valve annulus as in this patient and Figure 3. Computationally, a recently published model of arrhythmias in a three-dimensional geometric model of normal human atria incorporating fibre orientations and wall thicknesses derived from the literature developed atrial flutter and a reentrant rotor in the high lateral crista terminalis region after nearby burst pacing.³⁵ Locally increased wall thickness at the crista terminalis was visible in the CT imaging data of our patient, and included in the geometric model.¹⁶ Electrotonic effects due to this thickening may theoretically aid in the permanent attachment of the rotor to this region. Both the fibre discontinuity and wall thickening in the crista terminalis region are supported by anatomical and histological measurements in cadaver hearts.¹³

Of note, while the patient in Figure 1 had an AF rotor in lateral right atrium, several other right (and left) atrial locations have been noted for human AF rotors.¹⁵ Moreover, AF rotor locations often do not demonstrate signal characteristics consistent with dense scar or borderzone, in that voltages may be preserved and signals may lack fractionation.¹¹ Detailed studies are thus required to define a structure–function relationship for AF rotor and focal impulse locations.

The importance of abrupt changes in the fibre architecture on rotor dynamics demonstrated here builds on previous experimental, computational, and analytical analyses. Indeed, much of our understanding of rotor behavior comes from simple two-dimensional computational models or chemical systems.⁵ Early experimental findings in excitable chemical media showed that spatial inhomogeneities are not required to sustain a rotor and that stable meander could result from the interaction between a spiral wave and its refractory tail.³⁶ Early numerical studies demonstrated that smooth gradients in fibre orientation,¹⁹ refractory period³⁷ or excitability³⁸ can lead to spiral wave drift. More recently, Kuklik et al. identified inhomogeneity of conduction anisotropy as one functional mechanism that can permanently trap rotors but stable meandering was not observed.³⁹ A limitation for these investigations was the use of a simple two-dimensional geometry as surface curvature is an important determinant of rotor behaviour.^37,40,41 The complex three-dimensional atrial geometry may require additional stabilizing influences to trap or confine rotors. A more recent simulation study using an atrial myocyte ionic model showed that functional heterogeneities alone are capable of constraining rotors to small regions of space, at least for the time course of seconds;⁴² whether or not functional heterogeneities or fibre discontinuities are able to spatially constrain rotors for longer periods of time (hours to days) is unclear.

These data also demonstrate how structural remodelling can convert a fibrillatory rotor to excitable gap reentry. In Figure 5 the precessing AF rotor anchored to inexcitable scar, with development of an excitable gap. Similarly, the rotor in Figure 6 released from the fibre discontinuity at the crista terminalis and anchored to the scar. Increasing the size of this scar altered the dynamics of re-entry as anticipated, decreasing the rotational frequency and widening the spatially excitable gap. A depolarization wave was then able to invade the rotor core and displace reentry away from its original location (Figure 6B). These data support a mechanism, previously suggested by Kawase et al.,⁴³ by which increasing the excitable gap of a rotor can result in its termination.

Limitations

One limitation of the present study is that the model uses a phenomenological ionic model (Fenton–Karma) rather than a biophysical ionic model such as Courtemanche–Ramirez–Nattel⁴⁴ or Maleckar–Giles–Trayanova.⁴⁵ This limitation means that the present work can only suggest phenomenological mechanisms, not more meaningful biophysical mechanisms. For example, the Fenton–Karma model can be used to examine the effect of depressed excitability and of spatial variations in excitability, but cannot distinguish between changes in the biophysical constituents of excitability such as sodium channel remodelling, increased cardiomyocyte-fibroblast coupling, or resting membrane potential elevation. Moreover, the parameter governing excitability in the Fenton–Karma model ($\overline{g_{fi}}$) is not based on an actual biophysical measurement; in contrast, excitability in biophysical models is based on measurements of the fast inward sodium current. Additionally, inhibiting the fast inward current by modifying $\overline{g_{fi}}$ decreases both excitability and APD in the Fenton–Karma model, whereas in biophysical models of the action potential, decreasing the conductance of the fast sodium channel may increase APD (e.g. class 1a antiarrhythmic drugs). The extent to which these differences lead to different conditions for wavebreak and wave fractionation is unknown.

On the other hand, several insights gained into rotor dynamics and specifically into AF by computational models are completely attributable to the shape of the action potential waveform and its effect on spiral tip meander, dominant frequency, and fractionation.^26,46 Consequently, results depending principally on the wave shape, such as the number of wavelets that can be supported in a normal vs. an enlarged atrium, should be unchanged if the Fenton–Karma model can recapitulate the action potential shape of a more detailed model. A principal reason that we used the Fenton–Karma model in the present study is that in a recent computational study⁴⁷ both ‘normal’ and ‘AF’ parameter values in five recent human atrial myocyte models failed to capture clinically measured APD and CV restitution behaviours observed by groups including our own.²¹ Specifically, the restitution curves for ‘normal’ and ‘AF’ parameters were far more flat than has been observed experimentally, and the disagreement was worst at the fast rates (>4 Hz) of sources typical for rotors mapped by FIRM. In the future, the current study should be completed with more biophysically detailed models if parameter values can be found that agree with experimental APD and CV restitution curves.

Our model incorporated patient-specific CT anatomy, electrophysiological mapping of rotors and ablation results, although a limitation is that patient-specific APD and CV restitution curves were not incorporated. Unfortunately, with current technology such data cannot be obtained at high resolution in vivo. In explanted hearts, however, APD and CV restitution curves could be used to modify the parameters of the ionic model (whether phenomenological or biophysical) to make it subject specific although at the expense of an altered metabolic, haemodynamic, and autonomic milieu. Accordingly, while no model based on human measurements is currently available, Cherry et al. have published a similar model based on canine measurements.⁴⁸ Like many of the biophysically detailed models, the restitution behavior of this model at fast rates is not as steep as clinical measurements.

Finally, this study is limited because it considers only the geometry of one patient. Future studies should test if these results can provide patient-specific information on rotor stability; these simulations might differ from the results presented here due to differences in the distance of a focal source from a boundary, the location of sources relative to high-curvature regions (e.g. the pulmonary vein ostia), or the location of sources relative to well-known locations of fibre discontinuity.

Conclusion

Results from the computational model suggested mechanisms for the maintenance of rotors for human AF. Our data are consistent with the concept that discontinuities in the fibre architecture and inexcitable regions are important structural features that can trap rotors transiently or permanently. The addition of structural remodelling (inexcitable scars) can convert precessing AF rotors to macro-reentry, whose spatially excitable gap can be a target for extermination by external stimuli.

Conflicts of interest: S.M.N. serves as a consultant for and holds stock in the company Topera. He also serves as a consultant for the American College of Cardiology and has received honoraria from Medtronic, Biotronik, St Jude Medical and Boston Scientific. A.D.M. is a co-founder, shareholder and scientific advisor to Insilicomed, Inc., a licensee of UCSD software used in this research. Insilicomed had no involvement in the design, funding or conduct of this research.

Funding

This work was supported by the National Institutes of Health [1R01HL105242, 1R01HL96544, 8P41 GM103226, P50 GM0945503, A.D.M.]; [HL083359, S.M.N. and W.J.R.]; [HL103800, S.M.N.]; and an NIH pre-doctoral training grant [T32 EB009380, M.J.G. and K.P.V.].