Abstract
The dynamic crossover behavior of supercooled water as described by the first-principle based WAIL potential was investigated. Below the second liquid–liquid critical point, the viscosity shows a discontinuous jump consistent with a first-order phase transition between the high density liquid and the low density liquid. Above the critical point, a continuous transition occurs with only the first derivative of viscosity being discontinuous, and the dynamic crossover temperature is about 8 K below the thermodynamic switchover temperature. The 8 K shift can be explained by a delay in dynamic crossover, which does not occur until the more viscous liquid starts to dominate the population and jams the flow. On the basis of finite-size effects observed in our simulations, we believe that dynamic discontinuity may be observable above the critical point in confined water when the confinement is on a length scale shorter than the spatial correlation.
Despite the ubiquity and importance of water, the properties of deeply cooled water below the homogeneous nucleation temperature around 237 K are still a subject of debate.1−13 At the glass-transition temperature of 136 K, water is the strongest liquid ever identified.14−16 On the contrary, above the homogeneous nucleation temperature, water is a very fragile liquid.14 Somewhere between the glass-transition temperature and the homogeneous nucleation temperature, there has to be a crossover between strong and fragile dynamics.17 The exact nature of such a dynamic crossover has been elusive and controversial.
Experimental investigation of the dynamic crossover is typically done under confinement,18−21 or with another solute to suppress freezing.22,23 Theoretical simulations with the Jagla,24 ST2,25 SPC/E,26,27 and TIP4P28 models showed crossover behaviors, although how realistic these models reflect the physics of true water is an open question.4,12 Most of the water models used for the simulations were created by fitting to experimental properties. Recently, a water model, WAIL,29 has been developed by fitting to electronic structure calculations30,31 performed at coupled cluster quality.32 The WAIL model predicts the melting temperature (TM) of water to be ∼270 K and a temperature of maximum density (TMD) around 9 °C, in good agreement with experimental values. A simulation with the WAIL potential is less susceptible to biases, which could be introduced when a model was fit to experimental observables. Simulations with WAIL reflect the prediction from the underlying first-principle method used for parametrization,33 under the limitation of the simple energy expressions used for the potential.
It has been shown that the WAIL potential supports two forms of liquid water in the supercooled regime with distinct densities.15 The two forms,34 high density liquid (HDL) and low density liquid (LDL), have a critical temperature around 207 K at 50 MPa. Above the critical point, the two microscopic forms coexist in one phase across the Widom line;35,36 below the critical point, a sharp transition between the two forms is observed consistent with a first-order phase transition in our simulation.
The structural relaxation kinetics of the WAIL water has not been studied. While most existing simulations on dynamic crossover in supercooled water have focused on the diffusion constant by fitting to the power law scaling predicted by the mode-coupling theory,37 viscosity is one of the most direct experimental observables for determining fragility.38 Computational study of the viscosity of supercooled water is rare in literature. In this work, we measured the viscosity of water using nonequilibrium molecular dynamics (NEMD) by applying an external force with a sinusoidal profile.39 The approach is frequently referred to as the cosine acceleration method.40 Hess compared four different approaches for calculating viscosity of water and found the cosine acceleration method to be the most reliable.40 Compared with a Green–Kubo based approach, an NEMD approach generally converges faster. This is important for supercooled water simulations due to the long trajectories needed at low temperatures.
Unless otherwise noted, the viscosity measurements were performed in an orthorhombic box with an average dimension of 2.2 nm × 2.2 nm × 4.4 nm containing 686 water molecules. The box was constructed from the initial configurations sampled previously by Li et al.15 and replicated in the Z dimension. The longer Z dimension is required to ensure the validity of the Navier–Stokes equation.40 The new box was equilibrated for 7 ns. The cosine acceleration was applied after equilibration over a 20 ns period with the velocity profile measured for the last 15 ns. Such a long measurement is required due to the slow dynamics in supercooled temperatures. For selected temperature and pressure points described later, a large simulation box containing 2744 water molecules was used to assess the finite size effect. The larger box has an approximate dimension of 4.4 nm × 4.4 nm × 4.4 nm. A total of 3200 viscosity measurements were performed to reduce the error bar of the measured viscosities. This translates to approximately 70 μs worth of trajectory.
The Ewald summation method was used to treat long-range electrostatics. The equation of motion was integrated with a time step size of 0.5 fs with the hydrogen assuming the mass of the deuterium isotope. The Vogel–Fulcher–Tammann (VFT) and Arrhenius fit were performed by minimizing the weighted sum of squared residuals (WSSR), where the contribution of each point was weighted by the inverse of the square of the error. The error bars were determined by bootstrap resampling of the measured viscosities. The resampling was performed with replacements.
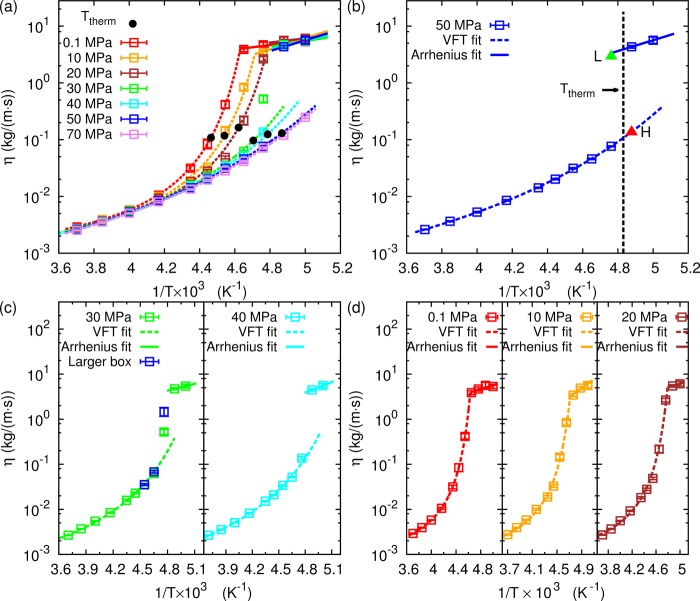
Figure 1a shows the viscosity as a function of temperature for pressures from 0.1 to 70 MPa. A clear strong-to-fragile transition is observed with the low-temperature viscosity showing the Arrhenius dependence and the high-temperature viscosity showing VFT kinetics.41 WAIL water has a first-order liquid–liquid transition above 50 MPa. At 70 MPa, the liquid–liquid transition occurs below 200 K, which is the lowest temperature investigated in this work. Thus, only VFT kinetics of HDL can be seen at this pressure.
Figure 1.
(a) Viscosity of supercooled water as a function of temperature for pressures from 0.1 to 70 MPa. The LDL-HDL thermodynamic transition temperatures (Ttherm) are shown as black dots. (b) Viscosity of supercooled water at 50 MPa shows a discontinuity between the two liquid forms. The viscosity of the metastable HDL at 205 K is labeled as H, and the viscosity of the metastable LDL at 210 K is labeled as L. (c) Viscosity of supercooled water at 30 and 40 MPa. The blue dots were calculated with a simulation box that is 4 times larger. (d) Viscosity of supercooled water at 0.1, 10, and 20 MPa shows a continuous transition between LDL and HDL forms. In the top panels, the error bars can be seen through the hollow symbols. In many cases, the error bar is virtually zero in the log scale graph and can be seen as one horizontal line at the center.
The viscosity at 50 MPa is highlighted in Figure 1b. At this pressure, the WAIL water undergoes a first-order phase transition at ∼207 K.15 The HDL shows a precise fit to fragile kinetics above the transition temperature, and the LDL viscosity was fit to Arrhenius kinetics below the transition temperature. The viscosity shows a discontinuous jump at ∼207 K. Although the first derivative of a dynamic variable, such as viscosity, is expected to be discontinues along a strong-to-fragile transition, most existing studies assume a continuous change in the dynamic variable itself when fitting across the transition line. Our simulation suggests that, during a first-order phase transition between two liquids, a discontinuity in the dynamic variable itself should be expected. This is not surprising considering the two liquids have different viscosities. Similar discontinuity in diffusion constant has been shown in previous studies using the Jagla model.24
To confirm this observation, we calculated the viscosity of metastable liquids across the transition line. In supercooled water, although ice is more stable thermodynamically, it is not accessible in our simulation time scale. At 210 K and 50 MPa, although the HDL phase is more stable, LDL can exist for hundreds of nanoseconds before transforming spontaneously and irreversibly to the HDL.15 In Figure 1b, the viscosity of the metastable LDL phase before the spontaneous transition is marked as L. Similarly, the viscosity of the metastable HDL phase at 205 K is marked as H. The metastable points stay close to the extrapolated viscosity curves obtained by fitting to the more stable liquid viscosities, clearly showing a kinetic discontinuity across the liquid–liquid transition line. This confirms that the discontinuity in viscosity observed is not an artifact of our fitting procedure.
The viscosity of supercooled WAIL water at 30 and 40 MPa is shown in Figure 1c. At these pressures, LDL and HDL are no longer two distinct phases. For a macroscopic system, one would expect the viscosity to be continuous as the two liquid forms fluctuate in a one phase regime. However, Figure 1c clearly shows a discontinuity in viscosity across the Widom line.
Close to the critical point, the structural fluctuation is correlated over an extended distance, which is larger than or comparable to the size of our simulation box. The time trace of box density, as shown in Figure 2, indicates that the system oscillates strongly between HDL and LDL conformations, with the entire box being HDL or LDL rather than a mixture. For a macroscopic system, only domains of the system rather than the whole will assume HDL or LDL forms, and thus the measured viscosity does not reflect the true viscosity of a macroscopic system.
Figure 2.
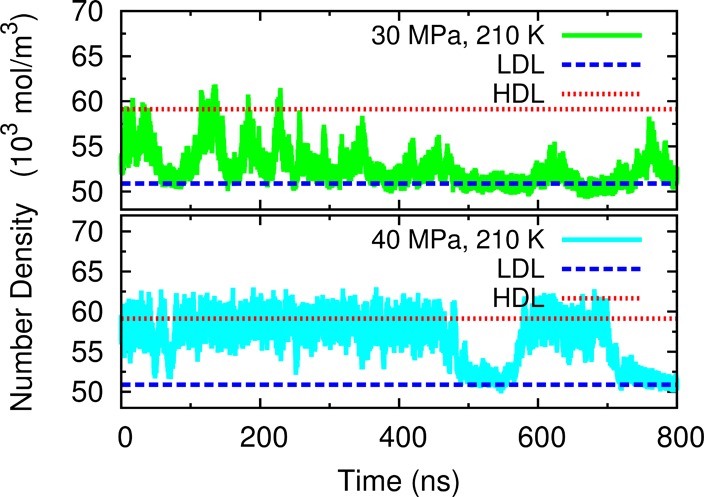
Time trace of the box density at 30 MPa 210 K (top) and 40 MPa 210 K (bottom). The horizontal lines are the expected density for HDL and LDL, respectively.
To assess whether the finite size effect indeed explains the apparent discontinuity in viscosity, we repeated the viscosity calculations for selected points using a box containing 2744 water molecules, which is 4 times as large as the other boxes. The blue dots in Figure 1c mark the viscosity calculated with the larger box. Close to the critical point at 210 K, the larger box resulted in a much larger viscosity, consistent with a continuous crossover slightly above 205 K.
Although the viscosity measured with the larger box is significantly larger at 210 K, the difference decreases as the temperature moves further away from the critical temperature, consistent with the expectation that shorter spatial correlation lengths further away from the critical point minimize the finite size effect.
Figure 1d shows the viscosity as a function of temperature for 0.1, 10, and 20 MPa. The viscosity shows a continuous transition from fragile to strong as temperature decreases. Only the first derivative of viscosity is discontinuous. At these pressures, the correlation length is sufficiently short due to the further distance from the critical point. Even for temperature and pressure close to the Widom line, only domains of LDL and HDL exist in a 686 water simulation box.
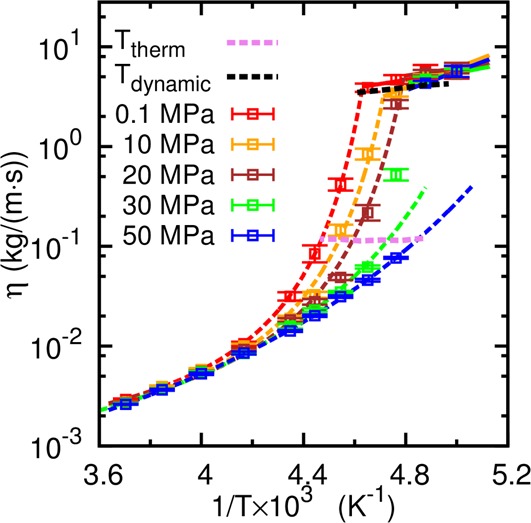
The temperature for dynamic crossover at 0.1, 10, and 20 MPa can be determined by the point where the VFT viscosity is the same as the Arrhenius viscosity. The dynamic crossover temperature at pressures higher than 20 MPa is estimated by a linear extrapolation of the low pressure behavior because a direct measurement of the crossover temperature at these pressures is challenging due to finite size effects. The dynamic crossover line is terminated at the critical temperature of 207 K. Below this temperature, discontinuous kinetics is observed across a phase transition line.
In Figure 3, the dynamic crossover line is plotted along with the thermodynamic transition line. The thermodynamic transition line follows the phase boundary below the critical point. Above the critical point, there is no phase transition, the population switches over from LDL dominate to HDL dominate across the Widom line. Thus, the thermodynamic “transition” line in the figure follows the Widom line, which is approximated using the inflection points of the density isobars and the maxima of isothermocompressibilities published previously.15 From Figure 3, it is clearly that the dynamic crossover occurs at a lower temperature than the thermodynamic switchover above the critical point. This difference is also evident in Figure 1a.
Figure 3.
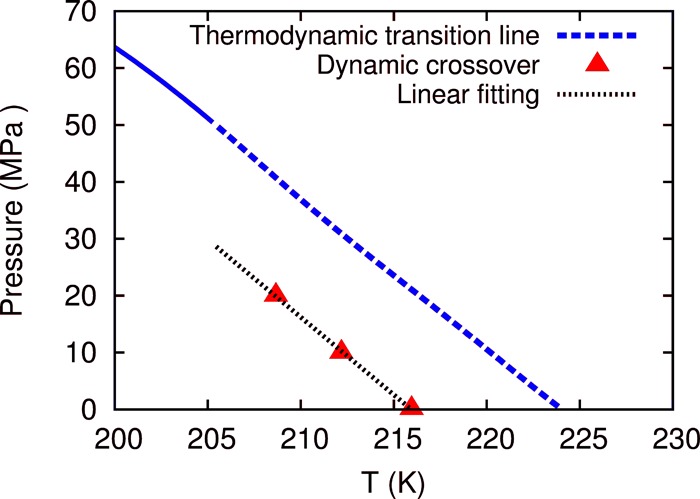
Dynamic crossover line and the thermodynamic transition line. The thermodynamic transition line follows the phase-transition line (solid) below the critical temperature and the Widom line above the critical temperature (dashed). The dynamic crossover line ends at the critical point. Below the critical point, the viscosity becomes discontinuous when the phase boundary is crossed.
It has been shown that, away from the critical point, the locus of maximum for different response functions, such as heat capacity and isothermocompressibility, do not necessarily agree.42 In this work, we will assume the Widom line35 is close to the 50–50 line, where each of the two microscopic forms of liquids has about 50% mole fraction. The shift between the dynamic crossover and the thermodynamic switchover can be understood considering an ice–water mixture with small ice crystals dispersed in water. A mechanical measurement of viscosity of such a mixture,43 using methods such as the capillary flow technique43 or a falling sphere viscometer,44 will not reveal the viscosity of ice because ice flows inside the more fluid liquid when the viscosity is measured. Dynamic crossover will not occur until a sufficient amount of ice has developed so that ice no longer flows without pushing into each other, which, intuitively, should occur when the mole fraction of ice is significantly over 50%.
We postulate that in supercooled water above the critical temperature, two microscopic forms of the liquid fluctuate quickly, and the viscosity of the liquid is dominated by the form with lower viscosity, which is HDL. Above the critical point, the VFT dynamics at higher temperature is caused by the increased population of LDL domains and the crossover to Arrhenius regime is caused by the formation of a sufficient amount of LDL to jam the system. This will explain the observation that the kinetic crossover temperature occurs below the thermodynamic, Widom, switchover temperature. It has been shown previously that the jamming of granular particles is expected to follow VTF kinetics.45
It is worth pointing out that our observation of the shift of the dynamic crossover line to the lower temperature from the Widom line has also been observed experimentally.46 For example, figure 1 of ref (46), by Chen et al., clearly showed the dynamic crossover in α-relaxation to be at lower temperature than the maximum in differential scanning calorimetry, although Chen concluded the two temperatures agree within the experimental error bars. If our explanation of the shift is indeed true, we anticipate similar shifts between the two lines to appear in some other liquids.
We note the HDL form by itself also shows VFT dynamics because the HDL liquid below the critical temperature shows fragile kinetics. This is consistent with the observation of VFT kinetics of other glass formers. Without formation of LDL in the HDL phase, the viscosity of HDL remains relatively low and a discontinuity is observed across the phase transition line.
We note that the discontinuity in viscosity with the WAIL model does not prove a first order liquid–liquid phase transition in real water. However, the WAIL model was created based only on electronic structure information as input and is thus a first-principle based model. In WAIL water, the viscosity of a mixture of LDL and HDL forms in one phase is dominated by the viscosity of the less viscous HDL form. The dynamic crossover occurs only when the LDL population starts to dominate the liquid. Although this argument explains the shift in dynamic crossover in viscosity from the thermodynamic switchover line, it is not immediately clear to us whether a similar conclusion can be drawn when diffusion constant is used to characterize dynamics because the Stokes–Einstein equation may not hold when crossing to the Widom line. The validity of the conclusion when other dynamic variables are used to characterize dynamic crossover requires further investigation.
Close to the critical point, the finite size effect of the simulation leads to a deviation from VFT kinetics; this leads to a discontinuity in the apparent viscosity across the Widom line. Such a discontinuity above critical temperature should not exist in macroscopic samples but may be observable experimentally in confined systems. Below the critical point, the viscosity in our simulation shows a clear discontinuity, which can only be explained by a first-order transition between two different phases. Many existing studies of the fragile-to-strong transition in supercooled water and other glass formers have fit the VFT and Arrhenius kinetics with a discontinuous first derivative but a continuous viscosity. Our work shows that the viscosity itself can be discontinuous when the underlying transition is truly first order.
Acknowledgments
This work was supported by NIH COBRE 8P30GM103450, Arkansas Biosciences Institute, and NSF CAREER award CHE0748628. The computer resources for this study were provided by the Arkansas High Performance Computational Center through grant MRI-R2 #0959124 provided by the NSF.
The authors declare no competing financial interest.
References
- Mishima O.; Stanley H. E. The Relationship between Liquid, Supercooled and Glassy Water. Nature 1998, 396, 329–335 10.1038/24540. [DOI] [Google Scholar]
- Hecksher T.; Nielsen A. I.; Olsen N. B.; Dyre J. C. Little Evidence for Dynamic Divergences in Ultraviscous Molecular Liquids. Nat. Phys. 2008, 4, 737–741 10.1038/nphys1033. [DOI] [Google Scholar]
- Mallamace F.; Branca C.; Corsaro C.; Leone N.; Spooren J.; Chen S.-H.; Stanley H. E. Transport Properties of Glass-Forming Liquids Suggest That Dynamic Crossover Temperature Is as Important as the Glass Transition Temperature. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 22457–22462 10.1073/pnas.1015340107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Limmer D. T.; Chandler D. The Putative Liquid-Liquid Transition Is a Liquid-Solid Transition in Atomistic Models of Water. J. Chem. Phys. 2011, 135, 134503. 10.1063/1.3643333. [DOI] [PubMed] [Google Scholar]
- Xu L.; Molinero V. Is There a Liquid–Liquid Transition in Confined Water?. J. Phys. Chem. B 2011, 115, 14210–14216 10.1021/jp205045k. [DOI] [PubMed] [Google Scholar]
- Holten V.; Anisimov M. A. Entropy-Driven Liquid-Liquid Separation in Supercooled Water. Sci. Rep. 2012, 2, 713. 10.1038/srep00713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holten V.; Limmer D. T.; Molinero V.; Anisimov M. A. Nature of the Anomalies in the Supercooled Liquid State of the Mw Model of Water. J. Chem. Phys. 2013, 138, 174501. 10.1063/1.4802992. [DOI] [PubMed] [Google Scholar]
- Palmer J. C.; Martelli F.; Liu Y.; Car R.; Panagiotopoulos A. Z.; Debenedetti P. G. Metastable Liquid-Liquid Transition in a Molecular Model of Water. Nature 2014, 510, 385–388 10.1038/nature13405. [DOI] [PubMed] [Google Scholar]
- Holten V.; Palmer J. C.; Poole P. H.; Debenedetti P. G.; Anisimov M. A. Two-State Thermodynamics of the St2Model for Supercooled Water. J. Chem. Phys. 2014, 140, 104502. 10.1063/1.4867287. [DOI] [PubMed] [Google Scholar]
- Gallo P.; Corradini D.; Rovere M. Widom Line and Dynamical Crossovers as Routes to Understand Supercritical Water. Nat. Commun. 2014, 5, 5806. 10.1038/ncomms6806. [DOI] [PubMed] [Google Scholar]
- Sellberg J. A.; Huang C.; McQueen T. A.; Loh N. D.; Laksmono H.; Schlesinger D.; Sierra R. G.; Nordlund D.; Hampton C. Y.; Starodub D.; et al. Ultrafast X-Ray Probing of Water Structure Below the Homogeneous Ice Nucleation Temperature. Nature 2014, 510, 381–384 10.1038/nature13266. [DOI] [PubMed] [Google Scholar]
- Limmer D. T.; Chandler D. Time Scales of Supercooled Water and Implications for Reversible Polyamorphism. Mol. Phys. 2015, 1–5 10.1080/00268976.2015.1029552. [DOI] [Google Scholar]
- Smallenburg F.; Sciortino F. Tuning the Liquid-Liquid Transition by Modulating the Hydrogen-Bond Angular Flexibility in a Model for Water. Phys. Rev. Lett. 2015, 115, 015701. 10.1103/PhysRevLett.115.015701. [DOI] [PubMed] [Google Scholar]
- Ito K.; Moynihan C. T.; Angell C. A. Thermodynamic Determination of Fragility in Liquids and a Fragile-to-Strong Liquid Transition in Water. Nature 1999, 398, 492–495 10.1038/19042. [DOI] [Google Scholar]
- Li Y.; Li J.; Wang F. Liquid–Liquid Transition in Supercooled Water Suggested by Microsecond Simulations. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 12209–12212 10.1073/pnas.1309042110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amann-Winkel K.; Gainaru C.; Handle P. H.; Seidl M.; Nelson H.; Böhmer R.; Loerting T. Water’s Second Glass Transition. Proc. Natl. Acad. Sci. U. S. A. 2013, 110, 17720–17725 10.1073/pnas.1311718110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S.-H.; Mallamace F.; Mou C.-Y.; Broccio M.; Corsaro C.; Faraone A.; Liu L. The Violation of the Stokes–Einstein Relation in Supercooled Water. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 12974–12978 10.1073/pnas.0603253103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertrand C. E.; Zhang Y.; Chen S.-H. Deeply-Cooled Water under Strong Confinement: Neutron Scattering Investigations and the Liquid-Liquid Critical Point Hypothesis. Phys. Chem. Chem. Phys. 2013, 15, 721–745 10.1039/C2CP43235H. [DOI] [PubMed] [Google Scholar]
- Liu L.; Chen S.-H.; Faraone A.; Yen C.-W.; Mou C.-Y. Pressure Dependence of Fragile-to-Strong Transition and a Possible Second Critical Point in Supercooled Confined Water. Phys. Rev. Lett. 2005, 95, 117802. 10.1103/PhysRevLett.95.117802. [DOI] [PubMed] [Google Scholar]
- Cupane A.; Fomina M.; Piazza I.; Peters J.; Schirò G. Experimental Evidence for a Liquid-Liquid Crossover in Deeply Cooled Confined Water. Phys. Rev. Lett. 2014, 113, 215701. 10.1103/PhysRevLett.113.215701. [DOI] [PubMed] [Google Scholar]
- Chu X. Q.; Kolesnikov A. I.; Moravsky A. P.; Garcia-Sakai V.; Chen S. H. Observation of a Dynamic Crossover in Water Confined in Double-Wall Carbon Nanotubes. Phys. Rev. E 2007, 76, 021505. 10.1103/PhysRevE.76.021505. [DOI] [PubMed] [Google Scholar]
- Murata K.-i.; Tanaka H. Liquid–Liquid Transition without Macroscopic Phase Separation in a Water–Glycerol Mixture. Nat. Mater. 2012, 11, 436–443 10.1038/nmat3271. [DOI] [PubMed] [Google Scholar]
- Kobayashi M.; Tanaka H. Possible Link of the V-Shaped Phase Diagram to the Glass-Forming Ability and Fragility in a Water-Salt Mixture. Phys. Rev. Lett. 2011, 106, 125703. 10.1103/PhysRevLett.106.125703. [DOI] [PubMed] [Google Scholar]
- Corradini D.; Gallo P.; Buldyrev S. V.; Stanley H. E. Fragile-to-Strong Crossover Coupled to the Liquid-Liquid Transition in Hydrophobic Solutions. Phys. Rev. E 2012, 85, 051503. 10.1103/PhysRevE.85.051503. [DOI] [PubMed] [Google Scholar]
- Poole P. H.; Becker S. R.; Sciortino F.; Starr F. W. Dynamical Behavior near a Liquid–Liquid Phase Transition in Simulations of Supercooled Water. J. Phys. Chem. B 2011, 115, 14176–14183 10.1021/jp204889m. [DOI] [PubMed] [Google Scholar]
- Starr F. W.; Sciortino F.; Stanley H. E. Dynamics of Simulated Water under Pressure. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1999, 60, 6757–6768 10.1103/PhysRevE.60.6757. [DOI] [PubMed] [Google Scholar]
- Gallo P.; Rovere M.; Chen S. H. Dynamic Crossover in Supercooled Confined Water: Understanding Bulk Properties through Confinement. J. Phys. Chem. Lett. 2010, 1, 729–733 10.1021/jz9003125. [DOI] [Google Scholar]
- Gallo P.; Rovere M. Mode Coupling and Fragile to Strong Transition in Supercooled Tip4p Water. J. Chem. Phys. 2012, 137, 164503. 10.1063/1.4759262. [DOI] [PubMed] [Google Scholar]
- Pinnick E. R.; Erramilli S.; Wang F. Predicting the Melting Temperature of Ice-Ih with Only Electronic Structure Information as Input. J. Chem. Phys. 2012, 137, 014510. 10.1063/1.4731693. [DOI] [PubMed] [Google Scholar]
- Akin-Ojo O.; Song Y.; Wang F. Developing Ab Initio Quality Force Fields from Condensed Phase Quantum-Mechanics/Molecular-Mechanics Calculations through the Adaptive Force Matching Method. J. Chem. Phys. 2008, 129, 064108. 10.1063/1.2965882. [DOI] [PubMed] [Google Scholar]
- Akin-Ojo O.; Wang F. The Quest for the Best Nonpolarizable Water Model from the Adaptive Force Matching Method. J. Comput. Chem. 2011, 32, 453–462 10.1002/jcc.21634. [DOI] [PubMed] [Google Scholar]
- Song Y.; Akin-Ojo O.; Wang F. Correcting for Dispersion Interaction and Beyond in Density Functional Theory through Force Matching. J. Chem. Phys. 2010, 133, 174115. 10.1063/1.3503656. [DOI] [PubMed] [Google Scholar]
- Hu H.; Ma Z.; Wang F., Chapter Two - On the Transferability of Three Water Models Developed by Adaptive Force Matching. In Annu. Rep. Comput. Chem.; Ralph A. W., Ed.; Elsevier: Boston, 2014; Vol. 10, pp 25–43. [Google Scholar]
- Poole P. H.; Sciortino F.; Essmann U.; Stanley H. E. Phase Behaviour of Metastable Water. Nature 1992, 360, 324–328 10.1038/360324a0. [DOI] [Google Scholar]
- Xu L.; Kumar P.; Buldyrev S. V.; Chen S.-H.; Poole P. H.; Sciortino F.; Stanley H. E. Relation between the Widom Line and the Dynamic Crossover in Systems with a Liquid–Liquid Phase Transition. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 16558–16562 10.1073/pnas.0507870102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wikfeldt K. T.; Huang C.; Nilsson A.; Pettersson L. G. M. Enhanced Small-Angle Scattering Connected to the Widom Line in Simulations of Supercooled Water. J. Chem. Phys. 2011, 134, 214506. 10.1063/1.3594545. [DOI] [PubMed] [Google Scholar]
- Gallo P.; Sciortino F.; Tartaglia P.; Chen S. H. Slow Dynamics of Water Molecules in Supercooled States. Phys. Rev. Lett. 1996, 76, 2730–2733 10.1103/PhysRevLett.76.2730. [DOI] [PubMed] [Google Scholar]
- Angell C. A. Formation of Glasses from Liquids and Biopolymers. Science 1995, 267, 1924–1935 10.1126/science.267.5206.1924. [DOI] [PubMed] [Google Scholar]
- Ciccotti G.; Jacucci G.; McDonald I. R. Thought-Experiments” by Molecular Dynamics. J. Stat. Phys. 1979, 21, 1–22 10.1007/BF01011477. [DOI] [Google Scholar]
- Hess B. Determining the Shear Viscosity of Model Liquids from Molecular Dynamics Simulations. J. Chem. Phys. 2002, 116, 209–217 10.1063/1.1421362. [DOI] [Google Scholar]
- Angell C. A. Relaxation in Liquids, Polymers and Plastic Crystals — Strong/Fragile Patterns and Problems. J. Non-Cryst. Solids 1991, 131–133Part 113–31 10.1016/0022-3093(91)90266-9. [DOI] [Google Scholar]
- Luo J.; Xu L.; Lascaris E.; Stanley H. E.; Buldyrev S. V. Behavior of the Widom Line in Critical Phenomena. Phys. Rev. Lett. 2014, 112, 135701. 10.1103/PhysRevLett.112.135701. [DOI] [PubMed] [Google Scholar]
- Hallett J. The Temperature Dependence of the Viscosity of Supercooled Water. Proc. Phys. Soc., London 1963, 82, 1046–1050 10.1088/0370-1328/82/6/326. [DOI] [Google Scholar]
- Sutterby J. L. Falling Sphere Viscometer. J. Phys. E: Sci. Instrum. 1973, 6, 1001–1005 10.1088/0022-3735/6/10/016. [DOI] [Google Scholar]
- Keys A. S.; Abate A. R.; Glotzer S. C.; Durian D. J. Measurement of Growing Dynamical Length Scales and Prediction of the Jamming Transition in a Granular Material. Nat. Phys. 2007, 3, 260–264 10.1038/nphys572. [DOI] [Google Scholar]
- Chen S. H.; Zhang Y.; Lagi M.; Chong S. H.; Baglioni P.; Mallamace F. Evidence of Dynamic Crossover Phenomena in Water and Other Glass-Forming Liquids: Experiments, Md Simulations and Theory. J. Phys.: Condens. Matter 2009, 21, 504102. 10.1088/0953-8984/21/50/504102. [DOI] [PubMed] [Google Scholar]