Functional Magnetic Resonance Imaging Methods

Abstract

Since its inception in 1992, Functional Magnetic Resonance Imaging (fMRI) has become an indispensible tool for studying cognition in both the healthy and dysfunctional brain. FMRI monitors changes in the oxygenation of brain tissue resulting from altered metabolism consequent to a task-based evoked neural response or from spontaneous fluctuations in neural activity in the absence of conscious mentation (the “resting state”). Task-based studies have revealed neural correlates of a large number of important cognitive processes, while fMRI studies performed in the resting state have demonstrated brain-wide networks that result from brain regions with synchronized, apparently spontaneous activity. In this article, we review the methods used to acquire and analyze fMRI signals.

1 Introduction

Functional Magnetic Resonance Imaging (fMRI) is a neuroimaging tool that employs MRI to image dynamic changes in brain tissue that are caused by changes in neural metabolism. Alterations of neural activity may be caused by asking the subject to perform a task designed to target a specific cognitive process, or can occur spontaneously while the subject is resting in the absence of conscious mentation (i.e., in the “resting state”). Both types of studies- task-based and resting state, have become indispensible tools for studying cognition in healthy as well as diseased brains, and tens of thousands of studies have been published (>150,000 listed in http://www.ncbi.nlm.nih.gov/pubmed under “fMRI; brain”) in the 2+ decades since nearly simultaneous introduction of the technique by three independent groups (Bandettini, Wong et al. 1992, Kwong, Belliveau et al. 1992, Ogawa, Tank et al. 1992).

The MR contrast mechanism used for virtually all fMRI relies on blood oxygenation level dependent (BOLD) changes in brain tissue, exhibited when a brain region experiences altered levels of oxygen consumption consequent to up- or down-regulated metabolic activity caused, e.g., by performing a cognitive task (Ogawa, Tank et al. 1992). When there is a local increase in neural (and glial) activity, concomitant increases in aerobic and anaerobic oxygen consumption trigger increased delivery of fully oxygenated hemoglobin through vasodilatory (Raichle, Grubb et al. 1976, Roland and Larsen 1976, Sokoloff, Reivich et al. 1977, Fox, Raichle et al. 1988, Malonek and Grinvald 1996) processes that increase Cerebral Blood Flow (CBF) to the region. For reasons that are still not fully understood (Fox and Raichle 1986, Frahm, Merboldt et al. 1994, Buxton, Wong et al. 1998), oxygen supply transiently exceeds demand, which results in a net increase in local oxygenation for several seconds (Fig. 1). Thus, the endogenous deoxyhemoglobin (Hb) is dynamically replaced with oxyhemoglobin (HbO2), and is accompanied by a transient increase in intravascular blood volume, resulting in a change in oxygenation state. Because Hb is paramagnetic while HbO2 is diamagnetic, the change in state from paramagnetic to diamagnetic results in a decrease in R2 and R2* relaxivity rates (Thulborn, Waterton et al. 1982, Ogawa, Lee et al. 1990). Thus, an MRI sequence with T2 (1/R2) or T2* (1/R2*) weighting can demonstrate BOLD contrast, and therefore signal neural activity changes through this hemodynamically driven process.

Figure 1.

BOLD contrast results from hemodynamically driven changes in blood oxygen level due to the difference in magnetic state of oxygenated hemoglobin (diamagnetic) molecules versus deoxygenated hemoglobin (paramagnetic) in capillaries and surrounding tissue. During activation (B) increased blood flow and blood volume causes reduction in endogenous Hb, increasing the T2*-weighted MRI signal relative to the baseline state (A).

The microgradients in magnetic field that surround vessels and capillaries filled with Hb result in two forms of BOLD contrast (Bandettini, Wong et al. 1994, Weisskoff, Zuo et al. 1994). The first is due to intravoxel dephasing, which is most prominent near larger vessels, and which causes T2* weighted signal loss. This contrast increases linearly with magnetic field strength and is readily observed with gradient recalled echo (GRE) imaging. The second type of contrast is due to diffusion of spins through the microgradients, causing a reduction in T2-weighted signal detected by spin echo (SE) MRI. The diffusion mechanism is most prominent when the distance the spins diffuse during the signal acquisition is comparable to the spatial extent of the microgradients, which thereby tunes this mechanism to be most sensitive to detecting BOLD contrast in capillaries (Weisskoff, Zuo et al. 1994). Diffusion contrast is proportional to the square of the magnetic field strength. Therefore, as the field is increased, the weighting of T2 contrast increases relative to T2* weighted contrast, with the result that in fields of 4T and higher BOLD contrast is more localized to tissue than to the larger veins when SE acquisitions are employed (Yacoub, Shmuel et al. 2001). By contrast, with GRE acquisitions at 7T the T2* of veins is so short the venous contribution becomes small and diffusion weighting from tissue microstructure dominates (Geissler, Fischmeister et al. 2013). Because of this, SE acquisitions are to be preferred at 7T, although SE methods have higher RF power deposition (Specific Absorption Rate, SAR), which may reduce the number of slices that can be collected.

Gradient recalled acquisitions suffer signal loss from static magnetic field distortions that are caused by magnetic susceptibility differences at air-tissue interfaces, for example in frontal orbital or lateral parietal brain regions. These gradients in magnetic field (~9 ppm difference in susceptibility between air and brain tissue) are large enough to cause signal dropout artifacts from intravoxel dephasing in GRE acquisitions. Spin echo methods refocus the static field heterogeneities, and therefore do not have signal dropout. The relationships between contrast, artifacts and field strength are summarized in Table 1.

Table 1.

Relationships between field strength for GRE & SE acquisition type, BOLD contrast mechanism, dropout severity (IvD = intravoxel dephasing, Diff = diffusion)

B0	Acquisition	BOLD Contrast	Dropout Artifact
≤3T	GRE	(veins : IvD) > (tissue : Dif)	↑
	SE	(tissue : Diff)	-
7T	GRE	(tissue : Diff) ↑	↑↑
	SE	(tissue : Diff) ↑	-

At this time, 7T and higher field magnets are not in widespread use, so that the majority of fMRI studies are performed at 3T (in which T2 and T2*-weighted contrasts are comparable or 1.5T, which is mostly sensitive to BOLD contrast in the draining veins (Kruger and Glover 2001, Kruger, Kastrup et al. 2001). Therefore, it would be wise to avoid 1.5T for neuropsychological studies whenever possible, to obtain the most accurate depiction of cognitive processes.

As we have indicated, there are two primary types of fMRI studies- those in which a cognitive task is used to modulate specific neuronal activity, and resting state studies. In either case, a dynamic series of T2*-weighted scans is acquired, resulting in (Kruger, Kastrup et al. 2001) a time series of signals for every brain voxel. These time series are submitted to various levels of correction and denoising (preprocessing steps) before model- or data-driven analyses are applied to obtain maps of activity. Because BOLD signals are tiny- typically a few percent or less- such analyses use statistical methods to discern false from true activation at a given confidence level.

This article reviews the methods employed to acquire and process BOLD fMRI data, with which to draw inferences regarding neural processes. We will not examine other methods often used in conjunction with fMRI such as Diffusion Tensor Imaging (DTI) (Le Bihan, Breton et al. 1986), which can depict or summarize structure of white matter, or Arterial Spin Labeling (ASL) (Williams, Detre et al. 1992), used to map the CBF either in stasis or during task manipulation. Similarly, despite the increasing interest in combining fMRI with other imaging modalities in order to obtain complementary information in the spatiotemporal (e.g., Electorencephalography (EEG) (Teplan 2002), or metabolic (e.g., Near Infrared Spectroscopy (NIRS) (Ferrari, Giannini et al. 1985) and Positron Emission Tomography (PET) (Raichle 1989) domains, these topics are beyond the scope of this review.

2. The fMRI experiment

2.1 Task-based fMRI

In task-based fMRI, time series data are compared against a hypothesized model of neural function based upon the cognitive task being performed. Through the use of statistical inference the hypothesis can be accepted or rejected for every voxel. In this way, a map of those brain regions that respond to the task is constructed, and can be further tested against phenotypical or genotypical models or parametric manipulations of the task, e.g., difficulty.

The typical fMRI experiment employs sensory stimuli to cue the participant to perform a behavioral task while BOLD contrast images are acquired for a fixed duration of minutes (see Fig. 2). Such stimuli can be visual, auditory or of other forms depending on the desired behavioral manipulation. In all cases, the task design employs a modulation of the behavior being studied within each scan (state A – experimental and state B – control in Fig. 2) so that the range of BOLD contrast elicited by the manipulation between experiment and control conditions is captured within one scan. This is important because MRI signal intensities are subject to drifts from instrument instability or changes in participant habitus or physiology that are unrelated to the effect of interest, which makes it difficult to develop accurate estimates of BOLD contrast changes from separate scans.

Figure 2.

Task-based fMRI experiment acquires a time series of images while participant performs cognitive manipulation that causes a change between brain states A and B. The functional map depicts those regions that were more metabolically activated in state A than B, using a statistical test to demonstrate significant signal differences in each voxel.

Task designs are commonly of the “Block Trial” type, “Event-related (ER) Trial” type (Dale and Buckner 1997, Dale 1999, Miezin, Maccotta et al. 2000, Ollinger, Corbetta et al. 2001, Liu 2012) or “Mixed Trials” (Chawla, Rees et al. 1999, Visscher, Miezin et al. 2003, Petersen and Dubis 2012), as shown in Fig. 3. In each case the effect size is inferred from the difference in BOLD contrast between the two states. However, note that because the measured signal is a hemodynamic response to changes in local brain metabolism and therefore only an indirect measure of neural responses, the hemodynamic process itself must be considered in the design of the signal model used to test for activation. A typical Hemodynamic Response Function (HRF), i.e., the BOLD signal obtained from a single brief activation event, is shown in Fig. 4 (Friston, Josephs et al. 1998). The HRF has the characteristic of a low-pass temporal filter, and under the linear assumption for BOLD contrast (Boynton, Engel et al. 1996, Dale and Buckner 1997), it must be convolved with the task design vector to provide the regressor that is used to test for significant activation in any voxel’s time series (see statistical analysis of task data below). As seen by the example in Fig. 4, the HRF’s filtering action can significantly attenuate short duration activity of event-related designs. It has been shown that Block designs are optimum for detecting an activation, while ER designs are most efficient for characterizing the time course of activation, and Mixed designs lie in between (Liu, Frank et al. 2001). Thus, when it is desired to simply decide whether a hypothesized activation occurs in a brain region, the Block design is most effective, but an ER design should be employed when more detailed characteristics of the neural response to the cognitive manipulation are desired (Dale 1999, Birn, Cox et al. 2002, Petersen and Dubis 2012). Of course, there are many variations on these basic designs, and some additional considerations for experimental design are described in (Huettel 2008).

Figure 3.

Types of basic task designs, showing (A) Block design, (B) Event-Related (ER) design and (C) Mixed design. The “on” and “off” levels indicate that the stimulus is either presented for the cognitive manipulation being tested or for a control condition, respectively. Block designs provide maximum detection sensitivity, while ER designs optimize the ability to characterize the time course of BOLD responses. Mixed designs can accomplish signal detection as well as response quantification.

Figure 4.

Hemodynamic Response Function (A) is convolved with an event-related design (B) to derive a regressor (C) with which to model an ER experiment. The regressor can be used either with convolution analysis or in a general linear model.

From the preceding description, statistical inferences regarding task-based brain function are drawn by testing for BOLD signal variations that significantly correlate with a hypothesized model. Therefore, any signal fluctuations unrelated to the effect of interest will degrade the power of the test because of the added unrelated variance. Examples include thermal noise (Edelstein, Glover et al. 1986), and physiological noise resulting from cardiovascular pulsatility or quasi-periodic respiration effects (Hu, Le et al. 1995, Glover, Li et al. 2000), as well as from longer-term vaso-dilatory effects (Birn, Diamond et al. 2006, Shmueli, van Gelderen et al. 2007, Chang, Cunningham et al. 2009). Corrections for these effects are discussed later as preprocessing steps. Of course, there can be cases (e.g., aversive pictures) where the task manipulation causes the participant to alter cardiac function or respiration, which can become a direct confound by causing BOLD signal changes stemming solely from the vascular response of changes in physiology (Birn, Murphy et al. 2009, Chang, Metzger et al. 2013). See later discussion of Preprocessing.

Other considerations important when setting up psychiatric fMRI experiments include possible confounds of medications and hormones. Many medications alter the brain’s vascular function, which in turn causes changes in BOLD response that can result in group differences when comparing medicated experimental populations against healthy controls. For example, even the relatively benign agent caffeine causes elevation in resting CBF and results in reduced BOLD responses due to reduced vascular reserve (Liu, Behzadi et al. 2004). Thus, it may be difficult to perform fMRI studies aiming to investigate cognitive effects of pharmacological treatments because of possible BOLD signal changes unrelated to the neural processes being explored.

2.2 Resting state fMRI

In the resting state (RS) case, the implicit hypothesis is that there are distinct brain regions whose fluctuations are temporally synchronized, and thereby are connected as nodes of networks, such as the Default Mode Network (Greicius, Krasnow et al. 2003, Buckner, Andrews-Hanna et al. 2008). Multiple networks are regularly observed (Damoiseaux, Rombouts et al. 2006, Smith, Fox et al. 2009). The acquisition of RS data is similar to that of task-basked studies, described below. The subject is typically prompted to remain still and avoid targeted mentation, while maintaining eyes open or closed for the scan duration. The latter instruction is important because it has been shown that FC differs between eyes open and closed (e.g., (Patriat, Molloy et al. 2013)). Typically heart rate and respiration data are collected for physiological denoising (see section 4.1.7 physiological noise correction).

3. Acquisition of fMRI data

FMRI scan sequences typically employ single-shot acquisitions using EPI (Mansfield 1977) or Spiral-in/out (Glover and Law 2001) k-space trajectories. Slices are typically acquired in an interleaved order (e.g., 1,3,5, …2,4,6,…), which diminishes “slice-bleed” effects (Bernstein, King et al. 2004), but which must be accounted for during “slice-timing” corrections. The main issues to be controlled during data acquisition are tradeoffs between spatial and temporal resolution, signal dropout in frontal and parietal regions and subject motion. In general, as the spatial resolution is increased, the duration of the readout increases, which makes it more sensitive to signal loss from magnetic susceptibility effects near heterogeneous brain regions. Acceleration using parallel imaging (multiple receiver coil channels) (Sodickson and Manning 1997, Pruessmann, Weiger et al. 1999, Griswold, Jakob et al. 2002) and simultaneous multiple slices (SMS) (Feinberg, Moeller et al. 2010, Setsompop, Gagoski et al. 2012) can change these tradeoffs by reducing the amount of data that need to be acquired and thereby increasing scan efficiency. SMS methods, for example, reduce the repetition time (TR) needed to acquire whole brain coverage by factors of 8 or more (e.g., (Chen, Vu et al. 2015)). The faster acquisition in turn allows more time frames to be collected, increasing the statistical power or enabling more complex temporal inferences, e.g., identifying dynamically changing brain repertoires in the temporal domain (Smith, Miller et al. 2012), but is often accompanied by reduced SNR. The higher scan efficiency afforded by acceleration can alternatively allow scan time to be reduced, thereby decreasing chances for head motion and increasing access for, and compliance by, populations such as children, older adults and patients.

Functional acquisition protocols include other sequences as well as the functional scan(s) themselves, and thus their scan times must also be considered when setting up a protocol to minimize the protocol duration. T2-weighted sequences (FSE or TSE) can be used to rapidly acquire high resolution slices with the same scan prescription as the functional scan. These are typically replaced or accompanied by T1 Inversion Recovery prepared whole brain acquisitions (3D MPRAGE or 3DFSPGR (Mugler and Brookeman 1990)) to enable normalization of subject data to a brain template in order to make group inferences (see Preprocessing below). In addition, many investigators collect diffusion tensor information in order to derive structural connectivity maps (“white matter tracks”) (Le Bihan, Breton et al. 1986), and to correlate structure with function (Werring, Clark et al. 1998, Zhu, Zhang et al. 2014). Infrequently, because of the added scan time and complexity, some studies also employ Arterial Spin Labeling (ASL) methods (Williams, Detre et al. 1992, Detre and Wang 2002, Borogovac and Asllani 2012), or hypercapnic challenges using CO2 breathing (Davis, Kwong et al. 1998, Kim, Rostrup et al. 1999) or breath holding (Kastrup, Kruger et al. 1999, Thomason, Foland et al. 2007, Chang, Thomason et al. 2008) to derive more quantitative measurements or correct for confounds such as inter-subject differences in vascular reactivity

As described previously, T2* weighting is usually employed for BOLD signal contrast, which requires long echo times (Bandettini, Wong et al. 1992), but which unfortunately also results in geometric distortion (Hutton, Bork et al. 2002) due to off-resonance near frontal-orbital and parietal regions, where the susceptibility difference between air and tissue generates substantial static magnetic field gradients. The distortion can be corrected using maps of magnetic field (see 4.1.4 distortion correction); therefore, field maps are often also acquired.

4. Analysis

4.1 Preprocessing

As fMRI detects neural activity indirectly via hemodynamic response to changes in metabolic consumption of oxygen, the collected time series are inevitably confounded by non-neurally related sources of variations, such as subjects’ head motion, physiological cycles, and magnetic field inhomogeneity. If not corrected, these unwanted fluctuations may obscure the intrinsic patterns of neural activity, reduce the detection power of further statistical analysis, or in worst cases, alter experimental conclusions by introducing structured noise that contaminates the real neurally-related results.

Several computational procedures, collectively termed as the preprocessing pipeline, have been proposed to remove the confounding sources of variations from the fMRI time series, and increase the functional signal to noise ratio (fSNR) before further analysis. The most frequently employed steps are detailed below.

4.1.1 Quality assurance

quality assurance (QA) testing is an indispensible but often ignored aspect of preprocessing in fMRI studies nowadays. The corruption of fMRI data may occur during data acquisition due to extreme scanner noise, e.g., “spike noise” or other scanner problems such as signal drift (even for the best-maintained scanner). If unnoticed, these corrupted datasets may propagate artifacts into final results of a study. To avoid frustration later with unusable data, the imaging data should be examined immediately post scan (e.g., check subjects’ motion parameters, physiological data, or view the stack of 3D brain images in a movie). In this way, it may be possible to prompt the subject to diminish excessive motion or observe and correct for instrument failures before continuing. QA procedures should also be employed throughout the preprocessing pipeline using visual inspection and simple tests (e.g., examining the mean intensity and standard derivation of slices, calculating the fSNR for each dataset (Murphy, Bodurka et al. 2007)) to guarantee the data quality prior to the next step of analysis.

4.1.2 Slice timing correction

the majority of fMRI studies use a two-dimensional pulse sequence that images one slice at a time, resulting in inconsistent acquisition time among different brain slices within one TR. Such slice-timing errors, if uncorrected, may pose severe inaccuracy in cases where the temporal information is critical, e.g., studies positing a causal relationship among different cortical regions or in rapid event-related experiments. A most common approach to correct for slice-timing errors is temporal interpolation, which estimates the signal amplitude of each slice/voxel at a reference time point by interpolating information from neighboring TRs. This method works most effectively when the single-slice sampling rate is much faster than the signal variability induced by the on-going experiment (Huettel 2008).

4.1.3 Head motion correction

subjects’ head motion is a prominent concern in most fMRI studies, particularly those involving hour-long scan duration (subjects may become increasingly drowsy and restless as time goes by), tasks requiring physical responses (subjects’ motion synchronizes with the on-going stimulus), or particular types of subjects (the young, the elderly and the diseased people).

Subjects’ head motion can affect the collected data quality in various ways. To list a few: motion mixes signals from neighboring voxels, yielding dramatic signal variability at the edge of distinct cortical regions; motion induces spurious distance-dependent variance (more similar between voxels nearby than far apart) that may alter the intrinsic correlation structure of the data; motion interplays with field inhomogeneity and slice excitation, bringing in more complicated noisy fluctuations (Huettel 2008, Van Dijk, Sabuncu et al. 2012, Power, Schlaggar et al. 2015).

Disruptive as it appears, motion can be considerably suppressed by strategies during or post acquisition. Head immobilization techniques, such as fixation devices (bite bars, masks, fixation pads- including inflatable air bags) and use of a mock scanner (training subject in a simulated environment) (Barnea-Goraly, Weinzimer et al. 2014), can diminish head movement during the scans. In addition, myriad retrospective methods have been proposed to correct for motion post acquisition (see (Power, Schlaggar et al. 2015) for a review of approaches and associated concerns). These approaches generally rely on motion parameters characterized by rigid body realignment, which assumes the brain to be a rigid object and estimates at each time point its displacement from a reference position (along three translational and three rotational axes). Motion induced signal variance can be mitigated by projecting the motion measures together with their higher order derivatives out of the data (Friston, Williams et al. 1996, Satterthwaite, Elliott et al. 2013, Yan, Cheung et al. 2013, Power, Mitra et al. 2014), or realigning the brain volume acquired at each time point to a fixed position using spatial interpolation. One may also identify those problematic time points by visually inspecting the time series of motion parameters, and apply censoring (excluding those volumes from further analysis, e.g., (Barch, Sabb et al. 1999, Lemieux, Salek-Haddadi et al. 2007, Kennedy and Courchesne 2008)), or temporal interpolation (extrapolating adjacent volumes, (Power, Mitra et al. 2014)) to suppress motion artifacts. Alternative to approaches that employ the estimated motion parameters, several other techniques attempt to extract motion-related fluctuations from the collected data itself based on its disparity with neural-related fluctuations in spatial distribution and temporal characteristics (Liao, Krolik et al. 2005, Behzadi, Restom et al. 2007, Kundu, Inati et al. 2012, Satterthwaite, Elliott et al. 2013, Patel, Kundu et al. 2014).

As an alternative to retrospective motion correction applied during preprocessing, prospective motion correction (“Promocor”) techniques can be employed during acquisition (see (Maclaren, Herbst et al. 2013) for a review). These methods utilize head position information to adjust the slice plane as the scan progresses so that the imaging plane orientation attempts to follow that of the head. One class of methods uses motion information acquired from the fMRI images or a navigator to alter the scan plane for the next TR. While this method requires no additional instrumentation, it is only applicable for motion that is slow compared to the slice collection time (TR/number_slices) because the correction always lags the motion by one TR. Another class of Promocor methods employs external instruments (visual (Forman, Aksoy et al. 2011) or electrical (Sengupta, Tadanki et al. 2014) to track head orientation in order to obtain truly real-time (<TR) orientation information. Such methods have improved correction but entail additional setup time for the tracking device.

4.1.4 Distortion correction

fMRI signals may suffer from geometric or intensity distortion due to inhomogeneity in the static/excitation fields. Field heterogeneity distorts the shape and location of tissue in the image because the reconstruction assumes a linear relationship between signal frequency and space. Hardware shimming embedded in the MR system can compensate for the magnetic field non-uniformity to a certain extent. In addition, techniques have been developed to correct for distortion in the reconstructed MR images by measuring the field heterogeneity with an additional acquisition of a magnetic field map and employing image or k-space interpolation during reconstruction (Jezzard and Balaban 1995, Hutton, Bork et al. 2002, Cusack, Brett et al. 2003, Sutton, Noll et al. 2003), or in cases when the field maps are not available (Sled, Zijdenbos et al. 1998, Arnold, Liow et al. 2001, Lewis and Fox 2004, Studholme, Cardenas et al. 2004, Vovk, Pernus et al. 2004).

4.1.5 Temporal filtering

in cases where the spectrum distributions of signal and noise components do not strictly overlap with each other, temporal filtering – which eliminates noisy frequencies but preserves signal frequency – can help enhance fSNR of the data. For instance, in studies employing block-design paradigm (the task-related signals reside in very narrow frequency bands), the detection power of the experiments can be effectively improved by suppressing the power of frequencies other than that of the task. Another common type of temporal filtering is to remove the slow fluctuations induced by scanner drift. Such high-pass filtering procedure is also referred to as detrending (Tanabe, Miller et al. 2002), and has been included as a routine step in most software packages. Besides improving fSNR of a time series, moderate temporal filtering can also reduce the bias in ensuing statistical analysis by obscuring the disparity between assumed and intrinsic models of the data (Friston, Josephs et al. 2000).

4.1.6 Spatial smoothing

Benefits from spatial smoothing are mainly threefold. First, spatial smoothing can improve the fSNR of the data. Due to functional similarity of adjacent brain areas and signal blurring caused by vascular origins, fMRI data are inherently spatially correlated as acquired. As a result, proper spatial smoothing, i.e., typically implemented by convolving the data with a Gaussian kernel that matches the inherent spatial correlation of fMRI data, could suppress noise sources uncorrelated among adjacent imaging voxels and increase the tSNR of the data (Lowe and Sorenson 1997, Skudlarski, Constable et al. 1999, Parrish, Gitelman et al. 2000, LaConte, Anderson et al. 2003). Second, spatial smoothing may also improve the validity of ensuing statistical analysis by mitigating the difference between inherent spatial structure of the data and the assumed model, e.g., increasing the Gaussianity of the data (a key assumption of the general linear model, and random field theory (Worsley, Cao et al. 1998)), or achieving valid estimation of the degrees of freedom in ensuing multiple comparisons (Worsley 2005). Lastly, proper spatial smoothing can also ameliorate the anatomical or functional variations among different subjects. Unfortunately, the optimum kernel sizes determined by different goals above are not consistent. For example, to maximize fSNR, the kernel size should match the spatial correlations of each region, while to approximate the assumed smooth Gaussian field, the ideal kernel size should be at least twice the size of a voxel (Worsley 2005). Meanwhile, several drawbacks of spatial smoothing should be considered as well. For instance, a larger kernel size will reduce the spatial resolution of acquired data, and may blur the functional boundaries or shift the activation loci of a task to an unacceptable level (Geissler, Lanzenberger et al. 2005, Sacchet and Knutson 2013). Therefore, there is inherent difficulty in choosing an appropriate kernel size (see (White, O'Leary et al. 2001, Worsley 2005, Scouten, Papademetris et al. 2006, Mikl, Marecek et al. 2008, Weibull, Gustavsson et al. 2008) for exploratory studies and detailed discussions). As oversimplified recommendations for conventional studies adopting fixed kernel size throughout the brain (in contrast to adaptive smoothing strategies, e.g., (Penny, Trujillo-Barreto et al. 2005, Yue, Loh et al. 2010)), a modest smoothing kernel size (~4mm) is suggested for single subject analysis, while a wider kernel size (6~8mm) can be applied for a group-level analysis. However, examining the results with no or modest kernel width is always recommended when a wide smoothing kernel is applied.

4.1.7 Physiological noise correction

as BOLD contrast originates from hemodynamically-driven changes in tissue and vessel oxygenation, it naturally contains non-neural fluctuations incurred by physiological processes, such as cardiac pulsatility and respiration (Birn 2012).

Briefly, the cardiac and respiratory-related physiological noise can be classified into two categories based on their spectral distributions. The first category refers to time-locked fluctuations directly synchronized with the cardiac (~0.8–1.3 Hz) and respiratory cycles (~0.1–0.3 Hz): cardiac pulsatility induces tissue movement and blood inflow that may cause signal fluctuations adjacent to large brain vessels (Dagli, Ingeholm et al. 1999); respiration engenders chest movement that can alter the magnetic susceptibility and MR signal intensity (Raj, Anderson et al. 2001, Brosch, Talavage et al. 2002). Such periodical noises have been demonstrated to be greater than system and thermal noise at 3T or higher magnetic field (Kruger and Glover 2001). With effectively faster acquisition (e.g., TR < 0.5s), the cyclic fluctuations can be resolved and temporally filtered out of the data (Biswal, DeYoe et al. 1996, Mitra and Pesaran 1999). However, despite the emergence of fast acquisition techniques, the majority of fMRI studies nowadays still use TR ≥ 2s for the whole brain acquisition, causing the cardiac noise to be aliased onto lower frequencies. To correct for the aliased physiological noise, several retrospective techniques have been proposed (Hu, Le et al. 1995, Le and Hu 1996, Glover, Li et al. 2000, Chuang and Chen 2001, Pfeuffer, Van De Moortele et al. 2002, Verstynen and Deshpande 2011). These approaches first characterize the physiological noise by either modeling them from external physiological recordings (e.g., photoplethysmography, respiratory belt and pulse oximetry (Verstynen and Deshpande 2011)), or estimating them directly from the acquired data, then extract the estimated noisy fluctuations out of the time course of each voxel.

A second category of physiological noise relates to variations of respiratory volume and heart rate. Variations of breathing depth and rate lead to altered levels of arterial CO₂, a potent vasodilator modulating blood flow and consequently the amplitude of BOLD signals (Modarreszadeh and Bruce 1994, Van den Aardweg and Karemaker 2002, Wise, Ide et al. 2004, Birn, Diamond et al. 2006, Birn, Murphy et al. 2008, Chang and Glover 2009). The variability of heart rate possesses, which extends to broader spectrum compared to pulsalitity cycles, has been shown to account for considerable amounts of BOLD fluctuations in resting state (Shmueli, van Gelderen et al. 2007, Chang, Cunningham et al. 2009). Numerous studies have been proposed to model such noisy fluctuations from external recordings of physiological data (Birn, Smith et al. 2008, Chang, Cunningham et al. 2009, Verstynen and Deshpande 2011) or the data itself (in a manner similar to the removal of motion artifacts) (Beall and Lowe 2007, Behzadi, Restom et al. 2007, Perlbarg, Bellec et al. 2007, Weissenbacher, Kasess et al. 2009, Jo, Saad et al. 2010, Anderson, Druzgal et al. 2011).

4.1.8 Functional-structural co-registration

the collected 3D stack of anatomical and functional images generally do not match each other due to different MR contrasts and acquisitions (e.g., inconsistent slice orientation, voxel resolution and image distortion), causing problems in mapping activity (from functional data, e.g., the task-activation map) to the anatomical image. Computational procedures that map functional and structural images to each other are termed functional-structural co-registration. These procedures typically resample the anatomical data to the spatial resolution of functional data first, then employ a rigid body transformation where a cost function (e.g., mutual information) is minimized (see (Gholipour, Kehtarnavaz et al. 2007, Klein, Andersson et al. 2009) for reviews).

4.1.9 Spatial normalization

In most neuroscience studies, we may need to aggregate brain activities across multiple individuals. Given that the shape and size of brains are rather inconsistent across subjects, a standard approach is to normalize each individual’s brain to a template estimated locally from specific populations (Guimond, Meunier et al. 2000) or published ones (Talairach atlas (Talairach 1988) and MNI templates are most commonly used, see (Brett, Johnsrude et al. 2002, Devlin and Poldrack 2007, Lancaster, Tordesillas-Gutierrez et al. 2007) for differences and transformations between the two coordinate systems). Spatial normalization can be intensity, landmark, or surface based (see (Gholipour, Kehtarnavaz et al. 2007, Klein, Andersson et al. 2009) for reviews). It is typically implemented by either registering each individual’s functional images to a functional template directly, or in two steps: (1) co-registering functional and structural images; (2) registering the anatomical image to a high-resolution structural template. These two approaches each have their own advantages and shortcomings – the former approach avoids inconsistent geometric distortions induced by different imaging contrasts; while the latter approach appears more robust due to improved resolution and quality of the structural image – the employment of which depends on the particular scanning environment and imaging protocols.

For reference, Fig. 5 offers a summary framework for preprocessing of fMRI data. Notably, the determination of specific preprocessing pipeline interacts with numerous factors, e.g., types of stimulus, experimental hypothesis, and acquisition environment (Strother 2006, Huettel 2008). For instance, it is more proper to perform slice time correction prior to motion correction with interleaved slice acquisition, while the order should be switched in a sequential acquisition (green rectangle). Moreover, for processes that operate linearly on the datasets, switching orders would yield no differences in the final results (e.g., procedures in the pink rectangle). Furthermore, it can be questioned whether to normalize the functional images prior to or after statistical analysis. The former avoids extra smoothing, image distortions introduced by imperfect normalization in the ensuing analysis, whereas the latter makes statistical analysis demanding matched voxels from different subjects plausible (e.g., group independent component analysis (Calhoun, Adali et al. 2001), atlas-based graph analysis).

Figure 5.

The basic scheme of preprocessing pipelines.

The preprocessing steps listed above apply to different task paradigms as well as resting state scans. Compared to block trial type designs, event-related designs have relatively lower detection power and high demand on the temporal precision. Therefore, removal of various non-neural confounds and slice timing correction are essential and indispensible for event-related studies. In resting state studies, an additional procedure – global signal regression (GSR) is sometimes included in the preprocessing pipeline. GSR averages the time series across all brain voxels and projects the averaged global signal out of each voxel’s time series using linear regression, assuming that the averaged signal is dominated by non-neural fluctuations that affects brain’s time series globally. GSR has been shown to improve the specificity of functional connectivity, mitigate motion artifacts (Satterthwaite, Elliott et al. 2013, Yan, Cheung et al. 2013, Power, Mitra et al. 2014), and yield prominent anti-correlations in resting state studies (Fox, Snyder et al. 2005, Fox, Zhang et al. 2009). However, this procedure has been controversial in resting state studies, because global signal may also carry information related to neural activity (Scholvinck, Maier et al. 2010, Wong, Olafsson et al. 2013). Moreover, it has been shown both theoretically and practically that GSR shifts the center of correlation values (by reducing positive correlations and introducing artificial negative correlations) such that all the correlation values across the brain sum to a negative value (Murphy, Birn et al. 2009, Weissenbacher, Kasess et al. 2009, Saad, Gotts et al. 2012, Gotts, Saad et al. 2013). Therefore, the inclusion of GSR as a preprocessing procedure is advised with great caution. Generally, noise sources that affect large areas of the brain (e.g., physiological noise, motion) can be modeled by reasonable alternatives discussed earlier (see 4.1.3 head motion correction, 4.1.7 physiological noise correction above). However, there are a few situations where GSR can be considered. For instance, if the alternative methods are not accessible (e.g., without external recordings of cardiac or respiratory waveforms) or the data contain global confounds that cannot be effectively modeled by existing approaches, GSR could be tested, but it is highly recommended to reexamine the results without GSR. Besides, in studies that do not directly investigate the interaction patterns among different brain regions, e.g., using pattern recognition methods to classify two mental states, GSR could be employed as a common data manipulation procedure. One needs to be careful with the interpretation of results, because the inherent interaction structure of the brain has already been altered.

As introduced in the acquisition section, there has been growing interest in fMRI studies with faster sampling rates (from conventional seconds to sub-second scales). Faster acquisition promises higher temporal resolution, increased statistical power (more sampling points with a fixed scan duration), and the examination of neural information in higher frequency bands. The majority of existing studies with faster acquisition (Wu, Gu et al. 2008, Boubela, Kalcher et al. 2013, Boyacioglu, Beckmann et al. 2013, Lee, Zahneisen et al. 2013, Chen and Glover 2015, Gohel and Biswal 2015) still follow the routine preprocessing pipeline employed in conventional studies, which may lack rigorous validation. We mention a few concerns regarding this issue that warrant careful explorations in the future. First, as BOLD contrast results from an inherently slow hemodynamic process, the spectrum of observed neural information (<0.3 Hz according to the canonical HRF model in SPM8, Wellcome Trust Centre for Neuroimaging, University College London, UK) is less likely to accommodate the observation of functional connectivity at very high frequencies. It is therefore not yet clear whether one can apply similar de-noising procedures as used previously to the observed high-frequency (> 0.1 Hz) BOLD functional connectivity data (see (Chen and Glover 2015) for discussion of HRF in the resting state and tSNR vs. frequency).. Second, BOLD time series are inherently auto-correlated, suggesting that the effective number of degrees of freedoms will not scale linearly with the number of time frames collected at a fixed scan duration. Unfortunately, properly accounting for the degrees of freedom is ignored in many studies, leading to over-estimation of statistical significance. Third, the energy of BOLD time series is dominated by low-frequency signals (e.g. at resting state, power spectrums of spontaneous fluctuations mainly reside below 0.1 Hz). As a result, if we apply the conventional preprocessing pipeline to acquired full band time series, parameter fittings involved in different steps may be driven by the low-frequency data and cannot effectively de-noise the high-frequency band data. For instance, if we linearly project motion regressors (see 4.1.3 motion correction above) out of each voxel’s time series, the scaling parameter of each regressor would to a large extent depend on the low-frequency component (main fluctuation) of each time series. However, there has been no clear evidence that the relative relationships between signals and motion noises are consistent across different frequencies. Indeed, additional noise (high-frequency components of the motion regressors) may be introduced due to this preprocessing step and alter the structure of true neural-related high-frequency signals.

4.2 Analysis of task studies

After preprocessing, the next step is to examine the research hypothesis of the designed experiment. In this section, we take the two-condition blocked design (experimental vs. control), a widely adopted experimental paradigm in fMRI studies, as an example to illuminate several common methodologies of statistical analysis.

In this particular setting, we want to identify voxels actively involved in the imposed task, i.e., voxels whose temporal behaviors differ significantly between the experimental and control conditions. Specifically, we test the research hypothesis H₁: experimental condition ≠ control condition, against its null hypothesis H₀: experimental condition = control condition.

4.2.1 The t test

To introduce the concept of statistical inference in fMRI, the simplest procedure is to treat each time point as an independent sample (at least initially we assume so), and compare signal amplitudes under different conditions using a standard two-sample student’s t test. This procedure is repeated for each brain voxel. To quantify the statistical significance of the estimated t-value, a p value is defined – the chance of observing a statistic t-value or more extreme results under the null hypothesis. If a voxel’s p value is smaller than a user defined significance level α, we can hence reject the null hypothesis and classify the voxel as ‘active’.

Primary challenges of the t-test analysis are twofold. First, the fMRI time series is filtered by a sluggish hemodynamic process; as a result the actual response of an active voxel may lag ~5s of the condition boxcar, requiring that this delay be accounted for in assigning time points to one or the other state. More importantly, the transition between brain states cannot be represented as belonging uniquely to either state, which can represent a serious loss of statistical power. Therefore, straightforward as it appears, this t-test approach is rarely used directly with time series data in fMRI studies.

4.2.2 Correlation Analysis

A more elegant approach is to examine the temporal synchrony between each voxel’s time series and the predicted response of the experiment (Bandettini, Jesmanowicz et al. 1993) – derived by convolving the task-control boxcar waveform with a canonical HRF. The correlation coefficient (eqn. (1)) is the most frequently used metric to quantify the correspondence (or sometimes referred to as functional connectivity) between two time series x and y (equal length):

$$r=\frac{1}{n-1}\frac{\mathrm{\Sigma }(x-\overline{x})(y-ȳ)}{{\sigma }_x{\sigma }_y}$$ eqn. (1)

where n denotes the number of time points per signal, x̄/ȳ and σ_x/σ_y denote the means and standard deviations of x and y.

The correlation coefficient r ranges from −1 to 1, with 0 meaning no correlation (the null hypothesis), and ±1 meaning perfect positive/negative correlations. An r value can be converted to student’s t-value based on its degrees of freedom (unconstrained number of parameters), and we can therefore identify active voxels using similar ways introduced above (see the t test above). To allow for the variability of temporal delays in HRFs across different brain voxels, cross correlation – which estimates the correlation coefficient as a function of the temporal lag of one signal relative to the other, may be applied (Friston 1994).

Correlation analyses can only be applied when a single hypothesis is to be tested, i.e.,, to test a voxel’s time series against another time series, such as that generated as a model for activation as described above, or to test for similarity with the time series of another voxel in resting state studies. However, fMRI experiments frequently involve more than one manipulation or condition to characterize responses during different temporal events within the scan, i.e., there are multiple hypotheses to be tested. In this case, correlation analysis cannot be used, and a more general method must be employed, as described next.

4.2.3 The general linear model (GLM) analysis

As an alternative to or expansion upon correlation analysis, the GLM analysis has been widely employed in the fMRI community to examine the temporal synchrony between experimental observations and the predicted responses (see Fig. 6A) (Friston 1995). Briefly, the fMRI time series y, is modeled as a linear mixture of several model factors (e.g., predicted task response) and white Gaussian distributed additive noise term ε as below:

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2\dots +{\beta }_n{x}_n+\epsilon$$ eqn. (2)

Figure 6.

The majority of model-based and model-free analyses in fMRI studies can be incorporated into a coherent scheme of matrix decomposition. Specifically, the 4-D fMRI dataset can be rearranged into a 2-D matrix by aligning all voxels of the same time point in a row; different approaches (e.g., GLM (A), MVPA (B), ICA/PCA (C)) attempt to decompose the 2-D matrix into sub-components by imposing various assumptions of the de-composed matrix structure (blue rectangles), then extract the spatial patterns (network patterns, pink rectangles) of neural-related contributions.

where x_i denotes each model factor, and the parameter weight β_i is the scaling term indicating the contribution of a model factor to the dependent variable y. When y refers to a large number of dependent variables, such as different time points across a scan in an fMRI study, eqn. (2) represents the GLM.

Statistical testing of the GLM estimates how well each voxel’s time series is fit by the linear combination of model factors. There exist routine ways (if the autocorrelation structure of ε is known) of converting the fitted results to t-, or F-statistics to assess the significance of each model factor’s contribution to y (assuming the null hypothesis: β_i = 0, i > 0, i.e., no contribution from x_i) (Friston, Holmes et al. 1995, Worsley and Friston 1995).

For instance, in the two-conditioned block task case, we can estimate each voxel’s task relevance by including a single model factor x₁ (the predicted response), and testing the statistical significance of β₁. This is equivalent to correlational analysis. Through versatile modifications of model factors, this approach allows more flexible shapes of the predicted response (originating from inconsistent temporal delays and variability of HRF shapes across different brain regions), details can be found in chapter 5 of (Poldrack 2011), and chapter 10 of (Huettel 2008).

Compared to correlation analysis, the GLM approach allows for more flexible experimental designs (e.g., experiments involving three or more cognitive conditions), and can include any known sources of variability as model factors, such as nuisance components (e.g., motion parameters, physiological fluctuations) and non-imaging information (e.g., subjects’ age and behavioral data, genotypical information, multi-site scanning environment). Other applications of GLM also include characterizing the impulse responses in event-related designs (Dale 1999, Glover 1999), studying the psychophysiological interactions (PPI) among different regions (Friston, Buechel et al. 1997), and investigating the coupling between fMRI and other imaging modalities (e.g., EEG recordings (Goldman, Stern et al. 2000, Laufs, Kleinschmidt et al. 2003)).

The major limitation of the GLM lies in the validity of model assumptions in specific fMRI applications (pertaining to relationships among model factors, between noise and model factors, and the assumed serial structure of the noise term, see (Monti 2011, Poline and Brett 2012) for reviews), which unfortunately, is rarely discussed in most cases. Of course, the GLM also presupposes linearity of BOLD responses (Boynton, Engel et al. 1996), which may not be valid. In such cases, higher order models must be utilized (Friston, Josephs et al. 1998).

4.2.4 Multivariate pattern analysis

Correlation analysis and the GLM introduced above treat each brain voxel independently and examines its intensity differences irrespective of all other voxels. However, such a univariate assumption may not hold rigorously, given that our brain is a complex system with tight interactions between different cortical regions. For instance, it is possible that an experimental condition modulates the activity pattern among multiple voxels without altering the averaged intensity levels of each voxel. In such cases and others, it may be statistically advantageous to examine groups of voxels simultaneously. Therefore, in contrast to univariate analyses focusing on the independent activity of individual voxels, a multivariate pattern analysis (MVPA) scheme, which integrates responses of multiple voxels/regions in an experiment, may be exploited (see Fig. 6B) (Haxby, Gobbini et al. 2001). Briefly, this set of approaches reference the concept of pattern classification, seeking to characterize the combination of activities among multiple voxels/regions to differentiate between experimental conditions (see (O'Toole, Jiang et al. 2007, Pereira, Mitchell et al. 2009, Haxby 2012, Mahmoudi, Takerkart et al. 2012) for reviews). Since 2001, MVPA has been actively applied in fMRI studies to investigate activity patterns in visual systems and various cognitive processes (see (Haynes and Rees 2006, Norman, Polyn et al. 2006, Tong and Pratte 2012) for reviews); several MVPA toolboxes are readily available for non-technical users (e.g., a matlab-based Princeton MVPA toolbox (http://code.google.com/p/princeton-mvpa-toolbox/), a Python-based PyMVPA toolbox (http://www.pymvpa.org)). Although MVPA is more sensitive and informative than univariate analysis, several technical challenges still exist, which potentially prevent it from being the dominant approach in revealing brain activity patterns (see (Norman, Polyn et al. 2006, Haxby 2012, Tong and Pratte 2012) for more complete discussions). First, it is hard to identify the neural representations of the learnt classification patterns, e.g., questions such as what information is encoded in the pattern, remain unclear. Second, technical factors (e.g., which voxels/regions should be covered, what spatial/temporal scales should be encoded) interplay with the performance of MVPA in very complicated manners, but are not easily determined. Finally, due to the high demand of fine-grained topographies in distinguishing subtle differences across states, MVPA are typically done in each individual’s native dataset, posing problems in characterizing activity patterns at a group level (see (Haxby, Guntupalli et al. 2011) for a plausible solution).

4.2.5 Correction for multiple comparisons

As mentioned above, the ‘p value’ is defined so to rigorously assess the statistical significance associated with each observed metric. If a voxel’s p value is smaller than a user defined significance level α, we reject the null hypothesis and classify the voxel as ‘active’.

However, in a standard fMRI analysis, we are faced with the challenge of multiple comparisons. For instance, if we attempt to identify ‘active’ voxels across 100,000 voxels under the significance level α = 0.05, ~ 5,000 voxels may be falsely classified as active by random chance under the null hypothesis. To correct for these false positive errors (voxels identified as ‘active’ but which are indeed not) induced by multiple comparisons, several approaches have been proposed (see (Nichols 2012) for a review). These approaches generally fall into two categories. A first category directly introduces more stringent voxel-wise significance level α (the threshold of p values) by assigning new error criteria, e.g., Familywise Error Rate (FWE, the chance of one or more false discoveries (Nichols and Hayasaka 2003)) and False Discovery Rate (FDR, the expected proportion of false positives among detected activation (Genovese, Lazar et al. 2002)). FWE is typically controlled by Bonferroni procedure and is effective in suppressing false positives, however, it has less power than FDR in general. A second category of methods controls the false positive probability of an entire cluster (contiguous voxels) instead of a single voxel. These methods first define clusters by retaining ‘active’ voxels above a primary p threshold, then evaluate the statistical significance of cluster activation by testing its size against the null hypothesis of no active voxels in that cluster. Popular approaches include random field theory (Worsley, Evans et al. 1992, Worsley, Taylor et al. 2004), Monte Carlo simulation (Forman, Cohen et al. 1995) and nonparametric permutation (Holmes, Blair et al. 1996, Nichols and Holmes 2002). Compared to the first category of approaches, these methods are advantageous in less stringent thresholds, high sensitivity, and incorporation of the spatial correlation, but have limited spatial specificity for large clusters (see (Woo, Krishnan et al. 2014) for detailed discussion).

4.2.6 Inter-subject analysis

The analyses discussed above have focused on identifying task activations in a single subject. However, an fMRI study typically recruits several or many subjects in order to probe biodiversity and generalize across a population or disease state. Therefore, we need to combine results across subjects to better test the experimental hypothesis. There exist two main approaches to make the group-level inference of task activation (Huettel 2008).

The first, and more straightforward way is to combine (through temporal concatenation or averaging) the time points of all the examined subjects in a single time series, and perform single-subject level analysis as introduced above. This approach relies on the key assumption that the experimental effect is fixed across all the recruited subjects, so it is termed a fixed-effect analysis. If this assumption (inter-subject variation = 0, only intra-subject variation exists) holds true, temporal combination of each subject’s data can improve the detection power by either increasing the degrees of freedom (concatenation) or reducing intra-subject variations (averaging). However, due to this assumption, the result of fixed-effect analysis is very sensitive to outliers within the recruited subjects (subjects with extreme task responses). Consequently, the conclusions are restricted to the specific subjects scanned within the study, and may not generalize to a larger population.

In contrast to fixed-effect analysis, a random-effect analysis is more commonly applied in fMRI studies nowadays. This analysis assumes that each subject is drawn from a large population of subjects, and that his response represents an independent sample from the overall distribution of task effects. The random-effect analysis is performed in two stages. In the first stage, summary statistics regarding task activation from each individual subject is analyzed independently. In the second stage, the distribution of summary statistics derived from the first stage is tested for significance. For instance, we can use a simple t-test to examine whether the summary statistics from all the subjects are drawn from a distribution with a mean of zero. If intra-subject variations in the first stage are carried up to the second stage, this analysis can also be referred to as mixed-effect analysis (Poldrack 2011). Because random-effect analysis permits the inferences of the entire population from which the subjects are drawn, it is preferable to fixed-effect analysis in most applications, and has been made available with various fMRI statistical toolboxes (see Table 2).

Table 2.

Several of the major fMRI toolboxes with flexible preprocessing pipelines and statistical analysis models

Toolbox	website
AFNI	http://afni.nimh.nih.gov/afni/
Brain Voyager	http://www.brainvoyager.com
FIASCO	http://www.stat.cmu.edu/~fiasco/
FreeSurfer	http://surfer.nmr.mgh.harvard.edu
FSL	http://fsl.fmrib.ox.ac.uk/fsl/
MEDx	http://ftp.medicalnumerics.com/products/medx/index.html
REST	http://restfmri.net/forum/index.php
SPM	http://www.fil.ion.ucl.ac.uk/spm/
Stimulate	https://www.cmrr.umn.edu/stimulate/

4.3 Analysis of resting state data

In task-based experiments (blocked, event-related, or mixed designs), we can target brain regions/patterns associated with the on-going stimulus by examining each brain voxel’s temporal synchrony with the task waveform. By contrast, during task-free mental conditions (e.g., resting state, levels of consciousness, continuous hypercapnia/hypocapnia challenges), we do not have explicit timing information to model the temporal behavior of neural-related fluctuations inherent in each brain voxel. To reveal the patterns of functional connectivity governing a task-free condition, several schemes of analyses have been proposed in the past two decades.

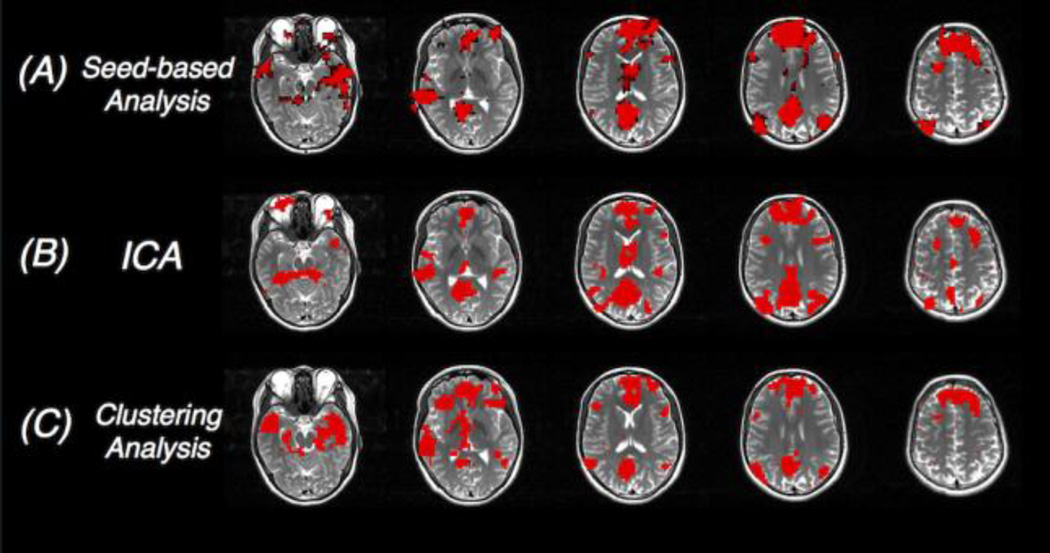
The first approach is seed-voxel based analysis (see Figs. 6A and 7A) (Biswal, Yetkin et al. 1995, Cordes, Haughton et al. 2000, Greicius, Krasnow et al. 2003, Hyde and Jesmanowicz 2012). This approach extracts the time series of a seed region, typically the activation/deactivation locus delineated from a prior task scan or a node within the network under investigation, and estimates its temporal synchrony with the rest brain voxels using GLM or correlation analysis introduced earlier. The topography of the network, i.e., regions significantly coupled with the seed voxel, informs the functional interaction patterns of the seed/network, and can be further compared under types of mental conditions or groups of subjects (healthy controls vs. clinical population) to examine its modulation by cognitive loads and neuropsychiatric disorders.

Figure 7.

Network patterns of the default mode network (a special resting state network) generated by different analyses approaches (red overlays). Results from the seed-based correlation analysis and ICA are thresholded for display.

A second type of analysis enables the exploration of whole-brain functional connectivity configuration without prior selections of network seeds using data-driven or model-free methods. Among all these model-free approaches, i.e., approaches without prior assumptions, independent component analysis (ICA) is the most frequently employed in task-free fMRI studies (see Figs. 6C and 7B) (McKeown and Sejnowski 1998, Calhoun, Adali et al. 2001, van de Ven, Formisano et al. 2004, Beckmann, DeLuca et al. 2005, Smith, Fox et al. 2009, Beckmann 2012). Very briefly, ICA separates the whole brain voxels into additive subcomponents by assuming that the subcomponents are non-Gaussian and they are statistically independent from each other. The spatial patterns of the obtained independent components (ICs) resemble those network patterns resolved by seed-based analysis (Greicius, Srivastava et al. 2004), and are consistent across different studies or subjects (Damoiseaux, Rombouts et al. 2006). Besides, ICA is able to identify certain non-neural sources of variability, such as motion or physiological noise, as separate subcomponents, and can therefore aid preprocessing (Liao, Krolik et al. 2005, Beckmann 2012). Major shortcomings of this approach include: (1) ICs correspond to more complicated representation of the raw fMRI data than seed-based functional connectivity maps, making it difficult to interpret group differences in clinical or neuropsychiatric applications; (2) the resolved ICs and their spatial patterns vary as a function of the number of subcomponents specified by the user; and (3) the classification of components into noise or signal is subject to user-induced interpretation bias.

In addition to ICA, several other model-free approaches have been proposed to characterize the functional connectivity patterns in task-free states. For instance, principal component analysis (PCA) projects the raw fMRI data into orthogonal spaces – principal components (PCs), and only focuses on the space spanned by the leading few PCs (i.e., PCs explaining the most variance of the original dataset) (Friston, Frith et al. 1993). A number of clustering techniques (Fig. 7C), such as hierarchical clustering (Cordes, Haughton et al. 2002), Normalized-cut (van den Heuvel, Mandl et al. 2008), Laplacian based clustering (Thirion, Dodel et al. 2006), fuzzy clustering (Chuang, Chiu et al. 1999), and spectral clustering (Craddock, James et al. 2012), have been applied to produce resting state networks as well. Clustering analysis attempts to parcellate the brain into distinct clusters such that intra-cluster similarity is higher than inter-cluster similarity. Naturally, voxels belonging to the same functional network (with strong temporal synchrony) will fall within the same cluster, if the cluster number is properly chosen.

A third type of analysis simplifies cortical regions as distributed functional nodes, and computes the pair-wise functional correlations of these nodes to achieve a global view of functional organization. The functional nodes can be derived by spatially parcellating the brain voxels into functionally homogeneous ROIs, or more conveniently, employing the recently reported functional atlas (Craddock, James et al. 2012, Shirer, Ryali et al. 2012). Obviously, this approach offers a more intuitive, comprehensive characterization of the connection patterns. However, as it assumes functional homogeneity within each functional ROI/node and is assumed to inherit the information carried at individual-voxel level, whether these atlas ROIs can be generalized to broader populations or mental disorders is questionable. For instance, it has been demonstrated that the functional connectivity map at rest may reorganize under different types of neuropsychological disease or age modulation (see (Fox and Greicius 2010, van den Heuvel and Hulshoff Pol 2010, Rosazza and Minati 2011, Lee, Smyser et al. 2013) for reviews). At the very least, given that alternations of atlas topography may be more or less reflected as changes in the node-level connectivity, we can still use this functional node level analysis as a preliminary step to target candidate brain regions, then employ approaches such as seed-based analysis to examine in detail the disruptive functional dissociations in more detailed manners.

4.4 Advanced analysis

4.4.1 From functional connectivity to effective connectivity

The vast majority of clinical inferences drawn from resting fMRI studies stem from quantifications of functional connectivity – the direct temporal synchrony among distributed cortical regions. Nonetheless, these metrics do not inform further the directional causal influence between neuronal systems that underlie the observed macroscopic correlation. Therefore, there have been growing efforts exploiting effective connectivity, the directed causal influence that one neuronal system exerts on another (see (Friston 2009, Friston 2011, Poldrack 2011, Valdes-Sosa, Roebroeck et al. 2011, Stephan and Roebroeck 2012) for reviews). Approaches estimating the effective connectivity generally start with sets of assumptions on the inherent data structure (time series, correlation matrix or higher-order statistics) or underlying biophysics to be modeled, then seek the optimum models using criteria such as maximum likelihoods or Bayesian inferences, and finally invoke the learned model parameters to conclude causality or conditional dependences. The most common approaches include dynamic causal modeling (DCM) (Friston, Harrison et al. 2003, Penny, Stephan et al. 2004, Lee, Friston et al. 2006, Stephan, Weiskopf et al. 2007, Marreiros, Kiebel et al. 2008, Stephan, Kasper et al. 2008, Penny, Stephan et al. 2010, Schuyler, Ollinger et al. 2010, Seghier, Zeidman et al. 2010, Stephan, Penny et al. 2010, Daunizeau, David et al. 2011, Friston, Li et al. 2011, Li, Daunizeau et al. 2011, Lohmann, Erfurth et al. 2012, Friston, Kahan et al. 2014), Granger causality analysis (Granger 1969, Goebel, Roebroeck et al. 2003, Harrison, Penny et al. 2003, Roebroeck, Formisano et al. 2005, Deshpande, LaConte et al. 2009), structural equation modeling (SEM) (McIntosh 1994, Buchel and Friston 1997, Horwitz, Tagamets et al. 1999, Bullmore, Horwitz et al. 2000), psychophysiological interaction (Friston, Buechel et al. 1997), graphical causal modeling (Pearl 2000, Spirtes 2000), dynamic Bayesian networks (Rajapakse and Zhou 2007), and switching linear dynamic system (Smith, Pillai et al. 2010); and have been actively employed in clinical studies to identify abnormal interactions in patients (e.g., Alzheimer’s disease (Agosta, Rocca et al. 2010, Rytsar, Fornari et al. 2011, Liu, Zhang et al. 2012, Neufang, Akhrif et al. 2014, Zhong, Huang et al. 2014), depression (Schlosser, Wagner et al. 2008, Almeida, Versace et al. 2009, Goulden, McKie et al. 2010, Moses-Kolko, Perlman et al. 2010, Hamilton, Chen et al. 2011, Iwabuchi, Peng et al. 2014, Liu, Wu et al. 2015), and schizophrenia (Schlosser, Gesierich et al. 2003, Kim, Burge et al. 2008, Benetti, Mechelli et al. 2009, Crossley, Mechelli et al. 2009, Dima, Roiser et al. 2009, Allen, Stephan et al. 2010, Diaconescu, Jensen et al. 2011, Deserno, Sterzer et al. 2012, Guller, Tononi et al. 2012, Mukherjee, Whalley et al. 2012, Birnbaum and Weinberger 2013, Zhang, Wei et al. 2013, de la Iglesia-Vaya, Escarti et al. 2014, Hutcheson, Sreenivasan et al. 2015)). As suggested by the way it is termed, effective connectivity opens a promising avenue to perceive the neural-related couplings of our brain systems. Nevertheless, such goals are challenging to achieve in real implementations due to the biophysics of fMRI and several technical limitations. First, fMRI by nature inevitably contain spatiotemporal variability from hemodynamic sources. Without rigorously correcting for hemodynamic variability, it may not be sensible to claim that the observed causal relationship reflects a neuronal origin (Chang, Thomason et al. 2008, David, Guillemain et al. 2008, Deshpande, Sathian et al. 2010, Roebroeck, Formisano et al. 2011, Webb, Ferguson et al. 2013). Second, to make integrative and precise inferences of information flow at the neuronal level, an ideal model should include the whole set of brain regions (even for cases assessing the effective connectivity between two regions) and superior to all alternative possible structures. The problem is thus problematic due to computational complexity (enormously large dimension expanded by the model space) and inadequate samples (the number of unknown free parameters is much larger than the number of time points per fMRI scan). To tackle the problem, we can enforce specific constraints on the model space by prior assumptions or briefly characterizing the causal structure of the data using approaches such as graphical causal modeling (Ramsey, Hanson et al. 2010). Apart from the two major concerns discussed here, effective connectivity faces other challenges, e.g., modeling causal structure across multiple subjects, see (Ramsey, Hanson et al. 2010, Poldrack 2011, Valdes-Sosa, Roebroeck et al. 2011) for discussions and plausible solutions.

4.4.2 From voxel/ROI-wise correlations to complex network behavior

As mentioned earlier (see analysis of resting state data above), a systematic view of the brain’s functional organization could be achieved by parcellating brain voxels into discrete functional nodes and examining the global interactions among these nodes. Indeed, such data manipulation and simplification also make it plausible to characterize the network-wise, or community-wise behavior of the data. Numerous quantitative metrics, originally proposed in graph theory, have been introduced to learn the complex network behavior of our brain’s functional structure, such as small-world topology (Watts and Strogatz 1998), scale-free network patterns (Barabasi and Albert 1999), rich club behavior (van den Heuvel and Sporns 2011), efficiency of global/local information flow (Latora and Marchiori 2001), hierarchies and modular structures (Meunier, Lambiotte et al. 2010), etc. (see (Bullmore and Sporns 2009, Meunier, Lambiotte et al. 2010, Rubinov and Sporns 2010, Bullmore and Sporns 2012, Sporns 2013) for reviews of complex network measures). These metrics, complimentary to conventional node-wise measures, have provided new opportunities to understand brain functions and neuropsychological diseases under the setting of a complex system (see (Bassett and Bullmore 2009, Stam and van Straaten 2012, Filippi, van den Heuvel et al. 2013, Hulshoff Pol and Bullmore 2013, Stam 2014) for reviews of clinical investigations). Despite the wide application of complex measures in clinical explorations, several potential challenges still lie ahead. For instance, the robustness of the estimated network-wise behavior is apparently vulnerable to choice of functional ROIs (Smith, Miller et al. 2011). If the ROIs employed to extract node time series for further network analysis do not match the actual functional boundaries of the data well, time series from different functional regions may mix with each other and obscure the actual community behavior of our brain. In this sense, functional, locally derived atlases are generally preferable to anatomical, standard atlases defined from large groups of subjects. Besides, these metrics from graph theory usually summarize the brain’s complex network-wise behavior in one single value. One can question whether the observed differences between groups of subjects (e.g., healthy controls vs. clinical populations) originate from neural sources, or from those confounds that affect brain voxels globally, e.g., motion and physiological processes (Smith 2012). Therefore, rigorous modeling and careful removal of potential noise confounds are essential for relevant studies. Examining the dependence of derived metrics to the processing pipeline (by including or excluding certain skeptical steps) can also enhance the reliability of the results. Furthermore, these complex network behaviors typically deviate substantially from the bottom-level temporal synchrony among functional nodes, making clinical interpretations on the results not easy.

4.4.3 From static functional connectivity to brain dynamics

Until a few years ago, studies investigating the RS functional connectivity have invoked the key assumption of temporal constancy, i.e., that interactions among different cortical regions remain unchanged during the entire scan. However, such assumptions are invalidated by recent observations that the network patterns may undergo substantial changes across a single RS scan (Chang and Glover 2010, Kiviniemi, Vire et al. 2011, Handwerker, Roopchansingh et al. 2012, Jones, Vemuri et al. 2012, Hutchison, Womelsdorf et al. 2013, Allen, Damaraju et al. 2014). In contrast to extracting the functional connectivity metrics by integrating time points over the whole scan as performed in conventional static studies, these dynamic analyses investigate the variability of brain connectivity metrics at sub time periods across the scan session (see (Hutchison, Womelsdorf et al. 2013, Calhoun, Miller et al. 2014) for reviews of methodology). The dynamic property of RS functional connectivity may carry information (at least) as important as those time-averaged metrics widely explored in neuroscience studies or clinical applications, e.g., it is entirely possible that clinical populations possess disrupted dynamics, which taken together with abnormal time-averaged metrics, may offer better understanding of the associated disorders. Preliminary applications include mental disorders such as schizophrenia (Sakoglu, Pearlson et al. 2010, Damaraju, Allen et al. 2014, Ma, Calhoun et al. 2014, Rashid, Damaraju et al. 2014, Shen, Li et al. 2014, Yu, Erhardt et al. 2015), major depression (Allen and Cohen 2010), Alzheimer’s disease (Jones, Vemuri et al. 2012), opioid analgesia (Robinson, Atlas et al. 2015), temporal lobe epilepsy (Morgan, Abou-Khalil et al. 2015) and childhood autism (Price, Wee et al. 2014). Of note, as studies of brain dynamic functional connectivity are at quite an exploratory stage, the associated interpretations of disrupted dynamics in disorders are still very cursory – it is yet hard to identify the true mechanism from candidates such as changes in autonomic processes, vigilance states, or behavioral origins (see (Hutchison, Womelsdorf et al. 2013) for a review). Hence, external measurements of physiological processes (e.g., galvanic skin response, respiratory and cardiac data) will be surely beneficial for confound reduction or identification of potential mechanisms.

It is important to highlight two technical challenges of dynamic studies. The first challenge lies in the inability of a standard fMRI scan (with minutes-long duration) to characterize the complete patterns of time-varying functional connectivity (an implicit premise for between group comparison). The total number of interaction patterns that different cortical regions may exhibit, although not quantified yet, is presumably huge. In contrast, the patterns that can be captured by ~10 minute long scanning snapshots are very limited. It is therefore speculative whether the altered patterns of brain dynamics in a clinical group (if they exist) indeed result from the associated disorder, or simply the stochastic nature of limited samples per scan. A second challenge relates to the number of time points (independent observations, if not considering the hemodynamic autocorrelation in time series) involved in the estimation of each connectivity pattern. Most current dynamic analyses implicitly assume that the time our brain spends in each network pattern is substantially shorter than the total scan duration. There is therefore a tradeoff between the statistical power of a limited snapshot of the brain’s behavior and the temporal resolution with which it is desired to test for dynamic changes. The consequent danger is that the number of time points collected when the brain is in a certain network pattern may not be adequate to yield statistically robust estimations. Collectively, at the current stage, longer scan durations (more network patterns) and faster acquisition rates (more samples) may improve the reliability of dynamic brain connectivity.

4.5 Analysis software

Many software packages have been developed for the analysis of fMRI data. These programs have flexible pipelines for preprocessing and multilevel task and resting state analysis (see Table 2 for some popular toolboxes).

Conclusions

Functional MRI has had a long history of development for, and application to, a large body of basic systems-level neuroscience investigation (see (Bandettini 2012) for a review). The original block design experiments have been augmented by many other types of experimental design, but remain a workhorse method for psychiatric studies. While most aspects of BOLD contrast are by now well understood, it remains an active area of research. Furthermore, acquisition methods are reasonably standardized by now with the use of single-shot EPI, although faster, more efficient methods such as SMS have been recently introduced. Both task-based and resting state experiments have shown great promise in understanding the brain’s behavior in healthy and diseased populations, and in guiding clinical therapy. Pattern classification and other forms of multivariate analyses are being employed to develop biomarkers of disease (Nash, Wiley et al. 2013), and with which to predict outcome for therapeutic intervention (Hoeft, McCandliss et al. 2011). Because BOLD fMRI relies on an indirect indicator of metabolic contrast, and because the signals are small, it is crucial to perform adequate compensation for confounds such as physiological noise, dynamic brain states, and subject motion, and to use great rigor in the acquisition and analysis pipelines to make sure the imaging data and derivative results are robust and reproducible across the duration of the study. With proper attention to all these factors, fMRI has become an invaluable tool for psychiatric investigations.