Population Intervention Models to Estimate Ambient NO₂ Health Effects in Children with Asthma

Abstract

Health effects of ambient air pollution are most frequently expressed in individual studies as responses to a standardized unit of air pollution changes (e.g., an interquartile interval), which is thought to enable comparison of findings across studies. However, this approach does not necessarily convey health effects in terms of a real-world air pollution scenario. In the present study, we employ population intervention modeling to estimate the effect of an air pollution intervention that makes explicit reference to the observed exposure data and is identifiable in those data. We calculate the association between ambient summertime NO₂ and forced expiratory flow between 25% and 75% of forced vital capacity (FEF_25–75) in a cohort of children with asthma in Fresno, California. We scale the effect size to reflect NO₂ abatement on a majority of summer days. The effect estimates were small, imprecise, and consistently indicated improved pulmonary function with decreased NO₂. The effects ranged from −0.8% of mean FEF_25–75 (95% Confidence Interval: −3.4 , 1.7) to −3.3% (95% CI: −7.5, 0.9). We conclude by discussing the nature and feasibility of the exposure change analyzed here given the observed air pollution profile, and we propose additional applications of the population intervention model in environmental epidemiology.

INTRODUCTION

Epidemiology has played a central role in the elucidation of health effects associated with ambient air pollution. However, several issues make interpretation of the findings from traditional models somewhat problematic and less than optimal for use in health risk assessment.¹

Ambient air pollution elicits health effects in ways that differ across geographical and temporal space, according to the specific local emission sources and meteorology, as well as characteristics of the exposed population. Despite the broad variability of air pollution health effects, and despite the fact that real-world health effects are of great regulatory interest,² health effects related to air pollution exposures are most frequently expressed as responses to a standardized unit of air pollution changes (e.g., an interquartile range [IQR] or a 10-unit change in pollutant concentration). While this approach may enable comparison of pollutant-specific exposure responses when using a constant scaling interval across studies (e.g., 10 units), IQRs are more problematic. A pollutant’s concentration interquartile interval is not constant between studies and may not correspond to real-world changes experienced by individuals in a given population. For example, it is not commonly stated whether an IQR-sized concentration change of a given ambient pollutant is feasible in the region being studied; in some cases, such daily variability of exposure is not observed in the data.³ Expressing health effects standardized by IQR also conflates factors related to study design and analysis (e.g., inclusion criteria, choice of confounders) with meaningful exposure-related effects.^{4, 5} There are also statistical issues associated with these scaling techniques. For example, they assume a linear (or log–linear) relationship between the pollution and the outcomes regardless of the concentration range observed within a region or across different studies, tacitly assuming a constant slope across the entire concentration range found in different cities. Although this is the prevailing approach in air pollution epidemiology, to our knowledge, this issue has not yet been addressed in the large literature on air pollution health effects.

Most analytical approaches up to this point have analyzed ambient air pollution using conditional methods, analyzing what is an ecologic, group-level exposure within strata of confounders. In epidemiologic studies, especially those of air pollution, population associations and effects are of interest. Log linear models are necessarily conditional, since the marginal odds ratios (ORs) are not estimated by the adjusted ORs. Moreover, the use of interactions to assess subgroup makes marginal estimation unachievable in typical linear regression or log-linear models.⁴ In light of this, methods for marginal estimation are particularly applicable to air pollution epidemiology.

Policy questions are of great interest in air pollution epidemiology; researchers in the field have long used policy changes and other natural experiments such as traffic changes and plant closures as opportunities for estimation of health effects attributable to real-world environmental changes.^{6, 7} A small number of studies have estimated health effects of hypothetical policy interventions, using techniques such as health impact functions to simulate the impact of rollbacks of air pollution levels (e.g., to meet regulatory standards ⁸). In this paper, we apply another method that expresses air pollution health effects scaled to real-world air pollution changes using observational data. We employ a method from the causal inference literature, the population intervention model.^{9, 10} This method relies on the counterfactual framework to calculate health effects that are not conditional on confounders, and analyzes the ambient air pollution as a marginal exposure.¹¹ The method targets an investigator-specified parameter that is observed in the data (i.e., an identifiable effect), scaling the health effect to a specific intervention. This approach also reflects epidemiology’s recent shift toward policy-relevant parameter estimation and scaling.^{12, 13} In addition to translating health effects for a policy audience, we aim to demonstrate the mechanics of one causal inference technique.

In this paper, to demonstrate the calculation of an intervention-scaled health effect, we analyze data from the Fresno Asthmatic Children’s Environment Study, using ambient NO₂ as an exposure and forced expiratory flow between 25% and 75% of forced vital capacity (FEF_25–75) as an outcome. In addition, we compare the inferences that can be drawn from this approach to those from a more traditional approach.

We chose to focus on ambient nitrogen dioxide (NO₂), which results primarily from automobile and diesel engine tailpipe emissions and has been shown to be associated with asthma onset, exacerbations, and symptoms.^14–16 Prior research has examined acute NO₂ health effects in children with asthma using outcomes such as symptoms, peak expiratory flow, and more recently, forced expiratory volume in 1 section and FEF_25–75.^17–20 FEF_25–75 is a logical outcome for studies of asthma, because it has been demonstrated to be a sensitive measure of small airway constriction and impaired pulmonary function in people with asthma.^{21, 22}

The specific air pollution intervention whose health effects we estimate is defined as decreasing ambient NO₂ concentrations on a majority of summertime study days (reducing the highest 75% of days down to the 25^th percentile concentration). We present marginal health effects scaled to this particular air pollution change, and also comment on the nature and feasibility of this exposure change given the observed air pollution profile of our study site. In addition to analyzing the impact of NO₂ exposure specifically in Fresno, we hope to demonstrate how this method could be applied to other geographical regions, other pollutants of interest, and other topics, when investigators wish to express identifiable, intervention-scaled findings specific to a particular region or setting.

MATERIALS AND METHODS

Fresno Asthmatic Children’s Environment Study

Sample

The Fresno Asthmatic Children’s Environment Study (FACES) was a prospective, longitudinal cohort study that was designed to examine the acute and long-term effects of ambient air pollution on respiratory health in children with asthma. Details of participant enrollment and study protocol have been published previously.^{23, 24} Briefly, between 2000 and 2005 the study enrolled 315 children with asthma in Fresno and Clovis, CA through school nurses, doctor’s offices, radio and print advertisements. The study site is located in California’s San Joaquin Valley, one of the most polluted air basins in the United States.²⁵ Eligibility requirements for the study included child’s age between 6 and 11 years old upon recruitment, physician-diagnosed asthma, active symptoms and/or the use of asthma medications in the previous 12 months, and residence within 20 kilometers of the California Air Resources Board’s (CARB) Downtown Fresno monitor (a United States Environmental Protection Agency Supersite during the study period). Study participants were followed through 2008. The Committee for the Protection of Human Subjects at the University of California, Berkeley approved the study protocol; written informed consent was obtained from parents/legal guardians for all procedures.

Outcome

At baseline, each child and parent/legal guardian completed a field office visit and interview, where extensive background data were collected on medical history, residence, and socio-demographic factors. Experienced field study staff also trained children and parents in the use of the EasyOne^® portable spirometer (ndd Medical Technologies Inc., Zurich, Switzerland), including how to perform the forced expiratory maneuver and how to answer questions programmed into the device’s interface. After the initial baseline visit, participating families were followed up through periodic clinic visits and phone calls, allowing collection of up-to-date socio-demographic, medical, and anthropometric data.

The pulmonary function outcome data come from periodic panel sessions during which participants performed home-based spirometry. Participating children completed two or three panel sessions per year, across different seasons (defined based on the local meteorology and air quality profile: spring, February – May; summer, June – September; and winter, October - January). In each of these 14-day panel sessions, children performed spirometry maneuvers using EasyOne spirometers. Participants provided data twice daily during their panel sessions: the first time at 7:00 – 9:00AM after waking up, and again at 7:00 – 10:00PM, before going to bed. At the beginning of the study, children were assigned to eight separate groups that completed panels during the same time period; therefore the periods of intensive data collection do not overlap between all children. These panel sessions give rise to the repeated panel structure of the data. See Supplemental Material, Figure 1 for a detailed schematic of the FACES data collection protocol, including panel sessions and clinic visits. Panel data were subject to rigorous quality assurance protocols, both automatic algorithms programmed into the spirometer and manual procedures administered by FACES study personnel.²⁶

Morning FEF_25–75 (measured in liters/second [L/sec]) was chosen as the outcome variable to minimize the heterogeneity in activities and exposure that children experienced immediately before the forced expiratory maneuver (children would be expected to be sleeping for most of the time prior to morning testing). Also, because spirometric measures are at their lowest upon awakening, the morning measure is likely more sensitive to detecting impaired pulmonary function.²⁷

Exposure

Hourly ambient air pollution and meteorological data were collected at the EPA Supersite monitor in downtown Fresno. Various air pollutants were measured, including NO₂, particulate matter, elemental carbon, black carbon, and ozone. This analysis analyzes only the effects of NO₂ to focus on a relatively simple hypothetical intervention. Quality-assured exposure data from the study time period were obtained from CARB, and daily ambient exposure levels were assigned to individual children from these central-site measurements. For all ambient pollution and meteorological variables, the same value (as measured at the central site) was assigned to all children on a given day. NO₂ concentration in parts per billion (ppb) was calculated as a 24-hour average. In addition to the extensive quality assurance measures implemented by CARB (including frequent instrument calibration, performance testing, and auditing of field and laboratory operations,²⁸) the FACES team performed additional quality checks on air pollution data before analysis. These verifications included range checks, consistency checks for temporal and diurnal pollutant variation, and comparison with data from nearby monitoring sites.

We restricted the analysis of ambient NO₂ health effects to the summer months (June – September) because of the seasonal variations in air pollution profile, meteorology, and underlying respiratory health. Prior research has argued that for some pollutants, season-stratified analyses are likelier to produce valid/meaningful results.²⁹ Therefore, we chose a restricted analysis to estimate NO₂ effects in time periods where the associations were more likely to be homogeneous. Acute NO₂ effects were estimated using three averaging times. The first was lag 0: the 24 hours preceding the morning outcome measurement (8:00AM the previous day – 8:00AM on the index day). We also analyzed the 2-day and 4-day moving averages of ambient NO₂ concentration to examine the impact of further-removed exposure, in light of prior studies that have found significant results at lags greater than 0–1.¹⁴

To define the hypothetical NO₂ intervention whose health effects were being estimated, we selected the 25th percentile of NO₂ across study days as the intervention cutoff level, which was 9.7 ppb for the entire sample of summer days.

Confounders

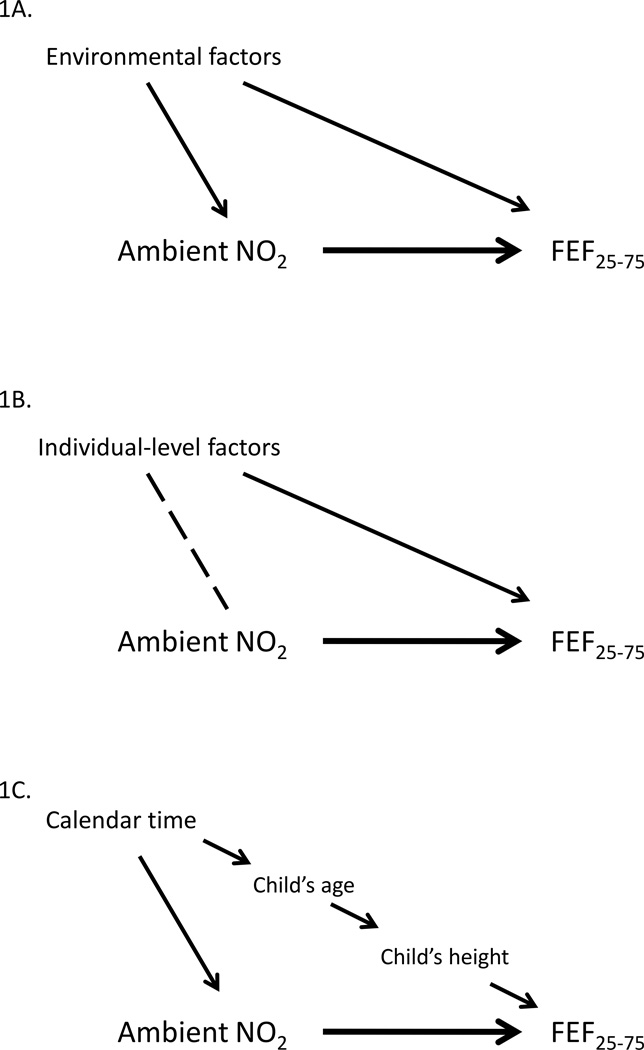
We identified three categories of potential confounders. Each is represented by a causal diagram (Figure 1). The first class of potential confounders were the environmental factors frequently considered in epidemiologic studies on the effects of ambient air pollution (Figure 1A).^{19, 30} Ecologic-level variables such as temperature and day of week may be associated with both ambient NO₂ and FEF_25–75, warranting their consideration as potential confounders. Secondly, individual-level covariates such as race/ethnicity and age at asthma diagnosis were considered as potential confounders (Figure 1B). Such factors are likely to be associated with pulmonary function, and less obviously, they may also be association with central-site exposure measurements. This owes to the repeated panel data structure of FACES, which resulted in different groups of children being observed on different study days. Imbalance in one of these factors across the panel groups could introduce confounding (see Supplemental Material, Figure 1 and Mann et al.²³ for further discussion of this topic).

Figure 1.

Causal diagrams demonstrating potential confounding by the three classes of confounders: environmental factors (A), individual-level factors (B), and factors relating to calendar time (C).

The casual effect of interest is the heavy arrow between ambient NO₂ and FEF_25–75. Solid arrows represent postulated causal associations and the dashed line represents a possible association due to chance, not causation.

The third class of potential confounders was factors associated with long-term time trends (e.g., calendar year, child’s age, or height, Figure 1C). During the nine-year study period, physiologic parameters of children changed with age, and air pollution levels could also reasonably be expected to change. Preliminary review of the data confirmed these hypothesized associations, demonstrating both a decrease in pollutants over the study period and an increase in the children’s height. Since age and height strongly predict pulmonary function, we considered age a proxy for several time-related factors and an a priori stratification variable. We performed an age-stratified analysis to control for this confounding. Another factor motivating the age-stratified analysis was the desire to study the effects of air pollution on pulmonary function in sub-samples of children that were more homogeneous with regard to age, stage of development, and height; this allowed the assessment of effect modification. For this acute effects analysis, child-days were divided between 6 to 9 year olds, 10 – 12 year olds, and 13 – 17 year olds. The specific cut-points were chosen based on the distribution of the and on subject matter considerations (i.e., splitting the pre-pubertal years from the pubertal years, and sub-dividing the pubertal years, which are characterized by hormonal changes that affect asthma prognosis.³¹)

Statistical methods

Population intervention model and G-computation

The population intervention model (PIM) builds on the counterfactual framework for causal inference.¹¹ The PIM approach estimates the effects of a hypothetical intervention by comparing a mean counterfactual outcome (e.g., the population outcome that would have been observed under some intervention scenario) to the mean observed outcome. Other authors have demonstrated how this approach can be applied to questions in social epidemiology which, like air pollution, deals with population-wide exposures.^{32, 33} The potential outcomes under the air pollution abatement were calculated using G-computation.^{34, 35} This technique employs a regression model (the Q-model) to compute counterfactual (i.e., unobserved) outcomes at exposure levels designated by the investigator, based upon the intervention of interest. In this paper, the hypothetical exposure scenario is an alternate air pollution profile in which NO₂ concentrations have been lowered to a level observed in our data (hereafter, the intervention) that might be expected to improve respiratory health in this vulnerable population.

Letting Y denote the random variable for outcome (i.e., FEF_25–75) and A the exposure (NO₂), Y_a denotes the counterfactual outcome when exposure is set to the level a (or A = a). With a representing the decreased NO₂ concentration profile, E[Y_a] is equal to the mean outcome under this intervention, and E[Y] is the mean observed outcome. The population intervention model quantifies the effects of the hypothetical intervention by comparing these two mean outcomes, using a parameter that is analogous to a marginal population attributable fraction ^{10, 32}:

$$E[Y]-E[Y_a]$$ (1)

The hypothetical exposure level a is selected by the investigator based upon the available data and the research or policy question of interest. Below, we discuss the selection of the intervention applied in this study.

Model-fitting

Within each of the three age strata, we conducted parallel processes of confounder selection and model-fitting. All analyses were conducted using R (version 2.10.0; R Foundation for Statistical Computing, Vienna Austria). Based on knowledge of the subject matter and prior studies, the covariates considered as environmental confounders were day of week and apparent temperature, a composite meteorological variable describing the perceived temperature accounting for relative humidity; see Basu et al.³⁶ for details. The individual-level confounders considered were: race/ethnicity (African-American, white, Hispanic), asthma diagnosis at two years old or younger (a surrogate for severity³⁷), skin-prick test sensitization (positive to at least one allergen on a skin-test panel or reported history of severe reaction to prior allergy skin test), asthma severity as defined by the Global Initiative for Asthma (mild-intermittent, mild-persistent, moderate, severe)³⁸, and income (categorized in 4 groups). We selected height-cubed to control for potential residual confounding by calendar time within age strata. Height-cubed was analyzed because any residual confounding by calendar time would be expected to be associated with the outcome through height (Figure 1C), and because prior research has demonstrated this power of height to be most strongly predictive of spirometric outcomes, due to the volumetric shape of the lung.³⁹

We first reduced this list of candidate covariates to a list of potential confounders for each age-group-specific analysis, on the basis of moderate association with exposure and outcome (P<0.20 for both). These confounders were considered in the fitting of the Q-model. We then fit Q-models for the association between NO₂ and FEF_25–75 in each of the three age groups using a flexible model-fitting algorithm, Deletion/Substitution/Addition (DSA), to select the optimal Q-model for each age group.⁴⁰ The model specification selected during this step served as the Q-model for the G-computation procedure in each age group. See Supplemental Material, p. 7 for a detailed description of model-fitting.

Parameter estimation

For each age group, we fit a Q-model using linear regression with the confounders and model specification selected in the previous step. To ensure that each child contributed equally to the regression, we weighted each observation by the inverse number of observations contributed by the child. This Q-model was then used to predict the unobserved outcomes needed for this analysis: the potential outcome under the intervention pollution profile (Y_a). We mechanically implemented the prediction of potential outcomes by generating a dataset in which no NO₂ level exceeded the intervention level (the hypothetical NO₂ reduction threshold, i.e., the 25^th percentile of ambient NO₂ concentrations). This cutoff level corresponded to 9.9 ppb for the younger age group, 9.7 ppb for the middle age group, and 9.1 ppb for the older age group. In this intervention dataset, NO₂ levels above the intervention cutoff level were reduced to the intervention level, while NO₂ levels at or below the intervention level were kept at their observed concentrations.

We applied the Q-model to this counterfactual dataset to predict the Y_a potential outcomes, given the NO₂-reduction intervention. The mean intervention outcome (E[Y_a]) was calculated for each age group using the Q-model with the intervention dataset, which held all confounders at their observed levels but lowered exposure levels for some observations. The outcome under the observed exposure distribution (E[Y]) was calculated from the empirically observed FEF_25–75 values. Both E[Y] and E[Y_a] were calculated as weighted averages, weighting each child equally. Finally, we calculated a risk difference comparing the mean outcome under observed exposure and the mean outcome when NO₂ levels were reduced to the 25th percentile: the population intervention parameter (expression 1). To permit comparison to a more conventional approach, we also used scaled the regression model results to the IQR of NO₂ concentration for all lags/moving averages studies.

Statistical inference

To calculate standard errors for the effect estimates, we conducted a bootstrap of the Q-model regression, the G-computation procedure, and the risk difference calculation in each age stratum, using resampling with replacement by child. In each bootstrap repetition, the same absolute NO₂ levels (9.9 ppb, 9.7 ppb, and 9.1 ppb) were implemented as the population intervention. The bootstrap was conducted with 1,000 repetitions.

RESULTS

Of the 299 children who contributed panel data to the FACES study, 42 children were excluded from analysis because they did not contribute any panel data during the summer months. Table 1 provides descriptive statistics of demographic and health characteristics at baseline for both the entire sample of 299 children who contributed panel data and the subset of 257 children that contributed panel data during summer months. The subset of children that were analyzed did not differ from the group of children that were excluded from analysis (P>0.1 for chi-square/Fisher’s Exact tests), except by 2 factors: race (P=0.002, African-Americans were more likely to be excluded and whites less likely), and age at asthma diagnosis (P=0.002, children diagnosed with asthma at ≤ 2 years old were more likely to be excluded).

Table 1.

Descriptive statistics of the sample at baseline, for children included in the summertime analysis and for all children who contributed panel data (overall sample).

	Summertime analysis (n=257)	Overall sample (n=299)
	n(%)	n(%)
Age (Median [IQR])	8 (6 – 9)	8 (7 – 9)
Male	146 (56.8)	170 (56.9)
Race/ethnicity
African-American	33 (12.8)	48 (16.0)
Asian-American	1 (0.4)	2 (0.7)
Hispanic	103 (40.1)	118 (39.5)
White (non-Hispanic)	113 (44.0)	124 (41.5)
Missing	7 (2.7)*	7 (2.3)
Income
< $15,000	46 (17.9)	58 (19.4)
$15,000 – $30,000	63 (24.5)	73 (24.4)
$30,000– $50,000	60 (23.3)	72 (24.1)
> $50,000	80 (31.1)	86 (28.8)
Missing	8 (3.1)	10 (3.3)
Asthma severitya
Mild intermittent	73 (28.4)	87 (29.1)
Mild persistent	125 (48.6)	139 (46.5)
Moderate or severe	59 (23.0)	73 (24.4)
Skin-test positiveb	142 (55.3)	165 (55.2)
Asthma diagnosis ≤ 2 y.o.	92 (35.8)*	118 (39.5)

Abbreviations: IQR, interquartile range; y.o., years old.

^*Chi-square or Fisher’s exact test P<0.01, compared to children not included in summertime analysis.

^aBased on the Global Initiative for Asthma severity guidelines ³⁸.

^bPositive to at least one allergen on skin-test panel or reported history of severe reaction to prior allergy skin test.

Table 2 presents the distribution of ambient NO₂ (lag 0) during summer months (June – September), as measured at the U.S. EPA Supersite monitor in Fresno, California. The NO₂ concentrations are described for the entire study period and within the age-stratified groups. The ambient NO₂ concentration ranged from 4.2 to 37.6 ppb, with a median value of 12.9 and an interquartile range (IQR) of 7.9 ppb. Across age groups the concentration of NO₂ was slightly lower on the study days in which the older group was observed (13 – 17 year-olds), because this sample of days did not include many of the days that occurred early in the study period when NO₂ concentrations were higher. The number of children and the number of unique study days in each age group followed the same pattern: the middle age group (10 – 12 year-olds) had the most observations, followed by the younger group (6 – 9 year-olds) and then the older group (13 – 17 year-olds). See Supplemental Material, Table 2 for details of the number of children observed across multiple age groups. This analysis focused solely on the health effects of NO₂; details about the distributions of additional summertime pollutants and environmental variables are available in Supplemental Materials, Table 2.

Table 2.

Overall and age-stratified distributions of ambient NO₂ concentrations (lag 0) measured at the central site monitor during summer months in Fresno, CA, 2001 – 2008.

NO2 (ppb)	Min.	25th %a	Median	Mean	75th %	Max.	IQR	Unique days	Days missing
Overall (n=257)	4.2	9.7	12.9	14.3	17.6	37.6	7.9	648	9
6–9 y.o (n=151)	4.7	9.9	13.0	14.5	17.7	37.6	7.8	563	6
10–12 y.o (n=196)	4.2	9.7	12.9	14.3	17.6	37.6	7.9	607	9
13–17 y.o (n=101)	4.2	9.1	11.5	13.3	15.9	37.6	6.8	329	8

Abbreviations: %, percentile; IQR, interquartile range; Max., maximum; Min., minimum; ppb, parts per billion; y.o., years old.

^a25^th percentile values were used as the age-specific thresholds for the hypothetical population intervention

The confounders and models selected by DSA are presented in Table 3. In the younger age group, asthma diagnosis when the child was ≤ 2 years old and an income category were the potential confounders; only young age at asthma diagnosis was selected in the final Q-model. In the middle age group, height³ was selected as a potential confounder of the NO₂-FEF_25–75 association as a squared term. Hispanic ethnicity and the weekend variable were the potential confounders in the older age group, but neither was selected into the model, leaving the unadjusted model as the final Q-model for this age group. Positivity is one of the testable assumptions for causal inference, and requires that there be observed exposure data to support estimation of the effect of interest in all covariate strata of the data.⁴¹ Supplemental Material, Figure 2 demonstrates the range of NO₂ concentrations across strata of age at asthma diagnosis and quartiles of height, providing evidence that the assumption is satisfied for this exposure and these covariates, and that the effect of the intervention is identifiable in the dataset.

Table 3.

Confounders selected by candidate reduction routine (P<0.2) and Q-models selected by DSA algorithm.

Age group	Confounders	Model selected by DSA
6 – 9 year-olds	Asthma diagnosis ≤ 2 years old Income category: $15,000 – $30,000	E(FEF25–75|NO2,AsthLe2)= α0+α1*NO2+α2* AsthLe2a
10 – 12 year-olds	Height3	E(FEF25–75|NO2,Height3)= α0+α1*NO2+α2* (Height3)2
13 – 17 year-olds	Hispanic Weekend	E(FEF25–75|NO2)= α0+α1*NO2

Abbreviation: FEF_25–75, mean forced expiratory flow between 25% and 75% of forced vital capacity.

^aAsthLe2: Asthma diagnosis when the child was ≤ 2 years old

Table 4 presents additional details of the population intervention, namely the distribution of changes in ambient NO₂ concentrations implied by reducing NO₂ levels on all days with concentrations exceeding the 25^th percentile. The age-group-specific median change in ambient NO₂ concentration was between −3.3 and −2.4 ppb, with mean changes between −5.1 and −4.6 ppb and maximum changes between −28.5 and −27.7 ppb. These distributions indicate that the majority of days are lowered by relatively small amounts under the population interventions and confirm that a quarter of days are not intervened on at all, by definition. At the tail end of the distribution, a small number of days see greatly reduced concentrations.

Table 4.

Distribution of ambient NO₂ concentration changes between the observed NO₂ concentration and the NO₂ population intervention (ppb).

Age group	Min.	25th %	Median	Mean	75th %	Max.
6 –9 y.o.	0	0	−3.1	−5.1	−7.8	−27.7
10 – 12 y.o.	0	0	−3.3	−5.1	−8.0	−27.9
13–17 y.o.	0	0	−2.4	−4.6	−6.8	−28.5

Abbreviations: %, percentile; Max., maximum; Min., minimum; No., number; ppb, parts per billion; y.o., years old.

The results of the population intervention model are presented in Table 5. Results are presented as point estimates and 95% confidence intervals in relative terms, as a percentage of the age-specific mean outcome (mean FEF_25–75). Given the parameter , a negative magnitude indicates that FEF_25–75 improved under the intervention of lower NO₂ levels (i.e., the hypothesized inverse association between air pollution and pulmonary function). These results demonstrate a consistent, small, inverse association between NO₂ and FEF_25–75 across all ages and lag/moving averages analyzed, though none of the estimates are significant at the P<0.05 level. Most relative parameter magnitudes were in the −3% to −1% range. The younger age group varied little, with all effect estimates of all NO₂ lags/moving averages in the −1.9 to −1.4% range. Both the younger and the middle age groups had the highest relative magnitude at the 2-day moving average NO₂ exposure, with a larger magnitude size (−3.3%) for the middle group as compared to the younger group (−1.9%). The older age group demonstrated the greatest range in magnitudes, with the magnitude size increasing from lag 0 (−0.8%) to moving average 4 (−2.9%).

Table 5.

Relative effect estimates^a for PIM analysis of ambient NO₂, expressed as percentage change of mean FEF_25–75.

	Mean FEF25–75 (L/sec)	Lag 0		2-day M.A.		4-day M.A.
		P.E.	95% C.I.	P.E.	95% C.I.	P.E.	95% C.I.
6 – 9 year-olds	1.35	−1.7	−5.1 , 1.7	−1.9	−6.1, 2.3	−1.4	−6.6, 3.7
10 – 12 year-olds	1.77	−2.5	−6.4 , 1.3	−3.3	−7.5, 0.9	−1.8	−5.9, 2.3
13 – 17 year-olds	2.59	−0.8	−3.4 , 1.7	−1.6	−4.4, 1.1	−2.9	−6.6, 0.7

Abbreviations: C.I., confidence interval; FEF_25–75, mean forced expiratory flow between 25% and 75% of forced vital capacity; L/sec, liters per second; M.A., moving average; P.E., point estimate; PIM, population intervention model.

^aNegative parameter magnitude indicates that FEF_25–75 improved under the intervention of lower NO₂ levels.

Results from a more conventional approach, scaling health effects to an IQR interval, are presenting in Table 6. In all cases, the IQR-scaled results were greater in magnitude than the population intervention model-scaled results. This finding is logical, given that the IQR intervals (Table 2) were consistently greater than the mean intervention NO₂ concentration changes (Table 4) by 50 – 60%. The overall pattern of effect sizes was the same, with associations being small to moderately-sized (−1.2 to −5.5% of average FEF_25–75), non-significant, and in the hypothesized inverse direction.

Table 6.

Relative effect estimates^a for conventional IQR scaling of ambient NO₂ effects, expressed as percentage change of mean FEF_25–75.

	Lag 0		2-day M.A.		4-day M.A.
	P.E.	95% C.I.	P.E.	95% C.I.	P.E.	95% C.I.
6 – 9 year-olds	−2.3	−6.8, 2.3	−2.7	−8.6, 3.2	−2.1	−9.8, 5.5
10 – 12 year-olds	−3.9	−9.6, 1.9	−5.2	−11.6, 1.2	−3.2	−10.5, 4.1
13 – 17 year-olds	−1.2	−5.1, 2.6	−2.5	−6.9, 1.8	−5.5	−12.5, 1.6

Abbreviations: C.I., confidence interval; FEF_25–75, mean forced expiratory flow between 25% and 75% of forced vital capacity; L/sec, liters per second; M.A., moving average; P.E., point estimate; PIM, population intervention model.

^aNegative parameter magnitude indicates that FEF_25–75 improved under the intervention of lower NO₂ levels.

DISCUSSION

This study estimated the health impact of a hypothetical NO₂ abatement using a method that allows for marginal (population-based) estimates, and which can be understood in reference to an air pollution intervention. The study found a small but consistent inverse association between ambient NO₂ and lung function (as measured by FEF_25–75) across various ages and exposure moving averages among this cohort of asthmatic children, though none of the findings reached statistical significance at the P<0.05 level.

The PIM approach employed here focused on estimating health effects scaled to an intervention that can be understood in relation to the observed air pollution profile of our study. Limitations that must be taken into account when interpreting these findings include the use of central site exposure data, which introduces exposure measurement error, and the possibility of informative censoring which could bias associations calculated here. In addition to the exclusion of some children from analysis, our analysis excluded child-days on which children did not use the portable spirometer (or used it but resulted in tracings that did not meet quality control standards); if NO₂ exposure were related to missing outcome days, then censoring would be informative. To enable a detailed explication of the method we only analyzed data for one exposure variable at three lags in one season; in future work we will apply the same approach to other pollutants and other seasons to provide a more comprehensive picture. This approach could also be implemented to estimate the effects of multi-pollutant exposure regimens (including co-exposures at different lags), an area of growing interest in environmental epidemiology.⁴²

The methodological approach employed here estimated marginal effects of ambient air pollution, and scaled the health effect size in a novel way. The advantages of marginal parameter estimation relative to conditional parameters are especially evident when analyzing policy-relevant exposures such as ambient air pollution, which is experienced by the target population as an ecological, population-wide exposure.. This approach has the additional advantage of enabling the investigator to estimate marginal health effects even in the presence of exposure/covariate interaction, or multivariable exposure regimens. It is worth noting that the issues of scaling interval (e.g., IQR versus some population interval) and marginal versus conditional effect estimation are separate; IQR-scaled effects may also be calculated not conditioned on model covariates.

To calculate the health effects of ambient NO₂, we defined an intervention in which three quarters of study days would have NO₂ concentrations lowered to a uniform threshold. While this results in a post-intervention air pollution profile that is unrealistic or overly ambitious, this focus on the actual exposure scenario behind the effect estimate is central to this the approach. The air pollution changes in this analysis are conservative compared to the IQR interval (Table 4 and Table 2, respectively). This is reflected by the increased magnitude of the associations in the IQR-scaled analysis as compared to the intervention-scaled analysis. Results were otherwise similar between the two analyses, highlighting the fact that while the scaling interval can help translate effects into real-world terms, it is of secondary importance to the modeling technique. Still, the population intervention approach enabled us to assess how realistic the intervention that we targeted is, and how likely these results are to map onto a real-world scenario, factors that are often obscured when scaling health effects to an IQR interval without reference to an intervention. The population intervention model is not without limitations. For example, although we defined a hypothetical intervention, it is unexplained how this decreased air pollution profile was achieved (e.g., through decreased traffic due to an economic downturn, decreased emission of precursor pollutants, or meteorological conditions), and the specific timing/sequence of the abatement (e.g., prolonged versus intermittent). It is likely that such different methods of achieving a population intervention would produce different health effects; in such a case we have no guidance as to which version is most relevant to our calculated health effect. This represents failure to meet the under-appreciated causal assumption of positivity.⁴³

Future applications of this method could help analyze policy scenarios and answer questions of greater real-world importance. For example, the PIM approach could be implemented to estimate the health impact of regulatory attainment in highly polluted areas characterized by regular non-attainment (conceptually similar to the approach of Hubbell et al.⁸), or to estimate the health impact of changing regulatory standards. While the PIM approach does not necessarily aid comparison across studies by scaling health effects to a single interval, it is perhaps better suited to estimate effects that take into account the existing exposure distribution of a given region. For example, a PIM analysis comparing the impact of ambient air pollution standard attainment in a highly polluted versus a less polluted area would scale the effects of abatement by a greater magnitude for the highly polluted region, reflecting the specific real-world consequences of abatement (analogous to a population attributable fraction).