Separation of Cellular and BOLD Contributions to T2* Signal Relaxation

Abstract

Purpose

The development of a reliable clinical technique for quantitative measurements of the parameters defining the BOLD effect, i.e. oxygen extraction fraction, OEF, and deoxygenated cerebral blood volume, dCBV, is needed to study brain function in health and disease. Herein we propose such a technique that is based on a widely available gradient recalled echo (GRE) MRI.

Methods

Our method is based on GRE with multiple echoes and a model of signal decay (Yablonskiy, MRM 1998) that takes into account microscopic cellular (R2), mesoscopic (BOLD), and macroscopic (background field gradients) contributions to the GRE signal decay with additional accounting for physiologic fluctuations.

Results

Using 3T MRI, we generate high resolution quantitative maps of R2*, R2, R2', and tissue concentration of deoxyhemoglobin, the latter providing a quantitative version of SWI. Our results for OEF and dCBV in gray matter are in a reasonable agreement with the literature data.

Conclusion

The proposed approach allows generating high resolution maps of hemodynamic parameters using clinical MRI. The technique can be applied to study such tissues as gray matter, tumors, etc.; however, it requires further development for use in tissues where extra- and intra-cellular compartments possess substantially different frequencies and relaxation properties (e.g. white matter).

Introduction

The presence of deoxygenated blood changes the local magnetic field around and within the blood vessels creating inhomogeneous distribution of local frequency shifts of water molecules. As a result, a faster transverse decay rate (R2*) of MRI signal can be observed, i.e. BOLD (blood-oxygen-level dependent) effect (1). In a gradient recalled echo (GRE) experiment the contribution of the BOLD effect to the tissue R2* relaxation rate constant is usually called R2'. The other part of R2* is usually called R2 which describes the part of the GRE signal decay resulting from water interaction with cellular components of biological tissue. Hence it is commonly assumed that

$$R{2}^{*}=R2+R2\prime$$ [1]

In other words, the parameter R2 represents the GRE signal decay that would exist in the absence of the BOLD effect. One should keep in mind that the parameter R2 in Eq. [1], that we call “cellular contribution” to the R2*, generally does not represent irreversible (with respect to the spin echo) part of the MRI signal transverse relaxation. This would only be the case for a single compartment tissue in the static dephasing regime (2). For a multi-compartment tissue, Eq. [1] should be written in the form of $R{2}^{*}=R{2}_c^{*}+R2\prime$, however in this manuscript we are using traditional notations, as defined in Eq. [1] (see further comments in the Discussion section). Separating the MRI signal decay due to the BOLD effect, that is R2', from R2*, could provide important information on tissue metabolic properties which is important for understanding normal human brain operation (3) as well as the pathophysiology of neurological disorders such as stroke (4), Alzheimer’s disease (5–7), Huntington’s disease (8), Parkinson’s disease (9,10) and others (11–14). It can also be of great importance for the evaluation of hypoxia within brain tumors and other organs (15,16).

Quite a few techniques have been proposed in the past to use BOLD effect for studying brain hemodynamic properties (see (17) and references therein). One of such techniques, quantitative BOLD (qBOLD) (18), is based on the theory of MRI signal formation in the presence of blood vessel network (2) and experimental method – Gradient Echo Sampling of Spin Echo (GESSE) proposed and tested on phantoms in (19). Similar method was later explored in human brain in (20,21). While results in phantom accurately reflect phantom parameters, the human data (20,21), being encouraging, reflect blood volume and blood oxygenated level only in an “apparent” manner. This was corrected in (18) by introducing a realistic model of human brain tissue that accounted for multi-compartment tissue structure (intra- and extra-cellular water and intravascular blood). qBOLD technique was also validated in animal studies by correlating qBOLD measurements of blood oxygenation level with direct measurements (22).

To fully explore the advantages of the qBOLD technique, one would require very high SNR in the data because of the high demand in the multi-parameter fitting of the qBOLD model (18,19,23–25). The robustness of qBOLD quantification could potentially be improved by independent measurements of some model parameters (26–28). Because of the complexity of the qBOLD mathematical model, many researchers are trying to evaluate the BOLD effect by estimating R2' part of tissue transverse relaxation rate constant R2*, by separately measuring R2* from a gradient recalled echo (GRE) experiment and R2 from a spin echo (SE) experiment (29–33).

However the R2' obtained in such a manner is very sensitive to the measurement protocol (29). Indeed, the signal we measure in the GRE experiment is a combination of signals from multiple tissue compartments having different R2* and different frequency shifts (18). For the same reason, the “irreversible” transverse decay rate constant, R2, which represents the properties mostly related to the tissue cellular content, is also an average parameter depending on details of the SE MRI pulse sequence. Importantly, the “weighted” contributions of the compartments in GRE and SE experiment are different. For example, if we measure R2* using multi-gradient echo sequence with short TR and TE, then the signal is highly weighted by short T1 and T2 compartments. If one applies multiple spin echo scans to measure R2, which usually requires long TR and SE times, then the signal is highly weighted by long T2 compartments. Thus combining these R2* and R2 measurements would not allow calculating the true BOLD-related R2'. To limit the problem, one should try using consistent TR and TE for both GRE and SE experiments and sample the signal within a time frame where signal variations between compartments are minimal.

In this paper, we present a simple and robust technique for separating the BOLD-related R2' contribution to R2* without using SE sequences. Our method relies on the GRE sequence with multiple gradient echoes and theoretical BOLD model (2,19). We also use recently-developed techniques allowing correction of GRE signal for compounding effects of magnetic field inhomogeneities (34) and physiological fluctuations (35). This new method provides high resolution maps of R2*, R2, R2' and hemodynamic parameters, i.e. tissue concentration of deoxyhemoglobin, oxygen extraction fraction (OEF), and deoxygenated cerebral blood volume (dCBV).

Theory

The MR signal decay from an imaging voxel in a gradient echo experiment can be represented as a product of several factors (19):

$$S(TE)=S_0·\text{exp}(-R2·TE+i·2\pi ·\mathrm{\Delta }f·TE)·F_{\mathit{\text{BOLD}}}(TE)·F(TE)$$ [2]

where TE is the gradient echo time, R2=1/T2 is the tissue transverse relaxation rate constant (describing GRE signal decay in the absence of BOLD effect), Δf is the frequency shift (dependent on tissue structure and also macroscopic magnetic field created mostly by tissue/air interfaces), function F_BOLD (TE) describes GRE signal decay due to the presence of blood vessel network with deoxygenated blood (veins and adjacent to them part of capillaries), and function F(TE) describes effect of macroscopic magnetic field inhomogeneities. In this paper we use voxel spread function (VSF) method (34) for calculating F(TE). Details are provided below in the Methods section.

In our previous publications, we used a statistical approach (2) assuming that a statistically significant amount of randomly positioned and randomly oriented blood vessels are present in each imaging voxel. In this case, F_BOLD (TE) is (2):

$$F_{\mathit{\text{BOLD}}}(TE)=\text{exp}[-\zeta ·f_s(\delta \omega ·TE)]$$ [3]

where ζ is the deoxygenated cerebral blood volume fraction (dCBV) and δω is the characteristic frequency determined by the susceptibility difference between deoxygenated blood and surrounding tissue (2):

$$\delta \omega =\frac{4}{3}\pi ·\gamma ·B_0·Hct·\mathrm{\Delta }{\chi }_0·(1-Y)$$ [4]

In this equation, Δχ₀ = 0.27 ppm (36) is the susceptibility difference between fully oxygenated and fully deoxygenated blood, Y is the blood oxygenated level (with Y = 0 being fully deoxygenated), Hct is the blood hematocrit, and γ is the gyromagnetic ratio. Function f_s describes the signal decay due to the presence of blood vessel network which was defined in (2). Herein we use a mathematical expression for the function f_s in terms of a generalized hypergeometric function ₁F₂ (17):

$$f_s(\delta \omega ·TE)={}_1{F}_2\left(\right[-\frac{1}{2}];[\frac{3}{4},\frac{5}{4}];-\frac{9}{16}{(\delta \omega ·TE)}^2)-1$$ [5]

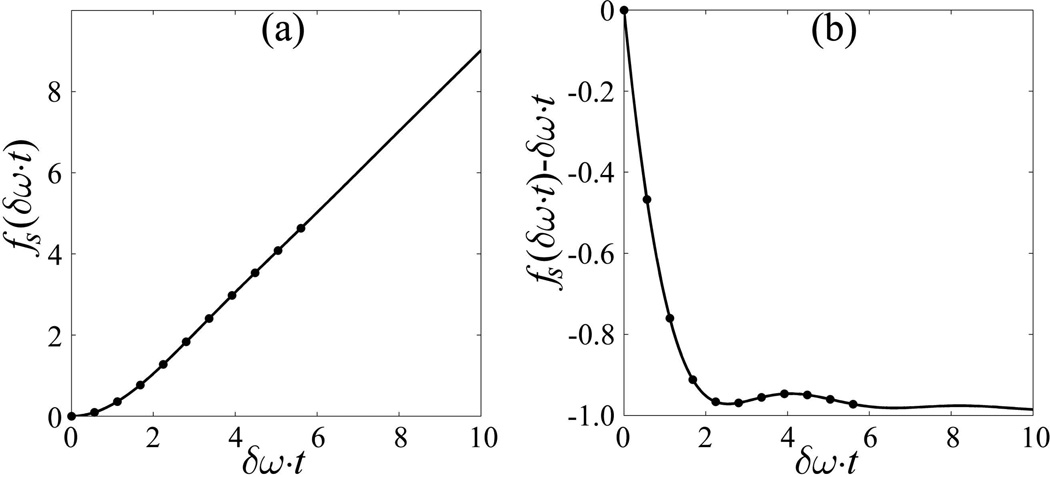
This non-linear function is presented in Fig. 1a. The non-linearity of f_s is very important for our method because it allows us to separate BOLD (R2') and cellular (R2) contributions to the GRE signal decay. In fact, because of this non-linearity, the R2* parameter can only be introduced for characterizing the GRE signal decay if TE >> δω⁻¹. In this case the function f_s becomes linear (2) and we can calculate BOLD-related R2' as:

$$R2\prime =\zeta ·\delta \omega$$ [6]

Figure 1.

(a) Function f_s, Eq. [5], versus (δω·t). The dots are values at our echoes (t=TE_n) assuming Y= 60%. (b) f_s(δω·t)−(δω·t) versus (δω·t), where t is the time after RF excitation pulse.

The residual of the function f_s(δω·t)−δω·t is shown in Figure 1b demonstrating substantially non-linear quasi-oscillating behavior at short times.

In the current paper, we still use an assumption that blood vessels are randomly oriented in each imaging voxels (which, of course, can be violated in voxels containing large vessels) but we are not using statistical requirement of a large number of randomly positioned blood vessels. In this case, F_BOLD (TE) can be obtained by averaging Eq. [35] in (2) for a single blood vessel with respect to random orientations of the vessel’s axis. The result is:

$$F_{\mathit{\text{BOLD}}}(TE)=1-\frac{\zeta }{1-\zeta }·f_s(\delta \omega ·TE)+\frac{1}{1-\zeta }·f_s(\zeta ·\delta \omega ·TE)$$ [7]

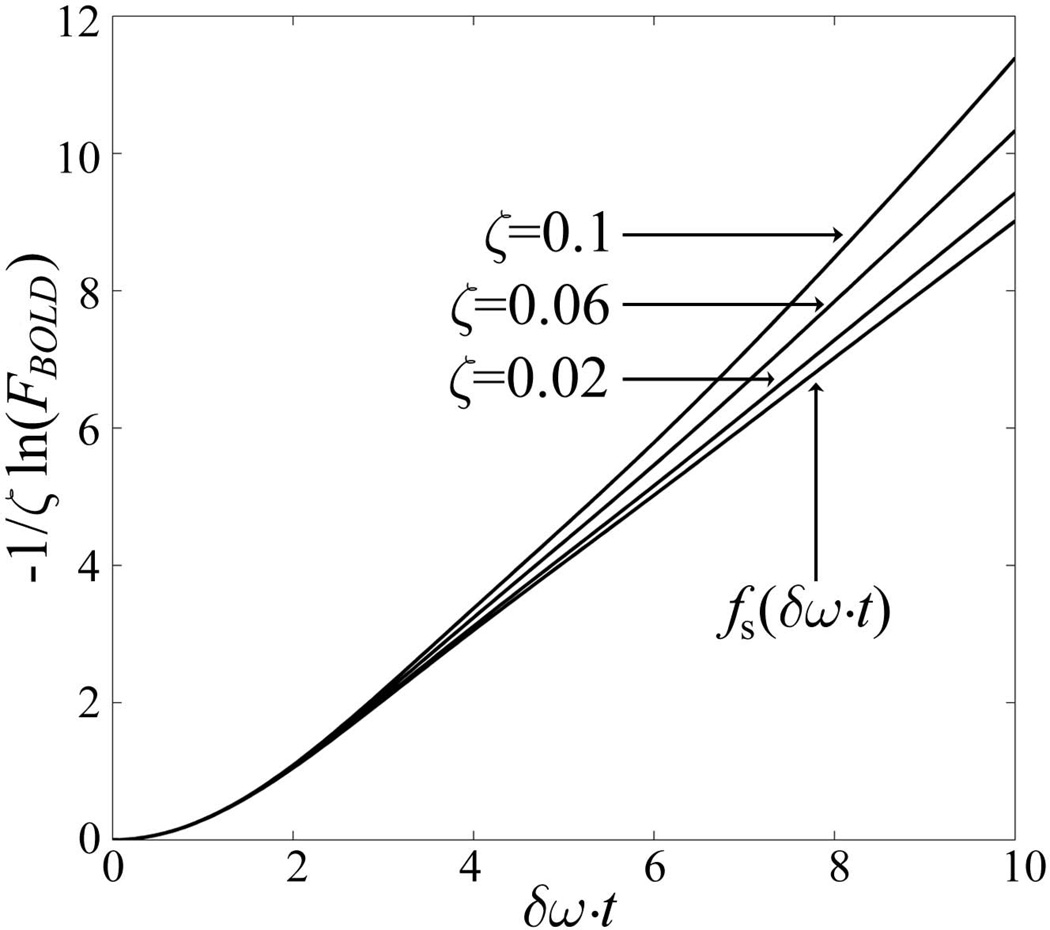
The dependence of the function F_BOLD (TE) in Eq. [7] on dCBV (ζ) is shown in Fig. 2. One can see that this function’s general behavior is similar to the original exponential function in Eq. [3]: it describes a non-linear behavior for a short period of time and quasi-linear after that (as seen in Figure 1). One should keep in mind that Eq. [7] does not represent an exact solution for the extravascular BOLD signal but is rather an empirical formula that provides a reasonable approximation for both limiting cases – small volume fractions of blood vessels (see Fig. 2) and a case of a few large vessels (as it was originally derived in (2)).

Figure 2.

The dependence of the function F_BOLD, describing the BOLD-related contribution to the extra-vascular signal decay, Eq. [7], on the deoxygenated blood volume fraction ζ. The function f_s defining BOLD signal in a standard exponential form, Eq. [3], is also shown. The plots demonstrate that Eq. [7] is more sensitive to ζ as compared to function f_s in Eq. [3].

By making use of Eqs. [4] and [6] we can also evaluate the concentration of deoxyhemoglobin per unit tissue volume (18):

$$C_{\mathit{\text{deoxy}}}=\frac{3}{4}·\frac{\zeta ·\delta \omega ·n_{Hb}}{\gamma ·\pi ·\mathrm{\Delta }{\chi }_0·B_0}$$ [8]

Where n_Hb is the total intracellular Hb concentration equal to 5.5×10⁻⁶ mol/mL (18).

By fitting equation [2] to the complex signal using nonlinear regression algorithm, we are able to find the five parameters: S₀, R2, Δf, ζ and δω for each voxel in the brain. In addition, we also calculate a standard relaxation rate constant R2* using a simplified model without separating BOLD effect but accounting for macroscopic field inhomogeneities:

$$S(t)=S_0·\text{exp}(-R{2}^{*}·TE+i·2\pi ·\mathrm{\Delta }f·TE)·F(TE)$$ [9]

Methods

Image acquisition

All studies were approved by the Institutional Review Board of Washington University in St. Louis. MRI data were obtained from eight healthy volunteers (4 Female and 4 male, age 23–30) using Siemens 3T Trio MRI Scanner (Siemens, Erlangen, Germany) and a 12-channel head coil. A 3D multi gradient echo sequence was used to obtain the data. Sequence parameters were: resolution 1×1×2 mm³ (read, phase, slab), FOV 256 mm×192 mm, repetition time TR = 50ms, 10 gradient echoes with first echo time TE₁ = 4 ms, echo spacing ∆TE = 4ms. Additional phase stabilization echo (the navigator data) was collected for each line in k-space to correct for image artifacts due to the physiological fluctuations (35). Field inhomogeneity effects were removed by using an advanced version (37) of the voxel spread function (VSF) approach (34). Standard clinical MP RAGE (38) images with high resolution (voxel size: 0.9×0.9×1.5 mm³) were also collected for segmentation purposes. After data acquisition, raw k-space data were read into MATLAB (The MathWorks, Inc.) for processing.

Image processing

Correction for physiologic motion artifacts

The correction of data for physiological artifacts (i.e. the background frequency fluctuations due to the physiological motions such as breathing, etc.) is accomplished using procedures developed in (35). In brief, the phase stabilization data (navigators) are collected as the last gradient echo for each line in k-space by rewinding phase encoding gradients prior to acquisition. Then each echo train, including the navigator, is Fourier transformed in the read-out direction only and we subtract a corresponding phase drift from the k-space data for each gradient echo time TE in the same echo train before doing the Fourier transform in the phase encoding directions.

$$S(x,k_y,k_z,TE,ch)\Rightarrow S(x,k_y,k_z,TE,ch)·\text{exp}[-i·d{\phi }_{\mathit{\text{nav}}}(x,k_y,k_z,ch)\frac{TE}{T{E}_{\mathit{\text{nav}}}}]$$ [10]

Here, dφ_nav is the phase difference of a current navigator from the 1^st navigator recorded and TE_nav is the navigator echo time.

RF channel combination

After we correct the k-space data for physiological artifacts, we apply FFT in the phase-encoding directions to get images. 3D spatial Hanning filter is then applied to the data in the image domain. To achieve an optimal signal-to-noise ratio, we use the following equation to combine the data of all channels (39):

$$S_n(TE)=\sum _{ch=1}^M{\lambda }_{ch}·{\overline{S}}_n^{ch}(T{E}_1)·S_n^{ch}(TE);{\lambda }_{ch}=\frac{1}{M·{\epsilon }_{ch}^2}\sum _{ch\prime =1}^M{\epsilon }_{ch\prime }^2$$ [11]

where the sum is taken over all M channels (ch), S̅ denotes complex conjugate of S, λ_ch are weighting parameters and ε_ch are noise amplitudes (r.m.s.). Index n corresponds to the voxel position (n=x,y,z). This algorithm allows for the optimal estimation of quantitative parameters, and also removes the initial phase incoherence among the channels (39,40).

Correction for B₀ field inhomogeneities

Background magnetic field inhomogeneities are known to adversely affect measurement of R2* and parameters of qBOLD model (19). Herein we use an advanced approach (37) of the VSF (voxel spread function) method (34) that provides a solid platform for correcting images. VSF method relies on the solution of the VSF equation

$$S_n(TE)={\sum }_m{\mathrm{\Psi }}_{nm}(TE)·{\sigma }_m(TE)$$ [12]

where S_n(TE) is the measured MRI signal in the voxel n at the gradient echo time TE, σ_m(TE) is the ideal “non-contaminated” signal from the voxel m that would exist in the absence of Gibbs artifacts and magnetic field inhomogeneities, and the matrix Ψ_nm(TE) defines the signal leakage to the voxel n from the neighboring voxels m (see definition in (37)). In (37) the VSF equation was solved using similarity approximation – an assumption that the ideal signal σ_m(TE) from the voxel m can be approximated as

$${\sigma }_m(TE)={\sigma }_n(TE)·|S_m(T{E}_1)/S_n(T{E}_1)|$$ [13]

where TE₁ is the first gradient echo time. This approximation is justified if neighboring voxels belong to “similar” tissues but it could lead to image artifacts at the boundaries between tissues with different MR properties where the MR signal can decay at neighboring voxels with different transverse relaxation rates R2*. To address this issue we proposed (37) to improve similarity approximation by a substitution

$${\sigma }_m(TE)={\sigma }_n(TE)·|S_m(T{E}_1)·\text{exp}[-R{2}_m^{*}(TE-T{E}_1)]/S_n(T{E}_1)·\text{exp}[-R{2}_n^{*}(TE-T{E}_1)\left]\right|$$ [14]

Since information on R2* is not initially available, we use an iterative procedure - the original similarity approximation, Eq. [13], is used to calculate initial values of R2* that are used subsequently in Eq. [14]. This allows solution of VSF equation in the form of

$$S_n(TE)={\sigma }_n(TE)·F_n(TE)$$ [15]

with F-function calculated based on Eq. [14] in the following form:

$$F_n(TE)=\sum _m|S_m(T{E}_1)|·\text{exp}(-R{2}_m^{*}·TE)/\left[\right|S_n(T{E}_1)\left|·\text{exp}\right(-R{2}_n^{*}·TE\left)\right]$$ [16]

After calculation, Eq. [16] is normalized to 1 at TE =0.

Data fitting procedure

The combined MR signal, in Eq. [11], is analyzed on a voxel-by-voxel basis by fitting Eq. [2] with F-function calculated according to the algorithm in Eq. [16]. While the hypergeometric function in Eq. [5] is in the MatLab library, its calculation is very slow. To speed up calculation, we use the Taylor expansion of this up to the 30^th order (note that only 15 terms are present in this expansion as function is even). The square root of the fitting amplitude produces image of S₀ in Eq. [2] which, for our sequence parameters, is T1-weighted image. Non-linear least square curve fitting algorithm is used to find the optimum parameters. To avoid the singularities in Eq. [2] and save computing time, we set the boundaries for fitting parameters to be within the following values: dCBV is from 0.001 to 0.99, and Y is from 0.1 to 0.9 (10% to 90%). The fitting results are not sensitive to the initial values of the parameters within the boundaries. All codes for image processing and fitting are written in MATLAB (R2011a, the MathWorks Inc, USA). To accelerate the computation, we also apply a brain mask that excludes the skull and the outside regions.

Image segmentation

Our method has an advantage of producing inherently co-registered T1W images with good WM/GM contrast and quantitative R2* maps. R2* maps have little contrast between GM and WM, so we use our T1W images to improve co-registration with MPRAGE using web-based tools, FSL (41–43). Image segmentation is done using FreeSurfer (Martinos Ctr for Biomed Imaging).

Results

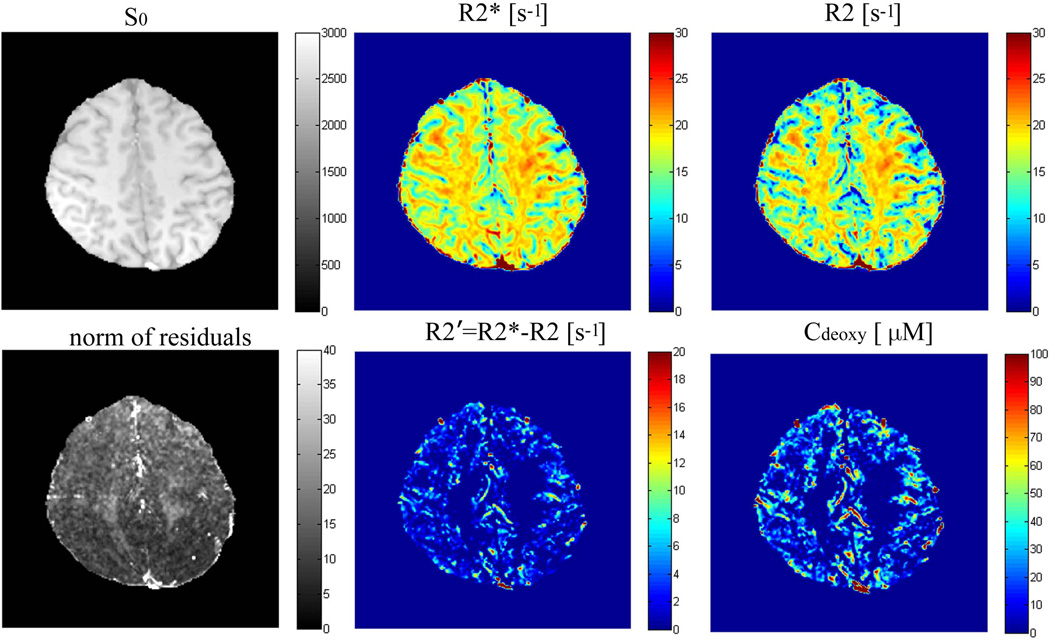
Example of the images and quantitative maps are shown in Figure 3. In this figure, S0 is the calculated signal intensity that would correspond to TE = 0, which for our sequence parameters represents T1-weighted image. While R2* map shows some WM/GM contrast, this contrast is substantially enhanced on the R2 map as a result of removing the BOLD contribution. Our results in cortical gray matter for all the subjects are summarized in Table 1.

Figure 3.

Fitting results and parameter maps from one subject. S₀ is a T1-weighted image which is a square root of the fitting amplitude; R2* is the apparent transverse decay rate obtained by fitting to data a mono-exponential function, Eq. [9], without accounting for the BOLD effect; R2 is the transverse decay rate after removal the BOLD effect, Eq. [2]; also shown are the R2' map (defined by the differences of R2* and R2) and C_deoxy map, Eq. [8]. Both these maps have higher values at the location of large veins. Residual map shows values mostly less than 1% of the total signal.

Table 1.

Values of the parameters for the cortical gray matter for eight subjects. The last row represents average values for all 8 subjects. Numbers are Mean (or peak) +/− STD. Y values are calculated assuming Hct = 0.4.

Subjects (Sex, Age)	Relaxation rate constants [s−1]								BOLD parameters
	R2*		R2		R2'=R2*-R2		R2'=ζ·δω		Cdeoxy [µM]		Y [%]		ζ [%]
	mean	peak	mean	peak	mean	peak	mean	peak	mean	peak	mean	peak	mean	peak
1 (F,23)	17.5±3.5	17.1	15.2±4.3	16.5	4.8±5.5	0.9	4.8± 3.0	2.7	20.0± 12.5	11.3	51.1±19.6	74.5	4.4±2.5	2.5
2 (F,28)	17.8±3.6	17.3	15.2±4.3	15.6	4.8±5.7	1.0	4.7± 3.0	2.7	19.9± 12.3	11.3	52.4±19.1	76.5	4.4±2.6	2.5
3 (M,28)	18.2±3.5	17.4	15.2±4.4	15.9	5.4±5.9	1.0	5.3±3.0	3.6	22.1±12.3	15.1	52.4±18.9	72.5	4.7±2.6	3.0
4 (F,26)	18.2±3.8	18.9	15.9±4.7	18.3	5.2±5.9	0.9	5.1±3.0	3.0	21.2±12.6	12.6	51.5±18.9	72.0	4.5±2.6	2.5
5 (M,29)	17.7±3.7	17.4	14.8±4.5	15.3	5.3±5.8	1.0	5.3±3.1	3.0	22.3±12.8	12.6	52.1±18.8	73.0	4.7±2.6	3.5
6 (F,30)	18.3±3.6	17.4	15.4±4.4	15.9	5.4±6.1	0.9	4.9±3.0	3.0	20.5±12.6	12.6	52.2±18.9	74.0	4.5±2.6	2.0
7 (M,22)	16.7±3.7	17.4	14.0±4.3	13.8	4.9±5.3	1.0	5.2±3.0	3.3	21.7±12.6	13.8	54.0±18.1	74.0	4.6±2.6	2.5
8 (M,26)	17.6±3.6	16.5	14.9±4.3	15.3	4.9±5.5	1.0	5.1±2.9	3.6	21.4±12.1	15.1	55.8±16.7	71.5	4.6±2.5	3.0
Mean ± STD	17.8±0.5	17.4 ± 0.7	15.1± 0.6	15.8 ±1.3	5.1±0.3	0.96±0.05	5.1±0.2	3.1±0.4	21.1±0.9	13.0±1.5	52.7±1.5	73.5 ±1.6	4.6±0.1	2.7±0.5

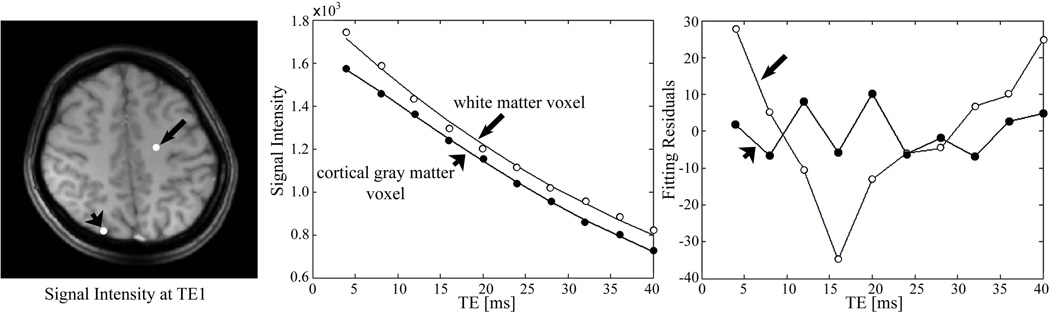
Examples of the signal decay and fitting curves are shown in Figure 4 for two representative voxels – in white and gray matter. While in GM fitting residuals are small and random, in WM our fitting returns the lower boundaries for Y and dCBV, and residuals show systematic (not related to noise) deviation from zero. This means that the BOLD effect in WM cannot be separated by the model described in Eq. [2]. This will be further discussed in the following section. Hence, we show only results for GM.

Figure 4.

Example of the fitting curves and residuals. The fitting results for gray matter voxel (short arrow) are R2=13.0 s⁻¹, f=0.41 Hz, δω=201 s⁻¹ (which implies 1-Y=38.28% if Hct=0.4), and ζ= 4.55%. For the white matter voxel (long arrow), the fitting results are R2=21.7 s⁻¹, f=−0.002 Hz, δω=52 s⁻¹ (1-Y=10% if Hct=0.4), and ζ= 0.1% (δω and ζ here hit the lower boundaries of ranges of the parameters).

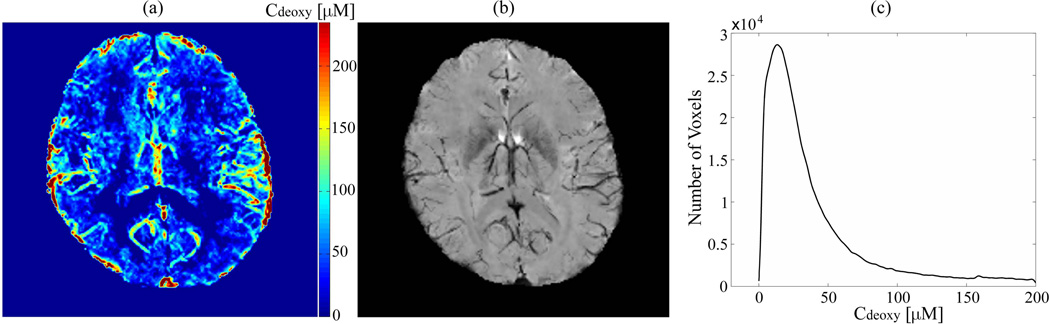
Our data for deoxyhemoglobin concentration are quite reasonable. It is important to note that, C_deoxy, Eq. [8], and R2', Eq. [3] (3), are different only by a numerical factor, but C_deoxy has clear physical meaning. As shown in Figure 3, C_deoxy is mainly seen in the cortical gray matter that has greater concentration of blood vessels as compared to WM. The concentration C_deoxy has the highest values in the areas of large veins. To further validate our results, we compare our results for C_deoxy with the results obtained by SWI calculated from GEPCI data using an algorithm described in (39). Example of the data is shown in Figure 5. The brighter area of Figure 5(a) means higher concentration of deoxygenated hemoglobin, which is consistent with the location of veins seen in SWI.

Figure 5.

A comparison between the maximum intensity projection of Cdeoxy maps over five slices (left) and the minimum intensity projection of SWIs over the same slices (middle). The brighter regions in Cdeoxy maps correspond to the darker ones in SWIs, which correspond to the voxels occupied by large veins. MIP of Cdeoxy maps also provides the information on capillaries which are not seen in the MIP image of SWI. The histogram (right) is an example of the distribution of Cdeoxy in cortical gray matter. All data are from the subject 1.

Discussion

The development of a reliable technique for quantitative measurements of the vascular characteristics affecting BOLD effect, such as oxygen extraction fraction, OEF, and deoxygenated cerebral blood volume, dCBV, can benefit diagnosis of brain tumors, stroke, and other neurological diseases (27,44–47). In this paper we have demonstrated successful separation of cellular (R2) and vascular (R2′) contributions to the transverse relaxation rate of GRE signal. Our method is based on the MRI signal acquisition using sequence with multiple gradient echoes and analytical model of signal decay, Eq. [2], that takes into account cellular (R2), extravascular (F_BOLD), and macroscopic (F) contributions to the GRE signal decay – Ref. (19). The extravascular BOLD effect is described in the framework of the theory that is an extension of the previously developed theory of BOLD effect (2) to tissue voxels that might have elevated volume fraction of blood vessel network with deoxygenated blood – dCBV. The macroscopic field inhomogeneity effects are accounted for in the framework of the VSF approach (34) with enhanced image contrast (37). Also, artifacts due to the physiologic fluctuations are minimized using technique developed in (35).

The restrictions of applying our method are mostly related to two factors. First, our method of separating cellular from vascular contributions to the tissue transverse relaxation relies on the specific behavior of the vascular (BOLD) contribution to the signal decay as described in Eqs. [5], [7], and illustrated in Figure 1 and Figure 2. As first proposed in (2) and demonstrated on phantom studies in (19), this behavior is not mono-exponential which allows separating it from the mono-exponential R2 decay. However, as is seen in Figure 1, we are sampling only very few initial points of the decay curve where this non-linear behavior is most pronounced. As demonstrated in (25) this might lead to rather large evaluation errors in parameters estimations. However, the use of the improved BOLD function, Eq. [7], slightly alleviates this problem because Eq. [7] shows non-monoexponential behavior in a broader range of TEs – see Figure 2. We should also mention that the BOLD model (2) that we are using was developed using the static dephasing regime when diffusion phenomena are not important. Computer Monte-Carlo simulations by Dickson et al (48) demonstrate that the diffusion effects do not significantly affect evaluation of BOLD parameters for a GRE experiment with relatively short TEs even for small blood vessels if additional δR2 correction is used (see Figure 7 in (48)).

Second, the model in Eq. [2] does not account for the multi-compartment structure of the brain tissue as was accounted for in the qBOLD approach (18,22). However, qBOLD, relying on the model with multiple parameters (compartments volume fractions, relaxation rate constants and frequencies) requires very high SNR and a very big number of sampling points which can be achieved only for images with rather big voxels (typical resolution 4×4×4 mm³). In this paper we use images with much higher resolution - 1×1×2 mm³ and found parameters in GM rather similar to the qBOLD technique – see Table 2. This is because in GM relaxation rate constants in the intracellular and extracellular compartments are rather similar (18) and the frequency shift between compartments (about 5 Hz at 3T) creates only very small additional signal decay in the time scale of 40 ms where our data are acquired. Indeed, as we can see from Figure 10 in (17), the multi-compartment structure of MR signal becomes pronounced only at gradient echo times around and beyond 40 ms. However, this is not the case for the GRE experiment in WM where contribution from the myelin water to the GRE signal is important as it has very strong signal decay and very high frequency shift from intra- and extra-cellular water (49–52). These two effects cause substantial non-linear behavior of the signal decay curve that is not accounted for in our model. Especially the large R2 of the myelin water compartment causes the signal to curve in the opposite direction to the curvature caused by the BOLD effect shown in Figure 1. Thus, the existence of myelin “interferes” with the BOLD effect. And indeed, our model fails in most parts of WM as it is demonstrated in Figure 4. This was not the case for qBOLD approach in (18) where data were acquired using GESSE (gradient echo sampling of spin echo) sequence (19) with the spin echo time of 60 ms where contribution of myelin water signal is practically negligible due to its short T2.

Table 2.

Summary of mean values of R2*, R2 and R2′ for cortical gray matter obtained at 3T MRI by different methods. There are two ways of calculating R2' in this paper: [a] R2'=R2*-R2, [b] R2'=ζ·δω

Source	Method	Number of subjects (age)	R2* [s−1] mean	R2 [s−1] mean	R2' [s−1] mean
This paper	mGRE	8 (23–30)	17.8±0.5	15.1± 0.6	5.1±0.3 [a] 5.1±0.2 [b]
Gelman et al., 1999 (30)	GESFIDE	6 (19–42)	Not available	14.4±1.8 (frontal cortex)	3.4±1.1 (frontal cortex)
He and Yablonskiy, 2007 (18)	GESSE	6	Not available	14.9±0.2	2.9±0.4
Paling et al., 2012 (31)	mGRE for R2* Fast SE for R2	21 (mean age 36)	Not available	Not available	9.2±1.1
West et al., 2013 (32)	QRAPMASTER (qMAP)	10 (21–29)	Not available	10.69±0.76 (frontal)	Not available
Sedlacik et al., 2014 (33)	mGRE for R2* mTES for R2	66 (only use age ≤ 30)	15.5 (14.8–16.2) (frontal cortex)	8.5 (8.2–8.9) (frontal cortex)	7.1 (6.5 to 7.8) (frontal cortex)
Ni et al., 2014 (29)	Multiple methods	10 (24–25)	Not available	Not available	2.7 to 3.5

In our model, Eq. [2], we also neglected contribution of the intravascular signal. While contribution of this signal is proportional to dCBV (as the contribution of extravascular BOLD – Eq. [7]), the vascular signal decays much faster due to the short blood T2* (30 ms for Y=0.6 at 3T) and additional signal decay due to the presence of randomly oriented blood vessels with the orientation-dependent frequencies (53). The latter leads to an additional signal decay with the time scale of about 3π/(2δω) (53) which is about 25 ms for Y=0.6 at 3T. These two mechanisms lead to substantially faster intravascular signal decay rate (apparent T2* less than 15 ms) as compared to T2 of GM that defines extravascular BOLD contribution to the GRE signal decay (about 60 ms per Tables 1 and 2).

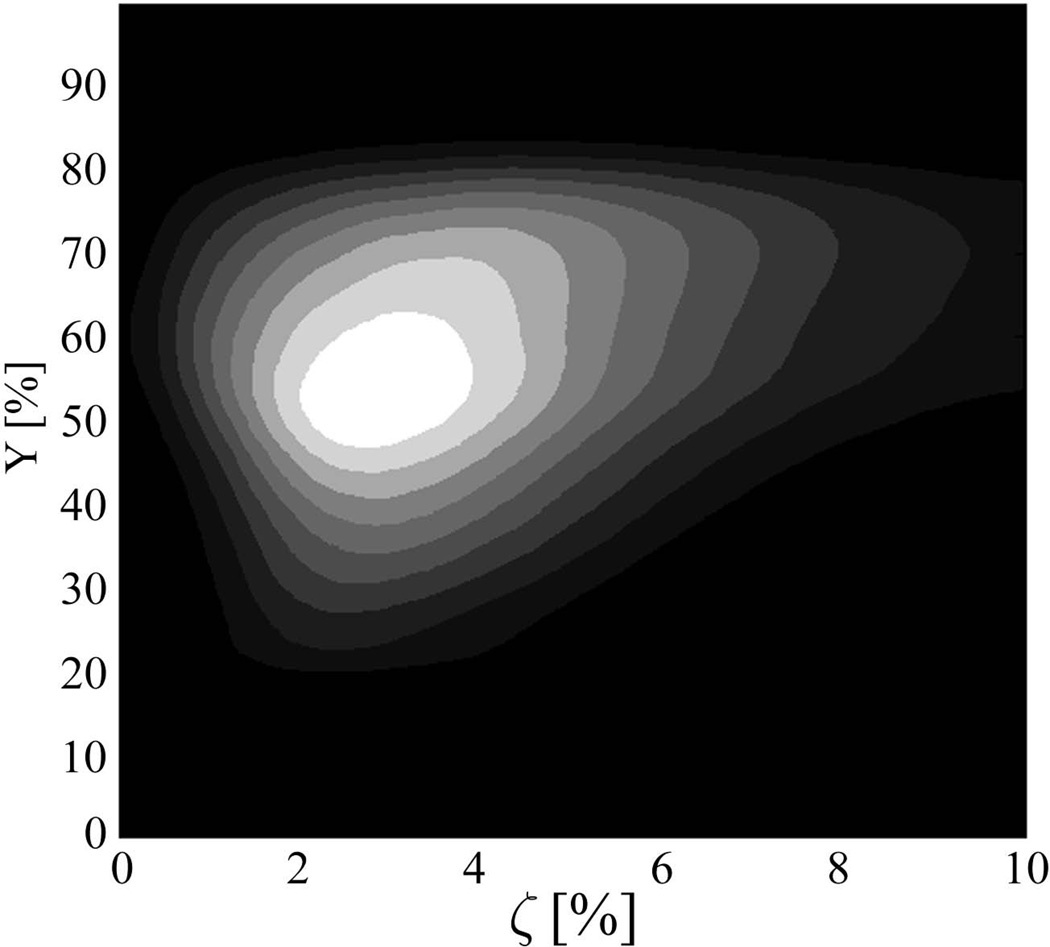
Despite these potential sources of errors, our results for the model parameters in GM are quite reasonable. Mean value of dCBV is 4.6% which includes contribution from blood vessels of different sizes, including large veins. The peak value of the distribution is much smaller – it is about 2.7% as seen in Table 1 and the example shown in Figure 6. This value is more consistent with the literature data for the total blood volume (arterial + venous) of 4.5%, 3%, and 2.7% reported by Carpenter et al. (54), Diringer et al. (55), and Derdeyn et al. (4), correspondingly. The mean value of blood oxygenation level in our subjects is 53% and the peak value is 73%. This values are in the range of MRI estimates of Y about 65% based on the measurements in the superior sagittal sinus by Lu and Ge (56), Jain et al (57) and Barhoum et al (58). Assuming that oxygenated level of the arterial blood is about 100%, we can estimate oxygen extraction fraction, OEF, from our data to be between 47% of mean value and 25% of peak value which is also in the range of the literature data. Indeed, Carpenter et al. (54), Yamauchi et al. (59), Diringer et al. (55), and Raichle et al. (60) reported OEF values of 35%, 42.6%, 41%, and 40%, correspondingly. An example of the 3D histogram of the voxels as a function of blood oxygenation level Y, and dCBV is shown in Figure 6. The histogram has a peak with Y around 0.55 and dCBV around 0.03, however, bigger dCBV, presumably originating from the voxels with large blood vessels, also present in this asymmetric histogram contributing to higher mean dCBV values.

Figure 6.

The plot represents an example of the 3D histogram of voxels as a function of blood oxygenation level Y, and dCBV (ζ) with bright white color corresponding to higher values. One can see that the peak value corresponds to Y around 0.55 and dCBV around 0.03.

The mean value of C_deoxy over the whole cortex that we found is 21.1 µM with the peak value of 13 µM and the average value in large veins about 200 µM (red color in Figure 5). For pure blood with Hct = 40%, Y= 0.6, we can estimate C_deoxy = Hct·(1−Y)·n_Hb to be about 880 µM. This number is higher than our measurements in large veins which is expected – our static dephasing regime model of BOLD signal can only describe signal dephasing in the blood in an apparent manner. More sophisticated models for the blood signal (see detail discussion in (17) can be implemented in our approach for obtaining quantitative measurements of blood oxygenation level in large veins. For voxels with dCBV between 2% and 3% we can expect C_deoxy to be between 18 µM and 26 µM which is consistent with our measurements. It is also consistent with C_deoxy of 14.3 µM measured in the neonatal brain surface by optical method (61).

Several papers have reported on different methods of separating R2 and R2′ contributions to the R2* signal decay. Their results are summarized in Table 2 together with our data. It is often assumed that the transverse relaxation of MR signal can be characterized by simple exponential functions:

$$S{(TE)}_{GRE}=S_0·\text{exp}(-R{2}^{*}·TE+i·2\pi ·\mathrm{\Delta }f·TE)S{(TE)}_{SE}=S_0·\text{exp}(-R2·TE);R{2}^{*}=R2+R2\prime$$ [17]

where R2 is assumed to represent an irreversible (with respect to 180° refocusing RF pulse) part of the signal decay and R2′ is assumed to represent a reversible part of the signal decay. However, as we already noticed in the Introduction, this assumption is not strictly correct because signal decay in biological tissue in either SE or GRE experiment is never monoexponential due to a number of reasons. First, biological tissue structure is always multi-compartment and not accounting for this effect can lead to substantial discrepancies in R2 and R2′ estimates even if considering them as apparent parameters. For example, Paling et al. (31) report R2′ values of 9.2 s⁻¹ and Sedlacik et al. (33) report R2′ values of 7.1 s⁻¹ obtained with 3T MRI. These values are too big to be attributed to vascular contribution to the R2* relaxation rate constant. The issue here is that in these papers the authors independently measured R2* and R2 assuming a monoexponential decay for both experiments ignoring the fact that the relative contributions of multi-compartments to the GRE and SE experiments are different (the compartments have different relaxation rate constants and different frequencies). Secondly, the extravascular BOLD contribution to the GRE signal decay is not monoexponential, as described by our Eqs. [7], [5] and illustrated in Figure 1 and Figure 2. Also, SE measurements can be affected by the SE sequence timing (62). Ignoring this effect can also lead to errors in estimating BOLD contribution – compare different ways of estimating R2′ presented in Table 1 and Table 2. Third, accounting for macroscopic field inhomogeneities is also essential for accurate estimates of tissue R2′. In our paper we use a VSF approach (34) with enhanced image contrast (37) as described by Eqs. [12]–[16]. This is an essential step in accurate estimate of BOLD contribution because macroscopic magnetic field inhomogeneities affect GRE signal decay in a non-mono-exponential manner (34) which can affect accuracy of all parameters estimates (19,34). Importantly, as was demonstrated in (34), an often-used sinc-function approach to correct for in-plane field inhomogeneities in 2D acquisition and for any direction in 3D acquisition, is not appropriate and only leads to additional errors in parameters estimates.

Conclusion

In this paper we have developed a technique for separating cellular and BOLD-related contributions to the R2* MRI signal decay. Our method is based on MRI signal acquisition using a single sequence with multiple gradient echoes (no spin echo sequences are involved) and analytical model of the signal decay that takes into account microscopic (cellular), mesoscopic (extravascular BOLD), and macroscopic (background field gradients) contributions to the GRE signal decay. The method provides reliable and realistic results for GM and is expected to work for any tissue where multiple compartments have similar magnetic properties (i.e. relaxation times and frequencies) which is the case in GM. We can also hypothesize that tissue tumors might satisfy such conditions. However, the method does not produce reliable BOLD results in WM due to the presence of myelin water compartment with substantially different magnetic properties. An approach that would account for this multi-compartment structure is necessary to provide accurate estimates in WM. Such an approach can also improve our results in GM.