Kinetic Dissection of the Pre-existing Conformational Equilibrium in the Trypsin Fold

Background: The pre-existing equilibrium between open (E*) and closed (E) conformations is a defining feature of the trypsin fold, but its kinetic signatures remain elusive.

Results: Kinetics of the E*-E interconversion are determined for protease and zymogen.

Conclusion: Protease and zymogen differ in the relative distribution of E* and E.

Significance: The role of the E*-E equilibrium in the trypsin fold is elucidated.

Abstract

Structural biology has recently documented the conformational plasticity of the trypsin fold for both the protease and zymogen in terms of a pre-existing equilibrium between closed (E*) and open (E) forms of the active site region. How such plasticity is manifested in solution and affects ligand recognition by the protease and zymogen is poorly understood in quantitative terms. Here we dissect the E*-E equilibrium with stopped-flow kinetics in the presence of excess ligand or macromolecule. Using the clotting protease thrombin and its zymogen precursor prethrombin-2 as relevant models we resolve the relative distribution of the E* and E forms and the underlying kinetic rates for their interconversion. In the case of thrombin, the E* and E forms are distributed in a 1:4 ratio and interconvert on a time scale of 45 ms. In the case of prethrombin-2, the equilibrium is shifted strongly (10:1 ratio) in favor of the closed E* form and unfolds over a faster time scale of 4.5 ms. The distribution of E* and E forms observed for thrombin and prethrombin-2 indicates that zymogen activation is linked to a significant shift in the pre-existing equilibrium between closed and open conformations that facilitates ligand binding to the active site. These findings broaden our mechanistic understanding of how conformational transitions control ligand recognition by thrombin and its zymogen precursor prethrombin-2 and have direct relevance to other members of the trypsin fold.

Introduction

Trypsin-like proteases are widely distributed in nature and constitute a very significant component (1–2%) of a typical genome (1). Substrate recognition in this family of enzymes is based on engagement of functional groups by distinct subsites whose structural architecture is preserved among different members of the family (2, 3). Selectivity and most of the substrate binding free energy are provided by the primary specificity pocket defined by residue 189 (chymotrypsinogen numbering) and secondary sites of recognition that decorate access to the active site region (4). Although much is known on the structural underpinnings of these interactions and the ensuing catalytic cycle leading to cleavage of the peptide bond downstream of the residue of substrate making contact with residue 189 (5), relatively little is known on whether substrate recognition entails conformational rearrangements that precede and/or follow the binding event. Lack of information on the mechanism of substrate recognition that precedes and informs catalysis makes it difficult to interpret the allosteric effect of cofactors so widely represented in trypsin-like enzymes involved in blood coagulation (6) and the complement (7).

Recent progress in the structural investigation of the trypsin fold has revealed an unexpected plasticity in both the protease and zymogen, especially in the region controlling substrate access to the active site (8, 9). Distinct arrangements have been reported for the segment comprising residues 215–217 on the west wall of the entrance to the active site (see Fig. 4 under “Discussion”), resulting in access to the primary specificity pocket that is either fully open or impeded to different extent. Most of this information is observational and rarely refers to the same protein, except in a few cases (10, 11), raising the question as to whether alternative conformations of the segment comprising residues 215–217 are indeed accessible in solution. NMR studies support the view of a highly plastic protease fold that is eventually rigidified upon ligand binding (12–14), but have failed to reveal any novel or mechanistically relevant information on the active site region of the enzyme so critical for substrate recognition and its regulation. Furthermore, any structural information remains phenomenological without functional validation and rapid kinetics are uniquely suited to address how binding and conformational transitions are intertwined in the process of ligand recognition (15). Such measurements are particularly relevant for the zymogen precursor of the protease, to establish if conformational plasticity exists prior to the proteolytic conversion to the mature enzyme and bears signatures that can be detected experimentally in solution.

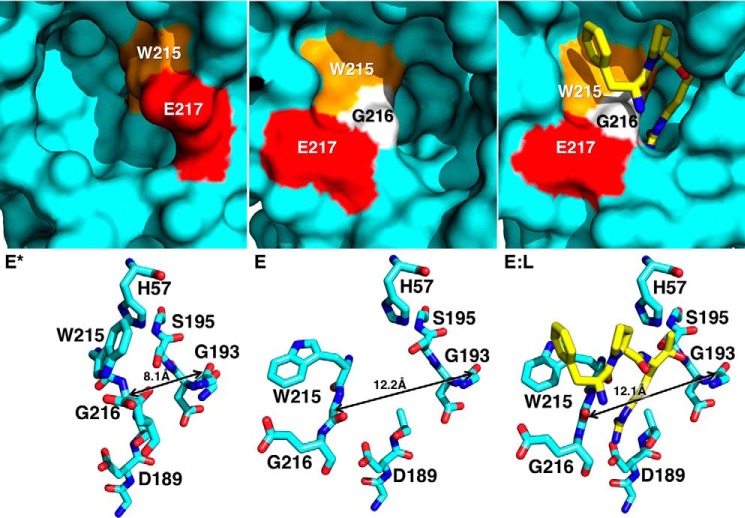
FIGURE 4.

X-ray crystal structures of thrombin mutant Y225P in the E* (Protein Data Bank 3S7H), E (Protein Data Bank 3S7K), and E:L (Protein Data Bank 1THP) conformations. Top panels depict surface representations of the active site of Y225P in three different conformations: free and closed (E*), free and open (E), and active site bound to PPACK (E:L). In the E* conformation the segment comprising residues Trp-215 (orange), Gly-216 (white), and Glu-217 (red) collapses into the active site, stabilized by interactions between His-57 and Trp-215 (bottom left). In the E conformation the same segment opens up, extending the aperture between the Cα atoms of residues Gly-193 and Gly-216 from 8.1 Å in the E* conformations to more than 12 Å in the E and EL conformations. The difference between the E* and E forms is significant, because PPACK (yellow) requires the wider 12-Å aperture to bind productively to the active site (bottom right).

Previous rapid kinetics studies support the existence of multiple conformations for the enzyme in the free form, but have been limited to small inhibitors making contacts with portions of the active site like the primary specificity pocket (11, 16, 17), or to allosteric effectors binding to domains distinct from the active site (18–20). These observations have been rationalized in terms of a pre-existing equilibrium between closed (E*) and open (E) forms bearing structural signatures consistent with the mobility of the segment comprising residues 215–217 (9, 11). Although the structure-function connection is compelling, key questions remain such as whether the E*-E equilibrium is detected upon binding of ligand to extended portions of the active site, and what is the precise distribution of E* and E forms for the protease and its zymogen precursor.

Measurements of substrate binding to the active site aimed at deciphering the mechanism of recognition and the rates of conformational changes preceding the binding step are potentially complicated by various factors. In the case of the zymogen, the widely accepted paradigm that ligands do not bind efficiently or at all to the active site given the lack of properly folded domains like the oxyanion hole or the primary specificity pocket (2, 3, 5) has historically discouraged kinetic studies of substrate recognition. The paradigm, however, is challenged by autoactivating zymogens such as proprotein convertases furin and kexin type 9 (21–23), plasma hyaluronan-binding protein (24), recombinant factor VII (25), and the membrane-bound matriptases (26, 27). Prothrombin and other thrombin precursors autoactivate upon suitable amino acid replacements in the activation domain (28), and so does the anticoagulant protein C (29). Obviously, the active site of a zymogen must be accessible to substrate to allow for autoactivation, and kinetic studies of substrate recognition by the zymogen are not only justified but highly desirable. In the case of the mature enzyme, the irreversible catalytic conversion of substrate into product that follows the binding step complicates resolution of the kinetic rates underscoring the mechanism of recognition (15). Furthermore, rapid kinetics of substrate recognition have historically focused on the steps that follow the initial binding step into the catalytic cycle (30, 31). The E*-E equilibrium of the trypsin fold refocuses attention on the steps that precede the binding interaction and requires an experimental approach where catalysis is eliminated by suitable amino acid replacements that do not perturb the recognition event.

Here we report rapid kinetic studies of substrate binding to the clotting protease thrombin (32) inactivated with the S195A substitution that does not alter the energetics of substrate recognition (33). Thrombin is a well studied trypsin-like enzyme involved in blood coagulation and endowed with allosteric regulation of its catalytic activity through the Na⁺ site and exosite I (34, 35). We extend our investigation to the zymogen precursor prethrombin-2, the physiological intermediate along the activation pathway of prothrombin to thrombin (36, 37), carrying the same S195A substitution. The importance and kinetic signatures of the pre-existing E*-E equilibrium for both the protease and zymogen emerge from measurements carried out in excess substrate or macromolecule and reveal the mechanism of ligand recognition in the trypsin fold.

Materials and Methods

Reagents

The S195A mutant of thrombin was expressed as prethrombin-1, activated and purified as previously described (38). The prethrombin-2 mutant S195A was expressed in E. coli and refolded as reported elsewhere (39). Full-length rabbit thrombomodulin was purchased from Hematologic Technologies, Inc. The C-terminal fragment of hirudin, hirugen phosphate (GDFEEIPEEY^PLQ), was synthesized using solid-phase Fmoc (N-(9-fluorenyl)methoxycarbonyl) chemistry on a model PS3 automated synthesizer (Protein Technologies International). The peptide was subsequently purified using reverse-phase high performance liquid chromatography and analyzed by matrix-assisted laser desorption mass spectrometry. The chromogenic substrate H-d-Phe-Pro-Arg-p-nitroanilide (FPR)² was purchased from Midwest Bio-Tech, Inc.

Stopped-flow Experiments

Rapid kinetic experiments were conducted on an Applied Photophysics SX20 stopped-flow spectrometer. For the experiments conducted in the presence of excess ligand, a final concentration of 50–75 nm thrombin S195A was used in a buffer containing 50 mm Tris, 0.1% PEG8000, pH 8.0, at 15 °C and additionally: 400 mm ChCl (free form); 400 mm ChCl, 100 nm rabbit thrombomodulin (thrombomodulin bound form); 400 mm ChCl, 30 μm hirugen (hirugen bound form); 400 mm NaCl (Na⁺ bound form). The solution containing the protein was mixed 1:1 with 60-μl solutions of FPR in the same buffer, but without rabbit thrombomodulin or hirugen. FPR is the cleavable analog of the irreversible active site inhibitor H-d-Phe-Pro-Arg-CH₂Cl (PPACK), for which detailed structural information exists on its interaction with the active site of thrombin (38, 40). Specifically, Arg at the P1 position of PPACK makes a strong double H-bonding interaction with Asp-189 at the bottom of the primary specificity pocket, Pro fits snugly in a hydrophobic pocket defined by the side chains of Trp-60d and Tyr-60a in the 60-loop, and Phe in the D-enantiomer makes a strong edge-to-face interaction with the indole side chain of Trp-215. The chloromethyl ketone moiety of PPACK engages covalently both the active site Ser-195 and its catalytic partner His-57. Except for this covalent interaction, FPR binds to thrombin with kinetic signatures almost identical to those of PPACK (33) and is therefore a relevant probe of the binding environment of the active site. Rapid kinetics of FPR binding to thrombin S195A were studied using an excitation of 295 nm and a cutoff filter at 320 nm. Baselines were measured by mixing thrombin into buffer in the absence of ligand. Each kinetic trace for a given FPR concentration was taken as the average of a minimum of six determinations. These traces were fit to single or double exponentials based on analysis of the residuals using software supplied by Applied Photophysics. Values of the relaxations for single and double exponential fits were taken from the average of at least three independent titrations with errors calculated as the standard deviation between titrations. Experiments conducted in excess macromolecule used fixed concentrations of FPR at 25 nm and varying concentrations of thrombin S195A in the presence of 50 mm Tris, 400 mm ChCl, 0.1% PEG8000, pH 8.0, at 15 °C. Excitation and emission wavelengths were as described above, as was the data analysis. Hirudin binding to prethrombin-2 was conducted in the presence of 50 mm Tris, 400 mm ChCl, 0.1% PEG8000, pH 8.0, at 15 °C using an excitation wavelength of 295 nm and a cutoff filter at 320 nm. For experiments conducted in the presence of excess hirudin, the concentration of prethrombin-2 was fixed at 75 nm, whereas the concentration of hirudin was varied between 1 and 100 μm. Experiments conducted in the presence of excess prethrombin-2 fixed the concentration of hirudin at 50 nm and varied the concentration of prethrombin-2 between 0.5 and 5 μm. At least 10-fold excess ligand or macromolecule was used under all conditions examined in this study.

Mechanism of Binding

Because of the potential complexity of even a simple kinetic mechanism, it is useful to review the basic principles that inform the analysis of ligand binding as detected by rapid kinetics. The simplest mechanism of binding is the lock-and-key model envisioning a rigid body association between the ligand and the macromolecule, i.e. Scheme 1.

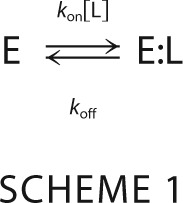Where k_on is the second-order association rate constant and k_off is the first-order dissociation rate constant. The ratio K_d = k_off/k_on defines the intrinsic equilibrium dissociation constant, or the concentration of free ligand at half-saturation. Of the two species in the mechanism (E and E:L), only one is independent due to conservation of mass. Consequently, only one independent relaxation describes how the system reaches equilibrium as (16).

The relaxation increases linearly with the ligand concentration [L] and yields k_on as the slope and k_off as the intercept. When conformational transitions are introduced in the kinetic scheme, the number of independent species increases and so does the number of independent relaxations. Because interconversion between alternative conformations does not involve ligand binding, the associated relaxation cannot grow without limits and saturates out. A saturable relaxation is the kinetic signature of conformational transition, whereas a relaxation that increases linearly with [L] at high [L] is a signature of binding.

In the simplest extension of the lock and key mechanism, a single conformational transition either precedes or follows the binding step. The former mechanism defines pre-equilibrium (41) and depicts a macromolecule existing in two possible conformations, from which the ligand selects only one, i.e. Scheme 2.

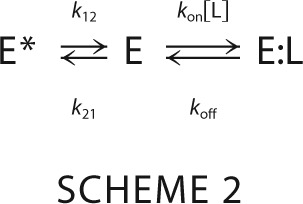Where k₁₂ is the first-order rate of isomerization from a “closed” E* form inaccessible to ligand to an “open” E form, k₂₁ is the first-order rate of isomerization for the reverse reaction from E to E*, and k_on and k_off have the same meaning as in the lock-and-key mechanism. Scheme 2 contains three species (E*, E, and E:L), of which only two are independent and define the relaxations (16).

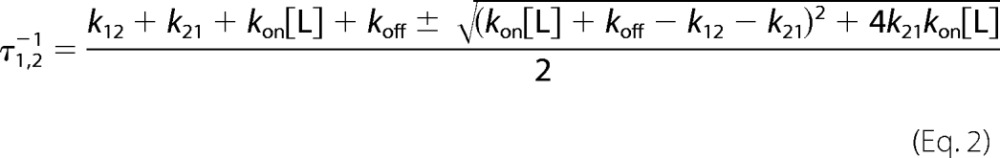The faster relaxation increases linearly at high [L], reflecting binding of L to E, but the slower relaxation saturates out at a value equal to the rate constants k₁₂, reflecting the interconversion from E* to E. It is particularly instructive to consider the derivative of the relaxations as a function of [L].

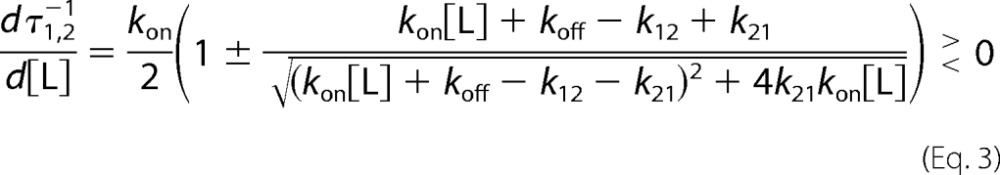The slope of the faster relaxation is always positive and becomes equal to k_on at high [L], On the other hand, the derivative of the slower saturable relaxation changes sign when k_off = k₁₂, underscoring its unique property of decreasing (k_off > k₁₂), increasing (k_off < k₁₂), or being independent (k_off = k₁₂) of the ligand concentration [L] based on the relative values of k_offand k₁₂.

In the alternative simplest extension of the lock-and-key mechanism, the conformational transition follows the binding step. This is the celebrated induced fit mechanism (42) where the macromolecule exists in a single conformation in the absence of ligand and the complex undergoes a rearrangement that optimizes the initial encounter i.e. Scheme 3.

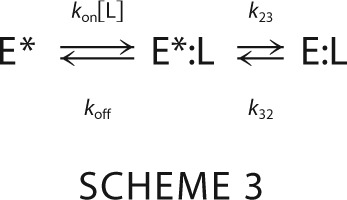Here, k₂₃ is the first-order rate constant for the isomerization of the initial E*:L complex into the final optimized E:L complex, k₃₂ is the first-order rate constant for the reverse transition, and k_on and k_off have the same meaning as in the lock-and-key model. As for pre-equilibrium, induced fit is associated with two independent relaxations given by Equation 4 (16).

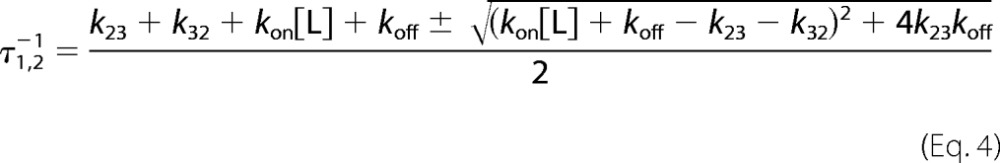Again, the faster relaxation increases linearly at high [L] and the slower relaxation saturates out. However, contrary to the case of pre-equilibrium, both relaxations in Scheme 3 have a positive slope, as readily seen from the derivative.

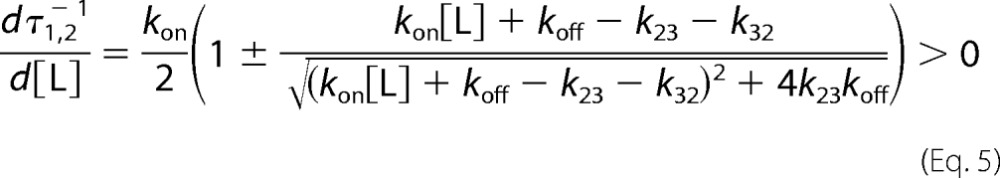Important conclusions can be drawn by inspection of the relaxations for pre-equilibrium and induced fit. The faster relaxation is unable to distinguish between the mechanisms, but the slower saturable relaxation becomes unequivocal proof of pre-equilibrium when it decreases or is independent of [L]. The only ambiguity remains when the saturable relaxation increases with [L], in which case it neither proves nor disproves pre-equilibrium or induced fit (16). Therefore, the widely held belief of a saturable relaxation that increases with [L] being unequivocal evidence of induced fit (15, 43) has no general validity (44, 45), and the assumed preponderance of induced fit as a mechanism of ligand binding (15, 43) should be critically re-evaluated (44, 45).

When a saturable relaxation increases with [L], distinction between induced fit and pre-equilibrium becomes of paramount importance in the analysis of ligand binding data and must rely on measurements carried out with excess macromolecule over the ligand (46–50). In the case of induced fit, excess in the macromolecule does not change the topology of the scheme and the relaxations remain unchanged compared with the experiment run with excess ligand. In the case of pre-equilibrium, on the other hand, excess in the macromolecule abrogates any information coming from the interconversion between pre-existing conformations because binding of ligand is insufficient to perturb significantly the pre-existing distribution. As a result, the saturable relaxation disappears and only the fast relaxation pertaining to binding can be measured experimentally.

Equilibrium Binding

Equilibrium binding titrations were carried out to validate parameters derived from stopped-flow measurements under the same solution conditions using a Horiba Spectrofluorometer 4. Wavelengths used were λ_ex = 295 nm and λ_em = 340 nm. All data were collected in triplicate and errors were taken as the standard deviation of the three independent titrations. Analysis was carried out according to the expression (51),

where ΔF is the change in intrinsic fluorescence at a given concentration of FPR, relative to the baseline at [L] = 0, ΔF_t is the maximum fluorescence change observed upon saturation, [E]_t and [L]_t are the total concentrations of thrombin S195A and FPR, respectively. The value of K_d(app) is the apparent equilibrium dissociation constant that depends on the intrinsic K_d = k_off/k_on and the contribution of conformational changes in the induced fit and pre-equilibrium schemes. Specifically, K_d(app) = K_d/(1 + k₂₃/k₃₂) for induced fit and K_d(app) = K_d(1 + k₂₁/k₁₂) for pre-equilibrium. Importantly, K_d(app) is the only measure of the strength of binding interaction accessible experimentally when no assumption is made on the mechanism of binding. It is instructive to remember that K_d(app) < K_d for induced fit, i.e. equilibrium measurements always overestimate the strength of the intrinsic protein-ligand interaction. The opposite is true for pre-equilibrium. This difference is particularly relevant in the study of structure-function relationships or the design of active site inhibitors (52).

Results

Rapid kinetics of substrate binding where carried out with the goal of detecting the E*-E equilibrium in solution and resolving the kinetic rates for the interconversion between the two forms.

Binding to the Free Form

Binding of FPR to the active site of thrombin carrying the S195A replacement to prevent substrate hydrolysis enables clear detection of a fluorescence change due to binding, which is not possible with the active form of the enzyme because of the large background signal due to catalysis. The fluorescence change entails a double exponential relaxation to equilibrium. The fast relaxation eventually increases linearly with increasing concentrations of FPR, whereas the slow relaxation increases hyperbolically and saturates out (Fig. 1). The presence of two observable relaxations, one linear and one saturable, suggests an underlying kinetic mechanism with at least three species, with one binding step (linear relaxation) and one conformational change (saturable relaxation). As explained under ”Materials and Methods,“ both pre-equilibrium and induced fit are consistent with the kinetic data of FPR binding to thrombin S195A and the quality of the fit is comparable in the two cases. This makes it difficult to establish whether thrombin exists in alternative conformations with FPR selecting the optimal one for binding, or whether the initial encounter between FPR and a unique conformation of thrombin is subsequently optimized by an induced fit. Experiments conducted in the presence of excess macromolecule distinguish between the two possibilities.

FIGURE 1.

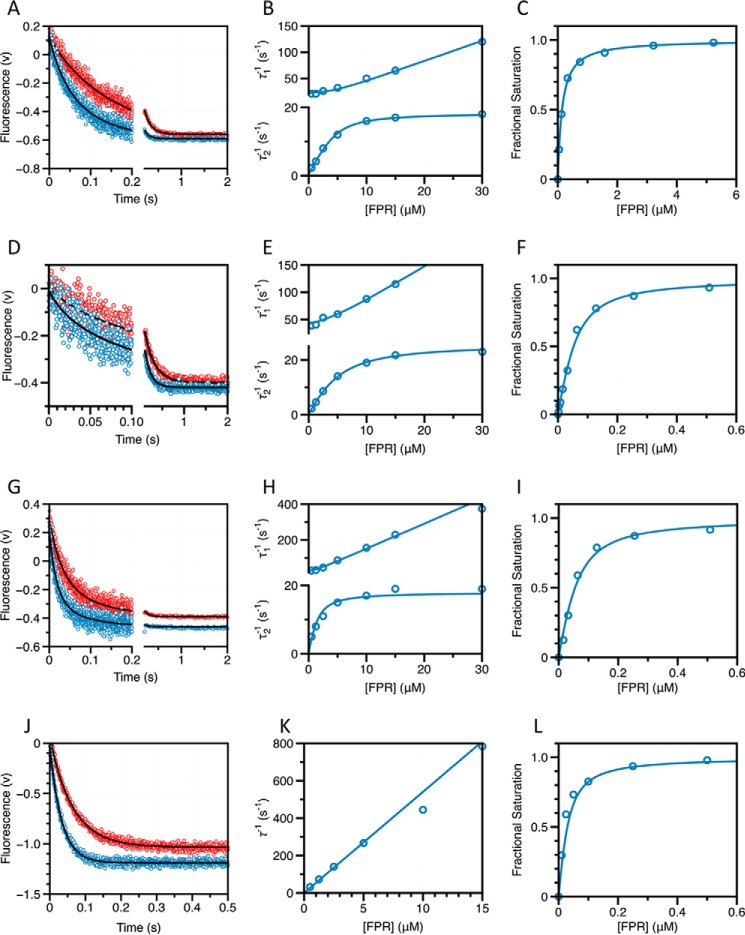
A–L, kinetic traces of FPR binding to thrombin in the free form (A), bound to thrombomodulin (D), hirugen (G), or Na⁺ (J), shown on the time scales resolved experimentally. Concentrations of FPR displayed are 1.25 μm (red) and 2.5 μm (cyan). Black lines were drawn according to the double-exponential equation: a exp(−t/τ₁) + b exp(−t/τ₂) + c, where τ₁ and τ₂ are the two relaxations associated with the decay. In the presence of Na⁺ (G) only one relaxation could be resolved. Plot of the relaxations derived from the double-exponential fit to the kinetic traces for FPR binding to thrombin in the free form (B), bound to thrombomodulin (E) or hirugen (H), and the single relaxation measured in the presence of Na⁺ (K). Solid lines were drawn according to Scheme 2 for the free form or in the presence of thrombomodulin or hirugen, and according to the lock-and-key mechanism (Scheme 1) in the presence of Na⁺, using best-fit parameters listed in Table 1. Equilibrium binding curves for FPR binding to thrombin in the free form (C), bound to thrombomodulin (F), hirugen (I), or Na⁺ (L). Solid line was drawn according to Equation 6 in the text with best-fit parameters listed in Table 1. Experimental conditions are: 50 mm Tris, 0.1% PEG8000, pH 8, at 15 °C, and 400 mm ChCl (free form), 400 mm ChCl and 50 nm rabbit thrombomodulin (+thrombomodulin), 400 mm ChCl and 15 μm hirugen (+hirugen), or 400 mm NaCl (+Na⁺).

Under conditions where the concentration of thrombin S195A is in significant excess over FPR, any pre-existing conformational equilibrium becomes undetectable by rapid kinetics and only events that take place upon and after the binding event are measured experimentally. If thrombin obeys pre-equilibrium, the two relaxations observed with excess substrate should collapse into a single one reflecting the binding interaction. If induced fit is at play, the two relaxations observed in the presence of excess substrate should be retained. Binding of FPR to thrombin S195A in the presence of excess macromolecule produces a single relaxation that increases linearly with the concentration of enzyme (Fig. 2). This result rules out that an induced fit conformational transition takes place after the binding step. FPR binding to the active site of thrombin occurs by selection of an optimal conformation from a pre-existing equilibrium. Therefore, the relaxations in Fig. 1 obey Scheme 2 and should be analyzed according to Equation 2. The results (Table 1) indicate that free thrombin is partitioned between closed (E*) and open (E) conformations in a 1:4 ratio, i.e. that 80% of free thrombin is in a conformation capable of binding FPR to the active site with k_on = 2.8 ± 0.2 μm⁻¹ s⁻¹ and k_off = 0.20 ± 0.05 s⁻¹, giving K_d = 71 ± 5 nm. The apparent affinity is reduced slightly by the 20% fraction of free thrombin in the closed E* conformation to yield K_d(app) = K_d(1 + k₂₁/k₁₂) = 85 ± 6 nm, which is the value measured from equilibrium titrations (Fig. 1) using the model-independent Equation 6. The E and E* conformations interconvert on a time scale of ∼45 ms, calculated as τ = 1/(k₁₂ + k₂₁) (15, 43).

FIGURE 2.

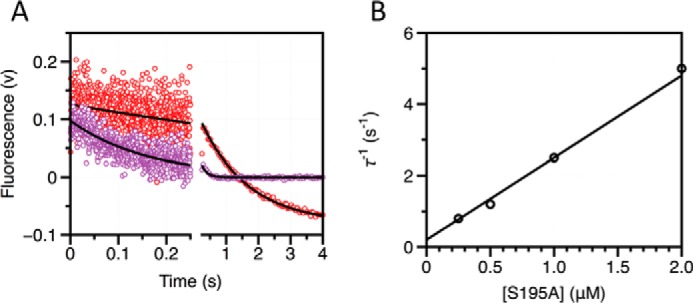
Kinetic traces of FPR binding to thrombin in the presence of excess enzyme. A, kinetic traces of a fixed concentration of FPR binding to excess thrombin in the free form shown on the time scales resolved experimentally. Concentrations of thrombin displayed are 0.25 μm (red) and 0.5 μm (purple). Black lines were drawn according to the single-exponential equation: a exp(−t/τ₁) + b. B, plot of the relaxation derived from the single-exponential fit to the kinetic traces for FPR binding. Solid line was drawn according to the lock-and-key mechanism (Scheme 1) using best-fit parameters k_on = 2.3 ± 0.2 μm⁻¹ s⁻¹ and k_off = 0.2 ± 0.1 s⁻¹, in good agreement with those derived from analysis of stopped-flow experiments with excess substrate (Table 1). Experimental conditions are: 50 mm Tris, 0.1% PEG8000, 400 mm ChCl, pH 8, at 15 °C.

TABLE 1.

Kinetic rate constants for FPR binding to thrombin mutant S195A

Rate constants refer to Scheme 2 in the text. Values of k₁₂ and k₂₁ could not be measured in the presence of Na⁺. The value of K_d(app) = K_d(1 + k₂₁/k₁₂) interprets the model-independent equilibrium dissociation constant in terms of the pre-equilibrium mechanism. The value of r = k₂₁/k₁₂ gives the relative population of the E* over E conformations. Experimental conditions are: 50 mm Tris, 0.1% PEG8000, pH 8.0, at 15 °C, and 400 mm ChCl (free form), 400 mm ChCl, and 50 nm rabbit thrombomodulin (+thrombomodulin), 400 mm ChCl, and 15 μm hirugen (+hirugen), or 400 mm NaCl (+Na⁺).

	k12	k21	kon	koff	Kd	Kd(app)	r
	s−1		μm−1s−1	s−1	nm
Free	18 ± 1	3.8 ± 0.8	2.8 ± 0.2	0.20 ± 0.05	71 ± 5	85 ± 6	0.21 ± 0.04
+Thrombomodulin	26 ± 2	16 ± 2	6.4 ± 0.4	0.11 ± 0.02	17 ± 1	27 ± 1	0.62 ± 0.08
+Hirugen	18 ± 1	10 ± 2	14 ± 1	0.27 ± 0.06	19 ± 4	30 ± 4	0.56 ± 0.09
+Na+			54 ± 2	0.9 ± 0.2	17 ± 1

These measurements represent a functional validation of the pre-existing E*-E equilibrium as an intrinsic structural feature of the trypsin fold (8, 9, 11). If E* and E are interpreted as alternative arrangements of the segment comprising residues 215–217, which either closes (E*) or opens (E) access to the active site, then the distribution unraveled for the E* and E forms may have a direct bearing on the activity of the enzyme. The action of allosteric effectors should be analyzed in this context. A new class of allosteric inhibitors of thrombin targeting the heparin binding site has been reported recently (53) and it would be of interest to establish if their mechanism of action involves a shift of the E*-E equilibrium in favor of the E* form. Physiological allosteric effectors of thrombin act as activators and enhance significantly the activity of the enzyme. These effectors include thrombomodulin and other molecules that bind to exosite I (35, 54–57) and Na⁺ (58). The effect of these ligands on the E*-E equilibrium becomes of interest.

Effect of Exosite I Binding

Binding of thrombomodulin to exosite I located >15 Å away from the active site (57) initiates an important regulatory feedback loop of the coagulation cascade through efficient activation of the anticoagulant protein C (59). Exactly how thrombomodulin exerts its allosteric effect resulting in a >2,000-fold increase in the rate of protein C activation by thrombin and whether this effect is on thrombin, protein C, or both macromolecules, has been a hotly debated issue over the years (29, 60–65). Recent data show that thrombomodulin affects the structure of both thrombin and protein C in ways that contribute almost equally to the energetics of protein C activation (29, 64). The effect on protein C results in exposure of Arg-169 in the activation domain for efficient proteolytic attack by thrombin (29). The effect on thrombin perturbs the active site and neighbor 30-loop (60, 64) and eventually influences the rotamer of the catalytic Ser-195 as an end point (66). Importantly, the effect of thrombomodulin on chromogenic substrate hydrolysis only depends on perturbation of the enzyme active site and is recapitulated by small peptides that bind to exosite I (54, 55). Prominent among these peptides is hirugen (56), the C-terminal fragment of the potent natural inhibitor hirudin (67). In the presence of saturating amounts of thrombomodulin, binding of FPR produces two relaxations that differ little from those observed in the free form of the enzyme (Fig. 1). Fitting the data to Scheme 2 yields rate constants for the E*-E transitions similar to those of the free form (Table 1), with a slight shift of the E*-E equilibrium in favor of the E* form. Binding of hirugen reproduces the effect of thrombomodulin almost completely (Fig. 1, Table 1). The lack of a significant effect on the E*-E equilibrium is consistent with structural biology of the E and E* forms where the architecture of exosite I does not change much in the conformational transition (11). The effect of thrombomodulin or hirugen on the enhanced affinity for FPR is not the result of a shift of the pre-existing E*-E equilibrium, but originates from a direct perturbation of the properties of the E form resulting in enhanced k_on and unchanged or reduced k_off.

Effect of Na⁺ Binding

Trypsin-like proteases, such as thrombin carrying Tyr at position 225, are endowed with Na⁺-dependent enhancement of catalytic activity (68). The Na⁺ binding site is located >15 Å away from residues of the catalytic triad and nestles between the 186 and 220 loops (34, 38) that also control the primary specificity of the enzyme (69). Binding of Na⁺ produces kinetic signatures of substrate recognition significantly different from those observed upon binding to exosite I. In the presence of Na⁺, FPR binding obeys a single linear relaxation consistent with a lock-and-key mechanism and abolishes the saturable relaxation reporting the E*-E pre-existing equilibrium (Fig. 1). This implies that binding of Na⁺ either completely shifts the E*-E equilibrium in favor of the E form, or silences the spectral reporter(s) of the E*-E equilibrium. The latter possibility is ruled out by measurements carried out with the active site inhibitor p-aminobenzamidine (PABA), where the fluorescence change comes from the inhibitor and not the enzyme. Binding of PABA to free thrombin obeys a single saturable relaxation that decreases hyperbolically with the inhibitor concentration (11), indicative of a pre-existing E*-E equilibrium. In the presence of Na⁺, only a fluorescence change too fast to resolve by stopped-flow is observed (data not shown), thereby proving that Na⁺ shifts the E*-E equilibrium in favor of the E form instead of simply silencing a spectral reporter of the protein. The value of k_on increases significantly (54 ± 2 μm⁻¹ s⁻¹ versus 2.8 ± 0.2 μm⁻¹ s⁻¹) in the presence of Na⁺. As seen in the case of thrombomodulin and hirugen, the increase is explained by a direct effect of Na⁺ on the properties of the E form. In the blood, thrombin is constantly exposed to a Na⁺ concentration of 140 mm that produces 64% saturation of the Na⁺ binding site (70). This further reduces the population of the E* form and makes the open E form, whether free or bound to Na⁺, the dominant physiological conformation of thrombin in vivo.

Binding to the Zymogen Prethrombin-2

Full activity in trypsin-like proteases ensues via a common mechanism that involves the irreversible processing of an inactive zymogen precursor. The zymogen is proteolytically cut at Arg-15 in nearly all members of the family to generate a new N terminus that ion pairs with the highly conserved Asp-194 next to the catalytic Ser-195 and organizes both the oxyanion hole and primary specificity pocket for substrate binding and catalysis (71). The widely accepted paradigm of the zymogen as an inactive precursor of the mature protease is supported by the incorrect architectures of the catalytic triad, oxyanion hole, and primary specificity pocket prior to the proteolytic cleavage at Arg-15 (2, 71). However, these features are not observed in all members of the trypsin fold. Zymogens such as trypsinogen (71, 72), the zymogen of MASP-2 (73), chymotrypsinogen (74), coagulation factor XI (75), and complement profactor B (76) crystallize in a conformation where the active site is fully accessible to substrate and organized as in the mature protease (8, 9). In the case of chymotrypsinogen (74) and prethrombin-2 (39), alternative conformations of the segment comprising residues 215–217 suggestive of a pre-existing E*-E equilibrium as in the mature protease have been trapped in the same crystal structure or different crystals harvested from the same crystallization well. Furthermore, functional evidence exists that PPACK can access the active site of prothrombin and prethrombin-2, and a structure of prethrombin-2 has recently been solved with the inhibitor argatroban bound at the active site (28). Finally, rapid kinetics of FPR binding to prethrombin-2 show a single relaxation that decreases hyperbolically at 35 °C, supporting a conformational transition that likely precedes a binding step that is either too fast to resolve by stopped-flow or spectroscopically silent (16). A compelling possibility is that the E*-E equilibrium also exists in the zymogen and that a key difference between zymogen and protease may reside in the relative distribution of E* and E forms. In general, the protease would favor the E form where access to the active site is wide open and the zymogen would favor the E* form where access to the active site is compromised (8). To test this hypothesis, direct measurements of the distribution of E* and E forms become necessary for the zymogen. Attempts to validate a pre-existing E*-E equilibrium in prethrombin-2 using stopped-flow measurements of FPR binding with excess macromolecule were unsuccessful due to the reduced affinity of the zymogen. An alternative approach was therefore used with the potent natural inhibitor hirudin.

Hirudin binds to thrombin with a K_d in the femtomolar range (67) and covers 20% of the available surface of the enzyme (77) bridging the active site and exosite I. As such, hirudin is an extraordinary reporter of the overall conformation of thrombin (78). Binding of hirudin to prethrombin-2 could be studied by stopped-flow under conditions of excess substrate and excess macromolecule (Fig. 3). In the former case, a single saturable relaxation increases hyperbolically with substrate concentration. The relaxation becomes linear when the experiment is carried out with excess macromolecule (Fig. 3). The scenario is analogous to that encountered for FPR binding to the mature enzyme (Figs. 1 and 2) and indicates that hirudin binding to prethrombin-2 is linked to conformational transitions that precede the binding step. Binding according to the induced fit would have left the relaxation seen with excess hirudin unaltered in the presence of excess prethrombin-2. We conclude that prethrombin-2 binds substrate with the same mechanism as the mature protease and that the E*-E equilibrium already exists in the zymogen prior to the irreversible conversion to thrombin. Resolution of all kinetic rates give values of k₁₂ = 21 ± 3 s⁻¹ and k₂₁ = 200 ± 100 s⁻¹, indicative of an E*-E equilibrium shifted significantly (10:1 ratio) in favor of the closed E* form. The equilibrium is reached over a time scale of only 4.5 ms, or 10-fold faster than that of the same equilibrium in the mature enzyme. Interestingly, the value of k₁₂ is practically identical to that measured for the mature enzyme (Table 1), indicating that the rate of the E* to E transition is not affected by the proteolytic conversion to thrombin. The difference between zymogen and protease in the case of thrombin stems from the value of the E to E* transition that is considerably faster in the case of prethrombin-2. Also notable is the value of k_off for hirudin dissociation that is about 2,000-fold faster in prethrombin-2 compared with thrombin (79).

FIGURE 3.

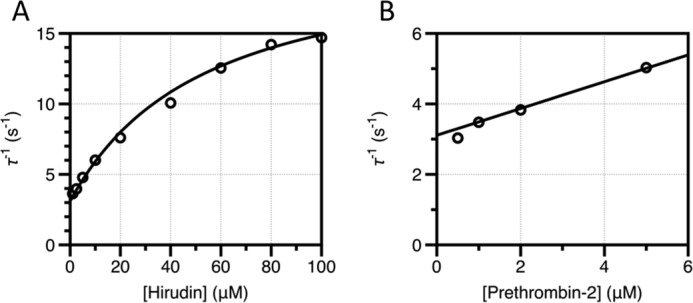
Pre-steady state kinetics of hirudin binding to prethrombin-2 showing the relaxation derived from the single exponential fit to the kinetic traces for hirudin binding to prethrombin-2 in the presence of excess hirudin (A) or prethrombin-2 (B). The continuous line was drawn according to Equation 2 in the text (A) or a modified version of Equation 1 with k_on replaced by the expression k_onk₁₂/(k₁₂ + k₂₁) to account for the fraction of prethrombin-2 in the E form (B). Both data sets were analyzed simultaneously with proper weighting to yield best-fit parameters: k₁₂ = 21 ± 3 s⁻¹, k₂₁ = 200 ± 100 s⁻¹, k_off = 3.1 ± 0.1 s⁻¹, k_on = 4 ± 2 μm⁻¹ s⁻¹. Experimental conditions are: 50 mm Tris, 0.1% PEG8000, 400 mm ChCl, pH 8, at 15 °C.

Discussion

Recent rapid kinetics studies of ligand binding to thrombin support the existence of a pre-equilibrium of alternative conformations, in keeping with the generality of this mechanism in biological systems (44, 45). Binding of PABA to the primary specificity pocket produces a single saturable relaxation that decreases with ligand concentration (11), a kinetic signature of pre-equilibrium between open and closed forms (16, 43). Likewise, Na⁺ binding to thrombin produces a saturable relaxation that decreases or changes little with ligand concentration (19, 20), again a signature of multiple pre-existing conformations with different accessibility of the binding site. In both cases, however, only a single saturable relaxation could be measured experimentally preventing unequivocal resolution of the k₁₂ and k₂₁ rate constants and leaving the important question about the distribution of the two conformations unanswered. The results reported in this study enable a complete resolution of the relaxations for binding and linked conformational transitions in thrombin and reveal a pre-existing equilibrium between closed (E*) and open (E) forms, in a 1:4 distribution, that unfolds on a time scale of 45 ms. The time scale is significantly slower than that inferred previously from analysis of PABA and Na⁺ binding. The difference between FPR and Na⁺ is easily explained in terms of the distinct binding sites, which may open and close independently of one another and on different time scales. The difference between PABA and FPR, on the other hand, requires attention. PABA binds to the primary specificity pocket of thrombin, like the Arg residue of FPR that in addition engages residues of the 60-loop and Trp-215. Recognition of FPR likely involves multiple pre-existing equilibria at separate subsites that altogether define the binding epitope. In the case of PABA, only the primary specificity pocket around Asp-189 is at play and the site is opened or closed by repositioning of Trp-215. In the case of FPR, additional subsites must become available thereby explaining the slower time scale probed by the substrate.

The kinetic signatures of FPR binding demonstrate that substrate selects a pre-existing conformation and no induced fit rearrangement follows formation of the complex. This conclusion is strongly supported by the structures of E*, E, and E bound to PPACK of the thrombin mutant Y225P (Fig. 4), the only existing example of a trypsin-like protease for which all three species of Scheme 2 have been solved crystallographically (11, 80). The segment comprising residues 215–217 moves and opens up access to the active site in the E conformation, extending the aperture defined by the Cα-Cα distance of residues Gly-193 and Gly-216 from 8.1 Å in the E* form to more than 12 Å in the E and E:L conformations. Notably, the distance does not change upon binding of PPACK to the E form, vouching for a mechanism where the E form is selected from the pre-existing equilibrium and without further induced fit rearrangement following formation of the complex. Similar conclusions have been drawn recently from the structure of thrombin bound to hirudin and Na⁺ where the enzyme assumes a conformation practically identical to the E form (45).

The existence of the open E form in significant amounts (80%) for the free enzyme and the lack of evidence of conformational transitions following the binding step invalidate completely recent gratuitous assertions such as free thrombin being zymogen-like (81), or ligand binding shuttling the enzyme from zymogen-like to proteinase-like states (82). If thrombin were zymogen-like, it would crystallize exclusively in the E* form when free, which is certainly not the case (11, 38, 66). Furthermore, the value of k₂₁ in Scheme 2 would largely exceed that of k₁₂, contrary to what is seen experimentally (Fig. 1, Table 1). If substrate binding shuttled the enzyme from zymogen-like to proteinase-like states, then thrombin would obey induced fit and there would be no difference between relaxations measured in excess substrate or protein, contrary to experimental evidence reported here (Figs. 1 and 2) and elsewhere (16, 44, 66).

The enhancement of substrate diffusion into the active site observed upon binding of thrombomodulin, hirugen, or Na⁺ far exceeds the intrinsic k_on of the E form (Fig. 1, Table 1) and must originate from a change of the properties of this conformation. In the case of thrombomodulin and hirugen, the new E form remains in equilibrium with the E* form and the E*-E distribution does not change significantly (Table 1). In the case of Na⁺, binding of the cation completely destabilizes the inactive E* form and shifts thrombin into the E form. It is possible that E* and E represent two ensembles of rapidly interconverting conformations and that binding of thrombomodulin or Na⁺ populates more active forms within the E ensemble that are poorly represented in free thrombin. Replacement of individual species with rapidly interconverting ensembles is inconsequential on the properties of a kinetic scheme (83) and would not affect analysis of the kinetic data presented in this study. Furthermore, rapid transitions within each ensemble may be spectroscopically silent if they do not perturb significantly the state of major reporters. A plausible scenario emerges where nested conformational transitions unfold over different time scales, consistent with recent NMR measurements (14) and molecular dynamics calculations (84, 85): a slow time scale (45 ms) for the interconversion of the E* and E ensembles detected by stopped-flow measurements, and a fast time scale, perhaps spectroscopically silent, for the interconversion of conformers within each ensemble. The rapid equilibrium within the E* ensemble likely involves different degrees of occlusion of the active site, all of them incompatible with substrate binding. The rapid equilibrium within the E ensemble, on the other hand, may involve open conformations where substrate diffusion into the active site takes place with different rates and different rotamers of Ser-195 ensure different levels of activity (66). Elucidation of this compelling new scenario will require further structural and kinetic analysis.

A final comment should be made about the role of the E*-E equilibrium in the trypsin fold, and especially in the zymogen. Observational evidence from the existing structural database vouches for alternative conformations of the segment comprising residues 215–217 for both the protease and zymogen (8, 9), but the present study validates the pre-existing E*-E equilibrium in solution with rapid kinetics and quantifies the relative distribution of the two forms and the time scale of their interconversion. Extension of the strategy presented here to other members of the trypsin family will be necessary to establish how E* and E are partitioned in each case, and to rationalize the distribution in the context of biological function. The relevant conclusion is that a finite population (10%) of zymogen may assume a conformation in solution that is compatible with ligand binding at the active site. Under experimental conditions favoring catalysis, the fraction of zymogen in the E form may promote activity. This scenario has physiological relevance in the context of autoactivation (8, 9, 28, 86). The long accepted paradigm where the zymogen is viewed simply as the inactive form of the mature protease (30, 31, 87, 88) needs revision (8). Zymogen and protease are two different incarnations of the underlying plasticity of the trypsin fold and are each capable of assuming closed (E*) and open (E) conformations of the active site. The difference between zymogen and protease resides in the covalent structure of the activation domain that controls not only the architecture of the catalytic residues, but also the relative distribution of E* and E and the time scale of their interconversion.

Author Contributions

A. D. V. and E. D. C. designed the research; A. D. V. and P. C. carried out the work; A. D. V., P. C., and E. D. C. analyzed the results; A. D. V. and E. D. C. wrote the manuscript.