The Pace of Hybrid Incompatibility Evolution in House Mice

Abstract

Hybrids between species are often sterile or inviable. This form of reproductive isolation is thought to evolve via the accumulation of mutations that interact to reduce fitness when combined in hybrids. Mathematical formulations of this “Dobzhansky–Muller model” predict an accelerating buildup of hybrid incompatibilities with divergence time (the “snowball effect”). Although the Dobzhansky–Muller model is widely accepted, the snowball effect has only been tested in two species groups. We evaluated evidence for the snowball effect in the evolution of hybrid male sterility among subspecies of house mice, a recently diverged group that shows partial reproductive isolation. We compared the history of subspecies divergence with patterns of quantitative trait loci (QTL) detected in F₂ intercrosses between two pairs of subspecies (Mus musculus domesticus with M. m. musculus and M. m. domesticus with M. m. castaneus). We used a recently developed phylogenetic comparative method to statistically measure the fit of these data to the snowball prediction. To apply this method, QTL were partitioned as either shared or unshared in the two crosses. A heuristic partitioning based on the overlap of QTL confidence intervals produced unambiguous support for the snowball effect. An alternative approach combining data among crosses favored the snowball effect for the autosomes, but a linear accumulation of incompatibilities for the X chromosome. Reasoning that the X chromosome analyses are complicated by low mapping resolution, we conclude that hybrid male sterility loci have snowballed in house mice. Our study illustrates the power of comparative genetic mapping for understanding mechanisms of speciation.

LEVELS and patterns of biodiversity are shaped by the process of speciation. As a result, speciation continues to captivate biologists. Under the biological species concept (Mayr 1942), the search for speciation mechanisms can be usefully focused on the genetic dissection of traits that confer reproductive isolation (Dobzhansky 1937). Among the many kinds of reproductive isolation, intrinsic genetic barriers between diverging lineages, especially in the form of reduced hybrid fertility and viability (postzygotic isolation), have received the greatest attention.

Studies of hybrid dysfunction have implicated deleterious interactions between loci as a common cause of reproductive isolation (Coyne and Orr 2004; Presgraves 2007; Maheshwari and Barbash 2011). These findings corroborate earlier theories postulating an epistatic basis for hybrid dysfunction (Bateson 1909; Dobzhansky 1937; Muller 1940, 1942). Commonly referred to as the Dobzhansky–Muller (DM) model, this supposition of epistasis explains hybrid dysfunction without requiring evolutionary transitions through unfit intermediates. These intermediates are bypassed by geographically separating the multiple substitutions responsible for an epistatic incompatibility into different populations (a derived–derived incompatibility) or temporally separating the substitutions in the same population (a derived–ancestral incompatibility).

The DM model has become highly influential in speciation research. It has helped investigators identify specific genes involved in hybrid incompatibilities (e.g., Sawamura and Yamamoto 1997; Bomblies et al. 2007; Lee et al. 2008; Seidel et al. 2008; Bikard et al. 2009; Mihola et al. 2009), and genetic studies of hybrid dysfunction are often interpreted in light of the DM model even when experiments lack the ability to detect epistasis. This attention has inspired multiple theoretical advances in speciation genetics, including treating fitness landscapes (Gavrilets 2004), protein evolution (Kondrashov et al. 2002), gene networks (Palmer and Feldman 2009; Livingstone et al. 2012; Tulchinsky et al. 2014), and developmental pathways (Porter and Johnson 2002; Johnson and Porter 2007) in the context of the DM model.

One especially interesting theoretical result predicts that the number of hybrid incompatibilities should increase faster than linearly with divergence time (or “snowball”) as lineages diverge (Orr 1995; Orr and Turelli 2001). This prediction arises from the opportunity for each new allelic substitution to act as both catalyst and substrate in the evolution of incompatibilities, potentially interacting with previous substitutions and their ancestral forms, as well as creating a target for interaction with future substitutions. This intriguing and mathematically tractable idea is difficult to test. To evaluate the snowball prediction, hybrid incompatibilities need to be counted in multiple species pairs for which good estimates of divergence time are available. As a result, empirical tests of the snowball effect did not appear until 15 years after the prediction was first made. Matute et al. (2010) used fine-scale deletion mapping to count lethal hybrid incompatibilities in two species pairs: Drosophila melanogaster–D. simulans and D. melanogaster–D. santomea. Moyle and Nakazato (2010) counted quantitative trait loci (QTL) for pollen and seed sterility in near isogenic lines featuring short introgressed regions from Solanum pennelli, S. habrochaites, and S. lycopersicoides on the genomic background of the domesticated tomato S. lycopersicum. Both studies estimated divergence time from the average number of synonymous substitutions between species across a small number of genes. Matute et al. (2010) and Moyle and Nakazato (2010) each found evidence for the snowball effect. Although the results from Solanum provided mixed support, with incompatibilities associated with pollen sterility accumulating linearly with divergence time (Moyle and Nakazato 2010), the pattern of incompatibility sharing among Solanum species as determined by tests of allelism subsequently revealed that this trait fits the snowball prediction as well (Sherman et al. 2014).

In light of the findings from Drosophila and Solanum, it is worth considering biological scenarios that do not predict a snowball effect. The connection between chromosomal rearrangements and hybrid sterility [especially in plants (Rieseberg and Willis 2007)] suggests that underdominance contributes to postzygotic isolation, despite the theoretical implausibility of this scenario (Lande 1985; Barton and Rouhani 1987; Gavrilets 1993). Genetic studies of hybrid dysfunction in Saccharomyces have also inspired a nonepistatic model in which the degree of isolation grows with sequence divergence (Chambers et al. 1996; Greig et al. 2003; Liti et al. 2006). If reproductive isolation is generated by the successive fixation of mildly underdominant (nonepistatic) mutations (White 1969; Walsh 1982; Barton and Bengtsson 1986; Spirito et al. 1991), the number of loci involved could accumulate linearly with divergence time. Finally, reproductive isolation could evolve according to the DM model without generating the snowball effect. For example, a mathematical formulation of the DM model that treats incompatibility evolution in the context of gene networks does not predict a snowball (Palmer and Feldman 2009). The generality of the snowball effect can be established only using data from additional groups of species.

In this study, we evaluate whether the evolution of hybrid incompatibilities in house mice follows the snowball prediction. House mice (Mus musculus) are a model system for understanding the genetics of speciation and feature an expansive genetic and genomic toolkit. The three subspecies diverged recently (Geraldes et al. 2008, 2011; White et al. 2009; Duvaux et al. 2011), perhaps <350,000 years ago (Geraldes et al. 2011). Two pairs of subspecies show partial reproductive isolation, particularly in the form of hybrid male sterility (Forejt and Iványi 1974; Britton-Davidian et al. 2005; Vyskočilová et al. 2005; Good et al. 2008a; White et al. 2012a), indicating speciation is in progress. House mouse subspecies also hybridize in the wild (Boursot et al. 1993; Sage et al. 1993; Duvaux et al. 2011; Jing et al. 2014), providing opportunities to connect the genetics of reproductive isolation phenotypes in the laboratory with gene flow in nature. The existence of gene flow violates the assumption of complete allopatry after divergence used in the snowball model. High levels of gene flow would likely erase the snowball signature. However, historical levels of gene flow between house mouse subspecies appear to have been relatively low (Duvaux et al. 2011; Geraldes et al. 2011), an inference supported by the phylogenetic history observed across the subspecies’ genomes (Keane et al. 2011).

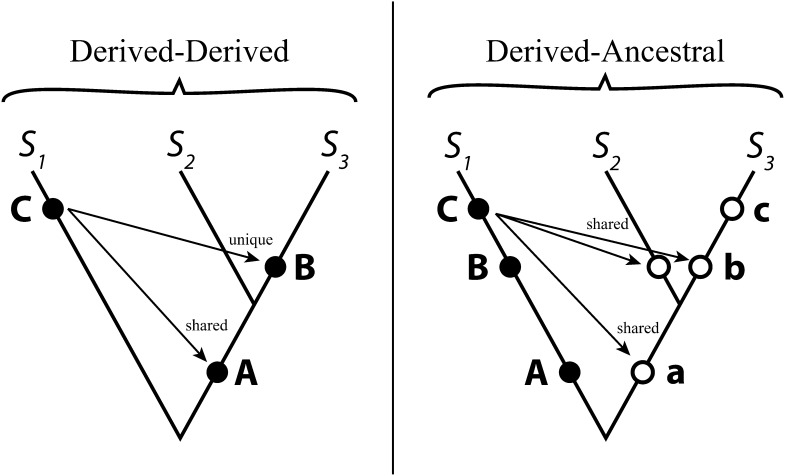
To test the snowball prediction, we use a recently developed phylogenetic comparative approach that takes into account the numbers of shared and unique incompatibilities among species pairs (Wang et al. 2013). In effect, this approach uses branch lengths to model the number of incompatibilities between species pairs and uses phylogenetic topology to model the relative number of shared and unique incompatibilities. Whether an incompatibility is shared between species pairs depends on the history of the substitutions involved, with a notable distinction between derived–derived and derived–ancestral incompatibilities (Figure 1). Unlike derived–derived incompatibilities, derived–ancestral incompatibilities between species pairs are shared even if the incompatible substitutions arose after their divergence. Compared to the nonphylogenetic analysis, which tests for a linear relationship between counts of hybrid incompatibilities with sequence divergence (e.g., Matute et al. 2010), this method offers increased statistical power and allows consideration of a wider variety of models (Wang et al. 2013).

Figure 1.

Schematic illustrating shared and unique incompatibilities between hybrids of species pairs S₁ × S₂ and S₁ × S₃. The point of substitution for each allele is diagrammed on the tree as a solid circle, while the respective ancestral allele for each substitution is diagrammed as an open circle; the ancestral alleles for both trees are “a”, “b”, and “c”. The tree on the left illustrates the pattern of sharing for derived–derived incompatibilities, which depend on substitution timing relative to the divergence of S₂ and S₃. The ancestral versions of alleles “A”, “B”, and “C” are not depicted on this tree. The tree on the right illustrates the pattern of sharing for derived–ancestral incompatibilities, which are shared regardless of timing relative to species divergence. A potential incompatibility between derived allele “B” and ancestral allele “a” is not depicted in this tree.

Materials and Methods

Identifying shared and unique incompatibilities

We used data from two studies that mapped QTL for hybrid male sterility between wild-derived inbred strains from the three subspecies of house mice: M. m. musculus (PWD/PhJ) and M. m. domesticus (WSB/EiJ) (White et al. 2011) and M. m. castaneus (CAST/EiJ) and M. m. domesticus (WSB/EiJ) (White et al. 2012a). These studies quantified five morphological traits strongly correlated with male fertility: testis weight, sperm density, proportion of abnormal sperm, sperm head shape, and stage VII seminiferous tubule area. The abnormal sperm trait was scored using five phenotypes: the proportion of sperm that exhibited proximal bent tail, distal bent tail, absence of head or tail, or amorphous sperm head and the proportion of total abnormal sperm. These studies were designed to be compared. The same strain of M. m. domesticus was used, similar numbers of F₂ males were generated, the same phenotypes were measured, and a common set of diagnostic SNPs was analyzed in QTL mapping.

We took two approaches to identify the number of shared QTL between the two intercrosses: (1) we compared the locations of QTL mapped separately in the two crosses and (2) we jointly mapped QTL from both crosses in a phylogenetic comparative context.

In the first approach, we considered single QTL identified by standard interval mapping in White et al. (2011, 2012a). For each QTL peak, we examined the physical positions of the maximum LOD score and the 1.5-LOD interval. QTL were identified as shared between the two crosses whenever the position of the maximum LOD score in one cross overlapped the 1.5-LOD interval for the same phenotype in the other cross. This approach relies on the intuition that overlapping QTL for the same trait in crosses between closely related subspecies are likely to share a common genetic basis.

Our second approach used the PhyloQTL method as implemented in R/qtl (Broman et al. 2012). This method assumes that the trait of interest is affected by a single diallelic QTL and that the effect of the QTL is the same in different crosses. The method jointly analyzes all of the crosses on a common genetic map and seeks to group the taxa according to which of the two alleles they possess (see Supporting Information, File S1). In addition to positioning the QTL along the phylogeny, this joint analysis of data from multiple crosses has the potential to increase the power to detect QTL (Broman et al. 2012). All of the QTL identified by our combined analysis with PhyloQTL reached the 5% significance level with thresholds calculated from 10,000 permutations for each trait.

Estimating the subspecies tree

To reconstruct the subspecies tree with branch lengths, we summarized gene trees estimated from whole-genome sequences of representatives of the three house mouse subspecies. The genomes of three wild-derived inbred strains, CAST/EiJ, WSB/EiJ, and PWK/PhJ (representatives of the castaneus, domesticus, and musculus subspecies, respectively), were sequenced by Keane et al. (2011). CAST/EiJ and WSB/EiJ were also used in our QTL analyses and PWK/PhJ is a close relative of the third strain we used (PWD/PhJ). Following the procedure described by White et al. (2009), the consensus sequences from these strains were mapped to an alignment of the mouse (MGSC37) and rat (version 3.4) genomes. This analysis by Keane et al. (2011) generated 43,255 loci. We analyzed these loci, using MrBayes (Huelsenbeck and Ronquist 2001; Ronquist and Huelsenbeck 2003) to generate 43,255 consensus gene trees (see File S1 and Figure S1).

The phylogenetic comparative approach to testing the snowball prediction requires estimates of branch lengths. In house mice, reconstruction of the subspecies phylogeny is complicated by significant gene tree discordance (Geraldes et al. 2008; White et al. 2009; Keane et al. 2011). Although the method used by Keane et al. (2011)—Bayesian concordance analysis (Ané et al. 2007)—accounts for discordance, it does not estimate branch lengths for a species tree. We reanalyzed the subspecies tree, using a class of methods that estimate branch lengths in the face of discordance and are computationally fast enough to handle 43,255 loci.

The collection of consensus gene trees was analyzed using three different methods: the Global LAteSt Split (GLASS) method (Mossel and Roch 2010) [also developed independently as the maximum tree (MT) by Liu et al. 2010], as implemented in Species Tree Estimation using Maximum likelihood (STEM) (Kubatko et al. 2009); the species tree estimation using average coalescent times (STEAC) method (Liu et al. 2009), as implemented in R/Phybase; and the shallowest divergence method (Maddison and Knowles 2006; Than and Nakhleh 2009), as implemented in R/Ape (Paradis et al. 2004). These methods all construct a species distance matrix from the gene trees, which is then used to hierarchically cluster the taxa and estimate the species tree. The pairwise distances between taxa in the distance matrix are calculated differently by each method. GLASS/MT/STEM finds the minimum pairwise coalescence time at each locus and takes the minimum across all loci, STEAC finds the mean coalescent time for each locus and takes the mean across all loci, and shallowest divergence finds the minimum coalescence time for each locus and takes the mean across all loci (see Helmkamp et al. 2012 for a review of these methods).

Evaluating models of hybrid incompatibility accumulation

We evaluated different models of hybrid incompatibility evolution, using a statistical approach that directly incorporates the phylogeny of the three subspecies and considers whether incompatibilities are shared or unique between hybrids in a maximum-likelihood framework (Wang et al. 2013). Specifically, we modeled the accumulation of substitutions as a Poisson process with equal fixation rates between populations and treated the emergence of incompatibilities as the result of Bernoulli trials among combinations of divergent substitutions (Orr 1995; Orr and Turelli 2001). A likelihood function was constructed according to the phylogeny, using both topology and divergence times; the observations for this likelihood included the numbers of incompatibilities between subspecies pairs and the subsets of these incompatibilities that were shared among species pairs. This likelihood function was then maximized to estimate the respective model’s parameters and Akaike information criterion (AIC) value, which was used to compare goodness-of-fit between models with different numbers of parameters. Following Wang et al. (2013), we compared four different models of incompatibility accumulation: a linear model of incompatibility accumulation (“linear”), a Dobzhansky–Muller model allowing only pairwise incompatibilities (“simple DM”), a DM model that also allows higher-order Dobzhansky–Muller incompatibilities (DMIs) (“pairwise + three-way DM”), and a DM model that allows derived–derived and derived–ancestral incompatibilities to arise with different probabilities (“p_a ≠ p_d DM”).

The approach described in Wang et al. (2013) uses six observed counts in the case of three taxa: the number of incompatibilities in each of the three hybrids and the number of shared incompatibilities in each of the three comparisons. In this study, we instead considered data from two crosses involving three subspecies, yielding three counts: the number of incompatibilities in each of the two hybrids and the number of shared incompatibilities between them. To account for this difference, we modified the likelihood function by reducing the number of elements in the vector of observations and the covariance matrix, respectively. For example, in a tree where A and B are sister taxa with C as the basal taxon, if the A × B cross is missing, the potential observations are I_AC, I_BC, and I_sharedC, making the observation vector

$$x=\{I_{\mathrm{AC}},I_{\mathrm{BC}},I_{\text{sharedC}}\}$$

and the covariance matrix

$$\mathrm{\Sigma }=\left[\begin{array}{ccc}{\sigma }^2{}_{\mathrm{AC}}& {\sigma }_{\mathrm{AC,BC}}& {\sigma }_{\mathrm{BC,sharedC}}\\ {\sigma }_{\mathrm{AC,BC}}& {\sigma }^2{}_{\mathrm{BC}}& {\sigma }_{\mathrm{AC,sharedC}}\\ {\sigma }_{\mathrm{AC,sharedC}}& {\sigma }_{\mathrm{BC,sharedC}}& {\sigma }^2{}_{\mathrm{sharedC}}\end{array}\right],$$

where σ² and σ are the variance and covariance calculated between incompatibility measures (Wang et al. 2013).

Data availability

Our QTL analysis used data from previously published studies (White et al. 2011, 2012a). Sequences used to estimate the subspecies trees and branch length are from Keane et al. (2011). Code used to implement maximum-likelihood methods developed in Wang et al. 2013 is available at https://github.com/Wang-RJ/speciation_on_trees.

Results

Phylogenetic partition of QTL

The combined analysis of the data from the castaneus × domesticus and musculus × domesticus intercrosses using PhyloQTL narrows confidence intervals around the positions of previously detected QTL, reveals some of the previously detected QTL to be shared between the subspecies, and identifies new QTL not reported by White et al. (2011, 2012a). Table 1 summarizes all hybrid male sterility QTL identified by the two intercrosses, including results from the combined analysis. Our analysis divides each QTL into one of three subspecies partitions: musculus | castaneus, domesticus (M|CD), castaneus | musculus, domesticus (C|MD), and domesticus | castaneus, musculus (D|MC). These partitions describe which subspecies share a common allele for the QTL (one of the subspecies must carry a different allele for a QTL to be detected). For example, a QTL with a common allele in the castaneus and domesticus subspecies but a different allele in musculus is given the M|CD partition. With one exception [sperm head morphology principal component 2 (PC 2)], PhyloQTL assigns QTL to partitions with high confidence (posterior probabilities >0.92).

Table 1. QTL identified with the combined analysis and their inferred phylogenetic partitions.

Phenotype	Chr.	Position (cM)	LOD score	Position (Mb)	1.5 LOD int. (Mb)	Partition	Posterior probability
Amorphous sperm head	2	66.0	4.70	168.3	131.9–178.7	C|MD	1.00
	5a	50.0	3.95	120.5	88.3–135.7	D|MC	0.94
	9	2.0	7.73	13.3	3.1–30.2	C|MD	1.00
	X	20.0	11.46	60.8	46.9–95.2	D|MC	0.97
	PAR	4.0c	3.87	—	—	C|MD	0.99
Distal bent tail	3	16.0	5.58	42.3	16.2–67.9	M|CD	1.00
	5	72.0	8.64	147.3	133.7–148.4	M|CD	1.00
	X	23.0	8.68	67.7	56.2–93.3	M|CD	1.00
Headless/tailless	15	0.0	3.96	16.5	16.5–46.7	M|CD	0.96
	X	23.0	10.10	67.7	51.5–97.1	D|MC	0.99
	PAR	0.0	3.95	—	—	C|MD	0.98
Proximal bent tail	10	8.0	4.86	48.5	33.8–81.9	M|CD	0.97
	X	31.5	10.05	90.8	56.2–97.1	M|CD	0.98
	Xb	58.0	3.36	146.9	95.2–62.9	C|MD	—
Testis weight	2	28.6	8.29	80.6	69.7–08.3	D|MC	1.00
	4	47.1	11.51	108.9	57.8–114.3	D|MC	0.98
	10	16.0	7.21	67.8	58.3–88.1	M|CD	0.94
	PAR	2.0	4.51	—	—	C|MD	0.99
Sperm density	17	13.5	6.02	29.9	3.1–64.8	M|CD	1.00
	X	4.0	4.22	20.7	10.2–56.2	D|MC	0.92
	Xb	56.0	3.82	142.4	86.6–162.9	C|MD	—
	PAR	2.0	6.06	—	—	C|MD	1.00
Sperm head PC1	2b	76.0	4.00	177.0	143.8–179.0	C|MD	—
	14a	46.0	10.26	96.8	89.4–104.1	M|CD	1.00
	19a	30.0	17.94	39.1	33.2–44.9	M|CD	1.00
	Xb	12.0	4.18	41.9	10.2–162.9	C|MD	—
	X	20.0	85.32	60.8	51.5–65.5	M|CD	1.00
	PAR	6.0	8.52	—	—	C|MDd	0.93
Sperm head PC2	X	18.0	10.80	56.2	45.1–70.3	D|MC	1.00
	PAR	0.0	8.35	—	—	C|MD	0.51
Seminiferous tubule area	2	26.0	7.25	76.3	57.7–102.4	C|MD	0.99
	8	51.1	4.33	125.0	113.0–130.8	C|MD	0.96
	16a	24.4	4.09	97.2	90.4–97.2	D|MC	0.93
	18	26.0	4.62	68.3	57.8–73.4	M|CD	0.97
	X	65.2	4.46	162.9	142.4–162.9	C|MD	1.00
	PAR	0.0	8.29	—	—	C|MD	1.00
Total abnormal sperm	5	64.0	4.96	137.7	123.6–148.4	M|CD	0.75
	15	4.0	4.66	28.6	16.5–68.7	M|CD	0.99
	X	34.0	15.98	93.3	56.2–99.1	D|MC	1.00
	PAR	0.0	5.44	—	—	C|MD	1.00

Posterior probabilities of the partitions were calculated using the approximate Bayes procedure in Broman et al. (2012). D|MC, M|CD, and C|MD describe the domesticus|musculus,castaneus; musculus|castaneus,domesticus; and castaneus|musculus,domesticus partitions, respectively. PAR, pseudoautosomal region.

^aQTL newly identified by the combined analysis.

^bQTL detected in separate analyses of the two crosses but not detected by the combined analysis.

^cPAR genetic positions are relative to the beginning of the region, not the X chromosome.

^dSperm morphology PC1 assigned to D|MC in PhyloQTL, but likely in error due to the high LOD score of QTL on the X in the musculus × domesticus cross (see text).

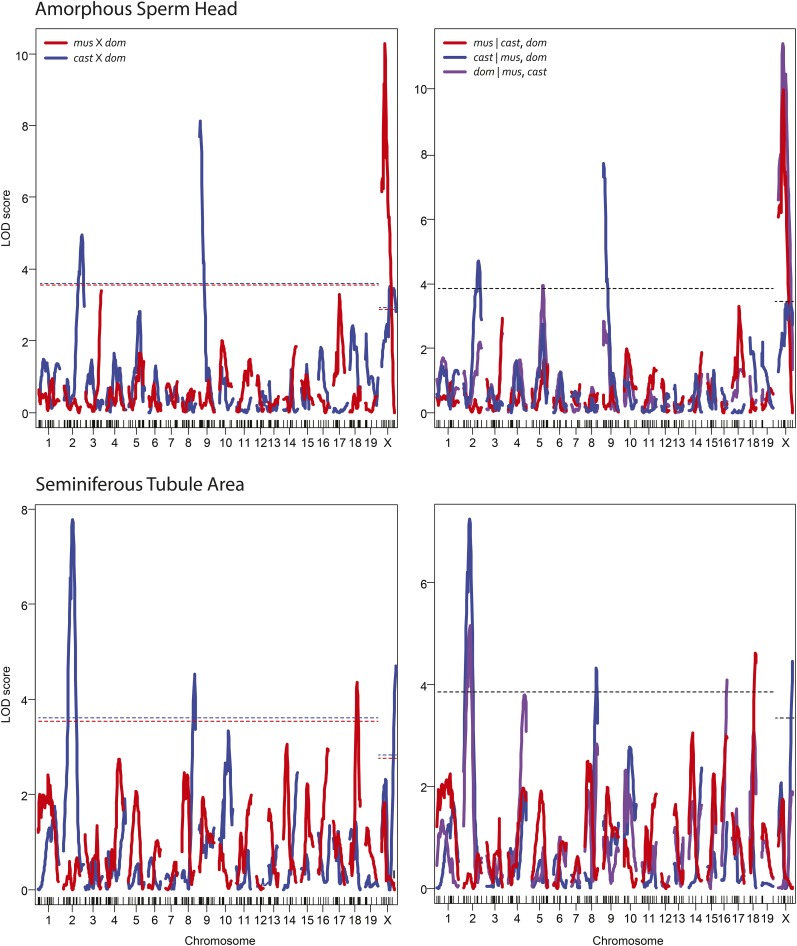
Figure 2 shows two example comparisons between LOD curves generated from separate and combined analyses. In the first example from Figure 2, a QTL for amorphous sperm head on the X chromosome—previously found to be significant in both crosses individually—is determined to be a single QTL shared between both crosses. Alternatively, QTL for amorphous sperm head on chromosome 5 and seminiferous tubule area on chromosome 16 are both novel (not present in the single-QTL scans from either of the two separate analyses). Interestingly, the shared QTL for seminiferous tubule area on chromosome 16 was also identified by a multiple-QTL scan specific to the musculus × domesticus cross (White et al. 2012a); this was the only new QTL identified by the joint analysis that was previously identified by a multiple-QTL scan.

Figure 2.

Example comparisons of heuristic and PhyloQTL methods for identifying shared QTL for amorphous sperm head (top) and seminiferous tubule area (bottom). LOD curves on the left show the results of mapping these phenotypes separately in the musculus × domesticus (red) and castaneus × domesticus (blue) crosses. LOD curves on the right show the results of joint mapping (PhyloQTL) with each curve representing a different partition [red, musculus ǀ castaneus, domesticus (mus|cast,dom); blue, cast|mus,dom; purple, dom|mus,cast]. Significance thresholds are at the 5% level and were determined by permutation.

Each QTL identified by White et al. (2011, 2012a) has a corresponding QTL in the combined analysis, except sperm head morphology PC1 and PC2. These exceptions are likely the result of a transformation on the values of this trait to compare them between the two crosses. Because the ranges of values from the principal component analysis of sperm head morphology are unique to each cross, a direct comparison of these values is not meaningful. To meaningfully compare this trait, we conducted principal component analysis on the combined sample of F₂’s from both crosses and arrived at new values for the principal components.

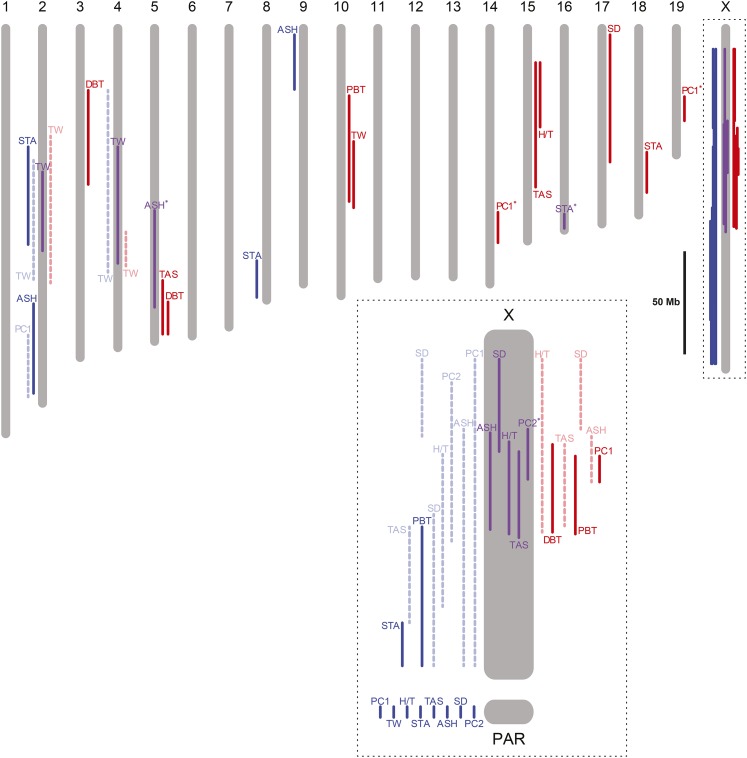
A drawback of the PhyloQTL analysis, because it is based on a single-QTL scan, is its limitation to detecting only one QTL per chromosome. QTL from the original analysis may be omitted if they occur on the same chromosome in both crosses but are identified as unshared; only the QTL with the greatest LOD score is reported. For example, a QTL for proximal bent tail is identified on the X chromosome in both individual crosses, but the combined analysis finds a single QTL for proximal bent tail on the X with the M|CD partition. This issue also arises for sperm density and sperm head morphology (PC1). For sperm head morphology (PC1), a QTL in the pseudoautosomal region (PAR) is partitioned in the PhyloQTL analysis as D|MC. However, this is likely an artifact due to a QTL for PC1 on the X chromosome from the musculus × domesticus cross; this QTL covers the entire X chromosome, including the PAR, but has no support in the PAR in a multiple-QTL analysis (White et al. 2012a). To ameliorate these problems in our analysis of the snowball model, we included all QTL that were significant in White et al. (2011, 2012a) and switched the partition of the PC1 QTL in the PAR to C|MD. The collection of all QTL identified as incompatibilities is illustrated with respect to their physical positions (NCBI36/mm8 assembly) in Figure 3.

Figure 3.

Hybrid sterility QTL identified by the combined analysis with their 1.5-LOD intervals depicted on a physical map of the mouse genome (NCBI36/mm8 assembly). QTL identified on the left (blue) of the chromosome pictograms represent incompatibilities partitioned to C|MD, QTL on the right (red) represent those partitioned to M|CD, and QTL in the middle (purple) represent those partitioned to D|MC. QTL shown by dashed lines are the positions and partitions identified by White et al. (2011, 2012a). QTL with an asterisk are newly identified by the combined analysis. Phenotypes are abbreviated: ASH, amorphous sperm head; DBT, distal bent tail; H/T, headless/tailless; PBT, proximal bent tail; TW, testis weight; SD, sperm density; PC1, sperm head morphology principal component 1; PC2, principal component 2; STA, seminiferous tubule area; and TAS, total abnormal sperm. Inset portrays the X chromosome with the same vertical scale as in the remainder of the figure.

To count the number of QTL in each phylogenetic partition, we enumerated them as in Table 1 with one exception. We counted all of the QTL in the PAR as arising from only one incompatibility. The small size of the PAR suggests that the many QTL partitioned to C|MD in this region are part of a single underlying locus. The totals across the genome for each partition according to the combined analysis are as follows: M|CD, 14; C|MD, 10; D|MC, 9 (autosome only count: M|CD, 11; C|MD, 8; D|MC, 4). The totals across the genome from the heuristic approach, which considers only overlap in single-QTL positions from the original studies, are M|CD, 13; C|MD, 12; and D|MC, 5 (autosome only count: M|CD, 9; C|MD, 5; D|MC, 2).

Two estimates of the subspecies tree

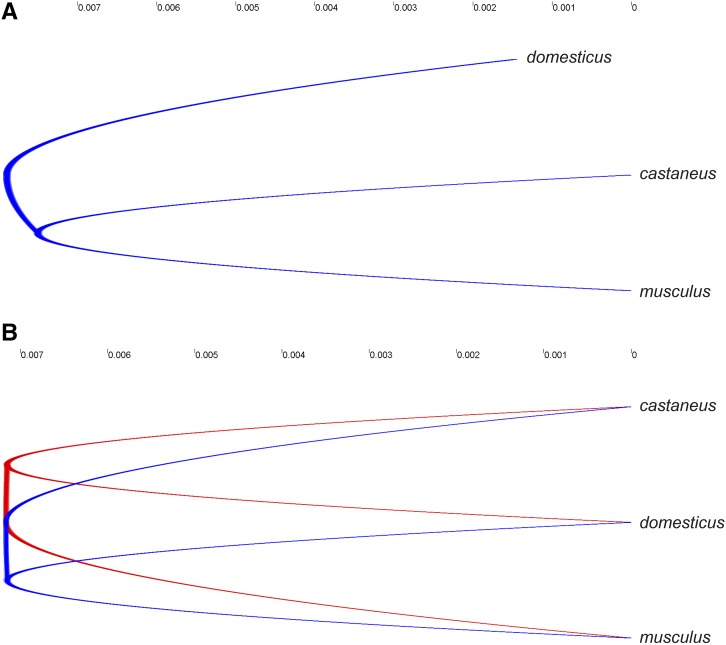
We used three different methods to determine the subspecies tree. We focus on the trees derived from the shallowest divergence (SD) and STEAC methods because results from STEM/GLASS/MT were uninformative. STEM returned branch lengths that were two orders of magnitude different from those of the SD or STEAC methods and trees in the neighborhood of the maximum-likelihood tree determined by STEM did not share the same topology. This result is consistent with studies showing that STEM’s accuracy can decrease substantially with larger numbers of loci when the population mutation parameter and tree height are relatively small (Leaché and Rannala 2011; DeGiorgio and Degnan 2014). The STEAC and SD trees are illustrated in Figure 4; note that these trees are rooted to Rattus norvegicus (not depicted).

Figure 4.

Subspecies trees reconstructed using the species tree estimation using average coalescence times (STEAC) (A) and the shallowest divergence method (SD) (B). The STEAC tree has castaneus and musculus as sister taxa in all 1000 of bootstrap replicates while the SD tree has domesticus and musculus as sister taxa in 52% of the replicates (dominant topology in blue). Trees are rooted to Rattus norvegicus (not depicted). Scale is in units of average substitutions per nucleotide.

The STEAC tree—which contains a short internal branch uniting castaneus and musculus as sister taxa—is consistent with previous estimates of the subspecies phylogeny (Geraldes et al. 2008; White et al. 2009; Keane et al. 2011; Suzuki et al. 2013). This tree is asymmetric: domesticus has a slightly shorter branch length (0.00642 substitutions per nucleotide) than castaneus (0.00750) and musculus (0.00749) (the internal branch length is 0.0004). When the loci were bootstrapped, 1000 replicates of the STEAC method consistently resulted in the same tree.

In contrast, the SD method returns an ultrametric tree that is essentially a polytomy, although the highest support has castaneus as the basal taxon with very minimal internal branch length. The sister taxa in this tree are separated from the node by 0.00715 substitutions per nucleotide and the internal branch length is estimated to be 1.3e-6. Only 52% of bootstrap replicates yielded this topology, revealing substantial uncertainty.

Incompatibility evolution along the phylogeny

Before reporting results from our statistical comparison of models of incompatibility evolution, we elaborate briefly on the structure of the tree topology and its relationship to the number of QTL expected in each partition. Figure 5 shows three different subspecies topologies with a fixed tree; the fixed tree preserves the structure when referencing the expected values. For example, the estimated number of incompatibilities between domesticus and musculus corresponds to I_AC—the number of incompatibilities between the outer branches in a tree with topology D|MC. Alternatively, with a C|MD tree topology, this same value would correspond to I_AB—the number of incompatibilities between sister taxa. Thus far, the number of QTL has been separated by partition. To determine the total number of incompatibilities between subspecies pairs, we must sum the shared incompatibilities with those specific to a single hybrid. Since domesticus is the common subspecies in our two crosses, all QTL partitioned to D|MC correspond to shared QTL from the domesticus branch. This number is then added to the number of incompatibilities partitioned to the branch specific to musculus or castaneus. Table 2 shows the relationship between tree topology, QTL partitions, and the number of incompatibilities between each species pair. The SD tree has the C|MD topology while the STEAC tree has the D|MC topology.

Figure 5.

Three different species topologies (right) and the constant structure to which they are referenced (left). The parameters, t₂ and t₁, represent time from present since divergence of the sister taxa and the time separating this divergence from the original split with the basal taxon, respectively.

Table 2. The number of incompatibilities based on QTL partitioned to each phylogeny.

	Tree partition
Incompatibility structure	D|MC	C|MD	M|CD
IAB	—	NC|MD + ND|MC	NM|CD + ND|MC
IAC	NM|CD + ND|MC	—	—
IBC	NC|MD + ND|MC	NM|CD + ND|MC	NC|MD + ND|MC
IsharedC	ND|MC	—	—
IsharedB	—	—	ND|MC
IsharedA	—	ND|MC	—

The number of incompatibilities is calculated based on the number of QTL partitioned to each phylogeny (N with respective partition subscripted). Tree topologies are labeled on the top row with incompatibility structure as depicted in Figure 5 in the left column. Each entry is the total number of incompatibilities for its respective phylogenetic partition. Three measures of incompatibilities can be calculated from our data while three measures are missing for each topology.

The number of incompatibilities between each species pair as measured by QTL is summarized in Table 3. Overall, the PhyloQTL method reveals a greater number of incompatibilities, both shared and unique. The number of incompatibilities, the tree topology, and the ratio of branch lengths (t₂/t₁) were used to calculate support for the four different models of incompatibility accumulation, as measured by AIC value (Table 3). AIC values were calculated for each of the 1000 bootstrapped SD and STEAC trees, with the mean and standard deviations from this analysis listed in Table 3; the variance in AIC values from bootstrapping the trees is very small. The mouse X chromosome has a substantial and complex role in hybrid male sterility (Storchova et al. 2004; Good et al. 2008b; Turner et al. 2014), evident in the large number of QTL that localize and overlap on the X chromosome (Figure 3). For this reason, we separately evaluated models of incompatibility evolution for three groups of loci: all QTL, autosomal QTL, and X-linked QTL. Because the tree estimated by the SD method closely resembles what is expected if the three subspecies split simultaneously, we also compared incompatibility models under the assumption of a polytomy. The results were nearly identical to the analysis under the SD tree, with AIC values for each model falling within the deviations from bootstrapping shown in Table 3.

Table 3. Summary of the number of incompatibilities, model selection, and AIC values.

Heuristic		NC|MD (mus × dom)	NM|CD (cast × dom)	ND|MC (shared)
Whole genome		13	12	5
Autosomes		9	5	2
X only		4	7	3
STEAC tree	Linear	Simple DM	2+3 DM	pa ≠ pd DM
Whole genome	24.59	19.64	21.64	21.64
	(1.E-2)	(5.E-2)	(5.E-2)	(4.E-6)
Autosomes	23.22	19.06	20.62	20.62
	(2.E-2)	(7.E-3)	(1.E-6)	(6.E-7)
X only	19.84	18.40	20.40	20.24
	(1.E-2)	(5.E-3)	(5.E-3)	(1.E-6)
SD tree	Linear	Simple DM	2+3 DM	pa ≠ pd DM
Whole genome	23.72	19.71	21.71	21.64
	(1.E-2)	(5.E-3)	(5.E-3)	(5.E-3)
Autosomes	22.64	18.86	20.62	20.62
	(2.E-2)	(2.E-2)	(2.E-2)	(2.E-2)
X only	19.48	18.59	20.59	20.24
	(1.E-2)	(1.E-2)	(1.E-2)	(2.E-2)
PhyloQTL		NC|MD (mus × dom)	NM|CD (cast × dom)	ND|MC (shared)
Whole genome		14	10	9
Autosomes		11	8	4
X only		3	2	5
STEAC tree	Linear	Simple DM	2+3 DM	pa ≠ pd DM
Whole genome	21.93	23.72	25.72	22.82
	(2.E-2)	(4.E-2)	(4.E-2)	(3.E-6)
Autosomes	23.02	19.30	21.30	21.30
	(2.E-2)	(6.E-4)	(6.E-4)	(2.E-6)
X only	17.63	24.59	26.59	19.96
	(1.E-2)	(4.E-2)	(4.E-2)	(1.E-3)
SD tree	Linear	Simple DM	2+3 DM	pa ≠ pd DM
Whole genome	21.47	24.98	26.98	22.82
	(2.E-2)	(2.E-2)	(2.E-2)	(3.E-2)
Autosomes	22.36	19.37	21.37	21.30
	(2.E-2)	(1.E-2)	(1.E-2)	(2.E-2)
X only	17.99	25.90	27.90	19.99
	(5.E-3)	(2.E-2)	(2.E-2)	(1.E-2)

AIC values are presented with standard deviations estimated from bootstrapped trees in parentheses. Models with lowest AIC values (favored) are in boldface type.

Analyses employing the heuristic approach of enumerating incompatibilities unanimously favor the simple DM model. The linear model is convincingly rejected (AIC difference >2) except when we restrict the analysis to the X chromosome. When considering all of the incompatibilities, other DM-type models have AIC values that are ∼2 greater than those of the simple DM model. When we examined parameter estimates from the more complex DM models, we found that for the 2+3 model, p₃ was at the lower limit of the search and was essentially zero. Similarly, estimates of the parameters p_a and p_d from the p_a ≠ p_d model were <20% different. These results indicate that these more complex models add little to the search space and confirm that the simple DM model is the best fit (suggesting the absence of three-locus incompatibilities and relatively equal probabilities of ancestral–derived and derived–derived incompatibilities).

In contrast, when the number of incompatibilities is enumerated per PhyloQTL, the favored model depends on whether we consider incompatibilities on the X chromosome. When the analysis is restricted to autosomal QTL, the simple DM model is again convincingly favored over other models. Inclusion of incompatibilities from the X chromosome results in superior fit for the linear model, although the p_a ≠ p_d model remains competitive. This signal appears to be driven by incompatibilities on the X chromosome, where the linear model is heavily favored when examining only the X.

To test the ability of our statistical method to distinguish between the linear and DM models given our data, we simulated incompatibility evolution under each of the four models we tested. We set the parameters of the simulation such that the expected number of incompatibilities between the two most diverged taxa would be 20 and used the divergence times and topologies from the SD and STEAC trees from our analysis. Given these trees, in the unrealistic limits that incompatibilities were either all unique or all shared, our method overwhelmingly favors or rejects the snowball prediction, respectively. Our simulations here do not account for uncertainty in assigning incompatibilities as shared vs. unique or uncertainty in the accuracy of the tree, but they do measure the power to differentiate models when other measures are accurate. Table 4 summarizes the results from 5000 simulations for each of the four models. We combined the results from each of the DM-type models as there was low power to distinguish between them. The tree estimated by the SD method is essentially polytomous. In this case, our analysis distinguishes between the linear and the DM model mainly by examining the fraction of shared incompatibilities. As depicted in Figure S2, the fraction of shared incompatibilities is expected to be higher for the linear model, especially when there is no internal branch. While this characteristic enables model distinction in the absence of phylogenetic structure, overall our method performs better with increasing internal branch length (Wang et al. 2013). Here, our statistical approach offers up to 88% sensitivity and 89% specificity for evaluating both linear and DM models.

Table 4. Contingency table of model simulations.

Tree	Linear simulation	DM simulation
SD
Linear best fit	0.876	0.119
DM best fit	0.124	0.881
STEAC
Linear best fit	0.890	0.112
DM best fit	0.110	0.888

Shown is the proportion of simulations that recover a best fit with the linear model vs. a DM-type model (simple DM, 2+3-locus DM, and p_a ≠ p_d DM). True (simulated) model is indicated by column.

Discussion

Our findings add the house mouse to the list of species groups that show evidence for a faster-than-linear accumulation of hybrid incompatibilities (Matute et al. 2010; Moyle and Nakazato 2010; Sherman et al. 2014). In contrast to previous studies of the snowball effect, our results explicitly incorporate phylogenetic information. We now address some of the challenges with testing the snowball prediction and connect our findings to the current understanding of speciation in house mice.

Error in phylogenetic reconstruction affects all comparative methods, including our test for the snowball effect. In house mice, phylogenetic discordance across the genome resulting from incomplete lineage sorting complicates inference of the subspecies phylogeny (Geraldes et al. 2008, 2011; White et al. 2009; Keane et al. 2011). To address this challenge, we used whole-genome sequences and two methods that incorporate discordance among gene trees for phylogenetic reconstruction. Two lines of evidence suggest that our inferences about the snowball effect are reasonably robust to uncertainty in the subspecies tree. First, measures of model fit (AIC values) were similar among bootstrapped trees. Second, although the two phylogenetic methods returned slightly different trees, the ranked fits of models were the same for these two trees.

Although it may seem disconcerting that different topologies yield similar results, the brevity of shared evolutionary history between subspecies pairs in both trees reduces the impact of topology on the model. Nevertheless, the phylogeny is informative for our analysis as our expectations for the numbers of shared and unique incompatibilities depend on the shape of the tree. Even in the absence of phylogenetic structure (simultaneous divergence of the three subspecies), there is a nonzero expectation for the number of shared incompatibilities between subspecies pairs. For example, consider a comparison between the linear model and the simple DM model in a three-species polytomy. Under the linear model, a single substitution confers incompatibility with the ancestral state; such a substitution along one lineage results in an incompatibility shared between the two potential hybrids with that lineage. Under the simple DM model, an incompatibility is shared between hybrids if (1) the participating substitutions interact as a derived–ancestral incompatibility or (2) one of the interacting substitutions became fixed during a period of shared ancestral history (see Figure 1). In the case of simultaneous divergence between species, there is no period of shared ancestral history and only derived–ancestral incompatibilities between hybrids can possibly be shared. This distinction between the two models in a polytomy manifests mathematically as an extra factor of 2 in the proportion of shared incompatibilities under the linear model as interdivergence time, t₁, goes to 0 (Wang et al. 2013) (Figure S2). Intuitively, the existence of unshared derived–derived incompatibilities under the simple DM model reduces the expected proportion of shared incompatibilities relative to the linear model.

In line with the original model (Orr 1995), our test of the snowball effect assumes that gene flow between subspecies ceased after their initial divergence (Wang et al. 2013). This assumption appears to be violated in house mice, although estimated levels of historical gene flow are low (Duvaux et al. 2011; Geraldes et al. 2011), with a potential increase in the hybridization rate very recently (Pool and Nielsen 2009). The potential impact of gene flow on our results is not easy to predict. Gene flow effectively shortens the amount of time that regions of the genome spend in allopatry, reducing the potential for incompatibility formation and inflating the expected number of incompatibilities under the snowball prediction. Alternatively, gene flow between subspecies might deflate estimates of divergence time, increasing the apparent number of incompatibilities with respect to divergence time and creating the appearance of faster incompatibility accumulation. Predicting the effects of gene flow that was asymmetrical or limited to certain pairs of subspecies would be even more difficult. How incompatibilities should accumulate along a phylogeny with gene flow after initial divergence is a question worthy of theoretical work.

Our use of hybrid male sterility QTL as proxies for hybrid incompatibilities relies on several assumptions that deserve attention. First, we counted single-locus QTL as hybrid incompatibilities, without identifying their epistatic partners. This assumes each QTL detected is from a single component of a unique epistatic incompatibility. This approach, which was also followed in previous tests of the snowball effect (Matute et al. 2010; Moyle and Nakazato 2010), recognizes that crosses with practical sample sizes usually lack power to locate interacting QTL. A second assumption involved treating phenotypic measures of hybrid male sterility as equivalent to reproductive isolation. If the QTL we identified instead are responsible for subspecies differences in the physiology and development of reproduction, then the prediction of epistasis and the snowball effect would break down. This problem plagues most genetic studies of reproductive isolation and is difficult to dismiss. But several lines of evidence suggest the QTL we found contribute to hybrid incompatibilities, including their involvement in X–autosome epistatic interactions (White et al. 2011), their overlap with regions of low introgression in the European hybrid zone (Janoušek et al. 2012), and their colocalization with trans-expression-QTL hotspots mapped in hybrids (Turner et al. 2014). Finally, we assumed that overlapping QTL from the two crosses reflect the same genetic changes. Confidence intervals on the locations of our QTL were wide (due to the limited amount of recombination in these F₂ mapping experiments), raising the chances that some QTL due to independent changes were falsely labeled as shared between the two crosses.

The heuristic approach for partitioning QTL as shared vs. unique leads to unanimous support for the snowball effect. In contrast, conclusions based on the PhyloQTL method depend on whether X-linked QTL are included in the comparative analysis. One explanation for this result is that the X chromosome contains more shared incompatibilities than the autosomes, and the PhyloQTL approach offers higher power than the heuristic method to detect these loci. The X chromosome confers hybrid male sterility between domesticus and musculus through complex regulatory mechanisms that remain unclear (Storchová et al. 2004; Good et al. 2008b, 2010; Oka et al. 2010; Campbell et al. 2013; Turner et al. 2014; Bhattacharyya et al. 2014; Oka and Shiroishi 2014). It is possible that incompatibilities involving the X chromosome differ from purely autosomal interactions in some way that affects the snowball prediction. For example, if X-linked changes participate in multiple incompatibilities, the assumption that incompatibilities experience independent fixation probabilities (Orr 1995) would be violated, potentially leading to a departure from the snowball expectation (Palmer and Feldman 2009).

Another possibility is that we have incorrectly reduced the number of unique incompatibilities in the domesticus × castaneus cross by assuming that multiple QTL in the PAR reflect a single incompatibility. Although this choice could introduce a bias away from the snowball effect, it seems reasonable because the PAR encompasses between 0.7 and 1.1 Mb of sequence (Perry et al. 2001; White et al. 2012b) (providing limited opportunities for multiple incompatibilities) and the hybrid sterility phenotypes that map to the PAR are highly correlated with one another (White et al. 2012a). This potential counting issue also fails to explain support for the snowball effect when using the heuristic approach to determine shared incompatibilities.

Overall, our results seem most consistent with a scenario in which the snowball effect is real across the genome, but the low mapping resolution and large numbers of X-linked QTL substantially violate the single-QTL model underlying PhyloQTL for the X chromosome. This violation results in an undue number of incompatibilities partitioned as shared between the crosses from the X chromosome. Our findings should motivate higher-resolution mapping of X-linked incompatibilities in house mice, as has been achieved for F₁ hybrid male sterility between musculus and domesticus (Bhattacharyya et al. 2014).

The conclusion that incompatibilities have accumulated faster than linearly with time has implications for the study of speciation in house mice. More incompatibilities contribute to F₂ hybrid male sterility in domesticus–musculus than in domesticus–castaneus, despite similar divergence times and similar power for QTL mapping in these crosses (White et al. 2012a). This pattern suggests that the snowball effect could disproportionately reflect substitutions along the musculus lineage, a possibility that could be addressed by genetic dissection of hybrid male sterility between castaneus and musculus. Another prediction that follows from our results is that a large number of incompatibilities are responsible for F₂ hybrid male sterility between house mice and other species of Mus. Loci have been identified that cause F₁ sterility between domesticus (C57BL/6) and M. spretus (Guénet et al. 1990; Matsuda et al. 1991, 1992), but a genome-wide search for F₂ sterility loci has yet to be conducted.

Tomatoes, flies, and mice differ in a wide spectrum of biological characteristics. The evidence in favor of the snowball effect in these three groups therefore indicates that the faster-than-linear accumulation of hybrid incompatibilities is likely to be a general phenomenon. Nevertheless, additional empirical testing of this influential theoretical prediction is needed. Although comparative genetic mapping in F₂’s or backcrosses presents its challenges, the amenability of this approach across a variety of species should facilitate evaluation of the universality of the snowball prediction beyond a handful of model genetic organisms. Along these lines, the fact that the snowball effect was detectable over the short timescale of divergence between subspecies of house mice should encourage investigators to examine groups of closely related species. A comparative framework is ultimately required for understanding how the genetic determinants of reproductive isolation evolve and hence how speciation occurs (Moyle and Payseur 2009).

The growing empirical support for the snowball effect should also inspire new theory. Examination of the polymorphic phase would illuminate intraspecific variation in interspecific hybrid dysfunction, which has been seen in house mice and other species (Rieseberg 2000; Reed and Markow 2004; Bomblies et al. 2007; Sweigart et al. 2007; Good et al. 2008a; Vyskočilová et al. 2009; Cutter 2012; Kozlowska et al. 2012; Corbett-Detig et al. 2013). The intraspecific variation of DMIs may affect both empirical and theoretical support for the snowball prediction, particularly in cases of recent divergence. The numbers of incompatibilities detected between species pairs are likely inflated by the existence of incompatibilities that are still polymorphic in the population. However, the polymorphism of incompatibilities is absent in the model upon which the snowball prediction is based. By assuming independence between incompatibilities (Orr 1995; Orr and Turelli 2001) and ignoring standing variation, the time incompatible substitutions spend in allopatry is likely exaggerated, resulting in an overestimation of the probability of incompatibility. Overestimated incompatibility probabilities and inflated incompatibility numbers have opposing effects on our inference; the former is conservative for the snowball hypothesis while the latter is not. Ultimately, understanding the consequences of a polymorphic phase for incompatibilities requires a new theoretical framework that considers the population genetic processes underlying the molecular evolution of incompatible substitutions. The emergence of transcriptomic data on hybrid dysfunction also has the potential to refine genetic models of speciation (Turner et al. 2014). Reconciliation of these data with predictions from models that constrain incompatibility evolution to developmental pathways and gene networks will offer an increasingly realistic portrait of speciation genetics.