Tree Topology Estimation

Abstract

Tree-like structures are fundamental in nature, and it is often useful to reconstruct the topology of a tree—what connects to what—from a two-dimensional image of it. However, the projected branches often cross in the image: the tree projects to a planar graph, and the inverse problem of reconstructing the topology of the tree from that of the graph is ill-posed. We regularize this problem with a generative, parametric tree-growth model. Under this model, reconstruction is possible in linear time if one knows the direction of each edge in the graph—which edge endpoint is closer to the root of the tree—but becomes NP-hard if the directions are not known. For the latter case, we present a heuristic search algorithm to estimate the most likely topology of a rooted, three-dimensional tree from a single two-dimensional image. Experimental results on retinal vessel, plant root, and synthetic tree datasets show that our methodology is both accurate and efficient.

Introduction

Trees are fundamental physical structures in nature. Aside from the eponymous large plants, other examples include retinal vessels, lung airways, neurons, lightning, plant roots, and more. Trees typically arise from a branching process that grows away from an initial root to efficiently distribute a fluid, a current, or signals between a central source and a set of end-points. Different growth processes produce strikingly different trees, both in terms of their geometry and their connectivity, as Figure 1 illustrates.

Fig. 1.

Images of physical trees: (This Figure is best viewed on-screen). Different combinations of internal and external factors yield remarkably different trees. However, all these trees facilitate a hierarchical flow between a central node and a series of end-points. (a) and (b) are samples from our experimental datasets, while (c) and (d) are public domain images.

A wide variety of imaging techniques—including fluorescein angiography, retinal fundus imaging, and x-ray and color photography—yield two-dimensional images of trees, from which it is often useful to reconstruct the tree's original connectivity. However, the three-dimensional location of each tree branch is lost after projection, and parts of different branches often map to the same point on the image. See Figure 1 again.

Specifically, the image of a tree obscures its original topology in two key ways:

1. There may be spurious branch crossings in the image that resemble true branchpoints.

2. The directionality (flow to or from the root) along the branches may be lost.

The resulting loss of information makes reconstructing tree connectivity and flow direction from an image an ill-posed problem, and a prior model must be introduced to regularize the solution. Fortunately, good theoretical and empirical models have been developed in several domains to describe the expected morphology or growth pattern of a particular type of tree. Well-studied trees include blood vessels [31], [33], plant roots [2], [20], neurons [24], [28], leafy trees [3], [34], and lightning [15], [29].

In this work, we present a comprehensive methodology for estimating the most likely topology of a rooted, directed, three-dimensional tree given a single two-dimensional image of it and a growth model for that type of tree. We address this challenging inverse problem through a combination of greedy approximation and heuristic search algorithms that efficiently explore the space of possible trees. Our main theoretical contributions are:

1. The formalization of the tree estimation problem from a single projection.

2. A proof that the tree estimation problem is NP-hard if flow direction is unknown.

3. A greedy linear-time algorithm for approximating the most likely topology of a tree.

4. A heuristic search algorithm that efficiently explores the space of possible trees starting from the greedy solution.

The rest of this paper is organized as follows: Section 2 discusses related work. Sections 3 and 4 describe the projection of three-dimensional trees onto two-dimensional images and elucidate the space of possible solutions, respectively. Section 5 presents a generative, parametric model of tree growth and defines the probability of a projected tree given the model. Section 6 examines the complexity of estimating the most probable tree. Section 7 presents both a greedy approximation algorithm and a heuristic search method that refines the greedy estimate. Finally, Section 8 presents experimental results on retinal vessel, plant root, and synthetic tree datasets, and Section 9 discusses future work.

2 Related Work

To the best of our knowledge, the only prior work on automatically determining the topology of a three-dimensional tree given a single, two-dimensional image of it is the method developed by Zeng et al. [44] for modeling visually plausible unfoliaged trees from images. Their algorithm greedily assigns to each branch segment the parent branch that has the most plausible thickness and forms the most plausible angle with the candidate branch. The results in their paper did not include any quantitative evaluation. We now survey other related work concerning tree imaging and modeling.

Tree reconstruction

Most previous tree estimation work focused on three-dimensional data, primarily from MRI, computed tomography (CT), and optical coherence tomography (OCT) scans of lung airways, cardiac vasculature, and retinal vessels. Reconstruction from three-dimensional images is a well-posed problem. The most popular methods in this field are region growing [16], [26], probabilistic branch tracking [12], [36], and dynamic programming [17], [18]. Tomographic reconstruction methods from conventional photographs have also been developed for plant roots grown in a clear medium using volumetric carving [20], [45]. We estimate the topology of a three-dimensional tree from a two-dimensional graph.

Tree segmentation

Two-dimensional analysis of tree structures, primarily of retinal vessels, has focused on binary segmentation, which seeks to extract the tree pixels but not the corresponding three-dimensional topology. Segmentation methods employ local filtering [42], [37], dynamic programming [4], [10], spanning tree sampling [14], [40], Steiner trees [19], or tubular tracking [30], [43]. Recent work also attempts to distinguish arteries from veins using a combination of color features and vessel tracking [7], [35].

Graphical tree modeling

Work on modeling trees using computer graphics follows three main approaches: Rule-based methods generate trees using fractals or other local deformations [1], [32]. In sketch-based tree modeling, a user draws one or more two-dimensional sketches and a tree is generated based on them [6], [38]. In image-based modeling, a set of input images is used to synthesize a plausible three-dimensional tree model [27], [44]. Overall, the goal of graphical tree modeling is to obtain a visually plausible three-dimensional geometry based on either a user's traced branches or a set of branch-generating rules. Our focus, on the other hand, is to faithfully estimate an input tree's topology.

Tree-growth models

There has been considerable work on modeling the growth of specific types of trees by accounting for the interactions between the various forces that affect the growing tree. Blood vessel models describe growth at multiple scales—from single cells to tissues—primarily through systems of differential equations that describe cell development and migration [31], [33]. Plant-root growth models generally employ similar principles, but also incorporate architectural constraints driven by gravity [2], [20]. Neuron growth modeling has focused on statistical techniques, such as Bayesian networks [24], [28]. Leafy tree models have used flow diffusion and fractals [3], [34], while lightning modeling has focused on the ambient electric field [15], [29]. We develop a generative probabilistic model that captures a wide class of trees with a modicum of parameters, and lends itself well to stochastic search.

3 Tree Projection

We study rooted trees in three-dimensional space that project onto graphs in two-dimensional images. More specifically, our trees carry a flow of something—a fluid, a current, information—from their roots to their leaves or vice versa, so that a direction consistent with this flow is associated to each of their branches. For simplicity, we assume that all flow is from the root, the reverse case being entirely equivalent. In our discussion, we often distinguish a graph from its embedding. Thus, for clarity, we use the term “directed tree” to refer to the graph of the three-dimensional tree and “arborescence” to refer to its embedding, even though “arborescence” is typically used for both in the literature.

Projecting an arborescence removes information about the distance of each of its branches to the image plane. Most of the time, projection also obscures information about the direction of flow associated with each branch, as branches taper very slowly, if at all, in typical images. As a result, projecting an arborescence yields an undirected graph in the image plane. This graph is planar if new branch intersections, formed as a result of projection, are considered to be new vertices.

Assuming that the undirected image graph G has been segmented out of the image (see Section 8.2.1 for segmentation) of an arborescence A with directed tree T, our task is to reconstruct T from G. Since projection is a many-to-one mapping, many different directed trees can project to the same graph, making the reconstruction problem ill-posed. To regularize it, we introduce a generative prior model M for the growth of any given type of tree—the dendrites of a neuron, the vessels in a retina, plant roots, or the branchings in a stroke of lightning. This model allows us to define a prior probability p_M(T) on the set of all possible directed trees, and we then seek a most likely tree given its image graph and the model:

$$T^{\ast }=\underset{T\in \mathcal{T}\left(G\right)}{\text{argmax}}{p}_M\left(T\right),$$ (1)

where $\mathcal{T}\left(G\right)\subset \mathcal{T}$ is the set of directed trees consistent with the graph G and $\mathcal{T}$ is the set of all directed trees.

The formulation in Eq. 1 can be interpreted as a special case of maximum a posteriori (MAP) estimation,

$$T^{\ast }=\underset{T\in \mathcal{T}}{\text{argmax}}{p}_O(G\mid T)p_M\left(T\right),$$

where the observation probability p_O(G|T) is uniform over graphs obtained by projecting T onto the image and zero elsewhere. Thus, our formulation leaves all regularization up to the prior model M, while any noise in the image is handled in the segmentation stage that extracts G from the image. We leave more nuanced models of image formation for future work.

The next two subsections describe how an arborescence projects to a planar graph and how to generate all possible directed trees consistent with this graph. Section 4 shows how to explore the space of all these trees.

3.1 Arborescence Projection

The topology of a tree T is endowed with geometry by embedding it in an arborescence A, which then projects to a planar graph G in the image. More formally, the edges of a directed tree T = (V_T, E_T, r_T) rooted at vertex r_T ∊ V_T are oriented away from the root; that is, every edge

$$e=(u,v)\in E_T\text{with}u,v\in V_T$$

is an ordered pair, with u the parent and v the child. The arborescence A = η(T) is an embedding of T in ${\mathbb{R}}^3$ such that every vertex v ∊ V_T maps to a vertex v = η(v) of A in ${\mathbb{R}}^3$ and every edge e = (u, v) ∊ E_T maps to a directed line segment e between the two vertices u = η(u) and v = η(v). In particular, we denote r_A = η(r_T). We assume that all the vertices of A are distinct points in space and all its edges are mutually disjoint [41]. Intuitively, an arborescence is a set of a non-intersecting, piecewise-linear, three-dimensional branches.

The image projection P(A) of A may intersect itself. More concretely, as Figure 2 illustrates:

1. Multiple vertices can project to the same point.

2. Distinct edges can intersect in the projection.

3. Vertices can project onto edges.

We exclude the degenerate cases of edges in A projecting to points in P(A), or distinct edges of A overlapping in line segments in P(A).

Fig. 2.

The projection P(A) of an arborescence A: (Best viewed in color.) The hollow circles are the roots of A and P(A). Both green and red dots project to crossings in P(A); that is, points in P(A) onto which distinct points in A project. Red dots are vertices of A and green dots, called refined vertices of A, are not. The red, green, and blue projection lines indicate vertex-vertex, edge-edge, and vertex-edge crossings, respectively.

The set P(A) is the embedding η(G_d) of a directed planar graph G_d = (V_Gd, E_Gd, r_Gd) with root r_Gd = P (r_A). This graph has one vertex v ∊ V_Gd for every vertex in A that projects to P(A) with no overlap, plus one for every point where two or more projected line segments overlap (including at their vertex endpoints). The latter type of vertex is called a crossing. In other words, v ∊ P(A) is a crossing whenever its multiplicity |P⁻¹(η(v))| is greater than 1. Here, |X| denotes the size of set X.

The graph has an edge e = (u, v) ∊ E_Gd for u, v ∊ V_Gd if and only if the line segment between its endpoints is fully contained in P(A) and e has the same direction as the projected line segment that contains it. Thus, every edge of G_d is either identical to a projected line segment of A or is a subset of one. Either way, the edge inherits the segment's direction.

It is useful to add a new vertex, called a refined vertex, to the original tree T for every non-vertex point of A = η(T) that projects to a crossing. These points are the green dots in Figure 2. Edges are split at refined vertices as illustrated in Figure 3. The resulting tree T′ is called the refined (directed) tree. This tree is homeomorphic (in the graph-theoretical sense) to T. Its embedding A′ = η(T′) is called the refined arborescence. By construction, only vertices can yield crossings in the projection of a refined arborescence.

Fig. 3.

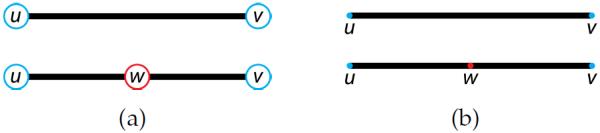
Edge subdivision: In (a), an edge subdivision replaces a single edge (u, v) with two new edges (u, w) and (w, v). In (b), the same subdivision in an embedded edge maintains the continuity of the embedding. Old vertices are highlighted in light blue, while the new vertex is shown in red.

Typically, the directed graph G_d is not observed in the image, since projecting an arborescence often obscures the directions of its edges. What is observed instead is an undirected graph G = (V_G, E_G, r_G) with the same vertex set V_G = V_Gd and root r_G = r_Gd as G_d and with an undirected edge e = {u, v} ∊ E_G if either (u, v) or (v, u) is in E_Gd. In other words, G_d is an orientation of G. Because of crossings, the number of vertices in G_d (and G) is at most equal to the number of vertices in T′. That is,

$$\mid V_G\mid =\mid V_{G_d}\mid \le \mid V_{T^{\prime }}\mid .$$

3.2 Crossings and Valid Partitions

In general, multiple directed trees are consistent with (i.e. project down to) a single directed planar graph G_d; we will now show how to generate these possible trees. To this end, we assume that (i) the root r_Gd is not a crossing, (ii) the pre-image of every point x on the embedding P(A) of G_d is finite—whether x is a crossing or not—and (iii) the number of crossings is finite. These conditions are mild. In particular, finite pre-images prevent any edge segment from projecting “edge-on”to a single point, and a finite number of crossings excludes infinitely tortuous edges.

Under these assumptions, crossings are exactly those vertices with in-degree greater than 1 in G_d. To see this, let deg(v) and deg⁻(v) denote the degree and in-degree of a vertex v ∊ V_Gd. Since G_d is the projection of tree T′, each (directed) edge entering v must enter a distinct vertex in T′, so the multiplicity of v is deg⁻(v). In particular, no vertex other than the root can have in-degree zero. Furthermore, all possible directed trees consistent with G_d yield the same crossings; thus, in what follows we will treat the “crossings of G_d”as intrinsic to the projected graph, without needing to reference any particular tree that is consistent with it.

Thus, to reconstruct T′, each crossing of G_d must be split into deg⁻(v) vertices, and the deg⁺(v) = deg(v) − deg⁻(v) edges out of v, if any, must be partitioned into deg⁻(v) sets. Such a partition is valid if each edge exiting v is associated to exactly one of the new vertices. Different combinations of valid partitions correspond to different trees that could have projected down to G_d, and the number of these trees is exponential in the number of crossings [9].

4 Graph Orientations

When only an undirected graph G is available from the image, we must first choose an orientation for each of its edges before we can generate a directed tree consistent with it. This section shows a systematic way to generate good graph orientations. First, Section 4.1 defines a “good”orientation as one for which every combination of valid partitions of its crossings yields a single, connected directed tree. Then, Section 4.2 shows that all good orientations for a given graph can be visited by flipping the orientation of one edge at a time, i.e. that they are connected. Based on these results, in Section 7 we present a heuristic search algorithm that explores this space by iteratively flipping edges to move between orientations. To the best of our knowledge, all the following results in this section are novel and may be of independent interest.

4.1 Flow Directed Acyclic Graphs

Figure 4 shows that some graph orientations cannot be transformed into connected directed trees by any set of valid partitions on its crossings, while Figure 5 shows that, for other orientations, only some combinations of valid partitions lead to a tree. In this section, we characterize the set of graph orientations for which every combination of valid partitions yields a single connected directed tree.

Fig. 4.

Some graph orientations cannot be transformed into connected directed trees by valid partitions. This directed graph has only one crossing v, which can only be partitioned in one way. Applying this valid partition yields two disconnected trees.

Fig. 5.

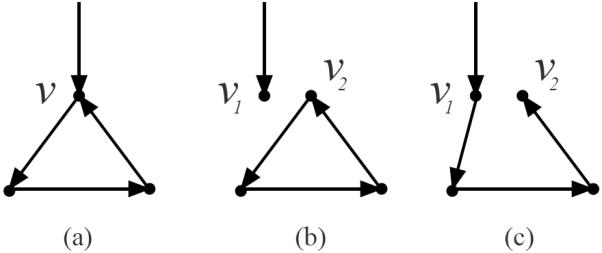
For crossings that are part of a directed circuit, only some of their valid partitions lead to trees. (a) A crossing v that is part of a directed circuit. (b) A valid partition of v into v₁ and v₂ that disconnects the graph and retains the circuit. Thus, the result is not a tree. (c) A different partition of v does yield a connected directed tree.

If we examine Figure 4 again, we can see that if we flip edge (w, v) to (v, w), then the resulting orientation is consistent with the tree u → v → w. We denote this new orientation as a flow orientation. More generally, an orientation G_d of an undirected graph G is a flow orientation if and only if there exists a vertex r_Gd from which every other vertex in V_Gd can be reached while respecting edge orientations.

Then, we propose that a directed graph G_d is the projection of at least one directed tree if and only if G_d is a flow orientation. To prove this, note that if G_d is not a flow orientation, then at least one vertex is unreachable from the root. Valid partitions can only eliminate paths between nodes, so there is no sequence of valid partitions that will create the necessary path and transform G_d into a directed tree. Conversely, if G_d is a flow orientation, a directed tree can be built in two steps: first, make a directed spanning tree rooted at r_Gd. Then, assign an arbitrary orientation to each of the edges that are not in the spanning tree to obtain a full orientation of G. By construction, the directed spanning tree guarantees that every vertex is reachable from r_Gd, thus ensuring that G_d is a flow orientation.

We denote graphs that are both flow orientations and Directed Acyclic Graphs (DAGs) as flow-DAGs. Flow-DAGs enjoy two important properties:

1. All connected, undirected graphs admit at least one flow-DAG. A simple way to build one is to first run breadth-first search starting at an arbitrary vertex to define a topological ordering of the graph's vertices. Then, orient every edge of the graph based on this ordering, i.e. orient every edge from the vertex that appears earlier in the ordering to the one that appears later.

2. Every combination of valid partitions for the crossings of a flow-DAG yields a directed tree. To see this, pick any node v in the flow-DAG other than the root. Since the graph is a flow orientation, v is reachable from the root. Since there are no cycles in a DAG, the parents of v must be on paths from the root to v. When v is validly partitioned, every child of v is connected to one of the parents of v, and is therefore reachable from the root. By this construction, after partitioning every crossing, every resulting vertex other than the root has exactly one parent, so the resulting graph is a connected directed tree.

Note, however, that not every tree projects to a flow-DAG. In particular, if some branches of the tree grow back towards the root, it may happen that the resulting true orientation of the image graph contains cycles. By restricting our attention to flow-DAGs we rule out these types of trees. These are rare in nature, however, because doubling back towards the root implies inefficiency in the flow mechanism that the tree embodies.

4.2 The Flow-DAG Meta-Graph

Any two flow-DAGs for a given undirected graph G differ only by the subset of edges that are oriented differently in the two orientations. Thus, one possible way to explore the set of flow-DAGs for a given undirected graph G is to build an initial flow-DAG for it (Section 4.1 showed that we can always do so) and then successively modify it by changing the direction of one of the edges—an edge flip—to obtain other solutions. In this section, we show that it is possible to reach every other flow-DAG for G given the initial solution through some sequence of flips, such that every intermediate orientation is also a flow-DAG.

Flipping edge (u, v) in G_d yields a flow-DAG $G_d^{\prime }$ if and only if (i) vertex v is a crossing of G_d, and (ii) the directed graph that results from the flip is acyclic. The first condition ensures that the in-degree of v is greater than 1, so v is still reachable from the root through one of the other incoming edges. The second condition retains the DAG nature of the resulting graph, and can be verified by a depth-first search of $G_d^{\prime }$ [39]. A flip that satisfies these two conditions is a valid flip, and G_d and $G_d^{\prime }$ are neighbors in the meta-graph whose undirected edges connect flow-DAGs that differ by one valid flip.¹ Figure 6 illustrates this point.

Fig. 6.

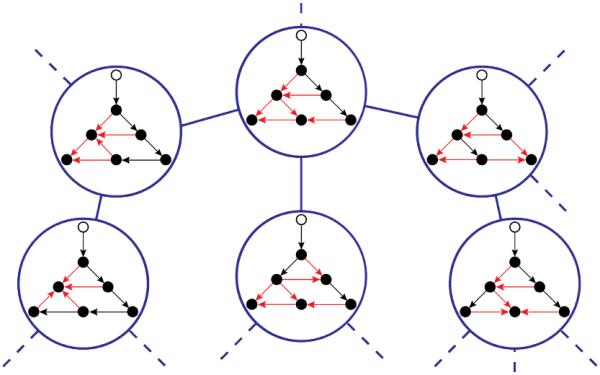
The flow-DAG meta-graph: (This Figure is best viewed in color.) The flow-DAG meta-graph for a small graph G. Neighboring orientations differ by one valid flip. The meta-graph is in blue. Edges entering a crossing in each flow-DAG are in red.

We now show that the flow-DAG meta-graph is connected. That is, any two flow-DAGs for the same graph can be reached from each other by sequences of valid flips. We will show this by relying on a similar property that relates all the directed spanning trees of a graph to each other.

Let S be a directed spanning tree of G_d. Adding a non-tree edge (u, v) of G_d to S creates a cycle called a fundamental circuit. The edge (u, v) is a forward edge if u is an ancestor of v in S, a backward edge if v is an ancestor of u in S, or a cross edge otherwise. If (u, v) is forward or cross, it can be exchanged with one of the tree edges in the fundamental circuit of (u, v) to form another (directed) spanning tree. Any two spanning trees related by exactly one such edge exchange are said to be adjacent to each other, and repeated exchanges can transform any directed spanning tree into any other [21]. Thus, the set of (directed) spanning trees of a given (directed) graph is connected with respect to this adjacency relation.

To extend this result to flow-DAGs, we say that a flow-DAG G_d for an undirected graph G is consistent with a directed spanning tree S of G if S is a (directed) subgraph of G_d. In the following, we show that (i) all the flow-DAGs consistent with a given directed spanning tree for G are connected to each other, and that (ii) for each pair of adjacent spanning trees, there is a flow-DAG that is consistent with both of them. This allows walking between any two flow-DAGs by valid flips: Given flow-DAGs G_d and $G_d^{\prime }$, find spanning trees S and S^′ consistent with them. Connect S to S^′ through a sequence of adjacent spanning trees S = S₀, …, S_n = S^′, and form the sequence of flow-DAGs $G_d=G_0,\dots ,G_n=G_d^{\prime }$ where flow-DAG G_i is consistent with trees S_i−1 and S_i for i = 1, …, n.

To prove property (i), let S be a directed spanning tree of G, and let G_d be a flow-DAG consistent with S. The set of non-tree edges of G_d cannot contain backward edges (with respect to S), as they would form cycles. For the same reason, the flip of a forward non-tree edge of G_d is not valid, as it would yield a backward edge. Flipping a cross edge, on the other hand, is always valid, as it creates no cycles. Thus, any two flow-DAGs consistent with S are related by one or more cross flips, and the flow-DAGs consistent with S form a connected component of the flow-DAG meta-graph.

To prove property (ii), let directed spanning trees S and S^′ of G be adjacent to each other. Specifically, S^′ is obtained from S by replacing edge e = (u, v) with edge e^′ = (w, v). Edge e^′ cannot be a backward edge in S. If it were, v would be an ancestor of w in S, and removing e from S would sever the only path from the root to v. Then, S^′ would not be a spanning tree. Because of this, e^′ must be either forward or cross, so that adding e^′ to S (without removing e) yields a flow-DAG G_d. So G_d contains both e and e^′ and therefore includes both S and S^′, and is consistent with both.

In summary, the flow-DAG meta-graph is connected. In Section 7, we define an algorithm to traverse this meta-graph to look for likely trees for a given image graph. We define this likelihood over trees in the following section.

5 Prior Model for Arborescences

In this section, we present a generative, parametric, tree-growth model that allows us to define a likelihood over the set of trees consistent with an input graph.

5.1 A Growth Model for Arborescences

Current research on tree growth models (see Section 2) reveals that the forces that guide growth patterns are often complex, multi-scale, and interdependent. Overall, the shape of a tree depends on a myriad of global and local interactions that determine when a given branch spawns new branches, how many children it has, and in what directions they grow.

In this paper, we describe the growth of an arborescence generatively as a stochastic, discrete, spatial Markov branching process that evolves over time. The resulting arborescence is a set of branches made of concatenated line segments. In our model, an arborescence can only grow by extending its leaf branches that are still “active”. Since we do not allow internal branches to increase in length, our model does not describe all actual growth processes in nature, but is rather to be seen as an abstract, generative model of the final shape of an arborescence. Although our model is simple, the experiments in Section 8 show that it adequately captures the morphology of a number of different types of trees, including retinal vessels and plant roots.

The frontierF(t) of a growing directed tree T(t) = (V_T (t), E_T (t), r_T) with embedding A(t) is the set of m(t) active vertices

$$F\left(t\right)=\{{\mathbf{v}}_1,\dots ,{\mathbf{v}}_{m\left(t\right)}\}\subset V_T\left(t\right)$$

in V_T (t) that are leaves and are still growing. The nonnegative integer t denotes the tree-depth of the leaves. At depth t = 0, the directed tree is a single point—its root r_T, embedded at the origin of space—and F(0) = {r_T}.

At depth t > 0, each leaf v in F(t) spawns a number c ≥ 0 of labeled branch stubs with probability p_s(c),where

$$\sum _{c=0}^{\infty }{p}_s\left(c\right)=1.$$ (2)

A stub is a short branch segment that connects a new leaf to its parent. If c > 0, we assign an ordered label i ∈ {1,2, …,c} to each of the children of v. For simplicity, we assume that p_s(c) is the same for all t. In our experiments, it is given by a one-inflated Poisson distribution [25] that behaves as a Poisson distribution with rate λ at all values except 1:

$$p_s\left(c\right)=\{\begin{array}{cc}\frac{1}{1+\alpha }\left(\text{Pois}\right(1;\lambda )+\alpha )\hfill & \text{if}c=1\hfill \\ \frac{1}{1+\alpha }\text{Pois}(c;\lambda )\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

In many physical trees, α ≫ Pois (1; λ) to account for the fact that extending a branch is much more common than stopping or splitting into two or more branches.

The vertex v is then removed from the frontier and the leaves of any of the stubs it has spawned are added to F(t + 1) and V_T(t + 1).

To model stub geometry, every new leaf v in the frontier F(t) records information about its parent π(v) = u and about its growth increment, a three-dimensional random vector δv = v − π(v) that depends on the following factors:

• 1)The stub's growth inertia
• 2)The preferred branching angle
• 3)The force field(s) surrounding u.

Growth inertia refers to the tendency of a branch to continue to grow in a steady direction. Factors 2 and 3 depend on the type of arborescence being modeled. A preferred branching angle captures the tendency of angles between a parent and its (multiple) child branches to take on similar patterns for a given type of arborescence and number of children. The force field encapsulates environmental forces that affect growth, such as a gravitational or electromagnetic field or the density of the growth medium.

These terms are combined as follows. The location of v_i, the i-th child of vertex u, is given by:

$$\begin{array}{cc}\hfill {\mathbf{v}}_i& =\mathbf{u}+\delta {\mathbf{v}}_i,\hfill \\ \hfill \delta {\mathbf{v}}_i& ~\text{VF}({\widehat{\mu }}_i,\kappa ,\gamma )=\gamma \frac{\kappa }{2\pi (e^{\kappa }-e^{-\kappa })}{e}^{\left(\kappa {\widehat{\mu }}_i^{⊺}\delta {\mathbf{v}}_i\right)}.\hfill \end{array}$$ (3)

The direction of the growth increment vector δ_vi is drawn from a von Mises-Fisher distribution [22] with concentration κ and its length is scaled by a parameter γ > 0, which can be either a constant or drawn from some distribution. The expected direction of growth ${\widehat{\mu }}_i=\frac{{\mu }_i}{\Vert {\mu }_i\Vert }$ is given by a vector sum that incorporates the three factors outlined above:

$${\mu }_i=\mathbf{s}\left({\rho }_c\right(i),{\varphi }_c(i),z_c(i\left)\right)+\mathbf{f}\left(\mathbf{u}\right),$$ (4)

where c is the number of children of u. Here,

• s(ρ_c(i), ϕ_c(i), z_c(i)) is the expected direction of growth of the i-th child of u. We parameterize s using cylindrical coordinates with origin u and cylindrical axis along δu.² Variables ρ_c(i) and z_c(i) are the radius and height, respectively, and ϕ_c(i) is the azimuth relative to a random reference plane.

• The vector f(u) captures environmental forces at u.

5.2 Directed Tree Probability

The growth model M can be used to define the probability p_M(T) of a directed tree T consistent with a projected graph G. This probability is a function of its topology (the number of children per vertex) and geometry (the angles between parent and child stubs).

Since there are an uncountably infinite number of arborescences consistent with a given T and G, we cannot enumerate the probability of every arborescence that could have projected to G. Instead, we approximate the probability of a directed tree as follows:

$$p_M\left(T\right)\approx \underset{{\mathbf{u}}_P\in V\left(T\right)}{\Pi }{p}_a({\mathbf{u}}_P\mid \pi ({\mathbf{u}}_P),c({\mathbf{u}}_P\left)\right)p_s\left(c\right({\mathbf{u}}_P\left)\right),$$ (5)

where u_P is the projection of u and where π(u_P) and c(u_P) are the parent and number of children of u_P, respectively. The probability p_s is defined in Eq. 2, and p_a is the probability of the angles between a parent stub and those of each of its children in the projection, rather than in the world:

$$p_a\left({\mathbf{u}}_P\right)=\{\begin{array}{cc}\underset{{\mathbf{v}}_{i_P}\in V_{{\mathbf{u}}_P}}{\Pi }\text{VM}(\delta {\mathbf{v}}_{i_P};{\widehat{\mu }}_{i_P},{\kappa }_{i_P})\hfill & \text{if}c\left({\mathbf{u}}_P\right)>0\hfill \\ 1\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (6)

Here, VM is the Von Mises distribution. The projected child v_iP has been assigned the i-th label, the unit vector ${\widehat{\mu }}_{\mathit{iP}}$ is the expected projected direction of growth of the i-th projected stub, and κ_iP is the concentration over the distribution of possible angles between the actual and expected projected stubs, as detailed further in [9].

6 Tree Estimation Complexity

In this section, we analyze the computational complexity of estimating the most likely tree for a class of local tree probability models, in which the probability of a tree is the product of the probability of each set of incident edges at each vertex. This class includes our model M.

More specifically, let T = (V_T, E_T, r_T) be a directed tree rooted at r_T. We restrict ourselves to models in which the probability of each vertex is a function of its incident edges:

$$\ell \left(T\right)=\sum _{v\in V_T}\ell (v\mid E_T(v),\theta ),$$ (7)

where l(T) is the log-probability of the directed tree, E_T (v) is the set of edges in T that are incident to v, and ϴ are any additional model parameters, such as the force field at v's location. We refer to models that satisfy Eq. 7 as local models. It is easy to see that Eq. 5 satisfies Eq. 7, so our growth model is local.

Assuming that calculating each vertex log-probability takes constant time, the overall probability of a tree can be computed in linear time by determining the probability of each of its vertices in turn. Given a flow-DAG G_d, we define its log-probability as

$$\ell \left(G_d\right)=\underset{T\in \mathcal{T}\left(G_d\right)}{\max }\ell \left(T\right).$$ (8)

If ℓ(T) is defined in terms of a local model, we can efficiently maximize this probability over the set of directed trees consistent with G_d by considering each crossing x in G_d in turn, evaluating all of its valid partitions, and picking the maximum-likelihood partition. Since changing the partition of x does not change any of the edges that are incident to it, the choice of a most likely valid partition for x is local; that is, it affects no vertex other than x, nor does it depend on any other vertices.

Therefore, if a directed graph G_d is available, we can find the most likely directed tree consistent with it by examining each of the vertices of G_d in turn. Since the degree of the vertices in G_d is assumed to be bounded, the time complexity at each vertex is constant, and the overall complexity of estimating the most likely directed tree is linear in the number of vertices of G_d.

However, if only the undirected graph G is available, finding an optimal directed tree consistent with G in a local model is NP-hard. We prove this in the appendix by reducing the minimum vertex cover problem [13] to the problem of estimating a tree from an undirected graph.

7 Algorithms

Since finding an optimal directed tree given an undirected graph is NP-hard, we resort to approximate methods. Specifically, this section present a two-step method for estimating a highly likely tree from an undirected, rooted graph G. The first step finds an approximate solution greedily, and the second improves this solution via a heuristic search in the space of possible flow-DAG orientations of G. The first step uses the arrival time of a flow sent from the root to every other vertex as a simple way to find an initial, reasonable flow-DAG. The second step then makes use of the prior growth model defined in Section 5 to establish the likelihood of each candidate tree. Intuitively, we heuristically search over possible topologies based on how likely their corresponding projected geometries (in terms of the prior growth model) are.

7.1 Greedy Directed Tree Search

Computing a directed tree from an undirected, rooted graph G = (V_G, E_G, r_G) involves two choices: first assign a direction to each of the edges of G—which defines an orientation G_d over G—and then apply a valid partition to crossing of G_d, as defined in Section 3.2. If the resulting orientation is a flow-DAG, any choice of valid partitions will yield a directed tree, so we restrict our search to these acyclic orientations.

To estimate a high-probability directed tree, we first obtain a flow-DAG G_d by completing a shortest-path spanning tree of G rooted at r_G. We then apply a valid partition to each vertex with in-degree ≥ 2 to convert G_d into a directed tree.

In more detail, a shortest-path tree S rooted at r_G is a spanning tree of G such that for any vertex v, the shortest distance dist (r_G, v) between r_G and v is the same in G and in S [23]. When the cost of each edge is the Euclidean distance between its two endpoints, then S approximates the arrival time of a flow sent from r_G to every other vertex in the graph. A (not necessarily unique) shortest-path tree S can be efficiently estimated in time O(|E_G| + |V_G| log(|V_G|)) using Dijkstra's shortest-path algorithm [8]. At each iteration, this algorithm extends the shortest-path tree by adding the unvisited vertex that is closest to the set of visited vertices,

$$v=\text{closest}\_\text{vertex}(G,V_{\text{visit}}).$$

A shortest-path tree induces a topological ordering of the vertices of G in which u < v if and only if dist (r_G, u) ≤ dist (r_G, v).³ Given S, we construct a flow-DAG G_d by orienting each edge in G according to this ordering. The resulting directed graph G_d is a flow-DAG: since it contains the spanning directed tree S as a sub-graph, it is a flow orientation and since its edges obey a topological ordering it is a DAG.

As noted in Section 6, we can determine a most likely directed tree from a flow-DAG in linear time by choosing a most likely valid partition independently at each crossing v ∈ V_Gd. The function

$$(\ell ,P)=\text{partition}(v,G_d,M)$$

computes the optimal probability ℓ(v) in model M by first evaluating the likelihoods of all the valid partitions of v that can be obtained given the edge directions of G_d and then picking the partition with

Algorithm 1 Greedy directed tree search

the highest probability. The function partition also returns a structure

$$P=(P.v,P.V,P.E,P.J)$$

that describes the surgery necessary to implement the partition. This includes the vertex P.v to be replaced, the set P.V of new vertices that replace P.v, the set P.E of oriented edges that are incident to P.v, and a set P.J of indices that for each edge e in P.E tells what vertex of P.V the edge e connects to. See Figure 8. A procedure

$$G=\text{transform}(G,P)$$

transforms the graph G to implement the optimal partition P: It replaces P.v with the elements of P.V and replaces the P.v endpoint of each edge in P.E with the vertex in P.V indicated by P.J. Algorithm 1 summarizes this greedy search.

Fig. 8.

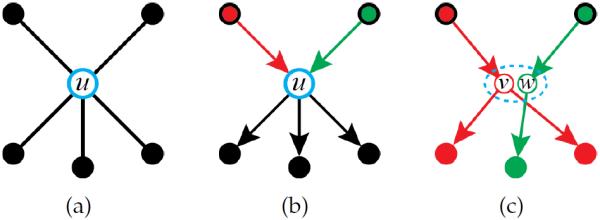
Valid partition formation: (This Figure is best viewed in color.) (a) A vertex u and its neighbors. In (b), the edges incident to u are assigned orientations. Since u has more than one incoming edge (red and green), it must be partitioned. In (c), u is split into two vertices v (red) and w (green), each with a single parent. The dashed oval indicates that v and w share the same location on the plane. Each of the outgoing edges of u is then assigned to one of the new vertices.

7.2 Heuristic Directed Tree Search

We now introduce a heuristic search algorithm that attempts to improve on the greedy solution by exploring variants of it that may increase its likelihood.

The expression in Eq. 8 in Section 6 defines a likelihood for every node of the flow-DAG meta-graph defined in Section 4.1. To efficiently explore this meta-graph, we make use of a heuristic that encourages moving towards an orientation of the input graph G that is not necessarily a flow orientation but has high probability and is easy to compute. This orientation G_L is called an anchor, because it is used as a reference point in the heuristic search. The idea is that although

Algorithm 2 Heuristic directed tree search

G_L is typically outside the flow-DAG meta-graph, any region of the meta-graph in the vicinity of G_L is worth exploring.

The anchor orientation G_L is defined as follows. For each crossing of G, find edge orientations that yield the best valid partition. Since these choices are made independently at each crossing, edges that connect two crossings may end up with conflicting orientations. In those cases, assign to that edge the direction of flow that is more likely given the force field at that location. Specifically, let p_u = VM((u, v); μ_fP (u), κ_fP (u)) and p_v = VM((v, u); μ_fP (v), κ_fP (v)) be the probabilities of two conflicting orientations (u, v) and (v, u) for an edge. Here, VM again denotes the Von Mises distributions, and μ_fP (v) and κ_fP (v) are the mean direction and concentration of the projections of the force field vectors whose origins lie along v's line of projection [9]. Then, the orientation with higher probability is chosen for that edge.⁴ The resulting anchor orientation G_L is generally not a flow orientation, but flow-DAGs that differ from it by a few edge flips are likely to be good.

Our search algorithm encourages exploring flow-DAGs that are near G_L. To this end, the heuristic value of exploring a flow-DAG $G_d^{\prime }$ from its neighbor G_d on the flow-DAG meta-graph is defined as follows:

$$h(G_d\to G_d^{\prime })=\lambda {\ell }_M\left(G_d^{\prime }\right)+(1-\lambda )\log (1-\Vert G_d^{\prime },G_L{\Vert }_f)$$

where λ is a parameter between 0 and 1 and ∥∥_f is the number of flips between the two orientations divided by the number of edges in $E_{G_d^{\prime }}$ (note that $\mid E_{G_d^{\prime }}\mid =\mid E_{G_L}\mid$). The first term is the likelihood of $G_d^{\prime }$ and the second term estimates its nearness to the anchor.

Using this heuristic in a best-first search of the meta-graph leads to Algorithm 2, which starts from the graph orientation for the tree found by Algorithm 1 and implement best-first traversal of the flow-DAG meta-graph with a priority queue. Using best-first ensures that this Algorithm is more likely to quickly find locally optimal orientations.

8 Experiments

We analyzed three datasets to validate the effectiveness of our algorithms: retinal vessel systems, roots of rice plants, and a synthetic leafy tree dataset. These datasets allowed us to test our algorithms on three very different types of trees. For each dataset, we constructed a set of planar graphs and obtained their ground-truth trees. We then quantified the similarity between the best trees obtained by our algorithms and the ground-truth trees, as explained below.

8.1 Materials

We constructed a new retinal vessel dataset (WIDE) of 15 high-resolution, wide-field, RGB images using an Optos 200Tx ultra-wide-field device (Optos plc, Dunfermline, Scotland, UK). All images were acquired at the Duke University Medical Center between August 2010 and October 2012. Each retinal image was taken from a different individual and captured as an un-compressed TIFF file at the widest setting available for the Optos device (3900×3072 pixels). We manually cropped out eyelashes and other non-retinal regions of the image. We downsampled each cropped image by a factor of 2 to obtain the final images (~900×1400 pixels).

We also constructed an 18-image rice-root dataset (RICE) by randomly selecting a subset of images from an earlier dataset [45], [20]. In the original dataset, 40 rice plants roots were grown in a transparent medium and imaged in Prof. Philip Benfey's lab at Duke University. Each plant was rotated around its center axis and imaged from 40 different angles and a three-dimensional tomographic model of each plant was then obtained from the images. To construct our RICE dataset, we first obtained 18 of the three-dimensional model/40 image sets corresponding to 13 different plants. Five plants were imaged twice, at 7 and 10 days of growth. For each volume, we randomly selected one of the ~1300×900 pixel RGB source images.

Finally, we constructed a synthetic leafy tree dataset (SKETCH) of 18 arborescences. Each arborescence was drawn by the first author on the tree modeling software developed by Chen et al. [6] using a Wacom Intuous 3 graphics tablet (Wacom Co. Ltd, Kazoshi, Saitama, Japan). This software estimates a three-dimensional arborescence given a set of input strokes that represent the tree's branches. Each vertex in the resulting graph is assigned a depth based on the chosen tree template. We used a maple tree template for all graphs. We then projected each arborescence at five different angles to obtain 90 planar graphs.

8.2 Methods

8.2.1 Planar graph estimation

For the WIDE and RICE datasets, we obtained each planar graph semi-automatically: we first computed a Gabor-enhanced image [11] and then extracted a noisy graph from it by building a set of tracks over the tree's branches [9]. We manually edited each graph using a graph editing software that we developed to correct any errors, such as missing or spurious edges due to low image quality or image artifacts.

For the SKETCH dataset, we first aligned the trunk of every arborescence with the z-axis. We then defined each vertex in the arborescence in terms of a cylindrical coordinate system. We obtained each planar graph by rotating an arborescence by a given angle of rotation ϕ and then collapsing the y-axis. We used five evenly spaced angles (0, 72, 144, 216, 288 degrees) per arborescence to obtain 90 planar graphs in total. To simulate the limited resolution of an imaging system, we defined a minimum separation radius r of 5 pixels. Any cluster of vertices that lied within a circle of radius r were merged into a single vertex. Then, for every vertex we determined the Euclidean distance d to the closest non-adjacent edge. If d < r, we shifted the vertex to lie directly over the edge with probability $\frac{r-d}{r}$; that is, the closer the vertex, the higher the probability that it would be merged.

8.2.2 Error quantification

There is no single metric that captures how similar two trees are because trees have properties at multiple scales. Thus, we determined the similarity between each estimated tree and the ground-truth tree using four weighted scores: the first two measure local errors in connectivity, while the latter two capture more global differences.

More specifically, the local similarities are defined as follows. Let T and T′ be two directed trees consistent with G and let d_c be the sum of the costs of the edges that are part of an undirected circuit.⁵ Then, let d_p be the sum of the costs of these circuit edges that have the same parent edge in both T and T′. Similarly, let d_f be the sum of the costs of the circuit edges that have the same orientation in the two trees. Then, the parent s_p and flow s_f similarities are given by:

$$s_p=\frac{d_p}{d_c}\text{and}{s}_f=\frac{d_f}{d_c}.$$

The global similarities are defined in terms of the paths from the root. In a tree, there is a unique path from the root to every one of its edges. Thus, let d_t be the sum of the costs of all the paths from the root to the circuit edges and let d_a be the sum of the subset of these paths that are identical in the two trees. Also, let r(e) be the sum of the costs of the edges in the path to edge e in T that are also part of the path to e in T′; intuitively r(e) is the percentage of the path to e that is shared by the two trees. Finally, let d_r be the sum of each r(e) for every circuit edge e. Then, the absolute s_a and relative s_r similarities are:

$$s_a=\frac{d_a}{d_t}\text{and}{s}_r=\frac{d_r}{d_t}.$$

8.2.3 Ground truth estimation

The SKETCH dataset already includes the ground truth trees. For the WIDE and RICE datasets, we manually obtained the ground truth trees using the aforementioned graph editing software. Our software allows a user to partition a vertex or undo an existing partition. To simplify the above process, we first obtained a non-optimized solution using our heuristic search algorithm and then replaced the invalid partitions with the correct ones. For the RICE dataset, we used the additional images and the three-dimensional volume to determine the correct topology.

For the WIDE dataset, on the other hand, our ground truth trees are based solely on human analysis. Since even human experts differ on their assessment of vessel topology, we quantified the degree of inter-observer variability or uncertainty in our ground truth by comparing the trees produced by two human raters (the first and last authors) using the two similarities defined above. We set the first rater's trees as ground truth. The similarity values of the second rater's trees in the test set of the WIDE dataset are listed in Table 1.

TABLE 1.

WIDE dataset results

(n = 8, μ(F) = 92.7, σ(F) = 25.5)
Method	sp	sf	Sa	sr	Time (min)
Human	0.9881 (± 0.01)	0.9911 (± 0.01)	0.8264 (± 0.13)	0.9398 (± 0.03)	~90
Heur. (100F)	0.9662 (± 0.02)	0.9719 (± 0.02)	0.7316 (± 0.15)	0.8599 (± 0.09)	1.4 (± 0.74)
Heur. (50F)	0.9518 (± 0.03)	0.9597 (± 0.03)	0.6996 (± 0.14)	0.8521 (± 0.07)	0.72 (± 0.37)
Heur. (10F)	0.9167 (± 0.03)	0.9292 (± 0.04)	0.5246 (± 0.20)	0.7730 (± 0.05)	0.18 (± 0.07)
Greedy	0.9059 (± 0.03)	0.9202 (± 0.03)	0.5071 (± 0.19)	0.7481 (± 0.06)	0.04 (± 0.02)

8.2.4 Directed tree estimation

We randomly split each dataset in half into a training and a testing set. We approximated the force field at each location using either a radially symmetric vector field centered at the root (WIDE) or a vector field in which every vector was parallel to the z-axis (RICE, SKETCH). Both vectors fields had constant magnitude. We then estimated the distributions of angles p_a and of numbers of children p_s of Section 5.2, as follows. For each vertex in each tree in the training set, we calculated the projected angles between its outgoing edges, as well as its out-degree (number of children). Given the empirical distributions of angles, we determined the means and concentration parameters of each von-Mises distribution defined in Eq. 6 to obtain p_a. We then determined p_s by fitting a one-inflated Poisson distribution to the empirical distribution of the out-degrees of all the vertices.

We then applied our greedy algorithm and our heuristic search algorithms to each planar graph. The number of possible solutions for a planar graph is an exponential function of the number F of its faces [5]. Accordingly, for each graph we adjusted our search algorithm to explore 100F trees.⁶ As we ran our search algorithm, we also recorded the best tree found after exploring 10F and 50F trees, and the mean running time in minutes for each method for each dataset. We ran our two algorithms on a Toshiba Satellite X870 laptop with a 2.4Ghz Intel I7 quad-core processor and 32GB of RAM.

8.3 Results

The results for each dataset are summarized in Tables 1–3 and two example results from each dataset are shown in Figures 9 and 10. In each table, n is the number of planar graphs in the test set and μ(F) and σ(F) are the mean and standard deviation of the number of faces per graph, respectively.

TABLE 3.

SKETCH dataset results

(n = 45, μ(F) = 37.68, σ(F) = 24.37)
Method	Sp	sf	Sa	Sr	Time (min)
Heur. (100F)	0.9551 (± 0.03)	0.9927 (± 0.01)	0.6837 (± 0.24)	0.9167 (± 0.07)	0.31 (± 0.24)
Heur. (50F)	0.9546 (± 0.03)	0.9920 (± 0.02)	0.6857 (± 0.24)	0.9170 (± 0.07)	0.17 (± 0.12)
Heur. (10F)	0.9516 (± 0.04)	0.9901 (± 0.02)	0.6793 (± 0.24)	0.9127 (± 0.08)	0.06 (± 0.02)
Greedy	0.9354 (± 0.04)	0.9823 (± 0.02)	0.6470 (± 0.24)	0.8736 (± 0.09)	0.03 (± 0.01)

Fig. 9.

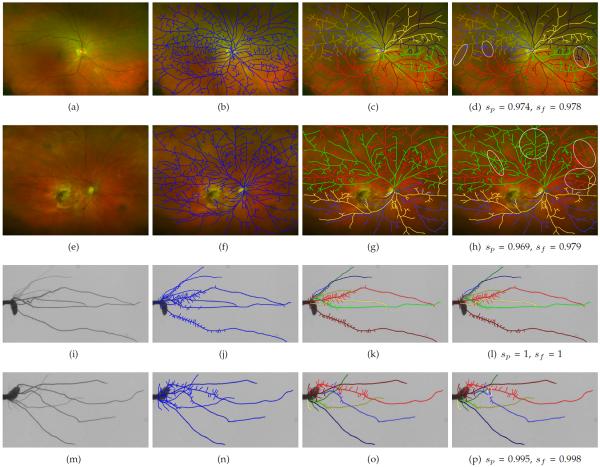
WIDE and RICE examples: (This Figure is best viewed on-screen). (a,e,i,m) Four sample test images. (b,f,j,n) The extracted graph for each image (in blue). (c,g,k,o) The ground-truth tree for each image. Different subtrees are shown in different colors. (d,h,l,p) The best tree found by our method. The parent and flow similarities for each graph are listed in the corresponding subcaption. The white ellipses highlight differences between computed and ground-truth trees.

Fig. 10.

SKETCH examples: (This Figure is best viewed on-screen). (a,d) Two sample test graphs (in blue). (b,e) The ground-truth tree for each image. Different subtrees are shown in different colors. (c,f) The best tree found by our method. The parent and flow similarities for each graph are listed in the corresponding subcaption. The white ellipses highlight differences between computed and ground-truth trees.

Our proposed methods accurately estimate a highly likely tree for each of the different input graphs in the three datasets. The estimated trees have over 95% of the same parent-child relationships and edge orientations as the correct trees. Our proposed approach is versatile and robust. The three different datasets represent three very different types of trees that vary in their branching behavior, the expected angles between their offspring, and how strongly they are influenced by surrounding forces. Also, the arborescences in the three datasets vary significantly in how close they are to being planar. Intuitively, an arborescence is close to being planar if it is very narrow along one of its axes; in contrast, a radially symmetric tree is very far from planar. In our case, the retinal vessels were the most planar, since the retina consists of a series of flat layers. The synthetic trees, on the other hand, were the least planar since the parameters of the tree modeling software favored radially symmetric trees. In spite of these structural differences between datasets, after properly tuning our model's parameters, our methods were generally able to accurately approximate the correct solution. We now discuss results on each dataset in more detail.

8.3.1 WIDE dataset

In this dataset, our algorithm was able to closely approximate the performance of an expert human rater on a set of challenging retinal images and with minimal specialized domain knowledge. That is, aside from the branching factor and expected angle statistics that we obtained from the training set, we did not exploit any other image features, such as vessel dilation or color. We expect that incorporating these additional features should further improve our results on traditional fundus images.

However, some novel imaging systems, such as the optical coherence tomography method described in [18], are able to capture retinal vasculature images at a higher resolution that conventional fundus cameras. The vessels in these higher resolution images often have no color and the smaller vessels in them have uniform dilation due to the imaging system's diffraction limit. Thus, the features described above are no longer informative. Since our method does not rely on conventional vessel features, we expect that we should also obtain good results with images from these next-generation imaging systems.

Furthermore, although the WIDE dataset had the highest mean number of faces, our algorithm obtained better parent similarity results for this dataset than for the SKETCH dataset. We speculate that this is because retinal vessels are very close to being planar. Thus, there is often very little difference between the original and the projected angles, which makes the prior on the angles between siblings very informative.

8.3.2 RICE dataset

We obtained the best results on this dataset relative to the other two. We speculate that these stronger results were primarily due to two factors: first, the graphs corresponding to the rice plants had fewer faces than the other datasets, particularly compared to the retinal graphs. Furthermore, although the rice roots were quite radially symmetric, they also had a strong tendency to grow downwards towards the ground, which made the projected angles between siblings less variable than in the SKETCH dataset.

8.3.3 SKETCH dataset

In this dataset, the difference between the parent and flow similarities was more pronounced than in the other two datasets. We speculate that this is because the graphs in this dataset had more instances of vertices of degree five or higher than the other two, due to the simulated limited resolution we imposed on the projections. For these vertices, it is often easy to determine the orientation of their adjacent edges if the edges are well aligned with the expected direction of growth. However, determining which of the incoming edges is the parent of which of the outgoing edges is generally more challenging, because there is often little difference in the projected angles between edges that are adjacent in the original tree compared to edges that are not.

9 Conclusions

In this work, we formalized the problem of estimating the topology of a three-dimensional tree from a single, two-dimensional image of it and presented a prior tree-growth model to regularize this ill-posed problem. We showed that estimating the most likely tree consistent with an undirected graph is NP-hard even when each tree's likelihood is defined by a local growth model. We then presented a heuristic search method to explore the space of possible trees and empirically showed that it effectively and efficiently approximates the most likely tree for various types of trees.

In our future work, we plan to analyze and compare alternative search methods for finding the most likely tree, including Markov Chain Monte Carlo, iterated local search, and stochastic gradient ascent. We also intend to refine our image formation model to enable our tree estimation methods to correct small errors in the estimated graph, including missing or spurious edges. Finally, we seek to extend our methodology to images that include incomplete trees.

Fig. 7.

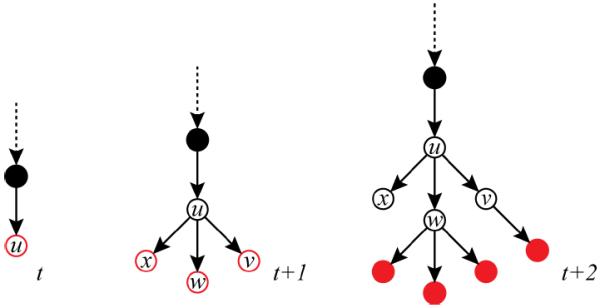
Arborescence growth: At each step, the frontier F_T (t) (highlighted in red) is updated. At depth t, a new vertex u is added to both F_T (t) and V_T (t). At depth t + 1, u is removed from F_T (t) and its offspring the {v, w, x} are added to frontier. At depth t + 2, the three vertices are removed from the frontier; v is succeeded by a single child and w spawned three children, while x has none.

TABLE 2.

RICE dataset results

(n = 9, μ(F) = 30.0, σ(F) = 9.3)
Method	sp	sf	Sa	Sr	Time (min)
Heur. (100F)	0.9831 (± 0.02)	0.9918 (± 0.01)	0.8984 (± 0.18)	0.9724 (± 0.05)	0.19 (± 0.08)
Heur. (50F)	0.9817 (± 0.02)	0.9905 (± 0.01)	0.8971 (± 0.18)	0.9717 (± 0.05)	0.10 (± 0.04)
Heur. (10F)	0.9649 (± 0.03)	0.9763 (± 0.03)	0.8625 (± 0.18)	0.9406 (± 0.07)	0.03 (± 0.01)
Greedy	0.9408 (± 0.04)	0.9583 (± 0.03)	0.7952 (± 0.17)	0.8945 (± 0.07)	0.01 (± 0.005)

Biographies

Rolando Estrada received a BS degree in computer science (magna cum laude) in 2005 and a BA degree in English (summa cum laude) in 2006, both from Louisiana State University. He then received a PhD degree in computer science, an MS degree in biomedical engineering, and a graduate certificate in cognitive neuroscience, all from Duke University in 2013. He completed a postdoctoral fellowship at the Department of Ophthalmology at the Duke University Medical Center in 2014 and is currently a research scientist at Teledyne Scientific Company. His research interests include computer vision, medical imaging, graph theory, and computational complexity.

Carlo Tomasi received a degree in Computer Science from Carnegie Mellon University in 1991. He was assistant professor at Cornell and Stanford, and is currently full professor of computer science at Duke University. He teaches undergraduate and graduate courses in computer vision and mathematics, and supervises students in computer vision research. His work emphasizes video analysis, image retrieval, and medical imaging.

Scott C. Schmidler received the BA degree in computer science from UC Berkeley in 1995, and the PhD degree in Biomedical Informatics from Stanford University in 2002. He joined Duke University in 2000 where he is currently an Associate Professor of Statistics and Computer Science. His research interests include Bayesian statistics, Monte Carlo algorithms, statistical shape analysis, computational biology, and computational statistical mechanics.

Sina Farsiu received the B.Sc. degree in electrical engineering from Sharif University of Technology, Tehran, Iran, in 1999, the M.Sc. degree in biomedical engineering from the University of Tehran, Iran, in 2001, and the Ph.D. degree in electrical engineering from the University of California, Santa Cruz in 2005. He is currently an Assistant Professor in the Departments of Biomedical Engineering, Ophthalmology, Electrical and Computer Engineering, and Computer Science at Duke University, Durham, NC. He is the principal investigator of NIH R01 and R21 grants and is the director of the Vision and Image Processing (VIP) laboratory at Duke University. He is an Associate Editor of the IEEE Transactions on Image Processing and his technical interests include ocular imaging and image analysis, computer aided diagnosis of ocular and neurological diseases, photonics, image enhancement and reconstruction, and statistical signal processing.

Appendix

Optimal Estimation from Undirected Graphs is NP-Hard

We show that finding an optimal directed tree $T\in \mathcal{T}\left(G\right)$ is NP-hard by reducing the minimum vertex cover (MVC, [14]) problem to a directed-tree estimation (DTE) problem. MVC is NP-complete even for graphs with bounded degree [2].

A vertex cover of a graph H = (V_H, E_H) is a subset C ⊆ V_H such that every edge of E_H is incident to at least one vertex in C. The bounded-degree version of MVC is defined as follows: Given a connected graph H with bounded degree, find a vertex cover of smallest possible size.

Let G be an undirected graph with root r_G. DTE is defined as follows: Find

$$T^{\ast }=\underset{T\in \mathcal{T}\left(G\right)}{\text{argmax}}\ell \left(T\right)$$

where ℓ(T) is defined in terms of a local model (see Eq. 7), and $\mathcal{T}\left(G\right)$ is the set of directed trees–for which every edge is directed away from the root–that project to G and P(r_T) = r_G. In this reduction, we assume, without loss of generality, that θ = ϕ; that is, a tree's probability does not depend on any additional model parameters.

In order to construct a polynomial-time transformation from MVC to DTE, we first give a way to interpret a graph orientation as a vertex cover. Let H_d be an orientation of the undirected graph H and define

$$C=\{v\in V_H\mid {\text{deg}}_{H_d}^{+}(v)>0\}$$ (9)

where ${\text{deg}}_{H_d}^{+}\left(v\right)$ is the out-degree of v in H_d. The set C is a vertex cover of H, because every edge starts at some vertex, and that vertex is in C by construction.

We now show a way to use DTE to find a minimum vertex cover for a given graph H, thereby reducing MVC to DTE. Let G = (V_G, E_G, r_G) be the rooted graph obtained from H by adding a new root vertex r_G and new edges to connect r_G to every vertex in V_H, and let $\mathcal{T}\left(G\right)$ be the set of directed trees consistent with G.

We will now define a local model over $\mathcal{T}\left(G\right)$. Let $T\in \mathcal{T}\left(G\right)$ be a directed tree consistent with G. Then, we define the log-probability of each of its vertices as follows:

$$\ell (v\mid E_T(v\left)\right)=\{\begin{array}{cc}-1\hfill & \text{if}{\text{deg}}_T^{+}\left(v\right)>0\text{and}v\ne r_T\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (10)

By definition of $\mathcal{T}\left(G\right)$, the root r_T of T has in-degree zero. In short, each vertex, other than the root, that has at least one child makes the tree less likely.

Every directed tree in $\mathcal{T}\left(G\right)$ projects to a unique flow orientation of G rooted at r_G. Conversely, given a flow orientation G_d of G rooted at r_G, we can obtain the most likely tree consistent with it by maximizing Eq. 10 at each node as follows.

We divide the nodes of G_d into four types: the root r_G, non-root nodes with out-degree zero, non-root nodes with positive out-degree and in-degree one, and non-root nodes with positive out-degree and in-degree greater than one. Nodes in the last category (and possibly some in the second) are crossings.

The maximum possible log-probability achievable at each node type is as follows. The root has in-degree zero because we do not allow roots to be crossings (see Section 3.2), and we show in [9] that under this assumption the root cannot have positive in-degree. Because of this, the root has a log-likelihood of zero by Eq. 10. Non-root nodes with out-degree zero can only be partitioned into tree leaves, and these have likelihood zero by Eq. 10 as well. Non-root nodes with positive out-degree and in-degree one are not split, and they get log-likelihood −1 by Eq. 10. Finally, any crossing v with positive out-degree in G_d must be split into a number of nodes equal to its in-degree in G_d. Since the out-degree of v is positive, its outgoing edges must be assigned to at least one of the nodes in the partition. Each such assignment results into a log-probability term of −1 by Eq. 10. As a consequence, the overall log-probability at this node is at most −1, because log-probabilities add up according to Eq. 7. This upper bound on the log-probability can be made tight by assigning all the outgoing edges of v to the same node of the partition.

To summarize, the maximum possible log-probability at each node of G_d given Eq. 10 is given by:

$$\ell (v\mid E_{G_d}(v\left)\right)=\{\begin{array}{cc}-1\hfill & \text{if}{\text{deg}}_{G_d}^{+}\left(v\right)>0\text{and}v\ne r_G\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Every possible orientation H_d of H corresponds to a unique flow orientation G_d of G rooted at r_G, because every vertex in V_H is reachable from r_G through at least one directed path in G_d. Furthermore, each vertex in V_H which has an outgoing edge in E_Hd (and consequently in E_Gd) makes the flow orientation less likely. Therefore, a flow orientation of G with maximum probability has a minimal number of vertices in V_H with non-zero out-degree in E_Hd. The set C resulting from the interpretation in Eq. 9 of H_d is a minimum vertex cover of H, so MVC reduces to DTE.

The above result holds even if the orientations of G are restricted to be flow-dags because, for every minimum vertex cover C, there always exists at least one flow orientation of G, rooted at r_G, consistent with C that is acyclic. To construct a flow-dag given C, first assign a topological ordering to the vertices in G such that:

$$\begin{array}{cc}\hfill & r_G<v,\forall v\in V_H\hfill \\ \hfill & v<u,\forall v\in C,u\in V_H\backslash C.\hfill \end{array}$$

In other words, all the vertices in V_H that are part of the vertex cover of H come before those not in the cover. Then, orient every edge in G according to the topological ordering. The resulting flow orientation is acyclic and a vertex in V_H has at least one outgoing edge in E_Hd if and only if it is part of C.